Abstract
We study a generalisation of relation algebras in which the underlying Boolean algebra structure is replaced with a Stone algebra. Many theorems of relation algebras generalise with no or small changes. Weighted graphs represented as matrices over extended real numbers form an instance. Relational concepts and methods can thus be applied to weighted graphs. All results are formally verified in Isabelle/HOL.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Binary relations, which are the main instance of relation algebras, are essentially Boolean matrices. In graph theory they occur as the adjacency-matrix representation of unweighted graphs. It is therefore not surprising that relation-algebraic methods have been used to reason about graphs and to develop graph algorithms [8, 9, 11, 45]. In this context weighted graphs are problematic simply because edge weights cannot be stored as entries of a Boolean matrix. Sometimes a workaround can be used, namely to represent weighted graphs by incidence matrices and weight functions [10]. However, keeping the direct representation of weighted graphs as matrices over numbers has benefits: it involves only one type of matrix, only a single matrix per graph, and only untyped (homogeneous) algebras which are better supported by theorem provers. Path problems and related algorithms have been treated successfully with this direct representation based on semirings with pre-orders and Kleene algebras [1, 6, 26, 33]. Other graph problems, in particular the minimum spanning tree problem, seem to require more structure. Relation algebras provide additional structure, but need to be generalised to capture weighted graphs.
In order to verify Prim’s algorithm for minimum spanning trees, we have proposed such a generalisation, Stone relation algebras, in [29]. Edge weights are typically numbers and form lattice and semiring structures (such as max-min and min-plus algebras). However, they do not form a Boolean algebra because a complement operation cannot be defined on the underlying linear order of numbers. The idea is to generalise the Boolean algebra structure just so much that edge weights can be represented while most of the structure is preserved. In particular, edge weights support a pseudocomplement operation and even form a Stone algebra. In Stone algebras, the involution property \(\overline{\overline{x}} = x\) and the law of excluded middle \(x \sqcup \overline{x} = \top \) are missing, but the weaker \(\overline{x} \sqcup \overline{\overline{x}} = \top \) still holds, as do De Morgan’s laws and \(x \sqcap \overline{x} = \bot \). By forming matrices over Stone algebras we can hope to preserve much of the structure of relations. These matrices represent weighted graphs and we capture their algebraic properties by Stone relation algebras. The axioms of Stone relation algebras are based on the axioms of Tarski’s relation algebras, which are modified to account for the weakening of the underlying lattice structure from Boolean algebras to Stone algebras.
Our previous paper gave the basic definitions and results with a focus on the verification of Prim’s algorithm. In this paper, we study the properties of Stone relation algebras in more detail. Related work is discussed throughout the present paper. Its structure and contributions are as follows:
-
In Sect. 2 we study pseudocomplemented algebras in general, and Stone algebras in particular. We also discuss the extended-real and matrix models of Stone algebras. Many results in this section are known from the literature; we contribute formally verified proofs of the algebraic properties and of the instantiation to the models.
-
In Sect. 3 we study Stone relation algebras. Our contribution is to show that many results of relation algebras generalise to Stone relation algebras directly or, in some cases, with small changes. This includes algebraic properties that hold for all elements and ones that hold for specific classes of elements. Again, we formally prove our results including the instantiation to models.
-
In Sect. 4 we study the weighted-graph model of Stone relation algebras. Our contribution is to characterise in logical terms the meaning of relation-algebraic properties when applied to weighted graphs. Also here, our results are formally stated and proved.
-
In Sect. 5 we study Stone-Kleene relation algebras, which extend Stone relation algebras with the Kleene star operation. We contribute a number of algebraic properties, again formally proved.
All of our results are verified in Isabelle/HOL [42] using its integrated automated theorem provers and SMT solvers [14, 43]. We omit the proofs, which can be found in the theory files available in the Archive of Formal Proofs [30, 31] and at http://www.csse.canterbury.ac.nz/walter.guttmann/algebra/. The Archive currently stores the theories for Stone algebras and Stone relation algebras including the results presented in Sects. 2–4. The theories for Stone-Kleene relation algebras including the results of Sect. 5 are being prepared for it.
2 Pseudocomplemented Algebras
This section covers basic algebraic structures used in the present paper, including lattices, pseudocomplemented lattices and Stone algebras. These structures are further discussed in a number of textbooks [7, 13, 16, 20, 27]. Many results given in this section can be found in these textbooks. All results given in this section have been formally verified in Isabelle/HOL, mostly as part of a proof of Chen and Grätzer’s construction theorem for Stone algebras [30].
Definition 1
A bounded semilattice is an algebraic structure \((S,\sqcup ,\bot )\) where \(\sqcup \) is associative, commutative and idempotent and has unit \(\bot \):
A bounded lattice is an algebraic structure \((S,\sqcup ,\sqcap ,\bot ,\top )\) where \((S,\sqcup ,\bot )\) and \((S,\sqcap ,\top )\) are bounded semilattices and the following absorption axioms hold:
A bounded distributive lattice is a bounded lattice where the following distributivity axioms hold (it is enough to postulate one of the two to obtain the other):
The lattice order is given by
A (distributive) p-algebra is an algebraic structure  such that \((S,\sqcup ,\sqcap ,\bot ,\top )\) is a bounded (distributive) lattice and the pseudocomplement
such that \((S,\sqcup ,\sqcap ,\bot ,\top )\) is a bounded (distributive) lattice and the pseudocomplement  the equivalence
the equivalence
A Stone algebra is a distributive p-algebra satisfying the equation
An element \(x \in S\) is regular if \(\overline{\overline{x}} = x\) and dense if \(\overline{x} = \bot \). A Boolean algebra is a Stone algebra whose elements are all regular.
Thus the pseudocomplement \(\overline{y}\) of an element y is the \(\le \)-greatest element whose meet with y is \(\bot \). The following result gives basic properties of pseudocomplements.
Theorem 2
Let S be a p-algebra and let \(x, y, z \in S\). Then the  \(\le \)-antitone, \(x \sqcup \overline{x}\) is dense, and
\(\le \)-antitone, \(x \sqcup \overline{x}\) is dense, and

In particular, the function \(\lambda x . \overline{\overline{x}}\) is a closure operation, that is, idempotent, \(\le \)-increasing and \(\le \)-isotone. The image of the  precisely the set of regular elements. They are closed under the operations
precisely the set of regular elements. They are closed under the operations  and \(\top \). The dense elements of a p-algebra are precisely those mapped to \(\top \) by the operation \(\lambda x . \overline{\overline{x}}\). They are closed under the operations \(\sqcup \), \(\sqcap \), \(\lambda x . \overline{\overline{x}}\) and \(\top \). Equational axioms for p-algebras are obtained by adding Theorems 2.1, 2.2 and 2.14 to any set of equational axioms for bounded lattices.
and \(\top \). The dense elements of a p-algebra are precisely those mapped to \(\top \) by the operation \(\lambda x . \overline{\overline{x}}\). They are closed under the operations \(\sqcup \), \(\sqcap \), \(\lambda x . \overline{\overline{x}}\) and \(\top \). Equational axioms for p-algebras are obtained by adding Theorems 2.1, 2.2 and 2.14 to any set of equational axioms for bounded lattices.
In distributive p-algebras, we also obtain the following properties. By Theorem 3.1, every element x can be represented as the meet of a dense and a regular element.
Theorem 3
Let S be a distributive p-algebra and let \(x, y \in S\). Then

In a Stone algebra we obtain one of De Morgan’s laws (the other is Theorem 2.10) and a number of weak shunting properties as the following result shows.
Theorem 4
Let S be a Stone algebra and let \(x, y, z \in S\). Then

The weak shunting property in Theorem 4.8 does not require the element z on the right-hand side to be regular. Another consequence is that the regular elements of a Stone algebra S are closed under the operation \(\sqcup \), whence they form a Boolean subalgebra of S [27]. The dense elements of a Stone algebra form a distributive lattice with \(\top \).
In the remainder of this section we look at instances of Stone algebras, notably extended real numbers and matrices over Stone algebras. Our considerations are motivated by weighted graphs. In this model we take edge weights from a Stone algebra and represent graphs by matrices containing edge weights.
For edge weights we use the extended real numbers  with the operations \(\max \) and \(\min \) and the order \(\le \) extended so that \(\bot \) is the \(\le \)-least element and \(\top \) is the \(\le \)-greatest element. The resulting structure is a Stone algebra; the following result also shows the operation \(\lambda x . \overline{\overline{x}}\) in this algebra.
with the operations \(\max \) and \(\min \) and the order \(\le \) extended so that \(\bot \) is the \(\le \)-least element and \(\top \) is the \(\le \)-greatest element. The resulting structure is a Stone algebra; the following result also shows the operation \(\lambda x . \overline{\overline{x}}\) in this algebra.
Theorem 5
 is a Stone algebra with
is a Stone algebra with
and the order \(\le \) on  as the lattice order. The regular elements are \(\bot \) and \(\top \). All elements except \(\bot \) are dense.
as the lattice order. The regular elements are \(\bot \) and \(\top \). All elements except \(\bot \) are dense.
The operation \(\lambda x . \overline{\overline{x}}\) checks whether its argument is different from \(\bot \) and returns one of the Boolean elements \(\bot \) or \(\top \).
Weighted graphs are represented as matrices whose entries are edge weights. We therefore need to lift the Stone algebra structure to matrices according to the following result. Let \(S^{A \times A}\) denote the set of square matrices with indices from a set A and entries from a set S. Such a matrix represents a directed graph with node set A and edge weights taken from S.
Theorem 6
Let  be a Stone algebra and let A be a set. Then
be a Stone algebra and let A be a set. Then  is a Stone algebra, where the operations
is a Stone algebra, where the operations  and the lattice order \(\le \) are lifted componentwise.
and the lattice order \(\le \) are lifted componentwise.
Using pointwise liftings, the result holds more generally for the set \(S^X\) of all functions from X to S, for any set X.
It follows that the regular elements among the matrices over extended reals are the matrices over \(\{ \bot , \top \}\). They represent unweighted graphs: an entry \({M}_{{i}{j}} = \bot \) means that there is no edge from node i to node j in graph M, while \({M}_{{i}{j}} = \top \) means that there is an edge but no information about its weight is provided. Hence, on the matrix level the operation \(\lambda x . \overline{\overline{x}}\) takes a weighted graph and produces an unweighted graph. The result \(\overline{\overline{M}}\) represents the structure of the weighted graph M after forgetting the weights. Under this interpretation, the dense elements among the matrices correspond to complete graphs.
There are several approaches related to obtaining the structure of a weighted graph. In [47] an operation that gives the least ‘crisp’ relation containing a fuzzy relation is discussed. In [21] the ‘shape’ is a relation that represents a superset of the non-zero entries of a matrix of complex numbers; an operation that gives the non-zero entries is not considered. In [39] the ‘support’ is an operation on matrices over natural numbers that maps 0 to 0 and each non-zero entry to 1. In [36] weighted graphs are represented by matrices over commutative semirings and their structure is obtained by a ‘flattening’ operation that maps each entry x to the smallest multiplicatively idempotent element whose product with x is x. The multiplicatively idempotent elements in  are 0 and 1.
are 0 and 1.
We conclude this section with a brief comparison of Stone algebras and Heyting algebras, which are bounded lattices where all relative pseudocomplements exist. The pseudocomplement of an element y relative to an element z is the \(\le \)-greatest element whose meet with y is below z. By specialising \(z = \bot \) it follows that Heyting algebras form distributive p-algebras. A counterexample generated by Nitpick [15] witnesses that, in general, Heyting algebras do not form Stone algebras this way. A counterexample given in [24, Example 4.6] shows that relative pseudocomplements need not exist in Stone algebras.
3 Stone Relation Algebras
In this section we further discuss the algebraic structure of matrices over Stone algebras. We have seen in Sect. 2 that such matrices form Stone algebras by lifting the operations componentwise. Moreover, they can be used to represent weighted graphs with edge weights taken from the extended reals. Finally, the subset of regular matrices obtained as the image of the closure operation \(\lambda x . \overline{\overline{x}}\) represents unweighted graphs in this case. Because unweighted graphs correspond to relations, these observations suggest a generalisation of relation algebras to cover weighted graphs.
Definition 7
A Stone relation algebra  is a Stone algebra
is a Stone algebra  with a composition \(\cdot \) and a converse \({}^\mathsf{T}\) and a constant \(\mathrm {1}\) satisfying the following axioms (1)–(10). We abbreviate \(x \cdot y\) as xy and let composition have higher precedence than the operators \(\sqcup \) and \(\sqcap \).
with a composition \(\cdot \) and a converse \({}^\mathsf{T}\) and a constant \(\mathrm {1}\) satisfying the following axioms (1)–(10). We abbreviate \(x \cdot y\) as xy and let composition have higher precedence than the operators \(\sqcup \) and \(\sqcap \).
A relation algebra  is a Stone relation algebra whose reduct
is a Stone relation algebra whose reduct  is a Boolean algebra.
is a Boolean algebra.
An element \(x \in S\) is a vector if \(x \top = x\), a co-vector if \(\top x = x\), reflexive if \(\mathrm {1}\le x\), co-reflexive if \(x \le \mathrm {1}\), irreflexive if \(x \le \overline{\mathrm {1}}\), symmetric if \(x = {x}^\mathsf{T}\), asymmetric if \(x \sqcap {x}^\mathsf{T} = \bot \), antisymmetric if \(x \sqcap {x}^\mathsf{T} \le \mathrm {1}\), transitive if \(x x \le x\), univalent if \({x}^\mathsf{T} x \le \mathrm {1}\), injective if \(x {x}^\mathsf{T} \le \mathrm {1}\), total if \(\mathrm {1}\le x {x}^\mathsf{T}\), surjective if \(\mathrm {1}\le {x}^\mathsf{T} x\), a mapping if x is univalent and total, bijective if x is injective and surjective, a point if x is a bijective vector, and an atom if both \(x \top \) and \({x}^\mathsf{T} \top \) are bijective.
Tarski’s relation algebras [46] require a Boolean algebra, axioms (1)–(6), and Theorem 8.20 below [40]. Axioms (7)–(10) follow from these properties. Another way to obtain relation algebras is by requiring a Boolean algebra and axioms (1)–(8) since axioms (9) and (10) immediately follow in Boolean algebras. There is a large body of research about Tarski’s relation algebras; recent monographs are [32, 41]. See [3] for an implementation of Tarski’s relation algebras in Isabelle/HOL.
The Dedekind formula (8) or variants of it are known from [12, 23, 35, 45]. In particular, Dedekind categories algebraically capture fuzzy relations, which are matrices over the real unit interval or complete distributive lattices used for modelling fuzzy systems [25, 47]. In Dedekind categories composition is required to have a left residual and each Hom-set must be a complete distributive lattice and therefore a Heyting algebra [34]. Stone relation algebras maintain the signature of relation algebras. Algebras of relations with a smaller signature have been studied, for example, in [2, 17]. In rough relation algebras [18] the lattice structure is required to be a double Stone algebra, which involves two dual pseudocomplement operations. A rough relation is a pair of upper and lower approximations of a relation with respect to a fixed indiscernibility relation [44].
Regular elements are closed under composition and its unit by axioms (9) and (10).
The following properties hold in Stone relation algebras.
Theorem 8
Let S be a Stone relation algebra and let \(w, x, y, z \in S\). Then

Theorems 8.21–8.24 are weak versions of the Schröder equivalences of relation algebras: the elements on the right-hand sides of both inequalities must be regular. On the other hand, the conjugation property
also holds in Stone relation algebras. Theorem 8.32 is another example how a property of relation algebras has been weakened, in this case by introducing double pseudocomplements. The original version is \(\overline{x y} \sqcup x z = \overline{x (y \sqcap \overline{z})} \sqcup x z\) and appears as [40, Theorem 24(xxiv)].
Counterexamples generated by Nitpick witness that neither the Schröder equivalences of relation algebras nor [40, Theorem 24(xxiv)] hold in Stone relation algebras. Nevertheless, Theorem 8 shows that many properties of relation algebras already hold in Stone relation algebras.
We reuse the characterisations of vectors, co-reflexivity, injectivity and other properties known from relation algebras [45]. Consequences of these definitions are given by the following result. Once again, it shows that many properties generalise from relation algebras without changes.
Theorem 9
Let S be a Stone relation algebra and let \(w, x, y, z \in S\).
-
1.
The regular elements of S are closed under the operation \({}^\mathsf{T}\).
-
2.
The set of vectors of S is closed under the operations
 and \(\top \).
and \(\top \). -
3.
Every mapping, every bijective element and every atom is regular.
If w and x are vectors, then

If w and x are co-reflexive, then

If w is univalent and x is injective, then

If w is a mapping and x is bijective, then

Finally,
-
28.
x is a vector/univalent/total \(\Leftrightarrow \) \({x}^\mathsf{T}\) is a co-vector/injective/surjective
-
29.
x is total \(\Leftrightarrow \) \(x \top = \top \)
-
30.
x is surjective \(\Leftrightarrow \) \(\top x = \top \)
While vectors are closed under pseudocomplements in Stone relation algebras, a counterexample generated by Nitpick witnesses that x need not be a vector if \(\overline{x}\) is a vector. In fact there are counterexamples in the weighted-graph model as shown below.
In order to instantiate Stone relation algebras by weighted graphs we proceed in two steps. First, we show how every Stone algebra gives rise to a Stone relation algebra by reusing some of the operations. Second, we lift the Stone relation algebra structure to matrices; this is similar to the lifting for Dedekind categories [47]. The following result also shows that every Stone relation algebra has a subalgebra that is a relation algebra. As a consequence we can work with weighted graphs in Stone relation algebras and use the full power of relation algebras for reasoning about their structure.
Theorem 10
-
1.
The regular elements of a Stone relation algebra S form a relation algebra that is a subalgebra of S.
-
2.
Let
 be a Stone algebra. Then
be a Stone algebra. Then  is a Stone relation algebra with meet as composition, \(\top \) as its unit, and the identity function as converse.
is a Stone relation algebra with meet as composition, \(\top \) as its unit, and the identity function as converse. -
3.
Let
 be a Stone relation algebra and let A be a finite set. Then
be a Stone relation algebra and let A be a finite set. Then  is a Stone relation algebra, where the operations \(\cdot \), \({}^\mathsf{T}\) and \(\mathrm {1}\) are defined by $$\begin{aligned} {(M \cdot N)}_{{i}{j}}&= \textstyle \bigsqcup _{k \in A} {M}_{{i}{k}} \cdot {N}_{{k}{j}} \\ {({M}^\mathsf{T})}_{{i}{j}}&= {({M}_{{j}{i}})}^\mathsf{T} \\ {\mathrm {1}}_{{i}{j}}&= \left\{ \begin{array}{ll} \mathrm {1}&{} \,\mathrm{if}\, i = j \\ \bot &{} \,\mathrm{if}\, i \ne j \end{array} \right. \end{aligned}$$
is a Stone relation algebra, where the operations \(\cdot \), \({}^\mathsf{T}\) and \(\mathrm {1}\) are defined by $$\begin{aligned} {(M \cdot N)}_{{i}{j}}&= \textstyle \bigsqcup _{k \in A} {M}_{{i}{k}} \cdot {N}_{{k}{j}} \\ {({M}^\mathsf{T})}_{{i}{j}}&= {({M}_{{j}{i}})}^\mathsf{T} \\ {\mathrm {1}}_{{i}{j}}&= \left\{ \begin{array}{ll} \mathrm {1}&{} \,\mathrm{if}\, i = j \\ \bot &{} \,\mathrm{if}\, i \ne j \end{array} \right. \end{aligned}$$
The weighted-graph model is an instance of this construction because edge weights are taken from the Stone algebra of extended reals. Thus for a finite set A, the set of matrices  is a Stone relation algebra with the following operations:
is a Stone relation algebra with the following operations:
The remaining operations are lifted componentwise from the underlying Stone algebra.
Recall that the regular elements are the matrices over \(\{ \bot , \top \}\) in this case; they represent unweighted graphs. In particular, the graphs \(\bot \), \(\mathrm {1}\) and \(\top \) are regular. Theorem 10.1 confirms that these matrices form a relation algebra.
We furthermore note that the way to obtain regular matrices (essentially relations) from weighted matrices by taking the image  similar to the way co-reflexive relations are obtained from relations by taking the image of the antidomain operation [22]. The operation \(\lambda x . \overline{\overline{x}}\) corresponds to the domain operation and, if vectors are used instead of co-reflexives, to the operation \(\lambda x . x \top \), which is a closure operation.
similar to the way co-reflexive relations are obtained from relations by taking the image of the antidomain operation [22]. The operation \(\lambda x . \overline{\overline{x}}\) corresponds to the domain operation and, if vectors are used instead of co-reflexives, to the operation \(\lambda x . x \top \), which is a closure operation.
Next, we further discuss the difference between relation algebras and Stone relation algebras. The following list shows a number of properties of relation algebras that do not generally hold in Stone relation algebras. We give counterexamples found by Nitpick in the weighted-graph model of matrices over extended reals  . Nitpick allows the user to set independent bounds for the size of matrices and the size of the set that approximates matrix entries in the search.
. Nitpick allows the user to set independent bounds for the size of matrices and the size of the set that approximates matrix entries in the search.
-
1.
\(x y \le z \Leftrightarrow {x}^\mathsf{T} \overline{z} \le \overline{y}\):
This Schröder equivalence fails for \(A = \{ a \}\) and \({x}_{{a}{a}} = {y}_{{a}{a}} = 0\) and \({z}_{{a}{a}} = -1\).
-
2.
\(\overline{x y} \sqcup x z = \overline{x (y \sqcap \overline{z})} \sqcup x z\):
This equation is [40, Theorem 24(xxiv)] and fails for \(A = \{ a \}\) and \({x}_{{a}{a}} = {z}_{{a}{a}} = 0\) and \({y}_{{a}{a}} = \top \).
-
3.
\(\overline{\overline{x} \top } \sqcap 1 \le x\) for each vector x:
This fails for \(A = \{ a \}\) and \({x}_{{a}{a}} = 0\).
-
4.
\((\overline{\overline{x} \top } \sqcap 1) \top = x\) for each vector x:
This fails for \(A = \{ a \}\) and \({x}_{{a}{a}} = 0\).
-
5.
x is a vector if \(\overline{x}\) is a vector:
This holds for graphs with a single node but fails for \(A = \{ a, b \}\) and \({x}_{{a}{a}} = 0\) and \({x}_{{a}{b}} = {x}_{{b}{b}} = 1\) and \({x}_{{b}{a}} = \top \).
-
6.
\(\overline{x} \sqcap y\) is regular for each \(x \ne \bot \):
This holds for graphs with a single node but fails for \(A = \{ a, b \}\) and \({x}_{{b}{a}} = \bot \) and \({y}_{{b}{a}} = 1\) and all other entries of x and y set to \(\top \).
Except in the last case, Nitpick indicated that the examples it found are potentially spurious, which might be due to the involved matrix products. All counterexamples have been verified manually.
Finally, we discuss two examples for proving properties of weighted graphs in Stone relation algebras. First, consider a graph G on a set of nodes A and a subset \(B \subseteq A\) of the nodes. We work in the Stone relation algebra  . The graph G is represented by an element \(x \in S\) and the subset B of nodes is represented by a regular vector \(v \in S\). The element \(v {v}^\mathsf{T}\) describes the complete unweighted graph formed by the nodes in B. The meet \(v {v}^\mathsf{T} \sqcap x\) restricts the edges of G to those that start and end in B; this is a weighted subgraph. By Theorem 9.10 we obtain
. The graph G is represented by an element \(x \in S\) and the subset B of nodes is represented by a regular vector \(v \in S\). The element \(v {v}^\mathsf{T}\) describes the complete unweighted graph formed by the nodes in B. The meet \(v {v}^\mathsf{T} \sqcap x\) restricts the edges of G to those that start and end in B; this is a weighted subgraph. By Theorem 9.10 we obtain
which shows that by following a sequence of two edges in the weighted subgraph we cannot leave the set of nodes in B. The claim extends to longer sequences of edges by using the Kleene star as in Sect. 5. Results like this are used for reasoning about Prim’s minimum spanning tree algorithm, where in each step the constructed tree is a subgraph of the input and a spanning tree of the nodes that have already been visited.
Second, in the same setting let \(e \in S\) such that \(e \le v {\overline{v}}^\mathsf{T}\). Such an e can represent a set of edges each of which goes from a node in B to a node outside of B. By Theorem 9.9 we obtain
which shows that it is not possible to follow two such edges in sequence. In Prim’s algorithm, the edges considered for extending the spanning tree in each step satisfy this property. The obtained result is used for showing that the extended tree is acyclic.
4 Relational Properties of Weighted Graphs
In this section we study the weighted-graph model of Stone relation algebras. In particular, we discuss how relation-algebraic properties are interpreted in this instance. Throughout this section, a graph is an element of the Stone relation algebra  introduced in Sect. 3.
introduced in Sect. 3.
4.1 Mappings and Related Properties
We first look at univalent, injective, total, surjective and bijective matrices and at mappings.
Theorem 11
Let  . Then M is
. Then M is
-
1.
univalent \(\Leftrightarrow \) in every row at most one entry is not \(\bot \)
-
2.
injective \(\Leftrightarrow \) in every column at most one entry is not \(\bot \)
-
3.
total \(\Leftrightarrow \) in every row at least one entry is \(\top \)
-
4.
surjective \(\Leftrightarrow \) in every column at least one entry is \(\top \)
-
5.
a mapping \(\Leftrightarrow \) in every row exactly one entry is \(\top \) and the others are \(\bot \)
-
6.
bijective \(\Leftrightarrow \) in every column exactly one entry is \(\top \) and the others are \(\bot \)
Moreover,
-
7.
\(\overline{M \top } = \bot \) \(\Leftrightarrow \) in every row at least one entry is not \(\bot \)
-
8.
\(\overline{\top M} = \bot \) \(\Leftrightarrow \) in every column at least one entry is not \(\bot \)
Note that univalent, injective, total and surjective matrices may have entries which are neither \(\bot \) nor \(\top \). In the graph interpretation, univalent means that every node has at most one outgoing edge. To specify at least one outgoing edge, we can use the property in Theorem 11.7, which is equivalent to \(\overline{\overline{M}}\) being total. Requiring M to be total is stronger: it means that at least one edge is labelled with \(\top \). Therefore, to specify exactly one outgoing edge per node, the conjunction of univalent with the property in Theorem 11.7 has to be used. Requiring a mapping is more restrictive; in fact mappings are regular by Theorem 9.3. Similar remarks apply for injective, surjective and bijective matrices and the property in Theorem 11.8 with respect to the incoming edges of each node.
4.2 Vectors and Related Properties
We next look at vectors, co-vectors, points and atoms in the weighted-graph model of matrices over  .
.
Theorem 12
Let  . Then M is
. Then M is
-
1.
a vector \(\Leftrightarrow \) in every row all entries are the same
-
2.
a co-vector \(\Leftrightarrow \) in every column all entries are the same
-
3.
a point \(\Leftrightarrow \) exactly one row is constant \(\top \) and the others are constant \(\bot \)
-
4.
an atom \(\Leftrightarrow \) exactly one entry is \(\top \) and the others are \(\bot \)
Also vectors and co-vectors may have entries which are neither \(\bot \) nor \(\top \). As in the relational case, a matrix with just one column/row is sufficient to store the information contained in a vector/co-vector. Points and atoms are regular by Theorem 9.3. Their interpretation for graphs is the same as in the relational model: a point represents a node of the graph and an atom represents an edge. Weaker properties can again be obtained by replacing surjective with the property in Theorem 11.8 in the definitions of point and atom. In this case, all rows in a point would be \(\bot \) except for one row, in which all entries would be the same, arbitrary non-\(\bot \) value. Similarly, an atom would have exactly one non-\(\bot \) value.
4.3 Orders and Related Properties
Finally, we look at reflexive, co-reflexive, irreflexive, symmetric, antisymmetric, asymmetric and transitive matrices over  .
.
Theorem 13
Let  . Then M is
. Then M is
-
1.
reflexive \(\Leftrightarrow \) the diagonal is constant \(\top \)
-
2.
co-reflexive \(\Leftrightarrow \) all entries not on the diagonal are \(\bot \)
-
3.
irreflexive \(\Leftrightarrow \) the diagonal is constant \(\bot \)
-
4.
symmetric \(\Leftrightarrow \) \({M}_{{i}{j}} = {M}_{{j}{i}}\) for each \(i, j \in A\)
-
5.
antisymmetric \(\Leftrightarrow \) \({M}_{{i}{j}} = \bot \) or \({M}_{{j}{i}} = \bot \) for each \(i \ne j \in A\)
-
6.
asymmetric \(\Leftrightarrow \) \({M}_{{i}{j}} = \bot \) or \({M}_{{j}{i}} = \bot \) for each \(i, j \in A\)
-
7.
transitive \(\Leftrightarrow \) \({M}_{{i}{k}} \le {M}_{{i}{j}}\) or \({M}_{{k}{j}} \le {M}_{{i}{j}}\) for each \(i, j, k \in A\)
Co-reflexive matrices share most properties of tests [28, 38] except they do not form a Boolean algebra. Nevertheless, they form a Stone relation subalgebra in which composition and meet coincide and composition is idempotent. For example, the composition MN of a co-reflexive matrix M and an arbitrary matrix N restricts the elements of N in row i to at most \({M}_{{i}{i}}\). In particular, rows are filtered out if \({M}_{{i}{i}} = \bot \) and left unchanged if \({M}_{{i}{i}} = \top \). The composition NM has a similar effect on the columns of N.
Matrices that are reflexive, transitive and symmetric have a block-diagonal structure (that is, the base set A can be suitably partitioned by an equivalence relation). The entries in each block are different from \(\bot \) but not necessarily \(\top \).
Similarly, matrices that are reflexive, transitive and antisymmetric have the structure of a partial order. Again the non-\(\bot \) entries may differ from \(\top \). In the graph interpretation, antisymmetric means that there is at most one edge between any two different nodes. Asymmetric additionally requires that there are no loops; the latter property amounts to being irreflexive. Symmetric matrices can be used to represent undirected weighted graphs.
5 Stone-Kleene Relation Algebras
In this section we discuss iterated composition in Stone relation algebras. This works analogously to adding the Kleene star operation to relation algebras. In the graph model, this allows us to talk about reachability. We use the axioms of the Kleene star given in [37].
Definition 14
A Stone-Kleene relation algebra  is a Stone relation algebra
is a Stone relation algebra  with an operation \({}^*\) satisfying the unfold and induction axioms
with an operation \({}^*\) satisfying the unfold and induction axioms
and the axiom
An element \(x \in S\) is acyclic if \(x x^*\) is irreflexive, and x is a forest if x is injective and acyclic.
Kleene algebras are based on idempotent semirings in [37], but we do not require more axioms than the above since all Stone relation algebras are idempotent semirings. Regular elements are closed under the Kleene star by axiom (11). The following properties hold in Stone-Kleene relation algebras.
Theorem 15
Let S be a Stone-Kleene relation algebra and let \(x, y \in S\).
-
1.
The regular elements of S are closed under the operation \({}^*\).
Moreover
-
2.
\(x{}^*{}^\mathsf{T}= x{}^\mathsf{T}{}^*\)
-
3.
\({x}^\mathsf{T} (x {x}^\mathsf{T})^* \le {x}^\mathsf{T}\) if x is a vector
-
4.
\((x {x}^\mathsf{T})^* = \mathrm {1}\sqcup x {x}^\mathsf{T}\) if x is a vector
-
5.
\({x}^\mathsf{T} y^* = {x}^\mathsf{T} ({({x}^\mathsf{T} y^*)}^\mathsf{T} ({x}^\mathsf{T} y^*) \sqcap y)^*\) if x is a vector
-
6.
\(x{}^\mathsf{T}{}^*\le \overline{x}\) if and only if x is acyclic
-
7.
x is asymmetric if x is acyclic
-
8.
\(x^* {x}^\mathsf{T}{}^*\sqcap {x}^\mathsf{T} x \le \mathrm {1}\) if x is a forest
As an example we discuss Theorem 15.5, which considers a graph y and a set of nodes x represented as a vector. Then \(y{}^\mathsf{T}{}^*x\) is a vector representing the set of nodes reachable from any node in x. The same set is represented by the left-hand side \({x}^\mathsf{T} y^*\) as a co-vector. The right-hand side uses the same construction except the graph y is restricted to those edges that start and end in this set of reachable nodes. Thus Theorem 15.5 states that to reach any of these nodes from x it suffices to take edges between these nodes. This property is used several times for proving the correctness of Prim’s minimum spanning tree algorithm.
As another example, Theorem 15.6 has the following interpretation for an acyclic graph x. The left-hand side describes backward reachability in x. The inequality states that if a node q is reachable from a node p by going backward any number of steps in x, then there must not be an edge from p to q; otherwise we could combine it with the path from q to p to obtain a cycle in x. Moreover, this condition is equivalent to being acyclic.
In order to instantiate Stone-Kleene relation algebras by weighted graphs we extend the two-step process we used for Stone relation algebras in Sect. 3 by the Kleene star operation. First, every Stone algebra gives rise to a Stone-Kleene relation algebra by setting \(x^* = \top \). This is because the underlying bounded lattice forms a semiring where \(\mathrm {1}= \top \). Second, we lift the Stone-Kleene relation algebra structure to matrices. Note that \(x^* = \top \) does not generally hold in the matrix algebra; only the entries on the diagonal of \(x^*\) will be \(\top \).
Theorem 16
-
1.
Let
 be a Stone algebra. Then, using the constant \(\top \) function as the Kleene star,
be a Stone algebra. Then, using the constant \(\top \) function as the Kleene star, 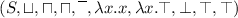 is a Stone-Kleene relation algebra.
is a Stone-Kleene relation algebra. -
2.
Let
 be a Stone-Kleene relation algebra and let A be a finite set. Then
be a Stone-Kleene relation algebra and let A be a finite set. Then  is a Stone-Kleene relation algebra, where the operation \({}^*\) on matrices is defined using Conway’s automata-based construction described in [19].
is a Stone-Kleene relation algebra, where the operation \({}^*\) on matrices is defined using Conway’s automata-based construction described in [19].
The subalgebra of regular elements of a Stone-Kleene relation algebra is both a relation algebra and a Kleene algebra.
The proof of Theorem 16 formally verifies the correctness of Conway’s construction for Kleene algebras. An implementation of the construction in Isabelle/HOL that extends [4] was given in [5] without a correctness proof.
6 Conclusion
In the present paper we have studied algebras for modelling weighted graphs. Stone relation algebras are designed to stay so close to relation algebras that relational methods and concepts can be reused, yet be general enough to capture weighted graphs. Like relation algebras, Stone relation algebras can be combined with Kleene algebras for reasoning about reachability. All of our results about these algebraic structures have been formally verified in Isabelle/HOL; this includes a proof that weighted graphs represented by matrices over extended reals form an instance.
We have applied these results in two case studies. The first is a formally verified proof of Chen and Grätzer’s construction theorem for Stone algebras [30]. It involves extensive reasoning about algebraic structures in addition to reasoning in algebraic structures. The second case study is a formal verification of Prim’s minimum spanning tree algorithm [29]. It uses Hoare logic and most of the proof can be carried out in Stone-Kleene relation algebras.
Section 4 interprets a number of relational properties for weighted graphs. Future work will consider further graph algorithms to understand the limits of what can be expressed algebraically in this model. The long-term goal of these efforts is a library for algebraic reasoning about weighted graphs and graph algorithms.
References
Aho, A.V., Hopcroft, J.E., Ullman, J.D.: The Design and Analysis of Computer Algorithms. Addison-Wesley Publishing Company, Reading (1974)
Andréka, H., Mikulás, Sz.: Axiomatizability of positive algebras of binary relations. Algebra Universalis 66(1–2), 7–34 (2011)
Armstrong, A., Foster, S., Struth, G., Weber, T.: Relation algebra. Archive of Formal Proofs (2016, first version 2014)
Armstrong, A., Gomes, V.B.F., Struth, G., Weber, T.: Kleene algebra. Archive of Formal Proofs (2016, first version 2013)
Asplund, T.: Formalizing the Kleene star for square matrices. Bachelor thesis IT 14 002, Department of Information Technology, Uppsala Universitet (2014)
Backhouse, R.C., Carré, B.A.: Regular algebra applied to path-finding problems. J. Inst. Math. Appl. 15(2), 161–186 (1975)
Balbes, R., Dwinger, P.: Distributive Lattices. University of Missouri Press, Columbia (1974)
Berghammer, R., Fischer, S.: Combining relation algebra and data refinement to develop rectangle-based functional programs for reflexive-transitive closures. J. Log. Algebr. Methods Program. 84(3), 341–358 (2015)
Berghammer, R., von Karger, B.: Relational semantics of functional programs (Chap. 8). In: Brink, C., Kahl, W., Schmidt, G. (eds.) Relational Methods in Computer Science, pp. 115–130. Springer, Wien (1997). doi:10.1007/978-3-7091-6510-2_8
Berghammer, R., von Karger, B., Wolf, A.: Relation-algebraic derivation of spanning tree algorithms. In: Jeuring, J. (ed.) MPC 1998. LNCS, vol. 1422, pp. 23–43. Springer, Heidelberg (1998). doi:10.1007/BFb0054283
Berghammer, R., Rusinowska, A., de Swart, H.: Computing tournament solutions using relation algebra and RelView. Eur. J. Oper. Res. 226(3), 636–645 (2013)
Bird, R., de Moor, O.: Algebra of Programming. Prentice Hall, Englewood Cliffs (1997)
Birkhoff, G.: Lattice Theory. Colloquium Publications, vol. XXV, 3rd edn. American Mathematical Society, Providence (1967)
Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending Sledgehammer with SMT solvers. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS (LNAI), vol. 6803, pp. 116–130. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22438-6_11
Blanchette, J.C., Nipkow, T.: Nitpick: a counterexample generator for higher-order logic based on a relational model finder. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 131–146. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14052-5_11
Blyth, T.S.: Lattices and Ordered Algebraic Structures. Springer, London (2005)
Bredihin, D.A., Schein, B.M.: Representations of ordered semigroups and lattices by binary relations. Colloq. Math. 39(1), 1–12 (1978)
Comer, S.D.: On connections between information systems, rough sets and algebraic logic. In: Rauszer, C. (ed.) Algebraic Methods in Logic and in Computer Science. Banach Center Publications, vol. 28, pp. 117–124. Institute of Mathematics, Polish Academy of Sciences, Warsaw (1993)
Conway, J.H.: Regular Algebra and Finite Machines. Chapman and Hall, London (1971)
Curry, H.B.: Foundations of Mathematical Logic. Dover Publications, New York (1977)
Desharnais, J., Grinenko, A., Möller, B.: Relational style laws and constructs of linear algebra. J. Log. Algebr. Methods Program. 83(2), 154–168 (2014)
Desharnais, J., Struth, G.: Internal axioms for domain semirings. Sci. Comput. Program. 76(3), 181–203 (2011)
Freyd, P.J., Ščedrov, A.: Categories, Allegories. North-Holland Mathematical Library, vol. 39. Elsevier Science Publishers, Amsterdam (1990)
Fried, E., Hansoul, G.E., Schmidt, E.T., Varlet, J.C.: Perfect distributive lattices. In: Eigenthaler, G., Kaiser, H.K., Müller, W.B., Nöbauer, W. (eds.) Contributions to General Algebra, vol. 3, pp. 125–142. Hölder-Pichler-Tempsky, Wien (1985)
Goguen, J.A.: L-fuzzy sets. J. Math. Anal. Appl. 18(1), 145–174 (1967)
Gondran, M., Minoux, M.: Graphs, Dioids and Semirings. Springer, New York (2008)
Grätzer, G.: Lattice Theory: First Concepts and Distributive Lattices. W. H. Freeman and Co., San Francisco (1971)
Guttmann, W.: Algebras for iteration and infinite computations. Acta Inf. 49(5), 343–359 (2012)
Guttmann, W.: Relation-algebraic verification of Prim’s minimum spanning tree algorithm. In: Sampaio, A., Wang, F. (eds.) ICTAC 2016. LNCS, vol. 9965, pp. 51–68. Springer, Cham (2016). doi:10.1007/978-3-319-46750-4_4
Guttmann, W.: Stone algebras. Archive of Formal Proofs (2016)
Guttmann, W.: Stone relation algebras. Archive of Formal Proofs (2017)
Hirsch, R., Hodkinson, I.: Relation Algebras by Games. Elsevier Science B.V., Amsterdam (2002)
Höfner, P., Möller, B.: Dijkstra, Floyd and Warshall meet Kleene. Form. Asp. Comput. 24(4), 459–476 (2012)
Kawahara, Y., Furusawa, H.: Crispness in Dedekind categories. Bull. Inform. Cybern. 33(1–2), 1–18 (2001)
Kawahara, Y., Furusawa, H., Mori, M.: Categorical representation theorems of fuzzy relations. Inf. Sci. 119(3–4), 235–251 (1999)
Killingbeck, D., Teixeira, M.S., Winter, M.: Relations among matrices over a semiring. In: Kahl, W., Winter, M., Oliveira, J.N. (eds.) RAMiCS 2015. LNCS, vol. 9348, pp. 101–118. Springer, Cham (2015). doi:10.1007/978-3-319-24704-5_7
Kozen, D.: A completeness theorem for Kleene algebras and the algebra of regular events. Inf. Comput. 110(2), 366–390 (1994)
Kozen, D.: Kleene algebra with tests. ACM Trans. Program. Lang. Syst. 19(3), 427–443 (1997)
Macedo, H.D., Oliveira, J.N.: A linear algebra approach to OLAP. Form. Asp. Comput. 27(2), 283–307 (2015)
Maddux, R.D.: Relation-algebraic semantics. Theoret. Comput. Sci. 160(1–2), 1–85 (1996)
Maddux, R.D.: Relation Algebras. Elsevier B.V., Amsterdam (2006)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002)
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: Sutcliffe, G., Ternovska, E., Schulz, S. (eds.) Proceedings of 8th International Workshop on the Implementation of Logics, pp. 3–13 (2010)
Pawlak, Z.: Rough sets, rough relations and rough functions. Fundamenta Informaticae 27(2–3), 103–108 (1996)
Schmidt, G., Ströhlein, T.: Relationen und Graphen. Springer, Heidelberg (1989)
Tarski, A.: On the calculus of relations. J. Symb. Log. 6(3), 73–89 (1941)
Winter, M.: A new algebraic approach to L-fuzzy relations convenient to study crispness. Inf. Sci. 139(3–4), 233–252 (2001)
Acknowledgement
I thank Georg Struth and the anonymous referees for pointing out related work and for other helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Guttmann, W. (2017). Stone Relation Algebras. In: Höfner, P., Pous, D., Struth, G. (eds) Relational and Algebraic Methods in Computer Science. RAMICS 2017. Lecture Notes in Computer Science(), vol 10226. Springer, Cham. https://doi.org/10.1007/978-3-319-57418-9_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-57418-9_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-57417-2
Online ISBN: 978-3-319-57418-9
eBook Packages: Computer ScienceComputer Science (R0)




 and
and  be a Stone algebra. Then
be a Stone algebra. Then  is a Stone relation algebra with meet as composition,
is a Stone relation algebra with meet as composition,  be a Stone relation algebra and let A be a finite set. Then
be a Stone relation algebra and let A be a finite set. Then  is a Stone relation algebra, where the operations
is a Stone relation algebra, where the operations  be a Stone algebra. Then, using the constant
be a Stone algebra. Then, using the constant 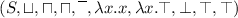 is a Stone-Kleene relation algebra.
is a Stone-Kleene relation algebra. be a Stone-Kleene relation algebra and let A be a finite set. Then
be a Stone-Kleene relation algebra and let A be a finite set. Then  is a Stone-Kleene relation algebra, where the operation
is a Stone-Kleene relation algebra, where the operation