Comparison of Adaptive Non-symmetric and Three-Field FVM-BEM Coupling

Abstract

The prototype for flow and transport in porous media in an interior domain is coupled to the Laplace equation on the complement, an unbounded domain. We approximate the solution of this interface problem either by the non-symmetric or the three-field coupling of the Finite Volume Method (FVM) and the Boundary Element Method (BEM). For these two coupling methods we introduce (semi-) robust a posteriori error estimators and use them in an adaptive algorithm to improve the convergence. Numerical experiments compare these two adaptive methods in terms of effectivity index, errors and mesh refinement.

1 Introduction and Model Problem

The finite volume method (FVM) is the method of choice for problems coming from fluid mechanics applications because of its direct flux conservation and the possibility to solve convection dominated problems via a simple upwind stabilization. When such a flow problem is coupled with a problem on an unbounded domain (e.g., to replace unknown boundary conditions) it is useful to reduce the exterior problem to a problem on the boundary. This leads to a formulation as an integral equation and its discretization to the boundary element method (BEM). There are several possibilities to couple FVM with BEM, in this work we compare the adaptive non-symmetric [3, 4] and the adaptive three-field FVM-BEM coupling approach [1, 2]. Both couplings have been analyzed for 2D and 3D cases. For simplicity we only consider the 2D case here.

Let $\varOmega \subset \mathbb {R}^2$ be a bounded domain with connected polygonal Lipschitz boundary $\varGamma$ with ${{\text {diam}}}(\varOmega )<1$ (possible by scaling) to ensure $H^{-1/2}(\varGamma )$ ellipticity of the single layer operator defined below. The corresponding unbounded exterior domain is $\varOmega _e=\mathbb {R}^2\backslash \overline{\varOmega }$. The coupling boundary $\varGamma =\partial \varOmega = \partial \varOmega _e$ is divided in an inflow and outflow part, namely $\varGamma ^{in}:=\left\{ x\in \varGamma \,\big |\,\mathbf {b}(x)\cdot \mathbf {n}(x)<0\right\}$ and $\varGamma ^{out}:=\left\{ x\in \varGamma \,\big |\,\mathbf {b}(x)\cdot \mathbf {n}(x)\ge 0\right\}$, respectively, where $\mathbf {n}$ is the normal vector on $\varGamma$ pointing outward with respect to $\varOmega$. Then the model problem reads, (see also [1, 3]): Find $u\in H^1(\varOmega )$ and $u_e \in H^1_{{\ell \mathrm{oc}}}(\varOmega _e)$ such that

$$\begin{aligned} {\text {div}}(-\mathbf {A}\nabla u + \mathbf {b}u)+cu&= f \quad&\text {in }\varOmega ,\end{aligned}$$

(1a)

$$\begin{aligned} -\varDelta u_e&=0 \quad&\text {in } \varOmega _e,\end{aligned}$$

(1b)

$$\begin{aligned} u_e(x)&=C_{\infty }\log |x|+\mathscr {O}(1/|x|) \quad&\text {for }|x|\rightarrow \infty ,\end{aligned}$$

(1c)

$$\begin{aligned} u&=u_e+u_0 \quad&\text {on } \varGamma , \end{aligned}$$

(1d)

$$\begin{aligned} ( \mathbf {A}\nabla u-\mathbf {b}u)\cdot \mathbf {n}&= \frac{\partial u_e}{\partial \mathbf {n}}+t_0\quad&\text {on } \varGamma ^{in},\end{aligned}$$

(1e)

$$\begin{aligned} ( \mathbf {A}\nabla u)\cdot \mathbf {n}&= \frac{\partial u_e}{\partial \mathbf {n}}+t_0\quad&\text {on } \varGamma ^{out}. \end{aligned}$$

(1f)

Here, $L^m(\cdot )$ and $H^m(\cdot )$, $m>0$ denote the standard Lebesgue and Sobolev spaces equipped with the corresponding norms $\Vert \cdot \Vert _{L^m(\cdot )}$ and $\Vert \cdot \Vert _{H^m(\cdot )}$. We will use $(\cdot ,\cdot )_{\omega }$ for the $L^2$ scalar product for $\omega \subset \varOmega$. The duality between $H^{m}(\varGamma )$ and $H^{-m}(\varGamma )$ is given by the extended $L^2$-scalar product $\langle \cdot ,\cdot \rangle _{\varGamma }$. We collect all functions with local $H^1$ behavior in $H^1_{{\ell \mathrm{oc}}}(\varOmega )$ and the Lipschitz continuous functions in $W^{1,\infty }$.

The diffusion matrix $\mathbf {A}:\varOmega \rightarrow \mathbb {R}^{2\times 2}$ has entries in $W^{1,\infty }(T)$ for every $T\in \mathscr {T}$, where $\mathscr {T}$ is a mesh of $\varOmega$ introduced below in Sect. 2. Additionally, $\mathbf {A}$ is bounded, symmetric and uniformly positive definite. Furthermore, $\mathbf {b}\in W^{1,\infty }(\varOmega )^2$ and $c\in L^{\infty }(\varOmega )$ satisfy the coerciveness assumption $({\text {div}}\mathbf {b}(x))/2+c(x)\ge 0$ for almost every $x\in \varOmega$. For the a posteriori estimators we assume slightly more regularity on the data than usual; $f\in L^2(\varOmega )$, $u_0\in H^{1}(\varGamma )$ and $t_0\in L^2(\varGamma )$. The constant $C_{\infty }$ is unknown; see [1, 3] for possible different radiation conditions. Note that we can rewrite the exterior problem (1b)–(1c) with the aid of the Calderón system and the Cauchy data $\xi :=u_e|_{\varGamma }\in H^{1/2}(\varGamma )$ and $\phi :=\partial u_e/ \partial \mathbf {n}|_{\varGamma }\in H^{-1/2}(\varGamma )$ into an equivalent integral equation. The model problem and the weak form are equivalent. There exists a unique weak solution $(u,u_e)\in H^1(\varOmega )\times H^1_{{\ell \mathrm{oc}}}(\varOmega )$; see [1, 3].

2 Non-symmetric and Three-Field FVM-BEM Coupling

This section introduces two different types of FVM-BEM couplings. In order to do this we first fix some notation.

Triangulations and discrete function spaces: With $\mathscr {T}$ we denote a regular triangulation of $\varOmega$ which consists of non-degenerate closed triangles. We assume that $\mathscr {T}$ is shape-regular, i.e., $\max _{T\in \mathscr {T}}h_T^2/|T|\le \sigma <\infty$ with $h_T:=\sup _{x,y\in T}|x-y|$ and that (possible) discontinuities of the known data $\mathbf {A}$, $\mathbf {b}$, $c$, f, $u_0$, and $t_0$ are aligned with $\mathscr {T}$. Then the sets $\mathscr {N}$ and $\mathscr {E}$ are the nodes and edges of $\mathscr {T}$, respectively. We denote by $\mathscr {E}_T\subset \mathscr {E}$ the set of all edges of T, i.e., $\mathscr {E}_T:=\left\{ E\in \mathscr {E}\,\big |\,E\subset \partial T\right\}$, by $\mathscr {E}_{\varGamma }:=\left\{ E\in \mathscr {E}\,\big |\,E\subset \varGamma \right\}$ the set of all edges on the boundary $\varGamma$, and by $\mathscr {E}_I=\mathscr {E}\backslash \mathscr {E}_{\varGamma }$ all interior edges. Furthermore, $h_E$ is the length of an edge $E\in \mathscr {E}$ and the unit normal vector $\mathbf {n}$ on a boundary always points outwards with respect to the domain.

For a vertex-centered FVM formulation we need a dual mesh $\mathscr {T}^*$, which can be constructed from the primal mesh $\mathscr {T}$. The so-called control volumes $V\in \mathscr {T}^*$ are constructed by connecting the center of gravity of an element $T\in \mathscr {T}$ with the midpoint of the edges $E\in \mathscr {E}_T$; see [3, Fig. 1]. Note that for every vertex $a_i\in \mathscr {N}$ ($i=1\ldots \#\mathscr {N}$), we can assign a unique box $V_i\in \mathscr {T}^*$ only containing $a_i$.

Finally, with $\mathscr {S}^1(\mathscr {T})$ we define the piecewise affine and globally continuous function space on $\mathscr {T}$ and $\mathscr {S}^1_*(\mathscr {E}_{\varGamma })$ is $\mathscr {S}^1(\mathscr {E}_{\varGamma })$ ($\mathscr {S}^1$ on $\mathscr {E}_{\varGamma }$) with integral mean zero. We denote by $\mathscr {P}^0(\mathscr {E}_{\varGamma })$ and $\mathscr {P}^0(\mathscr {T}^*)$ the $\mathscr {E}_{\varGamma }$-piecewise and $\mathscr {T}^*$-piecewise constant function spaces. For $v^*\in \mathscr {P}^0(\mathscr {T}^*)$ we may use $v^*:=\sum _{a_i\in \mathscr {N}}v_i^*\chi _i^*$, $v_i^*\in \mathbb {R}$, where $\chi _i^*$ is the characteristic function of $V_i\in \mathscr {T}^*$.

Non-symmetric FVM-BEM coupling: Now we can introduce the non-symmetric FVM-BEM coupling method which reads: Find $u_h\in \mathscr {S}^1(\mathscr {T})$ and $\phi _h\in \mathscr {P}^0(\mathscr {E}_{\varGamma })$ such that

$$\begin{aligned} \mathscr {A}_V(u_h,v^*)-\langle \phi _h,v^*\rangle _{\varGamma }&=(f,v^*)_{\varOmega } +\langle t_0,v^*\rangle _{\varGamma },\nonumber \\ \langle (1/2-\mathscr {K})u_h,\psi _h\rangle _{\varGamma }+\langle \mathscr {V}\phi _h,\psi _h\rangle _{\varGamma }&=\langle (1/2-\mathscr {K})u_0,\psi _h\rangle _{\varGamma } \end{aligned}$$

(2)

for all $v^*\in \mathscr {P}^0(\mathscr {T}^*)$, $\psi _h\in \mathscr {P}^0(\mathscr {E}_{\varGamma })$ with the finite volume bilinear form

$$\begin{aligned} \mathscr {A}_V(u_h,v^*)&:=\sum _{a_i\in \mathscr {N}}v^*_i\bigg ( \int _{\partial V_i\backslash \varGamma }(-\mathbf {A}\nabla u_h+\mathbf {b}u_h ) \cdot \mathbf {n}\,ds\nonumber \\&\qquad \qquad \quad +\int _{V_i}cu_h\,dx +\int _{\partial V_i\cap \varGamma ^{out}} \mathbf {b}\cdot \mathbf {n}\,u_h\,ds\bigg ), \end{aligned}$$

(3)

the single layer operator $(\mathscr {V}\phi _h)(x):=-\frac{1}{2\pi }\int _{\varGamma }\phi _h(y)\log |x-y|\,ds_{y}$, and the double layer operator $(\mathscr {K}u_h)(x):= -\frac{1}{2\pi }\int _{\varGamma }u_h(y)\frac{\partial }{\partial \mathbf {n}_{y}}\log |x-y|\,ds_{y}$, $x\in \varGamma$.

The system (2) approximates u by $u_h$ and the conormal $\phi$ by $\phi _h$. However, for convection dominated problems the central approximation of the convection term can lead to strong oscillations in the FVM solution. Since FVM is based on the balance equation we can easily apply a full upwinding stabilization which avoids these oscillations but still preserves local flux conservation: Given $V_i\in \mathscr {T}^*$, we consider the intersections $\tau _{ij}=V_i\cap V_j\ne \emptyset$ with the neighboring boxes $V_j \in \mathscr {T}^*$; see also [3, Fig. 1]. Then we replace $\mathbf {b}u_h$ on interior dual edges $\partial V_i\backslash \varGamma$ in $\mathscr {A}_V$ (3) by an upwind approximation. Instead of $u_h$ on $\tau _{ij}$ we use $u_{h,ij}:=u_h(a_i)$ if $\frac{1}{|\tau _{ij}|}\int _{\tau _{ij}}\mathbf {b}\cdot \mathbf {n}_i\,ds\ge 0$, otherwise $u_{h,ij}:=u_h(a_j)$. Here, $\mathbf {n}_i$ points outwards with respect to $V_i$.

The stability and convergence analysis (also with the upwind option) [3, Theorem 2 and 3] holds under a minimal eigenvalue condition on $\mathbf {A}$ (constraint from the ellipticity of the non-symmetric variational form  [3, Theorem 1]). With the usual regularity assumptions this scheme leads to first order convergence.

Three-field FVM-BEM coupling: The three-field coupling uses a different formulation of the exterior problem (i.e., the full Calderón system) and reads: Find $u_h\in \mathscr {S}^1(\mathscr {T})$, $\xi _h\in \mathscr {S}^1_*(\mathscr {E}_{\varGamma })$ and $\phi _h\in \mathscr {P}^0(\mathscr {E}_{\varGamma })$ such that

$$\begin{aligned} \mathscr {A}_V(u_h,v^*)-\langle \phi _h,v^*\rangle _{\varGamma }&= (f,v^*)_{\varOmega } +\langle t_0,v^*\rangle _{\varGamma },\nonumber \\ -\langle u_h,\psi _h\rangle _{\varGamma }-\langle \mathscr {V}\phi _h,\psi _h\rangle _{\varGamma } +\langle (1/2+\mathscr {K})\xi _h,\psi _h\rangle _{\varGamma }&= -\langle u_0,\psi _h\rangle _{\varGamma }, \nonumber \\ \langle (1/2+\mathscr {K}^*)\phi _h,\theta _h\rangle _{\varGamma }+ \langle \mathscr {W}\xi _h,\theta _h\rangle _{\varGamma }&= 0 \end{aligned}$$

(4)

for all $v^*\in \mathscr {P}^0(\mathscr {T}^*)$, $\theta _h\in \mathscr {S}^1_*(\mathscr {E}_{\varGamma })$, $\psi _h\in \mathscr {P}^0(\mathscr {E}_{\varGamma })$. Here, we additionally use the adjoint double layer operator $(\mathscr {K}^*\phi _h)(x):=-\frac{1}{2\pi }\int _{\varGamma }\phi _h(y)\frac{\partial }{\partial \mathbf {n}_{x}}\log |x-y|\,ds_{y}$ and the hypersingular integral operator $(\mathscr {W}\xi _h)(x):= \frac{1}{2\pi }\frac{\partial }{\partial \mathbf {n}_{x}}\int _{\varGamma }\xi _h(y)\frac{\partial }{\partial \mathbf {n}_{y}}\log |x-y|\,ds_{y}$, $x\in \varGamma$. Note that the system (4) additionally approximates the trace $\xi$ by $\xi _h$ and that the upwind option in $\mathscr {A}_V$ described above applies here as well. An a priori convergence analysis (also with the upwind option but without the eigenvalue restriction) can be found in [1]. With the usual regularity assumptions this scheme leads to first order convergence as well. Although the three-field coupling leads to a larger system of linear equations than the non-symmetric coupling one should apply it if the trace $\xi _h$ is explicitly important or if the right-hand side contribution $\mathscr {K}u_0$ is difficult to evaluate.

3 Residual Based a Posteriori Error Estimator

In order to introduce an element-wise refinement indicator, which is a part of our a posteriori error estimator, we define the residual $R:=R(u_h)=f-{\text {div}}(-\mathbf {A}\nabla u_h +\mathbf {b}u_h)-cu_h$ on $T\in \mathscr {T}$ and an edge-residual or jump $J:L^2(\mathscr {E})\rightarrow \mathbb {R}$ by

$$\begin{aligned} J|_E:=J(u_h)|_E= {\left\{ \begin{array}{ll}\displaystyle \big [(-\mathbf {A}\nabla u_h)|_{E,T}-(-\mathbf {A}\nabla u_h)|_{E,T'}\big ]\cdot \mathbf {n}&{} \text {for all }E\in \mathscr {E}_I, \\ \displaystyle (-\mathbf {A}\nabla u_h+\mathbf {b}u_h)\cdot \mathbf {n}+\phi _h+t_0 &{} \text { for all }E\in \mathscr {E}_{\varGamma }^{in},\\ \displaystyle -\mathbf {A}\nabla u_h\cdot \mathbf {n}+\phi _h+t_0 &{} \text { for all }E\in \mathscr {E}_{\varGamma }^{out}. \end{array}\right. } \end{aligned}$$

with $E=T\cap T'\in \mathscr {E}_I,$ $T,T'\in \mathscr {T}$. Note that $\varphi |_{E,T}$ denotes the trace of $\varphi \in H^1(T)$ on E and the normal vector $\mathbf {n}$ points from T to $T'$.

To prove a robust upper bound of the energy error we need some further notation. In order to apply a robust interpolant, the diffusion distribution in $\varOmega$ has to be quasi-monotone; for a definition we refer to [2, 4]. To simplify notation we restrict ourselves here to a piecewise constant diffusion coefficient $\alpha \in \mathscr {P}^0(\mathscr {T})$ with $\mathbf {A}=\alpha \mathbf {I}$. For the $\mathscr {T}$-piecewise constant function $\alpha \in \mathscr {P}^0(\mathscr {T})$ we write $\alpha _T:=\alpha |_T\quad$ for all $T\in \mathscr {T}$. Furthermore, we define $\alpha _E:=\max \big \{\alpha _{T_1},\alpha _{T_2}\big \}$ for $E\in \mathscr {E}_I$ with $E\subset T_1\cap T_2$, $\alpha _E:=\alpha _T$ for $E\in \mathscr {E}_{\varGamma }$ with $E\subset \partial T$. For convection and reaction we define $\beta _T:=\min _{x\in T}\{({\text {div}}\mathbf {b}(x))/2+c(x)\}$ for all $T\in \mathscr {T}$, $\beta _E:=\min \big \{\beta _{T_1},\beta _{T_2}\big \}$ for $E\in \mathscr {E}_I$ with $E\subset T_1\cap T_2$ and $\beta _E:=\beta _T$ for $E\in \mathscr {E}_{\varGamma }$ with $E\subset \partial T$. Next, we define $\mu _T:=\min \big \{\beta _T^{-1/2},h_T \alpha _T^{-1/2}\big \}$ and $\mu _E:=\min \big \{\beta _E^{-1/2},h_E\alpha _E^{-1/2}\big \}$ for all $T\in \mathscr {T}$ and all $E\in \mathscr {E}$, respectively. Note that we take the second argument if $\beta _T=0$ or $\beta _E=0$.

Then, the semi-robust refinement indicator for the non-symmetric coupling reads for all $T\in \mathscr {T}$

$$\begin{aligned} \eta _{T}^2&:=\mu _T^2\Vert R\Vert _{L^2(T)}^2+ \frac{1}{2}\sum _{E\in \mathscr {E}_I\cap \mathscr {E}_T}\alpha _E^{-1/2}\mu _E\Vert J\Vert _{L^2(E)}^2 +\sum _{E\in \mathscr {E}_{\varGamma }\cap \mathscr {E}_T}\alpha _E^{-1/2}\mu _E\Vert J\Vert _{L^2(E)}^2\nonumber \\&\quad +\sum _{E\in \mathscr {E}_{\varGamma }\cap \mathscr {E}_T}h_E\Vert \partial /\partial s\big ((1/2-\mathscr {K})(u_0-u_h)-\mathscr {V}\phi _h\big )\Vert _{L^2(E)}^2, \end{aligned}$$

(5)

where $\partial /\partial s$ denotes the arc length derivative. For the three-field coupling the semi-robust refinement indicator differs slightly, since the exterior trace is approximated separately. Hence, for all $T\in \mathscr {T}$ we get

$$\begin{aligned} \eta _{T}^2&:=\mu _T^2\Vert R\Vert _{L^2(T)}^2+ \frac{1}{2}\sum _{E\in \mathscr {E}_I\cap \mathscr {E}_T}\alpha _E^{-1/2}\mu _E\Vert J\Vert _{L^2(E)}^2 +\sum _{E\in \mathscr {E}_{\varGamma }\cap \mathscr {E}_T}\alpha _E^{-1/2}\mu _E\Vert J\Vert _{L^2(E)}^2\nonumber \\&\quad +\sum _{E\in \mathscr {E}_{\varGamma }\cap \mathscr {E}_T}h_E\Vert \partial u_h/\partial s -\partial /\partial s \big ( u_0-\mathscr {V}\phi _h+(1/2+\mathscr {K})\xi _h\big )\Vert _{L^2(E)}^2\\&\quad +\sum _{E\in \mathscr {E}_{\varGamma }\cap \mathscr {E}_T}h_E\Vert \mathscr {W}\xi _h+(1/2+\mathscr {K}^*)\phi _h\Vert _{L^2(E)}^2\nonumber \end{aligned}$$

(6)

If we apply the upwind stabilization option, an additional refinement quantity is necessary. For both coupling systems this reads for all $T\in \mathscr {T}$

$$\begin{aligned} \eta _{T,{up}}^2&:=\alpha _T^{-1/2}\mu _T \sum _{\tau _{ij}^T\in \mathscr {D}^T}\Vert \mathbf {b}\cdot \mathbf {n}_i(u_h-u_{h,ij})\Vert _{L^2(\tau _{ij}^T)}^2 \end{aligned}$$

(7)

with $\mathscr {D}^T:=\Big \{\tau ^T_{ij}\big |\tau ^T_{ij}=V_i\cap V_j\cap T \text { for }V_i,V_j\in \mathscr {T}^*, V_i\not =V_j, V_i\cap T\not =\emptyset , V_j\cap T\not =\emptyset \Big \}$ and the upwind value $u_{h,ij}$ from Sect. 2. With the refinement indicators (5) and (6) (plus (7)) we can define an error estimator

$$\begin{aligned} \eta :=\Big (\sum _{T\in \mathscr {T}}\eta _T^2(+\eta _{T,{up}}^2)\Big )^{1/2} \end{aligned}$$

(8)

for the non-symmetric (2) and the three-field (4) FVM-BEM coupling. For both couplings $\eta$ is reliable and efficient with respect to the error in the energy norm

$$\begin{aligned} E_h:={\left\{ \begin{array}{ll}\displaystyle |||u-u_h| ||_{\varOmega }+\Vert \phi -\phi _h\Vert _{\mathscr {V}} \qquad &{}\text {non-symmetric},\\ |||u-u_h| ||_{\varOmega }+\Vert \phi -\phi _h\Vert _{\mathscr {V}}+\Vert \xi -\xi _h\Vert _{\mathscr {W}} \qquad &{}\text {three-field} \end{array}\right. } \end{aligned}$$

(9)

with $|||v| ||_{\varOmega }:= \Vert \mathbf {A}^{1/2}\nabla v\Vert _{L^2(\varOmega )}^2+ \Vert \left( {\text {div}}\mathbf {b}/2+c\right) ^{1/2}v\Vert _{L^2(\varOmega )}^2$, $\Vert \cdot \Vert _{\mathscr {V}}^2:=\langle \mathscr {V}\cdot ,\cdot \rangle _{\varGamma }$ and $\Vert \cdot \Vert _{\mathscr {W}}^2:=\langle \mathscr {W}\cdot ,\cdot \rangle _{\varGamma }$. For both couplings the upper bound (reliability) is robust with respect to the variation of the model data. For the non-symmetric coupling, however, we have a minimal eigenvalue restriction of the diffusion matrix $\mathbf {A}$ again. The analytical proof for the lower bound (efficiency) in both couplings holds only for a quasi-uniform mesh on the boundary $\varGamma$. An improved efficiency result in slightly stronger norms (but for a shape regular triangulation also on the boundary) has recently been published in [4]. Additionally, the constant in the lower bound is only semi-robust, i.e., it depends on the local Péclet number. For more details and discussions on the bounds we refer to [4] (non-symmetric) and [2] (three-field).

4 Numerical Experiments

With the refinement indicators (5) and (6) (plus (7)) we devise an adaptive algorithm with the well known Dörfler marking strategy, where we consider a sequence $\mathscr {T}^{(k)}$, $k=0,1,\ldots$ of triangulations: Throughout, let $\theta =0.5$, then at refinement step k choose $\mathscr {M}^{(k)}\subset \mathscr {T}^{(k)}$ with minimal cardinality such that

$$\begin{aligned} \sum _{T\in \mathscr {M}^{(k)}} \left( \eta _T^2 (+\eta _{T,{up}}^2)\right) \ge \theta \sum _{T\in \mathscr {T}^{(k)}} \left( \eta _T^2 (+\eta _{T,{up}}^2)\right) . \end{aligned}$$

Then refine the elements in the set $\mathscr {M}^{(k)}$ with a red-green-blue refinement which ensures the shape regularity of the new mesh $\mathscr {T}^{(k+1)}$.

4.1 Convection-Diffusion Problem

For our first problem we choose $\varOmega =(0,1/2)\times (0,1/2)$ and prescribe the solution in the interior to be $u(x_1,x_2)=0.5\left( 1-\tanh \left( \frac{0.25-x_1}{0.02}\right) \right)$ for $x=(x_1,x_2)\in \varOmega$, and the solution in the exterior domain $\varOmega _e$ to be $u_e(x_1,x_2)=\log \sqrt{(x_1-0.25)^2+(x_2-0.25)^2}$. We choose the jumping diffusion coefficient as $\alpha =0.42$ for $x_2 < 0.25$ and 10 for $x_2 \ge 0.25$, the convection field $\mathbf {b}=(1000x_1,0)^T$ and the reaction coefficient $c=0$. Since this is a convection dominated problem we will use the full upwind stabilization. The right-hand side f and the jumps are calculated by means of the analytical solution.

Table 1 Errors for different refinement levels k for both coupling systems of the first example

Fig. 1

The effectivity index $\eta /E_h$ for the two coupling methods for the first example

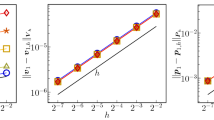
Table 1 shows the contributions to the error in the energy norm (9) of both adaptive couplings. Note that in the non-symmetric case we compute $\xi _h$ by $u_h|_{\varGamma }-u_0$ which is motivated by (1d). It can be observed that the error for the three-field coupling is slightly better (less elements but smaller errors). In Fig. 1 we show the effectivity index $\eta /E_h$ for $\mathbf {b}=\{(10x_1,0)^T;(100x_1,0)^T;(1000x_1,0)^T;(10000x_1,0)^T\}$. In both cases we observe the dependency on the local Péclet number, i.e., once we have resolved the shock region, the effectivity index convergences as well.

4.2 A More Practical Example

For the second example we do not know an analytical solution of (1). Additionally, we replace the radiation condition (1c) by $u_e(x)=a_\infty +\mathscr {O}(1/|x|)$ for $|x|\rightarrow \infty$. Thus we have to assume the scaling condition $\langle \partial u_e/\partial \mathbf {n},1\rangle _{\varGamma }=0$; see [2] and have to modify our discretization. The domain will be the classical L-shaped domain $\varOmega = (-1/4, 1/4)^2 \setminus [0, 1/4]\times [-1/4,0]$. We fix the piecewise constant diffusion coefficient $\alpha$ to 1 for $x_1 > 0$, 0.1 for $x_2\le 0$ and 0.5 else, $\mathbf {b}=(1500,1000)^T$, and $c=0.01$. The right-hand side will be $f(x_1,x_2)=5$ for $0.2\le x_1\le -0.1$, $-0.2\le x_2\le -0.05$ and 0 else and the jumps $t_0$ and $u_0$ are set to zero. This problem is again convection dominated, therefore, we use the full upwind stabilization. In Fig. 2 two adaptively generated meshes and contour lines are plotted to show the similarities between the two coupling approaches. Both meshes refine along the steepest parts of the solution, but they localize at slightly different areas. To generate the contour lines we calculate the values in $\varOmega _e$ from the Cauchy data $\xi _h$ and $\phi _h$ and the representation formula; see [1, 3]. Therefore, the contour lines show also the flow into the unbounded domain and show the difference in the accuracy of the approximation of the exterior solution.

Fig. 2

Adaptively generated mesh and contour lines for the non-symmetric FVM-BEM (left) and three-field FVM-BEM (right) for the second example

5 Conclusions

We presented the adaptive non-symmetric and the adaptive three-field FVM-BEM coupling. For both methods we established an error estimator which is reliable and efficient. In contrast to the three-field coupling the upper bound for the non-symmetric coupling imposes a lower bound on the smallest eigenvalue of the diffusion matrix which seems to be only a theoretical constraint. The effectivity index for both methods is semi-robust against variation of the model data. The three-field coupling leads to slightly better results than the non-symmetric coupling with respect to the same number of elements. However, the three-field coupling is computationally more expensive since it approximates the exterior trace directly. On the other hand the input data does not appear in an integral operator.