5.1 Definition of the DMDGP

We know that to ensure the finiteness of the solution set of the DGP, we can impose an order on the vertices of the associated graph. If such an order exists, it is not hard to find it in the DGP graph.

The DDGP3 assumes that, for all v i , i = 4, …, n, there exist (at least) three previous vertices a i , b i , c i with {{a i , v i }, {b i , v i }, {c i , v i }} ⊂ E, such that

$$\displaystyle{ d_{a_{i}b_{i}} + d_{b_{i}c_{i}} > d_{a_{i}c_{i}}. }$$
(5.1)

Depending on the DDGP3 instance, some distances between the vertices a i , b i , c i may be lacking, which may imply no solution in \(\mathbb{R}^{3}\) for the quadratic system

$$\displaystyle\begin{array}{rcl} \Vert x_{v_{i}} - x_{a_{i}}\Vert ^{2}& =& d_{ a_{i}v_{i}}^{2}, {}\\ \Vert x_{v_{i}} - x_{b_{i}}\Vert ^{2}& =& d_{ b_{i}v_{i}}^{2}, {}\\ \Vert x_{v_{i}} - x_{c_{i}}\Vert ^{2}& =& d_{ c_{i}v_{i}}^{2}. {}\\ \end{array}$$

A way to avoid this mishap is to require that, for all v i , i = 4, …, n, the distances between the vertices a i , b i , c i are known (note that this is not a requirement in the Definition of the DDGP3). Additionally, we may require that the vertices a i , b i , c i are the immediate predecessors to v i , which occurs in many applications [57].

Exercise 5.1

Geometrically, what does it mean for the quadratic system above to have no solution?

Exercise 5.2

If the vertices a i , b i , c i compose a clique, can we ensure that the related triangle inequality is strictly satisfied?

We are now interested in finding a vertex order in which the vertices used in the construction of each quadratic system compose a clique and are the immediate predecessors to the vertex whose coordinates we wish to calculate. Considering the same DGP instance as in Sect. 4.1, does there exist an order with these properties? Let us study this question before proceeding.

Let us return to that problem: a DGP with K = 3, where the associated graph is G = (V, E), with vertices V = {p, q, r, s, t, u, v} and edges

$$\displaystyle\begin{array}{rcl} E& & =\{\{ p,q\},\{p,r\},\{p,s\},\{p,u\},\{p,v\}, {}\\ & & \{q,r\},\{q,s\},\{q,t\},\{q,u\},\{q,v\}, {}\\ & & \{r,s\},\{r,t\},\{r,v\}, {}\\ & & \{s,t\},\{s,v\}, {}\\ & & \{t,u\},\{t,v\}, {}\\ & & \{v,u\}\}. {}\\ \end{array}$$

Consider a new ordering given by

$$\displaystyle{V =\{ p,u,v,q,t,r,s\}.}$$

We use the following notation in order to facilitate our analysis: p = u 1, u = u 2, v = u 3, q = u 4, t = u 5, r = u 6, and s = u 7 (u i is used instead of v i in order to emphasize that we are using a different order from the previous one). We can verify that this order has the desired properties, because in addition to the valid realization for {u 1, u 2, u 3}, we also have the following cliques:

$$\displaystyle\begin{array}{rcl} \{u_{1},u_{2},u_{3},u_{4}\},& & {}\\ \{u_{2},u_{3},u_{4},u_{5}\},& & {}\\ \{u_{3},u_{4},u_{5},u_{6}\},& & {}\\ \{u_{4},u_{5},u_{6},u_{7}\}.& & {}\\ \end{array}$$

To better follow the BP algorithm, we note that

$$\displaystyle\begin{array}{rcl} \{\{u_{1},u_{4}\},\{u_{2},u_{4}\},\{u_{3},u_{4}\}\}& \subset & E, {}\\ \{\{u_{2},u_{5}\},\{u_{3},u_{5}\},\{u_{4},u_{5}\}\}& \subset & E, {}\\ \{\{u_{1},u_{6}\},\{u_{3},u_{6}\},\{u_{4},u_{6}\},\{u_{5},u_{6}\}\}& \subset & E, {}\\ \{\{u_{1},u_{7}\},\{u_{3},u_{7}\},\{u_{4},u_{7}\},\{u_{5},u_{7}\},\{u_{6},u_{7}\}\}& \subset & E. {}\\ \end{array}$$

To obtain the coordinates of u 4, we consider the following quadratic system, with \(x_{u_{4}} \in \mathbb{R}^{3}\) as the only variable:

$$\displaystyle\begin{array}{rcl} \Vert x_{u_{4}} - x_{u_{1}}\Vert ^{2}& =& d_{ u_{1}u_{4}}^{2}, {}\\ \Vert x_{u_{4}} - x_{u_{2}}\Vert ^{2}& =& d_{ u_{2}u_{4}}^{2}, {}\\ \Vert x_{u_{4}} - x_{u_{3}}\Vert ^{2}& =& d_{ u_{3}u_{4}}^{2}. {}\\ \end{array}$$

We choose one of the two possible values for the coordinates of u 4, let us say \(x_{u_{4}}^{0}\), and we obtain the following quadratic system in order to find the coordinates of u 5,

$$\displaystyle\begin{array}{rcl} \Vert x_{u_{5}} - x_{u_{2}}\Vert ^{2}& =& d_{ u_{2}u_{5}}^{2}, {}\\ \Vert x_{u_{5}} - x_{u_{3}}\Vert ^{2}& =& d_{ u_{3}u_{5}}^{2}, {}\\ \Vert x_{u_{5}} - x_{u_{4}}^{0}\Vert ^{2}& =& d_{ u_{4}u_{5}}^{2}. {}\\ \end{array}$$

Again, we choose one of the two possible values for the coordinates of u 5, let us say \(x_{u_{5}}^{0}\), and we obtain a new quadratic system,

$$\displaystyle\begin{array}{rcl} \Vert x_{u_{6}} - x_{u_{3}}\Vert ^{2}& =& d_{ u_{3}u_{6}}^{2}, {}\\ \Vert x_{u_{6}} - x_{u_{4}}^{0}\Vert ^{2}& =& d_{ u_{4}u_{6}}^{2}, {}\\ \Vert x_{u_{6}} - x_{u_{5}}^{0}\Vert ^{2}& =& d_{ u_{5}u_{6}}^{2}. {}\\ \end{array}$$

We also have {u 1, u 6} ∈ E, that we can use to check which one of the possible coordinates obtained for \(u_{6},\ x_{u_{6}}^{0}\mbox{ and }x_{u_{6}}^{1}\), is feasible:

$$\displaystyle{\Vert x_{u_{6}}^{0} - x_{ u_{1}}\Vert = d_{u_{1}u_{6}}\quad \text{or}\quad \Vert x_{u_{6}}^{1} - x_{ u_{1}}\Vert = d_{u_{1}u_{6}}?}$$

Maybe none of the equations is satisfied, implying that we made a wrong choice for u 5. Let us suppose that it is the case. We need to return and recompute the coordinates using \(x_{u_{5}}^{1}\). The new quadratic system is

$$\displaystyle\begin{array}{rcl} \Vert x_{u_{6}} - x_{u_{3}}\Vert ^{2}& =& d_{ u_{3}u_{6}}^{2}, {}\\ \Vert x_{u_{6}} - x_{u_{4}}^{0}\Vert ^{2}& =& d_{ u_{4}u_{6}}^{2}, {}\\ \Vert x_{u_{6}} - x_{u_{5}}^{1}\Vert ^{2}& =& d_{ u_{5}u_{6}}^{2}. {}\\ \end{array}$$

Again, by using {u 1, u 6} ∈ E, we check each of the new possible positions obtained for \(u_{6}\ (y_{u_{6}}^{0}\mbox{ and }y_{u_{6}}^{1})\):

$$\displaystyle{\Vert y_{u_{6}}^{0} - x_{ u_{1}}\Vert = d_{u_{1}u_{6}}\quad \mbox{ or }\quad \Vert y_{u_{6}}^{1} - x_{ u_{1}}\Vert = d_{u_{1}u_{6}}?}$$

Supposing that the points \(\{x_{u_{1}},x_{u_{3}},x_{u_{4}}^{0},x_{u_{5}}^{1}\}\) are not coplanar, only one of these equations will be satisfied. Let us suppose that it is the first. Then, we discard \(y_{u_{6}}^{1}\) and we consider \(y_{u_{6}}^{0}\). The new quadratic system is

$$\displaystyle\begin{array}{rcl} \Vert x_{u_{7}} - x_{u_{4}}^{0}\Vert ^{2}& =& d_{ u_{4}u_{7}}^{2}, {}\\ \Vert x_{u_{7}} - x_{u_{5}}^{1}\Vert ^{2}& =& d_{ u_{5}u_{7}}^{2}, {}\\ \Vert x_{u_{7}} - y_{u_{6}}^{0}\Vert ^{2}& =& d_{ u_{6}u_{7}}^{2}. {}\\ \end{array}$$

By using {u 1, u 7} ∈ E and {u 3, u 7} ∈ E to check each of the new possible positions obtained for \(u_{7}\ (x_{u_{7}}^{0}\mbox{ and }x_{u_{7}}^{1})\), we have:

$$\displaystyle{\Vert x_{u_{7}}^{0} - x_{ u_{1}}\Vert = d_{u_{1}u_{7}}\quad \mbox{ or }\quad \Vert x_{u_{7}}^{1} - x_{ u_{1}}\Vert = d_{u_{1}u_{7}}}$$

and

$$\displaystyle{\Vert x_{u_{7}}^{0} - x_{ u_{3}}\Vert = d_{u_{3}u_{7}}\quad \mbox{ or }\quad \Vert x_{u_{7}}^{1} - x_{ u_{3}}\Vert = d_{u_{3}u_{7}}.}$$

Supposing that \(x_{u_{7}}^{1}\) is selected, we therefore obtain the solution to our problem as

$$\displaystyle{x_{u_{1}},x_{u_{2}},x_{u_{3}},x_{u_{4}}^{0},x_{ u_{5}}^{1},y_{ u_{6}}^{0},x_{ u_{7}}^{1}.}$$

Until this moment, it was not possible to see any advantage in this new order, besides the fact that it ensures that the quadratic systems have solutions. However, with the cliques {v i−3, v i−2, v i−1, v i }, for all i = 4, …, n, we can replace the solution of the quadratic systems by something numerically simpler and more stable. Before proceeding with explaining how to do this, we will formalize the definition of the new problem: the Discretizable Molecular Distance Geometry Problem (DMDGP).

Definition 5.1 (DMDGP)

Given a graph G = (V, E, d) of a DGP with K = 3 and an order on the vertices V, denoted by v 1, …, v n , such that

  • there is a valid realization for v 1, v 2, v 3,

  • for all v i , i = 4, …, n, there are (at least) three immediately previous vertices v i−3, v i−2, v i−1, where {v i−3, v i−2, v i−1, v i } is a clique, and

    $$\displaystyle{d_{v_{i-3}v_{i-2}} + d_{v_{i-2}v_{i-1}} > d_{v_{i-3}v_{i-1}},}$$

    find a function \(x: V \rightarrow \mathbb{R}^{3}\) such that

    $$\displaystyle{\forall \{v_{i},v_{j}\} \in E,\;\Vert x_{v_{i}} - x_{v_{j}}\Vert = d_{v_{i}v_{j}}.}$$

5.2 Complexity of the DMDGP

The existence of the cliques {v i−3, v i−2, v i−1, v i }, for all i = 4, …, n, provides us more information about the vertex order of the associated DGP graph. By using the distance information of the cliques {v i−3, v i−2, v i−1, v i }, we are able to obtain “almost” all of the following values:

  • d 1,2, …, d n−1, n : distances associated with the consecutive vertices,

  • θ 1,3, …, θ n−2, n : planar angles associated with three consecutive vertices,

  • ω 1,4, …, ω n−3, n : torsion angles associated with four consecutive vertices.

Exercise 5.3

What is the reason of the “almost” above?

Recall that the torsion angle ω i−3, i is the angle between the normal vectors associated with the planes determined by the vertices v i−3, v i−2, v i−1 and v i−2, v i−1, v i , respectively. The values d 1,2, …, d n−1, n are, obviously, obtained from the definition of the DMDGP, and the values θ 1,3, …, θ n−2, n are obtained by the law of cosines. However, from the DMDGP hypothesis, we can obtain only the values of the cosines of the torsion angles, given by (i = 4, …, n) [44, 49]:

$$\displaystyle{\cos \left (\omega _{i-3,i}\right ) = \frac{2d_{i-2,i-1}^{2}(d_{i-3,i-2}^{2} + d_{i-2,i}^{2} - d_{i-3,i}^{2}) - (d_{i-3,i-2,i-1})(d_{i-2,i-1,i})} {\sqrt{4d_{i-3,i-2 }^{2 }d_{i-2,i-1 }^{2 } - (d_{i-3,i-2,i-1 }^{2 })}\sqrt{4d_{i-2,i-1 }^{2 }d_{i-2,i }^{2 } - (d_{i-2,i-1,i }^{2 })}},}$$

where

$$\displaystyle\begin{array}{rcl} d_{i-3,i-2,i-1} = d_{i-3,i-2}^{2} + d_{ i-2,i-1}^{2} - d_{ i-3,i-1}^{2},& & {}\\ d_{i-2,i-1,i} = d_{i-2,i-1}^{2} + d_{ i-2,i}^{2} - d_{ i-1,i}^{2}.& & {}\\ \end{array}$$

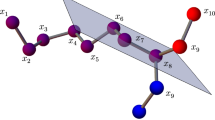
Actually, with the ordering structure of the DMDGP, we can imagine that we have molecular structures (Fig. 5.1), which explains the use of the extra term “molecular” to describe this new class of problems.

Fig. 5.1
figure 1

DMDGP instance as a molecule

Full size image

Exercise 5.4

What is the distance that appears only one time in the formula above for cos(ω i−3, i )? Why is it “different” from the other distances?

Remember that to define a three dimensional structure of a molecule, we can use the internal coordinates, given by the values d 1,2, …, d n−1, n , θ 1,3, …, θ n−2, n , and ω 1,4, …, ω n−3, n . However, as we mentioned above, in the DMDGP, we just have cos(ω i−3, i ),  i = 4, …, n, which generates two possible values for each torsion angle, since ω i−3, i ∈ [0, 2π]. This implies that we do not need to solve anymore quadratic systems! Moreover, the two possibilities for each torsion angle can be found by using the distances related to the cliques {v i−3, v i−2, v i−1, v i }. In order to prune using the given extra distances, we use the matrices given in Sect. 2.4 to obtain the Cartesian coordinates of the two possible solutions for each vertex v i , where we have already obtained the coordinates of v i−3, v i−2, v i−1, and then we just compare the distances we calculate with the given distances.

A question remains: “What is the computational cost in finding the DMDGP order?” This is different than the polynomial cost of obtaining the DDGP3 order. In fact, finding a DMDGP order may be difficult because it is an NP-hard problem [12]. It is the cost we pay for the new information. We escaped solving quadratic systems, but we exponentially increased the cost of finding a DGP order. However, depending on the application, that order can be obtained using the characteristics of the particular problem. It is what happens, for example, in problems related to 3D protein structures [48] (see Chap. 6).

Exercise 5.5

Why is there a “change of signs” in the formulas d i−3, i−2, i−1 = d i−3, i−2 2 + d i−2, i−1 2 − d i−3, i−1 2 and d i−2, i−1, i = d i−2, i−1 2 + d i−2, i 2 − d i−1, i 2 above?

Exercise 5.6

Derive the formula for cos(ω i−3, i ).

5.3 DMDGP Symmetry

We saw that the DMDGP order allows us to view the problem as a molecule with a finite possible configurations, and by using the internal coordinates and the distance information of the cliques {v i−3, v i−2, v i−1, v i }, i = 4, …, n, we can also find the two possible values for all torsion angles ω i−3, i . There exists another interesting property related to the symmetry of the DMDGP solutions.

In our example problem from Sect. 5.1, we realized that the two positions for \(v_{4}\ (x_{v_{4}}^{0},x_{v_{4}}^{1})\) can be considered since there are no extra edges which can invalidate one of them. This implies that, for any solution found in the left subtree, having the node \(x_{v_{4}}^{0}\) as its root, there exists another one that is symmetric to the plane defined by \(x_{v_{1}},x_{v_{2}},x_{v_{3}}\) [47]. Note the relation that exists among the finiteness of the solution set, the strict triangle inequality, and the symmetries.

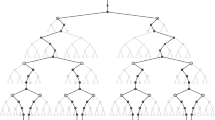
An immediate consequence of this fact is that the solution set has an even number of solutions. However, since the first computational results obtained for the DMDGP [53], we empirically observed that the number of solutions was always a power of two. Only recently, by using group theory, a mathematical proof of this fact was presented [58].

We illustrate the importance of this result by considering the following set, given a DMDGP graph G = (V, E, d) with the vertex order v 1, …, v n :

$$\displaystyle{S =\{ v \in V: \nexists \{u,w\} \in E\;\mbox{ such that }u + 3 < v \leq w\}.}$$

In order to simplify the notation, we denote by u + 3 the third vertex after u, and by u − 3 the third vertex before u. Initially, let us try to identify the elements in S. The first candidate is v 4, which is in S if there is no edge {u, w} ∈ E such that u + 3 < v 4 ≤ w. If there is some u ∈ V satisfying this property, we will have u < v 4 − 3. However, this is not possible because v 4 − 3 = v 1, which is the first element of V. That is, v 4 ∈ S for any DMDGP.

Let us see what happens with v 5 (we are supposing that the DMDGP has a solution):

  • Supposing that there exists {u, v 5} ∈ E, such that u < v 5 − 3, we have that v 5 ∉ S and {v 1, v 5} ∈ E, which implies that only one of the possibilities for v 5 is feasible: either \(x_{v_{5}}^{0}\) or \(x_{v_{5}}^{1}\).

  • Supposing that there is no {u, v 5} ∈ E, for u < v 5 − 3, we need to consider the two following cases:

    • If there is no {u, w} ∈ E, such that u + 3 < v 5 < w, then v 5 ∈ S.

    • If there exits {u, w} ∈ E, such that u + 3 < v 5 < w, then v 5 ∉ S.

Since the procedure above can be applied to all elements of V, we can obtain the set S by using just the DMDGP data, even before we apply BP to solve the problem. But what is the importance of the set S?

The set S identifies other symmetric planes for the DMDGP, in addition to the plane associated with the vertices {v 1, v 2, v 3}, defined for all DMDGP instances [58].

For example, if v 5 ∈ S, this implies that the two positions for v 5 are feasible, \(x_{v_{5}}^{0}\) and \(x_{v_{5}}^{1}\). At the same time, \(x_{v_{5}}^{0}\) and \(x_{v_{5}}^{1}\) are part of two different DMDGP solutions [66].

Considering the example problem of Sect. 5.1 and using the notation v i , we have:

$$\displaystyle\begin{array}{rcl} V & =& \{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}, {}\\ E& =& \{\{v_{1},v_{2}\},\{v_{1},v_{3}\},\{v_{1},v_{4}\},\{v_{1},v_{6}\},\{v_{1},v_{7}\}, {}\\ & & \{v_{2},v_{3}\},\{v_{2},v_{4}\},\{v_{2},v_{5}\}, {}\\ & & \{v_{3},v_{4}\},\{v_{3},v_{5}\},\{v_{3},v_{6}\},\{v_{3},v_{7}\}, {}\\ & & \{v_{4},v_{5}\},\{v_{4},v_{6}\},\{v_{4},v_{7}\}, {}\\ & & \{v_{5},v_{6}\},\{v_{5},v_{7}\},\{v_{6},v_{7}\}\}. {}\\ \end{array}$$

It is easy to see that S = {v 4}, since {v 1, v 7} ∈ E. That is, there exists only one symmetric plane (defined by \(x_{v_{1}},x_{v_{2}},x_{v_{3}}\)), which implies that we have only two solutions. As we have already obtained a solution, given by

$$\displaystyle{x_{v_{1}},x_{v_{2}},x_{v_{3}},x_{v_{4}}^{0},x_{ v_{5}}^{1},y_{ v_{6}}^{0},x_{ v_{7}}^{1},}$$

we have another one symmetric to the plane defined by \(\{x_{v_{1}},x_{v_{2}},x_{v_{3}}\}\) (see Fig. 5.2).

Fig. 5.2
figure 2

Solution obtained by BP algorithm

Full size image

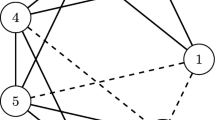
Suppose now that we have a little different DMDGP instance, given by

$$\displaystyle\begin{array}{rcl} V & =& \{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}, {}\\ E& =& \{\{v_{1},v_{2}\},\{v_{1},v_{3}\},\{v_{1},v_{4}\},\{v_{1},v_{6}\}, {}\\ & & \{v_{2},v_{3}\},\{v_{2},v_{4}\},\{v_{2},v_{5}\}, {}\\ & & \{v_{3},v_{4}\},\{v_{3},v_{5}\},\{v_{3},v_{6}\}, {}\\ & & \{v_{4},v_{5}\},\{v_{4},v_{6}\},\{v_{4},v_{7}\}, {}\\ & & \{v_{5},v_{6}\},\{v_{5},v_{7}\},\{v_{6},v_{7}\}\}. {}\\ \end{array}$$

Performing the calculations, we obtain

$$\displaystyle{S =\{ v_{4},v_{7}\},}$$

implying that we have another symmetric plane defined by {v 4, v 5, v 6} (see Fig. 5.3).

Fig. 5.3
figure 3

Symmetric solutions

Full size image

To simplify the notation, let us represent the first solution by a sequence of zeros and ones and denote the first tree positions by 0, 0, 0:

$$\displaystyle{s_{1} = (0,0,0,0,1,0,1).}$$

Since we know that we have a symmetry at vertex v 7, another solution is given by

$$\displaystyle{s_{2} = (0,0,0,0,1,0,0).}$$

Now, by considering the symmetry at vertex v 4, we obtain other two solutions given by

$$\displaystyle{s_{3} = (0,0,0,1,0,1,0)}$$

and

$$\displaystyle{s_{4} = (0,0,0,1,0,1,1).}$$

We have two important conclusions arising from these observations [1, 55, 66]:

  • We know, a priori, using only the data given by any DMDGP, that the cardinality of the solution set is 2| S |.

  • In order to find all the solutions of a DMDGP, it is enough to apply the BP algorithm to find only one solution, since all the others can be obtained using the DMDGP symmetries.

Exercise 5.7

What is the computational importance of knowing a priori the number of DMDGP solutions?

Exercise 5.8

Since the computational cost associated with the use of symmetries to obtain other DMDGP solutions is polynomial, what is the implication for the complexity of DMDGP?