3.1 Introduction

Ultrashort pulsed laser ablation has become a powerful technology in micro machining of transparent materials for more than a decade, such as waveguide writing [1], drilling [2, 3] and cutting [4]. Nonlinear absorption of laser energy by multi-photon ionisation and cascade ionisation allows localised material removal with high accuracy in the micrometer scale. As the time of laser energy deposition into the electron system of materials is much shorter than that of material removal and again much shorter than equilibrium heating of the atomic system, processing with ultrashort laser pulses has the potential to minimise destructive thermal and thermo-mechanical effects.

However, laser induced damage in the surrounding volume of the ablation front remains a relevant and intriguing issue in glass cutting with ultrashort laser pulses. Laser induced free electrons at the ablation threshold reach the critical electron density \(\rho_{crit}\). The energy stored in the electron plasma after thermal relaxation finally results in damage such as unwanted modifications of the electronic state, and also cracking if not removed together with the ablated material. This kind of damage is called electronic damage, because of residual refractive index modifications [5,6,7,8].

Thermal damage, however, is identified as happening in addition to electronic damage. This is a consequence of using highly productive high power lasers which allow for a high repetition rate of laser pulses, with a subsequent inherent risk of localised heat accumulation. A heat affected zone characterised by modifications of the atomic structure like softening and melting of the amorphous material is a result [9].

3.2 Phenomenology of Glass Processing with Ultrashort Laser Radiation

The numerous physical mechanisms involved in laser ablation of dielectrics have been widely investigated both experimentally and theoretically. In particular, investigations of laser-induced damage in bulk dielectrics used for laser fusion optics gives important insights [5, 7]. During the formation of bulk damage , the nonlinear effects of ionisation and propagation of radiation, such as the formation of filament s, are the two effects that appear to be most relevant for guiding the physical modelling of laser ablation . Laser damage , such as refractive index modification [5], molten regions [10] and micro-cracks [3] is crucial for the quality criteria of the processed glass product, such as the bending strength of the cut material. The laser-glass interaction with picosecond pulsed lasers therefore has to be investigated to control the evolving ablation front and avoid laser damage.

It is worth mentioning that in glass cutting with ultrashort pulsed laser radiation there are three observable quantities characteristic of the ablation mechanisms, which are useful in the identification of a reduced model. These characteristics are found to be

  1. 1.

    the rough shape of the ablation front: the shape of the ablation front shows a microscopically rough surface and the length scale fits the expected diffraction pattern present in the ablated region well. This diffraction pattern has a large Michelson contrast changing the laser intensity at the ablation front on a micrometer scale;

  2. 2.

    the saturation of the ablation rate after applying a specific number of single laser pulses [11]: the ablation rate turns out to be limited by a threshold value for the fluence related to a finite angle of incidence for the Poynting vector of the radiation incident at the ablation wall;

  3. 3.

    the different modification or damage patterns observed within the material volume emerging from the ablation front: there are at least 5 different damage patterns which can be related to their underlying nonlinear effects.

There are at least 5 different damage patterns related to different mechanisms, grouped into electronic damage and thermal damage :

  1. 1.

    Chipping of the glass at its non-irradiated rear side often happens previous to ablation at the irradiated front side and is often called rear side damage . Damage at the rear side is explained as a consequence of reflection of the radiation at the rear side raising the radiation intensities above the ablation threshold.

  2. 2.

    dense short spike s, which are needle-like or spike-shaped damage appearing along the full length of the ablation wall, see Figs. 3.2a, and 3.5a, b, e, f; they are related to diffraction and are also referred to as interference damage;

  3. 3.

    sparse long spikes , which are sparsely distributed over the length of the ablation wall and an order of magnitude longer than the dense short spikes, see Fig. 3.5b; they are related to (multiple) reflections [12] at the ablation wall and are prominent in the case of single pulse ablation along single tracks of the scanned laser beam axis;

  4. 4.

    effects normally referred to as filamentation damage emerging at the entrance edge of the ablation front having a length up to a few millimetres; see Fig. 3.2d. This kind of damage is understood as a focusing effect of the radiation, which is focussed at a spatially extended and curved entrance edge acting like a focusing lens. Filamentation damage is pronounced for single pulse ablation along multiple tracks of laterally shifted passes of the scanning laser beam axis.

  5. 5.

    Last not least thermal damage happens for large overlap of subsequent laser pulses or high repetition frequencies at larger averaged laser power.

Two kinds of electronic damage are observable in Fig. 3.4d. Filamentation damage is initiated at the entrance edge and subsequently propagates deeply into the material sometimes even penetrating the whole thickness of the glass sheet. Interference damage happens along the whole ablated wall and consists of needle-like modifications or cracks. Thermal damage is distinguished by its smooth shape as shown in Fig. 3.5c, d, g, h.

3.3 Modelling the Propagation of Radiation and the Dynamics of Electron Density

Several numerical models [11, 13, 14] of laser ablation with ultrashort pulses have been presented and the critical free-electron density for laser breakdown has been widely used as an ablation criterion. For laser ablation with a single pulse, the time-resolved ultrafast radiative transport equation (TE) is solved [13] to simulate the energy deposition and predict the crater shape. The TE model, however, cannot describe the diffraction and refraction of the following laser pulse induced by the ablated crater, and is thus limited to single-pulse ablation . To analyse multi-pulse ablation, Vázquez de Aldana et al. introduced a numerical simulation for the propagation of light within the ablation channel in dielectrics with femtosecond laser pulses based on the integration of the scalar wave equation. However, the underlying model is to be preferred when the laser pulse is shorter than 50 fs. Enormous computational power and time are required for longer pulses because a high resolution in space and time is required. Therefore, the time-resolved wave equation is not favourable for laser ablation with multiple picosecond pulses.

The study of Sun et al. [15] presents a numerical simulation , called GlassCut , focusing on both laser ablation and laser damage in transparent dielectrics with multiple picosecond laser pulses. The simulation code combines the numerical implementation of a beam propagation model (BPM ) and a model for the dynamics of the electron density generated by the radiation propagating into the initially transparent material. The beam propagation model is based on the paraxial Helmholtz equation, whereas the model for electron dynamics describes the nonlinear absorption of photons in dielectrics. Simulation runs show nearly quantitative agreement with experimental evidence concerning the evolution of the ablated shape and the morphology of the well-known 5 different kinds of modified and damaged regions induced by multiple incident laser pulses in the glass. The numerical simulation GlassCut describes the laser energy deposition in the sample by coupling of non-linear beam propagation (Beam Propagation Method BPM ) to a plasma model for the dynamics of the electron density. BPM is used to solve the paraxial Helmholtz equation. The plasma generation is described by a rate equation for the free-electron density. The shape of the ablated region and the damaged region are determined by tracking two related isolines for the spatial distribution of the free-electron density from the solution. The values of the two isolines for the electron density are \(\rho_{ablation} \,: = \,\rho_{crit}\) and \(\rho_{damage} \,: = \,\rho_{material}\) for the positions of the ablation front and the damage region, respectively.

The well-known critical electron density [16].

$$\rho_{crit} = \frac{{\omega^{2} \varepsilon_{0} m_{e} }}{{e^{2} }}$$

is nearly independent of the material and its composition, depending only slightly on the effective mass m e of the electronselectrons . Here ε 0 is the vacuum electrical permittivity and e is the electron charge. However, ablation of borosilicate glass sets in at an electron density \(\rho_{crit} = 4.2 \times 10^{21} \;{\text{cm}}^{ - 3}\) for radiation with wavelength \(\lambda = 1\) μm and is strongly dependent on the laser frequency equal to \(2\pi c\,/\,\lambda\). The electron density \(\rho_{damage} \,: = \,\rho_{material}\) is strongly material dependent and has to be measured by experiments for the material that is being processed.

3.4 Radiation Propagation Solved by BPM Methods

Suppose that the laser beam propagates into the glass sample in the z direction and the \(x - y\) plane is perpendicular to the z direction. The general ansatz for the electric field \(\overline{E} \left( {x,\,y,\,z} \right)\) is expressed as

$$\overline{E} \left( {x,y,z} \right) = E\left( {x,y,z} \right)\,\,{ \exp }\left( {in_{0} k_{0} z} \right),$$

where \(k_{0} = 2\pi \,/\,\lambda\) and n 0 are the wave number and index of refraction of the material, while E(x, y, z) is the envelope of the electric field. With the Slow Varying Envelope Approximation of the Helmholtz equation the ansatz yields

$$2ik_{0} \frac{\partial E}{\partial z} = -\Delta _{x,y} E - k_{0}^{2} (\varepsilon - 1)E$$

where the dielectric function ε of the material is given by

$$\varepsilon = 1 - \frac{{\rho_{b} e^{2} }}{{\varepsilon_{0} m_{e} }}\frac{{\omega^{2} - \omega_{0}^{2} - i\chi \omega }}{{\left( {\omega^{2} - \omega_{0}^{2} } \right)^{2} + \chi^{2} \omega^{2} }},\quad \chi = \chi_{max} \frac{{\rho_{max} }}{{\rho_{max} + \beta \rho_{crit} }}$$

Here ρ b is the bound electron density, ω 0 is the material resonance frequency. The damping constant χ at resonance equals the reciprocal of the electron relaxation time, which varies from 0.1 to 10 fs in transparent dielectrics [17].

The response of the material to the incident radiation is determined by the complex dielectric function \(\varepsilon\), where the real and imaginary parts represent refraction and loss terms, respectively. Thus, the diffraction and refraction of the electric field caused by the ablation front, its entrance edge acting like a slit provoking a diffraction pattern, and the laser-induced solid-state-plasma within the material volume are considered by the simulation.

3.5 The Dynamics of Electron Density Described by Rate Equations

In transparent dielectrics, the electrons in the valence band can be excited as free electrons by strong electric fields via multi-photon ionisation MPI . The intensity I of the electric field drives the temporal change of the free electrons density ρ and is described by the term for multi-photon ionisation, \(\sigma I^{k}\). The number k of photons necessary to overcome the band gap energy Δ is determined experimentally. The free electrons are then excited to even higher energy levels by single-photon absorption called inverse bremsstrahlung absorption. Reaching a typical energy \(E_{cas} = 1.5\Delta\) the electron has enough energy to ionise an additional bound electron and both electrons are once more excited by inverse bremsstrahlung absorption; this absorption mechanism is called cascade ionisation and is described by the rate Envelope Approximation \(a_{c} I\rho\). However, there are some losses for the free-electron density due to electron-hole recombination \(\eta_{rec} \rho^{2}\) and electron diffusion \(\eta_{diff} \rho\). On the picosecond scale, recombination dominates and diffusion can be ignored. As result, the temporal evolution of the free-electron density ρ is described by a rate equation of the generic form [16, 18, 19].

Fig. 3.1
figure 1

Photo-ionisation rate for the glass sample at 532 nm calculated from the complete Keldysh model (red solid line), with Keldysh’s approximation in the tunnelling ionisation limit (green dash-dotted line) and in the MPI limit (blue dotted line), and with Kennedy’s approximation of the Keldysh model in the MPI limit (black dashed line). Reproduced from [21] with the permission of The Optical Society

Full size image
$$\frac{d\rho }{dt} = \sigma I^{k} + \alpha_{c} I\rho - \eta_{rec} \rho^{2} .$$

It is worth mentioning that considering Keldysh’s theory of electronic ionisation [20], the competing tunnel ionisation takes place in the low frequency limit and can be neglected compared to the multi-photon ionisation at a photon energy of 1 eV which turns out to be the high frequency limit (Fig. 3.1). In more detail, the Keldysh parameter \(\gamma = \omega \left( {c\varepsilon_{0} n_{0} m\Delta /I} \right)^{1/2} /e\) is a quantitative measure for the ratio of multi-photon and tunnelling ionisation. Here m is the reduced mass of the electron and the hole \(m = m_{e} /2\) and c is the speed of light in a vacuum.

A typical laser intensity for ps-laser systems is up to 1013 Wcm−2 and the well-known Keldysh parameterg \(\gamma\) [20] is larger than 1.8. The MPI coefficient σ is therefore chosen in the Kennedy approximation [18] for multi-photon ionisation. When \(\gamma \, \ge \,1\), Kennedy’s approximation in the MPI limit is consistent with the complete Keldysh model so that the coefficient of the MPI rate reads

$$\sigma = \frac{2\omega }{9\pi }\left( {\frac{m\omega }{h\,/\,2\pi }} \right)^{3/2} \left( {\frac{{e^{2} }}{{16\omega^{2} c\varepsilon_{0} n_{0}\Delta }}} \right)^{k} \text{exp}\,(2k)\Phi \left[ {\left( {2k - 4\pi \frac{\Delta }{h\omega }} \right)^{1/2} } \right]$$

where Φ[.] denotes the Dawson probability integral.

Considering the cascade ionisation \(\alpha_{c} I\rho\) as already mentioned, the free electrons absorb energy from the electric field by inverse bremsstrahlung absorption after being generated. When the kinetic energy of the free electron in the conduction band accumulates the typical energy \(E_{cas} = 1.5\Delta\), it will shortly produce a new free electron while colliding with atoms or molecules. Neglecting the collisional losses and the excitation time of free electrons to gain the energy \(E_{cas}\) then the cascade ionisation coefficient α c [18] takes the form

$$\alpha_{c} = \frac{1}{{1 + \omega^{2} \tau^{2} }}\frac{{e^{2} \tau }}{{c\varepsilon_{0} n_{0} m_{e} E_{cas} }}$$

in the formula where \(\tau\) is the electron-electron collision time typically taking the value τ = 1 fs.

3.6 Properties of the Solution with Regard to Ablation and Damage

Heating by the electrons that constitutes energy deposition in the material, and heating of the atoms until material removal occurs are separated in time in ultrashort pulsed laser processing. The electric field excites the electrons to the conduction band by multi-photon ionisation followed by cascade ionisation. The free electron density goes up during the laser pulse until reaching the critical electron density ρ crit [16] that leads to strong absorption and almost no reflection, ultimately leading to breakdown. Laser ablation induced by electron energy transition to the atoms takes place after the laser pulse has passed. This ablation mechanism allows the use of the critical free-electron density ρ crit as the criterion ρ ablation  = ρ crit for ablation in the model. As result, in the model the material is removed in the region where the free-electron density exceeds the critical value ρ crit .

The material near the ablated crater wall is characterised by a free electron density ρ < ρ crit . Here the material is indeed not ablated but will be modified or damaged due to the energy released by high-density free electrons. Once more, a threshold value ρ damage for the free electron density can be identified. In the bulk of fused silica, the free-electron density corresponding to the damage threshold is close to ρ damage  = 1020 cm−3 [5, 6]. The damage patterns are formed along the interference patterns of the laser radiation propagating into the material and changing the optical properties. Within the zones where the electron density is above this threshold electron density ρ damage , modification and damage are observed. For ablating boroaluminosilicate glass the threshold electron density for laser damage is assumed to be of the same order of magnitude as that for fused silica. Thus, the damage threshold free-electron density ρ damage  = 0.025 ρ crit is nearly two orders of magnitude lower than the ablation threshold criterion ρ ablation  = ρ crit in the model.

First of all, comparison of the simulation results with experimental evidence successfully guides reduction of the complexity of the physical model successfully. Figure 3.2a, b show the cross-sections of the ablated craters and the damaged regions after 5 and 10 pulses in the experiment, which agree well with the numerical results shown in Fig. 3.2c, d. The experimental results show that the crater width after 10 pulses was slightly larger than that after 5 pulses, whereas it was constant in the numerical results. It is worth to mention, that forward propagation of the laser radiation is taken into account by the Beam Propagation Method BPM only, neglecting the propagation of the radiation backwards. The comparison with experiments supports the Slow Varying Envelope SVE approximation to the wave equation.

Fig. 3.2
figure 2

Cross-sections of the ablated craters and the damage regions after experiments: 5 pulses (a) and 10 pulses (b) and after the numerical work: 5 pulses (c) and 10 pulses (d). In c and d, the damage region is denoted by the red contour region where the electron density is larger than ρ damage  = 1020 cm−2. Reproduced from [21] with the permission of The Optical Society

Full size image

Figure 3.2a, b show a thin dark layer near the crater wall and some needle-like structures beneath the crater wall, namely the damage region. Due to the laser-induced free-electron density and its energy release, the refractive index of the sample was permanently changed and some other defects were generated, such as colour centres, influencing the interaction of the material with the next incident pulse. In the numerical simulation, using the damage criteria \(\rho_{ablation} > \rho \ge \rho_{damage}\), the damage regions shown in Fig. 3.2c, d are in nearly quantitative agreement with the experimental results.

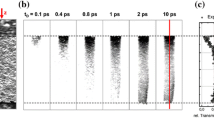
Estimates for the thickness of the damaged layer from Fig. 3.2 may give values that are too large owing to the thickness of the glass sample. As shown in Fig. 3.3e, a regular 2 μm thick layer of damage is generated near the crater surface after the first pulse. For subsequent pulses, refraction and diffraction on the crater wall play a significant role in the propagation of the electric field and drastically change the energy deposition in the material. As a result, the damaged regions become different after the first pulse, and several needle-like damaged regions in a distance of several microns were formed beneath the crater wall and surrounding the whole crater. In particular, two extremely long spike s of about 10 μm depth inside the sample body were generated by the crater edges after the second pulse, which can also be observed in the experimental results shown in Fig. 3.2a, c.

Fig. 3.3
figure 3

Numerical results for the cross-sections at different numbers of pulses for the intensity distributions in air (a) and in glass (b), the free-electron density (c) during the nth pulse, the ablated crater profile (d) and the damage region (e) after the nth pulse. The number of pulses n is shown in the lower left corner of each graph; the intensity in (a) is in 1016 W m−2 unit, in (b) is logarithmic in W m−2. Electron densities in (c) and (e) are logarithmic in cm−3. For each graph in (e), the damaged region is indicated by the red contour region where the electron density is greater than ρ damage  = 1020cm−2. All the graphs have the same horizontal scale as shown in (e). Reproduced from [21] with the permission of The Optical Society

Full size image

The laser pulse propagates into the target glass from above in the normal direction. Using numerical simulation, the ablation processes for 10 incident pulses were obtained. Figure 3.3a–e show the cross-sections for laser intensity in air (a), laser intensity in the glass (b), free-electron density (c), crater profile (d), and damage region (e), respectively. The characteristics of the ablated crater are the most intuitive and of primary interest in the laser ablation process. The profiles and the fine structure of the ablated craters are shown in Fig. 3.3d. The crater shape after the first pulse is nearly parabolic because of energy deposition through the initial planar interface and the Gaussian beam shape. This non-planar crater will reflect, refract and diffract the incident electric field when the second laser pulse arrives. The interference pattern of the laser field in the crater cavity, as shown in Fig. 3.3a, induces the fine structure of the crater wall. The crater structure becomes more complex and pronounced for subsequent laser pulses. The interference effect of the laser beam is therefore the main cause for the fine structure of the crater wall.

3.7 Electronic Damage Versus Thermal Damage

The nearly quantitative agreement of the morphology in the damage d region between experiments and simulation reveals that the damage near the ablated wall is strongly related to the evolving high electron density. It is remarkable that the additional effects of the numerous subsequent processes such as thermalisation of the electron energy and the thermomechanical response of the material finally leading to damage, only slightly change the results. However, additional thermal effects come into play for larger vales of the average power absorbed. With a higher repetition rate and increasing overlap of subsequent pulses the specific effects of ultrashort pulses change and become more similar to the appearance of long pulse or even continuous wave laser radiation. In order to verify the electronic nature of the damage mechanism and to distinguish it from thermally induced modification, the effect of heat accumulation on the damaged region was investigated experimentally by comparing different repetition rates and spatial overlaps of the adjacent pulses.

With increasing pulse number and corresponding depth of the groove the shape of the walls approaches an asymptotic shape; the inclination of the ablated wall is limited as seen in Fig. 3.4c. A pass of the laser beam along the contour to be cut, Fig. 3.4a, consists of single laser pulses with beam radius w 0 ablating the material while moving in the direction of the scan with a step size s between two pulses. A repetition rate f and speed of scanning v s result in an overlap O of subsequent pulses, Fig. 3.4b. As sketched in Fig. 3.4c, the ablated depth of the groove increases during every subsequent pass of the single pulses until the ablation rate saturates and no more material is ablated.

Fig. 3.4
figure 4

Cutting glass samples (a) is carried out by shifting the scanned track perpendicular to the scan direction in order to increase the overall cut depth. Preparation of cross-sections (d) clearly indicates the saturation of the reachable cut depth. Heat accumulation effects are investigated by ablating single tracks without shifting the scanned track. Ablation with pulses with an overlap O generate a single track (b) where the laser beam is scanned multiple times along the single track. The number of scans along a single track is called the number of passes (c). Reproduced from [15] with permission of ELSEVIER LTD in the format Book via Copyright Clearance Center

Full size image

The scaled overlap O s is defined by

$$O_{s} = \left( {1 - \frac{s}{{2w_{0} }}} \right)\quad {\text{for}}\quad 0 < s \le 2w_{0} ,\quad s = \frac{{v_{s} }}{f}$$

The cross-sections of the ablated channels obtained at different spatial overlaps and number of passes are shown in Fig. 3.5, where the pulse energy is 40 μJ (50 μJ for 0.54 overlap) and the repetition rate is 400 kHz. In the glass volume near the ablated wall, two groups of damage morphology can be clearly distinguished, namely damage induced by the excited free electrons (spike shaped) and by heat accumulation (smooth shape). Spike shaped damage happens at lower spatial overlap (O s  = 0,0.54) and smooth shapes are observed at a higher spatial overlap (O S  = 0.85, 0.90).

Fig. 3.5
figure 5

Influence of overlap O s (a)–(d) and repetition rate (e)–(h) on damage morphology while scanning 5 and 10 passes, respectively. Pulse energy 50 µJ at overlap O s  = 0.54 and 40 µJ at overlap 0.0, 0.85, 0.9. Overlap Os is a 0.0, b 0.54, c 0.85, d 0.9. Results for different repetition rates f of 10, 100 and 400 kHz are shown: e 0.54, 10 kHz; f 0.54, 400 kHz; g 0.85, 40 μJ, 100 kHz; d 0.85, 40 μJ, 400 kHz. Reproduced from [15] with permission of ELSEVIER LTD. in the format Book via Copyright Clearance Center

Full size image

The simulated damage morphology with a pulse energy of 40 μJ, spatial overlap of O s  = 0 and pass number of 10 is shown in Fig. 3.2d. The simulated ablated shape and the damage morphology agree well with the experiments. The temporal evolution of the simulated damage morphology shows that the two long spikes starting at the entrance edge, Fig. 3.5e, are partly obscured by the numerous additional effects of the subsequent pulses and thus cannot be clearly distinguished after 5 pulses, which is consistent with Fig. 3.5a and e. We found that all the three types of spike shaped damage are well reproduced by the corresponding free electron density and therefore described as electronic damage .

Simulation of the time dependent temperature near the entrance edge at a sampling point (shown in Fig. 3.5e–h by red dots) and comparing the maximum temperature reached with the softening temperature \(T_{s} = 971\,^{ \circ } {\text{C}}\) [22] of the glass reveals the conditions for the transition from electronic to thermal damage (Fig. 3.6). Material heated above the softening temperature responds with residual thermal modification visible as darkening as shown in a pronounced manner in Fig. 3.5c, d, g, h.

Fig. 3.6
figure 6

Simulation of heat accumulation of the glass sample near the entrance edge at the sampling point (x, y, z) = (6.5, 0.0, 5.0) μm, (indicated in Fig. 3.5e–h as dots) during one pass of ablation at different repetition rates \(f \in \left\{ {10,100,400} \right\}\,{\text{kHz}}\): a \(O_{s} = 0.54,50\,\) μJ, b \(O_{s} = 0.85,40\,\) μJ. The laser passed after irradiating the sample with 2 pulses (a) and 7 pulses (b), respectively. The softening temperature of the glass is \(T_{s} = 971\,^{ \circ } {\text{C}}\) is indicated by the dotted lines. Reproduced from [15] with permission of ELSEVIER LTD in the format Book via Copyright Clearance Center

Full size image

With the scanning speed reduced and therefore with reduced step size s of the beam axis between adjacent pulses, the step size s = 6 μm approximately equals the beam radius w 0 = 6.5 μm and the spatial overlap is O s  = 0.54. There are about two pulses hitting each position on the surface; see Fig. 3.6a.

The initial heated volume and the thermal diffusion rate can be determined by time-resolved observation of the thermal diffusion. Applying the transient lens method to irradiation of borosilicate glass with 200 fs pulses Sakakura et al. measured the heated length \(d_{\kappa } \, \approx \,5\,\) μm and the thermal diffusivity \(\kappa \, \approx \,4.6 \times 10^{ - 7} \,{\text{m}}^{2} {\text{s}}^{ - 1}\). As a result, the typical thermal relaxation time \(\tau_{\kappa } = d_{k}^{2} /\kappa = 10\,\) μs is in the range of a tenth of a microseconds [23]. At a repetition rate of f = 400 kHz, the time Δτ = 2.5 μs between two subsequent laser pulses is much larger than the typical relaxation time τ ep  = 100 ps [24] of the free-electron energy to the phonons in borosilicate glass but shorter than the typical thermal relaxation time τ κ = 10 μs. Thus although heat accumulation is expected to happen for all the simulated repetition rates 10, 100, 400 kHz it is worth mentioning that due to the small overlap O s  = 0.54 of the laser spot for 50 mJ pulses, the temperature rise remains fairly moderate. In particular, the temperature remains below the softening temperature \(T_{s} = 971\,^{ \circ } {\text{C}}\) of the material and no darkening of the glass occurs. The cross-sections of the ablated channels and damaged regions after 5 and 10 passes of ablation with 50 μJ laser pulses are shown in Fig. 3.5b, f, respectively. The shape of the ablated wall as well as the damage morphology are both similar to those at the spatial overlap of O s  = 0, which indicates that electronic damage is still dominant in the damaged regions and thermal damage is not pronounced because of the limited pulse number irradiating the same material position.

Thus although heat accumulation prevails over free electron energy release at an overlap of \(O_{s} = 0.54\) the softening temperature is not reached and darkening is absent.

Increase the spatial overlap \(O_{s} = 0.85\), as shown in Fig. 3.6b, with the pulse number increased to 7 pulses at every position of the sample. At a low repetition rate of 10 kHz the situation is qualitatively unchanged and the peak value remains smaller than the softening temperature T s . However, at higher repetition rates greater than 100 kHz heat accumulation becomes dominant; see Fig. 3.6b, where darkening happens and also see Fig. 3.5c, d, g, h.

3.8 Glass Cutting by Direct Ablation or Filamentation?

A substantial time ago researchers predicted self-focusing of light in dielectric media [25, 26]. In 1964 Hercher [27] first demonstrated the Kerr effect causing a change of the index of refraction in the medium, resulting in self-focusing of the beam accompanied by modification damage within an extremely narrow and elongated tubular region. For a few years now various industries have started to become interested in the self-focusing effect and are investigating the potential for low damage cutting of thin glass sheets for display applications, for example (Fig. 3.7).

Fig. 3.7
figure 7

The typical appearance of a Townes-like beam (white insert) referred to as a filament, which consists of a built up length followed by a narrow, slightly oscillating beam until the intensity of radiation due to absorption becomes too small to establish an equilibrium between Kerr-focusing and plasma defocusing. The figure shows a simulation of self-focusing radiation for different focal positions of a Gaussian beam irradiated onto glass from the left

Full size image

Self-focusing happens due to the fact that the real part of the index of refraction n = n 0 + n2 I + n 4 I 2 in nonlinear optical media depends additionally on the linear contribution n 0 as well as the second n 2 and fourth n 4 power of the electric field E. As is already well-known, plasma generation in dielectrics needs strong absorption to establish a high electron density and consequently leads to modification or even damage and cracking after thermal relaxation of the electron energy. However, the potential of glass cutting as well as its challenge is to tailor a suitable combination of material composition as well as laser radiation, which will enable stable propagation of an optical and electronic channel; both might be called filament s.

Introducing the vacuum wave number \(\omega /c\) and the number k of photons to overcome the band gap energy (multi-photon ionisation ), the corresponding wave equation reads

$$i\frac{\partial }{\partial z}E + \frac{1}{2}\left( {\frac{{\partial^{2} E}}{{\partial x^{2} }} + \frac{{\partial^{2} E}}{{\partial y^{2} }}} \right) + \frac{\omega }{c}n_{2} \left| E \right|^{2} E + \frac{{i\beta^{k} }}{2}\left| E \right|^{2k - 2} E - \frac{\omega }{c}n_{4} \left| E \right|^{4} E = 0$$

In addition to propagation (first term) and diffraction (second term), the equation has to cover at least two nonlinear effects relevant to propagation at high intensities \(I \propto \left| E \right|^{2}\). These are focusing by the Kerr-effect (third term) and defocusing by the plasma of free electrons (fifth term) . In particular, a third necessary effect is introduced through the imaginary part of the index of refraction (fourth term). This term has to be considered taking into account the absorption of light that results in excitation of free electrons that generate the defocusing plasma within the dielectric material.