Keywords

FormalPara List of Abbreviations
Table 1
Full size table

1 Introduction

The use of mathematics to help understand the emergence of biological phenomena has occurred for over a 100 years. However, through recent advances and an ever-closer collaborative effort between theoretical and experimental biologists, the field of Systems Biology has come to prominence. The history of Systems Biology can be traced back to Alfred Lotka at the start of the twentieth century. Through numerical analysis of chemical reactions that produce damped oscillations, Lotka observed that conditions matching those of larger biological systems may be able to sustain stable periodic rhythms (Lotka 1920). This led to the development of models describing population dynamics that are now regularly taught as part of mathematics courses (Murray 2002a). Importantly, Lotka’s aim was not merely to obtain an expression that can describe oscillations (such as a trigonometric function: sine or cosine), but to obtain an understanding of how oscillations can emerge through interactions between individual components within a system.

Over the last century further comparisons of the mathematics describing behaviour on a systems level were made. Consequently, scientists such as Ludwig von Bertalanffy aimed to derive a General System Theory whereby many different systems could be described by the same mathematical structure (von Bertalanffy 1968). In fact, some of the arguments made by von Bertalanffy in the 1960s are still prevalent today:

Modern science is characterised by its ever-increasing specialisation, necessitated by the enormous amount of data, the complexity of techniques and of theoretical structures within every field. Thus science is split into innumerable disciplines continually generating new subdisciplines. In consequence, the physicist, the biologist, the psychologist and the social scientist are, so to speak, encapsulated in their private universes…This, however, is opposed by another remarkable aspect…Independently of each other, similar problems and conceptions have evolved in widely different fields.

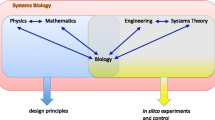
Such a quote, essentially, highlights the modus operandi of Systems Biology: to bring together the biologist, the physicist, the mathematician, and the computer scientist to deal with the masses of experimental data currently being produced and understand phenomena that emerge from biological systems. In Systems Biology one aims at predictive models, but it should be made clear what is actually meant by this term. Any correlation can be used for the purpose of a probabilistic prediction. However, what is meant in many cases is the construction of a genuinely explanatory model. The prediction should also hold for the manipulated system, which requires that the model captures changes of specific molecular components internal to the system. Thus, an understanding of the internal causal structure is needed to offer mechanistic explanations of system phenotypes (Westerhoff and Kell 2007; Brigandt 2013). This is a demanding task, requiring the integration of mathematical-modelling efforts, data detailing molecular interactions, and information on the physics of cellular structures (Mogilner et al. 2012).

There are a number of recent publications and books that have summarised aspects of the Systems Biology field and show how Systems Biology approaches can be implemented to solve biological problems (Kitano 2002a,b; Klipp et al. 2005). Some reviews highlight how spatial signals or organ development can be linked to intracellular networks, that have themselves been covered in books by Kholodenko (2006), Alon (2007), and Brady and Benfey (2009). On the other hand, mechanical forces that influence the growth of organs have been treated mathematically using methods that are generally independent of internal cellular processes (Goriely and Tabor 2008). Finally, for an overview of mathematical models describing a wide range of temporal and spatial biological phenomena, we direct interested readers to the excellent books by J. D. Murray and R. Phillips et al. that go into greater depths of mathematical analysis than the reviews listed above (Murray 2002a,b; Phillips et al. 2013).

In this chapter, we aim to supplement the reviews and book chapters listed above by considering the range of potential steps and questions that occur throughout the creation of a mathematical model within Systems Biology. We start by discussing model creation and how different types of model can be used to answer different biological questions. Then, we provide an overview of methods to infer kinetic rates within a biological system. This should, in principle, leave the user with a model that provides an accurate depiction of their biological data. Finally, we highlight methods to analyse a model and how to extract new understanding or experimental hypotheses about a biological network. Whilst we primarily consider what is referred to as the ‘bottom-up’ approach to Systems Biology (namely that we start with a limited amount of information and look to build upon this until our model is able to describe biological phenomena), we direct readers to other sources, such as Klipp et al. (2005), for more information about ‘top-down’ methods (whereby the causes of biological phenomena are unearthed from high-throughput ‘omics’ data).

2 Creating a Model

2.1 Prior Knowledge: What Is the System, the Data, the Question?

As with the start of any project, the most important consideration is what hypothesis does one wish to test, or what new understanding about the biological system does one wish to gain. The universal model from which all possible questions could be answered would be impossible to handle, even if it would exist. This is both a practical and an epistemological constraint. The behaviour of complex systems is often only understandable if one finds the correct level of description. In many cases the details of a system are not important and a coarse-grained description of the interactions between the constituent of a system is better to explore its behaviour. It is often the case that a rich yet structured picture emerges only if one asks the correct questions by allowing for controlled errors.

Furthermore, the question itself (and the modelling style used, as we shall see later) is constrained by the information and data that is available. A model reflects what is known about the system under inspection and what particular questions are asked. A seemingly simple reaction like receptor–ligand binding can be quite complicated and difficult to understand in detail, where the binding is governed by a combination of steric, electrostatic and van der Waals forces (Gilson and Zhou 2007). However, in many cases the binding process can be described by a second order reaction; all the details of the binding process are subsumed in a rate constant. The same is true, e.g. for protein degradation. In most models it is described by first order reaction kinetics, which is equivalent to a spontaneous decay of the protein, where in reality it is a sequence of reaction steps. The modelling of protein degradation by first order reaction kinetics is in many cases sufficient. However, if one is interested in the details of the degradation process itself, the description has to be expanded from a simple first order reaction to a system of coupled ordinary differential equations.

The type of available data also matters for the decision on the modelling approach. For example, one may have data that describes different levels of biology: temporal (time-dependent) or spatial dynamics of system components within single cells, changes in component concentration within a cell population over a period of time, concentration gradients through a tissue layer or across different cell types, and physiological readouts of a biological phenomena with limited knowledge about the components that cause them. Furthermore, such data could be measured across a range of environmental conditions or varied transgenic systems, allowing one to compare how external and internal changes or perturbations impact the system.

Each of these data sources can allow for a range of different questions to be asked. For example:

  • how does variability between single cells ultimately impact upon tissue generation or phenotypic responses?

  • how are temporal changes in component concentration, that in turn impact physiological responses, related to environmental fluctuations?

  • upon perturbing the concentration of a component, how is the spatial distribution of other components or tissue layers altered?

  • what potential cellular mechanisms could lead to non-linear physiological growth rates?

Additionally to the analysis of new data, one should also consider any available prior knowledge, both within the biological system of choice or from evolutionarily linked systems. This can have several positive effects upon the modelling strategy chosen for the study. For example, imagine that temporal changes of system components had been obtained but the researcher knew, qualitatively, about the spatial localisation of components through a tissue from published research. One could then construct a spatio-temporal model that captured the new data in detail and provided the broad pattern of expression across the spatial domain described by published observations. Another example would be combining information from different system perturbations. For example, a previous study may have implicated a particular component by observing altered responses in mis-expression studies. If another component was found to also alter the physiological response in new experiments, then a model could incorporate and link both of these components within a single system to explain biological phenotypes. Thus, combining data from multiple sources across a range of different scales can help model construction and analysis.

Finally, if a biological phenomena has been observed but little is known about the system responsible, then one possibility would be to look at analogous networks from different species or related systems—i.e. envisioning general systems principles for similar biological responses. A number of cases exist in plant biology. For example, simple models of the plant circadian clock (that coordinate daily physiological rhythms with the environment) were originally constructed assuming a similar network structure to that of the theoretical Goodwin oscillator that produces stable oscillations given certain kinetic rates (Goodwin 1965; Locke et al. 2005). By building on this simple theoretical system, a large number of components have been implicated in the regulation of plant circadian rhythms over the last decade (Pokhilko et al. 2012; McClung 2014). A further example has occurred through comparison of flowering phenotypes of different plants. The network that controls day-length-dependent flowering in short-day flowering rice, Oryza sativa, has been found to share components similar to the long-day flowering model plant Arabidopsis thaliana. By comparing system perturbations, researchers were able to understand how network connections differed between the two plant species, providing different flowering phenotypes despite having similar cellular components (Blumel et al. 2015). Thus, by viewing models as a general description of biological phenomena, rather than a description of very particular biological responses, one is able to elucidate a range of information about related systems that can act as starting points in more detailed examinations of a newly studied biological network.

Given a model and a hypothesis to test, one can now determine whether the current understanding of a biological system is correct or not. As described above, models integrate the current knowledge about a system and aim to answer specific questions. While deriving the mathematical model one idealises the actual biological situation and one, necessarily, simplifies certain aspects of the system. Usually, the derivation of a mathematical model is an iterative process. If the model describes the data and predicts correctly the manipulations—success. But, maybe, more interesting are model failures, because they point at not-well understood elements of the system; specific failures of the models may predict new regulatory interactions or components that can be tested by experimentation.

2.2 Model Characteristics: Which Model Is Suitable to Answer the Biological Question

Upon the decision of which level of biology one wishes to examine, the next step is to decide upon the modelling strategy required. As suggested in the previous section, this decision is limited by the data that the researcher possesses and what research questions are to be answered. In this section, we shall describe the mathematics and assumptions of different techniques from modelling individual molecules up to tissue level systems over both temporal and spatial dimensions (Fig. 13.1). For further information about these modelling strategies we refer readers to (Murray 2002a,b; Paulsson 2004; Kholodenko 2006; Gillespie 2007; Phillips et al. 2013). Whilst we shall not cover here large scale steady state models, such as those commonly found when analysing metabolic networks, we shall point out how these are a special case of dynamic systems and refer readers to Orth et al. (2010) for more details.

Fig. 13.1
figure 1

Spatial and temporal scales of biological systems. An illustration of the different scales that biology covers (a) spatially and (b) temporally from the smallest molecules to populations

Full size image

2.2.1 Assessing the State of a Single Interaction

At the basis of all biochemical reactions is the interaction between single molecules within a cell. In relation to Fig. 13.1, this implies that we are interested in reactions occurring on both temporal and spatial nano-scales. Here, we will introduce some of the important concepts to describe the effects of forces on such molecular interactions, but direct interested readers to the book by Phillips et al. for a more thorough treatment of the examples introduced here (Phillips et al. 2013).

A system is in thermodynamic equilibrium when it is in thermal, mechanical, and chemical equilibrium. This means there is no net flux of energy and matter between the system and its environment (Rao 2004; Phillips et al. 2013). A steady state of a system is more general; it is a fixed point of the system in which the influx and the efflux are in balance, but exchange of matter and energy is possible. A thermodynamic equilibrium is a special kind of steady state, i.e. every thermodynamic equilibrium is a steady state but not vice versa. Biological organisms always exchange matter and energy with their environment and therefore they are never in thermodynamic equilibrium unless they are dead. However, it is in many instances well-justified to consider a particular process to be in equilibrium, which is often the case if the time-scales of the relevant biological process, e.g. gene expression, and the process in question, e.g. binding of transcription factors, are very different. In this case one can use the wealth of concepts developed for equilibrium systems.

For example, imagine ligand molecules that can bind to receptor proteins (Fig. 13.2a). There are two possible states for the ligands, either bound or unbound, and with each of these states an energy state is related (Fig. 13.2b). The equilibrium state (i.e. how many of the ligands are bound or unbound) minimises the free energy of the system (Fig. 13.2b), where the free energy is the difference between the internal energy U and the product of temperature T and entropy S (F = U − TS). Note that for the sake of simplicity we do not distinguish between Helmholtz and Gibbs free energy (Rao 2004; Phillips et al. 2013). The entropy of a system measures the number of its microstates compatible with the macrostate of the system. For example, consider two receptors and two ligands. There is one microstate related to the macrostate with 100% of the ligands bound, one microstate related to the macrostate where 100% of the ligands unbound, and two microstates related to the macrostate where 50% of the ligands bound. In general, given N ligands and receptors, the number of microstates related to the macrostate with k ligands bound is W(k) = N! ∕(k! (N − k)! ). The entropy S of the receptor–ligand system is given by S = k B ln(W) (k B is the Boltzmann constant). If U u and U b are the binding energies of the unbound and bound state, respectively, then the free energy of the system with N receptors/ligands and k ligands being in the bound state is given by:

$$\displaystyle{ \frac{F(k)} {k_{B}T} = N \frac{U_{u}} {k_{B}T} + k\frac{U_{b} - U_{u}} {k_{B}T} -\ln (W(k)). }$$
Fig. 13.2
figure 2

Ligand binding to a receptor protein with a cell. (a) An illustration of the state switching between unbound and bound ligand with the receptor. Only one ligand can bind the receptor at any given time and this is influenced by its position within the cell. (b) An example of the double well energy landscape that such a system may generate. In this instance the states of unbound and bound ligand represent the minima in the binding energy landscape. The red line illustrates the gain of energy by the ligand–receptor complex to move from unbound state to bound state

Full size image

The question is which k, i.e. which number of bound ligands, minimises F? The first term on the right-hand side of this equation is a constant, which corresponds to the free energy of the system with all ligands unbound. To calculate some numbers, we set N = 100. In case U b = U u the obvious result is k = 50. For U b − U u = 0. 5 k B T one finds k = 62 and in case U b − U u = k B T one obtains k = 73.

There is another instructive way of looking at the above example. The state which minimises the free energy is the most probable state of the system. Other states are possible as well, but with lesser probability. The probability of finding the system in state k (short for having k ligands bound) is given by Phillips et al. (2013):

$$\displaystyle{ P(k) = \frac{e^{-F(k)/k_{B}T}} {\sum _{k^{{\prime}}=0}^{N}e^{-F(k^{{\prime}})/k_{B}T}}. }$$

Using the expression for F(k) given above and doing some algebra one obtains:

$$\displaystyle{ P(k) = \frac{N!} {(N - k)!k!} \frac{e^{-k(U_{b}-U_{u})/k_{B}T}} {(1 + e^{-(U_{b}-U_{u})/k_{B}T})^{N}}. }$$

The probability of finding the system in state k = 73 for U b − U u = k B T is P(73) ≈ 0. 09, while for k = 50, P(50) ≈ 5 × 10−7. What does this mean? If one does an experiment counting the number of bound states, in only 9% of the cases one will find exactly k = 73 bound receptors. But in 98% of the cases the number of bound receptors will be between k = 63 and k = 83.

Thus, starting from analysing microscale reactions between single molecules, we are able to understand snapshots of molecule populations containing mixed states through concepts of equilibrium statistical mechanics. Based on such ideas, several interesting results can be derived, including Hill functions that are often used to approximate the binding of transcription factors to promoters and the regulation of gene expression (Bintu et al. 2005; Phillips et al. 2013).

Using equilibrium approaches to analyse and describe a biological system can be very powerful, but time does not appear in these methods. There is no information of how long a process takes, how long one needs to wait in an experiment to reach equilibrium, or how long to measure to obtain sufficient statistics. If temporal and spatial information is needed on small scales molecular dynamics simulation can serve as a computational microscope, revealing the workings of biomolecular systems at a spatial and temporal resolution that is often difficult to access experimentally (Dror et al. 2012). On a coarse-grained or mesoscopic level the chemical master equation provides a description of what happens within molecule populations over time and space (Gillespie 2007).

2.2.2 Modelling Small Molecule Numbers in Single Cells

When examining the changes in small populations of molecules in single cells, we need to refer to stochastic processes. For stochastic processes it is impossible to know at any time the exact state of the system (besides the initial state). It is only possible to make statements about the probability to find the system in a given state at a given time. The time development of a system can be described by an equation for the time development of this probability. On a mesoscopic description level one is not concerned with forces or energies (like the microscopic level), but rather with the probability that a given change of the system occurs within a certain small time interval. The equation for the probability is a balance equation; it is concerned at each time point with a gain and a loss in the probability to find the system in a given state. As an example let us consider the ligand–receptor binding from the previous section. To simplify matters we analyse the situation for one ligand and one receptor (N = 1). We examine the reaction between state 0 (unbound) and 1 (bound):

$$\displaystyle\begin{array}{rcl} 0\mathop{\mathop{ \rightleftharpoons }\limits_{ k_{2}}}\limits^{k_{1}}1& & {}\\ \end{array}$$

The probability \(P(1,t + \Delta t)\) of finding the ligand in the bound state at time \(t + \Delta t\) is based on the probability at time t and the transition probabilities to either move from state 0 to 1 (gain) or vice versa (loss):

$$\displaystyle\begin{array}{rcl} P(1,t + \Delta t) = P(1,t) +\mathop{ k_{1}\Delta tP(0,t)}\limits_{\mathrm{gain}} -\mathop{ k_{2}\Delta tP(1,t)}\limits_{\mathrm{loss}}& & {}\\ \end{array}$$

Dividing by \(\Delta t\) and taking the limit \(\Delta t \rightarrow 0\) yields a differential equation for P(1, t):

$$\displaystyle\begin{array}{rcl} \frac{dP(1,t)} {dt} = k_{1}P(0,t) - k_{2}P(1,t).& & {}\\ \end{array}$$

This type of gain-loss equation for the probability is called the master equation. In steady state, i.e. when t → ∞ we find: P(1, t → ∞) = k 1∕(k 1 + k 2). Comparing this result to the result for P(k = 1) from the previous section yields:

$$\displaystyle\begin{array}{rcl} \frac{k_{1}} {k_{2}}& =& e^{-(U_{b}-U_{u})/k_{B}T}, {}\\ \end{array}$$

which relates the mesoscopic scale (reaction rates) to the microscopic scale (binding energies). For a birth and death process (∅ denotes the empty set; the molecules appear out of nothing—production—and vanish into nothing—degradation):

$$\displaystyle{ \emptyset \mathop{\longrightarrow }\limits^{k_{1}}X\mathop{\longrightarrow }\limits^{k_{2}}\emptyset, }$$

the corresponding master equation reads:

$$\displaystyle\begin{array}{rcl} \frac{dP(n,t)} {dt} & =& \mathop{k_{1}P(n - 1,t)}\limits_{\mathrm{gain:\, production}} +\mathop{ k_{2}(n + 1)P(n + 1,t)}\limits_{\mathrm{gain:\, degradation}} -\mathop{ k_{1}P(n,t)}\limits_{\mathrm{loss:\, production}} -\mathop{ k_{2}nP(n,t)}\limits_{\mathrm{loss:\, degradation}}{}\\ \end{array}$$

This equation describes the time development of the probability to find n molecules at time t and needs to be solved such that it obeys the initial condition P(n, t 0) = P 0(n). To find an equation for the mean or average number of molecules 〈n〉 one multiplies the master equation by n and sums over all possible values for n. This gives rise to:

$$\displaystyle\begin{array}{rcl} \frac{d\langle n\rangle } {dt} & =& k_{1} - k_{2}\langle n\rangle {}\\ \end{array}$$

The equation for the average of the stochastic process is identical to the deterministic equation one obtains using mass-action kinetics (Klipp et al. 2005). Thus, the average obtained from the master equation and the result from the mass-action kinetics agree. This only holds for linear systems; for non-linear reactions, such as protein–protein binding, the equation for the mean obtained from the master equation differs from the equation derived from mass-action kinetics. Additional assumptions, e.g. high molecule abundance, are required to find congruity between the stochastic and the deterministic description (Gardiner 2004).

For a general chemical reaction system the chemical master equation (CME) describes on a mesoscopic level the change of the chemical distribution. However, although being an exact description for the probability to find a given chemical composition of the biological system at a given time it is very difficult to obtain analytical solutions. This is due, in part, to biological networks breaking detailed balance through synthesis and degradation reactions. Numerical solutions to the CME can be obtained by using a variant of the Gillespie algorithm or the Stochastic Simulation Algorithm (SSA; see Gillespie (2007) for a review). However, to obtain information about the probability distribution several thousands of similar simulations need to be performed. Without computational parallelisation this process is thus highly time-consuming for complicated biological networks, but could be of use for small systems such as those created in the field of Synthetic Biology.

Since the CME is difficult to solve and computationally intensive to simulate for larger systems, several approximative schemes have been developed. Among these the linear-noise approximation and the Chemical Langevin Equation are widely used (van Kampen 1981; Gillespie 2000). Whilst we shall not go into the details of such a process, we would like the reader to note that this technique has allowed users to obtain accurate numerical estimates to the solution of the CME (Grima et al. 2011; Thomas et al. 2013).

2.2.3 Dynamics in Cell Populations

Ordinary differential equations (ODEs) are the most common modelling technique found in Systems Biology studies, and this is mainly reflected by the data that is available detailing cellular processes. For example, temporal evolution of system components is measured across a cell population, e.g. by quantitative real-time PCR (qRT-PCR), such that any internal fluctuations in the system are cancelled out. Consequently, a number of software packages have been developed to allow for the easy construction and simulation of such models (e.g. COPASI), whilst computer languages are under constant evolution to share these models around the Systems Biology community (e.g. SBML) (Hucka et al. 2003; Hoops et al. 2006).

From a mathematical perspective, the temporal dynamics of a reaction system can be described by the system of coupled ODEs:

$$\displaystyle{ \frac{dX_{i}} {dt} = f_{i}(\mathbf{k},\mathbf{X}(t)), }$$
(13.1)
Table 13.1 Example forms of function f i from (13. 1)
Full size table

where k is the vector of kinetic rates (or parameters) that determine the evolution of the variables X i (the number of molecules of type i per unit volume), f i is a function that relates the kinetic rates and components of the system with the regulation of X i (X is the vector of components X i ). The function f i can take many different forms depending on the reactions taking place within the system and will be, in general, a non-linear function of the X i ’s. We provide a few examples of such functions in Table 13.1 that can be summed together to form a complete ODE of synthesis, complex formation, and degradation rates.

The description using ODEs does not capture any stochastic effects; it is a solely deterministic description of the system under inspection. This means that for a given set of parameters k and initial conditions X(t = 0) the result will always be the same. One of the advantages of ignoring stochastic factors is that systems constructed by ODEs can be analysed in an easier fashion to obtain direct relations between certain biological rates and the emergence of system properties, such as oscillations. However, solving and analysing (e.g. how does the dynamic of the system depend on the parameters k?) a system of coupled non-linear ordinary differential equations can be a very challenging task. Therefore, one may seek to simplify the mathematical description such that the important features of the system remain sufficiently accurately described. For example, if a subset of the modelled processes occur at much shorter time-scales to the rest of the system, then their dynamics can be assumed constant (\(\dot{X}_{i} = 0\)) and thus greatly reduce the number of differential equations. We shall not provide any detailed methods here, these can be found in Murray (2002a), but we will highlight one classic example where an ODE system was simplified to produce a well-known relationship: Michaelis–Menten kinetics.

The Michaelis–Menten reaction is

$$\displaystyle{ E + S\mathop{\mathop{ \rightleftharpoons }\limits^{ k_{f}}}\limits_{k_{r}}C\mathop{\longrightarrow }\limits^{k_{c}}E + P, }$$

where E is an enzyme, S is a substrate, P is the product produced by the enzyme-substrate complex, C, and k j are the biological rates describing reversible complex formation and P synthesis.

This system can be written in the following ODE form:

$$\displaystyle\begin{array}{rcl} \frac{dE} {dt} & =& (k_{r} + k_{c})C - k_{f}ES, {}\\ \frac{dS} {dt} & =& k_{r}C - k_{f}ES, {}\\ \frac{dC} {dt} & =& k_{f}ES - (k_{r} + k_{c})C, {}\\ \frac{dP} {dt} & =& k_{c}C. {}\\ \end{array}$$

An important facet to this reaction is that the enzyme conservation law is maintained such that the total amount of enzyme (E + C) does not change with time. Thus, if E 0 is the initial concentration of enzyme, then E + C = E 0 for all time.

At this point, one of the two assumptions can be made as to the time-scales present within the system. The first is that the complex C is in instantaneous equilibrium (i.e. that binding of E and S is fast) which implies that (k r + k c )C = k f ES. Notably, this is similar reasoning to the rationale seen previously when comparing statistical approaches of gene regulation to using kinetic rates in the CME. The second is that the dynamics of C occur much more slowly than those of E and S. Mathematically, this implies that C is always at a quasi-steady state and, hence, dC∕dt = 0.

Ultimately, by setting E = E 0 − C, both approximations lead to the same mathematical conclusion, namely

$$\displaystyle\begin{array}{rcl} C& =& \frac{E_{0}S} {K + S}, {}\\ \frac{dS} {dt} & =& - \frac{E_{0}S} {K + S}, {}\\ \frac{dP} {dt} & =& \frac{V _{\mathrm{max}}S} {K + S}, {}\\ \end{array}$$

where V max = k c E 0 and K = (k r + k c )∕k f . Thus, by making two assumptions—the conservation law of E holds and that a subset of the biological processes occurs faster than the rest of the network—a system of four equations has been reduced to two (\(\dot{S}\) and \(\dot{P}\)). Note that these equations describe the dynamics of the system at larger times correctly, after an initial equilibration time such that \(\dot{C} \approx 0\) holds. If one is interested in the early time development of the system the full system needs to be considered.

We end this subsection with a quick note about larger scale models often encountered when modelling metabolic networks. Whilst these are not often encountered in Systems Biology studies of pollen tip growth they are a well-studied subclass of ODE models. The equation is formulated in matrix notation

$$\displaystyle{ \frac{d\mathbf{X}} {dt} = \mathbf{N}\mathbf{v}(\mathbf{X}), }$$

where N is the stoichiometry matrix of a reaction set and v is a vector of fluxes that depend on the concentrations of components X within the system.

These networks, generally, are very large and can be time-consuming to analyse numerically. Thus, researchers assume that enzymatic reactions occur at a much faster time-scale compared to observable changes in phenotypes of an organism (e.g. growth rate). This implies that the set of differential equations can be set to zero such that

$$\displaystyle{ \mathbf{N}\mathbf{v}(\mathbf{X}) = 0. }$$

This leaves us with a large set of linear equations from which a solution v ∗ can be found. Many methods have been derived to find the possible solutions of these equations that satisfy particular conditions and are mainly based on a process known as Flux Balance Analysis (FBA). We do not go into the details of these methods here, but the review by Orth et al. (2010) gives a general overview of the principles for interested readers.

2.2.4 Processes Across the Spatial Domain

Thus far we have concentrated on analysing the temporal changes within networks, however, many biological processes also vary across the spatial domain. Such networks and chemical gradients lead to phenomena like cell division, tissue generation, organ elongation, and skin coat patterning. For more examples we recommend the reader to look at the book by Murray (2002b). Here, we will briefly introduce the reaction–diffusion equation that mathematically describes a particular class of self-regulated spatial phenomena (Kondo and Miura 2010).

The question underlying spatial patterning of cellular tissue is how genetically identical cells can exhibit differentiated behaviour. A conceptually easy possibility is by using boundary layer information. A morphogen is produced at the boundary of the tissue and due to finite stability of the morphogen a gradient is established. Depending on the distance from the boundary cells experience disparate concentrations of the morphogen and by a threshold mechanism differentiate into different states (Wolpert 1996; Kondo and Miura 2010). In this scheme no feedback between cells is required. The challenge lies in the explanation of the threshold mechanism. Another possibility to achieve a spatial pattern is through the exchange of information between cells, which modifies the chemical reactions. One way to exchange information—or to achieve spatial coupling between cells—is by secretion of molecules. In many cases this can be described by a diffusion-like transport of molecules across the tissue. Using Fick’s Laws, the flux of a concentration q across spatial domains is related to the diffusion coefficient by

$$\displaystyle\begin{array}{rcl} J(x,t)& =& -D\frac{\partial q} {\partial x}, {}\\ \frac{\partial q} {\partial t} \sim -\frac{\partial J(x,t)} {\partial x} & =& \frac{\partial (D\partial q/\partial x)} {\partial x} \equiv \nabla (D\nabla q), {}\\ \end{array}$$

where ∇ = ∂∕∂x (or in three dimensions \(\nabla = ( \frac{\partial } {\partial x}, \frac{\partial } {\partial y}, \frac{\partial } {\partial z})\)) that tells us how the concentration of q changes across a spatial step \(\Delta x\). D is the diffusion coefficient that could be constant or depend on time and space. Adding this diffusion term to a chemical reaction system as described in the previous section results in a reaction–diffusion equation:

$$\displaystyle{ \frac{\partial \mathbf{q}} {\partial t} = \mathbf{f}(\mathbf{q}) + \nabla (D\nabla \mathbf{q}), }$$

where f describes the reaction kinetics. This is referred to as a partial differential equation (PDE). Because the reactions are typically non-linear, reaction–diffusion systems are mostly non-linear PDEs, which need to be solved numerically.

In the absence of reaction kinetics, f(q) above, the boundary conditions of the system will determine the final pattern. In the presence of reaction kinetics, different patterns can be obtained depending on the system parameters such as the initial conditions, the boundary of the system, and the kinetic rates. The diversity in these values leads to the rich variety of patterns observed across biological systems.

A number of other reaction–diffusion systems have now been studied due to the prevalence of patterns in biological systems. Generally, one can say that long-ranged inhibition and short-ranged activation of diffusing systems are necessary ingredients to produce stationary patterns as are seen in biology (Kondo and Miura 2010). For a system of two interacting and diffusing chemicals one can show that exactly two classes of pattern forming networks exist: activator-inhibitor and substrate-depletion (Murray 2002b). Many examples exist in the literature and interested readers can find further details in the textbooks by Murray and Edelstein-Keshet (including Edelstein-Keshet (1988) and Murray (2002b)).

2.2.5 Mechanical Descriptions of Tissue Growth

Thus far we have concentrated on methods of modelling individual molecules up to concentrations across temporal and spatial scales. Ultimately, these processes lead to the growth of tissues and organs. For example, in the case of pollen tip elongation, dynamic changes in ion concentration and subcellular localisation can have an impact on growth rate and organ development (Kroeger et al. 2008; Kato et al. 2010). However, once an organ has developed, mechanical forces start to play a role in growth dynamics, for example, friction and elasticity of the tissue surface (Goriely and Tabor 2008; Fayant et al. 2010). These sets of forces are different to those outlined at the start of this section (e.g. thermal forces). As with our previous discussions on the effects of forces in biological systems, we refer interested readers to Phillips et al. (2013).

If we go back to our previous description of biological interactions on the microscale, the system is in equilibrium states upon the minimisation of internal energy. When referring to mechanical growth of a tissue we are interested in potential energy or, rather, the amount of energy required for the organ to do ‘work’ and grow. Thus, a tissue is in mechanical equilibrium if the forces acting upon it are balanced and the potential energy is minimised. This implies that

$$\displaystyle{ \sum _{i}\mathbf{F}_{i} = 0, }$$

where F i is one of the i forces acting on the spatial structures of the tissue. These forces could include such effects as elasticity, elongation, weight, and friction.

The strain exerted on an extending tissue by a force can, for purely elastic material, be described by Hooke’s Law which states that the force required to stretch the growing tissue is proportional to the displacement of a position along the tissue

$$\displaystyle{ F = -k\Delta x, }$$

where F is the force, \(\Delta x\) is the displacement, and k is some positive constant. This can be rewritten as

$$\displaystyle\begin{array}{rcl} \frac{F} {A}& =& E\epsilon, {}\\ \epsilon & =& \frac{\Delta L} {L_{0}} = \frac{L - L_{0}} {L_{0}}, {}\\ \end{array}$$

where A is the cross-sectional area of the tissue, ε is the strain that describes the fractional extension of the tissue, and E is Young’s modulus that represents how stiff the tissue is. In general the relationship between stress (force per unit area) and strain (relative displacement) in three dimensions is described by a tensor equation, i.e. the scalars stress and strain are replaced by second-rank tensors (Jones and Chapman 2012). Further complication can stem from the fact that the biological material is not purely elastic, but rather yields under stress, which renders the material to be visco-elastic (Jones and Chapman 2012). Moreover, often biological materials exhibit non-linear stress–strain relationships, for which the linear approach sketched above is only valid for small relative displacements of the tissue (Jones and Chapman 2012).

An important factor for mechanical growth is the strain energy density that (for a linearly elastic material in one dimension) takes the form

$$\displaystyle{ W(\epsilon ) = \frac{1} {2}E\epsilon ^{2} = \frac{1} {2}E\Big(\frac{\Delta L} {L_{0}} \Big)^{2}. }$$

This function provides us with an estimate for the total stored strain energy contained per unit volume of the growing biological material. These relationships can be extended to relate growth across two- or three-dimensional spaces to forces exerted on the tissue from different directions. In the case of pollen tip elongation, such external forces have been shown to have an effect on tip shape and speed of elongation (Goriely and Tabor 2008; Kroeger et al. 2008). Phillips et al. present several examples showing how to calculate and analyse these functions for the effects of forces on growing biological material (Phillips et al. 2013).

In this section, we have covered some basic principles that can be used to model biological systems at different levels, from interactions between individual molecules to population level dynamics of system components in a cell to forces acting on tissue growth. Choosing the right modelling approach is a challenging task and requires knowledge about the corresponding mathematics, the physics, the biochemistry, or more generally, the biology of the system. Regardless of the modelling strategy employed in a study though, model analysis and the estimation of biological rates follow similar principles. However, before we turn our focus to these issues, we shall discuss one caveat to modelling, notably that if different models can describe the same phenomena, which model is correct?

2.3 Non-uniqueness of Models and Model Selection

In the previous section, we highlighted the methods used for modelling networks in Systems Biology across a range of different spatial and temporal scales. However, one should consider (and remember) that models are built with a specific purpose in mind and are constrained by the prior knowledge of the system. This raises an interesting epistemological question about the comparison of models. For example, could the same biological phenomena be described by multiple models? If so, is there a way of determining which model is more useful to obtain new biological insights? Could a different model exist to describe the same system and more?

Whilst this issue has not been fully realised yet in a number of Systems Biology fields, one such example where these ideas have been considered is that of the plant circadian clock. Due to the nature of obtaining qRT-PCR measurements from plant tissues (i.e. a population of cells), models of the circadian clock have been constructed using ODEs and the Langevin equation. Since the first mathematical model was published in 2005, a number of revisions to the model have been made as larger amounts of data have become available and incorporated into the mathematical analysis (see Locke et al. (2005, 2006), Guerriero et al. (2012), and Pokhilko et al. (2010, 2012)). Consequently, the number of components and biological rates has shot up from < 10 components and approximately 30 parameters, to nearly 30 components and over 100 parameters over the course of these model iterations. Notably, due to high levels of interest in the dynamics of plant circadian behaviour, one version of the plant circadian clock model was obtained independently by two research groups working with similar data and similar assumptions (Locke et al. 2006; Zeilinger et al. 2006).

Recent work has aimed to elucidate the basic core structure of the circadian clock that can describe the available datasets in a qualitative manner (De Caluwé et al. 2016). By reducing the model to 4 core subunits, the system size decreased to 9 components and 34 parameters. This core minimal model responded in similar manner to the data upon altered environmental conditions and when the system was perturbed through transgenic alterations. Whilst this may suggest that the larger, more complex models are overfitting the real biological system (i.e. the system is so complex that it can describe any simple systems), this is not really the case. Larger systems are able to describe a whole range of genetic perturbations in detail that reduced or coarse-grained models cannot due to the lack of appropriate mechanisms and components.

So which model is ‘best’—the minimal model or the more complex and detailed system? Importantly, the answer to this question depends on the research problem that one wishes to solve. For example, if the user was interested in understanding large scale effects of genetic perturbations within the system, or wished to understand how their new component could be incorporated into the current models, then using the more complex systems would be appropriate. However, for a conceptual understanding or if one wished to understand more qualitative effects, such as how an output of the network would be altered in different experimental settings, then the coarse-grained model would be easier for use.

Notably, mathematical and statistical methods of model comparison have been developed over the years. These methods range from the Akaike Information Criterion (AIC) to computing the probability of a model reproducing data given specific biological rates to characterising Pareto fronts that analyse a models ability to fulfill multiple different requirements (Akaike 1974; Friel and Pettitt 2008; Vyshemirsky and Girolami 2008; Simon 2013). For the purposes of understanding the evolution of biological networks, and how to manipulate them for the needs of Synthetic Biology, studying a range of model systems in conjunction (thus analysing a range of positive and negative model traits) promises to be a highly fruitful avenue of research over the coming decades.

3 Identification and Estimation of Biological Rates

Once a model has been constructed that describes the biological processes deemed important in producing specific responses, the next step in development is to obtain estimates for the rates that describe synthesis, degradation, complex formation, etc. As with obtaining equations by which a network is described, the parameter values used in simulations are also constrained by the available data. In this section, we shall discuss some of the key issues around parameter estimation and highlight to readers the principle ideas behind these concepts.

3.1 Experimental Variation of Data

The first step before attempting to estimate any parameter values is data collection with which to compare model simulations. As is well understood in experimental design, variation within a dataset can occur through two sources—intrinsic biochemical fluctuations (as is often captured mathematically by the CME) and external fluctuations (such as those in the environment or due to experimental equipment). Consequently, if one wished to match model simulations to data from a specific experimental condition, you would wish that the intrinsic variability is small. Thus, you would have confidence that you can find a specific set of parameters that describe this data. Alternatively, if the data is highly variable, then this would negatively impact the chances of finding a single optimal parameter set. Similarly, since changing experimental conditions can lead to alterations in biological networks, data for parameter estimation would ideally come from a single set of experimental conditions. Mixing of datasets across different experimental set-ups could lead to further variation in parameter estimates and the researcher cannot guarantee that the underlying system of equations do not need altering between different experimental conditions.

Another source of variation in data collection can occur through species comparisons. To illustrate this issue, we shall draw on one pertinent example. Let us assume that a large network of metabolic reactions is known but that there are limited amounts of experimental data obtained to aid parameter estimation. This is often referred to as an underdetermined problem, i.e. there is not enough data available to get good estimates of the biological rates (Orth et al. 2010). In some instances, large online databases have been developed that contain a wide range of experimentally measured catalytic rates and equilibrium constants (Schomburg et al. 2004; Flamholz et al. 2012; Wittig et al. 2012). Thus, if a model was being built to understand metabolism of a relatively understudied species, one could be pragmatic and obtain estimates for a large number of rates from closely related species. This assumes, of course, that the two species are evolutionarily close such that the underlying metabolic networks for the two species are relatively similar.

3.2 Parameter Estimation Methods

Using the available data, one needs to find a method of estimating the system parameters such that the model simulations match with what is observed experimentally. This could either be done by manual tweaking of parameter values within the model or through a more automated and unbiased approach. There is a wide range of literature related to this problem (Simon 2013; Raue et al. 2014). Here we shall go through the basic principles of how to obtain estimates for the parameter rates of a model given specific data.

Arguably, the most important facet of this procedure is to construct a scoring function that is smooth and has defined finite maxima or minima. By smooth, we mean that if one was to plot the scoring function in a multi-dimensional surface that no discontinuities exist. This means that for a given set of parameter values some finite score definitely exists and that no jumps within the surface occur. By finite maxima or minima, we mean the scoring function cannot extend to the realms of positive/negative infinity when calculated on a computer. The introduction of symbolic numbers (such as infinity in many computer software packages) can lead to problems when automating the optimisation process such that score values between different iterations are numerically compared.

In principle, one can construct a scoring function to match a particular model feature (such as oscillatory behaviour or relaxation to a steady state after an external pulse) or to measured data values. In the following we shall discuss the case where a modeller has data available to compare the model against. One of the simplest scoring functions is the calculation of the sum-of-squared residuals

$$\displaystyle{ C =\sum _{ i=1}^{n}\frac{(x_{i} - y_{i})^{2}} {\sigma _{i}^{2}}, }$$

where x i is the simulation at a given datapoint, y i is the measured datapoint, and σ i 2 is the variance of datapoint y i . The score, C, is calculated as the sum over the n measured datapoints. Importantly, one should notice that as the model simulations x get closer to the data y (denoted as x → y) then C → 0. Hence, the subset of parameter values where C = 0 are the set of potentially correct biological rates for the system under study. Importantly, the origins of such a scoring function can be found in the derivation of likelihood probabilities for Gaussian distributions, i.e. C ∼ logP(k | x, y) for parameter set k found given the model simulations x that is being matched to data y (Raue et al. 2009).

Due to the complexity of high-dimensional parameter spaces (that have as many dimensions as the number of parameters being estimated), one wishes to explore this space and obtain scores C to determine where the optimal parameter set lies. One possible method of doing this is by calculating C for all possible parameter combinations in an appropriately discretised parameter space, which is highly time-consuming from a computational perspective and infeasible for high-dimensional parameter spaces. Another option would be to use a Latin Hypercube sampling method (McKay et al. 2000), whereby the evaluated parameter sets are evenly distributed through parameter space, and calculate the scores C. This gives the user information about the global structure of the parameter space, but may also indicate subregions where the global optimum is likely to exist for closer inspection. One final option would be through the use of automated optimisation algorithms whereby, given an initial starting point in parameter space, the algorithm updates itself towards the direction of an optimal solution where C → 0.

Minimisation functions generally have the following steps (see Fig. 13.3 for a pictorial overview):

  • Pick random starting point in multi-dimensional parameter space, k 0.

  • Simulate the model using k 0 and calculate C 0.

  • Set i = 1.

  • Optional: set C threshold as some threshold that C must be lower than for k to be considered optimal.

  • While C i−1 > 0 (or C i−1 > C threshold):

    • Pick k i as perturbed parameter set of k i−1;

    • Simulate the model using k i to calculate C i ;

    • If C i < C i−1:

      • Set i = i+1.

    • Else if C i−1 ≤ C i :

      • Do not change i.

    • Else if C i = 0 or C i < C threshold:

      • Stop the algorithm as you have found the optimal parameter set.

Fig. 13.3
figure 3

An example of two-dimensional multimodal parameter space. Given variation in two parameters, optimisation routines aim to find the global minimum (dark blue) within the search space. However, due to the complexity of some mathematical models, several minima could exist. Here, we show three illustrative examples whereby the optimisation starts at a high-scoring parameter set (red regions) before moving towards (a) a low-scoring local minima, (b) a high-scoring local minima, and (c) the global optimum. What this highlights is that, depending on where within the search space an algorithm begins, the likelihood of finding the optimum result also changes

Full size image

Thus, one can see that with each iteration of the algorithm, the optimal parameter set is only updated when the score is less than the previous best result. Hence, upon reaching zero or the manually chosen threshold for optimal parameter sets, the algorithm stops and the optimal k can be obtained.

Multiple computational methods have been created to improve the accuracy and reliability of parameter estimation. These methods range from multi-start minimisation, whereby the minimisation procedure above is started from multiple different random positions to cover as much of the multi-dimensional parameter space as possible, to methods based on the principles of random walks, such as Simulated Annealing, whereby the jump to a new parameter set or region of parameter space is determined probabilistically. The interested reader can find details in (Simon 2013). One interesting point to make, though, is that the scoring function above can be generalised in two ways to incorporate multiple experimental conditions. In the following subsection we shall introduce these ideas.

3.2.1 Multi-Experiment Fits

The first way in which the scoring function can be generalised is to describe the match between data obtained from several experimental conditions and multiple model simulations. This can be used, for example, in cases where an input signal into a model is altered but the underlying network structure and biological rates should remain unchanged. Thus, one can rewrite the scoring function to be

$$\displaystyle\begin{array}{rcl} C& =& \sum _{j=1}^{m}C_{ j} {}\\ & =& \sum _{j=1}^{m}\sum _{ i=1}^{n_{j} }\frac{(x_{i,j} - y_{i,j})^{2}} {\sigma _{i,j}^{2}}. {}\\ \end{array}$$

Hence, one is not just taking into account the n j datapoints in experiment j, but also what takes place in m different experiments. The advantage of using multiple datasets is that this can result in the parameter space being constrained to subregions where both datasets are described equally well. In large systems, this is particularly important as the parameter space in some dimensions may be relatively flat (i.e. that the parameter could be any value without altering the score C).

3.2.2 Multi-Objective Optimisation

A second generalisation to the scoring function above is to include weights within our multi-experiment fit. Therefore

$$\displaystyle\begin{array}{rcl} C& =& \sum _{j=1}^{m}w_{ j}C_{j} {}\\ & =& \sum _{j=1}^{m}w_{ j}\sum _{i=1}^{n_{j} }\frac{(x_{i,j} - y_{i,j})^{2}} {\sigma _{i,j}^{2}}, {}\\ \end{array}$$

where w j is a vector of weight values given to particular comparisons to experimental conditions. Again, the advantage to doing this is that the parameter space can be constrained in such a way that only optimal parameter sets in particular subregions are considered.

What is interesting to note is if the optimisation procedure is carried out for multiple weight vectors, w j . The resulting multi-dimensional space of C(w) values forms what is known as a Pareto front. Pareto fronts are often used in other engineering disciplines where one wishes to consider trade-offs between multiple different optimal situations. Whilst this principle is only just starting to be used for biological problems, it can provide researchers with an interesting view of their systems (see Shoval et al. (2012) for an example). For example, given a specific biological system, model, and dataset, one could obtain a range of parameter sets but find that some are robust to environmental perturbations but sensitive to genetic manipulations, whilst other parameter sets have the opposite properties. Thus, researchers will understand how to manipulate their biological system for future applications depending on the functions they want the system to achieve (e.g. robustness to environmental variation).

3.3 Parameter Identifiability Problem

Upon obtaining your optimal parameter set, post-analysis of the parameter search space can be informative in deciding which experiments should be conducted in future to obtain more accurate information about the biological system of choice. As eluded to above, if a particular direction within parameter space is flat, this implies that the parameter can take any value without altering the scoring function C. Such a case leads to an identifiability problem, i.e. this parameter is non-identifiable from the current datasets being used during optimisation (Raue et al. 2009). Following the theory produced in Raue et al. (2009) (and sources therein), non-identifiability of a parameter can be assessed by looking at how the scoring function C changes as one parameter, α, is fixed and all others are re-optimised. If the difference between new and previous optimal scores (\(\Delta C_{\alpha } = C_{\alpha }^{\mathrm{new}} - C_{\alpha }^{\mathrm{opt}}\)) is less than a specific threshold, then the parameter is non-identifiable.

The question is whether any further experiments could be conducted that would render this parameter identifiable (Fig. 13.4). There are two forms of non-identifiability:

  • Practical non-identifiability (Fig. 13.4b)

    \(\Delta C_{\alpha }\) is less than the threshold in one or both directions. This implies that the confidence interval is infinite. In principle, this means that the amount and quality of the data is insufficient to obtain a good estimate for this kinetic rate.

  • Structural non-identifiability (Fig. 13.4c)

    \(\Delta C_{\alpha }\) is perfectly flat. This implies that a functional relationship between model parameters exists. To cure this one needs to change the model by taking into account qualitatively new data (e.g. from a new experimental condition).

Fig. 13.4
figure 4

Parameter identifiability as observed by re-optimising parameter α . (a) The parameter α is identifiable since fixing the value of α in both directions (increasing and decreasing) and re-optimising all other parameters increases the optimal score beyond a given threshold (dashed line). (b) The parameter α is practically non-identifiable since \(\Delta C_{\alpha }\) only increases above the threshold when α is decreased. (c) The parameter α is structurally non-identifiable since \(\Delta C_{\alpha }\) does not increase above the threshold regardless of α being increased or decreased

Full size image

Thus, by assessing multiple parameter fits between a model and data, one can understand where information is lacking about a given biological system and design experiments to appropriately remedy the situation. In the next section, we shall assume that a model has been constructed and an optimal, identifiable parameter set has been obtained. We shall then discuss how principles of biological phenomena can be validated and assessed to provide new insights into biological mechanisms.

4 Model Analysis, Validation, and Experimentation

At this point, the researcher should have a complete mathematical model with optimal rates that allow for simulations to closely match measured data. However, this is not the end of the modelling process. What we have currently is a model that describes the data that we already know. The next step is to assume that this model represents the idealised biological system—at least to the extent that it captures the relevant features—and to determine what new insights into the network can be made through analysis. The analysis of mathematical models does not necessarily follow a strict protocol and different researchers have different preferred techniques. Hence, although there have been some preliminary attempts at automation, we shall discuss here our own opinions on how model analysis can be performed (MacDonald et al. 2011; Rausenberger et al. 2011; Song et al. 2012; Rybel et al. 2014; Gabor and Banga 2015; Seaton et al. 2015).

4.1 Validating a Model Against Data Unused in Optimisation

An important aspect of mathematical analysis is the predictive power of the model. In principle, this means that although the model has been constructed to match a particular dataset, the model should still be able to match newly obtained data not used during model development and optimisation. Consequently, there are three possible results:

  • Case 1: the model quantitatively matches the validation dataset.

    This situation implies that the model (and the obtained kinetic rates) is a sufficient representation of the biological system.

  • Case 2: the model qualitatively matches the validation dataset.

    The model captures the main effects, but there is an error either in the model or the obtained parameter set.

  • Case 3: the model does not match the validation dataset.

    In this case, the model is, in some way, structurally incorrect and is missing elements. Thus, our initial idealisation of the biological system being studied is incorrect.

Arguably, cases 2 and 3 are the most interesting for researchers. These cases require further research and new experiments to be conducted to improve the model’s accuracy. This leads to an improved understanding of how biological systems function.

So how should one divide their datasets into test data (used in parameter optimisation) and validation data? This question often has no answer and differs from researcher to researcher, but in principle one requires the test dataset to be large enough that each parameter of the system can be adequately predicted but no more than that. Such a dataset could incorporate measurements obtained from wild-type or unperturbed conditions plus measurements from a small subsection of genetic perturbations. The validation dataset could then include measurements from the rest of the genetic perturbations plus data from different experimental conditions that would alter any model inputs.

4.2 Obtaining Experimentally Testable Hypotheses

Upon finding that model simulations do not match the validation dataset, the aim of the researcher is to find out why and whether any modifications to the model would allow one to describe both the test and validation data. As with model construction there are two issues at play. In the first, one could look to re-optimise the biological rates in a multi-experiment fit by incorporating the validation data into the test dataset. The resulting model would then need to be validated against new data to determine whether the model is describing biological reality. In the second case, one should look at whether the mathematical model needs to be altered in order to describe both the test and validation data. It is these steps that provide researchers with the opportunity to obtain new biological insights.

Let us say that, based on previous knowledge and assumptions, a model has been created that is able to match the biological process of an unperturbed system. However, simulations of a genetic perturbation do not match the experimental data. There could be two potential cases: the model shows no response to a genetic perturbation whereas experiments show changes to (e.g. increased) expression levels of a model component, or; the model shows the opposite response to those observed experimentally (decreased simulated expression compared to observed experimental increases). The first example could be rectified by a re-optimisation of the system parameters to produce a stronger simulated response upon network perturbations. In the second case, though, it is likely that the model is missing a particular type of regulation—in this instance, where the model simulates decreased expression given a genetic perturbation but data shows increased expression, then it is possible the network is missing some form of feedback regulation.

Only by computationally experimenting with the mathematical model can the range of plausible missing mechanisms be found. Such experimentation is quicker and cheaper than performing similar tests experimentally in the lab (a more practical advantage of mathematical modelling). Furthermore, if one is able to find a simple solution to match model simulations with experimental data, then this can be tested in the lab with extra genetic perturbations or conducting experiments under new conditions.

4.3 Design Principles: Relating Model Variables/Parameters to the Emergence of Biological Phenomena

By this point, one should now have a model (with corresponding parameter estimates) that can describe all the available datasets. As stated above, we can now believe that the mathematical system is an idealised version of biological reality. Consequently, one may be interested in more philosophical discussions. For example, what is the mechanism present in the model that is the most important for the emergence of a specific biological phenomena? What is the core model structure required that maintains the desired response? These questions can be highly illuminating for a number of reasons, but arguably the most important reason is that one can relate simple theoretical mechanisms to biological phenomena.

To highlight this point, we refer back to our earlier example of biological oscillators. The most recent mathematical model of the plant circadian clock is a highly complex system comprising multiple feedback mechanisms (Pokhilko et al. 2012). However, it has been known for nearly 50 years that stable oscillations can arise in simple negative feedback systems comprising of three components with a reaction that produces a sufficient amount of time delay within the network (Goodwin 1965). This has been experimentally shown by the creation of a synthetic oscillator in E. coli (Elowitz and Leibler 2000). Thus, why is such a complex network required for circadian regulation of plant function? It turns out, though, that the plant circadian model can be conceptually simplified to a model that is highly reminiscent of the synthetic oscillator (Pokhilko et al. 2012). Furthermore, model analysis has highlighted that this simple mechanism is able to qualitatively describe large amounts of data obtained from experiments in plants (De Caluwé et al. 2016). Thus, it appears that the circadian clock in plants (and potentially in other species) has evolved from a simple core structure to a more complex mechanism.

5 Conclusions

In this chapter we have attempted to cover as many of the topics that we feel are important to construct accurate and useful mathematical models of biological systems. We hope that one can observe that models can be constructed for a range of reasons, whether that be to design new biological systems or to understand the emergence of phenomena in existing networks. Crucially, the critical point of model construction is to determine which modelling technique one can use given the data that is available. Thus, it is vitally important that one understands the basic assumptions behind different mathematical concepts in order to create a meaningful coarse-grained model. Upon making this choice, the following steps of model construction and analysis are fairly homogeneous for all model types. Whilst modelling has proven useful in many areas of science and industry, we hope that this introduction will aid the development of future models to elucidate the biological mechanisms required for pollen tip elongation.