Graphical Method in CATIA for Side Mill Tool Profiling Using the Generating Relative Trajectories

Abstract

A new graphical solution is proposed, for profiling the side mill which generates a cylindrical helical surface with constant pitch. The method uses a specific complementary theorem: the generating trajectories theorem. This is a new express form of the theorems of surface generation. A graphical solution is presented. This solution is developed in the CATIA design environment. Examples of this new method application are presented, for profiling side mill tools which generate cylindrical helical surfaces with constant pitch used in industry.

1 Introduction

The issue of side mill tools’ profiling, tools bounded by revolution peripheral primary surfaces, for generation of cylindrical helical surfaces with constant pitch (e.g: helical flutes of the cutting tools; gear worms; driven screws or worms for pumps) has analytical solutions, [1], based on Olivier theorems, Gohman theorem, Nikolaev condition, as so as based on complementary theorem: the method of “minimum distance” or the method of “substitutive circles” [2].

Also, concerns for graphical solution of this problem exist: the grapho–analytical method, V.M. Vorobiev, for profiling side mill which generate the flute of the helical drill. This approach proposes a graphical representation of the in–plane sections curves of the drill’s flute and, from here, the graphical representation of the future side mill.

The development of the graphical design environment allows elaborating some graphical methods, as the method of the solid model, Baicu [3], which creates a solid model of the worm to be generated. Subsequent, this model is revolved around the axis of the future side mill. In this way, the determining of the solid model of tool is permitted and, from here, the axial section of the tool, as base for profiling the secondary order tool, which will generate the primary peripheral surface of the side mill.

Similarly solutions are proposed by Veliko and Nankov [4], regarding the profiling of tools for generation of helical involute tooth.

Also, the authors use the solid modelling for determining the shape of actually surface generated with a side mill of which model is determined [4, 5].

Berbinschi [6], using the capabilities of the CATIA software, developed an original methodology for modelling the side mill for generating a cylindrical helical surface with constant pitch—the normal projection of the side mill tool’s axis method, basic, the Nikolaev theorem. This method is very precise, intuitive and easy to apply.

The method allow determining the characteristic curve—the contact curve between the revolution surface and the helical surface to be generated—avoiding the uncertainties regarding the existence of the singular points onto composed profiles, as so as, the “shadow” zones in the relative position of side mill’s axis regarding the surface to be generated.

Also, the 3D modelling was used by Li et al. [7] for modelling the thread generation using the side mill tools. The contact with blank is modelled and the generating problems are analyzed for various positions of the tool regarding the blank’s axis.

In this paper, is proposed a new methodology, developed in the CATIA design environment, for profiling side mill which generate a cylindrical helical surface with constant pitch. The method is developed based on the complementary theorem of the “relative generating trajectories” method [8], as new approach for the enwrapping surfaces’ study.

The method is a graphical one and avoids the complicated equations which can be difficult to handle in case of analytical profiling for tools which generate certain piece’s profile.

The 3D tool’s models can be used for machining the tools using CNC machine–tools.

2 The Relative Generating Trajectories Method

The contact between the cylindrical helical surface with constant pitch and the revolution surface is analyzed regarding the primary peripheral surface of the side mill (revolution surface) in planes perpendicular to the axis of the side mill, see Fig. 1.

Fig. 1

Relative position of side mill tool’s axis regarding the helical surface; reference systems

They are defined the reference systems:

XYZ is the reference system joined with the Σ surface, with Z axis overlapped to the axis $\overrightarrow {V}$ of the helical surface;

X ₁ Y ₁ Z ₁—reference system joined with the axis of the future side mill, the Z ₁ axis, overlapped with the axis $\overrightarrow {A}$ of the side mill tool’s primary peripheral surface;

a—distance, measured on the common normal between the axes Z and Z ₁ (constructive value).

It is accepted that the Σ surface, in its own reference system, XYZ, is described by parametrical equations, in form:

$$ \varSigma \quad \left| {\begin{array}{*{20}c} {X = X\left( {u,v} \right);} \\ {Y = Y\left( {u,v} \right);} \\ {Z = Z\left( {u,v} \right),} \\ \end{array} } \right. $$

(1)

with u and v independent variable parameters.

For the in-plane crossing sections, Z ₁ = H (H—variable), it is defined the intersection curve between the plane and the Σ surface, the in-plane curve Σ _H :

$$ C_{{\varSigma_{H} }} \quad \left| {\begin{array}{*{20}c} {X_{1} = X_{1} \left( u \right);} \\ {Y_{1} = Y_{1} \left( u \right);} \\ {Z_{1} = H.} \\ \end{array} } \right. $$

(2)

The last equation of system (2) represents, in fact, a geometrical locus onto the helical surface, which, from algebraic point of view, is a dependency between the u and v variable parameters, on type:

$$ v = v\left( u \right). $$

(3)

The enwrapping of the relative trajectories of curves Σ _H , for H arbitrary variable, regarding the reference system of the tool’s peripheral surface, determines a geometrical locus which represents the side mill tool’s peripheral surface, reciprocally enveloping with the Σ helical surface. The generation process kinematics assumes to make the movements assembly presented in Fig. 2:

Fig. 2

Helical surface generation kinematics

• helical movement of the Σ surface (of the blank) with axis $\overrightarrow {V}$ and helical parameter p (the assembly of movements I and II);

• rotation movement of the side mill, the rotation around the axis $\overrightarrow {A}$, as cutting movement.

The relative generating trajectories are defined as trajectories of points belong to the helical surface regarding the reference system of the future side mill in the movement assembly I, II and III.

The characteristic curve of the Σ surface, in the 3 movements assembly does not depend from this component of moving in which the surface is self-generated. In this way, the characteristic curve will depend only by the rotation around the $\vec{A}$ axis.

Consequently, it is possible to state that: the enwrapping of a helical surface, in the rotation movement around a fixed axis is the enwrapping of the relative trajectories family generated in the rotation movement of the curves which represent the in-plane sections of the helical surface, perpendicular to the rotation axis.

In this way, the relative trajectories family, described by the curves on type (2), for H arbitrary variable, is described by the equations:

$$ \left( {C_{{\varSigma_{H} }} } \right)_{\upvarphi } \quad \left| {\begin{array}{*{20}c} {X_{1} = X_{1} \left( u \right)\,\cos \upvarphi - Y_{1} \left( u \right)\,\sin \upvarphi ;} \\ {Y_{1} = X_{1} \left( u \right)\,\sin \upvarphi + Y_{1} \left( u \right)\,\cos \upvarphi ;} \\ {Z_{1} = H,} \\ \end{array} } \right. $$

(4)

with H arbitrary variable.

The enwrapping of the $\left( {C_{{\varSigma_{H} }} } \right)_{\upvarphi }$ relative trajectories family, for H variable, represents the revolution surface, which is the side mill’s primary peripheral surface.

The enwrapping condition

The normal, in the current point of the Σ _H curve, see (2), has the parametrical equations:

$$ N_{{\varSigma_{H} }} \left| {\begin{array}{*{20}c} {X_{1} = X_{1} \left( u \right) + \lambda \,\mathop {Y_{{1_{u} }} ;}\limits^{ \bullet } } \\ {Y_{1} = Y_{1} \left( u \right) - \lambda \,\mathop {X_{{1_{u} }} ,}\limits^{ \bullet } } \\ \end{array} } \right. $$

(5)

with λ variable scalar parameter.

In the rotation movement of the Σ _H curve around the $\vec{A}$ axis, the normal (5) describes a straight lines family, with φ–family’s parameter:

$$ \left( {N_{{\varSigma_{H} }} } \right)_{\upvarphi } \,\left| {\begin{array}{*{20}c} {X = \left[ {X_{1} \left( u \right) + \lambda \mathop {Y_{{1_{u} }} }\limits^{ \bullet } } \right]\,\cos \upvarphi - \left[ {Y_{1} \left( u \right) - \lambda \mathop {X_{{1_{u} }} }\limits^{ \bullet } } \right]\,\sin \upvarphi ;} \\ {Y = \left[ {X_{1} \left( u \right) + \lambda \mathop {Y_{{1_{u} }} }\limits^{ \bullet } } \right]\,\sin \upvarphi + \left[ {Y_{1} \left( u \right) - \lambda \mathop {X_{{1_{u} }} }\limits^{ \bullet } } \right]\,\cos \upvarphi ,} \\ \end{array} } \right. $$

(6)

representing the family of normals to the Σ _H curves.

For λ = 0, the Eq. (6) represents the generating relative trajectories family (4).

The assembly of these points, for H variable, represents a geometrical locus onto the Σ surface, the characteristic curve, common for S and Σ.

The imposed condition is reduced to condition that the $\left( {N_{\varSigma } } \right)_{\upvarphi }$ family intersecting the $\vec{A}$ rotation axis, in the Z ₁ = H plane, hence, to pass through P point, with coordinates:

$$ P\quad \left| {\begin{array}{*{20}c} {X_{1} = 0;} \\ {Y_{1} = 0;} \\ {Z_{1} = H.} \\ \end{array} } \right. $$

(7)

The (6) and (7) conditions can be reduced to form:

$$ X_{1} \left( u \right)\,\mathop {X_{1u} }\limits^{ \bullet } + Y_{1} \left( u \right)\,\mathop {Y_{1u} }\limits^{ \bullet } = 0, $$

(8)

for H variable.

For a variation of H between limits constructively defined by Σ surface’s form and dimensions, let this H _min and H _max , see Fig. 1, the (4) and (8) equations assembly represents the coordinates of points from the characteristic curve, onto Σ, in principle in a matrix form:

$$ C_{\varSigma } = \left( {\begin{array}{*{20}c} {X_{11} } & {Y_{11} } & {H_{1} } \\ \vdots & \vdots & \vdots \\ {X_{1i} } & {Y_{1i} } & {H_{i} } \\ {X_{1n} } & {Y_{1n} } & {H_{n} } \\ \end{array} } \right), $$

(9)

where, X _1i , Y _1i , are coordinates of the current point onto the characteristic curve.

By revolving the (9) characteristic curve around the $\vec{A}$ axis, see Fig. 1, the side mill primary peripheral surface is determined:

$$ \left( {\begin{array}{*{20}c} {X_{1} } \\ {Y_{1} } \\ {Z_{1} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \,\theta } & { - \sin \,\theta } & 0 \\ {\sin \,\theta } & {\cos \,\theta } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {X_{i} } \\ {Y_{i} } \\ {H_{i} } \\ \end{array} } \right)_{i = 1,2, \ldots ,n} , $$

(10)

with θ angular parameter, in the rotation movement around the $\vec{A}$ axis.

The axial section of the side mill is determined in the (R, H) reference system, from (10), using equations:

$$ S_{A} \,\left| {\begin{array}{*{20}c} {R = \sqrt {X_{1i}^{2} + Y_{1i}^{2} } ;} \\ {H = H_{ix} ,} \\ \end{array} } \right. $$

(11)

with i = 1,…, n, regarding the form and dimensions of the generated helical surface, see Fig. 3.

Fig. 3

Side mill tool’s axial section

3 Applications

3.1 Side Mill for the Helical Flute of a Helical Drill

The helical flute of a drill is a composite cylindrical helical surface with constant pitch, see Fig. 4. This surface is a ruled helical surface, with generatrix $\overline{AB}$ and a helical surface with curved generatrix, the $\widehat{BC}$ arc, see Fig. 4.

Fig. 4

Composed helical surface of the flute

The XYZ reference system is defined, with Z axis overlapped to the dill’s axis. In this reference system the generatrix of the helical flute (AB and BC zones) are defined.

• The AB generatrix

In the XYZ reference system, the AB generatrix has equations:

$$ \left| {\begin{array}{*{20}l} {X = - u\,\sin \chi ;} \hfill \\ {Y = - \frac{{d_{0} }}{2};} \hfill \\ {Z = u\,\cos \chi ,} \hfill \\ \end{array} } \right. $$

(12)

with u variable parameter, between limits:

$$ u_{\hbox{min} } = 0;\,u_{\hbox{max} } = \sqrt {\frac{{D^{2} }}{4} - \frac{{d_{0}^{2} }}{4}} \cdot \frac{1}{\sin \chi }, $$

(13)

where d ₀ is the drill’s core diameter (constructive value).

So, the helical surface with axis $\vec{V}$ (Z) and p helical parameter has equations:

$$ \varSigma_{AB} \,\left| {\begin{array}{*{20}l} {X = - u\,\sin \chi \cdot \cos v + \frac{{d_{0} }}{2}\,\sin v;} \hfill \\ {Y = - u\,\sin \chi \cdot \sin v - \frac{{d_{0} }}{2}\,\cos v;} \hfill \\ {Z = u\,\cos \chi + pv.} \hfill \\ \end{array} } \right. $$

(14)

The Σ _AB helical surface is a cylindrical helical surface with constant pitch, with p helical parameter, see Fig. 2,

$$ p = \frac{D}{2 \cdot \tan \omega }, $$

(15)

where D is the drill’s diameter.

The specific enwrapping condition, see (8), assumes to know the surface’s equations in the side mill’s reference system, see Fig. 1 and transformation.

From (14), results the parametrical equations of the ruled helical surface in the X ₁ Y ₁ Z ₁ reference system, for the AB zone:

$$ \varSigma_{AB} \,\left| {\begin{array}{*{20}l} {X_{1} = - u\,\sin \chi \cdot \cos v + \frac{{d_{0} }}{2}\,\sin v - a;} \hfill \\ {Y_{1} = \left[ { - u\,\sin \chi \cdot \sin v - \frac{{d_{0} }}{2}\,\cos v} \right]\,\cos \alpha + \left[ {u\,\cos \chi + pv} \right]\,\sin \alpha ;} \hfill \\ {Z_{1} = - \left[ { - u\,\sin \chi \cdot \sin v - \frac{{d_{0} }}{2}\,\cos v} \right]\sin \alpha + \left[ {u\,\cos \chi + pv} \right]\,\cos \alpha .} \hfill \\ \end{array} } \right. $$

(16)

The $C_{{\varSigma_{H} }}$ curve is determined from the intersection condition between the Σ surface with plane

$$ Z_{1} = H. $$

(17)

From (17) results:

$$ u = \frac{{H - \frac{{d_{0} }}{2}\,\cos v \cdot \sin \alpha - pv \cdot \cos \alpha }}{\sin \chi \cdot \sin v \cdot \sin \alpha + \cos \chi \cdot \cos \alpha } $$

(18)

From (16) the partial derivatives are defined:

$$ \begin{aligned} \mathop {X_{1u} }\limits^{ \bullet } & = - \frac{du}{dv}\,\sin \chi \,\cos v + u\,\sin \chi \,\sin v - \frac{{d_{0} }}{2}\,\cos v \\ \mathop {Y_{1u} }\limits^{ \bullet } & = \left[ { - \frac{du}{dv}\,\sin \chi \,\sin v - u\,\sin \chi \,\cos v + \frac{{d_{0} }}{2}\,\sin v} \right]\,\cos \alpha \\ & \quad + \left[ {\frac{du}{dv}\,\cos \chi + p} \right]\,\sin \alpha , \\ \end{aligned} $$

(19)

$$ \frac{du}{dv} = \frac{{A\left( {u,v} \right)}}{{B^{2} \left( {u,v} \right)}}, $$

(20)

where:

$$ \begin{aligned} A\left( {u,v} \right) & = \left[ {\frac{{d_{0} }}{2}\sin v \cdot \sin \alpha - p\cos \alpha } \right] \cdot \left[ {\sin \chi \cdot \sin v \cdot \sin \alpha + \cos \chi \cdot \cos \alpha } \right] \\ & \quad - \left[ {H - \frac{{d_{0} }}{2}\cos v \cdot \sin \alpha - pv \cdot \cos \alpha } \right]\sin \chi \cos v\sin \alpha ; \\ B\left( {u,v} \right) & = \sin v \cdot \sin \chi \cdot \sin \alpha + \cos \chi \cdot \cos \alpha . \\ \end{aligned} $$

(21)

A solution for determining the enwrapping condition is proposed. The values X ₁ (u), Y ₁ (u), $\mathop {X_{1u} }\limits^{ \bullet }$ and $\mathop {Y_{1u} }\limits^{ \bullet }$ are defined from (16) to (21).

• The BC generatrix

The flute for chip removing corresponds with the circle arc BC, see Fig. 5.

Fig. 5

Geometric elements generated in CATIA

It is proposed a solution for generation of the helical drill’s flute, which avoid the singular points and the discontinuities onto the axial profile of the future side mill, see Fig. 4.

The generating profile of the flute for chip removing is composed from a circle arc with R ₀ radius, in a plane tangent to the cylinder which represent the drill’s core and, at the same time, tangent to the rectilinear profile of the cutting edge, Fig. 4.

The BC circle’s arc equations:

$$ \begin{aligned} & X = R_{0} \,\cos \kappa - R_{0} \,\cos \theta ; \\ & Y = - \frac{{d_{0} }}{2}; \\ & Z = - R_{0} \,\sin \kappa + R_{0} \,\sin \theta ; \\ \end{aligned} $$

(22)

with θ variable parameter.

The upper limit of the θ parameter is:

$$ \theta_{\hbox{max} } = \text{arc} \,\cos\,\left[ {\frac{1}{{R_{0} }}\left( {R_{0} \cos \kappa - \sqrt {\frac{{D^{2} }}{4} - \frac{{d_{0}^{2} }}{4}} } \right)} \right], $$

(23)

with κ working angle of the main cutting edge.

R ₀ is constructive value.

In this way, the equations of the helical flute Σ _BC have become:

$$ \varSigma_{BC} \left| \begin{aligned} X = & \left[ {R_{0} \,\cos \kappa - R_{0} \,\cos \theta } \right]\,\cos v + \frac{{d_{0} }}{2}\,\sin v; \\ Y = & \left[ {R_{0} \,\cos \kappa - R_{0} \,\cos \theta } \right]\,\sin v\, - \frac{{d_{0} }}{2}\,\cos v; \\ Z = & - R_{0} \,\sin \kappa + R_{0} \,\cos \theta + pv. \\ \end{aligned} \right. $$

(24)

In the reference system of the side mill, Fig. 1, the Eq. (24) become:

$$ \varSigma_{BC} \left| \begin{aligned} X_{1} =& R_{0} \,\left( {\cos \kappa - \cos \theta } \right)\,\cos v + \frac{{d_{0} }}{2}\,\sin v - a; \\ Y_{1} = & \left[ {R_{0} \,\left( {\cos \kappa - \cos \theta } \right)\,\sin v - \frac{{d_{0} }}{2}\,\cos v} \right]\,\cos \alpha \\ & + \left( { - R_{0} \,\sin \kappa + R_{0} \,\cos \theta + pv} \right)\,\sin \alpha ; \\ Z_{1} = & - \left[ {R_{0} \,\left( {\cos \kappa - \cos \theta } \right)\,\sin v - \frac{{d_{2} }}{2}\,\cos v} \right]\,\sin \kappa \\ & + \left( { - R_{0} \,\sin \kappa + R_{0} \,\sin \theta + pv} \right)\,\cos \alpha . \\ \end{aligned} \right. $$

(25)

The equations of the crossing section of Σ _BC surface, with orthogonal planes of the future side mill, are deduced, Fig. 1:

$$ Z_{1} = H\,,\left( {H{-\!\!-}{\text{arbitrary variable}}} \right), $$

(26)

$$ \begin{aligned} & \quad - \left[ {R_{0} \,\left( {\cos \kappa - \cos \theta } \right)\,\sin v - \frac{{d_{0} }}{2}\,\cos v} \right]\,\sin \alpha \\ & \quad + \left( { - R_{0} \,\sin \kappa + R_{0} \,\sin \theta + pv} \right)\,\sin \alpha = H. \\ \end{aligned} $$

(27)

Results:

$$ \begin{aligned} \theta & = \text{arc} \,\cos\left[ {\frac{{H + R_{0} \,\cos \kappa \,\sin v\,\sin \alpha + R_{0} \,\sin \kappa \,\cos \alpha }}{{R_{0} \,\left( {\sin v\,\sin \alpha + \cos \alpha } \right)}}} \right. \\ & \quad - \left. {\frac{{\frac{{d_{0} }}{2}\,\sin v\,\sin \alpha + pv\,\cos \alpha }}{{R_{0} \,\left( {\sin v\,\sin \alpha + \cos \alpha } \right)}}} \right]. \\ \end{aligned} $$

(28)

The derivatives are defined as:

$$ \begin{aligned} \frac{d\theta }{dv} & = \frac{1}{{R_{0}^{2} \,\left( {\sin v\,\sin \alpha + \cos \alpha } \right)^{2} }} \cdot \left[ {\left( {R_{0} \,\cos \kappa \,\cos v\,\sin \alpha - \frac{{d_{0} }}{2}\,\cos v\,\sin \alpha } \right.} \right. \\ & \quad - \left( { - p\,\cos \alpha } \right)\left( {\sin v\,\sin \alpha + \cos \alpha } \right)\,R_{0} - R_{0} \,\left( {H + R_{0} \,\cos \alpha \,\sin v\,\sin \alpha } \right. \\ & \quad \left. { + \left. {R_{0} \,\sin \kappa \,\cos \alpha - \frac{{d_{0} }}{2}\,\sin v\,\sin \alpha - pv\,\cos \alpha } \right)\left. {\cos v\,\sin \alpha } \right)} \right]. \\ \end{aligned} $$

(29)

Also, see (8), the partial derivatives are defined:

$$ \begin{aligned} \dot{X}_{1v} & = R_{0} \sin \theta \frac{d\theta }{dv}\sin v - R_{0} \left( {\cos \kappa - \cos \theta } \right)\sin v - \frac{{d_{0} }}{2}\cos v; \\ \dot{Y}_{1v} & = \left[ {\left( {R_{0} \cos \kappa - \cos \theta } \right)\cos v + R_{0} \sin \theta \frac{d\theta }{dv}\sin v + \frac{{d_{0} }}{2}\sin v} \right]\cos \alpha \\ & \quad + \left( { - R_{0} \sin v + p} \right)\sin \alpha . \\ \end{aligned} $$

(30)

The Eqs. (25), (29) and (30) allow to write the condition (8) and to determine the shape of side mill which generates the BC arc from the drill’s profile.

For a particular case, the values are: D = 20 mm, d ₀  = 2.5 mm, χ = 60°, a = 150 mm, p = 17.320 mm, α = 60°, R ₀  = 20 mm.

4 Graphical Method Developed in CATIA

The proposed graphical method supposes the following algorithm.

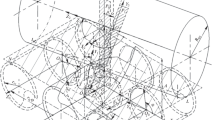
Two reference systems are generated in the Generative Shape Design module, see Fig. 5. The two reference systems are: XYZ as reference system joined with the Σ surface, with Z axis overlapped to the axis of helical surface and X ₁ Y ₁ Z ₁ reference system joined with the future side mill tool. This last reference system has the Z ₁ axis overlapped to the axis of the side mill. The distance between the origins of the reference systems is denoted with a and is measured on the common normal between the axes Z and Z ₁. The value of this distance is selected from constructive reasons.

The angle between the tool’s axis and the axis of the helical surface can be established as angular parameter and can be calculated as function of the helical parameter and the diameter of directrix helix of the Σ surface:

$$ \alpha = \text{arc} \,{ \tan }\left( {\frac{{p_{E} }}{\pi \cdot D}} \right), $$

(31)

where p _E is the helix pitch and D is the external diameter of the helical surface.

In the XYZ reference system, the cylindrical helix with constant pitch is defined. This helix is the directrix curve of helical surface.

In the XY plane of this reference system, the composed profile is constructed. This profile defined the frontal section of the helical drill’s flute.

Using the SWEEP command, the flute’s helical surface is generated, having as directrix the cylindrical helix with constant pitch and as generatrix the flute’s composite profile. The option for the swept surfaces is “with pulling direction”, the guide curve is the helix and the pulling direction is Z axis.

A length type parameter, H, is defined. This parameter will control the position of the plane Z ₁ = H.

Is constructed a plane parallel with X ₁ Y ₁, at distance H from this. Changing the value of the H parameter is easy to change the position of plane where is studied the contact between the helical surface and the revolution one. Intersecting this plane with the helical surface is obtained an in-plane curve, Σ _H , see Fig. 5.

It is generated the point M as intersection between the plane Z ₁ = H and Z ₁ axis. In the plane Z ₁ = H is drawn a skew composed by two line segments. The first segment, L₁ line from Fig. 5, is constricted to has an end onto the ∑ _H curve and the other end in the intersection point between Z ₁ = H plane and the Z ₁ axis.

The second segment, line L₂ from Fig. 5, is constricted to have the midpoint onto the end of first segment, which is onto the in-plane curve. One more restriction is imposed, the tangency between the L₂ line and the curve ∑ _H . After this, a last perpendicularity restriction between the two segments is applied. It is determined the intersection between the helical surface and the L₁ line.

In this way, is determined a point onto the ∑ surface, the C point, see Fig. 5. The normal to ∑ surface, which pass through this point, intersect the tool’s axis. According to the “generating trajectories” theorem, this point belongs to the characteristic curve.

This intersection point is retained with command ISOLATE and a new point onto the characteristic curve is determined, for a new value of the H parameter.

In this way, is possible to determine a discrete form of the characteristic curve, establishing enough points on it.

The characteristic curve’s coordinates as so as the axial section of the side mill are presented in Table 1.

Table 1 Coordinates of the characteristic curve and axial section

The axial section of the side mill is presented in Fig. 6.

Fig. 6

Axial section of the side mill

5 Conclusions

The relative generation trajectories method as complementary new method for study of geometrical process of surfaces enwrapping, applied for determining of active profile for side mill generating a helical flute with constant pitch is an original solution for profiling tools which generate by enwrapping.

Based on the proposed method was developed an graphical algorithm in CATIA design environment for determining the characteristic curve at contact between a cylindrical helical surface with constant pitch and a revolution surface, with known axis position.

The graphical method is prove as rigorous and easy to apply, allowing to avoid determining errors which can emerge due to inexact positioning of the side mill axis.

The graphical algorithm allows knowing the coordinates of points from characteristic curve in the reference system of the side mill primary peripheral surface.