1 Modelling Considerations

In plane strain conditions, the general system of equations under consideration consists of the momentum and energy balance equations which can be written as,

$$\begin{aligned} \sigma _{ji,j}= & {} 0 , \end{aligned}$$
(1)
$$\begin{aligned} \rho c \dot{T}= & {} \alpha T_{,ii} + \varPhi . \end{aligned}$$
(2)

where index notation is applied (\(i=1,2\)), the over imposed dot denotes time differentiation and comma denotes spatial differentiation. In this system, \(\alpha \) is the thermal conductivity, \(\sigma _{ij}\) is the stress tensor, T is the temperature, \(\rho \) the density, c the specific heat capacity and \(\varPhi \) the mechanical work dissipated into heat. The temperature diffusion equation (2), was derived by neglecting the higher order energy terms, like the thermo-elastic heating and by combining the energy balance law with the second law of thermodynamics.

In addition, we adopt the stress decomposition \(\sigma _{ij}= p \delta _{ij} + s_{ij}\), with p the volumetric mean stress and \(s_{ij}\) the deviatoric stress. For such a problem, we formulate the governing equations in the equivalent coordinate system where the stress tensor is rotated such that its elements are the mean stress \(p=I_1/3\) and the von Mises stress \(q = \sqrt{3 J_2}\). In these expressions \(I_1 = tr(\sigma _{ij})\) is the first invariant of the stress tensor and \(J_2 = s_{ij}s_{ij}/2\). The corresponding coordinate transformation dates back to Levy [4] and has the form:

$$\begin{aligned} \sigma _{11} = p - q \sin 2 \psi ,\quad \sigma _{22} = p + q \sin 2 \psi ,\quad \sigma _{12} = \sigma _{21} = q \cos 2 \psi , \end{aligned}$$
(3)

where \(\psi \) is the rotation angle of the coordinate system.

The mechanical dissipation takes the form (see also [7, 11]) \(\varPhi = \beta \sigma _{ij} \dot{\varepsilon }^p_{ij}\), where \(\beta \) is the Taylor-Quinney coefficient [10]. In order to close the system of equations, we need to provide a mechanical constitutive law. To that end, we first split the strain rate into elastic (reversible) and plastic (irreversible) parts \(\dot{\varepsilon }_{ij} = \dot{\varepsilon }^e_{ij} + \dot{\varepsilon }^p_{ij}\). For the elastic component we adopt a linear elastic law of the form \(\dot{\varepsilon }^e_{ij} = C^{-1}_{ijkl} \dot{\sigma }_{kl}\).

For the irreversible part, we assume that the Helmholtz free energy is invertible, such that the evolution of the plastic strain depends on the stress and temperature and takes the following form,

$$\begin{aligned} \dot{\varepsilon }^p_{ij} = \dot{\varepsilon }_0 \, e^{-T_0/T} \langle f(\sigma _{ij})\rangle \frac{\partial g}{\partial \sigma _{ij}}, \end{aligned}$$
(4)

where \(\dot{\varepsilon }_0\) is a reference strain rate, where \(T_0\) is the activation temperature for the thermal hardening mechanism, f is the so called over-stress function [8], g is the plastic potential function and the Macaulay brackets \(\langle \cdot \rangle \) ensure zero plastic strain before yield. This decomposition is supported by experimental data at elevated temperatures, below the phase transition temperature of the material [2] and the two most representative constitutive responses of temperature and rate dependent materials are an Arrhenius-type dependency on temperature, with either a power-law or an exponential dependency on stress. The function \(f(\sigma _{ij})\) is an arbitrary flow stress function.

The exact form of the constitutive equation is not prescribed during the analysis of the bifurcation in order to emphasize the generic nature of the formulation, where the onset of plastic deformation is derived from the basic assumptions of the energetics. The only important aspect of the constitutive response of the material is that it must obey a visco-plastic relationship linking the plastic strain-rate with the stress. This is required so that in the steady-state limit of the equations (\(\dot{\sigma }_{ij} = \dot{T} = 0\)) the mechanical dissipation remains non-zero. Finally, as shown in earlier studies (see for example [6]), the choice of the form of the temperature dependence of the plastic flow law is not central for the results of the present study and the Arrhenius type exponential dependency is the one that allows for the most convenient mathematical treatment.

2 Energy Bifurcation

We start by studying the steady-state limit of the system, in which \(\dot{T} = \dot{\sigma }_{ij} = 0\). Therefore, in this regime the elastic contribution is neglected and the problem reduces to that of the study of the response of a rigid (visco-)plastic material. This setting can therefore be considered to be a direct extension of the slip line field theory to thermo-visco-plastic materials. We note that in the present formulation the temperature equation (2) is active only when dissipation is non-zero. Since this is achieved in the post-yield regime, we expect that the orientation of possible localization planes would arise from the characteristics of the stress equilibrium, in accordance with the theory of plasticity [4].

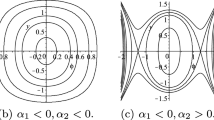
At the point of initial yield, where the temperature equation is inactive, the response of the system is governed by the stress equilibrium equations. We assume a generalized yield surface at a reference temperature of the form \(q = q_Y(p)\). In order to find the characteristics of the hyperbolic differential stress equilibrium equations (slip lines) we substitute the Levy stress transformations Eq. (3), into the stress equilibrium, Eq. (1). The slip lines are parametrized in terms of the arc-length s and the slopes of the characteristics along the \(x_1\)- and \(x_2\)-axes read

$$\begin{aligned} \frac{\partial x_1}{\partial s_k} = \frac{\mu ^{(k)}}{\sqrt{1+\mu ^{(k)2}}},\quad \frac{\partial x_2}{\partial s_k} = \frac{1}{\sqrt{1+\mu ^{(k) 2}}}, \quad (k = 1,2) \end{aligned}$$
(5)

where \(\mu ^{(k)}\) is the kth left eigenvalue of the stress equilibrium equations. For a general yield surface q(p)

$$\begin{aligned} \mu ^{(1,2)} = \frac{\mp \sqrt{1-h^2}+\cos (2\psi )}{h + \sin (2\psi )} \end{aligned}$$
(6)

and the quantity \(h = q'_Y(p)\) is a generalized pressure modulus. Note that in this expression p must be critical, i.e. equal to its yield value. For incompressible materials \(h = 0\).

Rescaling Eq. (1), along the characteristics Eq. (5) provide the generalized Hencky’s equations

$$\begin{aligned} 0 = \sqrt{1-h^2}\, p_s \pm 2 q \psi _s. \end{aligned}$$
(7)

In the case of a von Mises material, where \(q_Y = k =const.\), Eq. (6) simplifies (as \(h=0\)) to the familiar form \( \mu ^{(1)} = -\tan \psi , \, \mu ^{(2)} = \cot \psi \), and the corresponding traces are commonly known as \(\alpha \)/\(\beta \)-slip lines. Along the slip lines Eq. (7) reduce to the classical Hencky’s equations \(p \pm 2 k \psi = C_{\alpha ,\beta }\).

The energy balance can be brought into dimensionless form by setting

$$\begin{aligned} \theta = \frac{T - T_b}{T_b},\quad \hat{x}_i = \frac{x_i}{L_{i}}\ (i=1,2), \quad Ar = \frac{T_0}{T_b}, \end{aligned}$$
(8)

where \(T_b\) is the boundary temperature and \(L_{i}\) is an appropriate length scale. Since we are interested in deformation taking place under isothermal boundary conditions the final dimensionless equation is rescaled along the characteristics to obtain (the superimposed hats are dropped for convenience)

$$\begin{aligned} \frac{\partial ^2 \theta }{\partial s^2} + Gr^{1D} \exp \left( \frac{Ar\, \theta }{1 + \theta } \right) = 0, \end{aligned}$$
(9)

where the Gruntfest number admits the following form

$$\begin{aligned} Gr^{1D} = \frac{\beta \dot{\varepsilon }_0 L^2}{\alpha T_b} \frac{\mu ^2}{\left( 1+\mu ^2 \right) ^2}e^{-Ar} \sigma _{ij} \langle f(\sigma _{ij}) \rangle \frac{\partial g}{\partial \sigma _{ij}}, \end{aligned}$$
(10)

where L is a length scale. This Gruntfest number is spatially dependent through \(\mu \), and also incorporates the dimensionality of the system at hand, through L.

Fig. 1
figure 1

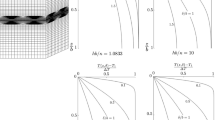
a Folded S-curve. Along the branch AB the solution of Eq. (9) corresponds to an isothermal temperature profile whereas along the section between the turning points B and C the solutions localizes. b Examples of the one-dimensional spatial pattern of the dissipation profile for \(Ar = 10\). The profiles are normalized with respect to the maximum value of dissipation

Full size image
Fig. 2
figure 2

a The thermal heat cross observed in warm metals when forged [5]. b Geometry of the problem configuration. A square is deformed by applying either a constant force F or constant velocity v at the right hand side of the sample. The sample is pinned on the left and in the y-direction. At the centre ‘A’ the sample is probed for various quantities. The theoretical analysis presented in the previous sections for a rate-dependent von Mises material suggests that the slip lines of this model run diagonally across the specimen and are represented by dashed lines [5]

Full size image
Fig. 3
figure 3

Heat lines under fast constant velocity loading. The heat lines emerge from an initially homogeneous temperature state. The heat lines follow the slip lines and can be observed as a localisation of a mechanical dissipation and b temperature

Full size image

In Fig. 1, we present the steady state response of the system with respect to the Gruntfest number, in a bifurcation diagram expressed for the dissipation function \(\phi \). We find three distinct steady states of alternating stability. The unstable branch BC corresponds to a localization instability across the characteristic trace for the normalized dissipation function \(\phi \). Since in Fig. 1a the branches AB and CD are stable in the dissipation the unstable branch BC cannot be admitted and the solution jumps from stable near isothermal homogeneous plastic deformation on AB to localized near adiabatic deformation on CD. The saddle point B therefore corresponds to the necessary condition for the loss of ellipticity of the thermomechanical system, after which localisation is progressively achieved. It is a similar condition to the traditional jump conditions for stress and velocity discontinuities in the classical slip line field solution but is expressed here in terms of their product, the dissipation.

This transition from homogeneous to localized deformation is shown in Fig. 1b, where the normalized dissipation is shown to localize towards the center of the domain as it crosses the unstable BC branch of the S-curve (see also the results of [6, 11]). The critical threshold for the transition from the stable branch AB to the new steady state CD is characterized by the turning point B.

To showcase this condition, we consider the simple heat cross localisation pattern of Fig. 2a. The mathematical problem can be idealised following Fig. 2b, to obtain localisation of temperature (dissipation) along the slip lines of the mechanical deformation when \(Gr > Gr_B\) (Fig. 3). No localisation is observed before the turning point of the S-curve.

3 Conclusion

In this work we have summarised an energy based localisation theory for temperature sensitive viscoplastic materials. The generalisation of this criterion for more complicated physics is straightforward as shown recently in the literature [1, 9, 12].