Keywords

1 Introduction

Previous chapters describe different types of additivity models (e.g., dose additivity, independent action) and examples of their application in toxicology (Chap. 9) and epidemiology (Chap. 10), while a later chapter deals with modeling additivity in risk assessment (Chap. 14). This chapter focuses on statistical considerations in applying concepts of dose additivity. The framework for testing hypotheses of additivity for chemical mixtures has transitioned beyond traditional multiple regression models with cross-product terms for interaction. Instead, mixture data are compared to an additivity model with statistically rigorous hypothesis tests. The motivating feature is that additivity models can be estimated with design support from only single chemical dose-response data instead of the impractical design required for estimation of a full response surface. For example, the design required to build an additivity model for a mixture of J components is J dose-response curves. Assuming a control group and 4 dose groups per chemical to allow for nonlinearity, the design would include 5 J design points. With 10 components, there would be 50 design points. In contrast, consider a factorial design to support a response surface with only two levels for each component (assuming linear relationships which cannot be tested with such a design); the full factorial design includes 2J design points. With 10 components, this would require an impractical 1024 design points. Fractional factorial designs reduce the number of design points but at the cost of assumptions about interactions that cannot be tested. As the number of components increases, the strategy of building additivity models that accommodate nonlinear dose-response shapes is appealing. Tests for interaction are based on comparing experimental mixture data or models of experimental mixture data to predictions constructed from single chemical data under an assumption of additivity.

This chapter illuminates this strategy using three different basic assumptions about the underlying response surface from single chemical data. When the dose-response curves for J components in a mixture of interest have a common maximum effect, the additivity model may be readily parameterized assuming the same parametric form for each component (e.g., Casey et al. 2004). In contrast, Rajapakse et al. (2004) consider parametric models from a set of possible models and select the “best model fit” for each component separately. The additivity surface is defined based on the dose addition definition using the selected models. This approach allows for different maximum effects per chemical. The limitation is that the prediction under additivity is constrained to be no greater than the maximum effect of the component with the lowest maximum. Finally, this limitation is not relevant when the dose-response curves are adequately represented by Hill functions with Hill parameter (slope factor) of 1 (e.g., Howard et al. 2010). Details of these strategies are described in the next section. The approaches are illustrated with mixture and corresponding single chemical data for six chemicals in an estrogen receptor-alpha reporter gene assay.

2 Definition of Additivity

Dose addition (used herein synonymously with concentration addition) is a widely used concept that assumes the expected combination effect of a mixture of chemicals is such that the components exert their effect without influencing each other’s action (Berenbaum 1985; Casey et al. 2004; Gennings et al. 2004; Scholze et al. 2014; U.S EPA 2000). Therefore, the expected combination effect may be predicted from single chemical dose-response data. In particular, consider a mixture of J chemicals where single chemical dose-response data are available on each. Dose addition satisfies the assumption of planar contours of constant response: i.e.,

$$ \sum \limits_{j=1}^J\frac{d_j}{{\mathrm{ED}}_{j,y}}=1 $$
(11.1)

where d j is the dose of the j th component in the mixture and ED j, y is the dose of the j th component alone that produces the same response level (y) as the mixture. Eq. 11.1 refers to a J-dimensional plane – i.e., planar contours of constant response. A schematic of a three-dimensional planar contour is given in Fig. 11.1 for chemicals X1, X2, and X3. An important consideration is the metameter (magnitude of the observed phenomenon) of the definition. Typically, the assumption is that additivity applies on the dose scale and not on the log-dose scale; or said another way, if the assumption holds on the dose scale, it generally will not be true on another scale (e.g., log-dose scale). Another definition of additivity is independent action which is based on statistical definitions of independence (e.g., Bliss 1939; Greco et al. 1992) but is not considered herein (see Chap. 9 for a discussion of independent action).

Fig. 11.1
figure 1

Schematic of a planar contour of constant response on an additivity surface

Full size image

3 Building Additivity Models

Several strategies have been used to build additivity models using single chemical data (see a conceptual discussion of additivity in Chap. 9). The most general is to use a “best fit” model to dose-response data from each chemical (Scholze et al. 2001). Various nonlinear regression models (e.g., logistic function, Hill function, Gompertz, exponential models; parameterizations of some are provided in Sect. 11.6) for monotonic sigmoidal (or partial sigmoidal) relationships are fit independently to the same data set, and the best fitting model is selected on the basis of a statistical goodness-of-fit test. The corresponding dose additivity model given by Eq. 11.1 is estimated for specified mixtures by defining the inverse functions for each dose-response curve (i.e., the ED values in Eq. 11.1). A limitation of this flexible approach is that the dose addition concept cannot be applied to effect levels that exceed the maximal effect of the least efficacious compound present in the mixture (Scholze et al. 2014). Scholze et al. (2014) extend the approach by using a novel toxic unit extrapolation method, which does not have this limitation.

Less generally, the same nonlinear dose-response function (e.g., Hill function with Hill parameter equal to 1; Howard et al. 2010) is assumed for each single chemical while allowing for different maximal effects for each chemical. Under the simplifying assumption of a common slope estimate, the combined effect of any combination of full and partial agonists can be calculated using the definition of additivity in Eq. 11.1. When the assumptions of a common background effect and maximum effect for all active chemicals are appropriate, simplifying forms of predicting under additivity are available (Casey et al. 2004).

To illustrate, without loss of generality, consider the combination of two chemicals A and B. Under the best fit model strategy, assume the dose-response relationship for chemical A is best fit with a four parameter nonlinear logistic model: \( {\mu}_0={\alpha}_A+\frac{\left({\gamma}_A-{\alpha}_A\right)}{1+{\left(\frac{d_A}{C_A}\right)}^{\beta_A}} \) with inverse function \( {\mathrm{ED}}_A=\exp \left[\frac{\log \left\{\frac{\gamma_A-{\mu}_0}{\mu_0-{\alpha}_A}\right\}+{\beta}_A\log {C}_A}{\beta_A}\right] \), where C is the inflection point (i.e., the ED50) and β is the Hill slope at C. Assume the dose-response curve for chemical B is best fit with a four parameter Gompertz model: μ 0 = α B  + (γ B  − α B ) exp [exp − (β 0,B  + β 1,B d B )] with inverse function \( {\mathrm{ED}}_B=\frac{-\log \left[\log \left\{\frac{\mu_0-{\alpha}_B}{\gamma_B-{\alpha}_B}\right\}\right]-{\beta}_{0,B}}{\beta_{1,B}} \). Under the assumption of dose addition, the combination [d A , d B ] associated with response μ 0 (i.e., the isobole) satisfies the equation \( \frac{d_A}{{\mathrm{ED}}_A}+\frac{d_B}{{\mathrm{ED}}_B}=1 \), which is the equation of a line with intercept ED A and slope \( -\frac{{\mathrm{ED}}_A}{{\mathrm{ED}}_B} \). Scholze et al. (2001) estimate the combination dose with the confidence interval constructed by bootstrap sampling of the original data and re-estimation of the combination dose associated with the mean of observed dose groups. This general strategy is readily generalized to J chemicals in combination.

In comparison, Howard et al. (2010) assumed all concentration-response curves were Hill functions with Hill parameter equal to 1, i.e., \( {\mu}_j=\frac{\alpha_j{d}_j}{\kappa_j+{d}_j} \), j = A,B, where κ j is the macroscopic dissociation equilibrium constant (i.e., equivalent to the effective concentration causing 50% of maximal response) and α j is the maximal effect level of the j th ligand in the tissue or system under study. In this case, substituting the Hill function into Eq. 11.1, under dose addition, the combination of [d A , d B ] associated with response μ 0 is given by \( {\mu}_0=\frac{\alpha_A{d}_A/{\kappa}_A+{\alpha}_B{d}_B/{\kappa}_B}{1+{d}_A/{\kappa}_A+{d}_B/{\kappa}_B} \). Howard et al. (2010) used a nonparametric Mann-Whitney test to assess the fit of the modeled response surface to experimental mixtures data. This general strategy is readily generalized to J chemicals in combination.

Finally, following the approach of Casey et al. (2004), without loss of generality that other nonlinear functions may be used, assume the dose-response curves for both chemicals are adequately represented by the nonlinear Gompertz function with common maximum effect parameter and intercept, i.e., μ A,B  = α + (γ − α) exp [exp − (β 0 + β A d A  + β B d B )]. This function is algebraically manipulated into the form of Eq. 11.1 for contour specified by μ 0 : i.e., \( \frac{d_A}{{\mathrm{ED}}_A}+\frac{d_B}{{\mathrm{ED}}_B}=1 \), where \( {\mathrm{ED}}_j=\frac{-\log \left(\log \left\{\frac{\mu_0-\alpha }{\gamma -\alpha}\right\}\right)-{\beta}_0}{\beta_j} \) and j = A,B. Thus, the additivity model has linear contours of constant response (i.e., isoboles). Goodness-of-fit of the additivity model to the single chemical data may be assessed graphically by overlaying observed and additivity model predicted dose-response estimates on the same graph. Again, this general strategy is readily generalized to J chemicals in combination.

4 Hypothesis Tests Comparing Mixture Data to Predicted Model Under Additivity

Goodness-of-fit tests are used by Howard et al. (2010) to assess the fit of the modeled additivity response surface to the experimental data. For example, the Mann-Whitney test (i.e., Wilcoxon rank sum test) tests the hypothesis that the experimental data and modeled data come from the same distribution. A significant p value (e.g., p < 0.05) indicates that the distributions differ.

In contrast, the strategy described by Scholze et al. (2014) for predicting additivity for a mixture with fixed mixing proportions by inverting Eq. 11.1 includes statistical uncertainty by applying bootstrap samples with repeated estimation of additivity – and the total dose associated with a fixed mean response. Differences between predicted and observed effect doses are considered statistically significant when the 95% confidence belt of the prediction (from the bootstrap sampling of single chemical data) does not overlap with those of the experimentally observed mixture effects.

The assumptions of the additivity model made by Casey et al. (2004) permit a statistical test of the hypothesis of additivity, which may be a Wald-type test, likelihood ratio test, or a score test. Specifically, mixture data are assumed to be available on one or more fixed-ratio ray(s). To set notation, the mixing proportion of the j th chemical in a mixture of J chemicals is a j and \( \sum \limits_{j=1}^J{a}_j=1 \). Thus, the dose of the j th chemical at total dose T is d j  = a j T. From the additivity model, using a Gompertz nonlinear model for two chemicals, the predicted dose-response curve for the mixture is given by

$$ {\displaystyle \begin{array}{c}{\mu}_{A,B}=\alpha +\left(\gamma -\alpha \right)\exp \left[\exp -\left({\beta}_0+{\beta}_A{d}_A+{\beta}_B{d}_B\right)\right]\\ {}=\alpha +\left(\gamma -\alpha \right)\exp \left[\exp -\left({\beta}_0+{\beta}_A{a}_AT+{\beta}_B{a}_BT\right)\right]\\ {}=\alpha +\left(\gamma -\alpha \right)\exp \left[\exp -\left({\beta}_0+\left({\beta}_A{a}_A+{\beta}_B{a}_B\right)T\right)\right]\\ {}=\alpha +\left(\gamma -\alpha \right)\exp \left[\exp -\left({\beta}_0+{\theta}_{\mathrm{add}}T\right)\right]\end{array}} $$

Following the approach of Casey et al. (2004), the mixture data with fixed mixing proportions are fit to a similarly parameterized model: e.g., μ mix = α mix + (γ mix − α mix) exp [exp − (β 0, mix + θ mix T)]. Then the test of additivity for the specified mixture is a test of coincidence with null and alternative hypotheses:

$$ {\displaystyle \begin{array}{c}{H}_0:\alpha ={\alpha}_{\mathrm{mix}}\;\mathrm{and}\ \gamma ={\gamma}_{\mathrm{mix}}\mathrm{and}\ {\beta}_0={\beta}_{0,\mathrm{mix}}\;\mathrm{and}\ {\theta}_{\mathrm{add}}={\theta}_{\mathrm{mix}}\\ {} vs\\ {}{H}_1:\mathrm{any}\ \mathrm{inequality}\end{array}} $$

An F test with 4 n–p degrees of freedom based on a Wald-type statistic can be used to test this hypothesis.

5 Sample Size and Power Considerations

Testing hypotheses of additivity which reject with evidence of departure from additivity should be based on study designs with adequate sample size to provide high power for detecting interaction (see Chap. 12 for further discussion of sample size and power considerations in experimental design of mixtures experiments). That is, not detecting interaction may not indicate additivity when the study design is poor (e.g., with small sample size). The location of dose/concentration groups in a study design and sample size at each group both impact the variance of slope parameters in a regression model and thereby the power for rejecting the null hypothesis of additivity. Strategies for addressing sample size and power have been described for comparison of mixture points to an additivity model (Meadows-Shropshire et al. 2005) and when comparing a model for a mixture with fixed mixing proportions compared under additivity (Casey et al. 2006).

6 Illustration

Data were extracted from graphs in Fig. 3 from Gennings et al. (2004) to provide an illustration of the methods described in this chapter and are provided in the appendix. The SAS code for the analysis presented herein is also in the appendix.

In short, six chemicals were selected for study by Gennings et al. (2004), including methoxychlor (MXC), o,p-DDT, beta-hexachlorocyclohexane (b-HCH), bisphenol A (BPA), octylphenol (OCT), and 2,3-bis(4-hydroxyphenyl)-propionitrile (DPN). An estrogen receptor-alpha (ER-α) gene transcription assay with MCF-7 human breast cancer cells was used to evaluate estrogenic activity. The data were assessed as units of luciferase activity normalized to the β-gal activity from individual wells. Experiments were evaluated with fold induction as the primary endpoint. A mixture was constituted with mixing proportions based on the no-observable-effect concentrations (NOECs) from preliminary concentration range-finding studies (data not shown). The resulting proportions were as follows: MXC = 0.4715; DPN = 0.0047; DDT = 0.4715; b-HCH = 0.0471; OCT = 0.0047; and BPA = 0.0005. Details are provided in Gennings et al. (2004).

Three models were considered for illustration of the methods and parameterized as follows:

  • Hill function with slope parameter 1 with background response of 1 for 100% fold induction: \( \mu =1+\frac{\gamma x}{{\mathrm{ED}}_{50}+d} \).

  • Four-parameter logistic model: \( \mu =\alpha +\frac{\left(\gamma -\alpha \right)}{1+{\left(\frac{d}{C}\right)}^{\beta }} \) where α is the minimum asymptote, γ is the maximum asymptote, C is the inflection point (i.e., the ED50), and β is the Hill slope at C. This model assumes symmetry around the inflection point.

  • Four-parameter Gompertz model: μ = α + (γ − α) exp [exp − (β 0 + βd)], where α and γ are as above, β 0 is a parameter associated with the lower plateau, and β is the slope parameter.

The single chemical data with model predicted curves from the Hill function, nonlinear Gompertz, and nonlinear logistic models are presented in Fig. 11.2. There is clear evidence of varying maximum effect levels across the single chemicals. Thus the strategy of Casey et al. (2004), which assumes a common maximum effect, is not justified.

Fig. 11.2
figure 2

Comparison of predicted models for single chemical data: Hill function with Hill parameter 1 (blue); nonlinear Gompertz (green); nonlinear logistic (red)

Full size image

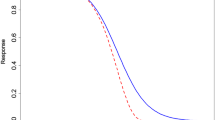
Following Howard et al. (2010), the Hill function with slope 1 was fit to each single chemical with the correction that the background response was set to 1 (i.e., the mean fold induction is 1 in the control groups): i.e., \( {\mu}_j=1+\frac{\alpha_j{d}_j}{\kappa_j+{d}_j} \) and j = 1,…,6. Under dose addition, the combination of [d 1, d 2, d 3, d 4, d 5, d 6] associated with response μ 0 is given by \( {\mu}_0=1+\frac{\sum \limits_{j=1}^6{\alpha}_j{d}_j/{\kappa}_j}{1+\sum \limits_{j=1}^6{d}_j/{\kappa}_j} \). A sign rank test was used to test the fit of the modeled additivity response surface to experimental mixture data with significant evidence of lack of fit (p < 0.001). The mixture data, predicted model, and additivity-predicted model are presented in Fig. 11.3. There is evidence that the mixture response is less than expected under additivity.

Fig. 11.3
figure 3

Observed and model predicted (blue solid) mixture data (with mixing proportion as specified in the text) using a Hill function assuming a slope of 1. The additivity model (green dashed) as predicted from single chemical data is also included, based on the Howard et al. (2010) strategy

Full size image

Following Scholze et al. (2001), the best fit models were used to estimate the additivity model for the mixture with fixed mixing proportions (Fig. 11.4) using minimum sum of squares error (SSE) as the model selection criterion. The selected models were the nonlinear Gompertz for β-HCH and OCT; the nonlinear logistic for MXC, DPN, BPA, and the mixture; and the Hill function with Hill slope and background parameters of 1 for DDT. The predicted curve under additivity for the specified mixture is restricted to the response region of the chemical component with the smallest maximum effect; here, β-HCH has maximum effect at 3.3 (Fig. 11.2); i.e., \( {t}_{\mathrm{add}}={\left(\sum \limits_{j=1}^6\frac{a_j}{\mathrm{ED}{\left({\mu}_0\right)}_j}\right)}^{-1} \) which is defined for μ 0 between 1.0 and 3.3. Scholze et al. (2014) have developed a “toxic unit extrapolation approach” to address this limitation of dose addition with combinations of chemicals with differing saturating effects; however, it is beyond the scope of this chapter.

Fig. 11.4
figure 4

Observed and model predicted (blue solid) mixture data (with mixing proportion as specified in the text) using best fit model (here, four parameter logistic model). The additivity model (green dashed) as predicted from single chemical data with best fit models is also included

Full size image

For these data, prediction of additivity was not possible for 4 of the mixture dose groups. In contrast to using a comparison of confidence bands from bootstrap samples suggested by Scholze et al. (2001), a likelihood ratio test can be conducted to test the hypothesis of additivity. The unrestricted (or full) model, based on the best fit model selection, is parameterized with each single chemical and mixture ray fit separately. Since the control group response of fold induction was set to a mean of 1.0, the models were parameterized as follows: μ = 1 + (γ j  − 1) exp [exp − (β 0j  + β j d)] for β-HCH (j = 1) and OCT (j = 2); \( \mu =1+\frac{\left({\gamma}_j-1\right)}{1+\exp \left(-\left({\beta}_{0j}+{\beta}_{1j}d\right)\right)} \) for MXC (j = 3), DPN (j = 4), BPA (j = 5), and the mixture (j = 6); and \( {\mu}_j=1+\frac{\alpha_j{d}_j}{\kappa_j+{d}_j} \) for DDT (j = 7).

Without clear evidence of a plateau, the maximum effect parameters for MXC, DPN, and BPA were set to 10, a value somewhat beyond the observed data. Thus, the total number of parameters estimated in the full model was 18, including an estimate for σ 2, with SSE(full) = 210.3 with N = 152. In comparison, the restricted model (under additivity) included only 15 parameters – those associated with the single chemical models omitting the mixture model. The prediction for the mixture is based on the dose addition model where the estimation of the restricted model is conducted with the full data set not just the single chemical data. The SSE (restricted) = 372.07. A likelihood ratio statistic is constructed as follows:

$$ {\displaystyle \begin{array}{c}{F}^{\ast }=\frac{\left(\mathrm{SSE}\left(\mathrm{rest}\right)-\mathrm{SSE}\left(\mathrm{full}\right)\right)/\Delta \mathrm{df}}{\mathrm{SSE}\left(\mathrm{full}\right)/\left(N-\mathrm{df}\left(\mathrm{full}\right)\right)}\\ {}=\frac{\left(372.07-210.31\right)/3}{210.31/\left(152-18\right)}\\ {}=34.4\end{array}} $$

Compared to an F distribution with (3, 134) degrees of freedom, p < 0.001, the hypothesis of additivity is rejected. Thus, there is evidence of departure from additivity, and the observed data are less than that predicted from additivity.

7 Summary

Generally, additivity models, supported from single chemical dose-response data, are statistically compared to mixture dose-response data (or models) to test the hypothesis of additivity. That is, single chemical dose-response data are used to estimate an additivity response surface (that satisfies the definition of additivity in Eq. 11.1) for any mixture of the components used in the estimation – assuming the same experimental conditions. Testing for evidence of departure from additivity using mixture dose-response data (i.e., a test of the goodness-of-fit of the additivity model) may follow standard statistical testing methods including Wald-type tests, likelihood ratio tests, and score tests. Wald-type tests may be based on comparison of model-based parameters (e.g., Casey et al. 2004) or predictions with bootstrap confidence bands (e.g., Scholze et al. 2014). In essence these tests are based on comparisons of prediction of mean responses for experimentally observed mixture data to that predicted from an additivity model. In contrast, likelihood ratio tests compare full and restricted likelihoods. Likelihood functions are joint probability distributions, which are evaluated at all data points (single chemical and mixture data) under the null hypothesis of additivity using only the parameters from the single chemical data. This restricted likelihood is compared to full likelihood using additional parameters to estimate the mixture mean response(s) (e.g., Gennings et al. 2004). The implementation of the likelihood ratio test simply requires the estimation of the full model (models for single chemical and mixture data) and the restricted model (including estimation of the model for the mixture data under additivity) with the likelihood calculated in each case and compared: i.e., −2(restricted loglikelihood – full loglikelihood). Finally, score tests – not illustrated herein – have the advantage of being estimated only under the null hypothesis (here, of additivity) but are not generally available in many software packages.