Abstract
As suggested by the title, it has recently become clear that theorems of Nonstandard Analysis (NSA) give rise to theorems in computability theory (no longer involving NSA). Now, the aforementioned discipline divides into classical and higher-order computability theory, where the former (resp. the latter) sub-discipline deals with objects of type zero and one (resp. of all types). The aforementioned results regarding NSA deal exclusively with the higher-order case; we show in this paper that theorems of NSA also give rise to theorems in classical computability theory by considering so-called textbook proofs.
This research was supported by FWO Flanders, the John Templeton Foundation, the Alexander von Humboldt Foundation, LMU Munich (via the Excellence Initiative), and the Japan Society for the Promotion of Science. The work was done partially while the author was visiting the Institute for Mathematical Sciences, National University of Singapore in 2016. The visit was supported by the Institute.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Computability theory naturallyFootnote 1 includes two sub-disciplines: classical and higher-order computability theory. The former deals with the computability of objects of types zero and one (natural numbers and sets thereof) and the latter deals with the computability of higher-order objects, i.e. including objects of type higher than zero and one. Friedman’s closely related foundational program Reverse Mathematics (RM for short; see [22, 23] for an overview) makes use of second-order arithmetic which is also limited to type zero and one objects; Kohlenbach has introduced higher-order RM in which all finite types are available [13].
As developed in [17, 18, 20, 21], one can extract higher-order computability results from theorems in Nonstandard Analysis. These results [18, 20, 21] involve the ‘Big Five’ of RM and also the associated ‘RM zoo’ from [7], but all results are part of higher-order RM. The following question thus naturally emerges:
(Q) Is it possible to obtain classical computability theoretic results, including second-order Reverse Mathematics, from NSA?
We will provide a positive answer to the question (Q) in this paper by studying an example based on the monotone convergence theorem in Sect. 3, after introducing Nonstandard Analysis and an essential fragment in Sect. 2. The notion textbook proof plays an important role. We also argue that our example generalises to many results in Nonstandard Analysis, as will be explored in [19].
Finally, we stress that our final results in (classical) computability theory are extracted directly from existing theorems of Nonstandard Analysis without modifications (involving computability theory or otherwise). In particular, no modification is made to the proofs or theorems in Nonstandard Analysis. We do consider special proofs in Nonstandard Analysis, which we christen textbook proofs due to their format. One could obtain the same results by mixing Nonstandard Analysis and computability theory, but one of the conceptual goals of our paper is to show that classical computability theory is already implicit in Nonstandard Analysis pur sang.
2 Internal Set Theory and Its Fragments
We discuss Nelson’s axiomatic Nonstandard Analysis from [15], and the fragment \(\textsf {P} \) from [1]. The fragment \(\textsf {P} \) is essential to our enterprise due to Corollary 2.6.
2.1 Internal Set Theory 101
In Nelson’s syntactic (or axiomatic) approach to Nonstandard Analysis [15], as opposed to Robinson’s semantic one [16], a new predicate ‘st(x)’, read as ‘x is standard’ is added to the language of ZFC, the usual foundation of mathematics. The notations \((\forall ^{\text {st}}x)\) and \((\exists ^{\text {st}}y)\) are short for \((\forall x)(\text {st}(x)\rightarrow \dots )\) and \((\exists y)(\text {st}(y)\wedge \dots )\). A formula is called internal if it does not involve ‘st’, and external otherwise. The three external axioms Idealisation, Standard Part, and Transfer govern the new predicate ‘st’; They are respectively definedFootnote 2 as:
- \({\varvec{\textsf {(I)}}}\) :
-
\((\forall ^{\text {st}~fin }x)(\exists y)(\forall z\in x)\varphi (z,y)\rightarrow (\exists y)(\forall ^{\text {st}}x)\varphi (x,y)\), for any internal \(\varphi \).
- \({\varvec{\textsf {(S)}}}\) :
-
\((\forall ^{\text {st}} x)(\exists ^{\text {st}}y)(\forall ^{\text {st}}z)\big ((z\in x\wedge \varphi (z))\leftrightarrow z\in y\big )\), for any \(\varphi \).
- \({\varvec{\textsf {(T)}}}\) :
-
\((\forall ^{\text {st}}t)\big [(\forall ^{\text {st}}x)\varphi (x, t)\rightarrow (\forall x)\varphi (x, t)\big ]\), where \(\varphi (x,t)\) is internal, and only has free variables t, x.
The system IST is (the internal system) ZFC extended with the aforementioned external axioms; The former is a conservative extension of ZFC for the internal language, as proved in [15].
In [1], the authors study fragments of IST based on Peano and Heyting arithmetic. In particular, they consider the systems \(\textsf {H} \) and \(\textsf {P} \), introduced in the next section, which are conservative extensions of the (internal) logical systems E-HA \(^{\omega }\) and E-PA \(^{\omega }\), respectively Heyting and Peano arithmetic in all finite types and the axiom of extensionality. We refer to [12, Sect. 3.3] for the exact definitions of the (mainstream in mathematical logic) systems E-HA \(^{\omega }\) and E-PA \(^{\omega }\). Furthermore, E-PA \(^{\omega *}\) and E-HA \(^{\omega *}\) are the definitional extensions of E-PA \(^{\omega }\) and E-HA \(^{\omega }\) with types for finite sequences, as in [1, Sect. 2]. For the former, we require some notation.
Notation 2.1
(Finite sequences). The systems E-PA \(^{\omega *}\) and E-HA \(^{\omega *}\) have a dedicated type for ‘finite sequences of objects of type \(\rho \)’, namely \(\rho ^{*}\). Since the usual coding of pairs of numbers goes through in both, we shall not always distinguish between 0 and \(0^{*}\). Similarly, we do not always distinguish between ‘\(s^{\rho }\)’ and ‘\(\langle s^{\rho }\rangle \)’, where the former is ‘the object s of type \(\rho \)’, and the latter is ‘the sequence of type \(\rho ^{*}\) with only element \(s^{\rho }\)’. The empty sequence for the type \(\rho ^{*}\) is denoted by ‘\(\langle \rangle _{\rho }\)’, usually with the typing omitted.
Furthermore, we denote by ‘\(|s|=n\)’ the length of the finite sequence \(s^{\rho ^{*}}=\langle s_{0}^{\rho },s_{1}^{\rho },\dots ,s_{n-1}^{\rho }\rangle \), where \(|\langle \rangle |=0\), i.e. the empty sequence has length zero. For sequences \(s^{\rho ^{*}}, t^{\rho ^{*}}\), we denote by ‘\(s*t\)’ the concatenation of s and t, i.e. \((s*t)(i)=s(i)\) for \(i<|s|\) and \((s*t)(j)=t(|s|-j)\) for \(|s|\le j< |s|+|t|\). For a sequence \(s^{\rho ^{*}}\), we define \({\overline{s}}N:=\langle s(0), s(1), \dots , s(N)\rangle \) for \(N^{0}<|s|\). For \(\alpha ^{0\rightarrow \rho }\), we also write \({\overline{\alpha }}N=\langle \alpha (0), \alpha (1),\dots , \alpha (N)\rangle \) for any \(N^{0}\). By way of shorthand, \(q^{\rho }\in Q^{\rho ^{*}}\) abbreviates \((\exists i<|Q|)(Q(i)=_{\rho }q)\). Finally, we shall use \({\underline{x}}, {\underline{y}},{\underline{t}}, \dots \) as short for tuples \(x_{0}^{\sigma _{0}}, \dots x_{k}^{\sigma _{k}}\) of possibly different type \(\sigma _{i}\).
2.2 The Classical System \(\textsf {P} \)
In this section, we introduce \(\textsf {P} \), a conservative extension of E-PA \(^{\omega }\) with fragments of Nelson’s IST. We first introduce the system E-PA \(_{\text {st}}^{\omega *}\) using the definition from [1, Definition 6.1]. Recall that E-PA \(^{\omega *}\) is the definitional extension of E-PA \(^{\omega }\) with types for finite sequences as in [1, Sect. 2] and Notation 2.1. The language of E-PA \(_{\text {st}}^{\omega *}\) is that of E-PA \(^{\omega *}\) extended with new symbols \(\text {st}_{\sigma }\) for any finite type \(\sigma \) in E-PA \(^{\omega *}\).
Notation 2.2
We write \((\forall ^{\text {st}}x^{\tau })\varPhi (x^{\tau })\) and \((\exists ^{\text {st}}x^{\sigma })\varPsi (x^{\sigma })\) for \((\forall x^{\tau })\big [\text {st}(x^{\tau })\rightarrow \varPhi (x^{\tau })\big ]\) and \((\exists x^{\sigma })\big [\text {st}(x^{\sigma })\wedge \varPsi (x^{\sigma })\big ]\). A formula A is ‘internal’ if it does not involve ‘\(\text {st}\)’, and external otherwise. The formula \(A^{\text {st}}\) is defined from internal A by appending ‘st’ to all quantifiers (except bounded number quantifiers).
The set \({\mathcal {T}}^{*}\) is defined as the collection of all the terms in the language of E-PA \(^{\omega *}\).
Definition 2.3
The system \( \textsf {E-PA}^{\omega *}_{\text {st}} \) is defined as E-PA \(^{\omega {*}} + {\mathcal {T}}^{*}_{\text {st}} + \textsf {IA}^{\text {st}}\), where \({\mathcal {T}}^{*}_{\text {st}}\) consists of the following axiom schemas.
-
1.
The schemaFootnote 3 \(\text {st}(x)\wedge x=y\rightarrow \text {st}(y)\),
-
2.
The schema providing for each closedFootnote 4 term \(t\in {\mathcal {T}}^{*}\) the axiom \(\text {st}(t)\).
-
3.
The schema \(\text {st}(f)\wedge \text {st}(x)\rightarrow \text {st}(f(x))\).
The external induction axiom IA \(^{\text {st}}\) states that for any (possibly external) \(\varPhi \):

Secondly, we introduce some essential fragments of IST studied in [1].
Definition 2.4
(External axioms of \(\textsf {P} \) )
-
1.
\(\textsf {HAC} _{\textsf {int} }\): For any internal formula \(\varphi \), we have
$$\begin{aligned} (\forall ^{\text {st}}x^{\rho })(\exists ^{\text {st}}y^{\tau })\varphi (x, y)\rightarrow \big (\exists ^{\text {st}}F^{\rho \rightarrow \tau ^{*}}\big )(\forall ^{\text {st}}x^{\rho })(\exists y^{\tau }\in F(x))\varphi (x,y), \end{aligned}$$(2.1) -
2.
\(\textsf {I}\): For any internal formula \(\varphi \), we have
$$\begin{aligned} (\forall ^{\text {st}} x^{\sigma ^{*}})(\exists y^{\tau } )(\forall z^{\sigma }\in x)\varphi (z,y)\rightarrow (\exists y^{\tau })(\forall ^{\text {st}} x^{\sigma })\varphi (x,y), \end{aligned}$$ -
3.
The system \(\textsf {P} \) is E-PA \(_{\text {st}}^{\omega *}+\textsf {I}+\textsf {HAC} _{\textsf {int} }\).
Note that I and \(\textsf {HAC} _{\textsf {int} }\) are fragments of Nelson’s axioms Idealisation and Standard part. By definition, F in (2.1) only provides a finite sequence of witnesses to \((\exists ^{\text {st}}y)\), explaining its name Herbrandized Axiom of Choice.
The system \(\textsf {P} \) is connected to E-PA \(^{\omega }\) by the following theorem. Here, the superscript ‘\(S_{\text {st}}\)’ is the syntactic translation defined in [1, Definition 7.1].
Theorem 2.5
Let \(\varPhi (\underline{a})\) be a formula in the language of E-PA
\(^{\omega *}_{\mathrm{st}}\) and suppose  . If
. If  is a collection of internal formulas and
is a collection of internal formulas and

then one can extract from the proof a sequence of closedFootnote 5 terms t in \({\mathcal {T}}^{*}\) such that

Proof
Immediate by [1, Theorem 7.7].
The proofs of the soundness theorems in [1, Sects. 5, 6 and 7] provide an algorithm \({\mathcal {A}}\) to obtain the term t from the theorem. In particular, these terms can be ‘read off’ from the nonstandard proofs.
In light of [18], the following corollary (which is not present in [1]) is essential to our results. Indeed, the following corollary expresses that we may obtain effective results as in (2.5) from any theorem of Nonstandard Analysis which has the same form as in (2.4). It was shown in [18, 20, 21] that the scope of this corollary includes the Big Five systems of RM and the RM ‘zoo’ [7].
Corollary 2.6
If  is a collection of internal formulas and \(\psi \) is internal, and
is a collection of internal formulas and \(\psi \) is internal, and

then one can extract from the proof a sequence of closed (See footnote 5) terms t in \({\mathcal {T}}^{*}\) such that

Proof
Clearly, if for internal \(\psi \) and \(\varPhi ({\underline{a}})\equiv (\forall ^{\text {st}}{\underline{x}})(\exists ^{\text {st}}{\underline{y}})\psi (x, y, a)\), we have \([\varPhi ({\underline{a}})]^{S_{\text {st}}}\equiv \varPhi ({\underline{a}})\), then the corollary follows immediately from the theorem. A tedious but straightforward verification using the clauses (i)–(v) in [1, Definition 7.1] establishes that indeed \(\varPhi ({\underline{a}})^{S_{\text {st}}}\equiv \varPhi ({\underline{a}})\).
For the rest of this paper, the notion ‘normal form’ shall refer to a formula as in (2.4), i.e. of the form \((\forall ^{\text {st}}x)(\exists ^{\text {st}}y)\varphi (x,y)\) for \(\varphi \) internal.
Finally, we will use the usual notations for natural, rational and real numbers and functions as introduced in [13, p. 288–289]. (and [23, I.8.1] for the former). We only list the definition of real number and related notions in \(\textsf {P} \).
Definition 2.7
(Real numbers and related notions in \(\textsf {P} \) )
-
1.
A (standard) real number x is a (standard) fast-converging Cauchy sequence \(q_{(\cdot )}^{1}\), i.e. \((\forall n^{0}, i^{0})(|q_{n}-q_{n+i})|<_{0} \frac{1}{2^{n}})\). We use Kohlenbach’s ‘hat function’ from [13, p. 289] to guarantee that every sequence \(f^{1}\) is a real.
-
2.
We write \([x](k):=q_{k}\) for the k-th approximation of a real \(x^{1}=(q^{1}_{(\cdot )})\).
-
3.
Two reals x, y represented by \(q_{(\cdot )}\) and \(r_{(\cdot )}\) are equal, denoted \(x=_{{{\mathbb {R}}}}y\), if \((\forall n)(|q_{n}-r_{n}|\le \frac{1}{2^{n}})\). Inequality \(<_{{{\mathbb {R}}}}\) is defined similarly.
-
4.
We write \(x\approx y\) if \((\forall ^{\text {st}} n)(|q_{n}-r_{n}|\le \frac{1}{2^{n}})\) and \(x\gg y\) if \(x>y\wedge x\not \approx y\).
-
5.
A function \(F:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) mapping reals to reals is represented by \(\varPhi ^{1\rightarrow 1}\) mapping equal reals to equal reals as in \((\forall x, y)(x=_{{{\mathbb {R}}}}y\rightarrow \varPhi (x)=_{{{\mathbb {R}}}}\varPhi (y))\).
-
6.
We write ‘\(N\in \varOmega \)’ as a symbolic abbreviation for \(\lnot \text {st}(N^{0})\).
3 Main Results
In this section, we provide an answer to the question (Q) from Sect. 1 by studying the monotone convergence theorem. We first obtain the associated result in higher-order computability theory from NSA in Sect. 3.1. We then establish in Sect. 3.2 that the same proof in NSA also gives rise to classical computability theory.
3.1 An Example of the Computational Content of NSA
In this section, we provide an example of the higher-order computational content of NSA, involving the monotone convergence theorem, \(\textsf {MCT} \) for short, which is the statement every monotone sequence in the unit interval converges. In particular, we consider the equivalence between a nonstandard version of \(\textsf {MCT} \) and a fragment of Nelson’s axiom Transfer from Sect. 2. From this nonstandard equivalence, an explicit RM equivalence involving higher-order versions of \(\textsf {MCT} \) and arithmetical comprehension is extracted as in (3.1).
Firstly, nonstandard \(\textsf {MCT} \) (involving nonstandard convergence) is:

while the effective (or ‘uniform’) version of \(\textsf {MCT} \), abbreviated MCT \(_{\textsf {ef}}(t)\), is:
We require two equivalent [13, Proposition 3.9] versions of arithmetical comprehension, respectively the Turing jump functional and Feferman’s mu-operator, as follows


and also the restriction of Nelson’s axiom Transfer as follows:

Denote by \(\textsf {MU}(\mu )\) the formula in square brackets in (\(\mu ^{2}\)). We have the following nonstandard equivalence.
Theorem 3.1
The system \(\textsf {P} \) proves that \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \leftrightarrow \textsf {MCT} _{\textsf {ns} }\).
Proof
For the forward implication, assume \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \) and suppose \(\textsf {MCT} _{\textsf {ns} }\) is false, i.e. there is a standard monotone sequence \(c_{(\cdot )}\) such that \(c_{N_{0}}\not \approx c_{M_{0}}\) for fixed nonstandard \(N_{0}, M_{0}\). The latter is by definition \(|c_{N_{0}}- c_{M_{0}}|\ge \frac{1}{k_{0}}\), where \(k_{0}^{0}\) is a fixed standard number. Since \(N_{0}, M_{0}\) are nonstandard in the latter, we have \((\forall ^{\text {st}}n)(\exists N, M\ge n) (|c_{N}- c_{M}|\ge \frac{1}{k_{0}})\). Fix standard \(n^{0}\) in the latter and note that the resulting \(\varSigma _{1}^{0}\)-formula only involves standard parameters. Hence, applying the contraposition of \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \), we obtain \((\forall ^{\text {st}}n)(\exists ^{\text {st}} N, M\ge n)(|c_{N}- c_{M}|\ge \frac{1}{k_{0}})\). ApplyingFootnote 6 the previous formula \(k_{0}+1\) times would make \(c_{(\cdot )}\) escape the unit interval, a contradiction; \(\textsf {MCT} _{\textsf {ns} }\) follows and the forward implication holds.
For the reverse implication, assume \(\textsf {MCT} _{\textsf {ns} }\), fix standard \(f^{1}\) such that \((\forall ^{\text {st}}n^{0})(f(n)\ne 0)\) and define \(c_{(\cdot )}^{1}\) as follows: \(c_{k}\) is 0 if \((\forall n\le k)(f(n)\ne 0)\) and \(\sum _{i=1}^{k}\frac{1}{2^{i}}\) otherwise. Note that \(c_{(\cdot )}\) is standard (as \(f^{1}\) is) and weakly increasing. Hence, \(c_{N}\approx c_{M}\) for nonstandard N, M by \(\textsf {MCT} _{\textsf {ns} }\). Now suppose \(m_{0}\) is such that \(f(m_{0})=0\) and also the least such number. By the definition of \(c_{(\cdot )}\), we have that \(0=c_{m_{0}-1}\not \approx c_{m_{0}}=\sum _{i=1}^{m_{0}}\frac{1}{2^{i}}\approx 1\). This contradiction implies that \((\forall n^{0})(f(n)\ne 0)\), and \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \) thus follows. \(\square \)
We refer to the previous proof as the ‘textbook proof’ of \(\textsf {MCT} _{\textsf {ns} }\leftrightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \). The reverse implication is indeed very similar to the proof of \(\textsf {MCT} \rightarrow \textsf {ACA} _{0}\) in Simpson’s textbook on RM, as found in [23, I.8.4]. This ‘textbook proof’ is special in a specific sense, as will become clear in the next section. Nonetheless, any nonstandard proof will yield higher-order computability results as in (3.1).
Theorem 3.2
From any proof of \(\textsf {MCT} _{\textsf {ns} }\leftrightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \) in \(\textsf {P} \), two terms s, u can be extracted such that E-PA \(^{\omega *}\) proves:
Proof
We prove the second conjunct and leave the first one to the reader. Corollary 2.6 only applies to normal forms and we now bring \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \) into a suitable normal form to apply this corollary and obtain the second conjunct of (3.1). Clearly, \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \) implies the following normal form:
The nonstandard convergence of \(c_{(\cdot )}\), namely \((\forall N,M\in \varOmega )[c_{M}\approx c_{N}]\), implies
in which we pull the standard quantifiers to the front as follows:
The contraposition of idealisation I applies to the underlined. We obtain:
and define \(K^{0}\) as the maximum of z(i) for \(i<|z|\). We finally obtain:
and (3.3) is a normal form for nonstandard convergence. Hence, \(\textsf {MCT} _{\textsf {ns} }\) implies:
and let the formula in square brackets be \(D(c_{(\cdot )}{, k, K})\), while the formula in square brackets in (3.2) is E(f, n). Then \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \) implies that
By the basic axioms in Definition 2.3, any standard functional \(\varPsi \) produces standard output on standard input, which yields
We may drop the remaining ‘st’ in the antecedent of (3.5) to obtain:
and bringing all standard quantifiers to the front, we obtain a normal form:
Applying Corollary 2.6 to ‘\(\textsf {P} \vdash \) (3.6)’, we obtain a term t such that
Define \(s(f, \varPsi )\) as the maximum of \(t(\varPsi , f)(i)\) for \(i<|t(\varPsi , f)|\). Then (3.6) implies
and we recognise the antecedent as the effective version of \(\textsf {MCT} \); the consequent is (essentially) \(\textsf {MU} (s(f, \varPsi ))\). Hence, the second conjunct of (3.1) follows. \(\square \)
Note that the normal form (3.3) of nonstandard convergence is the ‘epsilon-delta’ definition of convergence with the ‘epsilon’ and ‘delta’ quantifiers enriched with ‘st’. While the previous proof may seem somewhat magical upon first reading, one readily jumps from the nonstandard implication \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \) to (3.8) with some experience.
In conclusion, any proof of \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \leftrightarrow \textsf {MCT} _{\textsf {ns} }\) gives rise to the higher-order computability result (3.1). We may thus conclude the latter from the proof of Theorem 3.1. In the next section, we show that the latter theorem’s ‘textbook proof’ is special in that it also gives rise to classical computability-theoretic results. The latter is non-trivial since both \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \) and \(\textsf {MCT} _{\textsf {ns} }\) have a normal form starting with ‘\((\forall ^{\text {st}} h^{1})(\exists ^{\text {st}}l^{0})\)’ (up to coding). As a result, to convert the implication \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \) into a normal form, one has to introduce a higher-order functional like \(\varPsi \) to go from (3.4) to (3.5). Note that replacing the sequence of reals \(c_{(\cdot )}^{0\rightarrow 1}\) in \(\textsf {MCT} _{\textsf {ns} }\) by a sequence of rationals \(q_{(\cdot )}^{1}\) does not lower \(\varPsi \) below type two. In a nutshell, the procedure in the previous proof (and hence most proofs in Nonstandard Analysis) always seems to produce higher-order computability results.
3.2 An Example of the Classical-Computational Content of NSA
In the previous section, we showed that any proof of \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \leftrightarrow \textsf {MCT} _{\textsf {ns} }\) gives rise to the higher-order equivalence (3.1). In this section, we show that the particular ‘textbook proof’ of \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \leftrightarrow \textsf {MCT} _{\textsf {ns} }\) in Theorem 3.1 gives rise to classical computability theoretic results as in (3.13) and (3.14).
First of all, we show that the ‘textbook proof’ of Theorem 3.1 is actually more uniform than the latter theorem suggests. To this end, let \(\varPi _{1}^{0}\text {-}\textsf {TRANS} (f)\) and \(\textsf {MCT} _{\textsf {ns} }({c_{(\cdot )}})\) be respectively \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \) and \(\textsf {MCT} _{\textsf {ns} }\) from Sect. 3.1 restricted to the function \(f^{1}\) and sequence \(c_{(\cdot )}\), i.e. the former principles are the latter with the quantifiers \((\forall f^{1})\) and \((\forall c_{(\cdot )}^{0\rightarrow 1})\) stripped off.
Theorem 3.3
There are terms s, t such that the system \(\textsf {P} \) proves
All proofs are implicit in the ‘textbook proof’ of Theorem 3.1.
Proof
To establish (3.9), define the term \(t^{1\rightarrow 1}\) as follows for \(f^{1}, k^{0}\):
The proof of Theorem 3.1 now yields (3.9). Indeed, fix a standard function \(f^{1}\) such that \((\forall ^{\text {st}}k^{0})(f(k)\ne 0)\wedge (\exists n)(f(n)=0)\) and \(\textsf {MCT} _{\textsf {ns} }(t(f))\). By the latter, the sequence t(f) nonstandard convergences, while \(0=t(f)(n_{0}-1)\not \approx t(f)(n_{0})\approx 1\) for \(n_{0}\) the least (necessarily nonstandard) n such that \(f(n)=0\). From this contradiction, \(\varPi _{1}^{0}\text {-}\textsf {TRANS} (f)\) follows, and thus also (3.9).
The remaining implication (3.10) is proved in exactly the same way. Indeed, the intuition behind the previous part of the proof is as follows: In the proof of the reverse implication of Theorem 3.1, to establish \(\varPi _{1}^{0}\text {-}\textsf {TRANS} (f)\) for fixed standard \(f^{1}\), we only used \(\textsf {MCT} _{\textsf {ns} }\) for one particular sequence, namely t(f). Hence, we only need \(\textsf {MCT} _{\textsf {ns} }(t(f))\), and not ‘all of’ \(\textsf {MCT} _{\textsf {ns} }\), thus establishing (3.9). Similarly, in the proof of the forward implication of Theorem 3.1, to derive \(\textsf {MCT} _{\textsf {ns} }(c_{(\cdot )})\) for fixed \(c_{(\cdot )}\), we only applied \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \) to one specific \(\varSigma _{1}^{0}\) formula with a standard parameters \(n^{0}\) and \(c_{(\cdot )}\). \(\square \)
We are now ready to reveal the intended ‘deeper’ meaning of the term ‘textbook proof’: The latter refers to a proof (which may not exist) of an implication \((\forall ^{\text {st}}f)A(f)\rightarrow (\forall ^{\text {st}} g)B(g)\) which also establishes \((\forall ^{\text {st}}g)[A(t(g))\rightarrow B(g)]\), and in which the formula in square brackets is a formula in which all standard quantifiers involve variables of type zero. By Theorem 3.4, such a ‘textbook proof’ gives rise to results in classical computability theory.
We choose the term ‘textbook proof’ because proofs in Nonstandard Analysis (especially in textbooks) are quite explicit in nature, i.e. one often establishes \((\forall ^{st}g)[A(t(g))\rightarrow B(g)]\) in order to prove \((\forall ^{\text {st}}f)A(f)\rightarrow (\forall ^{\text {st}} g)B(g)\).
Before we can apply Corollary 2.6 to Theorem 3.3, we need some definitions, as follows. First, consider the following ‘second-order’ version of \((\mu ^{2})\):

where ‘\(\varphi _{e,s}^{A}(m)=n\)’ is the usual (primitive recursive) predicate expressing that the e-th Turing machine with input n and oracle A halts after s steps with output m; sets \(A, B, C, \dots \) are denoted by binary sequences. One easily defines the (second-order) Turing jump of A from \(\nu ^{1}\) as in \(\textsf {MU} ^{A}(\nu )\) and vice versa.
Next, we introduce the ‘computability-theoretic’ version of \(\textsf {MCT} _{\textsf {ef} }(t)\). To this end, let \(\textsf {TOT} (e, A)\) be the formula ‘\((\forall n^{0})(\exists m^{0}, s^{0})(\varphi _{e,s}^{A}(n)=m)\)’, i.e. the formula expressing that the Turing machine with index e and oracle A halts for all inputs, also written ‘\((\forall n^{0})\varphi _{e}^{A}(n)\downarrow \)’. Assuming the latter formula to hold for \(e^{0}, A^{1}\), the function \(\varphi _{e}^{A}\) is clearly well-defined, and will be used in \(\textsf {P} \) in the usualFootnote 7 sense of computability theory. We assume \(\varphi _{e}^{A}(n)\) to code a rational number without mentioning the coding. We now introduce the ‘second-order’ version of \(\textsf {MCT} _{\textsf {ef} }(t)\):

Here, t has type \((0\times 0)\rightarrow 0\) or \(0\rightarrow 1\), and we will usually treat the former as a type one object. Finally, let \(\textsf {MCT} _{\textsf {ef} }^{A}(t, e)\) and \(\textsf {MU} ^{A}(\nu , e,n)\) be the corresponding principles with the quantifiers outside the outermost square brackets removed.
Theorem 3.4
From the textbook proof of \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \), three terms \(s^{1\rightarrow 1}, u^{1}, v^{1\rightarrow 1}\) can be extracted such that E-PA \(^{\omega *}\) proves:
Proof
Similar to the proof of Theorem 3.2, a normal form for \(\varPi _{1}^{0}\text {-}\textsf {TRANS} (f)\) is:
while, for t as in (3.11), a normal from for \(\textsf {MCT} _{\textsf {ns} }(t(f))\) is:
Let C(n, f) (resp. B(k, K, f)) be the formula in (outermost) square brackets in (3.15) (resp. (3.16)). Then (3.9) is the formula
which (following the proof of Theorem 3.2) readily implies the normal form:
Applying Corollary 2.6 to ‘\(\textsf {P} _{0}\vdash \) (3.17)’ yields a term \(z^{2}\) such that
is provable in E-PA \(^{\omega *}\). Define the term \(s(f, \psi )\) as the maximum of all \(z(f, \psi )(i)\) for \(i<|z(f,\psi )|\) and note that (by the monotonicity of C):
Now define \(f_{0}^{2}\) as follows: \(f_{0}(e, n, A, k)=0\) if \((\exists m,s\le k)(\varphi _{e,s}^{A}(n)=m)\), and 1 otherwise. For this choice of function, namely taking \(f^{1}=_{1}\lambda k.f_{0}\), the sentence (3.18) implies for all \(A^{1}, \psi ^{1}, e^{0}, n^{0}\) that
where we used the familiar lambda notation with some variables of \(f_{0}\) suppressed to reduce notational complexity. Consider the term t from (3.11) and note that there are (primitive recursive) terms \(x^{1}, y^{1}\) such that for all m we have \(t(\lambda k.f_{0}(e,n,A,k))(m)=\varphi ^{A}_{x(e,n), y(e, n)}(m) \); the definition of \(x^{1}, y^{1}\) is implicit in the definition of t and \(f_{0}\). Hence, with these terms, the antecedent and consequent of (3.19) are as required to yield (3.14).
To prove (3.13) from (3.19), suppose we have \((\forall k')B(k', \xi (e,n)(k'), \lambda k.f_{0})\) for all \(e^{0}, n^{0}\) and some \(\xi ^{0\rightarrow 1} \) and \( A^{1}\), where \(\xi (e, n)\) has type 1. By (3.19) we obtain
Putting the previous together, we obtain the sentence:
Clearly, the consequent of (3.20) implies that \(s(\lambda k.f_{0}, \xi (e, n))\) provides the Turing jump of A as in \(\textsf {MU} ^{A}(\lambda e\lambda n.s(\lambda k.f_{0}, \xi (e, n)))\). On the other hand, the antecedent of (3.20) expresses that the sequence \(t(\lambda k.f_{0}(e, n, A, k))\) converges for all e, n as witnessed by the modulus \(\xi (e, n)\). In light of the definitions of \(f_{0}\) and t, the sequence \(t(\lambda k.f_{0})\) (considered as a type one object) is definitely computable from the oracle A (in the usual sense of Turing computability). Thus, the antecedent of (3.20) also follows from \(\textsf {MCT} _{\textsf {ef} }^{A}(\xi )\). In other words, (3.20) yields
which is as required for the theorem, with minor modifications to the term s. \(\square \)
Note that (3.14) expresses that in order to decide if the e-th Turing machine with oracle A and input n halts, it suffices to have the term s and a modulus of convergence for the sequence of rationals given by \(\varphi ^{A}_{u(e, n)}\). We do not claim these to be ground-breaking results in computability theory, but we do point out the surprising ease and elegance with which they fall out of textbook proofs in Nonstandard Analysis. Taking into account the claimsFootnote 8 by Bishop and Connes that Nonstandard Analysis be devoid of computational/constructive content, we believe that the word ‘surprise’ is perhaps not misplaced to describe our results.
In a nutshell, to obtain the previous theorem, one first establishes the ‘nonstandard uniform’ version (3.9) of \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \), which yields the ‘super-pointwise’ version (3.18). The latter is then weakened into (3.14) and then weakened into (3.13); this modification should be almost identical for other similar implications. In particular, it should be straightforward, but unfortunately beyond the page limit, to obtain versions of Theorems 3.3 and 3.4 for König’s lemma and Ramsey’s theorem [23, III.7], or any theorem equivalent to \(\textsf {ACA} _{0}\) in RM for that matter.
Furthermore, results related to weak König’s lemma, the third Big Five system of RM [23, IV] and the RM zoo [7], can be obtained in the same way as above. For instance, one can easily obtain \(\varPi _{1}^{0}\text {-}\textsf {TRANS} \rightarrow \textsf {WKL} _{\textsf {ns} }\) where the latter is the nonstandard modification of \(\textsf {WKL} \) stating the existence of a standard path for every standard infinite binary tree. However, the existence of a ‘textbook proof’ (as discussed right below Theorem 3.3) for this implication (or the reverse implication) leads to a contradiction.
In conclusion, higher-order computability results can be obtained from arbitrary proofs of \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \), while the textbook proof as in the proof of Theorem 3.1 yields classical computability theory as in Theorem 3.4.
3.3 The Connection Between Higher-Order and Classical Computability Theory
This paper would not be complete without a discussion of the \(\textsf {ECF} \)-translation, which connects higher-order and second-order mathematics. In particular, we show that applying the \(\textsf {ECF} \)-translation to e.g. (3.1) does not yield e.g. (3.14).
We first define the central \(\textsf {ECF} \)-notion of ‘associate’ which some will know in an equivalent guise: Kohlenbach shows in [14, Proposition 4.4] that the existence of a ‘RM code’ for a continuous functional \(\varPhi ^{2}\) as in [23, II.6.1], is equivalent to the existence of an associate for \(\varPhi \), and equivalent to the existence of a modulus of continuity for \(\varPhi \), Simpson’s claims from [23, I.8.9.5] notwithstanding.
Definition 3.5
The function \(\alpha ^{1}\) is an associate of the continuous \(\varPhi ^{2}\) if:
-
(i)
\((\forall \beta ^{1})(\exists k^{0})\alpha ({\overline{\beta }} k)>0\),
-
(ii)
\((\forall \beta ^{1}, k^{0})(\alpha ({\overline{\beta }} k)>0 \rightarrow \varPhi (\beta )+1=_{0}\alpha ({\overline{\beta }} k))\).
With regard to notation, it is common to write \(\alpha (\beta )\), to be understood as \(\alpha ({\overline{\beta }} k)-1\) for large enough \(k^{0}\) (See also Definition 3.8 below). Furthermore, we assume that every associate is a neighbourhood function as in [14], i.e. \(\alpha \) also satisfies
We now sketch the \(\textsf {ECF} \)-translation; Note that \(\textsf {RCA} _{0}^{\omega }\) is Kohlenbach’s base theory for higher-order RM [13]; this system is essentially E-PA \(^{\omega }\) weakened to one-quantifier-induction and with a fragment of the axiom of choice.
Remark 3.6
( \(\textsf {ECF} \) -translation). The translation ‘\([\cdot ]_{\textsf {ECF} }\)’ is introduced in [24, Sect. 2.6.5] and we refer to the latter for the exact definition. Intuitively, applying the \(\textsf {ECF} \)-translation to a formula amounts to nothing more than replacing all objects of type two or higher by associates. Furthermore, Kohlenbach observes in [13, Sect. 2] that if \(\textsf {RCA} _{0}^{\omega }\vdash A\) then \(\textsf {RCA} _{0}^{2}\vdash [A]_{\textsf {ECF} }\), i.e. \([\cdot ]_{\textsf {ECF} }\) provides a translation from \(\textsf {RCA} _{0}^{\omega }\) to (a system which is essentially) \(\textsf {RCA} _{0}\), the base theory of RM.
Thus, we observe that the \(\textsf {ECF} \)-translation connects higher-order and second-order mathematics. We now show that the \(\textsf {ECF} \)-translation is not a ‘magic bullet’ in that \([A]_{\textsf {ECF} }\) may not always be very meaningful, as discussed next.
Example 3.7
(The \(\textsf {ECF} \) -translation of \((\mu ^{2})\) ). The \(\textsf {ECF} \)-translation will interpret the discontinuous Footnote 9 functional \(\mu ^{2}\) as in \(\textsf {MU} (\mu )\) as a continuous object satisfying the latter formula, which is of course impossibleFootnote 10, and the same holds for theorems equivalent to \((\mu ^{2})\) as they involve discontinuous functionals as well. Hence, the \(\textsf {ECF} \)-translation reduces the implications in (3.1) to (correct) trivialities of the form ‘\(0=1\rightarrow 0=1\)’.
By the previous example, we observe that the answer to question (Q) is not just ‘apply \(\textsf {ECF} \)’ in the case of theorems involving \((\mu ^{2})\). Nonetheless, we could apply the \(\textsf {ECF} \)-translation to (3.13) and (3.14) to replace the terms s, u, v by associates. To this end, we require definition of partial function application (See e.g. [24, 1.9.12] or [12, Definition 3.58]) for the final corollary.
Definition 3.8
(Partial function application). For \(\alpha ^{1}, \beta ^{1}\), ‘\(\alpha (\beta )\)’ is defined as
and \(\alpha | \beta := (\lambda n^{0})\alpha (\langle n\rangle *\beta )\). We write \(\alpha (\beta )\downarrow \) to denote that \(\alpha (\beta )\) is defined, and \(\alpha |\beta \downarrow \) to denote that \((\alpha |\beta )(n)\) is defined for all \(n^{0}\). For \(\beta ^{1}, \gamma ^{1}\), we define the paired sequence \(\beta \oplus \gamma \) by putting \((\beta \oplus \gamma )(2k)=\beta (k)\) and \((\beta \oplus \gamma )(2k+1)=\gamma (k)\).
We now consider the following corollary to Theorem 3.4.
Corollary 3.9
From the textbook proof of \(\textsf {MCT} _{\textsf {ns} }\rightarrow \varPi _{1}^{0}\text {-}\textsf {TRANS} \), a term \(z^{1}\) can be extracted such that E-PA \(^{\omega *}\) proves:
Proof
Immediate from applying the \(\textsf {ECF} \)-translation to (3.13). \(\square \)
Note that (3.22) is part of second-order arithmetic.
Notes
- 1.
The distinction ‘classical versus higher-order’ is not binary as e.g. continuous functions on the reals may be represented by type one objects (See e.g. [23, II.6.1]).
- 2.
The superscript ‘fin’ in (I) means that x is finite, i.e. its number of elements are bounded by a natural number.
- 3.
The language of E-PA \(_{\text {st}}^{\omega *}\) contains a symbol \(\text {st}_{\sigma }\) for each finite type \(\sigma \), but the subscript is essentially always omitted. Hence \({\mathcal {T}}^{*}_{\text {st}}\) is an axiom schema and not an axiom.
- 4.
A term is called closed in [1] (and in this paper) if all variables are bound via lambda abstraction. Thus, if \({\underline{x}}, {\underline{y}}\) are the only variables occurring in the term t, the term \((\lambda {\underline{x}})(\lambda {\underline{y}})t({\underline{x}}, {\underline{y}})\) is closed while \((\lambda {\underline{x}})t({\underline{x}}, {\underline{y}})\) is not. The second axiom in Definition 2.3 thus expresses that \(\text {st}_{\tau }\big ((\lambda {\underline{x}})(\lambda {\underline{y}})t({\underline{x}}, {\underline{y}})\big )\) if \((\lambda {\underline{x}})(\lambda {\underline{y}})t({\underline{x}}, {\underline{y}})\) is of type \(\tau \).
- 5.
Recall the definition of closed terms from [1] as sketched in Footnote 4.
- 6.
To ‘apply this formula \(k_{0}+1\) times’, apply \(\textsf {HAC} _{\textsf {int} }\) to \((\forall ^{\text {st}}n)(\exists ^{\text {st}} N, M\ge n)(|c_{N}- c_{M}|\ge \frac{1}{k_{0}})\) to obtain standard \(F^{0\rightarrow 0^{*}}\) and define G(n) as the maximum of F(n)(i) for \(i<|F(n)|\). Then \((\forall ^{\text {st}}n)(\exists N, M\ge n)(N, M\le G(n)\wedge |c_{N}- c_{M}|\ge \frac{1}{k_{0}})\) and iterate the functional G at least \(k_{0}+1\) times to obtain the desired contradiction.
- 7.
For instance, written out in full ‘\(0\le \varphi _{e}^{A}(n)\le \varphi _{e}^{A}(n+1)\le 1\)’ from \(\textsf {MCT} _{\textsf {ef} }^{A}(t)\) is:
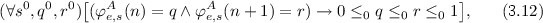
where we also omitted the coding of rationals.
- 8.
Bishop (See [4, p. 513], [2, p. 1], and [3], which is the review of [11]) and Connes (See [6, p. 6207] and [5, p. 26]) have made rather strong claims regarding the non-constructive nature of Nonstandard Analysis. Their arguments have been investigated in remarkable detail and were mostly refuted (See e.g. [8,9,10]).
- 9.
Suppose \(f_{1}=11\dots \) and \(\mu ^{2}\) from \((\mu ^{2})\) is continuous; then there is \(N_{0}^{0}\) such that \((\forall g^{1})(\overline{f_{1}}N_{0}={\overline{g}}N_{0}\rightarrow \mu (f_{1})=_{0}\mu (g))\). Let \(N_{1}\) be the maximum of \(N_{0}\) and \(\mu (f_{1})\). Then \(g_{0}:=\overline{f_{1}}N_{1}*00\dots \) satisfies \(\overline{f_{1}}N_{1}=\overline{g_{0}}N_{1}\), and hence \(\mu (f_{1})=\mu (g_{0})\) and \(f_{1}(\mu (f_{1}))=g_{0}(\mu (g_{0}))\), but the latter is 0 by the definition of \(g_{0}\) and \(\mu \), a contradiction..
- 10.
If a functional has an associate, it must be continuous on Baire space. We established in Footnote 9 that \((\mu ^{2})\) cannot be continuous, and thus cannot have an associate.
References
van den Berg, B., Briseid, E., Safarik, P.: A functional interpretation for nonstandard arithmetic. Ann. Pure Appl. Logic 163(12), 1962–1994 (2012)
Bishop, E.: Aspects of constructivism. Notes on the Lectures Delivered at the Tenth Holiday Mathematics Symposium, New Mexico State University, Las Cruces, 27–31 December 1972
Bishop, E.: Review of [11]. Bull. Amer. Math. Soc 81(2), 205–208 (1977)
Bishop, E.: The crisis in contemporary mathematics. In: Proceedings of the American Academy Workshop on the Evolution of Modern Mathematics, pp. 507–517 (1975)
Connes, A.: An interview with Alain Connes. EMS Newslett. 63, 25–30 (2007). http://www.mathematics-in-europe.eu/maths-as-a-profession/interviews
Connes, A.: Noncommutative geometry and reality. J. Math. Phys. 36(11), 6194–6231 (1995)
Dzhafarov, D.D.: Reverse Mathematics Zoo. http://rmzoo.uconn.edu/
Kanovei, V., Katz, M.G., Mormann, T.: Tools, objects, and chimeras: Connes on the role of hyperreals in mathematics. Found. Sci. 18(2), 259–296 (2013)
Katz, M.G., Leichtnam, E.: Commuting and noncommuting infinitesimals. Am. Math. Mon. 120(7), 631–641 (2013)
Keisler, H.J.: Letter to the editor. Not. Am. Math. Soc. 24, 269 (1977)
Keisler, H.J.: Elementary Calculus. Prindle, Weber and Schmidt, Boston (1976)
Kohlenbach, U.: Applied Proof Theory: Proof Interpretations and Their Use in Mathematics. Springer Monographs in Mathematics. Springer, Berlin (2008)
Kohlenbach, U.: Higher order reverse Mathematics. In: Reverse Mathematics 2001. Lecture Notes in Logic, vol. 21, pp. 281–295. ASL (2005)
Kohlenbach, U.: Foundational and mathematical uses of higher types. In: Reflections on the Foundations of Mathematics (Stanford, CA, 1998). Lecture Notes in Logic, vol. 15, pp. 92–116. ASL (2002)
Nelson, E.: Internal set theory: a new approach to Nonstandard Analysis. Bull. Am. Math. Soc. 83(6), 1165–1198 (1977)
Robinson, A.: Non-standard Analysis. North-Holland, Amsterdam (1966)
Sanders, S.: The Gandy-Hyland functional and a hitherto unknown computational aspect of Nonstandard Analysis (2015). Submitted. http://arxiv.org/abs/1502.03622
Sanders, S.: The unreasonable effectiveness of Nonstandard Analysis (2015). Submitted. arXiv: http://arxiv.org/abs/1508.07434
Sanders, S.: On the connection between Nonstandard Analysis and classical computability theory. In: Preparation (2016)
Sanders, S.: The taming of the reverse mathematics zoo. (2015). Submitted. http://arxiv.org/abs/1412.2022
Sanders, S.: The refining of the taming of the reverse mathematics zoo. Notre Dame J. Formal Logic (2016, to appear). http://arxiv.org/abs/1602.02270
Simpson, S.G. (ed.): Reverse Mathematics 2001. Lecture Notes in Logic, vol. 21. ASL, La Jolla (2005)
Simpson, S.G. (ed.): Subsystems of Second Order Arithmetic. Perspectives in Logic, 2nd edn. CUP, Cambridge (2009)
Troelstra, A.S.: Metamathematical Investigation of Intuitionistic Arithmetic and Analysis. Lecture Notes in Mathematics, vol. 344. Springer, Berlin (1973)
Acknowledgement
The author would like to thank Richard Shore, Anil Nerode, and Vasco Brattka for their valuable advice and encouragement.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Sanders, S. (2017). From Nonstandard Analysis to Various Flavours of Computability Theory. In: Gopal, T., Jäger , G., Steila, S. (eds) Theory and Applications of Models of Computation. TAMC 2017. Lecture Notes in Computer Science(), vol 10185. Springer, Cham. https://doi.org/10.1007/978-3-319-55911-7_40
Download citation
DOI: https://doi.org/10.1007/978-3-319-55911-7_40
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-55910-0
Online ISBN: 978-3-319-55911-7
eBook Packages: Computer ScienceComputer Science (R0)