Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the last fifteen years, the definition and the development of quantum programming languages catalyzed the attention of a part of the computer science research community. Quantum computers are a long term but concrete reality. Even if physicists and engineers have to continuously face tricky problems in the realization of quantum devices, the advance of these innovative technologies promises a noticeable speedup.

A calculus for quantum computable functions should present two different facets. On the first hand there is the unitary aspect of the calculus, that captures the essence of quantum computing as algebraic transformations of state vectors by means of unitary operators. On the other hand, it should be possible to control the quantum steps by means of classical computational steps, “embedding” the pure quantum evolution in a classical computation. Behind this second perspective we have the usual idea of computation as a sequence of discrete steps on (the mathematical description of) an abstract machine. The relationship between these different aspects gives rise to different approaches to quantum functional calculi (as observed in [1]). If we divide the two features, i.e. we separate data from control, we adopt the so called quantum data & classical control (\( qd \& cc\)) approach. This means that classical computation is hierarchical dependent from the quantum part: a classical program (ideally in execution on a classical machine) computes some “directives”: these directives are sent to a hypothetical device which apply them to quantum data. Therefore classical program controls quantum data or, in other words, classical computational steps control the unitary part of the calculus. In general, the classical control acts on the quantum side of the computation in two way: by means of the selection of unitary transformations to be applied and by means of data observations, i.e. by means of measurements. A different approach based on the quantum control is the superposition-of-programs paradigm. See [34], Part III, for details. This idea is inspired to an architectural model called Quantum Random Access Machine (QRAM). The QRAM has been defined in [10] and can be viewed as a classically controlled machine enriched with a quantum device. On the grounds of the QRAM model, Selinger defined the first functional language based on the quantum data-classical control paradigm [28]. This work represents a milestone in the development of quantum functional calculi and inspired a number of different investigations. A key research line tried to retrace, in the quantum setting, foundational results about computability. In this direction, calculi for quantum computable functions have been defined, and equivalence results with other computational models, such as Quantum Turing Machine and Quantum Circuit Families, have been proved [4, 11, 12, 35]. Moreover, interesting proposals to provide satisfactory denotational semantics for \( qd \& cc\) functional calculi have been proposed in [8, 19, 29]. Many quantum programming languages [7, 28, 29] implementing the (\( qd \& cc\)) approach have been proposed in literature. A recent and interesting proposal is Quipper which is an embedded, scalable functional programming language for quantum computing proposed in [28]. Quipper is essentially a high-level circuit description language: circuits can be created, manipulated, evaluated in a mixture of procedural and declarative programming styles. The most important quantum algorithms can be easily encoded thanks to a number of programming tools, macros, and extensive libraries of quantum functions. The idea of the separation between control and data is definitely reformulated in terms of quantum-coprocessor [31]. Quipper has been mainly developed as a concrete language. Authors are not interested in the foundational study of it. Quipper is based on the lambda calculus with classical control proposed in [28], and this relationship is discussed in [26], by means of a suitable calculus named Proto-quipper. In [14], the semantics of Proto-Quipper is further formalized by means of the linear specification logic SL. The type system is based on a linear logic approach that ensures the correct interaction of classical and quantum types. The “\( qd \& cc\)” philosophy, in particular the circuit generation oriented approach, has been also adopted in the purely linear core-language QWire, introduced in [22]: a low-level quantum language developed to be a “quantum plugin” for a hosting classical language like Haskell. QWire and \({\textsf {qPCF}}\) are based on some similar ideas. Differently from \({\textsf {qPCF}}\), QWire retains the focus on quantum states which is typical of the \( qd \& cc\) tradition. In \({\textsf {qPCF}}\) quantum states are not more atomic data, they are replaced by quantum circuits. In this paper we advance in the research on the languages for \( qd \& cc\) paradigm by formalizing a flexible quantum language. We propose qPCF, a simple extension of PCF. We quickly list the main features of qPCF.

  • Absence of explicit linear constraints: the management of linear resources is radically different from the ones proposed in languages inspired to Linear Logic such as [4, 11, 12, 14, 26, 28, 35]; so, we do not use linear/exponential modalities.

  • Use of dependent types: we decouple the classic control from the quantum computation by adopting a simplified form of dependent types that provide a sort of linear interface.

  • Emphasis of the Standardization Theorem: the Standardization Theorem, proved in [4, 35], and largely used in circuit description languages such as Quipper, decomposes computations in different phases, according to the quantum circuit construction by classical instructions and the successive, independent, evaluation phase involving quantum operations.

  • Unique measurement at the end of the computation: following the “principle of deferred measurement” which states that any quantum circuit is equivalent to one where all measurements are performed as the very last operations (see, e.g., [17]), we add an explicit measurement operator to qPCF syntax that models the (von Neumann) Total Measurement [17], a kind of measurement that reduces a quantum state to a classical one (a sequence of classical bit). Essentially we are using a monad-style programming, and we “embed” both, quantum evaluation and measurement into the operator \(\mathsf {dmeas}\) (see Sect. 3 for \(\mathsf {dmeas}\) operational behavior).

  • Implicit representation of quantum states: differently from other proposals (e.g. [4, 28, 35]), we hide quantum states we are working on. This can be achieved thanks to the monadic-style approach we mentioned above.

  • Turing Completeness: qPCF retains PCF expressive power. So, a qPCF term can represent an infinite class of circuits.

Synopsis: Section 2 introduces syntax and typing system of qPCF; the operational semantics of qPCF is in Sect. 3; Sect. 4 sketches some properties of qPCF; Sect. 5 contains some examples of qPCF circuit encodings; Sect. 6 is devoted to discuss conclusions and future work.

2 qPCF

In this section we describe qPCF, a programming language that pursue seriously the application of the standardization theorem of [4, 35]: it states that, in the “quantum-data & classic control languages”, the quantum evaluation can always be postponed after the classical execution. On the other hand, the classical evaluation designs a quantum circuit that can be evaluated in a second time. Ideally, qPCF computes a finite circuit description which is offloaded to a quantum co-processor for the execution. qPCF is definitively more flexible than the languages presented in [4, 19, 27,28,29]. It extends PCF with quantum circuits, viz. a new kind of classical data. Indeed, as observed in [22], quantum circuits can be freely duplicated and erased. We realized that the linearity of mainstream typing systems of “quantum-data & classic control” languages has been used to impose constraints on both the management of quantum-data and the management of classic control. qPCF neatly splits these linear facets by using two different solutions. On the one hand, qPCF shows that linearity for quantum control can be completely confined to atomic datatypes by using a simplified form of dependent types [23]. A dependent type picks up a family of types that bring in the type auxiliary information (just circuit arity in our case). On the other hand, the linearity needed to manage quantum state is hidden in a destructive measure operator (by means of an implicit form of monad) that model von Neumann Measurement [17] and allows us to avoid the explicit management of intermediate quantum states.

In the rest of the paper, we assume some familiarity with notions as quantum bits (the quantum equivalent of classical data), quantum states [15, 16, 32, 33] (systems of n quantum bits), quantum circuit and quantum circuit families [18]. A quantum circuit generalizes the idea of classical circuit, replacing the elementary classical gates (AND, OR, NOT...) by elementary quantum gates [17], that enjoy matemathical descriptions in terms of unitary operators on suitable Hilbert spaces. A quantum circuit family can be (quite informally) considered as a function \({{\mathbf {K}}}:{\mathbb {N}}\rightarrow {\mathcal {K}}\) (denotable as \((K_{i})_{i<\omega }\)), where \({\mathcal {K}}\) is the set of circuit descriptions; \({{\mathbf {K}}}({n})\) returns \(K_n\), i.e. the circuit of ariety n. See [35] for a friendly introduction to quantum computing. We remand to [17] for a complete overview about the topic. See also [9, 18] for details about quantum circuit families and some crucial discussions about the universality of sets of quantum gates. Finally, see [25] for a rigorous algebraic characterisation of quantum computing.

2.1 Syntax

Dependent types have been widely used in strongly normalizing settings (usually, with logic goals) where the evaluation of expressions is always terminating. But in programming settings the strong normalization [21] is not realistic. Unfortunately, to allow types that embeds undefined terms (viz. not strongly normalizing ones) requires the management of “undefined types” [3]. We circumvent this issue by identifying a subclass of terms (always normalizing) that we use in our dependent types. \({\textsf {qPCF}}\) extends \(\text {PCF}\) [5, 6, 24] to manage some additional atomic data structures: indexes (always normalizing number expressions) and circuits.

The row syntax of \({\textsf {qPCF}}\) follows.

In the first row we extended \(\text {PCF}\) with syntactic sugar to facilitate the bitwise access to digit: \(\mathtt {get}\) allows us to read the i-th digit of the binary representation of a numeral, i.e. its i-th bit; \(\mathtt {set}\) allows us to modify the i-th bit of a numeral.

Index expressions (ranged over by \(\mathtt {E}\)) are completely formalized via the typing (cf. Table 1). They include numerals and some total operations on expressions: (viz. sum, product).

We assume \(\mathtt {U}\) to range on a given set of selected gates (i.e. unitary operator, see [17]): if \({\mathcal {U}}\) is a fixed set of computable unitary operators then, we associate to each computable operator \({\mathbf {U}}\in {\mathcal {U}}\) a symbol \(\mathtt {U}\). We represent circuits by means of strings, viz. the Kleene-closure of the following symbols: the parallel composition of circuits denoted \(\parallel \) (i.e. side-by-side placing of circuits), the sequential composition of circuits and gate-names \(\mathtt {U}\). \(\mathtt {append}\) sequentializes two circuits of the same arity. \(\mathtt {iter}\) produces the parallel composition of a first circuit with a given numbers of a second one. The goal of the operator \(\mathtt {reverse}\) is to transform a circuit in its adjoint one (in case the gate-base has been chosen closed under adjunction, otherwise it will be meaningless).

\(\mathtt {size}\) is an operator that applied to a circuit returns its arity: an index information. It is worth to notice that \(\mathtt {size}\) do not add any expressivity to \({\textsf {qPCF}}\), because the programmer can explicitly manage pairs of “circuit together with arity”: so that, a projection provides the arity of the circuit. We added \(\mathtt {size}\) to \({\textsf {qPCF}}\) to emphasize the gain that dependent type can provide in a concrete context, although this makes the proofs of the language properties more complex.

Last, but not least, we use \(\mathtt {dMeas}\) (a.k.a. destructive measure) to evaluate circuits initialized via a numeral (representing a binary classical state): \(\mathtt {dMeas}\) returns the classic state (encoded in the binary representation of a numeral) obtained measuring the final quantum state of the considered circuit. Traditionally \( qd \& cc\) languages focus on quantum states, while \({\textsf {qPCF}}\) focuses on circuits (hiding states in an monadic measure).

Typically, \({\mathcal {U}}\) will include a universal base for quantum circuits (see [9]). We like to remark that we can instance \({\mathcal {U}}\) to interesting family of gate as reversible ones: in these cases we are not properly building a quantum programming language. If \(k\in {\mathbb {N}}\) then we denote \({\mathcal {U}}(k)\) the gates in \({\mathcal {U}}\) having arity \(k+1\), so \({\mathcal {U}}=\bigcup _0^\omega {\mathcal {U}}(k)\). Notice that we do not introduced explicit permutations, because they can be provided by means of a convenient choice of quantum gates (see, e.g. [30]). Thus, the choice \({\mathcal {U}}\) determines whose permutations our circuits can use. We also notice that the gate identity is a particular permutation.

2.2 Typing System

Standard \(\text {PCF}\) types are extended to manage circuits and their dependencies. We use types decorated by numerals to define a denumerable family of circuits. Our approach is closely inspired to that mentioned in [23, Sect. 30.5] to manage types of vectors (with dependencies): the decoration carry around some arity information. We avoided general dependent types systems (see [3] for a survey) because their great expressiveness is exceeding our need, we preferred to maintain the qPCFtype system as simple as possible by aiming to show the feasibility of the approach and its concrete benefits. Our approach to dependent types is based on a special kind of numeric expressions that can be managed in a limited way: index. Summing up, types of \(\text {PCF}\) (i.e. integers and arrows) are flanked by two new types: circuits (viz. strings typed with dependent types that carry around numeric information about arities) and indexes (that grasp a subset of numeric expressions that express only terminating expressions).

Types of \({\textsf {qPCF}}\) are formalized by the following grammar:

where \(\texttt {E}\) is an index expressions (morally, a strongly normalizing numeric expression). As in standard dependent type system, we replace arrows involving dependencies by quantified types, namely an arrow is replaced by whenever occurs in \(\tau \) in order to emphasize that \(\tau \) depends from \(\texttt {x}\).

Index. \(\textsf {Idx}\) aims to pick up a subset of expressions on natural numbers being strongly normalizing, i.e. we want to cut out undefined PCF-expressions as (viz. a looping forever term). The leading use of \(\textsf {Idx}\) is to type terms \(\mathtt {M}\) embodied in dependent types (i.e. used in types via \(\mathsf {circ(\mathtt {M})}\)). The goal is to select numeric expressions that made the equivalence decidable (when such expressions are closed). We focus on a restricted, but revealing, syntax of index expressions is where viz. operators denoting addition and multiplication. We are considering a very basic set of binary operators that can be conveniently extended in a concrete case, e.g. by adding the (positive subtraction) , or the \(\%\), or a selection and so on.

Above expressions are typed \(\textsf {Idx}\) by the following rules:

where B denotes a standard typing base, i.e. sets of pairs (variable and type).

Index expression are closed when they do not contain any free variable. As usual for \(\text {PCF}\), the evaluation is focused on closed expressions, and formalized by the following rules:

where we use the to denote both its name and its straighforward semantics. We remark that we are considering a strict subset of the index expressions of \({\textsf {qPCF}}\) in order to increase some intuition (e.g. by neglecting \(\mathtt {size}\)).

It is immediate that the above index expressions are normalizing with the proposed evaluation strategy, when we focus on closed terms. Moreover, we can informally claim that they are strongly normalizing in the straightforward lambda-calculus behind our semantics, that can be obtained as usual by including some \(\delta \)-rules for constants.

The most basic property of paradigmatic typing system is that well-typed terms do not “go wrong”, i.e. types are preserved by the evaluation and, if the evaluation stops then the result is a value.

Theorem 1

(Preservation & Progress). (i) If and then . (ii) If and then is a numeral.

Remaining typing. We can now extend the typing to the whole \({\textsf {qPCF}}\): the typing system is given in Table 1 (be careful to implicit assumption remarked in the caption).

Table 1. Typing Rules. Each typing rule contains implicit premises: (i) all occurrences of circuits types (also those in bases) embody a term typed \(\textsf {Idx}\) with the given base; (ii) all free variables (occurring in terms and types) are typed in the base.
Full size table

Finite sets of pairs variable, type are called bases whenever variable-names are disjoint: we use B to range on them. We write to denote the set where the pair is added (possibly replacing an pair involving x. As usual, dependent type systems include a typing rule making explicit some type inter-convertibility. We consider types up to a congruence \(\simeq \). We define \(\simeq \) as the smaller equivalence that includes: (i) the \(\alpha \)-conversion of bound variables and \(\beta \)-conversion, (ii) sum and product are associative and commutative; (iii) product distributes over the sum, i.e. \((*\, \texttt {E}\,(+\, \texttt {E}_0\,\texttt {E}_1))\ \simeq \ (+\, (*\,\texttt {E}\,\texttt {E}_0)(*\,\texttt {E}\,\texttt {E}_1))\); (iv) \(\mathtt{\underline{0}}\) is the neuter element for the sum; and, (v) \(\mathtt{\underline{1}}\) is the neuter element for the product. We use the type equivalence often implicitly. In particular in the typing system (cf. Table 1) types (containing dependencies) are considered up to equivalence.

Rules \((p_1),(p_2),(p_3),(p_4),(p_5),(p_6),(p_7),(p_8)\) are directly inherited from \(\text {PCF}\) and do not require special care. We also note that \((p_1)\) can be instantiated to \((i_1)\) (which has not been included in the system). Rules \((p_6)\), \((p_8)\) are restricted to excludes undefined index expressions. This restriction avoid types containing terms (i.e. index expressions) being not normalizing. The cases excluded by \((p_3)\), \((p_4)\) are managed by rules \((x_1)\), \((x_2)\). Rules \((x_1)\), \((x_2)\) reflect the usual approach of dependent types.

Rule \((b_1), (b_2)\) type \(\mathtt {get}\) and \(\mathtt {set}\) that use the second numeral to select a bit in the binary representation of the first argument: \(\mathtt {get}\) extract such bit, \(\mathtt {set}\) modify it. The rule \((x_3)\) allows us to transform an index in a numeral typed \(\textsf {Nat}\). The rule \((x_4)\) is typing an operator that allows us to recover in the computation the index information carried around by the circuit type.

Rules \((c_1)\), \((c'_1)\), \((c''_1)\),\((c_2)\), \((c_3)\), \((c_4)\), \((c_5)\) conclude our type-equipment. \((c_1)\), \((c'_1)\), \((c''_1)\) type strings representing circuits. \((c_2)\) allows to parallel compose circuits: a base circuit \(\texttt {M}\) and some copies of a circuit \(\texttt {N}\). \((c_3)\) allows to sequentialize circuits of the same arity. \((c_4)\) transforms a circuit in its adjoint one.

Example 1

An interesting example of typed term that provides evidence of the circularity arising from dependent types is: where M can be any term of \({\textsf {qPCF}}\) typed by a circuit.

The above example shows that in types can occur undefined terms, maybe containing open variables not typed \(\textsf {Idx}\). In particular, \(\mathtt {size}\) can contain any term (that can be typed as a circuit of a given arity). Luckily, the evaluation of \(\mathtt {size}\) does not need the normalization of its argument: it just requires the normalization of its type.

3 Operational Semantics

As standard for \(\text {PCF}\), the evaluation focuses on closed terms of ground types, viz. \(\textsf {Nat}\), \(\textsf {Idx}\), \(\mathtt {circ(E)}\). Because the inclusion of dependent types and the presence of the operator \(\mathtt {size}\), we assume that an evaluated terms brings implicitly in it, its whole typing information. We denote \(\mathtt {V}\) the closed values of ground types, namely numerals (typed either \(\textsf {Nat}\) or \(\textsf {Idx}\)), and strings (typed as circuits of a given arity). The operational evaluation is formalized by means of the evaluation predicate : it holds whenever it is the conclusion of a derivation built on the rules presented in Table 2 (we included also the rule for the evaluation of index expressions). Table 2 includes the standard call-by-name semantics of \(\text {PCF}\), namely the first two lines of rules. Since they are well-known, we do not insist further on them. The rules (sz), (op) compute some index expressions. In particular, (sz) recovers the numeral decorating the type circuit of a closed term. Since the involved expressions do not contain open variables, the evaluation does not pose any problem.

Table 2. Operational Semantics.
Full size table

Let be notation for \((\underbrace{(\mathtt{\underline{m}}\mathbin {/}\mathtt{\underline{2}})\ldots \mathbin {/}\mathtt{\underline{2}} }_{\mathtt{\underline{n}}})\%\mathtt{\underline{2}}\) where \(\mathbin {/}\) is the integer division and \(\%\) is the modulo. Thus, is the rightmost bit of the binary representation of \(\mathtt{\underline{m}}\). Moreover, if \(\mathtt{\underline{k}}\) is the logarithm (base 10) of \(\mathtt{\underline{m}}\) then and, for all \(\mathtt{\underline{h}}\) greater than \(\mathtt{\underline{k}}\), . The rule (gt) and (st) get/set a bit of the first argument (the one selected by the second argument). Notice that \(\mathtt {set}\), \(\mathtt {get}\) are syntactic sugar managing classical input states. In particular, the numeral \(\mathsf {set}\,\mathtt{\underline{0}}\,\mathtt{\underline{n+1}}\) represents the state \(1\underbrace{0\ldots 0}_{n}\).

The rules (u), \((u')\), \((u'')\), \((r_0)\), \((r_1)\), \((r_2)\), (a), (d) build circuits, i.e. strings on and the gate-names \(\mathtt {U}\). The semantics of \(\mathtt {append}\) is simply the sequential post-position of circuits. The semantics of \(\mathtt {iter}\) is the parallel composition of circuits, driven by an argument of type \(\textsf {Idx}\): thus the arity of the generated circuit is well defined. The semantics of \(\mathtt {reverse}\) is build to produce the adjoint circuits when a suitable endo-function \(\ddagger \) is provided by the co-processor. If the co-processor do not provide it (for instance, because the set \({\mathcal {U}}\) of unitary gate is not closed under adjunction) then we let \(\ddagger \) be the identity, so that \(\mathtt {reverse}\) is well-defined but uninteresting.

Let \(\mathtt{\underline{m}}{\mathop {\upharpoonright _{\! \mathtt{\underline{k}}}}}\) to denote the numeral \(\mathtt{\underline{k}}\) such that the binary representation of \(\mathtt{\underline{n}}\) is the restriction of the binary representation of \(\mathtt{\underline{m}}\) on the first \(\mathtt{\underline{k}}\) bits. It is worth to recall that, conventionally, each classic state is represented via an integer having (implicitly) a number of relevant bits as the arity of the circuit. The rule (m) evaluates the \(\mathtt {dMeas}\) arguments and uses the results of these evaluations to feed an external evaluation: morally, a quantum co-processor [31]. The co-processor call is done by using the auxiliary evaluation \(\text {circuitEval}\). It executes the quantum circuits on the provided classical initialization, then it returns the measure of the whole final state. The rule explicitly restricts the evaluation of the first argument to the relevant number of bits (i.e. the arity of the circuit).

In order to define our co-processor we need two ingredients. The first one is the semantic for the evaluation of the circuit. We denote Circ the valid strings of circuits, and \({\mathcal {O}}\) the set of unitary operators on finite dimensional Hilbert spaces (informally, we are mapping circuit descriptions into their mathematical denotation, i.e. into corresponding algebraic operators). So that we can define the circuit semantic by using the function defined as follows: ; ; . The second one is the semantic of the measure that rest on the von Neumann Measurement [9], here dubbed . We define to be the measure of the application of the circuit to our initial state (in the assumed base), namely .

Equivalence. The operational equivalence can be defined by just considering closed terms of type \(\textsf {Nat}\) because the operational differences in the other types can be traced back to \(\textsf {Nat}\) (the reverse can be easily proved be false).

For many reasons, we are remarking the relevance of the notion of program of \(\text {PCF}\), i.e. a closed term of type \(\textsf {Nat}\). First, the result of a circuit-measure is a list of bits, viz. a natural number. Second, the circuits are represented by using strings on a finite alphabet, that still (in a Turing-complete setting) can be straightforwardly represented by numbers (at worst, paying some code-obfuscation). These remarks should make clear why the evaluation of \({\textsf {qPCF}}\) is focused on natural numbers and the standard notion of program, as any \(\text {PCF}\)-like programming language.

4 Properties of qPCF

\({\textsf {qPCF}}\) is, morally, a PCF-like language endowed with a quantum co-processor. This co-processor allows us to execute a quantum circuits that has been designed by executing a classical control. The co-processor returns a measure (total, in the sense that we measure the whole quantum state) of a run of the given circuit on a given input, to our classical processor.

A first property of a paradigmatic programming language as \({\textsf {qPCF}}\) is some form of subject reduction. Moreover, we prove preservation, i.e. if a well-typed term takes a step of evaluation then the resulting term is also well typed. A second property expected for a programming language is progress [23]: well-typed terms evaluation do not stuck. Roughly, a term \(\mathtt {P}\) is stuck whenever the evaluation of \(\mathtt {P}\) ends in a normal form, which is not a ground value.

The main complexity in this proof comes from the fact that we have infinite (two plus a family) ground types (viz. \(\textsf {Nat}\), \(\textsf {Idx}\), \(\mathtt {circ(E)}\)). Example 1 shows that each term can occurs in a type (in an index expression using \(\mathtt {size}\)). To prove preservation and progress we must unravel the mutual relationship that holds between them.

Lemma 1

If and then and, moreover, if then .

Proof

The proof follows by induction on the derivation .

Theorem 2

(Idx -safety). If then .

Proof

The proof is quite complex but it can be done by defining a suitable predicate of computability à la Tait.

Remark that Theorem 2 is stronger than both preservation and progress, in fact it immediately implies both: (i) if \(\mathtt {M}\) is closed, and then \(\mathtt {N}\) is closed and , and (ii) if \(\mathtt {M}\) is closed, and then \(\mathtt {N}\) is a numeral.

Theorem 3

(Preservation). If \(\mathtt {M}\) is a closed term such that and then \(\mathtt {N}\) is a closed term such that .

Proof

The evaluation is applied only to terms typed by ground types, viz. \(\textsf {Nat}\), \(\textsf {Idx}\), \(\mathtt {circ(E)}\). Indeed, the rule in Table 2 are applied to them. The proof follows by proving by mutual induction on the following statements: (i) if \(\mathtt {M}\) is closed, and then \(\mathtt {N}\) is closed and ; and, (ii) if \(\mathtt {M}\) is closed, and then \(\mathtt {N}\) is closed and . The fact that we are restricting our attention on closed terms typed by ground types simplify our proof by conveniently restricting the possible cases. The proof of (i) involves only the rules \(\mathrm {(n)}\), \(\mathrm {(s)}\), \(\mathrm {(p)}\), \((\beta )\), \(\mathrm {({if}_l)}\), \(\mathrm {({if}_r)}\), \(\mathrm {(Y)}\), \(\mathrm {(gt)}\), \(\mathrm {(st)}\), \(\mathrm {(m)}\), because the others are excluded by hypothesis. The proof of (ii) involves only the rules \((\beta )\), \(\mathrm {({if}_l)}\), \(\mathrm {({if}_r)}\), \(\mathrm {(Y)}\), \(\mathrm {(u)}\), \(\mathrm {(u')}\), \(\mathrm {(u'')}\), \(\mathrm {(r_0)}\), \(\mathrm {(r_1)}\), \(\mathrm {(r_2)}\), \(\mathrm {(a)}\), \(\mathrm {(it)}\), because the others are excluded by hypothesis.

Likewise, a form of progress can be proved.

Theorem 4

(Progress)

  • If \(\mathtt {M}\) is a closed term such that and then \(\mathtt {N}\) is a numeral.

  • If \(\mathtt {M}\) is a closed term such that and then there is a numeral \(\mathtt{\underline{k}}\) such that and \(\mathtt {N}\) is a circuit of arity \(\mathtt{\underline{k}}\).

Proof

The proof is similar to the that of the Preservation Theorem.

Progress and preservation together tell us that a well-typed term can never reach a stuck state during evaluation.

We conclude this section with some preliminary comments about confluence. It is well-known that quantum-measures break the deterministic evolution of a quantum system. As a consequence, in presence of a measurement operator in a quantum language (equipped with an universal basis of quantum gates), one necessarily lost confluence. This loose of standard properties is typical in presence of “non classical” operators (this holds for examples also in languages including non deterministic or probabilistic choices [2, 13]). Given an evaluation of a program \(\mathtt {P}\), a second evaluation can ends with a different result; in particular, the results of two evaluations of a same program can be different natural numbers. Clearly, the “measurement-free” fragment of qPCF, i.e. the whole calculus minus \(\mathtt {dMeas}\) is patently deterministic. Finally, one can observe that the presence of the measure does not imply the loss of the determinism, if we limits the use of \({\textsf {qPCF}}\) to deterministic circuits (by a suitable choice of unitary operators included in \({\mathcal {U}}\), e.g. only swaps).

5 Examples

In this section we propose some higher-order encoding of quantum circuit families. In the following examples, we exploit the full expressive power of the language. A qPCF term can be parametric, viz. it can represent an entire (infinite) quantum circuit family. In general, given an input numeral \(\mathtt{\underline{n}}\) we define a term that generates the description of the n-dimensional circuit of the family. Notice that, in some sense, circuits can be parameterized both in “horizontal” and in “vertical”, that correspond to the two basic ways to built greater circuits from smaller ones, i.e. by sequential and parallel composition.

Example 2

The following term, applied to a circuit and a numeral \(\mathtt{\underline{n}}\), concatenates \(n+1\) copies of \(\mathtt {C}\).

, where

has type , with . It is easy to show that generates the circuit built upon a single copy of the circuit \(\mathtt {C}\) and so on.

It is straightforward to parameterize the above term in order to transform it in a template for a circuit-builder that can be used for any arity. It suffices to replace \(\mathtt{\underline{k}}\) with the variable and to abstract it; so that, the resulting term is typed .

Example 3

The following term, applied to a numeral \(\mathtt{\underline{n}}\) and two unitary gates \(\mathtt {U}_1\) and \(\mathtt {U}_2\) of arity \(\mathtt{\underline{k}}\) and \(\mathtt{\underline{h}}\) respectively, generates a simple circuit built upon a copy of gate \(\mathtt {U}_1\) in parallel with n copies of gate \(\mathtt {U}_2\):

It is straighforward to parameterize the above example. It suffices to replace numerals \(\mathtt{\underline{k}}\) and \(\mathtt{\underline{h}}\) in the above example by variables and to abstract, by obtaining a term typed .

Example 4

(Deutsch-Jozsa). We provide the qPCF encoding of the circuit that implements the generalised version of the Deutsch’s problem [17].

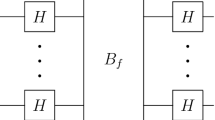
The “simple case” of Deutsch’s problem can be formulated as follows. Given a block box \({B}_f\) implementing some function \(f : \{0,1\} \rightarrow \{0,1\}\), determine whether f is constant or balanced. The classical computation to determine whether f is constant or balanced is very simple: one computes f(0) and f(1), and then check if \(f(0) = f(1)\). This requires two different calls to \({B}_f\) (i.e. one to compute f(0) and one to compute f(1)) in the classical computing model. By means of the “quantum superpower”, Deutsch showed how to achieve this result with a single call of \({B}_f\) in the quantum case.

The problem can be generalised considering a function \(f : \{0,1\}^{n} \rightarrow \{0,1\}\) which acts on many input bits. This yields the n-bit generalization of Deutsch’s algorithm, known as the Deutsch-Josza algorithm. The following picture represents the circuit, up to the last, measurement phase, for the Deutsch-Josza problem.

figure a

When fed with a classical input state of the form \(|0\ldots 01\rangle \), the output measurement of the first \(n-1\) bits reveals if the function f is constant or not. If all \(n-1\) measurement results are 0, we can conclude that the function was constant. Otherwise, if at least one of the measurement outcomes is 1, we conclude that the function was balanced. See [17] for details about Deutsch and Deutsch-Josza algorithm.

Consider now the following qPCF terms. They easily show how to encode different levels of the measurement-free parametric circuit for the Deutsch’s problem. The last, evaluation-measurement phase, will be performed by our evaluation \(\mathtt {dMeas}\), suitably fed with the representation of the classical input state (i.e. ). Let and be the (unary) Hadamard and Identity gates respectively (so the index is 0). Suppose is given for some n such that where is the \({\textsf {qPCF}}\S \)-circuit that represents the function f.

Observe that clearly generates \(x+1\) parallel copies of unary Hadamard gates \(\mathtt {H}\), and concatenates in parallel x copies of unary Hadamard gates \(\mathtt {H}\) and one copy of the unary identity gate .

Thus the generator term of the parametric measurement-free Deutsch-Jozsa circuit, here dubbed \(\mathsf {DJ^{-}}\) can be defined as

where

.

We finally evaluate \(\mathsf {DJ^{-}}\) by means of \(\mathtt {dMeas}\), providing the encoding

of the black-box function f having arity \(n+1\). Let us assume that the term evaluated by means of , yields the numeral \(\mathtt{\underline{m}}\): the rightmost \(\mathtt{\underline{n}}\) digit of the binary representation of \(\mathtt{\underline{m}}\) are the result. Notice that \(\mathsf {DJ^{-}}\mathtt{\underline{0}}{\mathsf {M}}^{B_{f}}\) returns the circuit description of Deutsch algorithm.

6 Conclusions and Future Work

We introduced qPCF, an extension of PCF for quantum circuit generation and evaluation. In this seminal work, we introduced qPCF syntax, typing rules and evaluation semantics. We started to study its properties and we provided some examples of parametric circuit families encoding. The presented research is the first step of some works in progress and for several short time investigations. First, we are further investigating qPCF properties sketched in Sect. 4. Second, we aim to deepen qPCF flexibility, e.g. studying specialization of qPCF: for example, we aim to focus on the (still “silent”) reverse operator (of the calculus), also in different settings w.r.t quantum computing. We like to remark that gates can range on different interesting sets. Since reversibility is nowadays one of the most interesting trend in computer science [20], a reversible specialization of qPCF seems to be intriguing. Even if the use of total measurement does not represent a theoretical limitation, a partial measurement operator can represent an useful programming tool. Therefore, another interesting task will be to integrate in qPCF the possibility to perform partial measures of computation results.