Keywords

1 Introduction

Overlapping Community Detection is an important approach in complex networks to understand and analysis large network character [3, 50], such as social network [30, 49], collaborative network [39], and biological network [1]. We can find most correlated overlapping sub-communities to simplify global structure to understand the network topology, and keep original network with overlapping structure especially in density network.

It is a recognition with community detection that nodes in same community are densely connected, and nodes in different communities are sparsely connected. A node can be allocated into different communities in overlapping situation [55]. We can find overlapping communities with methods as clique percolation techniques [23], random walk [18], label propagation [12, 51], seed expansion [47], objective function optimization (modularity or other function) [35], or statistical inference [11, 40, 48]. Overlapping communities can also be detected based on the graph partitioning approach, which tries to find underling clusters from minimize the number of edges between communities [8, 43].

Macropol et al. [29] propose a biologically sensitive algorithm based on repeated random walks (RRW) for discovering functional modules, e.g., complexes or pathways, within large-scale protein networks. RRW considers the element of network topology, edge weights, and long range interactions between proteins. Zhang et al. [53] propose a learning algorithm which can learn a node-community membership matrix via stochastic gradient descent with bootstrap sampling. Lee et al. [25] introduce a community assignment algorithm named Greedy Clique Expansion (GCE). GCE algorithm identifies distinct cliques as seeds and expands these seeds by greedily optimizing a local fitness function.

In many clustering applications, object data is nonnegative due to their physical nature, e.g., images are described by pixel intensities and texts are represented by vectors of word counts. As to a graph-based network, the adjacency matrix (or weighted adjacency matrix) \(\mathbf {A}\) as well as the Laplacian matrix completely represents the structure of network, and \(\mathbf {A}\) is non-negative naturally. Meanwhile, Nonnegative Matrix Factorization (NMF) was originally proposed as a method for dimension reduction and finding matrix factors with parts-of-whole interpretations [15, 27]. Based on the consideration that there is no any physical meaning to reconstruct a network with negative adjacency matrix, using NMF to obtain new representations of network with non-negativity constraints can achieve much productive effect in overlapping community analysis [52, 53]. It is likely an efficient network partition tool to find the communities because of its powerful interpretability and close relationship with other clustering methods. Overlapping community detection with NMF can capture the underlying structure of network in the low dimensional data space with its community-based representations [41]. Zhang et al. [54] propose a method called bounded nonnegative matrix tri-factorization (BNMTF) with three factors in the factorization, and explicitly model and learn overlapping community membership of each node as well as the interaction among communities.

NMF decomposes a given nonnegative data matrix \(\mathbf {X}\) as \(\mathbf {X}\approx \mathbf {UV^T}\) where \(\mathbf {U}\ge \mathbf {0}\) and \(\mathbf {V}\ge \mathbf {0}\) (meaning that U and V are component-wise nonnegative). Tan et al. [45] addresses the estimation of the latent dimensionality in nonnegative matrix factorization (NMF) with the \(\beta \)-divergence, and proposes for maximum a posteriori (MAP) estimation with majorization-minimization (MM) algorithms. Psorakis et al. [40] presents a novel approach to community detection that utilizes the Bayesian non-negative matrix factorization model to extract overlapping modules from a network.

In this paper, we propose an adaptive Bayesian non-negative matrix factorization (ABNMF) method for overlapping community detection. In a Bayesian framework, ABNMF assumpts that original matrix \(\mathbf {X}\) with object matrix \(\mathbf {U}\) and \(\mathbf {V}\) follow a certain probability distribution. In this way, we expect that ABNMF can obtain a relevant count of communities and quantized strength of each node related to every community from original network data. To achieve this, we design a new non-negative matrix factorization objective function by incorporating Bayesian Detection, and suggest an adaptive node-based threshold for different communities. Our experiments show that the proposed approach can validly estimate relevant dimension in lower space, find suitable overlapping communities, and also achieve better performance than the state-of-arts overlapping methods.

2 Related Works

Let \(\mathbf {X}\) be a \(m\times n\) non-negative matrix, and NMF consists in finding an approximation:

$$\begin{aligned} \mathbf {X}\approx \mathbf {U}\mathbf {V}^{T} \end{aligned}$$
(1)

where \(\mathbf {U}\) and \(\mathbf {V}\) are \(m \times k \) and \(n \times k \) non-negative matrices. The factorization rank \(\mathbf {k}\) is often chosen such that \(k\ll \min (m,n)\). The objective behind this choice is to summarize and split the information contained in \(\mathbf {U}\) into \(\mathbf {k}\) factors (the columns of \(\mathbf {U}\)). Depending on the application field, these factors are given different names: basis images, metagenes or source signals. In community detection, we equivalently and alternatively use the terms primary communities to refer to matrix \(\mathbf {U}\), and mixture coefficient matrix or communities assignment profiles to refer with matrix \(\mathbf {V}\). We examine each row of \(\mathbf {V}\), and assign node \(\mathbf {x}_j\) to community c if \(c=\arg \max \limits _{c} v_{jc}\) [44] in non-overlapping community detection like crisp clustering. If we define a proper threshold set \(\delta \), a node j can be assigned into community c if \(v_{jc}\ge \delta _c\) in overlapping situation like fuzzy clustering [37].

The main approach of NMF is to estimate matrices \(\mathbf {U}\) and \(\mathbf {V}\) as a local minimum with a cost function in some distance metric. Generally we use \(\beta \)-Divergence \(\mathbf {D_\beta (X;UV^T)}\) [7]. When \(\beta =0,1,2, \mathbf {D_\beta (X;UV^T)}\) is proportional to the (negative) log-likelihood of the Itakara-Saito (IS), KL and Euclidean noise models up to a constant.

Recently, Bayesian inference has been introduced into NMF with a noise E between \(\mathbf {X}\) and \(\mathbf {UV^T}\).

$$\begin{aligned} \mathbf {X}=\mathbf {U}\mathbf {V^T}+\mathbf {E} \end{aligned}$$
(2)

Morten et al. [31] demonstrate how a Bayesian framework for model selection based on Automatic Relevance Determination (ARD) can be adapted to the Tucker and CandeComp/PARAFAC (CP) models. By assigning priors for the model parameters and learning the hyperparameters of these priors the method is able to turn off excess components and simplify the core structure at a computational cost of fitting the conventional Tucker/CP model. Morten et al. [32] also formulate a non-parametric Bayesian model for community detection consistent with an intuitive definition of communities, and present a Markov chain Monte Carlo procedure for inferring the community structure.

Automatic Relevance Determination is a hierarchical Bayesian approach that widely used for model selection. In ARD, hyperparameters explicitly represent the relevance of different features by defining the range of variation for these features, and are usually by modeling the width of a zero-mean prior imposed on the model parameters. If the width becomes zero, the corresponding feature cannot have any effect on the prediction. Hence, ARD optimizes these hyperparameters to discover which features are relevant. While ARD based on Gaussian or Poisson priors, we can prune excess components by admitting sparse representation and retain active components. Applying ARD in some real network community detection process, we can effectively find the relevant communities number without knowing in advance.

Jin et al. [17] extend the stochastic model method to detection of overlapping communities with the virtue of autonomous determination of the number of communities. Their approach hinges upon the idea of ranking node popularities within communities and using a Bayesian method to shrink communities to optimize an objective function based on the stochastic generative model. Wang et al. [46] propose a probabilistic model, Dynamic Bayesian Nonnegative Matrix Factorization, for automatic detection of overlapping communities in temporal networks. Their model can not only give the overlapping community structure based on the probabilistic memberships of nodes in each snapshot network but also automatically determines the number of communities in each snapshot network based on automatic relevance determination.

Schmidt et al. [42] present a Bayesian treatment of NMF based on a Gaussian likelihood and exponential priors, and approximate the posterior density of the NMF factors. This model equals to minimize the squares Euclidean distance \(\mathbf {D_2(X;UV^T)}\) for NMF. Cemgil [5] proposes NMF models with a KL-divergence error measure in a statistical framework with a hierarchical generative model consisting of an observation and a prior component. We can see that this models of \(\mathbf {D_1(X;UV^T)}\) is equals to NMF model with Poisson noise likelihood:

$$\begin{aligned} P(n;\lambda )=\frac{\lambda ^n}{n!}exp(-\lambda ) \end{aligned}$$
(3)
$$\begin{aligned} P(X|U,V)=\prod _i\prod _j\frac{[UV^T]_{ij}^{{X}_{ij}}exp(-[UV^T]_{ij})}{{X}_{ij}!} \end{aligned}$$
(4)

We further assume that all entries of X are independent of each other (the dependency structure is later induced by the matrix product), we can write:

$$\begin{aligned} ln(P(X|U,V))=\sum _i\sum _j{{X}_{ij}ln[UV^T]_{ij}-[UV^T]_{ij}-ln(X_{ij}!)} \end{aligned}$$
(5)

We use Stirling’s formula \(ln(n!)\approx nln(n)-n\) for \(n>>1\) to get approximated expression:

$$\begin{aligned} ln(P(X|U,V))\approx \sum _i\sum _j{{X}_{ij}ln\frac{[UV^T]_{ij}}{{X}_{ij}}-[UV^T]_{ij}+X_{ij}} \end{aligned}$$
(6)

3 Overlapping Community Detection with Bayesian NMF

3.1 Bayesian NMF Model

In this section, we introduce Bayesian inference process of our Adaptive Bayesian NMF (ABNMF) method. Given a network \(\mathbf {G}\) consisting of n nodes \(\mathbf {a}_1,\mathbf {a}_2,\cdots ,\mathbf {a}_n\), we can represent the network as matrix \(\mathbf {X}\) transformed from adjacency matrix. In our ABNMF processing, the diagonal elements are defined to be 1 rather than 0 as in usual clustering cases, and \(\mathbf {X}\) is \(n\times n\) square matrix and non-negative.

We consider there lies a relation between original network matrix \(\mathbf {X}\) and combination of factorized matrix \(\mathbf {UV^T}\). The distribution of this relation can be Gaussian [42] or Poisson [26] model. As Poisson noise model algorithm have much better performance than Gaussian noise models [19, 21] to achieve better sparse estimation effect, we select Poisson likelihood in our ABNMF method. In maximum-likelihood solution to find \(\mathbf {U}\) and \(\mathbf {V}\), \(\mathbf {P(X|UV^T)}\) is maximized, or its energy function \(\mathbf {-logP(X|UV^T)}\) is minimized.

To simplify likelihood with positive error [10, 36], we chose the relation of \(\mathbf {U},\mathbf {V}\) and \(\mathbf {X}\) as \(X_{ij}\sim Poisson(\sum _kU_{ik}*V_{kj})\). In this Poisson model, the log-likelihood of \(\mathbf {X}\) and \(\mathbf {UV^T}\) is:

$$\begin{aligned} -ln(P(X|UV^T))=&-\sum _i\sum _j\left\{ {{X}_{ij}ln\frac{[UV^T]_{ij}}{{X}_{ij}}-[UV^T]_{ij}+X_{ij}}\right\} \\ =&-Xln({UV^T})+\mathbf 1 UV^T\mathbf 1 ^T+const(X) \nonumber \end{aligned}$$
(7)

where \(\mathbf 1 \) is an n \(\times \) n matrix with every elements equal to 1. We use independent half-normal prior over every column of \(\mathbf {U}\) and \(\mathbf {V}\), where the mean is zero and precisian is \(\beta _j\):

$$\begin{aligned} p(u_{ij}|\beta _j)=\mathcal {HN}(x|0,\beta ^{-1}_j) \\ p(v_{jk}|\beta _j)=\mathcal {HN}(x|0,\beta ^{-1}_j)\nonumber \end{aligned}$$
(8)

when

$$\begin{aligned} \mathcal {HN}(x|0,\beta ^{-1})=\sqrt{\frac{2}{\pi }}\beta ^{\frac{1}{2}}exp(-\frac{1}{2}\beta x^2) \end{aligned}$$
(9)

We define the diagonal matrix \(\mathbf {B}\) with [\(\beta _1,...,\beta _K\)] and zeros elsewhere, and the negative log priors of \(\mathbf {U}\) and \(\mathbf {V}\) are:

$$\begin{aligned} -ln(p(U|\beta ))=\sum _i\sum _j\frac{1}{2}{\beta _j}u^2_{ij}-\sum _j\frac{N}{2}log\beta _j+const\\ -ln(p(V|\beta ))=\sum _j\sum _k\frac{1}{2}{\beta _j}v^2_{jk}-\sum _j\frac{N}{2}log\beta _j+const \nonumber \end{aligned}$$
(10)

At last, we set the independent prior distribution of \(\beta _j\) as a Gamma distribution with parameters \(a_j\) and \(b_j\):

$$\begin{aligned} p(\beta _j|a_j,b_j)=\frac{b_j^{a_j}}{\varGamma (a_j)}{\beta _j^{a_j-1}}exp(-\beta _jb_j) \end{aligned}$$
(11)

The negative log of \(\beta _j\) is:

$$\begin{aligned} -ln(p(\beta ))=&\sum _j[\beta _jb_jk-(a_j-1)ln\beta _j]+const \end{aligned}$$
(12)

The MAP(Maximum a Posteriori) of ABNMF is:

$$\begin{aligned} \mathcal {U}=-lnP(X|UV^T))-lnP(U|\beta ))-lnP(V|\beta ))-lnP(\beta )) \end{aligned}$$
(13)

3.2 Iteration Rules of ABNMF

From Eq. (13), we can derive the multiplicative update rules of ABNMF with Poisson likelihood. Let \(\phi _{ij},\psi _{jk}\) be the Lagrange multiplier for constraint \(u_{ij}\ge 0\) and \(v_{jk}\ge 0\), respectively, and \(\mathbf {\Phi }=[\phi _{ij}],\mathbf {\Psi }=[\psi _{jk}]\). The Lagrange function \(\mathcal {L}\) is

$$\begin{aligned} \mathcal {L}=\mathcal {U}+\mathrm {tr}(\mathbf {\Phi }\mathbf {U^T})+\mathrm {tr}(\mathbf {\Psi }\mathbf {V^T}) \end{aligned}$$
(14)

Let the derivatives of \(\mathcal {L}\) with respect to \(\mathbf {U}\) or \(\mathbf {V}\) vanish, we have:

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial {U}} = -2*\frac{X}{UV^T}U + 2*\mathbf 1 U + 2*BU + \mathbf {\Phi }=0 \end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial {V}} = -2*\frac{X}{UV^T}V + 2*\mathbf 1 V + 2*BV + \mathbf {\Psi }=0 \end{aligned}$$
(16)

Using the KKT conditions \(\phi _{ij}u_{ij} = 0\) and \(\psi _{jk}v_{jk} = 0\), we get the following equations for \(u_{ij},v_{jk}\):

(17)
(18)

and the \(\beta _{j}\) will be updated below:

$$\begin{aligned} \beta _{j} \longleftarrow \frac{n+a_j-1}{\frac{1}{2}( \sum _{i}{u^2_{ij}} +\sum _{k}{v^2_{jk}} )+ b_j} \end{aligned}$$
(19)

We can get an approximate fixed value in convergence for iteration. Suppose the multiplicative updates stop after t iterations with parameters from Table 1, the overall computational complexity for ABNMF will be \(O(tn^2c+n^2)\). A relatively small initial c will save running time of the algorithm.

Table 1. Parameters used in complexity analysis
Full size table

3.3 Determination of Overlapping Community Number K and Threshold \(\delta \)

In regular NMF methods for clustering, the object factorized dimension K should be given. But in community detection situation, we just know the relation of nodes without prior information of community number K, and it’s hard to count out the suitable number. If K is too small, some communities will be very large and the model can not be fitted well. On contrary, If K is too large, we can not catch the group character effectively from an entire network and occur into overfitting. We need to find K with a appropriate solution between network fineness and overfitting.

To solve this problem, we propose a statistical shrinkage method in a Bayesian framework to find the number of communities and build a model selection method based on Automatic Relevance Determination [31, 45]. In ABNMF, we principally iterate out \(v_{jk}\) with gradual change, and the prior will try to promote a shrinkage to zero of \(v_{jk}\) with a rate constant proportional to \(\beta _j\). A large \(\beta _j\) represents a belief that the half-normal distribution over \(v_{jk}\) has small variance, and hence \(v_{jk}\) is expected to get close to zero. We can see the priors and the likelihood function (quantifying how well we explain the data) are combined with the effect that columns of V which have little effect in changing how well we explain the observed data will shrink close to zero. We can effectively estimate the communities number K by computer the non-zero column number from V with initial rank c.

In overlapping fuzzy detection, a sparse or dense network may have different overlapping degree. A dense network may contain more communities overlapped. Network density p describes the portion of the potential connections in a network that are actual connections. Every node potentially has a basic probability p to connect with rest nodes in a network, regardless of whether or not they actually connect:

$$\begin{aligned} p=\frac{2*|E|}{n*(n-1)} \end{aligned}$$
(20)

There is a fact that nodes shared multiple community memberships receive multiple chances to create a link in overlapping assumption. We may assume each overlapping sub-community is larger than a potential network, that refer every \(v_{ij}\) will large than one fixed threshold in each network. Yang et al. [52] suggest that the threshold value can be \(\delta =\sqrt{-log(1-p)}\) to achieve good performance. Note that this process adaptively generates an increasing relationship between edge probability and the number of shared communities.

3.4 Performance Comparisons in Different Networks

We compare our algorithm with other four popular overlapping community detection methods. Five algorithms are listed below:

  1. 1.

    CFinder tries to find overlapping dense groups of nodes in networks, and is based on method Clique Percolation Method (CPM) [38].

  2. 2.

    COPRA (Community Overlap PRopagation Algorithm) is based on the label propagation technique for finding overlapping community structure in large networks [12].

  3. 3.

    OSLOM (Order Statistics Local Optimization Method) locally optimizes the statistical significance information of a cluster with respect to random fluctuation with Extreme and Order Statistics [24].

  4. 4.

    LCM (Link Communities Method) organizes community structures spanning inner-city to regional scales while maintaining pervasive overlap, and builds blocks that reveal overlap and hierarchical organization in networks [2].

  5. 5.

    ABNMF (Adaptive Bayesian Non-negative Matrix Factorization) with Poisson likelihood. Its overlapping threshold is related with network density.

We run OSLOM, LFM and ABNMF in different six network datasets without groundtruth to evaluate its communities number, overlap fraction and modularity. Then we generate a synthetic network with 5000 nodes in different overlap fraction [22]. The details of experiments are stated below:

  1. (1).

    In ABNMF methods, we select 10 different initial communities count c and apply 10 independent experiments. Every experiment iterates for 500 times.

  2. (2).

    We test the ABNMF method in Email network [14] to evaluate the performance with different initial dimension number of c in Table 1.

  3. (3).

    We use six different size and different character networks to compare communities number, overlap fraction and Modularity [35]. Football (American College football), Email (Email network of University at Rovira i Virgili in Tarragona, Spain), and PGP (Pretty Good Privacy communication network) [9, 13, 14] are social networks. Erdos (Collaboration network with famous mathematician Erdos) and Cmat (Condensed matter collaborations 2003) [4, 34] are collaborative networks. Metabolic (Metabolic Network) [16] is biological network.

  4. (4).

    We use Omega Index [6, 33] to evaluate overlapping communities detecting performance with benchmark in a synthetic network.

Modularity has widely used to measure the strength of non-overlapping or overlapping community structure found by community detection methods. In Eq. (21), \(A_{ij}\) is the adjacency matrix, and \(k_i,k_j\) are node degree of i, j. \(\delta (c_i,c_j)\) is probability of having a link between i and j in the null model are weighted by the belonging of i and j to the same community, since \(\delta (c_i,c_j)\) is equal to 1 only when i and j belong to the same community, and it is 0 otherwise.

$$\begin{aligned} Q_{ov} = \frac{1}{n}\sum _{i,j\in {V}} \left[ {A_{ij}\delta (c_i,c_j)-\frac{k_{i}k_{j}}{2n}\delta (c_i,c_j)} \right] \end{aligned}$$
(21)

The Omega Index can evaluate the extent of two different solutions for overlapping communities in which each pair of nodes is estimated to share same community:

$$\begin{aligned} Omega(C_1,C_2) = \frac{\sum _{j=0}^{min(J,K)}\frac{A_j}{N}-\sum _{j=0}^{min(J,K)}\frac{N_{j1}N_{j2}}{N^2}}{1-\sum _{j=0}^{min(J,K)}\frac{N_{j1}N_{j2}}{N^2}} \end{aligned}$$
(22)

where J and K represent the maximum number of communities in which any pair of nodes appears together in solution \(C_1\) and \(C_2\), respectively, \(A_j\) is the number of the pairs agreed by both solutions to be assigned to number of community j, and N is the number of pairs of nodes. \(N_{j1}\) is the total number of pairs assigned to number of communities j in solution \(C_1\), and \(N_{j2}\) is the total number of pairs assigned to number of communities j in solution \(C_2\).

Table 2. Overlapping community number K with different initial c in ABNMF
Full size table

We run ABNMF method to test the impact of different initial communities numbers c in Email network. Table 2 lists the different result K, relevant overlap fraction(O) and Modularity(\(Q_{ov}\)). ARD is effective well on features extraction with large initial c, and contractive communities count K is around 30 in Email network. We can find that different c has weak influence for O and \(Q_{ov}\) results when c is set from 567 to 52. In ABNMF, we choose the initial count c from 1/5 to 1/10 of total nodes n to keep the performance of algorithm and keep the operational efficiency.

3.5 Overlapping Community Detection in Different Network

On American Football Game real network with 115 nodes and 613 edges, we run ABNMF for case study and the visualization of our found overlapping community structure is shown in Fig. 1, where same color nodes are allocated into same overlapping community. From Fig. 1, we can see that our proposed method ABNMF automatically finds 10 strong sense communities which are gathered by crisp clustering, and most of the football teams are correctly assigned into their corresponding communities in our found overlapping community structure. Moreover, it is very interesting to note that our proposed method ABNMF detects 32 overlapping nodes in different communities in total, in which each overlapping node has two different colors indicating different communities the node belongs to. This is because, besides against other football teams in the same conference, these football teams corresponding to the overlapping nodes also frequently play many games against football teams in other conferences. Therefore, we can see that our proposed method ABNMF has a good performance in detecting overlapping community structures in this real world social network.

Fig. 1.
figure 1

Overlapping communities of Football network obtained by ABNMF.

Full size image

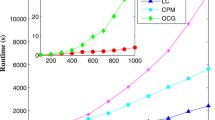
We select 6 popular networks with different size, and compare community number(K), overlap fraction(O) and overlap modularity(\(Q_{ov}\)) in OSLOM, LCM and ABNMF. We can find from Table 3 that, our method ABNMF can effectively find overlapping community number and is highly close to results of OSLOM and LFM. ABNMF detects much dense communities in overlap fraction and achieves high overlapping modularity than other two methods. In ABNMF with Multiplicative Update Rules [27], we achieve good performance in large PGP and Cmat networks both of which have more than ten thousands of nodes. We may also combine with Projected Gradient [28] method or Block Gradient Descent method [20] to solve Eq. (13) in larger datasets with millions of nodes.

Table 3. Overlapping community detection comparison on different networks
Full size table

We evaluate the performance of our proposed algorithm on the LFR synthetic networks with benchmark, and compare with other four overlapping community detection algorithms. The LFR (Lancichinetti-Fortunato-Radicchi) benchmark [22] provides a class of artificial networks in which both the degrees of the nodes and the sizes of the communities follows power laws the same as many real-world networks. Here, we adopt a LFR benchmark with 5000 nodes respectively from the benchmark generator source codeFootnote 1 in our experiment:

benchmark -N 5000 -k 10 -maxk 30 -mu 0.1 -minc 10 -maxc 50 -on 50 -om 2

In this LFR benchmark, we set the average degree of nodes \(davg=10\), the maximum degree of nodes \(dmax=30\), the minimum community size \(minc=10\), the maximum community size \(maxc=50\), the exponents of the power law of the community size distribution \(t_1=1\), the exponents of the power law of the community size distribution \(t_2=2\), the overlapping nodes in the entire network \(on=50\), and the number of communities that each overlapping node belongs to \(om=2\). Moreover, we define the mixing parameter \(\mu \) as the average percentage of edges that connect a node to those in other communities which indicates that every node shares a fraction (\(1-\mu \)) edges with other nodes in its community and a fraction \(\mu \) edges with nodes outside its community. The network community structure will be weakened by increasing \(\mu \).

Table 4. Omega index comparison on LFR 5000 network
Full size table

Five algorithms are executed on the LFR benchmark network, and the average Omega Index is used to measure the similarities between the known community structure and the obtained resultant community structure by these algorithms. The results of different algorithms in the LFR networks are shown in Table 4.

It can be seen that all these five algorithms perform well and our proposed ABNMF algorithm has slightly better performance comparing with the other four algorithms when the value of overlap fraction \(\mu \) is small on the LFR network. Moreover, as the value of \(\mu \) increasing, the performance of our proposed algorithm does not degrade rapidly as shown in Table 4. Therefore, our proposed algorithm has a good ability to detect overlapping community structures in complex networks no matter whether they have dense or sparse overlapping structure.

4 Conclusions

In this paper, we solve an overlapping community detection problem using Adaptive Bayesian NMF. We propose a model that considerate Bayesian inference process with Poisson model into NMF, and derive the updating rules and conduct experiments to valid our model. We also apply Automatic Relevance Determination method with sparse constrain to learn the community count of a network, and compare the detection impact of different initial community rank. At last, we adaptively select a most proper value related to network density as overlapping threshold for mixture coefficient matrix. Our method can be applied in real network data without any given information, and achieves good performance than other overlapping community detection methods.