Comments for the Continuation Method by A.F. Filippov for Discontinuous Systems, Part I

Abstract

The conventional existence-uniqueness theorems are not applicable for differential equations with right hand sides as discontinuous state functions. This is the case for the systems with discontinuous controls and sliding modes, when state trajectories belong to discontinuity surfaces. Many authors offered their methods of deriving sliding mode equations, or solution continuations on the discontinuity surfaces. Due to uncertainties of right hand sides, the proposed methods led to different solutions. These methods are compared, the reasons of ambiguity are discussed in the paper. It is assumed that any solution is under the umbrella of the method proposed by A.F. Filippov.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The systems with control actions as discontinuous state functions are under discussion. Relay systems and variable structure systems belong to this class. Relay systems were employed actively at the first stage of the control theory history, because of their ease of implementation, and to help control reach its full potential. Voltage control of a DC generator, already described in the paper Kulebakin [3] from 1932, may serve as an example; see Fig. 1, top. Any comments are hardly needed for a modern reader. The principle operation mode, called “vibrational” in these papers, is nothing but sliding mode in the modern terminology. The term “sliding mode” can be found in the paper Nikolski [5] from 1934 about ship course control; see Fig. 1, bottom. The theoretical methods of analysis and design were summarized in the monographs Flugge-Lotz [2] and Tsypkin [6], published in the USA and USSR, respectively. Sliding modes on a switching line for relay control were studied in these monographs. The state plane of the system

$$\begin{aligned} \ddot{x}=u \end{aligned}$$

(1)

with relay control

$$\begin{aligned} u=-u_0 {\text {sign}}(s), \quad s=cx+\dot{x}, \quad u_0,c>0. \end{aligned}$$

(2)

The state vector $(x,\dot{x})$ reaches the line $s=0$ after a finite time interval and then cannot leave it. This motion is called a sliding mode. The equation of switching line $cx+\dot{x}=0$ is used as the motion equation. Its solution depends on the switching line equation and does not depend on properties of the plant to be controlled.

Fig. 1

Examples of sliding mode control

The property of invariance was utilized actively in the 1960’s in variable structure systems, when the system behavior was studied in the space of an output variable and its time derivatives. In contrast to relay systems, the amplitude of the control signal $u_0$ depended on the state vector. All these facts are well-known for a long time, and mentioned in this paper to explain why development of new mathematical methods is needed for this class of systems. Formally the mathematical problem of describing sliding modes for the simplest second order systems (1) and (2) remains open. Indeed, a Lipshitz constant does not exist for discontinuous systems, and as a result the conventional uniqueness-existence theorems are not applicable. The above offered solution $x(t)=x_0 e^{-ct}$ to equation $cx+\dot{x}=0$ looks doubtful: if this function is the solution, then it should turn the equation into an identity, but it is not clear what the function sign(s) $=$ sign(0) is equal to.

A.F. Filippov offered a new method [1] of solution continuation on discontinuity surface for the systems with discontinuous right hand sides

$$\begin{aligned} \dot{x}=\left\{ \begin{array}{lll}f^+(x,t)&{}\mathrm{if}&{}s(x)>0,\\ f^-(x,t)&{}\mathrm{if}&{}s(x)<0,\end{array}\right. \quad x,f^+,f^-\in \mathbb R^n,\;\;s\in \mathbb R. \end{aligned}$$

(3)

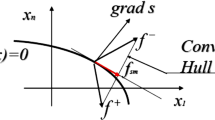
For now, we confine ourselves to the simplified formulation of Filippov’s method; see Fig. 2.

Fig. 2

Filippov method

An equation $\dot{x}=f_{sm}$, with a vector field $f_{sm}$, describes a sliding mode on the surface $s(x)=0$, found from the convex hull of vectors $f^+$ and $f^-$, which is a straight line connecting the ends of these vectors (Fig. 2), given by $f_{sm}=\mu f^++(1-\mu ) f^-$ for $0\ge \mu \ge 1$. The vector $f_{sm}$ lies in the intersection of the straight line with the tangential plane to the surface $s(x)=0$, and the coefficient $\mu$ is found from equation $[\nabla (s) ]^T f_{sm}=0$. Actually, the method by Filippov postulates the sliding mode equation, but other methods of solution continuation on the discontinuity surface were offered in a set of publications. These methods are discussed and compared in this short paper.

2 Problem Statement

The motion of a finite-dimensional system with vector control is governed by the equation

$$\begin{aligned} \dot{x}=f(x,t,u), \qquad x,f\in \mathbb R^n,\quad u\in \mathbb R^m. \end{aligned}$$

(4)

Similarly to the simple examples in the introduction, each component of the control is assumed to be a discontinuous state function

$$\begin{aligned} u_i=\left\{ \begin{array}{lll}u_i^+(x,t)&{}\mathrm{if}&{}s_i(x)>0,\\ u_i^-(x,t)&{}\mathrm{if}&{}s_i(x)<0,\end{array}\right. \quad i=1,\ldots ,m. \end{aligned}$$

(5)

Scalar functions $s_i (x)$ are continuous-differentiable and any solution of (4) for any of the functions $u_i^\pm (x.t)$ exists and is unique. Sliding modes in (4) and (5) can occur at each of the surfaces $s_i (x)=0$ and, on their intersection, $s(x)=0$, $s^T=(s_1,\ldots ,s_m)$; see Fig. 3. The set of problems of interest are then: how to find sliding mode equations, whether they are unique, and if not, how to substantiate a choice of motion equations for real processes.

Fig. 3

Multidimensional sliding mode

3 Systems with Scalar Control

From the first view, system (4) and (5) with a scalar control $u\in \mathbb R$ is equivalent to system (3), studied by Filippov, with $f^+=f(x,t,u^+ )$, $f^-=f(x,t,u^- )$. However, dependence of the right hand side on the control gave birth to many methods of deriving sliding mode equations, dictated by natural engineering arguments. For example, relay control was replaced by a linear relation ks with k tending to infinity [6], since the input of the relay s is close to zero (the trajectory belongs to the surface $s(x)=0$), while the output takes finite values. It was suggested to write down the solution in convolution form for linear systems, and to find a continuous control such that $s(t)=0$; see Neimark [4]. Another method was based on the replacement of discontinuous control by a continuous one such that $s(t) =0$; see Utkin [7]. These methods happened to result in different sliding motion equations and rather vivid discussions on what method was correct.

We start with the example which served as a reason for doubts in the correctness of Flippov’s method,

$$\begin{aligned} \dot{x}=Ax+bu_1+du_2, \quad u_1=-M_1 {\text {sign}}(s),\quad u_2=-M_2 {\text {sign}}(s). \end{aligned}$$

(6)

Both components of control undergo discontinuities on the same plane $s(x)=cx=0$ ($A,b,d,M_1,M_2,c$ are constants). From the first view, the unique sliding equation can be derived by Flippov’s method with $f^+=Ax-bM_1-dM_2$, $f^-=Ax+bM_1+dM_2$. Let the control $u_2$ be implemented as a relay function with small hysteresis, and $M_1\gg M_2$, then a sliding mode can be enforced for any value of $u_2=M_2$ or $u_2=-M_2$. Sliding mode equations can be derived following Flippov’s method for $f^+=Ax-bM_1+du_2$, $f^-=Ax+bM_1+du_2$. The control $u_2$ can take one of two possible values depending on initial conditions. This non-uniqueness was the reason of doubts. But these doubts can be easily eliminated if we use the exact recommendation of Filippov (in contrast to the simplified formulation in the introduction):

$$\begin{aligned} \dot{x}=f_{sm}, \quad f_{sm} (x,t)\in \lim _{\varepsilon \rightarrow 0}\;\mathsf{conv}\;f(x+\delta x,t,u+\delta x))\backslash N, \end{aligned}$$

where $\;\mathsf{conv}\;f(x+\delta x,t,u)$ means a minimal convex hull, corresponding to all values of control in the vicinity $||\delta x||<\varepsilon$, and the symbol $\backslash N$ means that a set of zero measure can be excluded from this vicinity (or points of the discontinuity surface where the control is not defined). There are four possible vectors in the right hand side of the above example, corresponding to different combinations of $u_1$ and $u_2$. The minimal convex hull of the four vectors is the polygon depicted in Fig. 4, and its intersection with the tangential plane defines the set of all possible right hand sides in the sliding mode equations. This set includes two different motion equations in the above example, when control $u_2$ could take one of two possible values.

Fig. 4

Non-unique sliding mode equations

Filippov’s method has a very simple interpretation in the time domain. Let the right hand side of (4) take one of k possible values $f_1,\ldots ,f_k$ in the vicinity of some point in the state space, and let the time interval $\Delta t$ consist of k subsets $\Delta t_1,\ldots ,\Delta t_k$, $\Delta t=\sum _{i=1}^k\Delta t_i$ with values of right hand sides $f_1,\ldots ,f_k$ correspondingly. Then

$$\begin{aligned} \dot{x}=\lim _{\Delta t0}\rightarrow \frac{1}{\Delta t}\sum _{i=1}^kf_i\Delta t_i=\Sigma _{i=1}^k\mu _i f_i ,\quad \mu _i=\frac{\Delta t_i}{\Delta t},\quad \mu _i\ge 0,\quad \sum _{i=1}^k\mu _i =1. \end{aligned}$$

The right hand side is nothing but the convex hull of $f_1,\ldots ,f_k$.