Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction and Statements of the Main Results

Let \(F^{\pm }(x,y)=A^{\pm }(x,y)^T+(b_1^{\pm },b_2^{\pm })\), \(A^{\pm }=(a^{\pm }_{ij})_{2\times 2},\) be linear vector fields. This work is concerned about crossing limit cycles of piecewise linear differential systems having the form

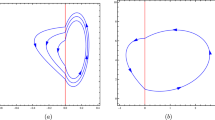
$$\begin{aligned} \big (\dot{x},\dot{y} \big )^T =Z(x,y)=\big (F^+,F^-\big )(x,y)=\left\{ \begin{array}{l} F^+(x,y) \quad \text {if}\quad x\ge 0,\\ F^-(x,y) \quad \text {if}\quad x\le 0. \end{array}\right. \end{aligned}$$
(1)

Denote by \(\Sigma =\{(x,y):\,y=0\}\) the set of discontinuity of (1). From now on, a crossing limit cycle will be called only by limit cycle.

It was conjectured in Han–Zhang [5] that a planar piecewise linear differential system with two zones separated by a straight line has at most two limit cycles. A negative answer for this conjecture was provided in Huan–Yang [6] via a numerical example having three limit cycles. Analytical proofs for the existence of these three limit cycles were given in [3, 7]. Finally, in Freire–Ponce–Torres [4] some general conditions were studied to obtain these three limit cycles. Recently, perturbative techniques (see [9, 10]) were used together with newly developed tools on Chebyshev systems (see Novaes–Torregrosa [12]) to obtain three limit cycles in such systems.

When a general curve of discontinuity is considered instead of a straight line, there is no upper bound for the maximum number of limit cycles that a differential system of this family can have. It is a consequence of a conjecture stated in Braga–Mello [1] and then proved in Novaes–Ponce [11].

It is easy to see that \(a^{\pm }_{12}>0\) is a necessary condition for the existence of crossing limit cycles (see Freire–Ponce–Torres [2]). So, define

$$ \delta ^{\pm }=\dfrac{a^{\pm }_{22}}{a^{\pm }_{12}}b^{\pm }_1-b^{\pm }_2. $$

Let \(\det (\cdot )\) and \(\text {tr}(\cdot )\) denote the determinant and the trace of a matrix, respectively. When \(\det (A^{\pm })\ne 0\) the vector field \(F^{\pm }\) vanishes at the point

$$ \big (x^{\pm },y^{\pm }\big )= \left( \dfrac{a^{\pm }_{12}b^{\pm }_2-a^{\pm }_{22} b^{\pm }_1}{\det (A^{\pm })}\, ,\,\dfrac{a^{\pm }_{21} b^{\pm }_1-a^{\pm }_{11} b^{\pm }_2}{\det (A^{\pm })} \right) . $$

Note that \(x^{\pm }=-a^{\pm }_{12}\delta ^{\pm }/\det (A^{\pm })\).

In Llibre–Novaes–Teixeira [8], tools and ideas to estimate bounds on the maximum number of limit cycles that the differential system (1) can have were introduced. The equality \(\text {tr}(A^+)\text {tr}(A^-)=0\) was assumed in some of the cases considered there. The ideas of [8] can be followed straightly to obtain the next result.

Theorem 1

If \(\text {tr}(A^+)\text {tr}(A^-)=0\), then the differential system (1) admits at most two limit cycles and this maximum is reached.

Among all the cases addressed in [8], assuming that the lateral differential systems are non–singular, the authors also proved that if one of the lateral differential systems, \(F^+\) or \(F^-\), has a singularity on the line of discontinuity \(\Sigma \) then the differential system (1) can have at most two limit cycles. This result can be generalized as follows.

Theorem 2

If \(\delta ^+\delta ^-=0\) then the differential system (1) admits at most two limit cycles and this maximum is reached.

In the above case, the equality \(\text {tr}(A^+)\text {tr}(A^-)=0\) is not assumed. In this direction a third result is obtained.

Theorem 3

If \(\text {tr}(A^+)+\text {tr}(A^-)=0,\) \(\det (A^+)-\det (A^-)=0\), and \(\delta ^++\delta ^-=0,\) then the differential system (1) does not admit limit cycles.

Let F(x, y) be a linear vector field, and let \(R(x,y)=(-x,y)\) be an involution. Assume that \(F^+(x,y)=F(x,y)\) and \(F^-(x,y)=-R\circ F\circ R(x,y+k)\), \(k\in \mathbb {R}\). It easy to see that \(Z=(F^+,F^-)\) satisfies the hypotheses of Theorem 3. The proof of Theorem 3 follows by showing that differential systems for which their hypotheses hold are actually equivalent to a differential system \(Z=(F^+,F^-)\) such that \(F^-(x,y)=-R\circ F\circ R(x,y+k)\). In this case, if \(k=0\) then Z is R–reversible which implies the non–existence of limit cycles. The parameter k breaks the reversibility, however limit cycles cannot appear.

In Sect. 2 some preliminary results are introduced. In Sect. 3 the proofs of Theorems 1, 2, and 3 are discussed. The proof of Theorem 3 is treated with more detail.

2 Preliminar Results

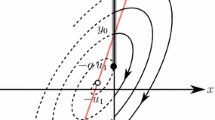
As usual, the following open regions are distinguished on \(\Sigma \): Crossing Region: \(\Sigma ^{c} = \{p \in \Sigma :\, F_1^+(p)F_1^-(p) > 0 \}\); Escaping Region: \(\Sigma ^{e} = \{p \in \Sigma :\, F_1^+(p) > 0, F_1^-(p) < 0 \}\); and Sliding Region: \(\Sigma ^{s} = \{p \in \Sigma :\,F_1^+(p) < 0, F_1^-(p) > 0 \}\). Let \(\Sigma ^{c^+}\subset \Sigma ^c\) denote the points \(p\in \Sigma ^c\) such that \(F_1^+(p)>0\) and \(F_1^-(p)>0\).

Denote by \(\varphi ^{\pm }(t,x,y)=\left( \varphi ^{\pm }_1(t,x,y),\varphi ^{\pm }_2(t,x,y)\right) \) the solutions of the lateral differential systems \((\dot{x},\dot{y} )^T=F^{\pm }(x,y)\) such that \(\varphi ^{\pm }(0,x,y)=(x,y)\). The existence of an interval domain \(I\subset \Sigma ^{c^+}\) and functions \(t^{\pm }:I\rightarrow \mathbb {R}^{\pm }\), such that, for \(y\in I\), \(\varphi _1^{\pm } (t^{\pm }(y), 0,y)=0,\) \(\varphi _1^+(t,0,y)>0\) for every \(0<t<t^+(y),\) and \(\varphi _1^-(t,0,y)<0\) for every \(t^-(y)<t<0\) is a necessary condition for the existence of limit cycles. In this case, the differential system (1) admits a limit cycle passing through \((0,y^*),\) \(y^*\in I,\) if and only if \(y^*\) is a solution of the equation

$$\begin{aligned} \begin{array}{rl} f(y)\doteq \varphi _2^+(t^+(y),0,y)-\varphi _2^-(t^-(y),0,y)=0. \end{array} \end{aligned}$$
(2)

In general the functions \(t^{\pm }(y)\) cannot be obtained explicitly. However, their inverse \(\xi ^{\pm }:t^{\pm }(I)\rightarrow I\) may be explicitly computed.

Proposition 4

Assume that there exist an interval domain \(I\subset \Sigma ^{c^+}\) and functions \(t^{\pm }:I\rightarrow \mathbb {R}^{\pm }\), such that, for \(y\in I\), \(\varphi _1^{\pm } (t^{\pm }(y), 0,y)=0,\) \(\varphi _1^+(t,0,y)>0\) for every \(0<t<t^+(y),\) and \(\varphi _1^-(t,0,y)<0\) for every \(t^-(y)<t<0\). Then, \(t^{\pm }(y)\) are invertible and their inverses \(\xi ^{\pm }:t^{\pm }(I)\rightarrow I\) satisfy \(\varphi _1^{\pm }(t,0,\xi ^{\pm }(t))=0\) for every \(t\in t^{\pm }(I)\).

In Freire–Ponce–Torres [2], assuming \(a_{12}^+a_{12}^->0,\) which is a necessary condition for the existence of limit cycles, the authors provided the following normal form for the differential system (1):

$$\begin{aligned} \big (\dot{\widetilde{x}},\dot{\widetilde{y}} \big )^T =\left\{ \begin{array}{l} \widetilde{F}^+(\widetilde{x},\widetilde{y}) \quad \text {if}\quad \widetilde{x}>0,\\ \widetilde{F}^-(\widetilde{x},\widetilde{y}) \quad \text {if}\quad \widetilde{x}<0, \end{array}\right. \end{aligned}$$
(3)
$$\begin{aligned} \begin{array}{l} \widetilde{F}^+(\widetilde{x},\widetilde{y})=\left( \begin{array}{cc}T^+&{}-1\\ D^+&{}0\end{array}\right) \left( \begin{array}{c}\widetilde{x}\\ \widetilde{y}\end{array}\right) -\left( \begin{array}{c}-k\\ a^+\end{array}\right) , \\ \widetilde{F}^-(\widetilde{x},\widetilde{y})=\left( \begin{array}{cc}T^-&{}-1\\ D^-&{}0\end{array}\right) \left( \begin{array}{c}\widetilde{x}\\ \widetilde{y}\end{array}\right) -\left( \begin{array}{c} 0\\ a^-\end{array}\right) , \end{array} \end{aligned}$$

with \(T^{\pm }=\text {tr}(A^{\pm }),\) \(D^{\pm }=\det (A^{\pm }),\) and

$$ a^-=a^-_{12}b^-_2-a^-_{22}b^-_1,\quad k=\dfrac{a^-_{12}}{a^+_{12}}b^+_1-b^-_1,\quad a^+=\dfrac{a^-_{12}}{a^+_{12}}\big (a^+_{12}b^+_2-a^+_{22}b^+_1\big ). $$

The homeomorphism h, which transforms the differential system (1) into the canonical form (3), leaves the line of discontinuity \(\Sigma \) invariant. The crossing and sliding sets, tangency points, and boundary equilibria of the original differential system (1) are transformed by h into sets and points of the same type by the differential system (3). Moreover, there is a topological equivalence between the differential systems (1) and (3) for all their orbits not having points in common with the sliding set.

3 Sketches of the Proofs of the Main Results

The proofs of Theorems 1 and 2 follow by finding explicitly at least one of times \(t^+(y)\) or \(t^-(y)\). It is assured by hypotheses. Without loss of generality, suppose that one is able to find \(t^-(y)\). Using Proposition 4 to invert the function \(t^+(y)\) (which from hypotheses can be found explicitly as \(\xi ^+(t)\)) Eq. (2) becomes equivalent to

$$ g(t)\doteq f(\xi ^+(t))=\varphi ^+(t,0,\xi ^+(t))-\varphi ^-(t^-(\xi ^+(t)),0,\xi ^+(t))=0, $$

for which the number of solutions can be estimated; see Llibre–Novaes–Teixeira [8].

To see Theorem 3, take \(F^{\pm }(x,y)=A^{\pm }(x,y)^T+(b_1^{\pm },b_2^{\pm })\), \(A^{\pm }=(a^{\pm }_{ij})_{2\times 2},\) and assume that \(\text {tr}(A^+)+\text {tr}(A^-)=0,\) \(\det (A^+)-\det (A^-)=0\), and \(\delta ^++\delta ^-=0.\) Thus the differential system (1) is transformed into the canonical form (3), where

$$ \begin{array}{l} \widetilde{F}^+( \widetilde{x},\widetilde{y})=\left( \begin{array}{cc}T&{}-1\\ D&{}0\end{array}\right) \left( \begin{array}{c}\widetilde{x}\\ \widetilde{y}\end{array}\right) -\left( \begin{array}{c} -k\\ a\end{array}\right) , \\ \widetilde{F}^-(\widetilde{x},\widetilde{y})=\left( \begin{array}{cc}-T&{}-1\\ D&{}0\end{array}\right) \left( \begin{array}{c}\widetilde{x}\\ \widetilde{y}\end{array}\right) -\left( \begin{array}{c} 0\\ -a\end{array}\right) , \end{array} $$

T and D are the trace and the determinant of the matrix \(A^+\), respectively, \(a=a^+\), and \(k=(a^-_{12}/a^+_{12})b^+_1-b^-_1.\) Taking the involution \(R(x,y)=(-x,y)\), the relation \(\widetilde{F}^-(x,y)=-R\circ \widetilde{F}^+\circ R(x,y+k)\) is obtained. From now on we shall drop the tildes. As before, \(\varphi ^{\pm }(t,x,y) =\left( \varphi ^{\pm }_1(t,x,y), \varphi ^{\pm }_2(t,x,y)\right) \) denote the solutions of the lateral differential systems \((\dot{x},\dot{y} )^T=F^{\pm }(x,y)\) such that \(\varphi ^{\pm }(0,x,y)=(x,y)\). It is easy to see that \(\varphi _1^-(t,x,y)=-\varphi _1^+(-t,-x,y+k)\) and \(\varphi _2^-(t,x,y)= \varphi _2^+(-t,-x,y+k)-k\).

As a necessary condition for the existence of periodic solutions, assume the existence of an interval domain \(I\subset \Sigma ^{c^+}\) and a function \(t^+=\tau :I\rightarrow \mathbb {R}^+\), such that, for \(y\in I\), \(\varphi _1^+(\tau (y),0,y)=0\) and \(\varphi _1^+(t,0,y)>0\) for every \(0<t<\tau (y).\) Note that, in this case, \(t^-(y)=-\tau (y+k)\). Indeed \(\varphi _1^-(-\tau (y+k), 0,y)=-\varphi _1^+(\tau (y+k),0,y+k)=0,\) and \(\varphi _1^-(t,0,y)=-\varphi _1^+(-t,0,y+k)<0\) for every \(-\tau (y+k)<t<0\) and \(y+k\in I\). Let \(\varphi _i=\varphi ^+_ i\) so, Eq. (2) reads

$$\begin{aligned} f(y)&=\varphi _2^+(\tau (y),0,y)-\varphi _2^-(-\tau (y+k),0,y)\\&=\varphi _2(\tau (y),0,y)-\varphi _2(\tau (y+k),0,y+k)+k=0. \end{aligned}$$

From the above expression it follows that the equation \(f(y)=0\), for \(k\ne 0\), does not have solution for \(y\in I\). Indeed, without loss of generality, assume that \(y>0\); if \(k>0\) then the first return of y to \(\Sigma \), \(\varphi _2(\tau (y),0,y)\), is strictly greater than the first return of \(y+k\) to \(\Sigma \), \(\varphi _2(\tau (y+k),0,y+k)\). Therefore, \(\varphi _2(\tau (y), 0,y) -\varphi _2(\tau (y+k),0,y+k)>0\) and consequently \(f(y)>0\). Analogously, if \(k<0\) we would conclude that \(f(y)<0\).