Nonlinear Transverse Vibrations of a Beam with Multiple Breathing Edge Cracks

Abstract

One step beyond the studies of transverse vibration of beams with a breathing edge crack is the verification of the theoretical crack beam models with an experimental test set up. Beams with a single breathing edge crack can be used as a specimen for the experimental test. However, there is no assurance against the unexpected additional cracks in the specimens, which may cause unexpected results. Therefore, in this paper nonlinear transverse vibration of a beam with multiple breathing edge cracks is considered as a preliminary study. The breathing effect of the cracks are modeled as piecewise linear stiffness and a harmonic force is applied to the cracked beam. Galerkin’s Method is applied with multiple trial functions and nonlinear differential equations obtained are solved by using harmonic balance method with multi harmonics. Utilizing the developed model, effects of crack parameters and crack locations are studied.

27.1 Introduction

Vibrations in structures may cause crack propagation which may result in unexpected failure. Therefore, vibration of beams with cracks has been an interesting area of research. Two comprehensive review articles were published by Dimarogonas [1] and Bovsunovsky et al. [2] covering the cracked beam vibration studies that had been done until that time in which studies about linear and nonlinear vibrations, continuous crack beam theories, vibration of cracked plates and beams with breathing edge cracks were considered. Some of the studies available in literature are based on transverse vibration of beams with multiple cracks. Khiem and Lien [3] utilized transfer matrix method and rotational spring model in order to evaluate natural frequencies of a beam with multiple open cracks. In another study, Khiem and Lien [4] formulated natural frequencies in the form of a non-linear optimization problem and proposed a procedure to find the crack depth, crack location and quantity. Mazanoglu et al. [5] used Rayleigh-Ritz approximation method in order to identify the vibrations of non-uniform Euler-Bernoulli beams with multiple open cracks. In the study, the beam model was developed by considering both strain energy change at cracked beam surface and stress field caused by the angular displacement. Caddemi et al. [6] proposed a closed form expression for the modes of an Euler-Bernoulli beam with multiple cracks. The cracks were modeled as open type and a sequence of Dirac’s delta generalized functions were utilized in order to express the flexural stiffness. Lee [7] used finite element method to model the beam with multiple open cracks. The author also used Newton-Raphson and singular value decomposition methods to find the crack quantity, depth and location. Xiao et al. [8] applied a method called reverse modal analysis and utilized strain energy density function to evaluate the additional flexibility induced due to the presence of crack. In the study, breathing effect of the crack was considered by defining contact on the colliding surfaces. Using finite element and experimental analysis, natural frequencies and mode shapes of the cracked beam were obtained. In a more recent study, Attar [9] proposed an analytical approach to investigate the natural frequencies and mode shapes of a stepped beam with multiple transverse cracks. Transfer matrix method was utilized as a function of beam properties and crack parameters. The calculated natural frequencies were used for crack identification by the method proposed in the study. Labib et al. [10] carried out a study in order to calculate natural frequencies of beams and frames containing multiple cracks. In the study, dynamic stiffness matrices for beams with multiple cracks were evaluated. The authors represented open cracks by rotational springs and utilized bilinear natural frequency in order to consider the breathing effect.

In this paper, a preliminary study is carried out in order to model the vibration of beams with double breathing edge cracks. An additional breathing edge crack is added to the model proposed by the authors in a previous study [11]. The beam is modeled by Euler-Bernoulli beam theory and a multi degree of freedom (MDOF) representation of the cracked beam is obtained by utilizing Galerkin’s method. Three different set of mass normalized eigenfunctions are utilized as trial functions, for instance, the eigenfunctions of a beam with double open cracks and eigenfunctions of a beam with a single open crack at two different locations. Each breathing edge crack is modeled as a piecewise linear stiffness. The state of each crack is determined by checking the slope difference at each crack location. Resulting set of nonlinear differential equations of motion are solved by utilizing harmonic balance method with multi harmonics coupled with a nonlinear equation solver.

27.2 Mathematical Modeling of the Problem

Equation of motion of a uniform continuous beam under the action of an external point force f(t) located at point L _f can be expressed by Euler-Bernoulli beam theory as follows

$$ EI\frac{\partial^4w\left(x,t\right)}{\partial {x}^4}+c\frac{\partial w\left(x,t\right)}{\partial t}+m\frac{\partial^2w\left(x,t\right)}{\partial {t}^2}=f(t)\delta \left(x-{L}_f\right), $$

(27.1)

where w(x, t) is the transverse displacement, EI is the flexural rigidity, m is the mass per unit length of the beam and c is the viscous damping coefficient. Utilizing the expansion theorem, transverse displacement can be expressed as follows

$$ w\left(x,t\right)=\sum_{j=1}{a}_j(t){\phi}_j(x), $$

(27.2)

where ϕ _j (x) is the j ^th trial function and a _j (t) is the corresponding modal coefficient. Substituting Eq. (27.2) into Eq. (27.1), the following expression is obtained

$$ \sum_j\left({EIa}_j(t)\frac{d^4{\phi}_j(x)}{dx^4}\right)+\sum_j\left({c\dot{a}}_j(t){\phi}_j(x)\right)+\sum_j\left({m\ddot{a}}_j(t){\phi}_j(x)\right)=f(t)\delta \left(x-{L}_f\right). $$

(27.3)

Multiplication of Eq. (27.3) by ϕ _i (x) and integration over the spatial domain of the beam results in the following equation

$$ \sum_j\left({m}_{ij}\right){\ddot{a}}_j(t)+\sum_j\left({c}_{ij}\right){\dot{a}}_j(t)+\sum_j\left({k}_{ij}\right){a}_j(t)={F}_i(t), $$

(27.4)

where

$$ {k}_{ij}=\underset{0}{\overset{L}{\int }} EI{\phi}_i(x)\frac{d^4{\phi}_j(x)}{dx^4} dx, $$

(27.5)

$$ {c}_{ij}=\underset{0}{\overset{L}{\int }}c{\phi}_i(x){\phi}_j(x) dx, $$

(27.6)

$$ {m}_{ij}=\underset{0}{\overset{L}{\int }}m{\phi}_i(x){\phi}_j(x) dx, $$

(27.7)

$$ {F}_i(t)={\phi}_i\left({L}_f\right)f(t). $$

(27.8)

Rearranging Eq. (27.4), the following matrix equation is obtained.

$$ \left[M\right]\left\{\ddot{a}\right\}+\left[C\right]\left\{\dot{a}\right\}+\left[K\right]\left\{a\right\}=\left\{F\right\} $$

(27.9)

Mass normalized eigenfunctions of the beam with double open cracks are utilized, therefore [M], [C] and [K] are the corresponding mass, damping and stiffness matrices of the beam with double open edge cracks. The details and the derivations of eigenfunctions of a beam with open edge crack can be found in [12].

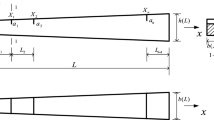
Fig. 27.1 shows a beam with double cracks under the action of a point force. Depending on the slope difference at the crack locations, each crack may be in open or closed state. Thus, for different time instants of the period, both of the crack at locations L _c1 and L _c2 may be closed, only one of the cracks may be closed while the other crack is open or both of them may be open. For the time instants when the cracks are at different states, for instance closed or open, [M] and [C] matrices do not change, however stiffness matrix [K] depends on the state of the cracks. Therefore, in order to consider the breathing effect of each crack, three different sets of eigenfunctions are utilized, i.e. eigenfunctions of a beam with double open edge cracks and eigenfunctions of a beam with a single edge crack for two different crack locations.

Fig. 27.1

Cantilever beam with double breathing crack

For the instant when only the crack at location L _c1 closes, the stiffness of the double open cracked beam increases. The increase in the stiffness is defined by the following expression,

$$ \left[{B}_1\right]=\left[{K}_{c2}\right]-\left[K\right], $$

(27.10)

where [K _c2] is the stiffness matrix of the beam obtained by utilizing the mass normalized eigenfunctions of the beam with a single open edge crack at location L _c2. Similarly, the increase in the stiffness at the instant when only the crack at location L _c2 closes is defined as follows,

$$ \left[{B}_2\right]=\left[{K}_{c1}\right]-\left[K\right], $$

(27.11)

where [K _c1] is the stiffness matrix of the beam obtained by utilizing mass normalized eigenfunctions of the beam with a single open edge crack at location L _c1. In case both of the cracks are closed, the stiffness of the beam with double cracks becomes equal to the stiffness of the beam with no crack. Therefore, the stiffness matrix of the beam with no crack is taken as follows without introducing any significant errors

$$ \left[{K}_{nc}\right]=\left[K\right]+\left[{B}_1\right]+\left[{B}_2\right]. $$

(27.12)

Including the breathing effect of the cracks at different locations, the equation of motion takes the following form,

$$ \left[M\right]\left\{\ddot{a}\right\}+\left[C\right]\left\{\dot{a}\right\}+\left[K\right]\left\{a\right\}+\left\{{R}_1\left(\left\{a\right\}\right)\right\}+\left\{{R}_2\left(\left\{a\right\}\right)\right\}=\left\{F\right\}, $$

(27.13)

where {R ₁({a})} and {R ₂({a})} are the nonlinear forcing terms that represent the periodic change in the stiffness of the beam due to the breathing effect of each crack and defined as follows

$$ \left\{{R}_1\left(\left\{a\right\}\right)\right\}=\left\{\begin{array}{c}\hfill \left[{B}_1\right]\left\{a\right\}\kern0.84em if\operatorname{}{\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c1}}^{+}}-{\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c1}}^{-}}\ge 0\hfill \\ {}\hfill \left\{0\right\}\operatorname{}\kern0.48em if\kern0.24em {\left.\kern1.32em \frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c1}}^{+}}-{\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c1}}^{-}}<0\hfill \end{array}\right., $$

(27.14)

$$ \left\{{R}_2\left(\left\{a\right\}\right)\right\}=\left\{\begin{array}{c}\hfill \left[{B}_2\right]\left\{a\right\}\kern0.84em if\operatorname{}{\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c2}}^{+}}-{\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c2}}^{-}}\ge 0\hfill \\ {}\hfill \left\{0\right\}\operatorname{}\kern0.48em if\kern0.24em {\left.\kern1.32em \frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c2}}^{+}}-{\left.\frac{\partial w\left(x,t\right)}{\partial x}\right|}_{x={L_{c2}}^{-}}<0\hfill \end{array}\right.. $$

(27.15)

In order to identify the state of the cracks, the slope difference at each crack location is checked. Positive slope difference at the crack location indicates that the crack is closed and the nonlinear forcing term is nonzero; whereas negative slope difference indicates that the crack is open, thus the nonlinear forcing term is zero.

27.3 Harmonic Balance Method with Multi Harmonics

Nonlinear differential equations of motion obtained is solved by utilizing harmonic balance method with multi harmonics. For periodic forcing, the response can also be assumed periodic. Therefore, modal coefficient of each trial function is expressed as follows

$$ {a}_j\left(\theta \right)={a}_{j0}+\sum_p{a}_{jcp} \cos \left( p\theta \right)+\sum_p{a}_{jsp} \sin \left( p\theta \right), $$

(27.16)

where a _j0 is the bias term of the j ^th modal coefficient, a _jcp and a _jsp are the coefficients of cosine and sine components of the p ^th harmonic of the j ^th modal coefficient, respectively and θ = ωt.

Similarly, the external periodic point force can be written as follows

$$ f\left(\theta \right)=\sum_p{f}_{cp} \cos \left( p\theta \right)+\sum_p{f}_{sp} \sin \left( p\theta \right). $$

(27.17)

In addition, each periodic nonlinear forcing term can be expressed by multi harmonic Fourier series as

$$ {R}_i={R}_{i0}+\sum_p{R}_{icp} \cos \left( p\theta \right)+\sum_p{R}_{isp} \sin \left( p\theta \right), $$

(27.18)

where i = 1 , 2 and

$$ {R}_{i0}=\frac{1}{\pi}\underset{0}{\overset{2\pi }{\int }}{R}_i d\theta, $$

(27.19)

$$ {R}_{icp}=\frac{1}{\pi}\underset{0}{\overset{2\pi }{\int }}{R}_i \cos \left( p\theta \right) d\theta, $$

(27.20)

$$ {R}_{isp}=\frac{1}{2\pi}\underset{0}{\overset{2\pi }{\int }}{R}_i \sin \left( p\theta \right) d\theta . $$

(27.21)

As given in [11], Eqs. (27.16), (27.17), (27.18), (27.19), (27.20), and (27.21) can be expressed in vector form. Substituting the vector form of the above mentioned equations into Eq. (27.13) and collecting the sine cosine terms leads to the following set of nonlinear equations

$$ \begin{array}{c}\hfill \left(\left[\begin{array}{ccc}\hfill \left[K\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[K\right]\hfill \end{array}\right]-{\omega}^2\left[\begin{array}{ccc}\hfill \left[M\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[M\right]\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill \left[I\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill {p}^2\left[I\right]\hfill \end{array}\right]\right)\left\{\begin{array}{c}\hfill \left\{{a}_{c1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{a}_{cp}\right\}\hfill \end{array}\right\}+\left\{\begin{array}{c}\hfill \left\{{R}_{1c1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{R}_{1 cp}\right\}\hfill \end{array}\right\}+\left\{\begin{array}{c}\hfill \left\{{R}_{2c1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{R}_{2 cp}\right\}\hfill \end{array}\right\}\hfill \\ [20pt]\hfill +\omega \left[\begin{array}{ccc}\hfill \left[C\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[C\right]\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill \left[I\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill p\left[I\right]\hfill \end{array}\right]\left\{\begin{array}{c}\hfill \left\{{a}_{s1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{a}_{sp}\right\}\hfill \end{array}\right\}-\left[\begin{array}{ccc}\hfill \left[{\phi}_{L_f}\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[{\phi}_{L_f}\right]\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {f}_{c1}\left\{I\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {f}_{cp}\left\{I\right\}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill \left\{0\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{0\right\}\hfill \end{array}\right\}\hfill \end{array}, $$

(27.22)

$$ \begin{array}{c}\hfill \left(\left[\begin{array}{ccc}\hfill \left[K\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[K\right]\hfill \end{array}\right]-{\omega}^2\left[\begin{array}{ccc}\hfill \left[M\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[M\right]\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill \left[I\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill {p}^2\left[I\right]\hfill \end{array}\right]\right)\left\{\begin{array}{c}\hfill \left\{{a}_{s1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{a}_{sp}\right\}\hfill \end{array}\right\}+\left\{\begin{array}{c}\hfill \left\{{R}_{1s1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{R}_{1 sp}\right\}\hfill \end{array}\right\}+\left\{\begin{array}{c}\hfill \left\{{R}_{2s1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{R}_{2 sp}\right\}\hfill \end{array}\right\}\hfill \\ [20pt] {}\hfill +\omega \left[\begin{array}{ccc}\hfill \left[C\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[C\right]\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill \left[I\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill p\left[I\right]\hfill \end{array}\right]\left\{\begin{array}{c}\hfill \left\{{a}_{c1}\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{{a}_{cp}\right\}\hfill \end{array}\right\}-\left[\begin{array}{ccc}\hfill \left[{\phi}_{L_f}\right]\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill \left[{\phi}_{L_f}\right]\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {f}_{s1}\left\{I\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {f}_{sp}\left\{I\right\}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill \left\{0\right\}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \left\{0\right\}\hfill \end{array}\right\}\hfill \end{array}, $$

(27.23)

$$ \left[K\right]\left\{{a}_0\right\}+\frac{1}{2}\left\{{R}_{10}\right\}+\frac{1}{2}\left\{{R}_{20}\right\}=\left\{0\right\}, $$

(27.24)

where [I] is the identity matrix, {I} is a vector whose elements are all 1, and

$$ \left[{\phi}_{L_f}\right]=\left[\begin{array}{ccc}\hfill {\phi}_1\left({L}_f\right)\hfill & \hfill \hfill & \hfill 0\hfill \\ {}\hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill \hfill & \hfill {\phi}_j\left({L}_f\right)\hfill \end{array}\right]. $$

(27.25)

27.4 Numerical Results

In this study, the concern is the effect of the extra breathing crack that is added to a cantilever beam which already has a breathing edge crack. Therefore, a case study is carried out by using the following beam properties and crack parameters:

L = 1 m, I = 1.6667 ⋅ 10⁻⁹ m⁴, A = 2 ⋅ 10⁻⁴ m², ρ = 7850 kg/m⁴, E = 206 GPa, ζ= 0.002, L _c1 = 0.2L, L _c2 = 0.6L and crack ratio α = 0.5. External point force is applied at location L _f  = 0.3L with a magnitude of f(t) = 100 cos (ωt). Galerkin’s method is applied utilizing the first three mass normalized mode shapes of a cantilever beam. Nonlinear equation of motion obtained is solved by utilizing multi harmonic balance method with five harmonics.

In Table 27.1, the first three natural frequencies of intact beam, single crack beam and double crack beam are given and the corresponding mass normalized mode shapes are plotted in Fig. 27.2. If single crack beams are considered, it is seen that the natural frequency is affected by the crack location and an additional crack increases the flexibility of the beam further; therefore, the natural frequencies of the beam with double cracks are the lowest. However, the decrease in the natural frequencies are not significant enough to be used for crack detection purposes, especially considering the effect of measurement noise.

Table 27.1 First three natural frequencies of beams with no crack, single crack and double crack

Fig. 27.2

First Three Mass Normalized Mode Shapes of Intact Beam, Beam with Open Crack at L_c = 0.2 L and Beam with Open Crack at L_c = 0.6 L

Response of the beam is obtained for three different cases, i.e., a beam with a single breathing crack at location 0.2L, a beam with a single breathing crack at location 0.6L and a beam with double breathing cracks at locations 0.2L and 0.6L. In Fig. 27.3a, b total transverse displacement and acceleration amplitudes of the free end point are plotted as functions of frequency. It is observed that the change in amplitudes is not significant for each case. In both plots, especially in acceleration amplitude plot, there are additional local peaks at frequencies other than the natural frequencies of the beams. These additional local peaks are related to the nonlinearity due to the breathing crack. However, by observing the amplitude plots, it is not possible to get information about the additional breathing crack. Therefore, higher harmonics of the response are also plotted for the same frequency range to in order to see the effect of the additional breathing crack.

Fig. 27.3

Beams with single crack at L_c = 0.2 L, at L_c = 0.6 L and beam with double cracks at L_c1 = 0.2 L, L_c2 = 0.6 L (a) tip point displacement amplitude, (b) tip point acceleration amplitude

In Fig. 27.4a, the first harmonic is given as a function of frequency which is the most dominant harmonic in the total response. It is slightly influenced by the crack parameters; therefore, it is not possible to perform crack identification by observing the first harmonic. However, from Fig. 27.4b, it is seen that the bias term is significantly affected by the crack parameters. Magnitude of the bias term of the beam with double breathing crack is similar to the magnitude of the bias term of the beam with a single crack at L _c  = 0.2L up to 20 Hz. Starting from about 40 Hz, up to about 100 Hz, the beam with double cracks has a magnitude of bias term similar to the magnitude of the bias term of a beam with single crack at location L _c  = 0.6L.

Fig. 27.4

(a) First harmonic, (b) Bias term

In Fig. 27.5 even numbered harmonics are presented as a function of frequency. At different frequency ranges, the beam with double breathing crack follows a pattern similar to the pattern of the beam with a single breathing crack at location L _c  = 0.2L or at location L _c  = 0.6L.

Fig. 27.5

Even numbered harmonics (a) second harmonic, (b) fourth harmonic

Odd numbered harmonics are shown in Fig. 27.6. Studying these figures, similar behavior of the double crack as in the odd numbered harmonics is observed. However, at higher frequencies the order magnitude gets smaller for the odd numbered harmonics. Therefore, when the crack detection is the concern, odd harmonics may not be as useful as the even harmonics.

Fig. 27.6

Odd numbered harmonics (a) third harmonic, (b) fifth harmonic

27.5 Conclusion

In this paper, a preliminary study is carried out in order to observe the effects of the additional breathing crack. The beam which is under the action of a harmonic point forcing is modeled by Euler-Bernoulli beam theory and the breathing effect is modeled in terms of bi-linear stiffness. Utilizing Galerkin’s method, a nonlinear system of differential equations is obtained for a beam with double cracks at locations L _c1 and L _c2. By the application of harmonic balance method with multi harmonics, a nonlinear set of algebraic equations is obtained and solved by utilizing Newton’s method. Higher harmonics of the total displacement of the tip point is plotted as a function of excitation frequency. The results obtained showed that, at different frequency ranges, the harmonics of the beam with double breathing edge crack is similar to the harmonics of the beam with a single breathing crack at locations L _c1 or L _c2. It is also shown that as the frequency increases, the order of magnitude of the odd numbered harmonics decreases, therefore even numbered harmonics might have more significance for detection purposes.