Recovering Pose and 3D Deformable Shape from Multi-instance Image Ensembles

Abstract

In recent years, there has been a growing interest on tackling the Non-Rigid Structure from Motion problem (NRSfM), where the shape of a deformable object and the pose of a moving camera are simultaneously estimated from a monocular video sequence. Existing solutions are limited to single objects and continuous, smoothly changing sequences. In this paper we extend NRSfM to a multi-instance domain, in which the images do not need to have temporal consistency, allowing for instance, to jointly reconstruct the face of multiple persons from an unordered list of images. For this purpose, we present a new formulation of the problem based on a dual low-rank shape representation, that simultaneously captures the between- and within-individual deformations. The parameters of this model are learned using a variant of the probabilistic linear discriminant analysis that requires consecutive batches of expectation and maximization steps. The resulting approach estimates 3D deformable shape and pose of multiple instances from only 2D point observations on a collection images, without requiring pre-trained 3D data, and is shown to be robust to noisy measurements and missing points. We provide quantitative and qualitative evaluation on both synthetic and real data, and show consistent benefits compared to current state of the art.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The joint estimation of 3D shape and camera pose from a collection of images either acquired from different viewpoints or by a single moving camera is one of the most active areas in computer vision. In the last two decades, many works have addressed this problem under the assumption of a rigid scene [1,2,3,4] (see Fig. 1-Left). More recently, a number of approaches have been proposed to tackle the non-rigid case, and estimating a deforming 3D shape together with the camera pose from solely 2D observations [5,6,7,8,9]. This is the so-called Non-Rigid Structure from Motion (NRSfM) problem, which is inherently ambiguous and requires introducing several priors. The most standard assumption holds on that the observed objects do not arbitrarily change their shapes, and that deformations can be ruled by low-rank models. For instance, low-rank shape models span the shape using a linear combination of rigid and global basis, weighted by time-varying coefficients [10,11,12]. This has led to a number of solutions for sparse [7, 13, 14], dense [15], and sequential [16, 17] reconstruction. A common characteristic of all these NRSfM algorithms is that the input images belong to one single object viewed from consecutive and smoothly changing viewpoints (see Fig. 1-Center), which has been exploited to introduce further constraints about temporal smoothness on the shape deformations [5, 11, 18], on the point trajectories [19, 20] and on the camera motion [21]. Temporal smoothness priors have proven to be a powerful constraint on sequential NRSfM [16, 22, 23], giving consistent and accurate solutions.

Fig. 1.

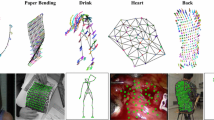
Schematic comparison of our approach (denoted as Manifold Non-Rigid SfM) against standard Rigid SfM and Non-Rigid SfM. Left: In Rigid SfM pipelines, a collection of images, either acquired from different cameras –even with a different calibration– and viewpoints or from a single moving camera, is used to recover pose and 3D shape of a rigid scene. Center: Non-Rigid SfM normally handles objects that deform between consecutive frames, but the collection of images normally needs to be temporally consistent and the object remain the same. Right: Our Manifold Non-Rigid SfM is applicable to image collections that do not retain temporal consistency, and most importantly, can estimate the shape of different deforming instances in the same family.

In this paper, we depart from the assumptions of previous NRSfM approaches, by proposing a solution that does not require temporal consistency of the input images, and most importantly, that it can be applied to simultaneously recover the 3D deformable shape and pose of different instances of the same class of objects. In essence, we bring the standard scenario of the rigid structure from motion depicted in Fig. 1-Left to a non-rigid domain, as shown in Fig. 1-Right, in which we learn pose and a 3D non-rigid shape manifold. To do so, we expand the NRSfM formulation using a dual low-rank shape model that independently represents the deformations between- and within-object instances. Each of these components and their corresponding set of weights is learned by means of a variant of the Probabilistic Linear Discriminant Analysis (PLDA) [24] and iterating between partial expectation and maximization steps. The resulting approach estimates all this from the sole input of 2D input tracks on a collection of images without requiring pre-trained 3D data, it is robust to noisy observations and it can handle missing tracks due to occlusions or lack of visibility. We demonstrate the effectiveness on both synthetic and real image collections, showing the advantages of the proposed approach with respect to state-of-the-art techniques. We believe our model opens up the NRSfM topic to a series of new problems in which the single instance and smooth camera viewpoint changes are no longer a requirement.

2 Related Work

Reconstructing the shape of a non-rigid object while recovering the camera motion from only 2D point trajectories is known to be a severely under-constrained problem that requires prior information in order to be solved. The prior most widely used in NRSfM consists in constraining the shape to lie on a global low-rank shape subspace, that can be computed over a set of training data [25], applying modal [26, 27] or spectral [28] analysis over a rest shape, or estimating it on-the-fly [10, 12, 29]. Most approaches build upon the well-known closed-form factorization technique used for rigid reconstruction [30], enforcing camera orthonormality constraints. This is also done in [5, 11, 18, 31] by incorporating temporal and spatial smoothness constraints on top of the low-rank ones. More recently, temporal smoothness is enforced by means of differentials over the 3D shape matrix by directly minimizing its rank [13, 15], or by means of a union of temporal low-rank shape subspaces [14].

Alternatively, pre-defined trajectory basis have been introduced to constrain the trajectory of every object point, turning the original trilinear problem to a bilinear one [19]. In [32], trajectory priors were used in terms of 3D point differentials. Subsequent works have combined shape and trajectory constraints [6, 33, 34]. More recently, both low-rank shape and trajectory subspaces have been linked to a force subspace, giving them a physical interpretation [9]. In any event, while achieving remarkable results, all previous approaches aim at modeling one single object, observed from smoothly changing viewpoints. The approach we propose here, gets rid of both these limitations.

We would also like to mention that our approach can be somewhat related to methods that model low-dimensional shape manifolds using, e.g., Gaussian Mixtures [35] or Gaussian Processes [36, 37]. However, note that all these techniques assume again smoothly changing video sequences, and the 3D shape to be aligned with the camera. Additionally, none of these approaches tackles the problem of besides retrieving 3D shape, estimating the camera pose, as we do.

Contributions. In short, we propose a novel NRSfM solution which brings together a number of characteristics not found in other methods: (1) It recovers 3D non-rigid shape and camera motion from image collections that do not exhibit temporal continuity, i.e., our approach does not require monocular videos as input; (2) It jointly encodes between- and within-object deformations; (3) It can simultaneously model several instances of a same family; and (4) the number of instances does not need to be known in advance. Our method is robust to artifacts such as noise or discontinuities due to missing tracks, and yields accurate reconstructions.

3 3D Deformable Shape Manifold Model

This section describes the proposed low-rank shape model, and specifically focuses on highlighting the main differences with respect to previous similar formulations.

Let $\mathbf {s}^k=[(\mathbf {x}_1^k)^\top ,\dots ,(\mathbf {x}_N^k)^\top ]^\top$ be the 3N-dimensional representation of the shape at the k-th frame of a collection of K images, with $\mathbf {x}_i^k=[x_i^k,y_i^k,z_i^k]^\top$ denoting the 3D coordinates of the i-th point. Traditional low-rank shape methods [5, 11, 22] approximate the shape $\mathbf {s}^k$ by a linear combination of a shape at rest $\mathbf {s}_0$ and Q rigid shapes $\mathbf {F}\in 3N\times Q$, weighted by time-varying coefficients $\varvec{\gamma }^k=[\gamma ^k_1,\ldots ,\gamma ^k_Q]^\top$:

$$\begin{aligned} \mathbf {s}^{k}=\mathbf {s}_0+\mathbf {F}\varvec{\gamma }^k . \end{aligned}$$

(1)

In all theses approaches the collection of images is assumed to be temporally ordered (i.e., the superscript $^k$ conveys time information), such that the deformation between two consecutive frames k and $k+1$ changes smoothly. Additionally, it is assumed that the shapes $\mathbf {s}^k$ for $k=\{1,\ldots ,K\}$ belong to the same object.

The proposed new formulation does not impose both these constraints: we let the K images of the collection to be acquired from different viewpoints that do not follow a smooth path, and the images may belong to C different instances of the same class of object (e.g., faces of different individuals). For doing so, we draw inspiration on the LDA [38, 39], and propose a model that besides the term $\mathbf {F}\varvec{\gamma }^k$ in Eq. (1) representing the deformations undergone by one single object (we call them within-object deformations), it incorporates a term that approximates the deformation among different objects of the same class (we call them between-object deformations). More specifically, an object instance $c\in \{1,\ldots ,C\}$ at image frame k can be approximated as:

$$\begin{aligned} \mathbf {s}^{k,c}=\mathbf {s}_0+\mathbf {B}\varvec{\psi }^c+\mathbf {F}\varvec{\gamma }^k , \end{aligned}$$

(2)

where $\mathbf {B}$ is a $3N\times B$ matrix containing the B shape basis vectors of the between-individual subspace and $\varvec{\psi }^c=[\psi ^c_1,\ldots ,\psi ^c_B]^\top$ are their corresponding class-varying weight coefficients.

Equation (2) can be interpreted as follows: the term $\mathbf {s}_0+\mathbf {B}\varvec{\psi }^c$ allows encoding the 3D shape manifold, but not the object particularities of the k-th frame, and thus, we do not index it with the superscript $^k$. On the other hand, the term $\mathbf {F}\varvec{\gamma }^k$ is intended to encode the within-individual deformations, which are specific for each frame k. Additionally, note that the formulation considers a vector of coefficients $\varvec{\psi }^c$ specific per each object c. This assumes that the partition of the K images into C object classes is known in advance. If this is not possible, or simply if the number of classes is unknown, we set $C=1$.

Eventually, in the following section, we may compactly represent Eq. (2) as:

$$\begin{aligned} \mathbf {s}^{k,c}=\mathbf {s}_0+\mathbf {M}_s\mathbf {m}^{k,c} , \end{aligned}$$

(3)

where we define a $3N\times (B+Q)$ matrix $\mathbf {M}_s\equiv [\mathbf {B}, \mathbf {F}]$ and a vector of coefficients $\mathbf {m}^{k,c}\equiv [{\varvec{\psi }^c}^{\top }, {\varvec{\gamma }^k}^{\top }]^{\top }$.

4 Learning 3D Deformable Manifold, Shape and Motion

We now describe our approach to simultaneously learn the 3D deformable shape manifold ${\mathbf {B}}$, the shape basis $\mathbf {F}$ to code the time-varying deformations, their corresponding coefficients $\{\varvec{\psi },\varvec{\gamma }\}$ and the camera motion from a collection of images.

4.1 Problem Formulation

Let us consider the 3N-dimensional shape $\mathbf {s}^{k,c}$ of Eq. (2) is observed by an orthographic camera. The projection onto the image plane of the 3D points in frame k can be written as a 2N vector $\mathbf {w}^{k,c}$:

$$\begin{aligned} \mathbf {w}^{k,c} = \mathbf {G}^{k} \mathbf {s}^{k,c} + \mathbf {h}^k + \mathbf {n}^{k} , \end{aligned}$$

(4)

where $\mathbf {G}^k=\mathbf {I}_N\otimes \mathbf {R}^k$ is the $2N\times 3N$ camera motion matrix, $\mathbf {I}_N$ is the N-dimensional identity matrix, $\mathbf {R}^k$ are the first two rows of a full rotation matrix, and $\otimes$ denotes the Kronecker product. Similarly, $\mathbf {h}^k=\mathbf 1 _N\otimes \mathbf {t}^k$ is a 2N vector resulting from concatenating N bidimensional translation vectors $\mathbf {t}^k$, and $\mathbf 1 _N$ is a N-vector of ones. Finally, $\mathbf {n}^k$ is a 2N dimensional vector of Gaussian noise that accounts for the unexplained data variation.

We can then define our problem as that of estimating for $k=\{1,\ldots ,K\}$, the shape $\mathbf {s}^{k,c}$ and camera pose parameters $\{\mathbf {R}^k,\mathbf {t}^k\}$, given the 2D point observations $\mathbf {w}^{k,c}$ corrupted by noise $\mathbf {n}^k$ and the list the classes $c=\{1,\ldots ,C\}$.

In order to make the problem tractable, we constrain the shape $\mathbf {s}^{k,c}$ to lie on the dual low-rank shape subspace defined by the manifold $\{\mathbf {B},\mathbf {s}_0\}$ and by the within-object subspace $\mathbf {F}$. We therefore inject Eq. (2) into Eq. (4) to rewrite our observation model as:

$$\begin{aligned} \mathbf {w}^{k,c} = \mathbf {G}^{k} (\mathbf {s}_0+\mathbf {B}\varvec{\psi }^{c}+\mathbf {F}\varvec{\gamma }^k) + \mathbf {h}^k + \mathbf {n}^k\;. \end{aligned}$$

(5)

4.2 Probabilistic Formulation of the Problem

To simultaneously learn the 3D deformable shape manifold, the instance-specific shape and the camera pose from 2D point correspondences as described in Eq. (5), we propose an algorithm similar to the Probabilistic LDA approach used to represent shape distributions [24, 40, 41]. However, these previous formulations are intended to retrieve mappings that do not change the dimensionality of the input data. In our case, we aim at estimating a mapping that brings the 2D observations to 3D interpretations, i.e., we solve an inverse problem. This will need from a substantially different methodology.

In order to proceed we assume the between- and within-object coefficient vectors to be normally distributed, i.e., $\varvec{\psi }^{c}\sim \mathcal {N}\left( \mathbf {0};\mathbf {I}_{B}\right)$ and $\varvec{\gamma }^{k}\sim \mathcal {N}\left( \mathbf {0};\mathbf {I}_{Q}\right)$, respectively. Assuming these probabilistic priors, both vectors become latent variables that can be marginalized out and never need to be explicitly computed. We can then propagate the previous distributions to the deforming shapes on Eq. (2), yielding:

$$\begin{aligned} \mathbf {s}^{k,c}\sim \mathcal {N}\left( \mathbf {s}^{k,c}|\mathbf {s}_0;\mathbf {B}\mathbf {B}^{\top }+\mathbf {F}\mathbf {F}^{\top }\right) . \end{aligned}$$

(6)

Let us also consider a Gaussian prior distribution with variance $\sigma ^2$ to model the noise over the shape observations, such that $\mathbf {n}^{k}\sim \mathcal {N}\left( \mathbf {0};\sigma ^2\mathbf {I}_{2N}\right)$. Any remaining variation on the observations that is not explained by the shape parameters is described as noise. Since both latent variables follow a Gaussian prior distribution, the distribution of the observed variables $\mathbf {w}^{k,c}$ on Eq. (5) is also Gaussian:

$$\begin{aligned} \mathbf {w}^{k,c} \sim \mathcal {N}\left( \mathbf {w}^{k,c}|\mathbf {G}^k\mathbf {s}_0+\mathbf {h}^k; \mathbf {G}^k\mathbf {B}\mathbf {B}^\top {\mathbf {G}^k}^\top +\mathbf {G}^k\mathbf {F}\mathbf {F}^\top {\mathbf {G}^k}^\top +\sigma ^{2}\mathbf {I}_{2N} \right) . \end{aligned}$$

(7)

In order to learn the parameters of this distribution we use an Expectation-Maximization (EM) algorithm, as done in other NRSfM approaches [5, 7, 9]. However, this approach will need a bit more of machinery, as previous methods did only consider one single latent variable. Here we are estimating two latent variables ($\varvec{\gamma }^k$ and $\varvec{\psi }^c$) which will require to re-define the algorithm by including multiple consecutive E-steps.

Fig. 2.

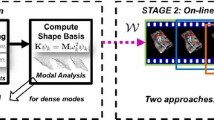
Left: Graphical representation of our probabilistic NRSFM formulation with a dual low-rank shape model. Given the 2D observations $\mathbf {w}^{k,c}$ of K shapes belonging to C different object instances, the proposed approach learns, for each image frame, the pose parameters $\varvec{\varTheta }^k$ and a shape model. The shape is represented by two low-rank matrices $\mathbf {B}$ and $\mathbf {F}$ approximating the deformation between- and within-objects, with their corresponding weights $\varvec{\phi }^c$ and $\varvec{\gamma }^k$, respectively. These latent variables and the 2D observations are assumed to be normally distributed with covariances $\mathbf {I}_B$, $\mathbf {I}_Q$ and $\sigma ^2\mathbf {I}_{2N}$, respectively, also learned from data. Right: Evolution of the log-likelihood function in Eq. (8) as a number of iterations, for a specific problem with 200 images and 157 points.

4.3 Expectation Maximization

We next describe the details of the EM algorithm to learn the PLDA-inspired model from 2D point correspondences. Let us denote by $\varvec{\varTheta }^{k}\equiv \{\mathbf {R}^{k},\mathbf {t}^{k}\}$ the set of pose parameters that need to be estimated per frame, and by $\varvec{\varUpsilon }\equiv \{\mathbf {B},\mathbf {F},\sigma ^{2}\}$ the set of parameters that are common for all frames of the collection. Regarding the latent space, let $\varvec{\varPsi }=[\varvec{\psi }^1,\ldots ,\varvec{\psi }^C]$ and $\varvec{\varGamma }=[\varvec{\gamma }^1,\ldots ,\varvec{\gamma }^K]$ be the between- and within-object latent variables, respectively.

Our problem consists in estimating the parameters $\varvec{\varTheta }=\{\varvec{\varTheta }^1,\ldots ,\varvec{\varTheta }^K\}$ and $\varvec{\varUpsilon }$, given the set of 2D positions of all points $\mathbf {w}=\{\mathbf {w}^{1,\mathcal {C}(1)},\ldots ,\mathbf {w}^{K,\mathcal {C}(K)}\}$, where $\mathcal {C}(k)=c$ is a function that returns the instance label c associated to the k-th frame. Recall that we do not assume temporal coherence between two consecutive observations $\mathbf {w}^{k,\mathcal {C}(k)}$ and $\mathbf {w}^{k+1,\mathcal {C}(k+1)}$. See Fig. 2-Left for a representation of the problem as a graphical model.

The corresponding data likelihood we seek to maximize is therefore given by:

$$\begin{aligned} p\left( \mathbf {w}|\varvec{\varTheta },\varvec{\varUpsilon }\right) \,\, \sim \prod _{k=1}^{K} p\left( \mathbf {w}^{k,\mathcal {C}(k)}|\mathbf {R}^{k},\mathbf {t}^{k},\mathbf {B},\mathbf {F},\sigma ^{2} \right) . \end{aligned}$$

(8)

In order to maximize this equation, the EM algorithm we propose iteratively alternates between two steps: the E-step to obtain the distribution over latent coordinates and the M-step to update the model parameters. However, since our model contains two types of latent variables and several model parameters, we use partial E- and M- steps, as we next explain.

E-Steps: To estimate the posterior distribution over the latent variables $\varvec{\psi }^{c}$ and $\varvec{\gamma }^{k}$ given the current model parameters and observations, we propose executing two consecutive E-steps. Assuming independent and identically distributed random samples, and applying the Bayes’ rule and the Woodbury’s matrix identity [42], the distribution over $\varvec{\varPsi }$ can be shown to be:

$$\begin{aligned} \nonumber p\left( \varvec{\varPsi }|\mathbf {w},\varvec{\varTheta }, \varvec{\varUpsilon }\right) = \prod _{c=1}^{C}p\left( \varvec{\psi }^c|\mathbf {w},\varvec{\varTheta }, \varvec{\varUpsilon }\right) \sim \prod _{c=1}^{C}\mathcal {N}\left( \varvec{\mu }^c_{\varvec{\psi }};\varvec{\varSigma }^c_{\varvec{\psi }}\right) , \end{aligned}$$

with:

where $\mathbb {I}(k)=1$ if $\mathcal {C}(k)==c$, and zero otherwise. Note that this indicator function enforces computing $\varvec{\mu }_{\varvec{\psi }}^{c}$, $\varvec{\varSigma }^{c}_{\varvec{\psi }}$ and $\varvec{\varLambda }^{c}_{\varvec{\psi }}$ using only the image frames k belonging to the object class c.

Once the distribution over $\varvec{\varPsi }$ is known, the distribution over $\varvec{\varGamma }$ can be estimated by:

$$\begin{aligned} \nonumber p\left( \varvec{\varGamma }|\mathbf {w},\varvec{\varTheta }, \varvec{\varUpsilon }, \varvec{\varPsi }\right) = \prod _{k=1}^{K} p\left( \varvec{\gamma }^k|\mathbf {w},\varvec{\varTheta }, \varvec{\varUpsilon }, \varvec{\varPsi }\right) \sim \prod _{k=1}^{K} \mathcal {N}\left( \varvec{\mu }_{\varvec{\gamma }}^k;\varvec{\varSigma }_{\varvec{\gamma }}^k\right) , \end{aligned}$$

with:

$$\begin{aligned} \begin{aligned} \varvec{\mu }_{\varvec{\gamma }}^k=&\varvec{\varLambda }_{\varvec{\gamma }}^{k}\Big (\mathbf {w}^{k,\mathcal {C}(k)}-\mathbf {G}^k\mathbf {s}_0-\mathbf {G}^k\mathbf {B}\varvec{\mu }^{c}_{\varvec{\psi }}-\mathbf {h}^k\Big )\;, \\ \varvec{\varSigma }_{\varvec{\gamma }}^k=&\mathbf {I}_Q-\varvec{\varLambda }^{k}_{\varvec{\gamma }}\mathbf {G}^k\mathbf {F},\\ \varvec{\varLambda }^{k}_{\varvec{\gamma }}=&\sigma ^{-2}\mathbf {F}^{\top }{\mathbf {G}^{k}}^\top \Big (\mathbf {I}_{2N}-\sigma ^{-2}\mathbf {G}^k\mathbf {F}\left( \mathbf {I}_{Q}+\sigma ^{-2}\mathbf {F}^\top {\mathbf {G}^{k}}^\top \mathbf {G}^k\mathbf {F}\right) ^{-1}\mathbf {F}^\top {\mathbf {G}^{k}}^\top \Big ). \end{aligned}\nonumber \end{aligned}$$

M-Steps: We then replace the latent variables by their expected values and update the model parameters by optimizing the following negative log-likelihood function $\mathcal {A}({\varvec{\varTheta },\mathbf {w}})$ with respect to the parameters $\varvec{\varTheta }^k$, for $k=\{1,\ldots ,K\}$ and $\varvec{\varUpsilon }$:

Since this function cannot be minimized in closed form for all parameters, we perform partial M-steps over each of the model parameters. For doing so, we first consider the compact model on Eq. (3) and define the following expectations:

where $\varvec{\phi }^{c}_{\varvec{\psi }\varvec{\psi }}=\mathbb {E}[\varvec{\psi }^{c}{\varvec{\psi }^{c}}^\top ]=\varvec{\varSigma }^{c}_{\varvec{\psi }}+\varvec{\mu }^{c}_{\varvec{\psi }}{\varvec{\mu }^{c}_{\varvec{\psi }}}^\top$ and $\varvec{\phi }^k_{\varvec{\gamma }\varvec{\gamma }}=\mathbb {E}[\varvec{\gamma }^k(\varvec{\gamma }^k)^\top ]=\varvec{\varSigma }_{\varvec{\gamma }}^k+\varvec{\mu }_{\varvec{\gamma }}^k(\varvec{\mu }_{\varvec{\gamma }}^k)^\top$.

To update each of the individual model parameters, we set $\partial \mathcal {A}/\partial \varvec{\varTheta }=0$ for each parameter on $\varvec{\varTheta }$. The update rules can be shown to be:

where $\mathbf {w}^{k,c}=[(\mathbf {w}_1^{k,c})^\top ,\ldots ,(\mathbf {w}_N^{k,c})^\top ]^\top$ is a 2N-dimensional vector, $\mathbf {w}^{k,c}_i$ are 2D coordinates of the i-th point in frame k, and $(\mathbf {M}_s\varvec{\mu }_{\mathbf {m}}^{k,c})_i$ is the i-th 3D point of the 3N vector $\mathbf {M}_s\varvec{\mu }_{\mathbf {m}}^{k,c}$. To solve the optimization for $\mathbf {R}^k$ we use a non-linear minimization routine.

The overall process is quite efficient, and requires, in average, a few tens of iterations to converge for collections of a few hundreds of images. Figure 2-Right plots the evolution of the log-likelihood of Eq. (8) for a collection of 200 images with 157 points each. In this case, the algorithm converged in 30 iterations, taking 323 seconds on a laptop with an Intel Core i7 processor at 2.4 GHz.

We initialize motion parameters by rigid factorization (similar to shape-based NRSfM approaches [5, 12, 15]) and the dual low-rank model by means of a coarse-to-fine approach, where each basis that is added explains as much of the deformable motion variance as possible. Additionally, since we are estimating global models we can handle occlusions, and missing observations can be easily inferred from the observed data. We will demonstrate this robustness in the results section.

5 Experiments

We next report quantitative and qualitative results of our method on face reconstruction. These results can be best viewed in the supplemental video¹. For the quantitative results, we report the mean 3D reconstruction error [%] as defined in [12, 15].

5.1 Synthetic Images

To quantitatively validate our method, we first consider a synthetic sequence with 3D ground truth. From the real and dense mocap data of [43], we render a sequence of 200 frames and 157 points per frame (denoted in the following as Face sequence), in which one person performs several face movements and gestures. We randomly shuffle the frames ordering in order to build a collection of images without temporal coherence. For this specific experiment we do not test the multi-object instance scenario. This is not a problem for our model though, despite it considers the between- and within-object subspaces. We could have forced the between-object subspace to be zero, but decided not doing so, and show that our approach can generalize from one to several objects.

Fig. 3.

Mean 3D reconstruction error in the Face sequence, as a function of basis rank Q for state-of-the-art methods: EM-LDS [5], MP [12], PTA [19], CSF2 [20], KSTA [6] and EM-PND [7]; and our approach. For the EM-PND [7], the 3D reconstruction error was 21.0% and 21.2% for the noise-less and noisy cases, respectively. For our approach, the between-object rank was set to a fixed value of $B=3$. Left: Noise-less 2D measurements. Right: Noisy 2D measurements. Best viewed in color.

We use this sequence to compare the proposed method against several low-rank shape, trajectory and shape-trajectory methods in state of the art. In particular, we consider: EM-LDS [5], the metric projections MP [12], SPM [13] and EM-PND [7] for shape space; the point trajectory approach (PTA) [19] for trajectory space; the column space fitting (CSF2) [20] and the kernel shape trajectory approach (KSTA) [6] for shape-trajectory methods. The parameters of these methods were set as suggested in the original papers. In our case, we only have to set the rank B and Q of the between- and within-object subspaces, respectively.

We conduced experiments with and without noise in the observations. For the noisy case, we corrupted the measurements using additive zero-mean Gaussian noise with standard deviation $\sigma _{noise}=0.02\kappa$, where $\kappa$ denotes the maximum distance of a 2D point observation to the mean position of all observations. In Fig. 3, we plot the mean 3D reconstruction error as a function of the within-object basis rank Q, for our method and the other seven methods aforementioned. In our formulation the between-object basis rank was not accurately tuned and it was set to a constant value of $B=3$. Observe that our approach consistently outperforms the rest of competing approaches for both the noise and noiseless experiments. Since EM-PND [7] does not need to set the basis rank, we did not include this method in the graph, and just report its reconstruction error, which is of 21.0%, far above from the rest of methods. Regarding SPM [13], the approach is not applicable to larger ranks as the number of linear-matrix-inequality constraints is not sufficient to solve this case, obtaining an error of 10.69% for $Q=1$. It is worth noting that our results for $Q=1$ are remarkably better than other approaches for $Q\ge 4$, that is our equivalent rank if we consider the 3 vectors of B. In Fig. 4 we represent the significance of the reconstruction error values, and show some qualitative results, including the 2D input data and our reconstructed 3D shape.

Fig. 4.

Synthetic results on the Face sequence. We show the input images at the top, and at the bottom a frontal and side views of the reconstructed shapes. For all cases, we display the results with $Q=3$ and $B=3$. Best viewed in color.

Fig. 5.

ASL database. In each row we show the same information. Top: 2D tracking data and reconstructed 3D shape reprojected into several images with green circles and red squares, respectively. Blue squares correspond to missing points. Bottom: Camera frame and side-views of the reconstructed 3D shape: our solution, CSF2 [20] and KSTA [6], respectively. We also represent the number of image k in the input data, showing as different objects are intercalated. Best viewed in color.

5.2 Real Images

For the real data we consider two experiments with human faces of two or more individuals.

In the first scenario we process an American Sign Language (ASL) database, that consists in a collection of 229 images belonging to 2 subjects (male and female) with 77 feature points per frame. One of the challenges of this dataset is that some of the frames are heavily occluded by one or two hands, or by the own rotation of the face. The dataset is built from two sequences previously used to test NRSfM algorithms: the ASL1, consisting of 115 frames with a 17.4% of missing data [33], and the ASL2 sequence, consisting of 114 frames with a 11.5% of missing data [20]. Before processing the collection of images, we shuffle the frames to break the temporal continuity. In Fig. 5 we show two views per image of the shape estimated by our method, CSF2 [20] and KSTA [6]. For our approach we set $C=1$. By doing this we ensure a fair comparison with the other two approaches, as we do not exploit the fact that the identity of each individual is known. Additionally we set $B=2$ and $Q=3$. From Fig. 5 we can observe that our model yields a qualitatively correct estimation of the shape. However, while CSF2 [20] provides very good results when processing the two sequences ASL1 and ASL2 independently, it is prone to fail when merging their data and shuffling the frames, using exactly the same rank of the subspace. Note the completely wrong estimation of the nose in some of the frames. This is relieved by KSTA [6], although by providing a quasi-rigid solution with almost no deformation adaption. Observe, for instance, that the lips remain always closed (see for example frames #105 and #62 of the upper and lower sequence in Fig. 5). Although only qualitatively, our approach correctly retrieves these deformations.

In order to bring some quantitative results to this analysis, we have built a pseudo-ground truth of this database (real 3D ground truth is not available) by independently processing ASL1 and ASL2 using the NRSfM approach proposed in [9] –the method that seems to provide best performance for these sequences– and compared its 3D reconstructions with the ones obtained when simultaneously processing the faces of the two persons. A summary of these results are provided in Table 1. In this case, we obtain the following errors: CSF2 [20] (14.93%), KSTA [6] (3.62%), EM-PFS [9] (8.37%), our approach (2.66%). If we specifically focus on the lips reconstruction, which is highly deformable, as expected the differences become more clear: CSF2 [20] (12.74%), KSTA [6] (11.08%), EM-PFS [9] (7.79%), our approach (4.53%). It is worth to point that the performance of EM-PFS [9] degrades when jointly processing images of ASL1 and ASL2. We presume the intrinsic physical model considered by this approach is sensitive to the differences between the two individuals. Additionally, we can exploit the list the classes c in our formulation. In this case, we obtain more accurate solutions: 2.50% considering all object shape and 4.35% for lips reconstruction.

Table 1. Quantitative comparison on ASL database. Comparison of our approach against CSF2 [20], KSTA [6] and EM-PFS [9] for the full face shape and the corresponding lips area in terms of 3D error [%]. In all cases we show the minimum error with the number of rank Q in the subspace (in brackets).

In the final experiment we evaluate our approach on a subset of the MUCT face database [44]. We gather an heterogeneous collection of 302 images belonging including very different face morphologies, poses and expressions. We ensure the input images contain similar numbers of males and females, and a cross section of ages and races. Once the images are chosen, we obtain the 2D observations using an off-the-shelf 2D active appearance model [45]. Again, in order to highlight the generality of our approach, we do not take advantage of the fact of knowing the object label of each input image, and we set $C=1$. Figure 6 shows the qualitative results of our approach. We can observe how our method provides results that seem very realistic and correlate with the appearance of the images. Note, for instance that some of the faces have an overall thin shape (see woman in the first column) while other convey a quite round shape (see woman in the second column).

Fig. 6.

MUCT database. In each row we show the same information. Top: 2D tracking data and reconstructed 3D shape reprojected into several images with green circles and red squares, respectively. Bottom: Camera frame and side-views of the reconstructed 3D shape. Best viewed in color.

6 Conclusion

In this paper we have proposed a new formulation of the NRSfM problem that allows dealing with collections of images with no temporal coherence, and including several instances of the same class of object. In order to make this possible we have proposed a dual low-rank space that separately models the deformations within each specific object and the deformations between individuals. These low-rank subspaces are learned using a variant of the probabilistic linear discriminant analysis, and an EM strategy that consecutively executes several expectation and maximization steps. We validate the approach in synthetic image collections –with one single object instance– and show improved results compared to state-of-the-art. Real results on datasets including faces of two or more persons, depict an even larger gap with previous NRSfM approaches. In the future we aim at extending our approach to different types of datasets, not only human faces. For instance, we believe we can readily exploit our formulation to learn deformable shape manifolds of human full body motions. Other fields, such as computer graphics animation could also benefit from this approach and transfer motion styles between different characters.