Harmonic Forcing of a Two-Segment Euler-Bernoulli Beam

Abstract

This study is on the forced motions of non-homogeneous elastic beams. Euler-Bernoulli theory is employed and applied to a two-segment configuration subject to harmonic forcing. The objective is to determine the frequency response function for the system. Two different solution strategies are used. In the first, analytic solutions are derived for the differential equations for each segment. The constants involved are determined using boundary and interface continuity conditions. The response, at a given location, can be obtained as a function of forcing frequency (FRF). The procedure is unwieldy. Moreover, determining particular integrals can be difficult for arbitrary spatial variations. An alternative method is developed wherein material and geometric discontinuities are modeled by continuously varying functions (here logistic functions). This results in a single differential equation with variable coefficients, which is solved numerically, for specific parameter values, using MAPLE^®. The numerical solutions are compared to the baseline analytical approach for constant spatial dependencies. For validation purposes an assumed-modes solution is also developed. For a free-fixed boundary conditions example good agreement between the numerical methods and the analytical approach is found, lending assurance to the continuous variation model. Fixed-fixed boundary conditions are also treated and again good agreement is found.

1.1 Introduction

This work is an extension of one given in reference [1] in which the determination of the bending natural frequencies of beams whose properties vary along the length was sought. Of interest were beams with different materials and varying cross-sections, which were layered in cells and could be uniform or not.

In reference [1] an approach was discussed, in which the discrete cell properties were modeled by continuously varying functions, specifically logistic functions, which had the considerable advantage of working with a single differential equation (albeit one with variable coefficients). Natural frequencies could be calculated via a forced motion strategy by means of MAPLE^®’s ODE¹ solver.

There are several references on vibrations of layered beams. For example reference [2], where free vibrations of stepped Timoshenko beams were treated via a Lagrange multiplier formalism. Results compared well with values obtained using other analytical methods. In reference [3] Euler-Bernoulli stepped beams were studied via exact and FEM approaches. FEM results using non-integer polynomials shape functions [4] compared well with exact solutions. General studies on media with discrete layers have been given, for example, in references [5,6,7,8]. Note that finite difference approaches to the dynamics of non-homogeneous media can be found in reference [9].

Here the objective is to determine the frequency response functions (FRF) of such beams. Euler-Bernoulli theory is used for a two-segment configuration under harmonic forcing. Analytic solutions can be obtained for each segment, for specific conditions, and the response calculated at a given location, thus providing the FRFs. But the procedure is unwieldy and particular solutions to the differential equations can be difficult to obtain for arbitrary spatial variations. The alternate approach utilized involves modeling material and geometric discontinuities by continuously varying functions. This results in a single differential equation with variable coefficients, which is solved numerically. These are compared to analytical solutions for constant spatial dependencies. An assumed-modes solution is also developed for validation purposes.

1.2 Basic Problem

In this study Euler-Bernoulli beam theory is used. The equation of motion is given below and Fig. 1.1 exhibits the underlying variables.

$$ \frac{\partial^2}{\partial {x}^2}\left(E(x)I(x)\frac{\partial^2w\left(x,t\right)}{\partial {x}^2}\right)+\rho (x)A(x)\frac{\partial^2w\left(x,t\right)}{\partial {t}^2}=f\left(x,t\right) $$

(1.1)

Fig. 1.1

Beam element

In the derivation of Eq. (1.1) no assumption was made in relation to the material type, therefore it can be either a homogeneous or a non-homogeneous material.

The layered configuration discussed here is a two-cell beam. Strategies for obtaining the steady state response, due to harmonic forcing, are investigated in the following.

1.3 Analytical Approach

In this section analytic solutions are sought using standard beam theory.

Consider the beam shown in Fig. 1.2 which is composed by two cells of different materials.

Fig. 1.2

Layered beam

The transversal displacement equation of motion for each segment (“i-th” segment) is:

$$ \frac{\partial^2}{\partial {x}^2}\left({E}_i(x){I}_i(x)\frac{\partial^2{w}_i\left(x,t\right)}{\partial {x}^2}\right)+{\rho}_i(x){A}_i(x)\frac{\partial^2{w}_i\left(x,t\right)}{\partial {t}^2}={f}_i\left(x,t\right),i=1,2... $$

(1.2)

where f _i are external transverse forces per unit length.

For harmonic forcing with frequency ω:

$$ {f}_i\left(x,t\right)={F}_i(x) \sin \left(\omega t\right) $$

(1.3)

Assuming solutions of the form:

$$ {w}_i\left(x,t\right)={R}_i(x) \sin \left(\omega t\right) $$

(1.4)

leads to

$$ \frac{d^2}{dx^2}\left({E}_i{I}_i\frac{d^2{R}_i(x)}{dx^2}\right)-{\rho}_i{A}_i{\omega}^2{R}_i(x)={F}_i(x) $$

(1.5)

For A _i , ρ _i , I _i and E _i constant in each segment:

$$ \frac{d^4{R}_i(x)}{dx^4}-\frac{\rho_i{A}_i}{E_i{I}_i}{\omega}^2{R}_i(x)=\frac{F_i(x)}{E_i{I}_i} $$

(1.6)

Define ${\gamma_i}^4=\frac{\rho_i{A}_i}{E_i{I}_i}{\omega}^2$ and ${P}_i(x)=\frac{F_i(x)}{E_i{I}_i}$, then for each segment:

$$ \frac{d^4{R}_i(x)}{dx^4}-{\gamma_i}^4{R}_i(x)={P}_i(x) $$

(1.7)

General solutions to the linear differential equation (1.7) can be written as:

$$ {R}_i(x)={R}_{ih}(x)+{R}_{ip}(x) $$

(1.8)

where R _ih (x) are the general solutions to the homogeneous equations and R _ip (x) are “particular integrals”.

For Eq. (1.7),

$$ {R}_{1h}(x)={B}_1 \cosh \left({\gamma}_1x\right)+{B}_2 \sinh \left({\gamma}_1x\right)+{B}_3 \cos \left({\gamma}_1x\right)+{B}_4 \sin \left({\gamma}_1x\right) $$

(1.9)

$$ {R}_{2h}(x)={B}_5 \cosh \left({\gamma}_2x\right)+{B}_6 \sinh \left({\gamma}_2x\right)+{B}_7 \cos \left({\gamma}_2x\right)+{B}_8 \sin \left({\gamma}_2x\right) $$

(1.10)

For arbitrary forcing P _i (x), finding tractable particular integrals can pose a problem (this is treated later numerically). In the following two examples are considered.

1.3.1 Constant Spatial Force

Here attention is restricted to constant spatial forcing: P ₁ (x) = P _1,0 , P ₂ (x) = P _2,0 ; P _1,0 , P _2,0 constants.

Then

$$ {R}_{1p}(x)=-\frac{P_{1,0}}{{\gamma_1}^4} $$

(1.11)

$$ {R}_{2p}(x)=-\frac{P_{2,0}}{{\gamma_2}^4} $$

(1.12)

Now the general solutions can be written:

$$ {R}_1(x)={B}_1 \cosh \left({\gamma}_1x\right)+{B}_2 \sinh \left({\gamma}_1x\right)+{B}_3 \cos \left({\gamma}_1x\right)+{B}_4 \sin \left({\gamma}_1x\right)-\frac{P_{1,0}}{{\gamma_1}^4} $$

(1.13)

$$ {R}_2(x)={B}_5 \cosh \left({\gamma}_2x\right)+{B}_6 \sinh \left({\gamma}_2x\right)+{B}_7 \cos \left({\gamma}_2x\right)+{B}_8 \sin \left({\gamma}_2x\right)-\frac{P_{2,0}}{{\gamma_2}^4} $$

(1.14)

The overall analytic solution requires that the boundary conditions be defined. Two sets are considered below.

1.3.1.1 Free-Fixed Boundary Conditions

For these conditions the moment and shear free end at x = 0 gives: ${\left.\frac{d^2{R}_1(x)}{dx^2}\right|}_{x=0}=0$ and ${\left.\frac{d^3{R}_1(x)}{dx^3}\right|}_{x=0}=0$, which, from Eq. (1.13), leads to B ₁  = B ₃ and B ₂  = B ₄ . Then Eq. (1.13) becomes:

$$ {R}_1(x)={B}_1\left( \cosh \left({\gamma}_1x\right)+ \cos \left({\gamma}_1x\right)\right)+{B}_2\left( \sinh \left({\gamma}_1x\right)+ \sin \left({\gamma}_1x\right)\right)-\frac{P_{1,0}}{{\gamma_1}^4} $$

(1.15)

The remaining constants involved in the solutions can be determined as follows. The boundary condition at the other end (fixed) gives: R ₂(x) = 0 and ${\left.\frac{dR_2(x)}{dx}\right|}_{x=L}=0,x=L\ \left(L={L}_1+{L}_2\right)$. Interface continuity conditions give: R ₁(x) = R ₂(x) , x = L ₁ (displacement continuity), $\frac{dR_1(x)}{dx}=\frac{dR_2(x)}{dx},x={L}_1$(slope continuity), ${E}_1{I}_1\frac{d^2{R}_1(x)}{dx^2}={E}_2{I}_2\frac{d^2{R}_2(x)}{dx^2},x={L}_1$(moment continuity) and ${E}_1{I}_1\frac{d^3{R}_1(x)}{dx^3}={E}_2{I}_2\frac{d^3{R}_2(x)}{dx^3},x={L}_1$(shear continuity). The conditions lead to a system of algebraic equations:

$$ \begin{array}{l}{B}_5 \cosh \left({\gamma}_2L\right)+{B}_6 \sinh \left({\gamma}_2L\right)+{B}_7 \cos \left({\gamma}_2L\right)+{B}_8 \sin \left({\gamma}_2L\right)=\frac{P_{2,0}}{{\gamma_2}^4}\\ {}{B}_5 \sinh \left({\gamma}_2L\right)+{B}_6 \cosh \left({\gamma}_2L\right)-{B}_7 \sin \left({\gamma}_2L\right)+{B}_8 \cos \left({\gamma}_2L\right)=0\\ {}{B}_1\left( \cosh \left({\gamma}_1{L}_1\right)+ \cos \left({\gamma}_1{L}_1\right)\right)+{B}_2\left( \sinh \left({\gamma}_1{L}_1\right)+ \sin \left({\gamma}_1{L}_1\right)\right)-\frac{P_{1,0}}{{\gamma_1}^4}=\\ {}{B}_5 \cosh \left({\gamma}_2{L}_1\right)+{B}_6 \sinh \left({\gamma}_2{L}_1\right)+{B}_7 \cos \left({\gamma}_2{L}_1\right)+{B}_8 \sin \left({\gamma}_2{L}_1\right)-\frac{P_{2,0}}{{\gamma_2}^4}\\ {}{B}_1\left( \sinh \left({\gamma}_1{L}_1\right){\gamma}_1- \sin \left({\gamma}_1{L}_1\right){\gamma}_1\right)+{B}_2\left( \cosh \left({\gamma}_1{L}_1\right){\gamma}_1+ \cos \left({\gamma}_1{L}_1\right){\gamma}_1\right)=\\ {}{B}_5 \sinh \left({\gamma}_2{L}_1\right){\gamma}_2+{B}_6 \cosh \left({\gamma}_2{L}_1\right){\gamma}_2-{B}_7 \sin \left({\gamma}_2{L}_1\right){\gamma}_2+{B}_8 \cos \left({\gamma}_2{L}_1\right){\gamma}_2\\ {}{B}_1\left( \cosh \left({\gamma}_1{L}_1\right){\gamma_1}^2- \cos \left({\gamma}_1{L}_1\right){\gamma_1}^2\right)+{B}_2\left( \sinh \left({\gamma}_1{L}_1\right){\gamma_1}^2- \sin \left({\gamma}_1{L}_1\right){\gamma_1}^2\right)=\\ {}\frac{E_2{I}_2}{E_1{I}_1}\left({B}_5 \cosh \left({\gamma}_2{L}_1\right){\gamma_2}^2+{B}_6 \sinh \left({\gamma}_2{L}_1\right){\gamma_2}^2-{B}_7 \cos \left({\gamma}_2{L}_1\right){\gamma_2}^2-{B}_8 \sin \left({\gamma}_2{L}_1\right){\gamma_2}^2\right)\\ {}{B}_1\left( \sinh \left({\gamma}_1{L}_1\right){\gamma_1}^3+ \sin \left({\gamma}_1{L}_1\right){\gamma_1}^3\right)+{B}_2\left( \cosh \left({\gamma}_1{L}_1\right){\gamma_1}^3- \cos \left({\gamma}_1{L}_1\right){\gamma_1}^3\right)=\\ {}\frac{E_2{I}_2}{E_1{I}_1}\left({B}_5 \sinh \left({\gamma}_2{L}_1\right){\gamma_2}^3+{B}_6 \cosh \left({\gamma}_2{L}_1\right){\gamma_2}^3+{B}_7 \sin \left({\gamma}_2{L}_1\right){\gamma_2}^3-{B}_8 \cos \left({\gamma}_2{L}_1\right){\gamma_2}^3\right)\end{array} $$

(1.16)

from which B ₁ , B ₂ , B ₅ , B ₆ , B ₇ and B ₈ can be determined.

In non-dimensional matrix form the complete set of equations is given by:

$$ \begin{array}{c}\left[\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cosh \left({\gamma}_r\lambda \right)\hfill & \hfill \sinh \left({\gamma}_r\lambda \right)\hfill & \hfill \cos \left({\gamma}_r\lambda \right)\hfill & \hfill \sin \left({\gamma}_r\lambda \right)\hfill \\ [4pt] {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \sinh \left({\gamma}_r\lambda \right)\hfill & \hfill \cosh \left({\gamma}_r\lambda \right)\hfill & \hfill - \sin \left({\gamma}_r\lambda \right)\hfill & \hfill \cos \left({\gamma}_r\lambda \right)\hfill \\ [4pt] {}\hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill - \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill - \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill - \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \\ [5pt] {}\hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill -{\gamma}_r \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{\gamma}_r \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {\gamma}_r \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{\gamma}_r \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \\ [5pt] {}\hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^2 \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^2 \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {E}_r{I}_r{\gamma_r}^2 \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {E}_r{I}_r{\gamma_r}^2 \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \\ [5pt] {}\hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^3 \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^3 \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^3 \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {E}_r{I}_r{\gamma_r}^3 \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \end{array}\right] \left[\begin{array}{c}\hfill {b}_1\hfill \\ [4pt] {}\hfill {b}_2\hfill \\ [4pt] {}\hfill {b}_3\hfill \\ [4pt] {}\hfill {b}_4\hfill \\ [4pt] {}\hfill {b}_5\hfill \\ [4pt] {}\hfill {b}_6\hfill \\ [4pt] {}\hfill {b}_7\hfill \\ [4pt] {}\hfill {b}_8\hfill \end{array}\right]= \left[\begin{array}{c}\hfill 0\hfill \\ [3pt] {}\hfill 0\hfill \\ [3pt] {}\hfill \frac{1}{{\gamma_r}^4}\hfill \\ [4pt] {}\hfill 0\hfill \\ [4pt] {}\hfill \left(1-\frac{1}{{\gamma_r}^4}\right)\hfill \\ [4pt] {}\hfill 0\hfill \\ [3pt] {}\hfill 0\hfill \\ [3pt] {}\hfill 0\hfill \end{array}\right]\frac{Q_0}{\lambda^4}\\ {}\equiv \left[\mathrm{A}\right]\left\{\mathrm{B}\right\}=\left\{\mathrm{F}\right\}\end{array}\\[-11pt]\vspace*{-3pt} $$

(1.17)

where ${b}_i=\frac{B_i}{L}$, L ₂ = αL ₁, L = (1 + α)L ₁, λ = γ ₁ L,${\gamma}_r=\frac{\gamma_2}{\gamma_1}$, ${I}_r=\frac{I_2}{I_1}$, ${E}_r=\frac{E_2}{E_1}$, Q ₀ = P ₀ L ³ and P _1,0  = P _2,0  = P ₀ .

Note that natural frequencies can found on setting the determinant of [A] to zero.

1.3.1.2 Fixed-Fixed Boundary Conditions

For these conditions the fixed end at x = 0 gives: R ₁(x) = 0 and ${\left.\frac{dR_1(x)}{dx}\right|}_{x=0}=0$, which, from Eq. (1.13), leads to ${B}_1+{B}_3=\frac{P_{1,0}}{\gamma_1^4}$ and B ₂ =  − B ₄. Following the procedure described above leads to the following non-dimensional system of equations for the unknowns coefficients (non-dimensional matrix form):

$$ \begin{array}{c}\left[\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cosh \left({\gamma}_r\lambda \right)\hfill & \hfill \sinh \left({\gamma}_r\lambda \right)\hfill & \hfill \cos \left({\gamma}_r\lambda \right)\hfill & \hfill \sin \left({\gamma}_r\lambda \right)\hfill \\ [4pt] {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \sinh \left({\gamma}_r\lambda \right)\hfill & \hfill \cosh \left({\gamma}_r\lambda \right)\hfill & \hfill - \sin \left({\gamma}_r\lambda \right)\hfill & \hfill \cos \left({\gamma}_r\lambda \right)\hfill \\ [4pt] {}\hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill - \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill - \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill - \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \\ [5pt] {}\hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill -{\gamma}_r \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{\gamma}_r \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {\gamma}_r \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{\gamma}_r \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \\ [5pt] {}\hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^2 \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^2 \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {E}_r{I}_r{\gamma_r}^2 \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {E}_r{I}_r{\gamma_r}^2 \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \\ [5pt] {}\hfill \sinh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \cosh \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill \sin \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill - \cos \left(\frac{\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^3 \sinh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^3 \cosh \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill -{E}_r{I}_r{\gamma_r}^3 \sin \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill & \hfill {E}_r{I}_r{\gamma_r}^3 \cos \left(\frac{\gamma_r\lambda }{1+\alpha}\right)\hfill \end{array}\right] \left[\begin{array}{c}\hfill {b}_1\hfill \\ [4pt] {}\hfill {b}_2\hfill \\ [4pt] {}\hfill {b}_3\hfill \\ [4pt] {}\hfill {b}_4\hfill \\ [4pt] {}\hfill {b}_5\hfill \\ [4pt] {}\hfill {b}_6\hfill \\ [4pt] {}\hfill {b}_7\hfill \\ [4pt] {}\hfill {b}_8\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 1\hfill \\ [4pt] {}\hfill 0\hfill \\ [4pt] {}\hfill \frac{1}{{\gamma_r}^4}\hfill \\ [4pt] {}\hfill 0\hfill \\ [4pt] {}\hfill \left(1-\frac{1}{{\gamma_r}^4}\right)\hfill \\ [4pt] {}\hfill 0\hfill \\ [4pt] {}\hfill 0\hfill \\ [4pt] {}\hfill 0\hfill \end{array}\right]\frac{Q_0}{\lambda^4}\\ [4pt] {}\equiv \left[\mathrm{A}\right]\left\{\mathrm{B}\right\}=\left\{\mathrm{F}\right\}\end{array}\vspace*{-3pt} $$

(1.18)

1.4 Continuous Variation Model

Here the transitions from one material to another are approximated via logistic functions (step functions are not used since they would generate numerical complications because of the singular derivatives):

$$ H(x)\approx \frac{1}{2}+\frac{1}{2} \tanh (Kx)=\frac{1}{1+{e}^{-2 Kx}} $$

(1.19)

Note that in Eq. (1.19) a larger K corresponds to a sharper transition at x = 0.

A non-dimensional version of the equation of motion can be obtained by taking:

τ = Ω₀ t, $\xi =\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$L$}\right.$, $Y\left(\xi, \tau \right)=w\left(x,t\right)\raisebox{1ex}{${\Omega}_0$}\!\left/ \!\raisebox{-1ex}{$L$}\right.$, $\nu =\raisebox{1ex}{$\omega $}\!\left/ \!\raisebox{-1ex}{${\Omega}_0$}\right.$, I(x) = I ₁ H ₂(Kξ) = I ₁ f ₂(ξ), A(x) = A ₁ H ₄(Kξ) = A ₁ f ₄(ξ),E(x) = E ₁ H ₁(Kξ) = E ₁ f ₁(ξ), ρ(x) = ρ ₁ H ₃(Kξ) = ρ ₁ f ₃(ξ). (H _i , logistic functions.)

Substituting these into Eq. (1.1) leads to:

$$ \frac{\partial^2}{\partial {\xi}^2}\left({f}_1\left(\xi \right){f}_2\left(\xi \right)\frac{\partial^2Y\left(\xi, \tau \right)}{\partial {\xi}^2}\right)+\frac{\lambda^4}{\nu^2}{f}_3\left(\xi \right){f}_4\left(\xi \right)\frac{\partial^2Y\left(\xi, \tau \right)}{\partial {\tau}^2}=g\left(\xi, \tau \right) $$

(1.20)

Ω₀ is a reference frequency, which is set to ${\Omega}_0=\sqrt{\frac{E_1{I}_1}{\rho_1{A}_1{L}^4}}$. This gives: ${\lambda}^4={\left({\gamma}_1L\right)}^4=\left(\frac{\rho_1{A}_1{L}^4{\omega}^2}{E_1{I}_1}\right)={\nu}^2$and $g\left(\xi, \tau \right)=\frac{L^3{\Omega}_0}{E_1{I}_1}f\left(x,t\right)$.

Analytic solutions may not be feasible for Eq. (1.20). Here the following approach is adopted. Given the material layout (stacked cells) and cross section variation, i.e., f ₁(ξ), f ₃(ξ), f ₂(ξ) and f ₄(ξ), a MAPLE^® routine is developed for obtaining numerical approximations to the frequency response function (FRF) of the system. The equation is subjected to a harmonic forcing function, for example g(ξ, τ) = F(ξ) sin (ντ), and response amplitudes are monitored for different values of ν.

An approach described by the authors in reference [10] can also be utilized for extracting resonances and amplitudes. In Eq. (1.20) vibration frequencies can be calculated by assuming Y(ξ, τ) = S(ξ) sin (ντ) and harmonic forcing g(ξ, τ) = F(ξ) sin (ντ). This leads to:

$$ \frac{d^2}{d{\xi}^2}\left({f}_1\left(\xi \right){f}_2\left(\xi \right)\frac{d^2S\left(\xi \right)}{d{\xi}^2}\right)-{\lambda}^4{f}_3\left(\xi \right){f}_4\left(\xi \right)S\left(\xi \right)=F\left(\xi \right) $$

(1.21)

where, it should be noted that ν ² = λ ⁴.

In this case the strategy consists of using MAPLE^®’s two-point boundary value solver to solve a forced motion problem. A constant value for the forcing function F is assumed and the frequency λ is varied. By observing the mid-span deflection of the beam, the resonant frequency can be found on noting where an abrupt change in sign occurs. Higher modes can be obtained by extending the search range.

1.5 Numerical Examples

Consider the beam shown in Fig. 1.2 and assume the following materials: Aluminum (E ₁  = 71 GPa, ρ ₁  = 2710 kg/m ³) and Silicon Carbide (E ₂  = 210 GPa, ρ ₂  = 3100 kg/m ³). These values are taken from a basic paper in the field [11].

1.5.1 Free-Fixed Boundary Conditions

For the free-fixed case and taking α = 1(L ₂ = L ₁), the determinant of [A] in Eq. (1.17) leads to the following values for the first two non-dimensional natural frequencies: λ ₁ = 2.3967 and λ ₂ = 5.2342. (The following parameters apply: γ _r  = 0.7886, E _r  = 2.9577, A _r  = A ₂/A ₁ = 1.00, ρ _r  = ρ ₂/ρ ₁ = 1.1481, Q ₀ = 1.00.)

For this case the non-dimensional version of Eq. (1.15) is given by:

$$ {R}_1\left(\xi \right)={b}_1\left( \cosh \left(\lambda \xi \right)+ \cos \left(\lambda \xi \right)\right)+{b}_2\left( \sinh \left(\lambda \xi \right)+ \sin \left({\lambda}_1\xi \right)\right)-\frac{Q_0}{\lambda^4} $$

(1.22)

Setting ξ = 0.50 (beam mid-span) and using b ₁ and b ₂ from Eq. (1.17), amplitudes can be calculated for different values of the frequency λ.

Using Eq. (1.22) the frequency response function spanning the first two natural frequencies for the mid-point of the beam is shown in Fig. 1.3.

Fig. 1.3

FRF for non-homogeneous beam mid-point—Free/Fixed

For the continuous variation model and this uniform beam, the non-dimensional logistic functions and cross-section functions can be written, for example, as (see Fig. 1.4):

$$ \begin{array}{l}{f}_1\left(\xi \right)=1+\frac{E_2-{E}_1}{E_1}\left(\frac{1}{2}+\frac{1}{2} \tanh \left(500\left(\xi -\frac{1}{2}\right)\right)\right),{f}_2\left(\xi \right)=1\\ {}{f}_3\left(\xi \right)=1+\frac{\rho_2-{\rho}_1}{\rho_1}\left(\frac{1}{2}+\frac{1}{2} \tanh \left(500\left(\xi -\frac{1}{2}\right)\right)\right),\kern0.5em {f}_4\left(\xi \right)=1\end{array} $$

(1.23)

Fig. 1.4

Relative properties variation for two-cell beam

Assuming a value of 1 for the external forcing and using the approach given in reference [10], the resultant deflections are plotted bellow for two distinct values of the frequency λ.

The resonance frequencies are taken to occur at λ = 2.40 and λ = 5.25 as seen in Figs. 1.5 and 1.6, respectively.

Fig. 1.5

Beam deflections for distinct values of λ–Free-Fixed: first resonance

Fig. 1.6

Beam deflections for distinct values of λ–Free-Fixed: second resonance

Amplitudes for the response at the center of the beam can be monitored from Eq. (1.21). This approach leads to the numerical FRF shown in Fig. 1.7.

Fig. 1.7

Results comparison—numerical and analytical approaches (ODE)—Free/Fixed

The figure shows an overlap of the numerical results and the results from the analytical approach, Eq. (1.22). It is seen that good agreement is obtained, the first two resonances are captured and the amplitude values correspond well.

Next the FRF is obtained via solutions to Eq. (1.20). The results are shown in Fig. 1.8.

Fig. 1.8

Results comparison—numerical and analytical approaches (PDE)—Free/Fixed

It is seen in the overlap that the PDE solutions lead to a reasonable approximation to the FRF for this case. The first resonance is captured within 12% but the second resonance is not. Obtaining better results from MAPLE^® would require considerable more effort and is not pursued here in view of the other successful approaches.

For validation purposes, an assumed mode method is pursued in the following. The solution to Eq. (1.1) is assumed to have the form of a Rayleigh-Ritz expansion:

$$ w\left(x,t\right)=\sum_{i=1}^n{\alpha}_i(t){\varphi}_i(x) $$

(1.24)

where the generalized coordinates α _i , in the linear combination of shape functions φ _i , are functions of time.

The shape functions φ _i must be chosen so they form a linearly independent set that possess derivatives up to the order appearing in the strain energy expression for the problem. They also must satisfy the prescribed boundary conditions.

Substituting Eq. (1.24) into the appropriate expressions for the kinetic and strain energy, and using Lagrange’s equations, leads to a set of n differential equations for the generalized coordinates α _i .

For the problem at hand, the discrete non-dimensional mass and stiffness matrices, for the differential equations set, can be obtained from:

$$ {m}_{i,j}=\underset{0}{\overset{\frac{1}{2}}{\int }}{\varphi}_i(x)\ {\varphi}_j(x)\ dx+{A}_r{\rho}_r\underset{\frac{1}{2}}{\overset{1}{\int }}{\varphi}_i(x)\ {\varphi}_j(x)\ dx,{k}_{i,j}=\underset{0}{\overset{\frac{1}{2}}{\int }}{\varphi}_i^{{\prime\prime} }(x)\ {\varphi}_j^{{\prime\prime} }(x)\ dx+{E}_r{I}_r\underset{\frac{1}{2}}{\overset{1}{\int }}{\varphi}_i^{{\prime\prime} }(x)\ {\varphi}_j^{{\prime\prime} }(x)\ dx $$

(1.25)

If the external transverse loads are taken to be sinusoidal with frequency ν, the following expression for calculating the generalized external forces can be used:

$$ {p}_i=\left[\underset{0}{\overset{\frac{1}{2}}{\int }}{f}_1{\varphi}_i(x)\ dx+\underset{\frac{1}{2}}{\overset{1}{\int }}{f}_2{\varphi}_i(x)\ dx\right] \sin \left(\nu \tau \right) $$

(1.26)

where f _i is the amplitude of the force acting on the i-segment.

The natural frequencies can then be evaluated via an eigenvalue problem and the system response to external forcing estimated via modal analysis. The procedure is tackled using MAPLE^®.

As a first approach, non-dimensional mode shapes for a homogenous cantilever beam are used for the shape functions set. They can be written as:

$$ {\varphi}_i(x)={N}_i\left\{\Big[ \cos \left({\beta}_i\right)+ \cosh \right.\left({\beta}_i\right)\left] \left[ \sin \left({\beta}_i\left(1-\xi \right)\right)- \sinh \left({\beta}_i\left(1-\xi \right)\right)\right] +\left[ \sin \left({\beta}_i\right)+ \sinh \left({\beta}_i\right)\right]\right. \\ \left. \left[ \cosh \left({\beta}_i\left(1-\xi \right)\right)- \cos \left({\beta}_i\left(1-\xi \right)\right)\right]\right\} $$

(1.27)

where N _i is a normalization parameter and ${\beta}_1=1.875,{\beta}_2=4.694,{\beta}_k=\left(2k-1\right)\frac{\pi }{2},k=3,...,n$. The normalization parameters are taken to be the inverse of the magnitude of the maximum values of the shape functions in the interval ξ = 0..1.

Using i = 3, f ₁ = 1 and f ₂ = 1, the discrete differential equations of motion for the generalized coordinates α _i are:

$$ \left[\begin{array}{ccc}\hfill 0.2518\hfill & \hfill 0.0053\hfill & \hfill 0.0053\hfill \\ {}\hfill 0.0053\hfill & \hfill 0.2659\hfill & \hfill 0.0192\hfill \\ {}\hfill 0.0053\hfill & \hfill 0.0192\hfill & \hfill 0.4670\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\ddot{\alpha}}_1(t)\hfill \\ {}\hfill {\ddot{\alpha}}_2(t)\hfill \\ {}\hfill {\ddot{\alpha}}_3(t)\hfill \end{array}\right]+\left[\begin{array}{ccc}\hfill 8.8339\hfill & \hfill 5.5380\hfill & \hfill -16.0001\hfill \\ {}\hfill 5.5380\hfill & \hfill 254.1732\hfill & \hfill 351.7299\hfill \\ {}\hfill -16.0001\hfill & \hfill 351.7299\hfill & \hfill 3255.3629\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\alpha}_1(t)\hfill \\ {}\hfill {\alpha}_2(t)\hfill \\ {}\hfill {\alpha}_3(t)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0.3915\hfill \\ {}\hfill 0.2170\hfill \\ {}\hfill 0.1678\hfill \end{array}\right] \sin \left(\nu \tau \right) $$

(1.28)

The natural frequencies are calculated as λ = 2.41 and λ = 5.33.

Following the procedure, the Rayleigh-Ritz approximation for the steady state response is obtained. Setting an arbitrary non-dimensional time τ = 100, for example, and monitoring the amplitudes at ξ = 0.5, for distinct values of the excitation frequency ν, leads to the results shown in Fig. 1.9.

Fig. 1.9

Results comparison—assumed modes and analytical approaches—Free/Fixed

The figure shows an overlap of the assumed modes results and the analytic results (solid line). It can be seen that very good agreement is obtained in terms of frequencies and FRFs for the first two resonances.

In the search for better convergence in the higher modes, one can increase the number of shape functions utilized in the approach. However, this increases the complexity of the numerical calculations in the algorithm developed, due to the presence of increasingly more complex trigonometric and hyperbolic functions in the integrals of Eqs. (1.25) and (1.26).

An alternative is to use polynomial shape functions. This is discussed next.

In this case, the shape functions φ _i are taken to be beam characteristic orthogonal polynomials, with each polynomial satisfying the prescribed boundary conditions of the problem. They are generated by the Gram-Schmidt process [12] as demonstrated by Bhat [13].

The first polynomial is taken to satisfy the two boundary conditions at the fixed end and to have the following form (free-fixed non-dimensional homogeneous beam static deflection under distributed load):

$$ {\varphi}_1(x)={s}_1\left({x}^4-5{x}^3+15{x}^2-19x+8\right) $$

(1.29)

The constant s ₁ is chosen such that:

$$ \underset{0}{\overset{1}{\int }}{\left({\varphi}_k(x)\right)}^2 dx=1 $$

(1.30)

The remainder polynomials are generated by the Gram-Schmidt approach. In addition, the set is also normalized as described above. For example, an approximation with three polynomials gives:

$$ \begin{array}{l}{\varphi}_1(x)=0.1250{x}^4-0.6250{x}^3+1.8750{x}^2-2.3750x+1.0000\\ {}{\varphi}_2(x)=5.4569\left(x-.1538\right)\left(0.2959{x}^4-1.4797{x}^3+4.4391{x}^2-5.6228x+2.3675\right)\\ {}{\varphi}_3(x)=29.5510\left(x-0.3238\right)\left(x-0.1539\right)\left(0.2959{x}^4-1.4797{x}^3+4.4391{x}^2-5.6228x+2.3675\right)-\\ {}\kern3em 0.1556{x}^4+0.7780{x}^3-2.3341{x}^2+2.9565x-1.2448\end{array} $$

(1.31)

which leads to the following discrete differential equations of motion for the generalized coordinates α _i :

$$ \left[\begin{array}{ccc}\hfill 0.1790\hfill & \hfill 0.0034\hfill & \hfill 0.0041\hfill \\ {}\hfill 0.0034\hfill & \hfill 0.5489\hfill & \hfill 0.0248\hfill \\ {}\hfill 0.0041\hfill & \hfill 0.0248\hfill & \hfill 0.5702\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\ddot{\alpha}}_1(t)\hfill \\ {}\hfill {\ddot{\alpha}}_2(t)\hfill \\ {}\hfill {\ddot{\alpha}}_3(t)\hfill \end{array}\right]+\left[\begin{array}{ccc}\hfill 9.3374\hfill & \hfill -54.7945\hfill & \hfill 114.6766\hfill \\ {}\hfill -54.7945\hfill & \hfill 963.8044\hfill & \hfill -2147.8536\hfill \\ {}\hfill 114.6766\hfill & \hfill -2147.8536\hfill & \hfill 9888.9234\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\alpha}_1(t)\hfill \\ {}\hfill {\alpha}_2(t)\hfill \\ {}\hfill {\alpha}_3(t)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0.3063\hfill \\ {}\hfill 0.3333\hfill \\ {}\hfill 0.2276\hfill \end{array}\right] \sin \left(\nu \tau \right) $$

(1.32)

The natural frequencies are calculated as λ = 2.42 and λ = 5.41.

Following the procedure and using the same non-dimensional time τ = 100, monitoring the amplitudes at ξ = 0.5 leads to the results shown in Fig. 1.10.

Fig. 1.10

Results comparison—assumed modes three polynomials and analytical approaches—Free/Fixed

The overlap of the assumed modes and the analytic results (solid line) shows that good agreement is obtained for the first two frequencies and FRFs.

Figure 1.11 shows results using six polynomials. The natural frequencies are calculated as λ = 2.41 and λ = 5.31.

Fig. 1.11

Results comparison—assumed modes six polynomials and analytical approaches—Free/Fixed

The overlap shows better agreement and demonstrates convergence of the approach.

Consider next an example in which the spatial force variations are such that the particular integrals in Eq. (1.8) are intractable analytically. As demonstrated above, the results can be found using the continuous variation model and the assumed modes method.

Take, for example, variable forces equal in both segments and given by an exponential function: ${P}_1(x)={P}_2(x)={e}^{-\left[{\left(x/L\right)}^2\right]}$. Then $F\left(\xi \right)={e}^{-{\xi}^2}$ (refer to Eqs. (1.20) and (1.21)) and ${f}_1={f}_2={e}^{-{\xi}^2}$in Eq. (1.26).

The frequency response functions given by the forced motion and assumed mode approaches, respectively, are seen in Fig. 1.12.

Fig. 1.12

FRF for varying spatial functions—Free/Fixed

In the forced motion plot, the FRF points are represented via a trend line. Very good agreement for the first frequency is seen.

1.5.2 Fixed-Fixed Boundary Conditions

For the fixed-fixed case (α = 1), the determinant of [A] in Eq. (1.18) leads to the following values for the first two non-dimensional natural frequencies: λ ₁ = 5.2329 and λ ₂ = 8.9156. (The parameters γ _r , E _r , A _r , ρ _r , and Q ₀ are the same as above.)

For this case the non-dimensional version of Eq. (1.13) is:

$$ {R}_1\left(\xi \right)={b}_1 \cosh \left(\lambda \xi \right)+{b}_2 \sinh \left(\lambda \xi \right)+{b}_3 \cos \left(\lambda \xi \right)+{b}_4 \sin \left({\lambda}_1\xi \right)-\frac{Q_0}{\lambda^4} $$

(1.33)

Setting ξ = 0.50 and using b ₁ and b ₂ from Eq. (1.18), amplitudes can be calculated for different values of the frequency λ. The frequency response function spanning the first two natural frequencies for the mid-point of the beam is shown in Fig. 1.13.

Fig. 1.13

FRF for non-homogeneous beam mid-point—Fixed/Fixed

Next only the numerical methods that led to consistent results in the previous example are used to obtain frequencies and FRFs for this case, i.e., the forced motion and assumed modes approaches.

The forced motion produces these resonance frequencies: λ = 5.25 and λ = 8.90. Monitoring amplitudes for the response at the center of the beam (Eq. (1.21)) leads to the numerical FRF shown in Fig. 1.14.

Fig. 1.14

Results comparison—numerical and analytical approaches (ODE)—Fixed/Fixed

The figure shows an overlap of the numerical results and the results from the analytical approach, Eq. (1.33). As in the previous example good agreement is obtained.

For the assumed modes method, in this case, the first polynomial is chosen to satisfy the fixed boundary conditions at the ends. It is given by (fixed-fixed non-dimensional homogeneous beam static deflection under distributed load):

$$ {\varphi}_1(x)={s}_1\left(4{x}^3-6{x}^2+2x\right) $$

(1.34)

The constant s ₁ satisfies Eq. (1.30).

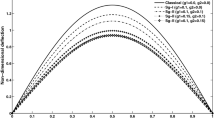
Utilizing six polynomials, the resulting frequencies are λ = 5.27 and λ = 8.95. Following the procedure given above and using the non-dimensional time τ = 100, monitoring amplitudes at ξ = 0.5 leads to the results shown in Fig. 1.15. Good agreement is also seen here.

Fig. 1.15

Results comparison—assumed modes six polynomials and analytical approaches—Fixed/Fixed

Lastly, the spatial force with exponential variation is considered. Results are given in Fig. 1.16 for this case.

Fig. 1.16

FRF for varying spatial functions—Fixed/Fixed

Good agreement for frequencies is seen while the assumed modes approach predicts somewhat higher amplitudes.

1.6 Conclusions

Replacing discrete property variations with continuously varying ones, in conjunction with numerical solutions, has been shown to lead to good results for resonant frequencies and FRFs of layered beams subject to harmonic excitation.

Both resonance monitoring of forced motion solutions of the resulting single ordinary differential equation and an assumed modes approach produced good results toward this objective. MAPLE^® software was utilized and it has been shown to lead to accurate solutions via the two approaches, based on a comparison to analytical results for a specific case.

Two sets of boundary conditions were studied. Namely, fixed-free and fixed-fixed for a uniform two-cell beam made of aluminum and silicon-carbide.

Very good agreement was observed for both cases, with some variation on the amplitudes for the FRFs. For improved accuracy it is conjectured that using more polynomials in the assumed mode approach will produce better agreement.