Keywords

10.1 Introduction

10.1.1 Characteristics of Biological Materials

Engineers have traditionally studied materials such as metals, ceramics, polymers, and their composites. Natural, including biological, materials are another class of materials which offer new opportunities for analysis and discovery (Fratzl and Weinkamer 2007; Chen et al. 2008; Meyers et al. 2008; Meyers et al. 2011; Meyers et al. 2013). Examples of biological materials are bone, cartilage, muscle, tendon, ligament, skin, brain tissue, enamel, dentin, and others. General characteristics of biological materials are that they self-assemble and self-organize from atomic level into complex hierarchical, composite, often porous, and fluid-filled structures (Cui et al. 2007; Bar-On and Wagner 2013). They are multifunctional, adapt to the environment, and can often self-heal (Meyers et al. 2008; Weinkamer and Fratzl 2011). They range from soft and highly deformable tissues such as skin to hard mineralized materials such as bone. Knowledge of biological materials is needed for various medical applications and to design new bioinspired synthetic materials (Munch et al. 2008; Studart 2012; Mirkhalaf et al. 2013; Libonati et al. 2014; Naleway et al. 2015).

10.1.2 Hierarchical Composite Structure of Bone

In this chapter, we focus on the mechanics of bone. Bone is a multifunctional biological material, which has a structural role in the body by providing the frame, facilitating movement, and protecting organs. In addition, it stores minerals, manufactures blood, maintains PH of blood, and detoxifies the body. As a structural material, bone has excellent mechanical properties when healthy as it is stiff, strong, tough, and lightweight (Rho et al. 1998; Weiner and Wagner 1998; Launey et al.2010; Ural and Vashishth 2014). In addition, by being a biological material, bone is in a constant state of remodeling as old or damaged tissues are being continuously replaced by a new bone. This allows bone to continuously change to adapt to its environment (stronger bone is built when subjected to exercise) and to self-heal (e.g., healing of bone fractures) (Weinkamer and Fratzl 2011; Zimmermann and Ritchie 2015).

The superior mechanical properties of bone are due to bone’s composite and hierarchical structure (Weiner and Traub 1992; Lakes 1993; Rho et al. 1998; Olszta et al. 2007; Hamed et al. 2010, 2012a, b). Bone consists of a soft organic phase with collagen type I and non-collagenous proteins, 33–43% by volume (vol%), a stiff inorganic phase with hydroxyapatite crystals, 32–44 vol%, and water-filled pores, 15–25 vol%. Collagen and water provide bone its ductility and toughness, and minerals give it high stiffness and strength, while porosity makes it lightweight.

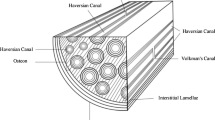
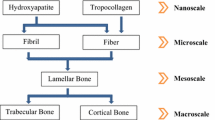
Bone self-assembles from atoms into a complex hierarchical structure up to a whole bone level, as shown in Fig. 10.1. In this paper, we distinguish six structural levels: macroscale, mesoscale, microscale, sub-microscale, nanoscale, and sub-nanoscale following (Rho et al. 1998; Hamed et al. 2010). These choices are not unique and other choices have been proposed in the literature (Weiner and Traub 1992; Katz et al. 2007). This is due to the fact that bone structure changes continuously with length scale, i.e., bone does not have clear scale separations.

Fig. 10.1
figure 1

Hierarchical structure of bone (Hamed and Jasiuk 2013)

Full size image

At the macroscale, bone is made of dense cortical (also called compact) bone which forms an outer shell of whole bone and a spongy trabecular (also called cancellous) bone which fills ends of bone. Cortical bone, in the form of a hollow shaft, provides stiffness and strength and superior bending and torsion resistance while trabecular bone absorbs energy. Such structure achieves optimal structural performance while being lightweight.

At the mesoscale, cortical bone (with 5–10% porosity) consists of concentric hollow cylinders, called osteons, embedded in an interstitial bone which is made of old osteons. The outer shell of cortical bone is made of softer periosteum and circumferential bone. Trabecular bone, present mainly at bone’s ends, has a highly porous structure (20–95% porosity) with porosity increasing in the direction away from the cortical bone giving it a functionally graded structure. Its architecture consists of randomly arranged rodlike or platelike struts, called trabeculae, which give it a foamlike appearance.

At the microscale level, bone is made of lamellar structures, resembling those of laminated composite materials. These include osteonal, interstitial, and circumferential bone types in cortical bone and trabecular pockets forming trabecular struts in trabecular bone.

At the sub-microscale, a single lamella, which is few microns thick, is made of preferentially oriented mineralized collagen fibrils.

At the nanoscale, the mineralized collagen fibril consists of tropocollagen molecules and nanosized minerals. It is considered a basic building block of bone. The tropocollagen molecules, which have a triple-helix structure, about one nanometer (nm) in diameter and 300 nm in length, are crosslinked with each other and arranged in a staggered way with gap and overlap zones and assembled into collagen fibrils which are 50–100 nm in diameters and microns in length. The gap and overlap zones in collagen fibrils result in a characteristic banded pattern which is visible under a transmission electron microscope. The minerals are in the shape of platelets and they are about 25 nm by 50–100 nm and few nanometers thick. Crystals are believed to be infused within the gaps, to fit between collagen molecules (intrafibrillar crystals) and to form cores outside the collagen fibrils (extrafibrillar crystals). There is still a lack of consensus on the percentages of minerals within and outside the collagen fibrils and their precise arrangements. Also, the role of non-collagenous proteins is not fully understood, but it is believed that they reside at collagen–crystal and crystal–crystal interfaces. Most of the models of bone at the nanoscale assume the matrix-fiber geometry with collagen being a matrix and crystals being inclusions (Fratzl et al. 2004). More recent studies observed that bone with organic phase removed still has a self-standing structure, which implies that crystals form a continuous phase (Chen et al. 2011; Hamed et al. 2015).

10.1.3 Overview on Modeling of Bone

Thus, bone is a complex natural nanocomposite material having distinct features at different structural scales. There are several geometric models proposed to represent bone at the nanoscale. Most popular is a matrix-inclusion model which assumes that isolated minerals are embedded in a collagen matrix (Fratzl et al. 2004). More recent propositions involve assumptions of bi-continuous collagen--mineral phases (Chen et al. 2011). At the sub-microscale, a single lamella can be represented as a collection of preferentially aligned fibers (mineralized collagen fibrils) and extrafibrillar minerals and pores (osteocytes and canaliculi canals). At the microscale, bone resembles a laminated composite material forming various lamellar structures (osteonal, interstitial, and circumferential bone) and trabecular struts. At the mesoscale, cortical bone can be considered as a hybrid composite material consisting of osteons and resorption cavities embedded in an interstitial bone, while trabecular bone can be modeled as a random or periodic foam.

Various computational approaches have been proposed to model bone. They can be classified into the following four categories: (a) approximate analytical models based on strength of materials theories, (b) analytical models based on micromechanics theories, (c) computational models using mainly a finite element method, and (d) atomic level simulations utilizing molecular dynamics (Hamed and Jasiuk 2012; Sabet et al. 2016).

Each approach has its advantages and limitations. Strength of materials models are approximate and they can provide quick estimates. Micromechanical approaches involve more rigorous mechanics formulations but they also utilize simplified geometric models. They have been used to estimate the elastic properties of bone. Computational models have addressed more complex geometries and have been used to model damage, plasticity, and fracture of bone. In particular, the finite element models, using images obtained by computed and micro-computed tomography (CT and micro-CT), provide a powerful tool to account precisely for bone’s complex geometries and architectures. Molecular dynamics simulations have been used to predict the mechanical properties of bone’s main constituents (collagen and crystals) and to provide insights on interfaces between them.

Numerous models have been proposed for modeling of bone at different structural scales. For a review of the literature on characterization and elastic modeling of bone, the reader is referred to a recent review paper (Novitskaya et al. 2011). Elastic modeling of bone at the nanoscale is summarized in Hamed and Jasiuk (2012). Modeling of bone fracture and strength at different structural scales is summarized in Sabet et al. (2016).

In the next section, we present a hierarchical approach for modeling the elastic properties of bone. It involves successive steps spanning from the nanoscale to the mesoscale. Effective elastic properties are computed analytically at each structural level by using a “bottom-up” approach in which the effective properties computed at a lower level serve as the inputs for a next higher up level. In the analysis, we employ micromechanics theories and a classical lamination theory. C and Φ denote, respectively, a stiffness tensor and a volume fraction of phases. The analysis follows our formulations presented in Hamed et al. (2010, 2012a, b, 2015).

10.2 Elastic Hierarchical Modeling of Bone

In this section, we present a representative approach to model the elastic properties of bone in order to illustrate how micromechanics methods can be used to study this biological material. This example also provides a framework for modeling other mineralized tissues. Note that scale definitions are not unique, effective medium choices are not unique, and there are various assumptions made on bone geometry at the defined length scales. Different modeling steps are summarized in Fig. 10.2.

Fig. 10.2
figure 2

Homogenization steps used in modeling the elastic properties of cortical bone following Hamed et al. (2010)

Full size image

10.2.1 Nanoscale

At the nanoscale, the mineralized collagen fibril is modeled as a bi-continuous composite material, following (Chen et al. 2011). We use a self-consistent method (Hill 1963; Budiansky 1965) to account for the two interpenetrating phases: collagen fibrils and hydroxyapatite crystals. In this model, there is no matrix and both phases are represented as inclusions. For simplicity, we assume that the bone constituents are linear elastic and isotropic. The properties used in the analysis and their volume fractions are given in Table 10.1. Note that there are a wide range of values reported in the literature as summarized in Table 1 in Hamed et al. (2010), so input choices are not unique.

Table 10.1 Elastic properties and volume fractions of bone constituents used in modeling
Full size table

Collagen fibrils are modeled as cylinders with an aspect ratio of 1000:1:1 following the dimensions reported in the literature ~100 μm length and ~100 nm diameter of collagen fibrils (Olszta et al. 2007; Hang and Barber 2011), while platelet-like crystals are represented as ellipsoidal inclusions with an aspect ratio of 50:25:3 (Robinson 1952) which are aligned in the direction of a long axis of the collagen fibril. Again, these aspect ratios reflect representative values. The effective stiffness tensor of a mineralized collagen fibril, C fib , is computed in terms of stiffness tensors of wet collagen, C wcol , and hydroxyapatite, C wHA , as follows:

$$ \begin{aligned} {\mathbf{C}}_{fib}=&\Bigg\{{\Phi}_{wcol}{\mathbf{C}}_{wcol}:{\left[\mathbf{I}+{\mathbf{S}}_{fib}^{cyl}:{\mathbf{C}}_{fib}^{-1}:\left({\mathbf{C}}_{wcol}-{\mathbf{C}}_{fib}\right)\right]}^{-1}\\ {} &+{\Phi}_{wHA}{\mathbf{C}}_{wHA}:{\left[\mathbf{I}+{\mathbf{S}}_{fib}^{ellipse}:{\mathbf{C}}_{fib}^{-1}:\left({\mathbf{C}}_{wHA}-{\mathbf{C}}_{fib}\right)\right]}^{-1}\Bigg\}\\ {} &: \Bigg\{{\Phi}_{wcol}{\bigg[\mathbf{I}{+}{\mathbf{S}}_{fib}^{cyl}:{\mathbf{C}}_{fib}^{-1}:\big({\mathbf{C}}_{wcol}{-}{\mathbf{C}}_{fib}\big)\bigg]}^{-1} \\ {} & {+}{\Phi}_{wHA}{\bigg[\mathbf{I}{+}{\mathbf{S}}_{fib}^{ellipse}:{\mathbf{C}}_{fib}^{-1}:\big({\mathbf{C}}_{wHA}{-}{\mathbf{C}}_{fib}\big)\bigg]}^{-1}\Bigg\}^{-1},\end{aligned} $$
(10.1)

where the expressions for C wcol and C wHA are given in the next paragraph. Subscripts in Eq. (10.1), “wcol,” “HA,” and “fib,” represent, respectively, the wet collagen, interfibrillar hydroxyapatite, and mineralized collagen fibril. The fourth-order Eshelby tensor (Eshelby 1959) \( {\mathbf{S}}_0^r \) accounts for the shape of phase r in a matrix with a stiffness tensor C 0, with 0 being a generic subscript.

Furthermore, the superscripts “cyl” and “ellipse” refer to the cylindrical and ellipsoidal shapes of collagen fibrils and hydroxyapatite crystals, respectively. Note that the effective stiffness tensor of the mineralized collagen fibril, C fib , is not isotropic since hydroxyapatite crystals are assumed to be aligned in the direction of collagen fibrils. Thus, the components of the Eshelby tensor need to be evaluated numerically by considering the problem of an ellipsoidal inclusion embedded in an anisotropic matrix using the approach of Gavazzi and Lagoudas (1990). C fib is computed by solving Eq. (10.1) iteratively, with the Eshelby tensors \( {\mathbf{S}}_{fib}^{cyl} \) and \( {\mathbf{S}}_{fib}^{ellipse} \) being updated at each iteration.

Water and non-collagenous proteins (NCPs) also influence the mechanical properties of bone, and solid phases are immersed in fluid (Yoon and Cowin 2008). Thus, in Eq. (10.1), we use the properties of wet collagen while the minerals are represented as a porous HA foam filled with water and NCPs (Fritsch and Hellmich 2007).

We compute the effective elastic properties of wet collagen, C wcol , following the approach of Fritsch and Hellmich (2007). More specifically, we use the Mori–Tanaka scheme (Mori and Tanaka 1973; Benveniste 1987), with the crosslinked collagen molecules modeled as a matrix and the voids (filled with water and NCPs) represented as inclusions as shown in Fig. 10.2b

$$ \begin{array}{l}{\mathbf{C}}_{wcol}={\mathbf{C}}_{col}+{\Phi}_w\left\{\left({\mathbf{C}}_w-{\mathbf{C}}_{col}\right):{\left[\mathbf{I}+{\mathbf{S}}_{col}^{sph}:{{\mathbf{C}}_{col}}^{-1}:\left({\mathbf{C}}_w-{\mathbf{C}}_{col}\right)\right]}^{-1}\right\}:\\ {}{\left\{{\Phi}_{col}\mathbf{I}+{\Phi}_w{\left[\mathbf{I}+{\mathbf{S}}_{col}^{sph}:{{\mathbf{C}}_{col}}^{-1}:\left({\mathbf{C}}_w-{\mathbf{C}}_{col}\right)\right]}^{-1}\right\}}^{-1}.\end{array} $$
(10.2)

Secondly, we obtain the stiffness of the interfibrillar hydroxyapatite, C wHA , using the Mori-Tanaka method, as follows

$$ \begin{aligned} &\mathbf{C}_{wHA}=\mathbf{C}_{HA}+\Phi_w\Big\{(\mathbf{C}_w-\mathbf{C}_{HA}):\Big[\mathbf{I}+\mathbf{S}_{HA}^{sph}:{\mathbf{C}_{HA}}^{-1}:(\mathbf{C}_w-\mathbf{C}_{HA})\Big]^{-1}\Big\}:\\ &\Big\{\Phi_{HA}\mathbf{I}+\Phi_w\Big[\mathbf{I}+\mathbf{S}_{HA}^{sph}:{\mathbf{C}_{HA}}^{-1}:(\mathbf{C}_{w}-\mathbf{C}_{HA})\Big]^{-1}\Big\}^{-1}. \end{aligned} $$
(10.3)

In Eqs. (10.3) and (10.4), the subscripts “col,” “w,” and “HA” denote, respectively, the dry collagen, water and NCPs, and hydroxyapatite crystals. The superscript “sph” refers to the spherical shape of voids. Furthermore, we assume equal water volume fractions in wet collagen composite and hydroxyapatite foam. In addition, 75% of the total hydroxyapatite crystals are taken as interfibrillar and the remaining 25% are extrafibrillar (Hamed et al. 2010). Again, these choices are not unique, as there is still no clear consensus on these percentages.

The nanoscale model, presented in this section and captured in Fig. 10.2b--c, applies to both cortical and trabecular bone. Alternatively, one can use molecular dynamics, finite element method, or other micromechanics theories. A comprehensive review of literature on elastic modeling of bone at the nanoscale is presented in Hamed and Jasiuk (2012).

10.2.2 Sub-microscale

At the sub-microstructural level, we use two modeling steps: (1) mineralized collagen fibrils interacting with an extrafibrillar hydroxyapatite matrix and (2) the matrix of step 1 combined with lacunar cavities to form a single lamella, following (Hamed et al. 2010).

Several experimental studies reported on the presence of extrafibrillar hydroxyapatite crystals on the outer surface of mineralized collagen fibrils (Katz and Li 1973; Prostak and Lees 1996; Sasaki and Sudoh 1997; Sasaki et al. 2002) and noted that these crystals are randomly dispersed (Lees et al. 1994; Fratzl et al. 1996; Benezra Rosen et al. 2002) (Fig. 10.3). Therefore, the extrafibrillar hydroxyapatite is modeled here as a HA foam with intercrystalline pores, filled with water and NCPs (Hellmich et al. 2004; Fritsch et al. 2006; Fritsch and Hellmich 2007; Fritsch et al. 2009). The effective stiffness tensor of this extrafibrillar foam, C Efoam , was evaluated using the self-consistent scheme with two interpenetrating phases, HA crystals and pores, as

$$ \begin{aligned} {\mathbf{C}}_{Efoam}&=\Big\{{\Phi}_w{\mathbf{C}}_w:{\left[\mathbf{I}+{\mathbf{S}}_{Ifoam}^{sph}:{\mathbf{C}}_{Ifoam}^{-1}:\left({\mathbf{C}}_w-{\mathbf{C}}_{Efoam}\right)\right]}^{-1}\\ &\quad+{\Phi}_{HA}{\mathbf{C}}_{HA}:{\left[\mathbf{I}+{\mathbf{S}}_{Ifoam}^{sph}:{\mathbf{C}}_{Ifoam}^{-1}:\left({\mathbf{C}}_{HA}-{\mathbf{C}}_{Efoam}\right)\right]}^{-1}\Big\}\\ &\quad:{\Big\{{\Phi}_w{\left[\mathbf{I}+{\mathbf{S}}_{Efoam}^{sph}:{\mathbf{C}}_{Efoam}^{-1}:\left({\mathbf{C}}_w-{\mathbf{C}}_{Efoam}\right)\right]}^{-1}}\\ &\quad{+{\Phi}_{HA}{\left[\mathbf{I}+{\mathbf{S}}_{Efoam}^{sph}:{\mathbf{C}}_{Efoam}^{-1}:\left({\mathbf{C}}_{HA}-{\mathbf{C}}_{Efoam}\right)\right]}^{-1}\Big\}}^{-1},\end{aligned} $$
(10.4)
Fig. 10.3
figure 3

Scanning electron microscopy images of bone at the nanoscale and sub-microscale. (a) The nanoscale with a mineralized collagen fibril (length bar is 125 nm) and (b) the sub-microscale with single lamella with preferentially aligned mineralized collagen fibrils and a lacuna cavity which houses a bone sensing cell (osteocyte)

Full size image

where the subscript “Efoam” denotes the extrafibrillar HA foam. The resulting stiffness tensor is isotropic due to the random arrangement of extrafibrillar HA crystals in the foam. Also, for simplicity, both phases, HA crystals and voids, are assumed to be spherical in shape, following (Hellmich and Ulm 2002).

Mineralized collagen fibrils, with the elastic properties obtained in Eq. (10.2), and the extrafibrillar HA foam, with the elastic properties obtained in Eq. (10.5), form two bi-continuous phases, resulting in coated fibrils. The self-consistent method is used to predict the effective elastic stiffness tensor of coated fibrils, C cfib , as

$$ \begin{aligned} {\mathbf{C}}_{cfib}&=\Big\{{\Phi}_{fib}{\mathbf{C}}_{fib}:{\left[\mathbf{I}+{\mathbf{S}}_{cfib}^{cyl}:{\mathbf{C}}_{cfib}^{-1}:\left({\mathbf{C}}_{fib}-{\mathbf{C}}_{cfib}\right)\right]}^{-1}\\ &\quad+{\Phi}_{Efoam}{\mathbf{C}}_{Efoam}:{\left[\mathbf{I}+{\mathbf{S}}_{cfib}^{sph}:{\mathbf{C}}_{cfib}^{-1}:\left({\mathbf{C}}_{Efoam}-{\mathbf{C}}_{cfib}\right)\right]}^{-1}\Big\}\\ &\quad:{\Big\{{\Phi}_{fib}{\left[\mathbf{I}+{\mathbf{S}}_{cfib}^{cyl}:{\mathbf{C}}_{cfib}^{-1}:\left({\mathbf{C}}_{fib}-{\mathbf{C}}_{cfib}\right)\right]}^{-1}}\\ &\quad{+{\Phi}_{Efoam}{\left[\mathbf{I}+{\mathbf{S}}_{cfib}^{sph}:{\mathbf{C}}_{cfib}^{-1}:\left({\mathbf{C}}_{Efoam}-{\mathbf{C}}_{cfib}\right)\right]}^{-1}\Big\}}^{-1}.\end{aligned} $$
(10.5)

In Eq. (10.6), the subscript “cfib” denotes the coated fibrils consisting of mineralized collagen fibrils coated with the extrafibrillar HA foam. The superscripts “cyl” and “sph” denote, respectively, the cylindrical shape of fibrils and spherical shape of voids in extrafibrillar HA foam. Here again, two bi-continuous phases are assumed, modeled as two different types of inclusions and no matrix.

A single lamella is represented as a material with coated fibrils as a matrix, with properties given in Eq. (10.6), containing ellipsoidal cavities, lacunae, which house bone cells osteocytes. The subscript “lac” denotes the ellipsoidal lacunae, with an aspect ratio of 5:2:1 following their approximate 25 × 10 × 5 μm3 dimension (Remaggi et al. 1998; Yoon and Cowin 2008). The osteocytes are stimuli sensing cells in bone which play a key role in bone remodeling. The major axes of lacunae are assumed to be oriented along the long axis of bone. The effective elastic stiffness tensor of a single lamella, C lamella , is computed by using the Mori–Tanaka scheme as

$$ \begin{array}{l}{\mathbf{C}}_{lamella}={\mathbf{C}}_{cfib}+{\Phi}_{lac}\left\{\left({\mathbf{C}}_{lac}-{\mathbf{C}}_{cfib}\right):{\left[\mathbf{I}+{\mathbf{S}}_{cfib}^{ellipse}:{\mathbf{C}}_{cfib}^{-1}:\left({\mathbf{C}}_{lac}-{\mathbf{C}}_{cfib}\right)\right]}^{-1}\right\}:\\ {}{\left\{{\Phi}_{cfib}\mathbf{I}+{\Phi}_{lac}{\left[\mathbf{I}+{\mathbf{S}}_{cfib}^{ellipse}:{\mathbf{C}}_{cfib}^{-1}:\left({\mathbf{C}}_{lac}-{\mathbf{C}}_{cfib}\right)\right]}^{-1}\right\}}^{-1}.\end{array} $$
(10.6)

In our model, the effect of canaliculi on elastic properties of the single lamella is neglected. Canaliculi are canals, about 50–100 nm in diameter, which connect lacunae and form an intricate network. They transport nutrients and waste in bone.

Again, the presented model applies to cortical and trabecular bones. Other models of bone at the sub-microscale have been reported in the literature but they are rather limited. They include predictions obtained using other micromechanics approaches (Yoon and Cowin 2008), finite element models (Hamed and Jasiuk 2013), and finite element beam network method (Jasiuk and Ostoja-Starzewski 2004). They are summarized in our review paper (Novitskaya et al. 2011) and in our more recent study (Hamed et al. 2015).

In Jasiuk and Ostoja-Starzewski (2004), mineralized collagen fibrils were represented as three-dimensional Timoshenko beam finite elements as shown in Fig. 10.4a. The inputs included dimensions of rectangular cross sections of fibrils and their lengths, the fiber volume fraction, and fiber orientations. Rigid or flexible connections were assumed at fiber contacts as shown in Fig. 10.4b, and the boundary value problem was solved under displacement boundary conditions. The elastic stiffness tensor was computed by equating the elastic strain energy stored in a discrete fiber network and the energy of the approximating homogeneous medium. Anisotropic stiffness tensor was obtained as a function of fiber volume fraction, aspect ratio, and orientation.

Fig. 10.4
figure 4

Finite element beam network approach to model a single lamella in bone. (a) Randomly oriented fibers with preferential orientation shown in black with fiber connections shown by red dots and (b) detail of the fiber–fiber connection (rigid or flexible)

Full size image

10.2.3 Microscale

At the microscale level, the lamellae in bone are arranged in orthogonal, rotated, or twisted plywood-like patterns (Weiner and Wagner 1998). In our model, we consider a twisted pattern which involves continuous rotation of lamellae and use the properties obtained in Eq. (10.7). There is still no consensus in the literature on the number of lamellae and their orientations in osteons and other lamellar bone types. Also, those orientations vary spatially. In our analysis, we choose the 0° starting angle for the innermost layer and we assume that the mineralized collagen fibrils complete a 180° turn from the innermost to the outermost layer. It was reported that if the layers are not orthogonal to each other, then the angle change between successive layers does not significantly influence the results (Cheng et al. 2008).

The elastic stiffness tensor of osteonal lamella is obtained using a composite laminate theory following the approach of Sun and Li (1988) developed for laminated composite materials. Details on applying this method to an osteonal lamella are given in Hamed et al. (2010).

The properties of an interstitial lamella are obtained using the same approach as for the osteonal lamella. The interstitial bone is more mineralized than the osteons and thus more stiff (Burr et al. 1988; Guo et al. 1998). To capture such behavior, one can use a higher mineral content for an interstitial lamella as compared to an osteonal lamella (Hamed et al. 2010).

Similar approach can be used to obtain the elastic properties of lamellar bone in trabecular bone forming trabecular pockets as discussed in Hamed et al. (2012a).

Next, we compute the effective properties of an osteon forming a basic building block of cortical bone. The osteon is modeled as a hollow cylinder with the osteonal lamella being a solid part and the Haversian canal being a cylindrical void. The osteon has an outer diameter of about 250 μm and is approximately 1 cm long, while the inner diameter (Haversian canal) is approximately 50 μm (Cowin 2001). The volume fraction of the Haversian canals is about 4%. Using the elastic properties of an osteonal lamella, a generalized self-consistent method (Christensen and Lo 1979) is used to calculate the effective elastic constants of an osteon, C ost , following the approach of Dong and Guo (2006).

10.2.4 Mesoscale Level

The mesoscale level represents cortical and trabecular bone levels. Here again, one can use micromechanics analysis or finite element models to model these two bone types.

First, focus on the modeling of cortical bone. The hybrid Mori–Tanaka scheme (Taya and Chou 1981), with an interstitial lamellar bone being a matrix and osteons and resorption cavities being two different types of inclusions, is used to compute the elastic stiffness tensor of cortical bone. The osteons and the resorption sites are assumed to be cylindrical in shape with an aspect ratio of 4:1:1, following the 1 cm length and 250 μm diameter of osteons (Cowin 2001), and aligned along the long axis of the bone. The volume fraction of osteons is assumed to be 70%. Resorption cavities form during bone remodeling process and in time new osteons are built in their place. The subscripts “inters,” “ost,” and “v” denote, respectively, the interstitial lamella, the osteons, and the voids.

Then, the transversely isotropic effective stiffness tensor of the cortical bone, C bone , is computed as

$$ \begin{aligned}\hspace*{-1pc}{\mathbf{C}}_{bone}&=\Big\{{\Phi}_{inters}{\mathbf{C}}_{inters}+{\Phi}_{ost}{\mathbf{C}}_{ost}:{\left[\mathbf{I}+{\mathbf{S}}_{inters}^{cyl}:{\mathbf{C}}_{inters}^{-1}:\left({\mathbf{C}}_{ost}-{\mathbf{C}}_{inters}\right)\right]}^{-1}\\ \hspace*{-1pc}&\quad+{\Phi}_v{\mathbf{C}}_v:{\left[\mathbf{I}+{\mathbf{S}}_{inters}^{cyl}:{\mathbf{C}}_{inters}^{-1}:\left({\mathbf{C}}_v-{\mathbf{C}}_{inters}\right)\right]}^{-1}\Big\}:\\ \hspace*{-1pc}&\quad{\Big\{{\Phi}_{inters}+{\Phi}_{ost}{\left[\mathbf{I}+{\mathbf{S}}_{inters}^{cyl}: {\mathbf{C}}_{inters}^{-1}:\left({\mathbf{C}}_{ost}-{\mathbf{C}}_{inters}\right)\right]}}^{-1}\\ \hspace*{-1pc}&\quad+{{\Phi}_v{\left[\mathbf{I}+{\mathbf{S}}_{inters}^{cyl}:{\mathbf{C}}_{inters}^{-1}: \left({\mathbf{C}}_v-{\mathbf{C}}_{inters}\right)\right]}^{-1}\Big\}}^{-1}.\end{aligned} $$
(10.7)

Trabecular bone has a random and highly porous structure with porosity ranging from 20 to over 90 vol%. Effective medium theories in general do not provide reliable estimates for materials with high porosity. Thus, alternate simplified strength of materials-based approaches have been used. For example, trabecular bone has been modeled as an idealized open-cell foam. Among other models, a simple anisotropic cell, which has a length of l in x1 and x2 directions and a height of h in the x3 direction, has been used. The degree of anisotropy in such a model is defined as D = h/l. Young’s modulus of trabecular bone in the x3 direction, E 3 , was obtained by Huber and Gibson (1988) as

$$ \frac{E_3}{E_{trabecula}}= CD\left(\frac{\rho_{bone}}{\rho_{trabecula}}\right) $$
(10.8)

whereE trabecula is Young’s modulus of a single trabecula as obtained at the microscale, ρ bone and ρ trabecula are, respectively, densities of trabecular bone and solid trabeculae, and C is a constant of proportionality. Gibson (1985) proposed two types of models for trabecular bone: an open cell (with rodlike elements) at relative densities smaller than 0.2 and a closed cell (with platelike elements) at relative densities greater than 0.2. The power n = 2 for an open cell and n = 3 for a closed cell (Gibson 1985). The relative density, ρ bone /ρ trabecula , is equal to the bone volume fraction. Young’s modulus of trabecular bone in the direction x 1 or x 2 , E 1  = E 2 , was determined as (Huber and Gibson 1988)

$$ \frac{E_1}{E_3}=\frac{1+1/{D}^3}{2{D}^2}. $$
(10.9)

The modeling results obtained at this scale, namely, E 1 and E 3 , represent the elastic moduli of trabecular bone. We utilized this approach for simplicity in Hamed et al. (2015).

However, the mechanical properties of trabecular bone are dependent not only on relative density but also on its architecture. Micro-computed tomography (micro-CT) is a powerful technique that can capture trabecular bone structure. This technique gave rise to micro-CT-based finite element modeling of trabecular bone. Elastic and inelastic properties have been obtained using this approach (Gross et al. 2012; Hambli 2013; Park et al. 2013; Panyasantisuk et al. 2015; Baumann et al. 2016; Gong et al. 2016; Schwiedrzik et al. 2016). An illustration of such an approach is given in Fig. 10.5 with more details in Hamed et al. (2012a).

Fig. 10.5
figure 5

Finite element model of trabecular bone: (a) finite element mesh and (b) strain energy density (Hamed et al. 2012a)

Full size image

Numerical results on effective elastic properties of bone, using a similar approach, were reported for cortical bone in Hamed et al. (2010, 2012b) and for trabecular bone in Hamed et al. (2012a, 2015). Very good agreement was found with measurements on bovine bone using experimentally obtained inputs. Cortical bone properties range from 15 to 25 GPa, depending on age, species, and anatomical location, while trabecular bone properties are much lower, ranging from 200 MPa to 1 GPa, depending on porosity.

In this section, we illustrated how micromechanics theories can be used to model the elastic properties of bone. Effective medium theories choices, selected scales, and geometric models used at each scale as well as materials inputs, which are not fully known, they all make this problem computationally and experimentally challenging.

10.3 Trabecular Bone Anisotropy

An important issue to consider when modeling trabecular bone is to account for its anisotropy. Trabecular bone is considered to be orthotropic. Cowin (1985) introduced a fabric tensor (second-order tensor) to capture the characteristics of microstructure of porous materials. In the formulation, it is assumed that the base material is isotropic and the anisotropy arises from the pore architecture. Cowin showed that the cases of three, two, and one distinct eigenvalues of the fabric tensor correspond to orthotropy, transverse isotropy, and isotropy of the material, respectively. This concept has been successfully applied to trabecular bone. Computation of fabric tensor allows to determine orthogonal symmetrical planes in trabecular bone. By determining those directions, the problem becomes simpler for computations as only nine elastic constants are needed to define trabecular bone properties. Fabric tensor has been incorporated in computational models of elastic stiffness tensor of bone (VanRietbergen et al. 1996; Odgaard et al. 1997; Zysset et al. 1998; Kabel et al. 1999; Homminga et al. 2003; Maquer et al. 2015; Moreno et al. 2016) and has been used to construct anisotropic yield/failure criteria in bone (Pietruszczak et al. 1999; Doblare et al. 2001; Garcia et al. 2009; Charlebois et al. 2010).

10.4 Modeling of Plasticity, Damage, and Fracture of Bone

Predictions of bone fracture and strength are of high scientific and clinical interest. In Sect. 10.2, we focused on the elastic properties of bone (stiffness). As mentioned in the “Introduction,” bone is also strong and tough. These properties are again due to bone’s composite and hierarchical structure, which includes complex architecture, various interfaces, and hierarchical porosity. There are a number of comprehensive reviews that have addressed the underlying mechanisms of bone fracture toughness and strength (Ritchie et al. 2005, 2006; Gao 2006; Gupta and Zioupos 2008; Launey et al. 2010; Ural and Vashishth 2014; Zimmermann et al. 2015).

Following Launey et al. (2010), high toughness of bone results from a mutual competition between intrinsic (local damage and plasticity) and extrinsic (crack-tip shielding) toughening mechanisms as shown in Fig. 10.6. At the sub-nanoscale, the molecular uncoiling and intermolecular sliding of tropocollagen molecules are present, and at the nanoscale, slipping at interfaces and microcracking of collagen take place within the mineralized collagen fibrils. At the sub-microscale (single lamella level), microcracking and fibrillar sliding are observed in the fibril arrays. Also, breaking of sacrificial bonds formed by non-collagenous proteins contributes to increasing the energy dissipation capacity of bone at the interface of fibril arrays, together with crack bridging by collagen fibrils. At larger length scales (the microscale and higher), the primary sources of toughening are extrinsic and they result from extensive crack deflections due to lamellar layering and interfaces between them (such as cement lines around osteons) and crack bridging by uncracked ligaments. It is important to note that damage zones filled with microcracks stimulate bone remodeling, resulting in damaged bone being replaced by a newly formed bone. Such a continuous process of bone resorption and formation allows bone to adapt to new loads and create thicker bone when loads are increased. When the applied force is too large and/or bone remodeling process does not have enough time to replace new bone, the macrocracks will form resulting in the whole bone fracture.

Fig. 10.6
figure 6

Bone toughness mechanism at different structural scales (Launey et al. 2010)

Full size image

Various models have been proposed to model bone damage, plasticity, and fracture. A comprehensive literature review on various modeling approaches applied at different structural scales is given in our recent review paper (Sabet et al. 2016). The open issues are as follows. Most of the models address only one or two structural scales, while bone fracture is a multiscale phenomenon. Also, no comprehensive multiscale models exist that address the fracture processes in bone across scales. Many studies considered idealized, two-dimensional representations of bone. Since crack initiation and growth are sensitive to microstructures, three-dimensional models would provide more accurate predictions. Also, spatial inhomogeneity and randomness are rarely accounted for, while fracture is a stochastic phenomenon. The bone structure and properties are still not fully characterized especially at smaller scales (nanoscale and below) in both healthy and diseased bone. Open issues remain on the collagen--HA crystal arrangements and interfaces. Most models assume isotropic properties for collagen and HA crystals, while these constituents are anisotropic. One reason is simplicity and the other is that the anisotropic properties are not readily available in the literature. Also, accurate constitutive laws of bone’s constituents and bone at different scales up to failure are needed. Finally, insights gained from theoretical and experimental studies on bone fracture and strength should be more closely linked to clinical practice, as they have potential to provide more accurate predictions of bone fracture risk in patients. The key challenge is to be able to incorporate clinically measured parameters in the computational models. There are some exciting advances which involve patient-specific models computed using tomography images in a finite element method to predict bone stiffness and strength (Giambini et al. 2016; Rossman et al. 2016).

There are several other challenges that will be discussed next. The transition between different structural scales is continuous rather than discrete. Do we have a representative volume element (RVE) at each structural scale? Studies on the effects of scale and boundary conditions on bone properties, in particular fracture and strength, are needed.

10.5 Apparent Properties

In the micromechanics analyses, described in Sect. 10.2, we assumed the existence of a representative volume element (RVE). The RVE is defined as a representative region such that it is much larger than the microstructural dimensions (inclusions) and the predicted properties are independent of applied uniform boundary conditions. However, in bone in general, we do not have an RVE. For example, at the nanoscale level, the mineralized collagen fibril is about 50–200 nm in diameter, while the size of mineral crystals is on average 50 × 25 × 3 nm3. Thus, these dimensions are of comparable size. This is also visible in Fig. 10.2, which illustrates collagen fibrils and HA crystals (which are the irregular shapes on collagen fibers). Another example is a trabecular bone at the mesoscale level. Trabecular bone has a spatially changing structure and porosity so only a relatively small region can be selected with constant porosity for testing or computations. Also, the trabecular bone region is limited in size. The typical dimensions of studied trabecular bone compression specimens are 2–4 mm in diameter and about twice that in height, while the voids in trabecular bone may reach up to 0.5 mm. Thus, specimen’s dimensions are of comparable sizes to microstructural features (pores) and the samples are smaller than the RVE.

When the size of a specimen is smaller than the RVE size, then experimental results depend on boundary conditions and the so-called apparent properties will be measured. Similarly, computationally, when the size of a region used for computations is smaller than the RVE, then the computed results will depend on boundary conditions unless one models a periodic microstructure and applies periodic boundary conditions. However, trabecular bone, for example, has a highly irregular structure, and thus periodic boundary conditions cannot be used. One can follow the approach of Huet (1990), who showed that when the size of the specimen is smaller than the RVE, the effective properties of composite are bound from above by the properties obtained by applying kinematic (displacement with uniform strain) boundary conditions and are bound from below by the properties obtained using static (tractions with uniform stress) boundary conditions. When the size of the specimen increases, these bounds will come closer and the results will converge when the RVE size is reached.

These findings of Huet (1990) can be described mathematically as follows. The apparent elastic properties are dependent on the size of a window (or specimen size) and boundary conditions which give rise to a hierarchy of bounds

$$ {\boldsymbol{C}}^R\equiv {\left({\boldsymbol{S}}^R\right)}^{-1}\equiv {\left\langle {\boldsymbol{S}}_1^t\right\rangle}^{-1}\le {\left\langle {\boldsymbol{S}}_{\delta^{\prime}}^t\right\rangle}^{-1}\le {\left\langle {\boldsymbol{S}}_{\delta}^t\right\rangle}^{-1}\le {\boldsymbol{C}}^{eff}\le \left\langle {\boldsymbol{C}}_{\delta}^d\right\rangle \le \left\langle {\boldsymbol{C}}_{\delta^{\prime}}^d\right\rangle \le \left\langle {\boldsymbol{C}}_1^d\right\rangle \equiv {\boldsymbol{C}}^V $$
(10.10)

where ∀δ ′  < δ, δ = d/L denotes the relative size of the window, d is the size of the microstructure, L is the size of the window, and 〈〉denotes ensemble averages. The inequality between any two tensors implies

$$ \boldsymbol{C}\ge \boldsymbol{D}\kern0.5em \iff \kern0.5em \left(\boldsymbol{C}-\boldsymbol{D}\right):a:a\ge 0,\kern1em for\ any\ tensor\kern0.75em {a}_{ij}\ne 0 $$

In Eq. (10.10), C is the fourth-order stiffness tensor C ijkl and S is the compliance tensor S ijkl , where S −1 = C. The superscripts R and V denote Voigt and Reuss bounds, respectively, while the superscripts t and d imply traction and displacement boundary conditions, respectively. Following Eq. (10.10), the effective properties are bounded from above and below by the apparent elastic moduli obtained using displacement and traction boundary conditions, respectively. The larger is the window size δ, the closer are the bounds. When δ reaches the size of the RVE, the bounds merge and the effective properties are obtained.

Mixed boundary conditions (combination of displacements and tractions) will give apparent properties which are between the two bounds but will not give effective properties until the RVE size is reached:

$$ {\left\langle {\boldsymbol{S}}_{\delta}^{tt}\right\rangle}^{-1}\le \left\langle {\boldsymbol{C}}_{\delta}^{dt}\right\rangle \le \left\langle {\boldsymbol{C}}_{\delta}^{dd}\right\rangle $$
(10.11)

Several studies addressed the apparent properties of trabecular bone both experimentally and computationally. They include experimental studies of BeVill et al. (2007) and Chevalier et al. (2007) and computational studies of Yeni and Fyhrie (2001), Wang et al. (2009), Gross et al. (2012), Park et al. (2013), Panyasantisuk et al. (2015), and Gong et al. (2016), among others.

In our exploratory computational study (Wang et al. 2009), we modeled trabecular bone, for simplicity, as two- and three-dimensional periodic networks and calculated the apparent orthotropic elastic properties of such idealized models as a function of boundary conditions (displacement, traction, and mixed), window size, and choice of a unit cell. We also obtained effective elastic moduli by applying periodic boundary conditions to obtain effective elastic stiffness tensor. We found that effective results are bound from above by the apparent elastic properties obtained using displacement boundary conditions and from below by apparent properties computed using traction boundary conditions as expected and apparent elastic mixed boundary conditions were very close to effective ones. In addition, we found that for materials like bone, which has one hard phase and one very soft phase (bone marrow, which is often modeled as void), these bounds are far apart and converge slowly. Also, the rate of convergence depends on a choice of the periodic unit cell. These results point out to challenges in obtaining effective properties of trabecular bone.

More advanced studies addressing the effects of window size and boundary conditions on apparent properties of bone, accounting for actual trabecular bone geometries, were done by Yeni and Fyhrie (2001) and Panyasantisuk et al. (2015).

10.6 Bone as a Cosserat Material

The concept of apparent properties which arises due to the fact that the size of tested samples or region used for computations may be smaller than the RVE was discussed in Sect. 10.5. In this section, we address a related problem. When dimensions of materials are comparable in size to the length of the microstructural features, such as pores in trabecular bone, then higher-order effects are present. Classical continuum mechanics theories do not include intrinsic length scales and give first-order approximations for materials behavior. Higher-order continuum theories such as micropolar, strain gradient, or non-local theories aim to account for such phenomena. Micropolar theory, also called the Cosserat theory, is a generalized continuum theory in which not only a force-stress is defined (from force vector) but also a couple-stress (from moment vector) is defined. In terms of kinematics, at a point, not only a translation but also a rotation is defined. Such enriched constitutive equations allow to better capture the mechanical behavior of heterogeneous materials like bone.

First experimental evidence of bone behaving like a Cosserat material is due to Lakes and his coworkers. These experiments on bone showed a stiffening effect in bending and torsion in bone (Lakes 1982; Yang and Lakes 1982; Park and Lakes 1986), and tougher notched bone than predicted by classical fracture mechanics theory (Nakamura and Lakes 1988; Lakes et al. 1990).

Several more recent studies aimed to predict Cosserat or couple-stress (special case of Cosserat theory) constants of trabecular bone. They include studies of Yoo and Jasiuk (2006), Tekoglu and Onck (2008), Fatemi et al. (2002), Onck (2002), and Fatemi et al. (2003).

10.7 Bone as a Viscoelastic Material

Bone is also a viscoelastic material. Characteristics of viscoelastic materials include an increase in strain with time under a constant stress (creep), a decrease in stress with time under a constant strain (relaxation), when properties depend on rate of application of the load and when hysteresis occurs under cyclic load, when acoustic waves experience attenuation, and rebound of an object following an impact is less than 100%. The viscoelastic constitutive law accounting for time effect is given as

$$ {\sigma}_{ij}(t)=\underset{0}{\overset{t}{\int }}{C}_{ij kl}\left(t-\tau \right)\frac{\partial {\varepsilon}_{kt}}{\partial \tau } d\tau $$
(10.12)

Viscoelastic constants involve storage and loss moduli. In bone viscoelastic damping, tan δ, exhibits a broad minimum at frequencies 1 to 100 Hz which are associated with normal activities. Thus, viscoelasticity is not a shock-absorbing mechanism. Interestingly, bone exhibits substantial damping at low frequencies and substantial creep at high frequencies. Tan δ has an intermediate value between that of polymers and metals (δ is ~0.01 at 1–10 Hz). Viscoelasticity of bone has been studied by a number of researchers both experimentally and theoretically. These studies date back to early works of Lakes and Katz (1974a, b), and Lakes et al. (1979) as well as more recent studies (Garner et al. 2000; Buechner and Lakes 2003; Ojanen et al. 2015). Most of these papers focus on the overall viscoelastic response of bone rather than micromechanics analyses of bone. An interesting micromechanics study of viscoelasticity of fluid-filled materials like bone or concrete was done by Hellmich and his coworkers (Eberhardsteiner et al. 2014; Shahidi et al. 2014). These studies addressed the effects of fluid-filled interfaces on viscoelastic properties of materials. In Sandino et al. (2015), they reported that “interface results in exponentially decaying macroscopic viscoelastic phenomena, with both creep and relaxation times increasing with increasing interface size and viscosity, as well as with decreasing elastic stiffness of the solid matrix; while only the relaxation time decreases with increasing interface density.”

10.8 Conclusions

In this study, we presented an overview on micromechanics modeling of bone. This subject is broad so this study only captures selected topics in this area. Bone is a highly complex composite material, with numerous challenges to model it. There are still many open topics for mechanicians to explore.