Simulation of Cyclic Loading Conditions Within Fluid-Saturated Granular Media

Abstract

In civil engineering, the installation of a reliable foundation is essential for the stability of the emerging structure. Already during the foundation process, a comprehensive survey of the mutual interactions between the preliminary established construction pit and the surrounding soil is indispensable, especially, when building in an existing context. In this regard, drawing our attention to the construction site at the Potsdamer Platz in Berlin, which resides within a nearly fully saturated soil and in the immediate vicinity of existing structures, measurements have revealed significant displacements of the retaining walls during the vibratory installation of the foundation piles via a so-called vibro-injection procedure. Herein, due to the gradual plastic strain accumulation and the small pore-fluid permeability of the granular assembly, the rapid cyclic loading conditions gave rise to a gradual pore-pressure build-up, which degraded the load-bearing capacity of the surrounding soil.

Addressing the simulation of cyclic loading conditions within a fluid-saturated soil, the present contribution proceeds from a multi-phasic continuum-mechanical approach based on the Theory of Porous Media (TPM), where the solid scaffold is described as an elasto-(visco)plastic material incorporating both an isotropic and a kinematic hardening model. The properties of the proposed solid-skeleton description are extensively discussed. Moreover, the model response is compared to experimental data.

1 Introduction

A soil is a complex aggregate of several mutual interacting components. On the one hand, it consists of the soil grains composing the solid skeleton and, on the other hand, of a single or multiple pore fluid(s), e.g. pore water or pore gas, occupying the intergranular pore space. Consequently, due to their granular structure, soils cannot be classified as solids or fluids, as their macroscopic observed state (solid- or fluid-like) strongly relies upon the loading conditions and the mutual interactions between the individual constituents. For instance, common failure scenarios, such as slope instabilities or soil liquefactions, can betraced back to a pore-pressure build-up. In particular, the contract tendency of the granular assembly gives rise to an excess of pore pressure, which degrades the intergranular normal contact forces and, thereby the intergranular frictional forces. In consequence, the load-bearing capacity of the overall soil compound decreased.

The present contribution is dedicated to the numerical simulation of liquid-saturated granular assemblies, which are subjected to cyclic loading conditions as they occur, for instance, during earthquakes or geotechnical installations processes (e. g. installation of vibro-injection piles). Aiming at the stability analysis of fluid-saturated granular media, there are several models available, see, e. g., [33, 44], from which most are based on the phenomenological and somehow ad hoc formulated Biot’s theory [4], however, proceeding from different approaches in order to describe the solid-skeleton behaviour. In this regard, special attention needs to be paid to the description of the contractant (densification) and dilatant (loosening) behaviour of the granular assembly under pure shear deformations as a consequence of the micro-structural grain motions, such as grain sliding and grain rolling. Depending on the initial density, the soil exhibits a macroscopically contractant (loose soil) or dilatant behaviour (dense soil) under shear loading, where in the latter, although the dilatant regime is more pronounced, the deformation behaviour is preceded by a slight contractant property at first. However, experimental observations have revealed that with ongoing shear deformation, independent of the initial soil state (loose or dense), the soil reaches a critical state from which on no further volumetric changes occur, see [8]. This observation motivated the development of so-called critical-state-line (CSL) models, see, e. g., [27, 34, 37]. In this regard, some are associated with the Cam-Clay-based descriptions, see, e. g. [27] or [34], and others with the hypoplasticity framework, see e. g. [41]. Furthermore, it is also worth to mention the more phenomenological approaches, such as [45, 46], which employ a direct stress-strain relation that distinguishes between loading and unloading stages. Other approaches account for the hardening (and softening) behaviour through kinematic hardening models. Herein, the yield surface is translated or rotated within the principle stress space through a so-called kinematic back-stress tensor and/or a rotation tensor, respectively. In this connection, further two concepts can be distinguished to handle the nonlinear hardening (or softening) material properties. On the one hand, there are the so-called multiple-yield-surface models, which have been introduced by [23, 30]. Herein, various nested yield surfaces are defined, where each subdomain is associated with constant hardening parameters. Upon loading, the individual hardening regimes are gradually activated and the hardening behaviour accumulates. These models suffer from their piece-wise linear hardening properties and theoretically require an infinite number of nested yield surfaces to accurately recover the non-linear behaviour and, in turn, a significant number of material parameters. On the other hand, there are the nonlinear kinematic hardening models, which already propose a non-linear relation for the evolution of the kinematic back-stress tensor, see, e. g., [1], or the evolution of the rotation tensor, respectively. A comparison between both concepts can be found in [28].

For the purpose of this contribution, the description of the soil aggregate proceeds from the thermodynamically consistent TPM as a suitable modelling approach. Herein, the overall soil is described as an immiscible biphasic aggregate composed of the soil grains and the percolating pore water. The description of the solid skeleton is based on the approach of [13], who proposed an elasto-(visco)plastic formulation incorporating an isotropic hardening model and a stress-dependent failure surface. The model has been validated through the simulation of small-scale slope-failure experiments. Subsequently, the solid-skeleton model was incorporated into a dynamic biphasic formulation by [19, 22] to cope with dynamic loading conditions and the related phenomena therein, such as dynamic soil liquefaction, thereby illustrating that the TPM-based modelling approach appropriately accounts for the important solid-skeleton-pore-fluid interaction. For the purpose of this contribution, the formulations of [13] will be further enhanced through a kinematic hardening model based on non-linear evolution of the kinematic back-stress tensor to overcome its shortcomings under quasi-static cyclic loading conditions.

2 Fluid-Saturated Soil Model

In what follows, a fluid-saturated soil model is presented. In this regard, at first, the theoretical framework namely the TPM is briefly reviewed. For a more detailed insight refer, e. g., to [6, 18] and references therein. Subsequently, the governing equations are tailored to describe a fluid-saturated soil, where particular focus is put on the description of the elasto-plastic behaviour of the solid skeleton.

2.1 Preliminaries

With respect to the TPM, the overall aggregate is treated as an immiscible mixture of various interacting components $\varphi ^\alpha$, which are assumed to be homogeneously distributed within a representative elementary volume (REV) $\mathrm{d}v$. However, addressing the simulation of fluid-saturated soils, the overall aggregate is composed of the solid skeleton ($\alpha =S$), assembled by the soil grains, and of the pore liquid ($\alpha =L$) representing the pore water. The composition of the bulk volume element is defined through the respective volume fractions $n^\alpha =\mathrm{d}v^\alpha /\mathrm{d}v$, where $\mathrm{d}v^\alpha$ is the partial volume of the component $\varphi ^\alpha$ within the REV. Note that the saturation condition $\sum _\alpha n^\alpha =n^S+n^L=1$ must hold.

Following this, two density functions are defined. The material (realistic or effective) density $\rho ^{\alpha R}=\mathrm{d}m^\alpha /\mathrm{d}v^\alpha$ relates the components local mass $\mathrm{d}m^\alpha$ to its volume $\mathrm{d}v^\alpha$, while the partial (global or bulk) density $\rho ^\alpha =\mathrm{d}m^\alpha /\mathrm{d}v$ is associated with the bulk volume. Moreover, both density definitions are related to each other through $\rho ^\alpha =n^\alpha \rho ^{\alpha R}$. As we assume materially incompressible and uncrushable grains, the realistic density of the solid remains constant under the prescribed isothermal conditions, but the bulk density can still change through a changing volume fraction $n^\alpha$.

2.2 Kinematics

In the framework of the TPM, the individual components $\varphi ^\alpha$ are treated as superimposed continua, where each spatial point is simultaneously occupied by particles of both components. Moreover, each component is moving according to its own motion function and, thus, has its own velocity field. In this regard, it is convenient to express the solid motion in the Lagrangean description through the solid displacement $\mathbf {u}_S$ and the motion of the pore-liquid component $\varphi ^L$ in the Eulerian setting relative to the solid motion through the seepage velocities $\mathbf {w}_{L}$ :

(1)

Therein, $\mathbf {X}_S$ denotes the position of a solid material point in the reference configuration ($t=t_0$), while $\mathbf {x}$ is the position of a point in the current configuration ($t>t_0$). Moreover, $(\mathbf {\cdot })^\prime _S$ and $(\mathbf {\cdot })^\prime _L$ denote the material time derivatives following the motion of the solid skeleton and the pore fluid, respectively.

2.3 Balance Relations

The underlying balance equations proceed from the balance equations of classical continuum mechanics. However, with respect to an efficient solution procedure, the set of governing balance laws is tailored to the particular application scenario of the present contribution by imposing several constraints on the general balance laws. In this regard, the individual constituents are assumed to be materially incompressible, i. e. $(\rho ^{\alpha R})^{\prime }_{S}=0$, and mass-exchange processes among them are excluded. Moreover, only quasi-static processes are considered, i. e. the acceleration terms are dropped, and the investigations are restricted to isothermal processes. Note that, in order to obtain a thermodynamically consistent model, the entropy inequality is exploited additionally. However, its lengthy evaluation is not carried out here, instead, only the final results are given. An interested reader is referred, for instance, to [12, 16] and references therein. Following these elaborations, the underlying balance laws are the momentum balance and the volume balance both associated with the overall aggregate:

$$\begin{aligned} 0=\mathrm {div}\,(\mathbf {T}^S_E-p\,\mathbf {I})+(\rho ^S+\rho ^L)\mathbf {g}, \end{aligned}$$

(2)

$$\begin{aligned} 0=\mathrm {div}(\mathbf {v}_S+\displaystyle \frac{k^L}{\gamma ^{LR}}\{\rho ^{LR}\mathbf {b}-\mathrm {grad}\,p\}). \end{aligned}$$

(3)

Therein, $\mathbf {g}$ is the unique mass-specific body force (gravity), $k^L$ is the hydraulic conductivity (Darcy permeability) and $\gamma ^{LR}=g\rho ^{LR}$ is the effective fluid weight with $g=|\mathbf {g}|=\mathrm{const.}$ as the scalar gravitational acceleration. Moreover, $\mathbf {T}^S_E$ is the effective solid stress, which is associated with the intergranular forces, p is the pore-fluid pressure and $\mathbf {I}$ is the second-order identity tensor. The corresponding primary variables of the resulting independent field variables are the solid displacement $\mathbf {u}_S$ and the pore-liquid pressure p.

2.4 Solid Skeleton

Due to its granular microstructure, the solid skeleton exhibits a complex material behaviour. In particular, the macroscopic behaviour of the granular assembly is a result of the microstructural grain motions leading to irreversible (plastic) deformations on the macroscopic level. These plastic deformations are of particular importance during multiple loading-unloading loops, see, for instance, the comprehensive experimental observations of [2], where irreversible deformations have been found during both pure deviatoric and pure isotropic loading conditions. To mimic the gradual accumulation of plastic deformations during cyclic loading, kinematic hardening model are commonly used, thereby usually proceeding either from a rotation or a translation of the yield surface within the principle stress space. An example of the former can be found in [29], where the yield surface is allowed to tilt over the hydrostatic axis of the principle stress space. In contrast, other authors, for instance [1, 5], follow the latter approach. For the purpose of this contribution, the latter is used, as it, in contrast to the rotational hardening approach, additional allows for a plastic strain accumulation observed during cyclic isotropic compression see e. g. [2].

For the purpose of this contribution, the constitutive description of the solid skeleton is based on [13], where an elasto-plastic formulation proceeding from comprehensive quasi-static monotonic experiments has been proposed. In particular, the experiments have revealed that the shape of the failure surface, which, in turn, governs all admissible stress states, is not constant but depends on the current isotropic stress state. Moreover, an isotropic hardening formulation has been used to account for material hardening. To additionally account for the hardening properties of granular assemblies under cyclic loading conditions, the given formulation of [13] is extended through a translational kinematic hardening model yielding a mixed isotropic-kinematic hardening model. Following the elasto-plastic modelling framework, this section comprises the individual model components, in particular, the description within the elastic domain, the yield criterion, the evolution of the plastic strains, the isotropic and the kinematic hardening models, and the stress-dependent failure surface.

Preliminaries. The description of the solid skeleton is constrained to the small strain regime. Consequently, the linear solid-strain tensor is given by

$$\begin{aligned} \varepsilon _{S}=\displaystyle \frac{1}{2}(\mathrm {grad}\,\mathbf {u}_S+\mathrm {grad}^T\mathbf {u}_S)\qquad \longrightarrow \qquad \varepsilon _S=\varepsilon _{Se}+\varepsilon _{Sp}, \end{aligned}$$

(4)

which, in the framework of elasto-plasticity, is additively split into an elastic $\varepsilon _{Se}$ and a plastic part $\varepsilon _{Sp}$. Following this, the solid volume fraction can be written as, see [20],

$$\begin{aligned} n^S=n^S_{0S}(1-\varepsilon ^V_S) = n^S_{0S} (1-\varepsilon ^V_{Sp})(1-\varepsilon ^V_{Se}) = n^S_p (1-\varepsilon ^V_{Se}). \end{aligned}$$

(5)

Fig. 1.

Illustration of the failure surface $\overset{*}{F}$ and of the isotropic and kinematic hardening concepts.

Therein, $n^S_{0S}$ denotes the initial solid volume fraction and $\varepsilon ^V_{S}=\mathrm {div}\,\mathbf {u}_{S}=\varepsilon _{S}\cdot \mathbf {I}$ is the volumetric solid strain, which is split into its corresponding elastic part $\varepsilon ^V_{Se} = \varepsilon _{Se}\cdot \mathbf {I}$ and plastic part $\varepsilon ^V_{Sp}= \varepsilon _{Sp}\cdot \mathbf {I}$. Moreover, with respect to the assumed small strain regime, the effective solid stress tensor is approximated by its linearised formulation $\varvec{\sigma }^{S}_{E}$, i. e. $\varvec{\sigma }^{S}_{E}\approx \mathbf {T}^S_E$. Note that, as we proceed from a continuum-mechanical framework, volumetric compression corresponds to negative volumetric quantities, i. e. $\varvec{\sigma }^S_E\cdot \mathbf {I} < 0$ and $\varepsilon ^V_{S} < 0$, whereas volumetric expansion corresponds to positive volumetric quantities, i. e. $\varvec{\sigma }^S_E\cdot \mathbf {I} > 0$ and $\varepsilon ^V_{S} > 0$. Within the elasto-plastic setting, the investigation, whether the current stress state yields purely elastic, or elasto-plastic deformations, is made based on the yield criterion $F(\varvec{\sigma }^{S}_{E})$, where the deformation is purely elastic for $F<0$ and elasto-plastic for $F=0$. In a graphical representation, the yield limit, $F=0$, is depicted through the so-called yield surface in the principle stress space. It bounds the elastic domain and, consequently, defines all elastic stress states. Once plastic deformations are commenced, the load cannot increase any further unless the elastic domain is altered through a suitable hardening mechanism. In this regard, in order account for hardening or softening effects, the hardening model has to alter the shape of the yield-surface (isotropic hardening) or translate the yield locus through the principle stress space (kinematic hardening), where in any case the failure surface bounds the ultimately allowable stress states, see Fig. 1 ¹.

In this regard, in order account for hardening or softening effects, the hardening model needs to alter the shape of the yield-surface (isotropic hardening) or translate the yield locus through the principle stress space (kinematic hardening), where the failure surface $\overset{*}{F}$ bounds the ultimately allowable stress states, see Figure 1. Note that, following the findings of [13], the failure surface is not constant but depends on the current stress state, i. e. $\overset{*}{F}=\overset{*}{F}(\varvec{\sigma }^{S}_{E})$. Proceeding from the isotropic hardening model, the shape of the yield surface is altered, e. g., via expansion or shrinkage, from its initial state $F_{0}$ towards its current state $\widetilde{F}$ through a variation of the yield surface parameters. In case of kinematic hardening, the yield locus is shifted from its initial position $\mathcal {O}$ towards $\overline{\mathcal {O}}$ within the principle stress space $\{{\sigma }_{1}, {\sigma }_{2}, {\sigma }_{3}\}$ via the back-stress tensor $\mathbf {Y}^{S}_{E}$ (shifting tensor), viz.

$$\begin{aligned} \varvec{\sigma }^{S}_{E} = \overline{\varvec{\sigma }}^{S}_{E} + \mathbf {Y}^{S}_{E}\,. \end{aligned}$$

(6)

Combining both hardening concepts, the yield surface is simultaneously shifted (kinematic hardening) and altered (isotropic hardening) simultaneously, where the latter is described within the shifted principle stress space $\{\overline{{\sigma }}_{1}, \overline{{\sigma }}_{2}, \overline{{\sigma }}_{3}\}$.

Elastic domain. In order to capture the materially non-linear behaviour of sand, in the geometrically linear regime, the following stress-strain relation based on a non-linear elastic potential is introduced [13]:

(7)

Therein, $\varepsilon ^D_{Se}=\varepsilon _{Se}-1/3\,\,\varepsilon ^V_{Se}\,\mathbf {I}$ denotes the deviator of the elastic strain tensor. Moreover, $\mu ^S$ is the constant elastic shear modulus, $k^S_0$ and $k^S_1$ are volumetric bulk moduli, and $\varepsilon ^V_{Se\,\mathrm {crit}}$ is the critical volumetric strain, which is given by

$$\begin{aligned} \varepsilon ^V_{Se\,\mathrm {crit}}=1-\frac{n^S_\mathrm {max}}{n^S_P}, \end{aligned}$$

(8)

where $n^S_\mathrm {max}$ is a material parameter defining the densest packing.

Yield surface. Within the framework of elasto-plasticity, the elastic domain is bounded by an appropriate yield surface. For soils, or granular matter in general, a suitable criterion is provided in [17]. It reads:

$$\begin{aligned} \begin{array}{crcl} &{}\overline{F}&{}=&{}\sqrt{\varGamma \overline{\mathrm {I\!I}}^D_{\sigma }+\displaystyle \frac{1}{2}\alpha \overline{\mathrm {I}}^2_{\sigma }+\delta ^2\overline{\mathrm {I}}^4_{\sigma }}+ \beta \overline{\mathrm {I}}_{\sigma }+\varepsilon +\overline{\mathrm {I}}^2_{\sigma }-\kappa =0,\\ &{}\varGamma &{}=&{}(1+\gamma \displaystyle \frac{\overline{\mathrm {I\!I\!I}}^D_{\sigma }}{(\overline{\mathrm {I\!I}}^D_{\sigma })^{3/2}})^m. \end{array} \end{aligned}$$

(9)

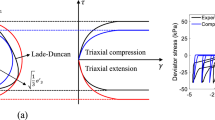
Therein, $\overline{\mathrm {I}}_{\sigma }$, $\overline{\mathrm {I\!I}}^D_{\sigma }$ and $\overline{\mathrm {I\!I\!I}}^D_{\sigma }$ are the first principal invariant of $\overline{\varvec{\sigma }}^S_E$ and the (negative) second and third principal invariants of the effective stress deviator $(\overline{\varvec{\sigma }}^S_E)^D$ all given in the shifted principle stress space. The material parameter sets $\mathcal {S}_h=(\delta ,\varepsilon ,\beta ,\alpha ,\kappa )^T$ and $\mathcal {S}_d=(\gamma ,m)^T$ define the shape of the yield surface in the hydrostatic ($\mathcal {S}_h$) and deviatoric plane ($\mathcal {S}_d$) (Fig. 2).

Fig. 2.

Sketch of the evolution of the plastic flow in the hydrostatic (left) and deviatoric plane (right).

Evolution of plastic strains. In order to evaluate the evolution of the plastic strains, following the experimental findings of several authors, see, e. g., [26] or [43], the concept of non-associated plasticity needs to be applied for frictional geomaterials as an associated flow rule would overestimate the volumetric deformations. In this regard, a suitable plastic potential, which allows for an adequate description of the contractant and dilatant behaviour of the granular assembly is introduced:

$$\begin{aligned} \overline{G}=\sqrt{\psi _1\overline{\mathrm {I\!I}}^D_{\sigma }+\frac{1}{2}\alpha \,\overline{\mathrm {I}}^2_{\sigma }+\delta ^2\overline{\mathrm {I}}^4_{\sigma }}+ \psi _2\beta \,\overline{\mathrm {I}}_{\sigma }+ \epsilon \,\overline{\mathrm {I}}^2_{\sigma }. \end{aligned}$$

(10)

Therein, $\psi _1$ and $\psi _2$ are material parameters, which serve to relate the dilatation angle $\nu _{D}$ to experimental data. The flow rule governing the plastic strain rate $(\mathbf {\varepsilon }_{Sp})^\prime _S$ reads

$$\begin{aligned} ({\varvec{\varepsilon }}_{Sp})^\prime _S = \varLambda \frac{\partial \overline{G}}{\partial \overline{\varvec{\sigma }}^S_E}, \end{aligned}$$

(11)

Therein, $\varLambda$ is the so-called plastic multiplier, which in the framework of viscoplasticity using the overstress concept of Perzyna [32] is determined from

$$\begin{aligned} \varLambda =\frac{1}{\eta }\Big <\frac{F}{\sigma _0}\Big >^r, \end{aligned}$$

(12)

where $\big < \cdot \big>$ are the Macaulay brackets, $\eta$ is the relaxation time, $\sigma _0$ is the reference stress and r is the viscoplastic exponent. Note that the overstress concept regularises the ill-posed problem, for instance at the onset of shear bands, see [14] and the references therein, through a careful choice of the parameters $\eta$ and r.

Isotropic and kinematic hardening. In granular assemblies, any macroscopically observed plastic deformation is a result of the microstructural grain motions leading to macroscopic hardening or softening effects. In this regard, experimental observations have revealed an anisotropic material behaviour, see, e. g., [25] or [35], which originates from the preceded loading history, see [5]. This anisotropy is of particular importance upon the stress reversal under cyclic (dynamic and quasi-static) loading conditions. An explanation is found by the similarities between the established theory of dislocation movement in solid materials, e. g. metals, known as the Bauschinger effect [3], and the grain motions and the related grain-to-grain interactions. Additionally, a densification or loosening of the granular assembly leads to isotropic hardening or softening, respectively, which needs to be considered as well.

Fig. 3.

Sketch of the combined isotropic-kinematic hardening concept considering the failure surface.

Any hardening model needs to ensure that the current stress state is admissible. In particular, it has to satisfy the yield criterion, i. e. $\overline{F}({p}_{i}) \le 0$, and, in addition, the failure criterion

$$\begin{aligned} \overset{*}{F}=F(\overset{*}{p}_{i})\le 0 \end{aligned}$$

(13)

as the ultimate loading boundary, where $\overset{*}{p}_{i}\in \{\overset{*}{\alpha }, \overset{*}{\beta }, \overset{*}{\delta }, \overset{*}{\epsilon }, \overset{*}{\gamma }\}$ denotes the set of material parameters governing the failure surface. In order to ensure the admissibility of the computed stress state, the commonly used predictor-corrector scheme, see [38], is used. Herein, a preliminary overstress is computed based on the current strain increment (predictor step), which is, subsequently, checked whether the current increment is elastic ($F<0$) or elasto-plastic ($F\ge 0$). In case of plasticity, the governing equations of the plasticity model are solved such that the resulting stress state lies on the yield surface ($F=0$) (plastic corrector step), where, in the scope of the present formulation, the shape of the yield surface is adjusted (isotropic hardening) and the yield locus is shifted through the principle stress space (kinematic hardening). In the scope of the kinematic hardening part, the translation direction is of particular interest. In this regard, Mróz [29] proposed an approach based on the geometric requirement that the tangential plane on the yield surface, which is associated with the current stress state, has to correspond to a tangential plane on the failure surface, thereby defining a second stress state on the failure surface. The evolution of the plastic strain is then governed by the vector defined through the current stress state and the second stress state leading to neither an associated nor a plastic-potential-driven non-associated flow rule. Note that the approach of [29] prevents an intersection of the yield and failure surfaces.

The current model also proceeds from a stress-projection method, but in contrast to [29], following a non-associated flow rule exploiting a plastic potential. In particular, the projection is carried out utilising the current stress state $\varvec{\sigma }^{S}_{E}$ and the normalised flow direction $\mathbf {N}$, which proceeds from the plastic potential (10). The projected stress state $\overset{*}{\varvec{\sigma }}{}^{S}_{E}$, which lies on the failure surface, is then found with the help of the scaling factor $\zeta$, see Figure 3. In particular, following the concept of the volumetric and deviatoric splitting, the projection is carried out independently along the hydrostatic and the deviatoric direction via

$$\begin{aligned} (\overset{*}{\varvec{\sigma }}{}^{S}_{E})^V=\varvec{\sigma }^S_E+\zeta ^V\mathbf {N}^V,\qquad (\overset{*}{\varvec{\sigma }}{}^{S}_{E})^D=\varvec{\sigma }^S_E+\zeta ^D\mathbf {N}^D, \end{aligned}$$

(14)

where the projected stress tensors $(\overset{*}{\varvec{\sigma }}{}^{S}_{E})^V$ and $(\overset{*}{\varvec{\sigma }}{}^{S}_{E})^D$, the scalar multipliers $\zeta ^{V}$ and $\zeta ^{D}$ and the normalised projection directions $\mathbf {N}^{V}$ and $\mathbf {N}^{D}$ are the corresponding contributions in the hydrostatic and deviatoric direction, respectively. The projection directions are computed through

$$\begin{aligned} \mathbf {N}^{V}=&\displaystyle \frac{1}{3}\,\text {sgn}(G^{V})\mathbf {I} \quad \text {with}\,\,G^{V}=\displaystyle \frac{\partial \overline{G}}{\partial \overline{\varvec{\sigma }}^{S}_{E}}\cdot \mathbf {I},\\ \nonumber \mathbf {N}^{D}=&\displaystyle \frac{1}{\Vert \mathbf {G}^{D}\Vert }\mathbf {G}^{D} \quad \text {with}\,\,\mathbf {G}^{D} =\displaystyle \frac{\partial \overline{G}}{\partial \overline{\varvec{\sigma }}^{S}_{E}} - \frac{1}{3}\left( \frac{\partial \overline{G}}{\partial \overline{\varvec{\sigma }}^{S}_{E}}\cdot \mathbf {I}\right) \mathbf {I}, \end{aligned}$$

(15)

where $\text {sgn}(\cdot )=(\cdot )/\Vert \cdot \Vert$ denotes the signum function with $\Vert (\cdot )\Vert =\sqrt{((\cdot )\cdot (\cdot ))}$ being the Euklidian norm. Exploiting the relations (14)$_{1}$ and (14)$_{2}$, $\zeta ^{V}$ and $\zeta ^{D}$ can be computed² through the requirement that the projected stresses have to lie on the failure surface, i. e.

$$\begin{aligned} \overset{*}{F}\!\left( \zeta ^{V} \right) \overset{!}{=}0 \qquad \text {and}\qquad \overset{*}{F}\!\left( \zeta ^{D}\right) \overset{!}{=}0. \end{aligned}$$

(16)

Consequently, the presented formulation always ensures the admissibility of the resulting stress state. To make this point more clear, lets assume an invalid stress state, i. e. where the current stress point lies outside the domain bound by the failure surface. In this case, at the onset of plastic deformations, the scaling factor $\zeta$ will be negative and the plastic strain increment, will be in the opposite direction, thereby leading to a softening material behaviour.

Next, the isotropic and kinematic hardening laws are addressed. In this regard, concerning the isotropic hardening, suitable evolution laws for the parameter subset $p_i \in \{\beta , \delta , \epsilon , \gamma \}$ of the yield surface $\overline{F}$ have been proposed by [15], viz.

$$\begin{aligned} \begin{array}{l} (p_i)^\prime _S = (p^V_i)^\prime _S + (p^D_i)^\prime _S = (\overset{*}{p_i}-p_i) [\,C^V_{pi}\,(\varepsilon ^V_{Sp})^\prime _S + C^D_{pi}\,\Vert (\varvec{\varepsilon }^D_{Sp})^\prime _S \Vert \,]\\ \text {with}\qquad p_i(t=0)=p_{i0}, \end{array} \end{aligned}$$

(17)

which, however, are adopted to match the present mixed isotropic-kinematic hardening concept and yield

$$\begin{aligned} \begin{array}{l} (p_i)^\prime _S = (p^V_i)^\prime _S + (p^D_i)^\prime _S = \zeta ^{V} C^V_{pi} (\varepsilon ^V_{Sp})^\prime _S +\zeta ^{D}C^D_{pi}\Vert (\varvec{\varepsilon }^D_{Sp})^\prime _S \Vert \\ \text {with} \qquad p_i(t=0)=p_{i0}. \end{array} \end{aligned}$$

(18)

In both cases, the evolution equation $(p_i)^\prime _S$ for the parameters $p_i$ is separated into volumetric and deviatoric parts, $(p^V_i)^\prime _S$ and $(p^D_i)^\prime _S$, which are driven by the corresponding plastic strain rates, $(\varepsilon ^V_{Sp})^\prime _S$ and $(\varepsilon ^D_{Sp})^\prime _S$, together with the volumetric and the deviatoric evolution constants, $C^V_{pi}$ and $C^D_{pi}$. Moreover, $p_{i0}$ denotes the initial values of the parameters $p_i$. Evidently, the deviatoric part only governs plastic hardening, whereas the volumetric part $(p^V_i)^\prime _S$ can take positive or negative values and, therefore, describes both hardening and softening processes [13].

The evolution of the kinematic back-stress tensor $\mathbf {Y}^{S}_{E}$ is based on the approach of Armstrong & Frederick (AF) [1]. However, it has been modified to match the present framework:

$$\begin{aligned} \begin{aligned} (\mathbf {Y}^{S}_{E})^\prime _S&= \zeta ^V(C^V_0-C^V_1 |\mathrm {Y}^{SV}_{E}|)(\varepsilon ^V_{Sp})^\prime _S\,\mathbf {I} \\&\quad +\zeta ^D[\,C^D_0 (\varvec{\varepsilon }^D_{Sp})^\prime _S- C^D_1\Vert (\varvec{\varepsilon }^D_{Sp})^\prime _S \Vert \mathbf {Y}^{SD}_{E}\,]. \end{aligned} \end{aligned}$$

(19)

Therein, $(\mathbf {Y}^{S}_{E})^\prime _S$ denotes the rate of the kinematic back-stress tensor. Furthermore, $\mathrm {Y}^{SV}_{E}=\mathrm {Y}^{S}_{E}\cdot \mathbf {I}$ and $\mathbf {Y}^{SD}_{E}=\mathbf {Y}^{S}_{E}-1/3\,\mathrm {Y}^{SV}_{E}\mathbf {I}$ denote the volumetric and the deviatoric part of the back-stress tensor, and $|(\cdot )|$ is the absolute value of $(\cdot )$. Moreover, $C^V_0$ and $C^V_1$, and $C^D_0$ and $C^D_1$ are the volumetric and the deviatoric evolution constants, respectively. In contrast to a pure linear kinematic hardening model, which, for instance, was proposed by [5], the nonlinear extension in (19) gives a better representation of the material behaviour. The differences between the linear kinematic, i. e. $C^{V}_{1}=0$ and $C^{D}_{1}=0$, and the AF hardening model are schematically depicted in Fig. 4.

Fig. 4.

Comparison between a linear kinematic hardening law and the model of Armstrong and Frederick [1].

In particular, at the onset of yielding, the nonlinear part is initially inactive. With ongoing (monotonic) loading it becomes more and more pronounced, thereby slowing down the rate of the back-stress tensor. Upon load reversal, the back-stress tensor and its rate have opposite directions and, therefore, the additional term increases the stress rate. For more details on the AF model, the interested reader is referred, for instance, to the work of [9, 10, 24] or [31]. where, however, the latter three in particular focus on its extension within the scope of metal-plasticity.

A suitable model for the description of granular media needs to account for the contract and dilatant properties of the granular assembly, which are, within the current setting, driven through the plastic potential. In consequence, the used hardening models adapt, in addition to the yield surface, the plastic potential and, therefore, the direction of the plastic flow as well. The impact on the plastic strain increment proceed from the isotropic and the kinematic hardening model are qualitatively sketched in Fig. 5 (left) and (right), respectively.

Fig. 5.

Comparison of the evolution of the plastic strains in case of pure isotropic (left) and pure kinematic hardening (right).

Herein, both hardening models are subjected to the same loading scenario starting with an isotropic compression to reach the stress state A and followed up by an pure deviatoric load from A to C. At first, the attention is drawn to the pure isotropic hardening model. Herein, the evolution of the volumetric contribution of the plastic strain increment gradually changes from a contractant behaviour at A towards a dilatant behaviour at C, see Fig. 5 (left). In contrast, in case of the kinematic hardening model, the volumetric part in the plastic strain increment merely exhibits contractant and isochoric properties, see Fig. 5 (right). Consequently, only the isotropic hardening part in the combined isotropic-kinematic hardening model mimics the commonly observed contract-dilatant property of granular matter under pure shear deformation.

Stress-dependent failure surface. To complete the model, the attention is drawn to the stress-dependent failure surface. In this regard, the comprehensive experimental investigations under monotonic quasi-static loading conditions carried out by [13] have revealed that the failure surface is not constant, but depends on the hydrostatic stress state, i. e. on the confining pressure $\mathrm {I}_{\sigma }$. In particular, different confining pressures lead to slightly different granular configurations and, consequently, to different grain movements upon loading. Therefore, at failure the granular configuration and consequently, the corresponding stress states are different. Following [13], the evolution of the stress-dependent failure surface is conducted via

$$\begin{aligned} \overset{*}{\epsilon }(\mathrm {I}_{\sigma }) = \overset{*}{\epsilon _0}(1+\overset{*}{C}_\epsilon \,\mathrm {I}_{\sigma }) \qquad \text {with}\qquad \overset{*}{\epsilon }\ge \overset{*}{\epsilon }_{lim}, \end{aligned}$$

(20)

Therein, $\overset{*}{C}_\epsilon$ is a constant evolution parameter of the failure surface, while $\overset{*}{\epsilon _0}$ theoretically defines the failure surface for the unloaded virgin material, which is adjusted as small as possible but large enough for the smallest confining pressure used in a triaxial experiment. The failure-surface limit is defined by $\overset{*}{\epsilon }_{lim}$.

Fig. 6.

Schematic sketch of stress path resulting in a not admissible stress state.

Next, the behaviour of the plasticity model and, in particular, its interplay with stress-dependent failure surface is elaborated in terms of a load-unload-reload cycle. For this purposed a possible loading scenario as depicted in Figure 6 is considered. Note that, therein, $\overset{*}{{F}}_{B}$ and $\overset{*}{{F}}_{E}$ denote the failure surfaces associated with stress states B and E, respectively. In the considered load case, a soil specimen is subjected to a hydrostatic compression and a triaxial load (($\mathcal {O}$-A-B). Next, the specimen is unloaded and the hydrostatic stress level is reduced (B-C-D) and, finally, the specimen is reloaded ($D-E$). Following the considered load path, the stress path $\mathcal {O}$-A-B causes a consolidation and, thereby an load-path-associated granular configuration represented through a shift and an expansion of the elastic domain through the kinematic and isotropic hardening models. During the unloading stage B-C-D, the granular configuration is mainly maintained. However, in the subsequent reload D-E, the stress state violates the yield criterion, thereby representing the interlocked granular configuration and, in consequence, allowing for stresses states violating the failure criterion. However, once the applied load exceeds the yield limit, plastic deformations are commenced and the granular assembly rearranges such that granular configuration and the current hydrostatic stress state match, which is represent in the plasticity model by returning the current stress onto the failure surface.

Summarised solid-skeleton model. With the previous elaborations at hand, two different solid-skeleton descriptions can be summarised, each composed of a set of ordinary differential equations (ODE). In particular, the mixed isotropic-kinematic hardening (IKH) model comprises the Eqs. (11), (12), (18), (19), (16)$_{1}$ and (16)$_{2}$ and reads

$$\begin{aligned} {\varvec{\mathcal {L}}}_{\mathrm {IKH}}= \left[ \begin{array} {c} ({\varvec{\varepsilon }}_{Sp})^{\prime }_{S}\\ 0\\ (p_{i})^{\prime }_{S}\\ (\mathbf {Y}^{S}_{E})^{\prime }_{S}\\ 0\\ 0\\ \end{array} \right] - \left[ \begin{array}{c} \displaystyle \varLambda \frac{\partial \overline{G}}{\partial \overline{\varvec{\sigma }}^{S}_{E}}\\ \displaystyle \varLambda - \frac{1}{\eta }\Big <\frac{\overline{F}}{\sigma _0}\Big >\\ \displaystyle \zeta ^{V}C^V_{pi}\,(\varepsilon ^V_{Sp})^{\prime }_{S} + \zeta ^{D}C^D_{pi} \Vert (\varvec{\varepsilon }^D_{Sp})^{\prime }_{S}\Vert \\ \begin{array}{c} \zeta ^V(C^V_0-C^V_1 |\mathrm {Y}^{SV}_{E}|)({\varepsilon }^V_{Sp})^{\prime }_{S}\,\mathbf {I} \\ \quad +\, \zeta ^D[C^D_0 \dot{\varvec{\varepsilon }}^D_{p} - C^D_1\Vert (\varvec{\varepsilon }^D_{Sp})^\prime _S \Vert \mathbf {Y}^{SD}_{E}] \end{array}\\ \overset{*}{F}\left( \zeta ^{V}\right) \\ \overset{*}{F}\left( \zeta ^{D}\right) \\ \end{array} \right] = \mathbf {0}. \end{aligned}$$

(21)

The purely isotropic-hardening (IH) model, composed of the relations (11), (12) and (17) is summarised as

$$\begin{aligned} {\varvec{\mathcal {L}}}_{\mathrm {IH}}= \left[ \begin{array} {c} ({\varvec{\varepsilon }}_{Sp})^{\prime }_{S}\\ 0\\ (p_{i})^{\prime }_{S}\\ \end{array} \right] - \left[ \begin{array} {c} \displaystyle \varLambda \frac{\partial \overline{G}}{\partial \overline{\varvec{\sigma }}^{S}_{E}}\\ \displaystyle \varLambda - \frac{1}{\eta }\Big <\frac{\overline{F}}{\sigma _0}\Big >\\ \displaystyle (\overset{*}{p_i}-p_i) [\,C^V_{pi}\,({\varepsilon }^V_{Sp})^{\prime }_{S} + C^D_{pi}\,\Vert (\varvec{\varepsilon }^D_{Sp})^\prime _S\Vert \,]\\ \end{array} \right] = \mathbf {0}. \end{aligned}$$

(22)

Note that, alternatively, (22)$_{2}$ may be solved for $\varLambda$ and inserted into (22)$_{1}$, in order to reduce the number of ODE within the local system on the one hand and to allow for explicit time-discretisation schemes on the other hand.

3 Numerical Treatment

The present section briefly outlines the spatial and temporal discretisation methods as well as the associated solution procedure of the underlying problem. For a more detailed insight into the numerical treatment of elasto-plastic porous materials, the interested reader is referred to, e. g., [13] and references therein.

The spatial discretisation is based on the finite-element method (FEM), thereby following a variational approach of Bubnov-Galerkin-type. Note that the ansatz and test functions need to fulfil the inf-sup condition (Ladyshenskaya-Babu $\check{s}$ ka-Brezzi (LBB) condition) [7] for the sake of a stable solution procedure. In particular, the solid displacements $\mathbf {u}_S$ and their corresponding test functions are approximated by quadratic shape functions, whereas linear shape functions are used for the pore pressure p and its associated test function. Addressing the simulation of quasi-static process, the unconditionally stable backward (implicit) Euler scheme, see e. g. [21], is used for the temporal discretisation.

The resulting system of a non-linear algebraic equations is composed of a global system associated with the finite-element (FE) discretisation and a local system related to the ODE of the elasto-plastic model. The coupled system is solved iteratively through the Newton-Raphson method. To be more precisely, in order to obtain an efficient solution strategy, the system is solved in a decoupled manner through a generalisation of the block Gauss-Seidel-Newton method, thereby exploiting the block-structured nature of the coupled system. This procedure results in two nested Newton iterations, where at each global iteration step, which seeks the solution to the primary variables, the local system is iteratively solved at first for the internal state variables with frozen primary variables. Note that the solution of the local system is found, as usual in elasto-plasticity, through the commonly used predictor-corrector scheme, see [38].

Following this, the discrete governing equations are implemented into the coupled FE solver PANDAS, which is then linked to the commercial FE package Abaqus via a general interface, see [36].

4 Simulation

The simulations address the investigation of the model responses under quasi-static cyclic loading conditions of the pure isotropic and the mixed isotropic-kinematic hardening model both in comparison to experimental data. In this connection, at first, a triaxial test on a cylindrical sand sample (diameter: 0.1 m, height: 0.1 m) subjected to slow cyclic load cycles is carried out, which will serve as a reference for the subsequent simulations. Herein, on the one hand, the isotropic hardening (IH) model with the material parameters depicted in Appendix A, and, on the other hand, the mixed isotropic-kinematic hardening (IKH) model with the parameters of Appendix B are used. Note that the material constants of the IKH are, in contrast to the IH model, not found through an calibration procedure. Instead, they are adapted from the parameters of the IH model. Therefore, the present investigations merely serve as a proof-of-concept rather than a validation of the material models.

Fig. 7.

Geometry and loading of the triaxial test (left) and the deduced IBVP (right).

The governing triaxial test and the deduced IBVP are depicted in Fig. 7. Note that in the numerical model, the axial symmetry of the problem is exploited, thereby simplifying the actual three-dimensional problem to a axial-symmetric two-dimensional FE model, which is solely composed of a single axial-symmetric finite element. The solid displacements normal to the symmetry lines (left and bottom edge) are equal to zero, i. e. $\overline{u}_{S1}=\overline{u}_{S2}=0$, whereas the edges associated with the free surfaces of the specimen, i. e. the top and bottom edge, are free to move and are perfectly drained, i. e. $\overline{p}={0}$. The sample is subjected to a quasi-static cyclic loading, through a prescription of the axial $\sigma _{a}(t)$ and the radial stresses $\sigma _{r}(t)$. In particular, the confining pressure, i. e. $\sigma _{a}(t)=\sigma _{r}(t) = 0.1\,\mathrm{\,MPa}$, is applied in the interval $t\in [\,0\,\mathrm{\,s},600\,\mathrm{\,s}\,]$ in a first step. Subsequently, the radial stress is kept constant and the axial stress periodically increases and decreases with an amplitude of $\varDelta \sigma _{a}=0.05\,\mathrm{\,MPa}$, see Fig. 8.

Fig. 8.

Evolution of the axial $\sigma _{a}(t)$ and the radial stress $\sigma _{r}(t)$ applied on the cylindrical soil specimen.

Fig. 9.

Evolution of the total axial strain $\varepsilon _{a}$ for the IH and the IKH model in comparison to the experimental records.

The evolution of the axial solid strain of the experiment, and the computed responses of the IH and IKH model are depicted in Fig. 9. At first, the elaboration of the experimental records is addressed. As illustrated by the evolution of the axial strain, the subsequent loading-unloading loops alter the granular configuration, thereby allowing for a gradual axial settlement of the top end of the specimen. These findings are in agreement with the experimental observations of other authors, see, e. g., [11] or [42]. Comparing the experimental observations with the model responses, it can be seen that only the IKH model is capable of predicting the axial settlement under the prescribed quasi-static loading conditions. The predictions of the IKH model are in very good agreement with the test result.

5 Conclusions

The present contribution addressed the simulation of granular assemblies under quasi-static cyclic loading conditions, thereby exploiting the TPM and the elasto-plasticity as suitable modelling frameworks. For the sake of a complete representation, the entire numerical model starting from the governing balance laws, over the constitutive relations towards the numerical treatment has been presented. In particular, two hardening models describing the solid-skeleton behaviour have been elaborated, namely an isotropic and a mixed kinematic-isotropic hardening model. Both formulations have been compared to experimental data, which has been obtained from quasi-static cyclic triaxial tests. It has been shown that the pure isotropic hardening model fails to mimic the axial settlement under slow cyclic loading conditions. In contrast, the mixed isotropic-kinematic hardening model was able to qualitatively reproduce the experimental observations at least to some extent. However, it was also illustrated that the proposed model does not reproduce the exact characteristics of the axial-strain evolution, i. e. the curvature in the zigzag pattern. To trace back the origin of the mismatch, further experimental investigations are necessary to optimise the governing material parameters on the one hand and to identify further physical processes, which might be essential for the mimicking of the experimental observations on the other hand.

Appendices

Appendix A: Material Parameters of the IH Model

Fig. 10.

Microscopic picture of the soil grains (left) and grain size distribution (right) of the sand of the research unit FOR1136.

Following the DIN 18196 of the German Institute for Standardisation, the underlying granular material, in particular, the sand³ of the research unit FOR 1136 “GeoTech”, can be classified as closely graded sand with an average grain diameter of $d_{50}=0.55\,\mathrm{mm}$, see Fig. 10. The density of an individual soil grain, which corresponds to the realistic solid density of the overall aggregate, is $\rho ^{SR}=2\,650\,\mathrm{kg/m^{2}}$.

Fig. 11.

Comparison of the experimental data with the simulation results of the triaxial tests at different confining pressures (left) and of the isotropic loading-unloading loop (right).

Table 1. Material parameters of the solid skeleton of the sand of the research unit FOR1136.

Table 2. Material-parameter adjustments of the solid skeleton for the mixed isotropic-kinematic hardening (IKH) model.

In order to identify the solid-skeleton material parameters associated with the FOR1136 sand, the course of actions as described in [13] is followed. Herein, initially several triaxial tests on cylindrical sand specimens (height: $0.1\,\mathrm{m}$, diameter: $0.1\,\mathrm{m}$) have been carried out, from which, subsequently, the materials parameters are identified through a staggered identification scheme, In particular, at first, the elastic shear modulus $\mu _S$ is determined straightforward from triaxial loading-unloading loops and the compression-extension-ratio parameter $\overset{*}{\gamma }$ of the failure surface is found from compression and extension experiments at different confining pressures. Subsequently, several triaxial tests at different confining pressure, in particular, $\sigma _{c,1}=0.1\,\mathrm{MPa}$, $\sigma _{c,2}=0.2\,\mathrm{MPa}$ and $\sigma _{c,3}=0.3\,\mathrm{MPa}$, have been carried out, where the axial $\sigma _{a}$ and radial stresses $\sigma _{r}$, the axial strain $\varepsilon _{a}$, and the volumetric strain $\varepsilon ^{V}$ have been recorded. The material parameters are then found through a minimisation of the squared error between simulation and experiment, which is known as Least-Squares optimisation method. In particular, a gradient-based constrained optimisation is used, in which the Hessean matrix is approximated through the BGFS (Broyden, Fletcher, Goldfarb, Shannon) procedure, see e. g. [39], and the parameter constraints are considered via the sequential-quadratic-programming (SQP) technique, see [40]. The identified solid-skeleton material parameters of the research-unit sand FOR 1136 are summarised in Table 1.

A comparison between the simulation and the experiments for the triaxial experiments at different confining pressures and for the isotropic compression test are depicted in Fig. 11. As can been seen, the model responses are in a quite good agreement with the experimental observations.

Appendix B: Material Parameters of the IKH Model

Proceeding from the material constants of the pure isotropic hardening (IH) model, see Table 1, the governing parameters of the mixed isotropic-kinematic hardening (IKH) model are guessed and the adjustments according to Table 2 are made.