A Zero Elastic Range Hypoplasticity Model for Sand

Abstract

The theory of zero purely elastic range in stress space within the framework of bounding surface plasticity is applied to sand constitutive modelling. With a vanished yield surface, plastic loading occurs for any direction of the stress ratio rate on which the loading and plastic strain rate directions now depend, rendering the model incrementally non-linear. The resulting model falls into the category of hypoplasticity in the sense of dependence of the plastic strain rate direction on the stress rate direction, that is different from another constitutive hypoplasticity theory, which does not involve classical plasticity loading-unloading criteria and additive decomposition of total strain rate into elastic and plastic parts. The simplicity of the conceptual structure of the model is particularly attractive as it consists of only one surface, the bounding/failure surface, and the stress point itself in the deviatoric stress ratio plane. The model follows the basic premises of the SANISAND family of models that unify the description for any pressure and density within critical state theory. Elimination of the classical yield surface concept circumvents the complexity associated with satisfying the consistency condition; however, the incrementally non-linear hypo-plastic nature of the new formulation requires special handling of its numerical implementation. The work shows the simulative capabilities of the model that are comparable with those of the classical model with very small yield surfaces, including simulations under cyclic and rotational shear loading.

1 Introduction

The idea of zero elastic range in plasticity theory where the yield surface size shrinks to zero and the surface degenerates to the current stress point in stress space was first presented in [3] as a corollary of bounding surface (BS) plasticity where such disappearance of yield surface is compensated by the still finite bounding surface that determines now the loading direction and plastic modulus. The physical motivation was the effort to simulate the response of artificial graphite [3, 8, 9], a material used in nuclear reactor technology and which exhibits zero purely elastic range in loading and unloading.

Several other materials do show either a zero or an extremely limited purely elastic range response described by a very small yield surface, prominent among them being soils, in particular granular soils or sands. In sand constitutive modeling the consequence of this trait was reflected in the adoption by various models of a very small size yield surface (YS) in stress-ratio space $\varvec{r}=\varvec{s}/p$, with $\varvec{s}$ the deviatoric and p the hydrostatic parts of the stress $\varvec{\sigma }$, respectively, obeying a kinematic hardening rule. Among such models the most relevant to the current paper are the two-surface model in [7, 21], and its variation in [26] where the name SANISAND was firstly adopted. Such a model is illustrated in Fig. 1(a) where the YS is shown as a very small circle in $\varvec{r}$ space with the back stress-ratio $\varvec{\alpha }$ as its center. The larger surface represents the bounding surface (BS) that varies in size, on which the image stress point $\varvec{r}^{b}$ is defined as shown by the unit norm deviatoric direction $\varvec{n}$ along $\varvec{r}-\varvec{\alpha }$. The $\varvec{R}^{\prime }$, normal to the BS at $\varvec{r}^{b}$, is the plastic deviatoric strain rate direction. As usual with BS plasticity, the plastic modulus $K_{p}$ depends on the projected on $\varvec{n}$ distance $(\varvec{r}^{b}-\varvec{r}):\varvec{n}$ such that $K_{p}=0$ when $\varvec{r}=\varvec{r}^{b}$, i.e., when the stress ratio is on the BS. The $\theta$ represents the relevant Lode angle.

It is then natural to consider the possibility that this very small yield surface can be taken in the limit to be of vanishing size becoming identical to the back-stress ratio that is its center, and consequently the YS surface degenerates to the stress point $\varvec{r}$ itself. In passing one can observe that in the counterpart of the above for the classical triaxial $q-p$ space, the yield surface is represented by a very narrow wedge, which for vanishing elastic range collapses onto the stress ratio line q / p = $\eta .$ The conceptual framework of the working of the model is illustrated in Fig. 1(b). The stress ratio rate is denoted by $\dot{\varvec{r}}$ (a superposed dot indicates henceforth the rate), and the stress ratio increment $d\varvec{r}=\dot{\varvec{r}}dt$, is shown as an arrow emanating from $\varvec{r}$, with dt the time increment. The extension of $\dot{\varvec{r}}$ direction defines the image (or bounding) stress ratio $\varvec{r}^{b}$ (mapping rule) at its intersection with the BS, where again $\varvec{n}$ and $\varvec{R}^{\prime }$ are defined. Figure 1(c) illustrates the process when the Lode angle $\theta$ effect on the BS is omitted and the BS becomes circular, but the Lode angle effect on $\varvec{R}^{\prime }$ is maintained. Notice that whichever is the direction of $\dot{\varvec{r}}$ for $\varvec{r}$ inside or on the BS (see later for the case of $\varvec{r}$ outside the BS), there will be always a unique bounding stress ratio point $\varvec{r}^{b}$ and associated $\varvec{n}$ for convex BS shape, and furthermore $\varvec{n}:\dot{\varvec{r}}>0$ guaranteeing there will be always plastic loading. Both $\varvec{n}$ and $\varvec{R}^{\prime }$ depend on the stress rate direction. Such dependence in conjuction with the mapping rule shown in Figs. 1(b) and (c), while originally proposed in [3, 8, 9] for artificial graphite, it was also proposed for soils in a qualitative sense in [4], and applied to sands within a full constitutive modeling framework in [2, 14, 29], and more recently in [12], in constitutive frameworks quite different than the present ones. According to [6] these models, which are also incrementally non-linear (the first such model was proposed in [11] in a different setting) are named hypoplasticity models; the same word hypoplasticity is used for a different class of models (e.g. [15, 16]) that do not involve classical plasticity loading-unloading criteria and additive decomposition of total strain rate into elastic and plastic parts. Incorporating the zero elastic range model within the framework of SANISAND models, introduces what has been called the SANISAND-Z model, Z standing for zero elastic range [10]. Its presentation and further elaboration is the objective of this paper.

Fig. 1.

Illustration of the concept of the SANISAND-Z model (a) small yield surface, bounding surface, mapping rule, loading direction $\varvec{n}$ and deviatoric plastic strain rate direction $\varvec{R}'$, (b) shrinking of the yield surface to the stress ratio point $\varvec{r}$, and (c) elimination of the Lode angle effect on the bounding surface.

Before closing this introduction it is instructive to delineate the present zero elastic range model from several other models that claim, erroneously, to be also of zero elastic range. Prominent among them are the stress-reversal surfaces models in [22, 23]. This is illustrated in Fig. 2, where after reversal at $\varvec{r}_{in}$ a new loading process begins and the current stress ratio point $\varvec{r}$ is projected at $\varvec{r}^{b}$ on the BS by a radius emanating from $\varvec{r}_{in}$; at $\varvec{r}^{b}$ the loading direction $\varvec{n}$ is defined and transferred at $\varvec{r}$. But this projection process creates an implied reversal/loading surface shown by dashed line which is homothetic to the BS with center of homothecy the $\varvec{r}_{in}$ and on which the current $\varvec{r}$ lies. If now the stress rate $\dot{\varvec{r}}$ is in a tangent direction to the created reversal/loading surface, i.e. it is normal to $\varvec{n}$ as shown in Fig. 2, purely elastic response is induced during such neutral loading path, allowing the stress ratio $\varvec{r}$ to move around the loading surface without causing any plastic deformation, thus, violating the concept of zero elastic range. The second large family of erroneously called zero elastic range models is that of generalized plasticity, where a loading direction $\varvec{n}$ and its opposite $\varvec{n'}=-\varvec{n}$ are defined in stress space and plastic loading is postulated for both $\varvec{n}:\dot{\varvec{r}}>0$ and $\varvec{n}:\dot{\varvec{r}}=-\varvec{n}':\dot{\varvec{r}}<0$ with different plastic moduli in each case giving the impression of non existence of purely elastic range. However, again in this scheme a neutral loading path defined by $\varvec{n}:\dot{\varvec{r}}=0$ causes only elastic deformation around an implied loading surface (the definition of $\varvec{n}$ is tantamount to the definition of such surface), that negates again the zero elastic range character of generalized plasticity. Bottom line is that zero elastic range must be exactly what the name signifies, i.e., a null yield surface that collapses onto the stress point itself, within a scheme that guarantees realistic description of plastic strain rate norm and direction.

Fig. 2.

Geometrical explanation why stress reversal surfaces and generalised plasticity models are not zero elastic range models.

2 The SANISAND-Z Constitutive Model

The sensitivity of sands to stress-ratio changes renders the stress-ratio space the appropriate one for the development of any sand constitutive model. Additional plastic deformation due to a change of stress under constant stress ratio, requires a modified formulation [26], which will not be considered in this work. The additive decomposition of total strain rate into an elastic and plastic part will be assumed, with the former given in terms of shear G and bulk K elastic moduli, and the latter occurring along a direction $\varvec{R}=\varvec{R}^{\prime }+(1/3)D\varvec{I}$ with $\varvec{R}^{\prime }$ the deviatoric part of $\varvec{R}$, and D the dilatancy. A deviatoric unit norm loading direction $\varvec{n}$ is defined at stress ratio space as discussed before in conjunction with Fig. 1, such that $\text {tr}\varvec{n}=0$ and $\text {tr}\varvec{n}^{2}=1$.

According to standard plasticity formulation as shown in [21], and with the loading index (or plastic multiplier) L defined in terms of stress or total strain rates and the plastic modulus $K_{p}$, the strain rate - stress rate direct and inverse relations for a stress ratio dependent response are given as follows:

$$\begin{aligned} \dot{\varvec{\varepsilon }}=\frac{1}{2G}\dot{\varvec{s}}+\frac{1}{3K}\dot{p}\varvec{I}+\langle L\rangle (\varvec{R}^{\prime }+\frac{1}{3}D\varvec{I}) \end{aligned}$$

(1)

$$\begin{aligned} \dot{\varvec{\sigma }}=2G\dot{\varvec{e}}+K\dot{\varepsilon }_{v}\varvec{I}-\langle L\rangle (2G\varvec{R}^{\prime }+KD\varvec{I)} \end{aligned}$$

(2)

$$\begin{aligned} L&= \frac{1}{K_{p}}\varvec{n}:p\dot{\varvec{r}}=\frac{1}{K_{p}}\varvec{n}:(\dot{\varvec{\sigma }}-\frac{\dot{p}}{p}\varvec{\sigma }) =\frac{1}{K_{p}}\varvec{n}:(\dot{\varvec{s}}-\dot{p}\varvec{r}) \nonumber \\&=\frac{2G\varvec{n}:\dot{\varvec{e}}-K(\varvec{n}:\varvec{r})\dot{\varepsilon }_{v}}{K_{p}+2G\varvec{n}:\varvec{R}^{\prime }-KD(\varvec{n}:\varvec{r)}} \end{aligned}$$

(3)

where $\langle L\rangle =L$ if $L>0,$ and $\langle L\rangle =0$ if $L\le 0$, the latter signifying the event of unloading, $\varvec{\varepsilon }$ denotes the strain tensor, $\varvec{e}$ its deviatoric part and ${\varepsilon }_{v}$ its volumetric with a superposed dot implying their rates. It is important to notice that for hardening response $K_{p}>0$ while for softening and perfectly plastic response $K_{p}\le 0.$ In the latter case it follows that necessarily $\varvec{n}:\dot{\varvec{r}}\le 0$ so that $L>0$. Because for elastic unloading also $\varvec{n}:\dot{\varvec{r}}\le 0$, the distinction between softening plastic loading and elastic unloading is made based on the sign of L calculated from the last expression of Eq. (3) in terms of the total strain rates.

In addition, since the model is developed within the framework of Critical State Soil Mechanics, the Critical Stress Ratio (CSR) in triaxial p–q space and Critical State Line (CSL) in void ratio e – pressure p space are given by the equations [20]

$$\begin{aligned} \frac{q}{p}=\eta =\eta _{c}=M;~~~~~e=e_{c}=e_{0}-\lambda (\frac{p}{p_{at}})^{\xi } \end{aligned}$$

(4)

where the M assumes different values in compression and extension and becomes function of the Lode angle in multiaxial stress space, while $e_{0}$, $\lambda$ and $\xi$ are material constants. The forgoing formulation requires the specification of the hypoelastic moduli G and K, and the plastic constitutive ingredients $\varvec{n}$, $\varvec{R}^{\prime }$, D, and $K_{p}$.

The Hypoelastic Moduli G and K

The G and K are given as functions of p and current void ratio e by the relations

$$\begin{aligned} G=G_{0}p_{at}\frac{(2.97-e)^{2}}{1+e}\left( \frac{p}{p_{at}}\right) ^{1/2};~~~~~K=\frac{2(1+\nu )}{3(1-2\nu )}G \end{aligned}$$

(5)

where the expression for G is given in [25]. Here $G_{0}$ is a model parameter, $\nu$ is a constant Poisson’s ratio, and $p_{at}$ is the atmospheric pressure for normalization.

Fig. 3.

Illustration of the working of the SANISAND-Z model in conjunction with bounding $F^b=0$, dilatancy $F^d=0$ and Critical State $F^c=0$ surfaces, for (a) stress ratio point $\varvec{r}$ inside the bounding surface, and (b) stress ratio point $\varvec{r}$ outside the bounding surface.

Definition of Bounding, Dilatancy and Critical State surfaces

Excluding for simplicity the Lode angle dependence of M, the BS is shown schematically as a circle $F^{b}=0$ in the stress ratio space of Fig. 3. Following [19, 21], and denoting by $\varvec{r}^{b}$ a stress ratio on the BS, its analytical expression is given by

$$\begin{aligned} F^{b}=(\varvec{r}^{b}:\varvec{r}^{b})^{1/2}-\sqrt{\frac{2}{3}}M^{b}=0;~~~~~M^{b}=M\exp (-n^{b}\psi ) \end{aligned}$$

(6)

where the value of M is taken as the average between its triaxial compression and extension values, $M_{c}$ and $M_{e}$, respectively, to compensate for the exclusion of Lode angle dependence, $\psi =e-e_{c}$ is the state parameter [1], $n^{b}$ a positive model constant and $\sqrt{(2/3)}M^{b}$ is the variable with $\psi$ radius of the BS.

With $\varvec{r}^{d}$ denoting a stress ratio on the dilatancy surface (DS) $F^{d}=0$ which is homocentric to the BS as shown in Fig. 3, its analytical expression is

$$\begin{aligned} F^{d}=(\varvec{r}^{d}:\varvec{r}^{d})^{1/2}-\sqrt{\frac{2}{3}}M^{d}=0;~~~~~M^{d}=M\exp (n^{d}\psi ) \end{aligned}$$

(7)

with $n^{d}$ a positive model constant. At critical state $\psi =0$ and $M^{b}=M^{d}=M$, thus, BS and DS collapse to the Critical State surface (CS) $F^{c}=0$, shown in Fig. 3 as a circle of radius $\sqrt{(2/3)}M$. The placement of BS and DS outside and inside CS surface, respectively, can be interchanged due to the value of $\psi$ being negative (denser than critical samples) or positive (looser than critical samples) [21].

The Loading Direction $\varvec{n}$

(i) Stress Ratio Inside or on the BS: Consider first the current stress ratio $\varvec{r}$ inside or on the BS as shown in Fig. 3(a), which implies $(\varvec{r}:\varvec{r})^{1/2}\le \sqrt{(2/3)}M^{b}$. For future reference a unit norm deviatoric tensor $\varvec{n}^{r}=\varvec{r}/\!\left| \varvec{r}\right|$ is defined along $\varvec{r}$. The stress ratio rate $\dot{\varvec{r}}=\left| \dot{\varvec{r}}\right| \varvec{\nu }$ is defined in terms of its norm $\left| \dot{\varvec{r}}\right|$ and its unit norm deviatoric direction $\varvec{\nu }$ such that $\text {tr}\varvec{\nu }=0$ and $\text {tr}\varvec{\nu }^{2}=1$. As already elaborated, the image stress ratio $\varvec{r}^{b}$ on the BS is obtained as the intersection of $\dot{\varvec{r}}$ direction with the BS. For a given $\dot{\varvec{r}}$ in the case of a circular BS the $\varvec{r}^{b}$can be analytically specified by:

$$\begin{aligned} \varvec{r}^{b}=\varvec{r}+b\varvec{\nu };\;\;\;b=-\varvec{r}:\varvec{\nu }+\left[ (\varvec{r}:\varvec{\nu })^{2}+(2/3)(M^{b})^{2}-\varvec{r}:\varvec{r}\right] ^{1/2} \end{aligned}$$

(8)

where the foregoing expression for b is obtained by inserting $\varvec{r}^{b}=\varvec{r}+b\varvec{\nu }$ in Eq. (6) and solving for b in terms of the (non negative) largest real root of the resulting quadratic equation. The loading direction $\varvec{n}$ is defined normal to BS at $\varvec{r}^{b}$, hence, based on Eq. (6) one has

$$\begin{aligned} \varvec{n}=\frac{\partial F^{b}}{\partial \varvec{r}^{b}}=\frac{\varvec{r}^{b}}{\left| \varvec{r}^{b}\right| } \end{aligned}$$

(9)

where $\varvec{n}$ is shown in Fig. 3(a) along the radius $\varvec{r}^{b}$. The points $\varvec{r}^{d}$ and $\varvec{r}^{c}$ are defined as the intersections of $\varvec{n}$ with the dilatancy and critical state surfaces $F^{d}=0$ and $F^{c}=0$, respectively, as shown in Fig. 3(a).

(ii) Stress Ratio Outside the BS: It is possible that the current stress ratio $\varvec{r}$ finds itself outside the BS, shown in Fig. 3(b), as a result of diminishing radius of the latter due to its dependence on the state parameter $\psi$, Eq. (6)$_{2},$ that implies ${(\varvec{r}:\varvec{r})}^{1/2}\ge \sqrt{(2/3)}M^{b}$. In this case the plastic modulus becomes negative (see subsequent definition), hence, there are two possibilities: either continued plastic loading with softening response or elastic unloading. In both cases the stress ratio rate $\dot{\varvec{r}}$ points “inwards” of $\varvec{r}$ towards the BS and the distinction of which one of the aforementioned two cases occurs is based on the sign of L according to Eq. (3). L requires the determination of the image stress ratio $\varvec{r}^{b}$ to obtain the loading direction $\varvec{n}$ normal to BS at $\varvec{r}^{b}.$ If the $\varvec{r}^{b}$ is defined as before, i.e., as the intersection of $\dot{\varvec{r}}$ with the BS, the direction of $\dot{\varvec{r}}$ may not intersect the BS for $\varvec{r}$ outside the BS, as implied in the illustration of Fig. 3(b). Thus, a re-definition of the mapping rule for $\varvec{r}^{b}$ is necessary as the intersection with the BS of the radius connecting the origin to $\varvec{r}$, Fig. 3(b), and $\varvec{n}=\partial F^{b}/\partial \varvec{r}^{b}$ as in Eq. (10). Such definition of $\varvec{r}^{b}$ maintains the continuity of the mapping rule as the $\varvec{r}$ crosses the BS, and becomes independent of $\dot{\varvec{r}}$ when $\varvec{r}$ is outside the BS. Now the process of loading/unloading is as follows. If $L>0$ according to the last expression of Eq. (3) expressed in terms of the total strain rates, plastic loading with softening occurs; if $L<0,$ it signifies elastic unloading. In either case the direction of $\dot{\varvec{r}}$ points inwards the current $\varvec{r}$, which is updated to the position $\varvec{r}^{\prime }=\varvec{r}+\dot{\varvec{r}}dt$ as shown in Fig. 3(b). The $\dot{\varvec{r}}dt$ is obtained from the calculation of the $\dot{\varvec{\sigma }}$ from Eq. (2) for either case since $\langle L\rangle =L$ when $L>0$, and $\langle L\rangle =0$ when $L<0$. At $\varvec{r}^{\prime }$ one has $\varvec{r}^{\prime b}$ as shown in Fig. 3(b) and $\varvec{n}^{\prime }=\partial F^{b}/\partial \varvec{r}^{b\prime }.$ For this new $\varvec{n}^{\prime }$ the previous process is repeated. The $\varvec{r}$ will reach eventually the BS from outside. Observe that while $\varvec{r}$ is outside the BS no reverse plastic loading can occur according to the above scheme, but this is not expected to cause any problem because the excursion outside the BS is very small.

The Deviatoric Plastic Strain Rate Direction $\varvec{R}^{\prime }$

The specification of the plastic strain rate direction $\varvec{R}=\varvec{R}^{\prime }+(1/3)D\varvec{I}$ requires the definition of the deviatoric part $\varvec{R}^{\prime }$ and the dilatancy D. The total flow rule is non associative.

(i) Deviatoric Associative Flow Rule: If a deviatoric associative flow rule is postulated, then one can set

$$\begin{aligned} \varvec{R}^{\prime }=\varvec{n} \end{aligned}$$

(10)

It follows that $\varvec{n}:\varvec{R}^{\prime }=\varvec{n}:\varvec{n}=1$ in the last member of Eq. (3) for L.

(ii) Deviatoric Non-associative Flow Rule: Following [7] the relative inaccuracy of the deviatoric associative flow rule due to independence from the Lode angle $\theta$ in Fig. 3, can be corrected by a deviatoric non-associative flow rule obtained from a Lode angle dependent plastic potential surface $F^{p}=0$ defined in stress ratio space by

$$\begin{aligned} F^{p}=(\varvec{r}^{p}:\varvec{r}^{p})^{1/2}-\sqrt{\frac{2}{3}}M^{p}(\theta )=0 \end{aligned}$$

(11)

$$\begin{aligned} M^{p}(\theta )=g(\theta )M_{c};\;\;\;g(\theta )=\frac{2c}{(1+c)-(1-c)\cos 3\theta };\;\;\;c=\frac{M_{e}}{M_{c}} \end{aligned}$$

(12)

where $M_{c}$ and $M_{e}$ are the critical stress ratios in triaxial compression and extension, respectively, $g(\theta )$ is the Lode angle-dependent interpolation function, and $\varvec{r}^{p}$ is a stress ratio on $F^{p}=0$. The $F^{p}=0$ is not shown in Fig. 3 for reasons of clarity, but it has the usual rounded triangular shape caused by the $\theta$ dependence as shown for the BS in Fig. 1(a) and (b). For any $\varvec{r}^{b}$ defined according to the mapping rules of the previous subsection, there is a corresponding $\varvec{n}$, and for this $\varvec{n}$ there is a corresponding Lode angle $\theta$ defined by $\cos 3\theta =\sqrt{6}\text {tr}\varvec{n}^{3}$. The $\varvec{R}^{\prime }$ is defined as the gradient of $F^{p}=0$ with respect to the stress, at a point $\varvec{r}^{p}$ on $F^{p}=0$ that is along $\varvec{n}$, which is expressed in [7]:

$$\begin{aligned} \varvec{R}^{\prime }=B\varvec{n}-C(\varvec{n}^{2}-\frac{1}{3}\varvec{I});\;\;\;B=1+\frac{3}{2}\frac{1-c}{c}g(\theta )\cos 3\theta ;\;\;\;C=3\sqrt{\frac{3}{2}}\frac{1-c}{c}g(\theta ) \end{aligned}$$

(13)

For $c=1$ Eq. (13) yields as expected the associative deviatoric flow rule $\varvec{R}^{\prime }=\varvec{n}$ because $F^{p}=0$ becomes circular in $\pi$-plane. Based on Eq. (13) it follows again that $\varvec{n}:\varvec{R}^{\prime }=B-C\text {tr}\varvec{n}^{3}=1$ in Eq. (3) for L, where the equality of the last two members of the above equation is based on the expression $\cos 3\theta =\sqrt{6}\text {tr}\varvec{n}^{3}$.

The Dilatancy D

Following the original suggestion in [21], the dilatancy will depend on the distance $\varvec{r}^{d}-\varvec{r}$ of the current stress ratio $\varvec{r}$ from its image $\varvec{r}^{d}$ on the DS, projected on the unit direction $\varvec{n}$, Fig. 3, thus, the following expression holds accounting for $\varvec{r}^d=\sqrt{2/3}M^d\varvec{n}$ and $\varvec{n}^{r}=\varvec{r}/\left| \varvec{r}\right|$:

$$\begin{aligned} D=A_{d}(\varvec{r}^{d}-\varvec{r}):\varvec{n}=A_{d}(\sqrt{\frac{2}{3}}M^{d}-\left| \varvec{r}\right| \varvec{n}^{r}:\varvec{n}) \end{aligned}$$

(14)

with $A_{d}$ a model parameter and the reminder that $M^{d}$ depends on the state parameter $\psi$ according to Eq. (7). Equation (14) can yield a positive (contraction) or negative (dilation) value of D, depending on the relative placement of $\varvec{r}^d$ and $\varvec{r}$ in conjunction with $\varvec{n}$. The $A_{d}$ in the simplest case is constant, but it was found beneficial for the simulation of liquefaction to render it a function of a fabric dilatancy tensor $\varvec{z}$ as $A_{d}=A_{0}(1+\sqrt{({3}/{2})}\langle \varvec{z}:\varvec{n}\rangle )$, with $A_{0}$ a constant, where $\varvec{z}$ evolves according to $\dot{\varvec{z}}=-c_{z}\langle -\dot{\varepsilon }_{v}^{p}\rangle (\sqrt{({2}/{3})}z_{\max }\varvec{n}+\varvec{z})$. Notice that here the factors $\sqrt{(3/2)}$ and $\sqrt{(2/3)}$ were appropriately added to the original expressions of $A_{d}$ and $\dot{\varvec{z}}$, respectively, presented in [7], so that the values of the constants $A_{0}$, $c_{z}$ and $z_{\max }$ calibrated from a simpler triaxial formulation and data, can be used directly as input in the multiaxial expressions above.

Fig. 4.

Illustration of the loading and unloading/reloading domains for the direction of $\dot{\varvec{r}}$ in deviatoric stress space, and the updating of $\varvec{r}_{in}$.

The Plastic Modulus $K_{p}$

Consistent with a BS formulation the value of the plastic modulus $K_{p}$ will depend on the “distance” $\varvec{r}^{b}-\varvec{r}$ of the current stress ratio $\varvec{r}$ from its image $\varvec{r}^{b}$ on the BS, projected on the unit direction $\varvec{n}$. An extension of the proposition made in [7] will be adopted where the back-stress ratio $\varvec{\alpha }$ of their formulation is now substituted by the stress ratio $\varvec{r}$ (recall that for zero elastic range one obtains $\varvec{r}=\varvec{\alpha }$ as the yield surface shrinks to zero), which then reads:

$$\begin{aligned} K_{p}=\frac{2}{3}ph\frac{(\varvec{r}^{b}-\varvec{r}):\varvec{n}}{(\varvec{r}-\varvec{r}_{in}):\varvec{n}} \end{aligned}$$

(15)

The $\varvec{r}_{in}$ is the value of $\varvec{r}$ at the initiation of a plastic loading event and h is a model parameter which is function of the void ratio e and pressure p according to $h=G_{0}h_{0}(1-c_{h}e)(p/p_{at})^{-0.5}$, with $h_{0}$ and $c_{h}$ model parameters. The factor 2/3 was placed for maintaining the same value of h calibrated under triaxial conditions. The $\varvec{r}_{in}$ must be updated to a new value at initiation of a new plastic loading event in order to obtain the infinite value of the plastic modulus resulting from Eq. (15) when $\varvec{r}=\varvec{r}_{in}$, expected in such event. Since one has always $L>0$ when $\varvec{r}$ is inside the BS, a new plastic loading event is defined as follows. When in Eq. (15) the $(\varvec{r}-\varvec{r}_{in}):\varvec{n}\le 0$, it means that the current loading direction $\varvec{n}$, defined in terms of $\dot{\varvec{r}}$, forms an angle greater than 90$^{\circ }$ in the generalized stress ratio space with the tensor $\varvec{r}-\varvec{r}_{in}$, which is a measure of the overall direction of ongoing stress loading path that started at $\varvec{r}_{in}$. But such drastic change of loading direction in regards to ongoing loading path is tantamount to unloading and the beginning of a new loading process. Hence the $\varvec{r}_{in}$ is updated to the current $\varvec{r}$ value when the denominator of Eq. (15) becomes negative, and a new loading process begins with an initially infinite value of the plastic modulus because the denominator becomes zero after the update. In other words the unloading event is followed immediately by a new loading event, without any purely elastic response taking place. The foregoing process is further illustrated in Fig. 4 where a loading process begins at the origin which serves as $\varvec{r}_{in}$ at the start. At $\varvec{r}$ the directions of $\dot{\varvec{r}}dt$ that continue plastic loading and those that signify instantaneous unloading and a new plastic loading event, can be easily visualized and distinguished by the shaded sectors of the little circle drawn around $\varvec{r}$ in such way that the forward continued loading is defined by all $\varvec{n}$ for which $(\varvec{r}-\varvec{r}_{in}):\varvec{n}=\varvec{r}:\varvec{n} > 0$ while the new plastic loading event for all $\varvec{n}$ for which $(\varvec{r}-\varvec{r}_{in}):\varvec{n}=\varvec{r}:\varvec{n}\le 0.$ These two sectors are defined by connecting the point $\varvec{r}$ with the two ends of the diameter of the $F^{b}=0$ which is perpendicular to $\varvec{r}-\varvec{r}_{in}=\varvec{r}$, because at these two ends the corresponding $\varvec{n}$ is normal to $\varvec{r}-\varvec{r}_{in}=\varvec{r}$ and $\varvec{r}:\varvec{n}=0$. Upon unloading/initiation of new loading, the previous $\varvec{r}_{in}$ at the origin, is updated to the current $\varvec{r}$. Finally, when $\varvec{r}$ moves outside the BS and $\varvec{r}^{b}$ is defined along $\varvec{r}$ on the BS, Fig. 3(b), the quantity $(\varvec{r}^{b}-\varvec{r}):\varvec{n}<0$ in Eq. (15), which implies a $K_{p}<0$, signifying a softening material response as long as $L>0$ according to Eq. (3).

Fig. 5.

Illustration of the SANISAND-Z model in triaxial stress space where the deviatoric stress ratio point of Fig. 3 becomes the line $\eta =q/p$, and the bounding, dilatancy and critical state surfaces become the lines $M^b$, $M^d$ and $M^c$ with subscripts c and e for compression and extension, respectively.

The updating of $\varvec{r}_{in}$ in Eq. (15), necessary to obtain a smooth elasto-plastic transition by rendering $K_{p}=\infty$ at initiation of a loading event, creates also the so-called overshooting response upon reverse loading/immediate reloading associated with its updating, known since the time of its inception [3]. Overshooting implies a stress-strain curve which unrealistically overshoots the continuation of a previous curve had the event of reverse loading/reloading not taken place. In order to remedy overshooting, [6] outlined a way of updating $\varvec{r}_{in}$, which is implemented in the current model and has been presented in detail in [10]. In this reference one can also find the triaxial counterpart formulation of SANISAND-Z, that will not be presented here. It suffices for illustration purposes to show Fig. 5, which is the counterpart of Fig. 3(a) in triaxial space, where the stress ratio $\varvec{r}$ is now the line $\eta =q/p$ and the bounding, dilatancy and critical state surfaces are represented by the straight lines with slopes $M_{c}^{b}$, $M_{c}^{d}$, $M_{c}^{c}$, in compression and $M_{e}^{b}$, $M_{e}^{d}$, $M_{e}^{c}$, in extension, while loading occurs for any rate of $\eta$ in the compression or extension directions.

Table 1. SANISAND-Z model parameters for Toyoura sand$^{\text {a}}$

3 Model Performance

Detailed calibration process for the SANISAND models are presented in [27]; their calibrated parameters for Toyoura sand are used in the present study, and shown in Table 1. Simulation results are based on both the SANISAND-Z model with true zero elastic range and the [7] version of SANISAND with a tiny yield surface cone. The trace of the cone on the stress-ratio $\varvec{r}$ plane is a circular deviatoric yield surface with center $\varvec{\alpha }$ and radius (2 / 3) m. A small value of $m=0.01$ is used for the simulations with [7] model. The SANISAND-Z model uses a constant critical stress ratio M which is set equal to the compression value $M_{c}$ here, in order to properly capture the main part of the loading which is in triaxial compression in these simulations. The [7] model uses a Lode angle dependent critical stress ratio with M varying between $M_{c}$ in triaxial compression and $M_{e}=cM_{c}$ in triaxial extension, although no extension is relevant to these data.

Performance of the SANISAND-Z model in simulation of selected drained and undrained triaxial loading and unloading paths, in comparison with the data of Toyoura sand from [28], is already reported in [10] and similar to previous models examined in [7, 26, 27]. In this presentation the response under some more complicated stress paths will be examined. Figures 6, 7, 8, 9 and 10 presented in the following, are in fact variations of corresponding figures in [10].

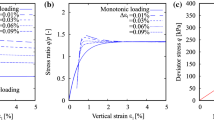
Figure 6 compares the experimental data [24] and model simulations for drained constant-p cyclic triaxial tests on isotropically consolidated loose samples of Toyoura sand. In this test the amplitude of shear strain ($\varepsilon _{{a}}-\varepsilon _{{r}}$) has been increased in different cycles of loading. The simulation with the SANISAND-Z model is done with a constant critical stress ratio M which is set equal to $M_{c}(1+c)/2$, in order to properly capture the average response in compression and extension. The simulation results are presented with solid lines in Figs. 6(d–f). The simulations with the [7] model are done in two different ways for the critical stress ratio with: (i) a constant $M=M_{c}(1+c)/2$ (for direct comparison with the results from the SANISAND-Z model), and (ii) a Lode angle dependent M. The simulations results for these two choices of M with the [7] model are presented with dashed and dot-dashed lines, respectively, in Figs. 6(d–i). The models show almost same results as each other, and very close to those observed in the experiments. Of course the simulations results with [7] and $M(\theta )$ are slightly closer to those observed in the experiments. Accumulation of compressive volumetric strain with cyclic loading can be observed in Fig. 6, and clearly when the stress ratio exceeds a certain value, which varies by the state, the specimen begins to dilate. Additional comparison for cyclic loading of a dense sample of Toyoura sand are presented in [10] showing again very similar trend.

Fig. 6.

Simulations vs. experiments in constant-p cyclic drained triaxial tests on isotropically consolidated relatively loose samples of Toyoura sand: experimental data (a–c) are after [24]; simulations (d–f and g–i) are using SANISAND-Z model with $M=M_c (1+c)/2$ (solid lines), [7] model with $M=M_c (1+c)/2$ (dashed lines), and [7] model with $M=M(\theta )$ (dot-dashed lines).

Simulation results under a particular rotational shear path comprising a circular stress path in the $\pi$-plane are presented in Figs. 7 and 8. The simulation results exhibit in a very illustrative way the performance of SANISAND-Z for such an unorthodox stress path. While the triaxial simulations can use the much simpler formulation of the triaxial space, the rotational shear requires the full general stress space formulation and numerical implementation, the latter being a problem to reckon with due to the incrementally non-linear feature of the equations. These simulations are intended to be compared with data from Fuji river sand for which no data for calibration were available. However, given the similarity of this sand with Toyoura sand, the model constants of the latter from Table 1 were used, instead. Figure 7 presents details of the simulation results for the following loading scenario: An isotropically consolidated sample with $p_{{in}}=\sigma _{{c}}=98$ kPa and $e_{{in}}=0.822$ is subjected to undrained triaxial compression by increasing the $\sigma _{{z}}$ until reaching $\tau _{{oct}}=12.5$ kPa, where $\tau _{{oct}}=(1/3)\left[ (\sigma _{{x}}-\sigma _{{y}})^{2}+(\sigma _{{x}}-\sigma _{{z}})^{2}+(\sigma _{{y}}-\sigma _{{z}})^{2}\right] ^{1/2}$; then keeping the $\tau _{{oct}}$ constant, the sample is subjected to a cyclically varying circular stress path in the $\pi$-plane under undrained condition. Three sets of simulation results are presented in Fig. 7 showing performance of SANISAND-Z model with $M=M_{c}(1+c)/2$ (dashed lines), [7] model with $M=M_{c}(1+c)/2$ (dashed lines), and [7] model with $M=M(\theta )$ (dot-dashed lines). The increasing amplitude helicoidal stress path in the stress ratio $\pi$-plane plot of Fig. 7(a) is due to the decrease of p, because of pore water pressure increase as shown in Fig. 7(b), hence, the increase of the ratio of stress / p.

Fig. 7.

Extended simulation results for undrained circular cyclic loading with $\tau _{oct}=12.5$ kPa on Fuji river sand for 5 cycles using model constants for Toyoura sand from Table 1: SANISAND-Z model with $M=M_c (1+c)/2$ (solid lines), [7] model with $M=M_c (1+c)/2$ (dashed lines), and [7] model with $M=M(\theta )$ (dot-dashed lines).

Figure 8 compares the effective stress path for undrained circular stress loading path between the simulations and the corresponding experimental results in [30] who explored three levels of $\tau _{{oct}}=9.7$, 11.1, and 12.5 kPa. In this figure $T_{{oct}}=\tau _{{oct}}\cos \varTheta$, where $\varTheta$ determines the angle of rotation of shear stress on the octahedral plane, shown in the original paper of [30]. Very similar general trend of response is observed between the simulation results and the experimental data. It is interesting to compare the plot of Fig. 7(b) with those of Figs. 8(f, i) for $\tau _{oct}$ = 12.5 kPa; the former is in fact a three dimensional perspective of the latter two. This is a good indicative of the overall performance of the SANISAND-Z model in such complex loading condition. A more specific calibration of the model parameters for Fuji river sand would likely provide better match between the simulations and experimental results.

Fig. 8.

Simulations vs. experiments in undrained circular cyclic tests on Fuji river sand using model constants for Toyoura sand from Table 1: experimental data (a–c) are after [30]; simulations (d–f and g–i) are using SANISAND-Z model with $M=M_c (1+c)/2$ (solid lines), [7] model with $M=M_c (1+c)/2$ (dashed lines), and [7] model with $M=M(\theta )$ (dot-dashed lines).

Because a stress ratio based model will not induce plastic deformation under constant stress ratio loading, the question arises on how the present model will respond to an oedometric test. Such test imposes a constant total volumetric to total deviatoric strain ratio that in triaxial space is equal to 3/2, which can become soon a constant stress ratio (fixed $K_0$); before constant stress ratio is reached, plastic deformation is induced by the model. In Fig. 9(a) the response of the model under such oedometric test in loading and unloading is shown in p, q stress space for two initial void ratio values, one for dense ($e_{in}=0.65$) and the other for loose ($e_{in}\,=\,0.95$) sample, starting at an initial $p=10$ kPa, using the constants of Table 1. The stress path attains a very close to constant value of the stress ratio $q/p=\eta =\eta _{K_0}\approx 1.26$ for the dense and $q/p=\eta =\eta _{K_0}\approx 0.91$ for the loose sample, which based on the relation $K_0\,=\,(3-\eta _{K_0})/(2\eta _{K_0}+3)$ yields the values $K_0\,=\,0.32$ and $K_0\,=\,0.43$ for dense and loose samples, respectively. Simultaneously Fig. 9(b) shows a volumetric strain $\varepsilon _v$ in the order of $2\%$ and $3\%$ at the end of loading, and remaining strain of $0.5\%$ and $2\%$ at the end of unloading, for dense and loose samples, respectively; clearly plastic volumetric deformation takes place also during the unloading phase. The foregoing $K_0$ and volumetric strain values are realistic, in particular accounting for the fact the model was not calibrated to obtain the $K_0$ value and strains under oedometric loading and unloading.

Fig. 9.

Numerical simulation results for $K_0$ compression loading and un-loading on isotropically consolidated ($p_{in}$=10 kPa) very loose ($e_{in} = 0.95$ in dashed lines) and very dense ($e_{in} = 0.65$ in solid lines) samples using constants of Table 1.

Fig. 10.

Numerical simulation results for conjugate Gudehus’ response envelopes. The initial state of the sample is $e_{in} = 0.88$, $p\,=\,100$ kPa (point A), then sheared with constant p to $\tau _{oct}=25$ kPa (point B). At points A and B the sample is subjected to constant norm stress increments of 10 kPa (thin lines) and 20 kPa (thick lines), dashed for point A and solid for point B.

The model can simulate general and unusual loading paths such as rotational shear and shows similar simulation capabilities as its dual model with a very small yield surface in [7]. The dependence of the loading direction $\varvec{n}$ and in particular the plastic strain rate direction $\varvec{R}'$ on the stress rate direction $\varvec{\nu }$, although supported qualitatively by experiments and DEM simulations, needs a more thorough investigation to compare the theoretical suggestions to experimental (real or virtual) evidence in a quantitative way. For example the following two response characteristics can be proposed for verification and calibration by DEM in the future, which are particularly suited for a model with zero elastic range. The first is related to the suggestion in [13, 17] to plot stress increments around a stress point corresponding to strain probes of same norm in various directions; the tips of the stress increments constitute what we can call the Gudehus’ response envelope. Here a conjugate Gudehus’ response envelope will be used, where a material sample is loaded till a point in stress space, and then very small stress increments of equal norm are applied in all directions, and the corresponding strain increments are plotted radially around an origin in strain space; the locus of their tips constitutes the aforementioned envelope. In fact this type of response envelope in strain space was first proposed in [18], a fact omitted to be mentioned by mistake in [10], but the option to call it a conjugate Gudehus’ response envelope stems from the focus given in [13] to such constitutive modeling features. This is a particularly appropriate test to perform by DEM to check the incremental non-linearity associated with the dependence of the strain increment direction on the stress increment direction. To illustrate this process such a test was performed in drained conditions by the SANISAND-Z model and the results shown on the deviatoric planes for stress and strain increments in Fig. 10(a) and (b), respectively. In Fig. 10(a) the material with initial void ratio $e_{in}=0.88$ is loaded hydrostatically by $p=100$ kPa, point A, and then sheared at constant p to $\tau _{oct} = 25$ kPa, point B. At each position A and B, the sample is probed by stress increments of constant norms 10 kPa and 20 kPa consecutively in various directions, the tips of which are plotted as smaller and larger circular envelopes, respectively, in Fig. 10(a). For each stress probing process the tips of the corresponding strain increments are plotted around the origin of the deviatoric plane for strain increments as shown in Fig. 10(b) for both points A and B, and the resulting shapes are the aforementioned conjugate Gudehus envelopes. The envelopes for the smaller stress probes are included in the envelopes for the larger stress probes at both points, but while at point A on the hydrostatic axis such envelope remains almost circular (there is only Lode angle dependence of the response), at point B the distortion of the envelopes are clearly intense, as a result of the zero elastic range and the plastic modulus dependence on the stress rate direction via the distance from the BS. The second response characteristic which is particular to the zero elastic range feature of the model, is shown by the plots for a circular rotational shear path in Figs. 7 and 8; these can be repeated by DEM (a 3D DEM code is required) and comparisons made.

4 Conclusion

The SANISAND-Z model is an elastic-plastic constitutive model for sands, which is obtained from a kinematic hardening model when the yield surface size vanishes and the surface shrinks to its back-stress center becoming identical to the stress point itself in the deviatoric stress ratio space. The finite bounding surface is used to define the loading and deviatoric plastic strain rate directions, both of which depend now on the direction of the deviatoric stress ratio rate. Consequently the model is incrementally non linear and falls into the category of hypo-plasticity models in the sense of the term first introduced in [5], and defined in detail in [6].

The non-existing yield surface eliminates the need to satisfy the consistency condition by requiring the stress to remain on the yield surface, but the stability and avoidance of drift of an explicit numerical implementation becomes more difficult to achieve and requires special methodologies. On the other hand the plastic deformation that takes place always for any loading direction (except for elastic unloading at softening regimes for the current formulation when the stress point is outside the bounding surface), renders the model suitable to address bifurcation and localization problems where elastic loading “to the side” is too stiff to accommodate the initiation of a bifurcation process in classical plasticity with neutral loading features, which do not exist in the present model.

Otherwise the simulations of SANISAND-Z are similar in nature to those obtained by its predecessors SANISAND models with small but finite yield surfaces. It is believed that the present model will be very promising in simulations of special loading paths such as multidirectional shear and rotation of principal stress directions, that recently became of importance in various areas, of geotechnical engineering.