Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this work we study metric and spectral properties of inhomogeneous random graphs, where edges are present independently but with unequal edge occupation probabilities. We obtain results about the diameter, typical distances and eigenvalues for the dense case in this random graph model, under weak assumptions.

A discrete version of this model was introduced in Söderberg [15]. The sparse case (when the number of edges is linear in the number n of vertices) was studied in detail in the paper Bollobás–Janson–Riordan [3]. Among other things, they give an asymptotic formula for the diameter of the giant component when it exists. Connectivity at the intermediate case was analyzed in Devroye–Fraiman [7]. The dense case (when the number of edges is quadratic in n) is closely related with the theory of graph limits started in Lovász–Szegedy [11] and further studied in depth by Borgs, Chayes, Lovász, Sós and Vesztergombi [4, 5] among others. For a thorough introduction to the subject of graph limits see the book Lovász [10].

The diameter of random graphs has been studied widely. In particular, for the Erdős–Rényi model G(n, p), Bollobás [2] generalized the results of Klee–Larman [9] characterizing the case of constant diameter. Later, Chung–Lu [6] proved concentration results in various different ranges. More recently, Riordan–Wormald [14] completed the program to give precise asymptotics for the sparse case.

The critical window for G(n, p) is much harder to analyze. Nachmias–Peres [13] obtained the order of the diameter. Addario-Berry–Broutin–Goldschmidt [1] proved Gromov–Hausdorff convergence of the rescaled connected components to a sequence of continuous compact metric spaces. In particular, the rescaled diameter converges in distribution to an absolutely continuous random variable with finite mean.

The spectral gap of G(n, p) was studied in Füredi–Komlós [8], and the convergence of the empirical spectral distribution to Wigner’s semicircle law [16] follows from the Stieltjes’ transform approach developed in Marchenko–Pastur [12].

2 Framework

Consider a separable metric space \(\mathcal{S}\) and a Borel probability measure μ on \(\mathcal{S}\). Let X 1, …, X n be μ-distributed independent random variables on \(\mathcal{S}\). Let \(\kappa: \mathcal{S}\times \mathcal{S}\rightarrow \mathbb{R}\) be a non-negative symmetric integrable kernel, κ ≥ 0 and \(\kappa \in L^{1}(\mathcal{S}\times \mathcal{S},\mu \otimes \mu )\).

Definition 1

The inhomogeneous random graph with kernel κ and window p is the random graph G(n, κ, p) = (V, E), where the vertex set is V = { 1, …, n} and we connect each pair of vertices i, j ∈ V independently with probability p ij  = min{1, κ(X i , X j )p}.

The asymptotic expansions for distances in the graph G(n, κ, p) are obtained by looking at upper and lower partition graphs, which are discrete approximations of κ. The formal definitions are given below. Given two subsets \(\mathcal{A},\mathcal{B}\subset \mathcal{S}\) let

$$\displaystyle\begin{array}{rcl} \kappa _{\ell}(\mathcal{A},\mathcal{B})& =& \mathop{\mathrm{ess\,inf}}\limits \{\kappa (x,y): x \in \mathcal{A},y \in \mathcal{B}\}, {}\\ \kappa _{u}(\mathcal{A},\mathcal{B})& =& \mathop{\mathrm{ess\,sup}}\limits \{\kappa (x,y): x \in \mathcal{A},y \in \mathcal{B}\}. {}\\ \end{array}$$

We say that \(\mathbb{A} =\{ \mathcal{A}_{1},\ldots,\mathcal{A}_{m}\}\) is an admissible partition of \(\mathcal{S}\) if

$$\displaystyle{\mu (\mathcal{S}\setminus \cup _{i=1}^{m}\mathcal{A}_{ i}) = 0\quad \text{and}\quad \Vert \mathbb{A}\Vert _{\mu }:=\min \{\mu (\mathcal{A}): \mathcal{A}\in \mathbb{A}\}> 0,}$$

i.e., it covers \(\mathcal{S}\) and contains no zero measure sets.

Definition 2

Given a kernel κ and an admissible partition \(\mathbb{A} =\{ \mathcal{A}_{1},\ldots,\mathcal{A}_{m}\}\) of \(\mathcal{S}\), the lower partition graph \(P_{\ell}(\mathbb{A})\) (resp., upper partition graph \(P_{u}(\mathbb{A})\)) induced by \(\mathbb{A}\) is the graph with vertex set \(\mathbb{A}\) and where \((\mathcal{A}_{i},\mathcal{A}_{j})\) is an edge if \(\kappa _{\ell}(\mathcal{A}_{i},\mathcal{A}_{j})> 0\) (resp., \(\kappa _{u}(\mathcal{A}_{i},\mathcal{A}_{j})> 0\)).

For two vertices u, v ∈ V belonging to the same connected component, denote by d(u, v) the graph distance between u and v, that is, the number of edges on a shortest path between them. For a connected graph G, let diamG = max u, v d(u, v).

We say that a partition \(\mathbb{A}\) is a refinement of \(\mathbb{B}\), denoted by \(\mathbb{A} \prec \mathbb{B}\), if for every \(\mathcal{A}\in \mathbb{A}\) there exists \(\mathcal{B}\in \mathbb{B}\) such that \(\mathcal{A}\subset \mathcal{B}\). Note that in this case, \(\mathcal{B}_{i} = \cup _{p=1}^{m_{i}}\mathcal{A}_{p}^{(i)}\ \mu\)-almost everywhere. Moreover, it holds that \(\mathop{\mathrm{diam}}\nolimits P_{u}(\mathbb{A}) \geq \mathop{\mathrm{diam}}\nolimits P_{u}(\mathbb{B})\) and \(\mathop{\mathrm{diam}}\nolimits P_{\ell}(\mathbb{A}) \leq \mathop{\mathrm{diam}}\nolimits P_{\ell}(\mathbb{B})\). By these properties it makes sense to consider the following constants.

Definition 3

The lower and upper partition diameters are given by

$$\displaystyle{\Delta _{\ell}:=\inf _{\mathbb{A}}\mathop{ \mathrm{diam}}\nolimits P_{\ell}(\mathbb{A})\qquad \text{and}\qquad \Delta _{u}:=\sup _{\mathbb{A}}\mathop{ \mathrm{diam}}\nolimits P_{u}(\mathbb{A}).}$$

Finally, we want to avoid trivial cases where \(\Delta _{\ell}\) or \(\Delta _{u}\) are infinite because of an structural obstruction for connectivity given by κ.

Definition 4

A kernel κ on \((\mathcal{S},\mu )\) is reducible if there exists a set \(\mathcal{A}\subset \mathcal{S}\) with \(0 <\mu (\mathcal{A}) <1\) such that κ = 0 almost everywhere on \(\mathcal{A}\times (\mathcal{S}\setminus \mathcal{A})\). Otherwise, κ is irreducible.

If κ is reducible then the whole graph G(n, κ, p) is disconnected since almost surely there are no edges between vertices of type in \(\mathcal{A}\) and \(\mathcal{S}\setminus \mathcal{A}\). Since we want to work with connected graphs, we restrict our attention to the irreducible case.

3 Our Results

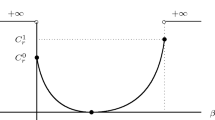
The results we prove are a generalization of previously known results for the Erdős–Renyi model obtained for the constant kernel κ = 1. We say that a sequence of events holds with high probability, if it holds with probability tending to 1 as n → ∞. We define the expansion factor \(\Phi:=\log n/\log np\). This quantity is about the diameter of G(n, p), as first shown in Bollobás [2]. Our main result about the diameter is the following.

Theorem 5

Let κ be irreducible and continuous (μ ⊗μ)-almost everywhere. Then,

  1. (i)

    if \(\Phi <\Delta _{u}\) then \(\mathop{\mathrm{diam}}\nolimits G(n,\kappa,p) = \Delta _{u}\) with high probability.

  2. (ii)

    if \(\Phi> \Delta _{\ell}\) then \(\mathop{\mathrm{diam}}\nolimits G(n,\kappa,p) = \Phi\) with high probability.

The proof relies on concentration inequalities which are inductively used to show that for all i, the i-th neighborhoods of vertices have good expansion properties. We also show that the upper and lower partition diameters cannot be very different.

Lemma 6

If \(\Delta _{\ell} <\infty\) then \(\Delta _{u} \leq \Delta _{\ell} \leq \Delta _{u} + 2\) .

Let λ i be the i-th eigenvalue (with multiplicity) of the adjacency matrix of G(n, κ, p). The empirical spectral distribution is

$$\displaystyle{\nu _{n} = \frac{1} {n}\sum _{i=1}^{n}\delta _{ \lambda _{i}/\sigma \sqrt{np}},}$$

where \(\sigma =\int _{\mathcal{S}}\int _{\mathcal{S}}\kappa (x,y)(1 -\kappa (x,y))d\mu (x)d\mu (y)\). Interlacing and the method of moments yield convergence to the semicircle law.

Theorem 7

Let κ be bounded and continuous (μ ⊗μ)-almost everywhere. Then,

$$\displaystyle{\nu _{n}\mathop{\longrightarrow }\limits^{w}\mathbf{1}_{\vert x\vert \leq 2}\frac{\sqrt{4 - x^{2}}} {2\pi } \,dx.}$$

Moreover, the eigenvalues normalized by np converge to the spectrum of T κ , the \(L^{2}(\mathcal{S},\mu )\) integral operator given by κ defined as

$$\displaystyle{T_{\kappa }\psi (x) =\int _{\mathcal{S}}\kappa (x,y)\psi (y)\,d\mu (y).}$$

Theorem 8

Let κ be bounded and continuous (μ ⊗μ)-almost everywhere. Then, for all eigenvalues of G(n,κ,p),

$$\displaystyle{ \frac{\lambda _{i}} {np}\longrightarrow \lambda _{i}(T_{\kappa }).}$$

Unlike in the empirical spectral distribution under this scaling, most of the normalized spectrum tends to the zero eigenvalue. The proof is based on the trace method and ideas for graph limits from Borgs–Chayes–Lovász–Sós–Vesztergombi [5]. A key ingredient is the following lemma. Let C k be a cycle on k vertices. The homomorphism densities are

$$\displaystyle{t(C_{k},G) = \frac{\vert \mathop{\mathrm{Hom}}\nolimits (C_{k},G)\,\vert } {(np)^{k}} \quad \text{ and }\quad t(C_{k},\kappa ) =\int \ldots \int _{\mathcal{S}}\prod _{i=1}^{k}\kappa (x_{ i},x_{i+1})\;d\mu (x_{1})\cdots d\mu (x_{k}).}$$

Lemma 9

Let κ be bounded, ɛ > 0 and G n = G(n,κ,p). Then,

$$\displaystyle{\mathbf{P}\left (\vert t(C_{k},G_{n}) - t(C_{k},\kappa )\vert>\varepsilon \right ) \leq 2\exp \left (-np \frac{\varepsilon ^{2}} {8k^{2}}\right ).}$$

4 Ongoing Work

The special case of rank 1 kernels, where κ(x, y) = ψ(x)ψ(y), is particularly interesting. In this case we have \(\Lambda (\kappa ) = \left \{\Vert \psi \Vert _{2}^{2},0\right \}\) because \(T_{\kappa }\psi (x) =\Vert \psi \Vert _{ 2}^{2}\psi (x)\), and T κ f(x) = 0, for all f ⊥ ψ.

Conjecture 10

Let κ be a rank 1, continuous (μ ⊗μ)-almost everywhere kernel. Then \(\lambda _{2} = O(\sqrt{np})\).

Theorem 8 implies that λ 2 = o(np). We are currently working on extending the method from Füredi–Komlós [8] to bound the Rayleigh quotient characterizing the second eigenvalue.