Abstract
Answer Set Programming (ASP) is a well-known problem solving approach based on nonmonotonic logic programs. Existing approaches towards integrating function terms into ASP can be organized in two classes: uninterpreted function symbols and interpreted functions; we focus on the latter. Existing approaches usually define interpreted functions in the program (e.g. using term equations), while evaluation wrt. to a pre-existing external semantics is neglected. However, this is useful if existing function libraries shall be accessed or if a function is more naturally implemented in procedural code. In this paper, we propose the declarative language of \(\textsc {hex}^{\textsc {ifu}}\) -programs which extends answer set programs (ASP) with such interpreted functions. However, rather than just providing a means for evaluating functions, it further turns interpreted functions into first-class citizens, i.e., functions are represented by accessible objects in the program. This paves the way for functionals (higher-order functions), i.e., functions that take other functions as arguments or return them. We provide then a rewriting of such programs to hex-programs, an extension of ASP with external sources, and an implementation based on this rewriting. Afterwards we present applications which motivated our work, e.g. the adoption of design pattern from software engineering. Finally, we discuss properties of the formalism and differences to related work.
This research has been supported by the Austrian Science Fund (FWF) project P27730.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Answer Set Programming (ASP) is a declarative programming paradigm based on nonmonotonic programs and a multi-model semantics [18]. For the integration of function symbols into ASP there exist basically two fairly different classes of approaches: viewing them either as uninterpreted function symbols or as interpreted functions.
The former view uses them as constructors for structuring information but with no inherent semantics. It is supported by many state-of-the-art grounders such as gringo [15] and recent releases of DLV [22]. In this case, the term \( multiply ( add (4,5),3)\) might be used to represent the computation \((4 + 5) \cdot 3\), but since all function terms have a Herbrand semantics (i.e., they evaluate to themselves), there is no way to actually evaluate the term wrt. the intended semantics. The second view is followed by some existing approaches which, however, define functions within programs with first-order-like interpretations using e.g. term equations in rule heads. This allows for detaching from Herbrand interpretations and syntactically different function terms can be equal, which yields new modeling possibilities. For instance, \( loc ( redCar ) = loc ( blueCar )\) represents that \( redCar \) and \( blueCar \) have the same location, in which case the comparison evaluates to true, while the terms would never be equal under a Herbrand semantics.
However, existing approaches do not support the call of functions whose semantics is defined outside of the logic program. Using such externally defined functions is motivated by practical observations. Some types of computations are more naturally implemented in a procedural languages, e.g. because numeric computations often lead to a large grounding. Moreover, pre-existing libraries of functions for special purposes (such as mathematical computations and physics simulations) are typically provided for procedural languages and it would be cumbersome to redefine them.
In this paper we suggest a new language, called \(\textsc {hex}^{\textsc {ifu}}\) -programs, to address this restriction. To this end, we associate function symbols with a given external semantics. However, rather than just adding a possibility to evaluate terms, it further turns interpreted functions into first-class citizens (accessible objects) that can be handled similarly as object constants and terms over uninterpreted function symbols; but at specific points, their semantics may be applied to parameters. This allows for passing them to other functions or retrieving them and paves the way for functionals (also known as higher-order functions), i.e., functions that take other functions as parameters or return them. Applications can be found in software design patterns such as the factory and the strategy pattern, accessing heterogeneous knowledge-bases via a generic interface, and typical use-cases in functional programming such as a mapping function.
\(\textsc {hex}^{\textsc {ifu}}\)-programs are based on (and further extend) hex-programs, an extension of ASP with external sources such as description logic ontologies and Web resources. hex-programs support external atoms to pass information from the logic program (given by predicate extensions and constants), to an external source, which in turn returns values to the program. For instance, the external atom  might be used to find the synonyms X of \( aircraft \), e.g. \( airplane \). However, unlike interpreted functions in \(\textsc {hex}^{\textsc {ifu}}\)-programs, external atoms in standard hex-programs are no first-class citizens and cannot be accessed as objects, which inhibits the aforementioned applications.
might be used to find the synonyms X of \( aircraft \), e.g. \( airplane \). However, unlike interpreted functions in \(\textsc {hex}^{\textsc {ifu}}\)-programs, external atoms in standard hex-programs are no first-class citizens and cannot be accessed as objects, which inhibits the aforementioned applications.
In more detail, after the preliminaries (Sect. 2), the organization of the paper and our contributions are as follows:
-
In Sect. 3 we present \(\textsc {hex}^{\textsc {ifu}}\)-programs as our main contribution. To this end, we first introduce a representation of interpreted functions by terms. Based on this, we introduce hex-programs with interpreted function (ifu-)atoms. A special case thereof are ASP programs with interpreted functions.
-
In Sect. 4 we define a rewriting of \(\textsc {hex}^{\textsc {ifu}}\)-programs to standard hex-programs. This is the basis for the implementation of a \(\textsc {hex}^{\textsc {ifu}}\)-reasoner.
-
In Sect. 5 we present applications of \(\textsc {hex}^{\textsc {ifu}}\)-programs motivated by design patterns in software engineering, existing applications of KR-formalisms, and typical applications of functionals in functional programming. We further discuss how they benefit from the features of \(\textsc {hex}^{\textsc {ifu}}\)-programs compared to standard hex-programs.
-
In Sect. 6 we discuss finiteness properties and the computational complexity of \(\textsc {hex}^{\textsc {ifu}}\)-programs. We show how a pre-existing framework for deciding finite groundability of hex-programs can also be applied to \(\textsc {hex}^{\textsc {ifu}}\)-programs. Overall, we show that important properties of hex-programs still hold for \(\textsc {hex}^{\textsc {ifu}}\)-programs.
-
In Sect. 7 we discuss related work, point out differences to our approach, conclude and give an outlook on future work.
2 Preliminaries
We recapitulate hex-programs as follows. Our alphabet consists of possibly infinite, mutually disjoint sets of constant symbols \(\mathscr {C}\) (including all integers), variables \(\mathscr {V}\), function symbols \(\mathscr {F}\), predicate symbols \(\mathscr {P}\), and external predicates \(\mathscr {X}\). We let the set of terms \(\mathscr {T}\) be the least set such that \(\mathscr {C} \subseteq \mathscr {T}\), \(\mathscr {V} \subseteq \mathscr {T}\), and \(f \in \mathscr {F}\), \(\bar{T_1}, \ldots , \bar{T_\ell } \in \mathscr {T}\) implies \(f(\bar{T_1}, \ldots , \bar{T_\ell }) \in \mathscr {T}\).Footnote 1 A term is called ground if it does not contain variables.
We start with basic concepts. A ground (ordinary) atom is of form \(p(t_1, \cdots , t_\ell )\) with predicate symbol \(p \in \mathscr {P}\) and ground terms \(t_1, \cdots , t_\ell \in \mathscr {T}\), abbreviated as \(p(\mathbf{t})\); we write \(t \in \mathbf{t}\) if \(t = t_i\) for some \(1 \le i \le \ell \). An assignment over the (finite) set \(\mathscr {A}\) of atoms is a set \(A \subseteq \mathscr {A}\), where \(a \in A\) expresses that a is true and \(a \not \in A\) that a is false. A builtin atom is of form \(t_1 \circ t_2\) with terms \(t_1, t_2 \in \mathscr {T}\) and comparison operator \(\circ \in \{ =, \not =, <, \le , \ge , > \}\). For a ground builtin atom \(t_1 \circ t_2\) and any assignment A we have that \(A \models t_1 = t_2\) if \(t_1\) is (syntactically) equal to \(t_2\) and \(A \not \models t_1 = t_2\) otherwise. Conversely, \(A \models t_1 \not = t_2\) if \(t_1\) and \(t_2\) are (syntactically) different and \(A \not \models t_1 \not = t_2\) otherwise. Operators <, \(\le \), \(\ge \) and > have the standard semantics and are defined only if \(t_1\) and \(t_2\) are integers.
We recall hex-programs, which generalize (disjunctive) logic programs under the answer set semantics [18]; for more details and background, see [12].
 hex-programs extend ASP programs by external atoms to enable a bidirectional interaction between a program and external sources. A ground external atom is of the form
hex-programs extend ASP programs by external atoms to enable a bidirectional interaction between a program and external sources. A ground external atom is of the form  , where \(\mathbf{y} = y_1, \cdots , y_k\) is a list of input parameters (predicate names or terms), called input list, and \(\mathbf{t} = t_1, \cdots , t_l\) are output terms.
, where \(\mathbf{y} = y_1, \cdots , y_k\) is a list of input parameters (predicate names or terms), called input list, and \(\mathbf{t} = t_1, \cdots , t_l\) are output terms.
Definition 1
A ground hex-program \(\varPi \) consists of rules
where each \(a_i\) is a ground ordinary atom, and each \(b_j\) is a ground ordinary, builtin or external atom; for such a rule r we let \(H(r) = \{ a_1, \ldots , a_h \}\) be its head and \(B(r) = \{ b_1, \ldots , b_m, \, \mathrm{not}\ b_{m+1}, \ldots , \, \mathrm{not}\ b_n \}\) be its body.
 In the following, assignments are over the set \(\mathscr {A}\) of ordinary atoms occurring in the program \(\varPi \) at hand. The semantics of a ground external atom
In the following, assignments are over the set \(\mathscr {A}\) of ordinary atoms occurring in the program \(\varPi \) at hand. The semantics of a ground external atom  wrt. an assignment A is given by the value of a \(1{+}k{+}l\)-ary Boolean oracle function
wrt. an assignment A is given by the value of a \(1{+}k{+}l\)-ary Boolean oracle function  that is defined for all possible values of A, \(\mathbf{y}\) and \(\mathbf{t}\). We say
that is defined for all possible values of A, \(\mathbf{y}\) and \(\mathbf{t}\). We say  is true relative to A if
is true relative to A if  , and false if
, and false if  . Satisfaction of rules and ASP programs [18] is then extended to hex-rules and programs as follows. An assignment A satisfies an atom a, denoted \(A \models a\), if \(a \in A\), and it does not satisfy it, denoted \(A \not \models a\), otherwise. It satisfies a default-negated atom \(\, \mathrm{not}\, a\), denoted \(A \models \, \mathrm{not}\, a\), if \(A \not \models a\), and it does not satisfy it, denoted \(A \not \models \, \mathrm{not}\, a\), otherwise. A rule r is satisfied under assignment A, denoted \(A \models r\), if \(A \models a\) for some \(a \in H(r)\) or \(A \not \models a\) for some \(a \in B(r)\).
. Satisfaction of rules and ASP programs [18] is then extended to hex-rules and programs as follows. An assignment A satisfies an atom a, denoted \(A \models a\), if \(a \in A\), and it does not satisfy it, denoted \(A \not \models a\), otherwise. It satisfies a default-negated atom \(\, \mathrm{not}\, a\), denoted \(A \models \, \mathrm{not}\, a\), if \(A \not \models a\), and it does not satisfy it, denoted \(A \not \models \, \mathrm{not}\, a\), otherwise. A rule r is satisfied under assignment A, denoted \(A \models r\), if \(A \models a\) for some \(a \in H(r)\) or \(A \not \models a\) for some \(a \in B(r)\).
The answer sets of a hex-program \(\varPi \) are defined as follows. Let the Faber-Leone-Pfeifer-reduct) [13], also called FLP-reduct (unrelated to functional logic programming), of \(\varPi \) wrt. an assignment A be the set \(f\varPi ^{A} = \{ r \in \varPi \mid A \models b \text{ for } \text{ all } b \in B(r) \}\) of all rules whose body is satisfied by A. We define:
Definition 2
An assignment A is an answer set of a hex-program \(\varPi \), if A is a \(\subseteq \)-minimal model of \(f\varPi ^A\).Footnote 2
Example 1
Consider the program  , where
, where  is true iff p is true. Then \(\varPi \) has the answer set \(A_1 = \emptyset \) as it is a \(\subseteq \)-minimal model of \(f \varPi ^{A_1} = \emptyset \). \(\square \)
is true iff p is true. Then \(\varPi \) has the answer set \(A_1 = \emptyset \) as it is a \(\subseteq \)-minimal model of \(f \varPi ^{A_1} = \emptyset \). \(\square \)
We also use programs with variables and consider them as shortcuts for all ground instances. The answer sets of a program \(\varPi \) with variables are defined as the answer sets of the program \( grnd (\varPi )\), which results from \(\varPi \) if all variables \(\mathscr {V}\) are substituted by all ground terms from \(\mathscr {T}\) in all possible ways. For now we assume that safety conditions guarantee the existence of a finite grounding which suffices for answer set computation and restrict our discussion to ground programs. We come back to safety in Sect. 6.
3 Interpreted Functions as First-Class Citizens
Function symbols are often uninterpreted, i.e., they are used for structuring information but have no intrinsic semantics. For instance, the term \( multiply ( add (4,5),3)\) might represent the expression \((4 + 5) \cdot 3\), but there is no way to evaluate it. Existing approaches towards interpreted functions typically define functions as part of the program, e.g. using term equations (see Sect. 7 for more details). However, the evaluation wrt. an external semantics was neglected. On the other hand, external atoms in hex-programs and VI-programs [8], have such a semantics. But unlike terms, they are not first-class citizens [6], i.e., they are not objects with an own identity that can be passed as arguments to or returned from (other) external atoms.
One might support the evaluation of ground terms under a given semantics by adopting the semantics of builtin atoms such that e.g. \(X = multiply ( add (4,5),3)\) evaluates to true if X is 27 (assuming that the semantics associated with the function symbols is as expected) and to false otherwise. However, the term \( multiply ( add (4,5),3)\) represents the application of the (unnamed) function \(\cdot (p_1,p_2,p_3) = (p_1 + p_2) \cdot p_3\) under the concrete parameters 4, 5 and 3, but not the function itself. Also the non-ground term \( multiply ( add (X,Y),Z)\) is only a shortcut for a number of evaluations of \(\cdot (p_1,p_2,p_3)\) under lists of parameters, but the function itself is not represented by an accessible object. This prohibits the composition of new functions, passing them as parameters to other functions, or retrieving them as return values. To address these restrictions, we propose an extension of hex-programs with interpreted functions featuring the following:
-
Function symbols from \(\mathscr {F}\) are associated with externally defined semantics.
-
Based on \(\mathscr {F}\), called basic functions, new functions can be composed.
-
Each basic or composed function is represented by a dedicated term t, which can be used wherever uninterpreted terms (such as constants) can also be used.
-
A term t in the program, which represents a function, can be applied to a list of parameters to compute the value of the respective function under the parameters.
We first show how functions can be represented by terms and introduce then the hex-extension of \(\textsc {hex}^{\textsc {ifu}}\)-programs.
Representing Interpreted Functions by Terms. We assume that each basic function \(f \in \mathscr {F}\) has an arity \(\ell \) and a (total) semantics function  defined for all \(\ell \)-ary vectors \(\mathbf{y} \in \mathscr {C}^\ell \) of constants. We let \(\mathscr {C}\) contain dedicated constant symbols \(\#i\) for all integers \(i \ge 1\), called placeholders, which are used to represent function parameters.
defined for all \(\ell \)-ary vectors \(\mathbf{y} \in \mathscr {C}^\ell \) of constants. We let \(\mathscr {C}\) contain dedicated constant symbols \(\#i\) for all integers \(i \ge 1\), called placeholders, which are used to represent function parameters.
We then use \(\mathscr {T}\) as function-representing (fr-)terms to turn interpreted functions into accessible objects. To this end, a ground fr-term \(t \in \mathscr {T}\) represents a \(\gamma (t)\)-ary function \(\hat{t}(p_1, \ldots , p_{\gamma (t)})\), which substitutes all occurrences \(\#i\) in t by \(p_i\), and then applies the semantics  of the function symbols f in t, where \(\gamma (t)\) is the largest i such that \(\#i\) occurs in t, or 0 if no \(\#i\) occurs. Intuitively, \(\gamma (t)\) is the number of parameters which are expected to be passed to the function represented by t.
of the function symbols f in t, where \(\gamma (t)\) is the largest i such that \(\#i\) occurs in t, or 0 if no \(\#i\) occurs. Intuitively, \(\gamma (t)\) is the number of parameters which are expected to be passed to the function represented by t.
Example 2
The fr-term \(t_1 = multiply ( add (\#1,\#2),\#3)\) represents in standard mathematical notation the function \(\hat{t_1}(p_1,p_2,p_3) = (p_1 + p_2) \cdot p_3\), assuming that the basic functions \( multiply \) and \( add \) have the expected semantics.
The fr-term \(t_2 = add (\#1, 1)\) defines the increment function \(\hat{t_2}(p_1) = p_1 + 1\) using basic function \( add \) by fixing the second operand to 1, while the first is the one of \(\hat{t_2}\). \(\square \)
It is important to note that an fr-term \(t = f(t_1, \ldots , t_\ell )\) with \(f \in \mathscr {F}\) and \(t_1, \ldots , t_\ell \in \mathscr {T}\) itself represents a (composed) function, and not the application of f to \(t_1, \ldots , t_\ell \). Instead, the subterms \(t_1, \ldots , t_\ell \) define how the function \(\hat{t}\) is composed of other functions, and constants \(\#i\) in t specify how the parameters of \(\hat{t}\) are passed to these basic functions (cf. \(t_1\) in the previous example). The actual parameters \(p_1, \ldots , p_{\gamma (t)}\) of \(\hat{t}\) are specified at the point when \(\hat{t}\) is applied as described below.
The semantics of basic functions \(f \in \mathscr {F}\) is directly defined by  . We now formalize the evaluation of the function \(\hat{t}\) given by an fr-term t under parameters \(p_1, \ldots , p_{\gamma (t)}\) recursively on top of functions
. We now formalize the evaluation of the function \(\hat{t}\) given by an fr-term t under parameters \(p_1, \ldots , p_{\gamma (t)}\) recursively on top of functions  for all \(f \in \mathscr {F}\) as follows:
for all \(f \in \mathscr {F}\) as follows:
Definition 3
For a list of ground terms \(t, p_1, \ldots , p_{\gamma (t)}\) we let

where \(\mathbf{t}\) and \(\mathbf{t'}\) are \(\ell \)-ary vectors with \(t'_i = val ( t_i , p_1, \ldots , p_{\gamma (t)})\) for all \(1 \le i \le \ell \).
The idea is as follows. If the fr-term t representing the function \(\hat{t}\) to be evaluated is a nested term \(f(\mathbf{t})\) (first two cases), then all subterms \(\mathbf{t} = t_1, \ldots , t_\ell \), which represent functions that \(\hat{t}\) is composed of, are first recursively evaluated. The results of these evaluations are given by \(\mathbf{t'} = t'_1, \ldots , t'_\ell \). If \(\mathbf{t'}\) is free of placeholders (first case), then the semantics of the outermost basic function f is applied. Due to functionals (shown in more detail in Example 8), the return value of  may contain further functions that must be interpreted, which is why we recursively apply \( val \) to the result. Otherwise (second case), the functional term \(f(\mathbf{t'})\) contains at least one placeholder and is returned as an fr-term representing a new function. For non-nested terms, placeholders are replaced by the respective parameters (third case), and all other constants are kept (fourth case).
may contain further functions that must be interpreted, which is why we recursively apply \( val \) to the result. Otherwise (second case), the functional term \(f(\mathbf{t'})\) contains at least one placeholder and is returned as an fr-term representing a new function. For non-nested terms, placeholders are replaced by the respective parameters (third case), and all other constants are kept (fourth case).
Example 3
(cont’d). Reconsider the functional term \(t = multiply ( add (\#1,\#2),\#3)\) and suppose \(\hat{t}\) is to be evaluated under parameters 4, 5 and 3, i.e., we compute \( val (t, 4, 5, 3)\).
We recursively evaluate the subterms \(t_1 = add (\#1,\#2)\) and \(t_2 = \#3\) of t under 4, 5, 3. To this end, we determine \(t_1' = val ( add (\#1,\#2), 4, 5, 3)\) and \(t_2' = val (\#3, 4, 5, 3)\). The former is recursively evaluated by computing \( val (\#1, 4, 5, 3) = 4\), \( val (\#2, 4, 5, 3) = 5\) and evaluating  . The latter yields \(t_2' = val (\#3, 4, 5, 3) = 3\).
. The latter yields \(t_2' = val (\#3, 4, 5, 3) = 3\).
Finally, since none of \(t_1', t_2'\) contains placeholders, we evaluate  , and thus we have \( val (t, 4, 5, 3) = 27\). \(\square \)
, and thus we have \( val (t, 4, 5, 3) = 27\). \(\square \)
Beginning from the deepest nesting level, \( val (\cdot )\) evaluates the functions \(\hat{t}\) is composed of recursively but stops if some \(\#i\) occur. Functions with a smaller nesting level than the placeholder remain uninterpreted until their parameters are specified. Although pre-existing placeholders in t are replaced during evaluation, new placeholders may be introduced by \(p_1, \ldots , p_\ell \).
Example 4
Consider \(t = add (\#1, 1)\) and suppose \(\hat{t}\) is evaluated under \(p_1 = add (\#1, \#2)\). Then \(t' = val (t, p_1) = add ( add (\#1, \#2), 1)\) represents the new function \(\hat{t'}(p_1, p_2) = (p_1 + p_2) + 1\) with two parameters that returns the increment of their sum. The fr-term \(t'\) can then be used to apply \(\hat{t'}\) to parameters, e.g. \( val (t', 10, 20) = 31\). \(\square \)
Programs with Interpreted Functions. Next, we need a means for applying functions given by fr-terms to parameters, i.e., for accessing \( val (\cdot )\) from the program. To this end, we introduce interpreted function (ifu-)atoms, whose syntax is inspired by builtin atoms:
Definition 4
An interpreted function (ifu-)atom is of kind \(\bar{R}=_{\$}\bar{T}[\bar{P_1}, \ldots , \bar{P_\ell }]\), where \(\bar{R} \in \mathscr {T}\) is a comparison operand, \(\bar{T} \in \mathscr {T}\) is an fr-term, and \(\bar{P_1}, \ldots , \bar{P_\ell } \in \mathscr {T}\) are parameters.
Here, the subscript \(_\$\) of the comparison operator is used to distinguish an ifu-atom from equality builtin atoms. While builtin atoms over \(=\) compares terms syntactically, \(=_{\$}\) evaluates the term on the right-hand side before comparison. We have that \(\bar{R}\), \(\bar{T}\), \(\bar{P_1}, \ldots , \bar{P_\ell }\) are possibly non-ground to allow exploiting the ASP grounder.
Informally, a ground ifu-atom \(r=_{\$}t[p_1, \ldots , p_{\gamma (t)}]\) is intended to be true iff r is equal to the value of the function represented by fr-term t under parameters \(p_1, \ldots , p_{\gamma (t)}\) holds. Based on Definition 3 we define:
Definition 5
A ground ifu-atom a of form \(r=_{\$}t[t_1, \ldots , t_n]\) is true wrt. assignment A, denoted \(A \models a\), if \(n = \gamma (t)\) and r has the value of \( val (t, t_1, \ldots , t_n)\), and false, denoted \(A \not \models a\), otherwise.
Example 5
The ifu-atom \(X =_{\$} add (\#1, 1)[Y]\) applies the increment function, represented by the fr-term \( add (\#1, 1)\), to the parameter Y and compares the result with X. \(\square \)
Note that because functions are represented by terms, an ifu-atom contains a pair of parentheses (from the fr-term) followed by a pair of brackets (from the parameter list). However, as we will see in the next example, using ASP variables as fr-term conceals the parentheses, which results in a syntax similar to standard mathematical notation. We formalize hex-programs with ifu-atoms as follows:
Definition 6
A hex-program with interpreted functions ( \(\textsc {hex}^{\textsc {ifu}}\) ) is a hex-program, where rule bodies may contain ifu-atoms.
The notions of models of rules/programs and of answer sets carry over.
Example 6
Consider the fact \( compInitials ( concat ( first (\#1), first (\#2))) \leftarrow \). The fr-term in the extension of \( compInitials \) represents a function that constructs a person’s initials from given first and last names. The function is based on the basic functions \( concat \) and \( first \) for string concatenation and extracting the first character of a string, respectively. If facts of kind \( person (F, L) \leftarrow \) represent persons with first name F and last name L, the rule \( initials (F, L, I) \leftarrow person (F, L), compInitials (C), I=_{\$}C[F, L]\) computes the initials of all persons by applying the function, which is accessible via C, to the parameters.
As the example demonstrates, terms that represent interpreted functions are accessible from the extension of predicates. That is, an fr-term t occurs as parameters of an atom of kind \( f (t) \leftarrow \). The application of the function to a list \(\mathbf{p}\) of parameters is then possible using a rule of kind \( res (T) \leftarrow f(T), R=_{\$}T[\mathbf{p}]\).
4 Implementation of Interpreted Functions Using hex-Programs
We realized \(\textsc {hex}^{\textsc {ifu}}\)-programs on top of standard hex-programs using a rewriting. The basic idea is to pass a ground fr-term t and \(\gamma (t)\) parameters to a dedicated external atom  , which resembles the function \( val (\cdot )\) from Definition 3 by substituting each placeholder \(\#i\) for the i-th argument \(p_i\) and recursively evaluating subterms.
, which resembles the function \( val (\cdot )\) from Definition 3 by substituting each placeholder \(\#i\) for the i-th argument \(p_i\) and recursively evaluating subterms.
For each integer n, let  be the semantics of an external predicate
be the semantics of an external predicate  which has as input a term t with \(n=\gamma (t)\) and parameter values \(p_1, \ldots , p_n\), and returns the value of the function term in r; as the number of parameters is also visible from the parameter list, we drop the subscript \(_n\) from
which has as input a term t with \(n=\gamma (t)\) and parameter values \(p_1, \ldots , p_n\), and returns the value of the function term in r; as the number of parameters is also visible from the parameter list, we drop the subscript \(_n\) from  in the following.
in the following.
Definition 7
For an assignment A and list of ground terms \(t, p_1, \ldots , p_n\) s.t. \(\gamma (t) = n\), let  where \(\sigma = \mathbf {T}\) if \(r = val ( t , p_1, \ldots , p_n)\) and \(\sigma = \mathbf {F}\) otherwise.
where \(\sigma = \mathbf {T}\) if \(r = val ( t , p_1, \ldots , p_n)\) and \(\sigma = \mathbf {F}\) otherwise.
The oracle function \( f_{ \& { eval }}\) may access semantics functions  of all basic functions \(f \in \mathscr {F}\). This allows for translating \(\textsc {hex}^{\textsc {ifu}}\)-programs to standard hex-programs:
of all basic functions \(f \in \mathscr {F}\). This allows for translating \(\textsc {hex}^{\textsc {ifu}}\)-programs to standard hex-programs:
Definition 8
The translation of an ifu-atom a of kind \(\bar{R}=_{\$}\bar{T}[\bar{P_1}, \ldots , \bar{P_\ell }]\) to an external atom is given by  .
.
For \(\textsc {hex}^{\textsc {ifu}}\)-program \(\varPi \), we let \(\tau (\varPi )\) be \(\varPi \) after replacing each ifu-atom a by \(\tau (a)\).
We demonstrate the translation with the following example:
Example 7
(cont’d). Reconsider the fr-term \(t= concat ( first (\#1), first (\#2))\). Then \(N=_{\$}t[ tom , johnson ]\) is translated to  . This external atom is true for \(N = tj \) and false otherwise. \(\square \)
. This external atom is true for \(N = tj \) and false otherwise. \(\square \)
This translation is sound and complete wrt. the semantics given by Definition 5.
Proposition 1
An assignment A is an answer set of a \(\textsc {hex}^{\textsc {ifu}}\)-program \(\varPi \) if an only if it is an answer set of the hex-program \(\tau (\varPi )\).
Interpreted functions have been implemented in the dlvhex solver, cf. http://www.kr.tuwien.ac.at/research/systems/dlvhex. The syntax is as in this paper, with \(=_{\$}\) written as  . The system comes with several examples with interpreted functions.
. The system comes with several examples with interpreted functions.
5 Applications of \(\textsc {hex}^{\textsc {ifu}}\)-Programs
We now present several applications of \(\textsc {hex}^{\textsc {ifu}}\)-programs. For each of them, we show how they benefit from the features of \(\textsc {hex}^{\textsc {ifu}}\)-programs compared to standard hex-programs.
Software Design Patterns. Our main motivation for \(\textsc {hex}^{\textsc {ifu}}\)-programs were functionals. They can be used to realize programming methods motivated by design patterns in software engineering, cf. e.g. [14]. An example is the abstract factory pattern which uses a factory class F for creating objects of one of several concrete classes \(C_1, \ldots , C_n\) which implement the same interface C. Instead of instantiating one of \(C_1, \ldots , C_n\) directly, the decision which class to instantiate is delegated to factory F. The client retrieves only a reference of type C and uses it abstractly without knowing (and caring) which of the concrete types \(C_1, \ldots , C_n\) the reference refers to.
Similarly, functionals in \(\textsc {hex}^{\textsc {ifu}}\)-programs allow for retrieving a function from an external atom that can later be used without knowing its exact type.
Example 8
Consider function \( getHashFunction ()\) that serves as a factory and returns a unary function, which is unknown to the implementer of the hex-program but still has an associated semantics that can be applied. Then \(r(H) \leftarrow F=_{\$} getHashFunction ()[], H=_{\$}F( padl )\) evaluates \( getHashFunction ()\) (without parameters) to retrieve a concrete hash function F, which is subsequently applied to compute the hash value H of \( padl \). \(\square \)
A similar example is the strategy pattern, where the algorithm/technique to be applied is selected at runtime based on the data at hand. For instance, a validation to be performed for incoming data usually depends on the type of the data. As a concrete example, consider matching strings against regular expressions. The regular expression for checking phone numbers is clearly different from one for checking email addresses. In such cases, the selection of an appropriate validation function can be done by a dedicated function  which implements the logic of the decision, i.e., the construction of an appropriate regular expression, depending on the \( type \in \{ phone , email , url , \ldots \}\) of the given data. The concrete verification function returned by the selection function can then be applied to a \( value \):
which implements the logic of the decision, i.e., the construction of an appropriate regular expression, depending on the \( type \in \{ phone , email , url , \ldots \}\) of the given data. The concrete verification function returned by the selection function can then be applied to a \( value \):
Example 9
Suppose  returns a function V for verifying data of the given \( type \). Provided that the returned verification functions evaluate to 1 if the check is passed and to 0 otherwise, a concrete \( value \) is verified by the ifu-atom \(1=_{\$}V( value )\).
returns a function V for verifying data of the given \( type \). Provided that the returned verification functions evaluate to 1 if the check is passed and to 0 otherwise, a concrete \( value \) is verified by the ifu-atom \(1=_{\$}V( value )\).
Suppose employee data is given by facts of form \( emp ( id , attType , attValue )\), where \( id \) is a unique identifier for each employee, and \( attType \) and \( attValue \) specify the value of a certain attribute. For example, \( emp ( 3 , firstname , john )\) defines that the first name of employee 3 is \( john \). In the following, \(r_1\) imports a verification function for each attribute type specified for at least one employee and \(r_2\) applies it to all values of this type.

The program derives \( invalid ( id )\) for all identifiers \( id \) of employee with invalid entries.
Benefits: Without functionals and interpreted functions as accessible objects, one must implement separate validation rules for all attribute type, which differ only in the external atom which performs the evaluation, but be of the same structure otherwise. This would introduce redundancies which make it more cumbersome to maintain the program. \(\square \)
Integrating Heterogeneous Knowledge Bases. Another example is the integration of multiple data sources which are possibly implemented in different formalisms, as realized e.g. by multi-context systems [5]. A functional can serve as a central dictionary that supports lookups of concrete knowledge-bases with a common query interface. Lookups are then answered with functions that allow for accessing the concrete knowledge-base abstractly without knowing its type and location.
Example 10
For instance, suppose \( lookup (\#1)\) provides access to the central dictionary and is accessible via predicate l. Then rule \( data (A) \leftarrow l(D), K=_{\$}D[ employee ], A=_{\$}K[ query ]\) can be used to answer queries over the \( employee \) knowledge-base using the access function D, which returns an abstract knowledge-base K that can be used to answer queries without knowing its type.
Benefits: As above, without functionals separate rules of the same basic structure must be defined for each type of knowledge-based, which differ only in the external atom. \(\square \)
Realizing Traditional Higher-order Functions. Also typical (generic) higher-order functions known from functional programming can be realized on top of \(\textsc {hex}^{\textsc {ifu}}\). These include, e.g., map for applying a custom function to all elements from a list, fold for aggregating values in a data structure, or sort with a custom comparison function.
Example 11
Consider the external atom  which applies function f, given as an fr-term, to all elements in the extension of predicate p and the function for computing a person’s initials as shown in Example 6. Then the rule
which applies function f, given as an fr-term, to all elements in the extension of predicate p and the function for computing a person’s initials as shown in Example 6. Then the rule  can be used to compute the initials of all persons in the extension of predicate \( person \).
can be used to compute the initials of all persons in the extension of predicate \( person \).
Benefits: Without functionals as accessible objects, one may define  where \( fn \) is the name of a function to be applied to p. However, all functions identified by such names must be known to the implementation of
where \( fn \) is the name of a function to be applied to p. However, all functions identified by such names must be known to the implementation of  and are not arbitrary. \(\square \)
and are not arbitrary. \(\square \)
Syntax Relaxation. Finally, interpreted function symbols are also a more natural alternative for external atoms with functional behavior such as string functions (concatenation, substring, etc.). The syntax is lightweight and similar to builtin atoms.
Discussion. While it is possible to simulate functionals by standard hex-programs if all involved external sources are provided by the implementer of the hex-program, this is in general not the case. For instance, Example 8 can be implemented such that not the hash function but only its name N is imported into the program. Consider the modified rule  . The name of the hash function N is passed to a dedicated external atom
. The name of the hash function N is passed to a dedicated external atom  , which internally selects the function identified by N and applies it to the given string. Now N plays the role of F from Example 8, but is instantiated with a string instead of an fr-term. The parameters of
, which internally selects the function identified by N and applies it to the given string. Now N plays the role of F from Example 8, but is instantiated with a string instead of an fr-term. The parameters of  do not contain fr-terms but only object constants, i.e.,
do not contain fr-terms but only object constants, i.e.,  is not a functional. However, now
is not a functional. However, now  must be aware of all possible hash functions; if a new one is added, the external source
must be aware of all possible hash functions; if a new one is added, the external source  must be modified. This is impractical if the function to be passed as argument and the functional itself are provided by different third parties, or if one is provided by a third party and the other one is newly developed. Then the programmer cannot modify the sources and moving functionality from one source to the other is not possible. Also if the set of possible functional parameters is unrestricted, such as for
must be modified. This is impractical if the function to be passed as argument and the functional itself are provided by different third parties, or if one is provided by a third party and the other one is newly developed. Then the programmer cannot modify the sources and moving functionality from one source to the other is not possible. Also if the set of possible functional parameters is unrestricted, such as for  , simulating functionals by a standard function is not possible, as it would need to be prepared for an infinite number of possible functions.
, simulating functionals by a standard function is not possible, as it would need to be prepared for an infinite number of possible functions.
6 Properties of \(\textsc {hex}^{\textsc {ifu}}\)-Programs
We now investigate relations to programs with uninterpreted function symbols, finiteness and computational properties of \(\textsc {hex}^{\textsc {ifu}}\)-programs.
Relations to Uninterpreted Function Symbols. One can show that ASP- or hex-programs with uninterpreted functions amount to a special case of \(\textsc {hex}^{\textsc {ifu}}\)-programs, where each function term is interpreted by itself.
Proposition 2
Let \(\varPi \) be a hex-program and let \(\varPi '\) be the \(\textsc {hex}^{\textsc {ifu}}\)-program resulting from \(\varPi \) if each builtin atom \(x \circ y\) is replaced by \(x =_{\$} y\) and  for all function symbols f and \(\mathbf{y} \in \mathscr {C}^{\gamma (f)}\). Then the answer sets of \(\varPi \) and \(\varPi '\) coincide.
for all function symbols f and \(\mathbf{y} \in \mathscr {C}^{\gamma (f)}\). Then the answer sets of \(\varPi \) and \(\varPi '\) coincide.
Finite Groundability. We call a program \(\varPi \) finitely groundable if there is a finite \(\varPi ' \subseteq grnd (\varPi )\) s.t. \(\varPi \) and \(\varPi '\) have the same answer sets. In this case, it is implied that all answer sets are also finite. For uninterpreted function symbols, several safety concepts have been introduced which allow for deciding finite groundability. For instance, the notion of \(\omega \)-restricted logic programs, which hinges on predicate dependencies, allows function symbols under a level mapping to control the introduction of new terms with function symbols to ensure decidability [29]. More expressive variants thereof are \(\lambda \)-restricted [17], argument-restricted programs [23] and bounded programs [19]. For an overview of classes of programs with uninterpreted function symbols, cf. e.g. [1].
However, since we consider interpreted functions, these notions are not directly applicable. A \(\textsc {hex}^{\textsc {ifu}}\)-program might be finitely groundable, while it is not finitely groundable if functions are left uninterpreted, or vice versa.
Example 12
Consider the \(\textsc {hex}^{\textsc {ifu}}\)-program \(\varPi = \{ p(a); \ p(Y) \leftarrow p(X), Y =_{\$} id (X) \}\) where \( id \) is an interpreted function s.t.  for all terms \(t \in \mathscr {T}\). Its only answer set is \(A = \{ p(a) \}\). In contrast, if \( id \) is considered as an uninterpreted function symbol as in \(\varPi ' = \{ p(a); \ p(Y) \leftarrow p(X), Y = id (X) \}\), then there is no finite grounding as the rule derives infinitely many atoms of form \(p( id ^n(a))\) for all \(n \ge 0\). \(\square \)
for all terms \(t \in \mathscr {T}\). Its only answer set is \(A = \{ p(a) \}\). In contrast, if \( id \) is considered as an uninterpreted function symbol as in \(\varPi ' = \{ p(a); \ p(Y) \leftarrow p(X), Y = id (X) \}\), then there is no finite grounding as the rule derives infinitely many atoms of form \(p( id ^n(a))\) for all \(n \ge 0\). \(\square \)
Conversely, it can also happen that a hex-program with uninterpreted function symbols is finitely groundable, but after assigning a semantics to the functions it is not.
Example 13
Consider the hex-program \(\varPi = \{ a \leftarrow 2= inc (1); \ int (X) \leftarrow a, X > 0 \}\). Then its only answer set is \(A = \emptyset \) because \(2= inc (1)\) is false, thus a is unsupported and the rule \( int (X) \leftarrow a, X > 0\) is never applicable. However, if function \( inc \) is interpreted with  for all \(n \ge 0\), as in the \(\textsc {hex}^{\textsc {ifu}}\)-program
for all \(n \ge 0\), as in the \(\textsc {hex}^{\textsc {ifu}}\)-program  , then \(2=_{\$} inc (1)\) is always true, a is derived and \( int (X) \leftarrow a, X > 0\) derives infinitely many atoms, i.e., \(\varPi '\) is not finitely groundable. \(\square \)
, then \(2=_{\$} inc (1)\) is always true, a is derived and \( int (X) \leftarrow a, X > 0\) derives infinitely many atoms, i.e., \(\varPi '\) is not finitely groundable. \(\square \)
Because interpreted functions are closely related to external atoms, as evidenced by our rewriting, it is appropriate to reuse concepts for hex-programs. The liberal safety framework [11] is defined for hex-programs and derives finite groundability of programs based on its syntactic structure and semantic properties of external atoms, where the latter are asserted by the provider of an external source. Such properties are, e.g., the existence of a well-ordering (the output of an external source is no greater than its input according to some ordering), monotonicity/antimonotonicity, and finite domains of external atoms.
Example 14
 . Without any knowledge about the semantics of the external atom
. Without any knowledge about the semantics of the external atom  , the program potentially introduces infinitely many new values because e is involved in a cycle, finitely groundability is not guaranteed. However, if the output domain of e is known to be finiteFootnote 3, then the framework identifies the program as finitely groundable. \(\square \)
, the program potentially introduces infinitely many new values because e is involved in a cycle, finitely groundability is not guaranteed. However, if the output domain of e is known to be finiteFootnote 3, then the framework identifies the program as finitely groundable. \(\square \)
For a \(\textsc {hex}^{\textsc {ifu}}\)-program \(\varPi \), the basic idea is to apply the framework to the hex-program \(\tau (\varPi )\). Known properties of basic functions are exploited similarly as for external atoms. Equivalence of \(\varPi \) and \(\tau (\varPi )\) wrt. answer sets establishes then the following result.
Proposition 3
A \(\textsc {hex}^{\textsc {ifu}}\)-program \(\varPi \) is finitely groundable iff \(\tau (\varPi )\) is finitely groundable.
Due to the result, convenient finiteness properties of hex-programs carry over to \(\textsc {hex}^{\textsc {ifu}}\)-programs.
Computational Complexity. For the computational aspect, one can first observe that unlike external atoms, ifu-atoms can only have input terms but no input predicates. Therefore, ifu-atoms can be evaluated once the program’s grounding is available, but there is no need for interleaving this process with model building.
In the following, we assume that the program at hand is finitely groundable and analyze the complexity wrt. the program’s grounding. This is because the grounding size depends on the semantics of the involved basic functions and, unlike ordinary ASP, one cannot specify an upper bound for the size of the grounding in terms of the size of the original program. For example, consider the rule \(p(Y) \leftarrow inc (I), p(X), Y =_{\$}I(X)\), where \( inc ( min ( add (\#1, 1), lim (c))) \leftarrow \) defines a bounded increment function. That is, the function increments parameter \(\#1\) up to a certain limit, which is given by the unary basic function \( lim (c)\). Obviously, the limit for the increment function, and thus the size of the grounding of \(\varPi \), depends on the value of \( lim (c)\).
In contrast to complexity results for hex-programs [12], we cannot reasonably restrict the Herbrand universe to be finite as this contradicts the idea of functionals which may introduce new functions. Instead, we can only rely on safety conditions (see above) which ensure that the grounding has a finite, but otherwise arbitrary size.
Then, if we assume that all functions have complexities in C, one can then show that complexity results of ordinary ASP [9] carry over to \(\textsc {hex}^{\textsc {ifu}}\)-programs:
Proposition 4
Deciding if a ground \(\textsc {hex}^{\textsc {ifu}}\)-program \(\varPi \) has an answer set is in \(C \circ \Sigma ^P_2\) in general and in \(C \circ NP \) if \(\varPi \) is disjunction-free.
Here, \(C \circ \Sigma ^P_2\) denote that the problem is decidable using the power of classes C and \(\Sigma ^P_2\) in sequence. Note that either of the two classes might dominate the overall complexity. For instance, \(C \circ \Sigma ^P_2\) reduces to \(\Sigma ^P_2\) if \(C = P\). Similarily for \(C \circ NP \).
Since deciding consistency of a ground hex-program is \((\Sigma ^P_2)^C\)-complete where C is the complexity of the external atoms [12], we conclude that \(\textsc {hex}^{\textsc {ifu}}\)-programs are potentially even easier but not harder, i.e., positive properties of hex-programs carry over.
7 Related Work and Conclusion
Related Work. We give an overview of existing approaches towards function terms with non-Herbrand semantics. They all have in common that the semantics is not given by an external theory but rather defined as part of the program and that none of the following approaches allows for accessing functions as first-class citizens.
The idea of integrating functions and logic programs is related to the field of functional logic programming (FLP), cf. [20, 21] for an overview. However, this integration aims at a tighter coupling of the two declarative paradigms, for instance by defining functions as equality clauses within the logic program. For example, the facts \( append ([],L) = L \leftarrow \) and \( append ([E|R],L) = [E| append (R,L)] \leftarrow \) might be used to define a list concatenation function. Arithmetic operators are allowed in some approaches such as [2]. This allows for identifying syntactically different terms as semantically equivalent. Functions defined in this way are then applied similarly as in term rewriting systems (cf. narrowing). However, FLP integrates features of functional programming directly into logic programs, while our approach aims at using externally defined functions within the program. Although our approach also supports the construction of new functions in the logic program, this works by composition of existing functions rather than equality clauses (cf. Example 4).
Intensional function symbols detach from Herbrand interpretations and use rules to define functions by other functions or predicates, cf. [3, 7, 24]. For instance, \( loc (X) = garage \leftarrow car (X), \, \mathrm{not}\, loc (X) \not = garage \) expresses that cars are in the garage by default. Although relations to ASP modulo theories and to SMT are identified, cf. [4], this analysis is limited to specific theories (e.g., arithmetics).
A different kind of approaches define functions as part of the program’s first-order-like interpretations, cf. e.g. [25, 26]. For instance, if \( color (n)\) represents the color of node n, the constraint \(\leftarrow edge (X,Y), color (X) \not = color (Y)\) represents that adjacent nodes have different colors. When computing the reduct of the program wrt. an interpretation, function terms are evaluated and replaced by the value of the function. As a consequence, the evaluation is a strictly non-recursive process. However, the possibility to evaluate a function term to a constant is similar as in our approach. The approach corresponds to the previously developed one by [26], as proven in [7]. The definition of the function \( color (\cdot )\) is part of the program’s answer.
HiLog-programs have a second-order syntax which allow arbitrary terms to occur as predicate names [27]. For instance, the program \(P = \{ closure (R)(X,Y) \leftarrow R(X,Y); \ closure (R)(X,Z) \leftarrow R(X,Y), closure (R)(Y,Z) \}\) defines the transitive closure of arbitrary relations R. In another rule, the closure of a concrete relation \( edge \) can be accessed using a HiLog literal of for \( closure ( edge )(X,Y)\). However, the semantics of HiLog is actually first-order, as evidenced by a translation of HiLog-programs to normal programs. To this end, general terms which are used as predicates are represented by standard predicates and function symbols. For instance, \( closure (R)(X,Y)\) is represented by \( call (u_3(u_2( closure , R), X, Y))\). The idea of using terms such as \( closure (R)\) to represent functions which depend on other functions is similar to our fr-terms, but relations and functions are defined within the program rather than externally.
The grounder gringo provides an interface which supports calls to functions written in the scripting language LuaFootnote 4 before grounding, after a model has been found, and after termination [16]. However, unlike in \(\textsc {hex}^{\textsc {ifu}}\)-programs, calls to such functions are constrained to happen only at specific evaluation phases and is not interleaved with model building. Also the use of functions as first-class citizens is not possible.
Last but not least, some reasoners such as DLV support pre-defined interpreted functions, e.g. for list processing (appending elements, retrieving the head element, etc.). However, the set of supported functions is fixed and hard-wired within the reasoner, while custom external functions are not supported. The same is true for well-known aggregate functions.
Uninterpreted function symbols are supported by ASP systems such as the grounder gringo [15] and recent releases of DLV [22]. Previous research often focused on the identification of classes of programs for which reasoning tasks, such as answer set computation or query answering, are decidable, cf. e.g. [1]. External sources as in hex-programs were exploited in context of uninterpreted function symbols for the composition and decomposition of nested function terms, cf. [8, 10]. However, the function symbols themselves do not have an externally defined semantics. In terms of our notation, the external predicates  with k input and 1 output parameter, and
with k input and 1 output parameter, and  with 1 input and k output parameters for each \(k \ge 0\) are used for composing and decomposing function terms. To this end,
with 1 input and k output parameters for each \(k \ge 0\) are used for composing and decomposing function terms. To this end,  with \(v=\mathbf {T}\) if \(x=f(t_1,\ldots ,t_k)\) and \(v=\mathbf {F}\) otherwise. However, all external predicates had fixed purposes and function symbols where not given a semantics.
with \(v=\mathbf {T}\) if \(x=f(t_1,\ldots ,t_k)\) and \(v=\mathbf {F}\) otherwise. However, all external predicates had fixed purposes and function symbols where not given a semantics.
Discussion. While having externally defined functions is central to our approach and motivated by practical observations (need for accessing pre-existing libraries, more natural or efficient implementation of some types of computations which invonve numeric computations, etc.), our approach can in principle also be instantiated in such a way that functions can be defined within the program, similarily to other approaches. To this end, one can pre-define a fixed set of basic functions which suffice to construct arbitrary functions (or at least arbitrary functions from a certain domain) by composition.Footnote 5
Conclusion. We introduced \(\textsc {hex}^{\textsc {ifu}}\)-programs, i.e., logic programs with interpreted functions. In contrast to existing approaches towards interpreted functions and also in contrast to hex-programs, the new approach paves the way for functionals, i.e., functions that take other functions as parameters or return them.
However, rather than functional logic programming (cf. e.g. [20, 21]), we do not aim at a tight integration of the two paradigms which allows for defining functions as part of the program, but rather at evaluating externally defined functions. Our approach is in particular flexible as it turns functions into objects that are accessible in the program.
Currently, interpreted functions are either externally defined basic functions or compositions thereof. Future work may include the support for additional means for defining new functions such as currying [28], i.e., the translation of a function \(f:D_1 \times \cdots \times D_n \rightarrow R\) with n parameters into a function \(f':D_1 \rightarrow (D_2 \rightarrow (\cdots (D_n \rightarrow R)))\) with one parameter that returns another function in the remaining \(n-1\) parameters. Also the support for functions with predicate parameters, such as supported by external atoms, is an interesting starting point. Finally, while we focused on functions in this work, also external atoms with non-functional behavior might be turned into first-class citizens. Both of the last two ideas might be realized based on parameters resp. return values whose domain consists of sets of elements.
Notes
- 1.
We let \(\bar{T}\) denote a meta-variable (not to be confused with ASP variables in the object language) which represents a constant from \(\mathscr {C}\), an ASP variable from \(\mathscr {V}\), or a ground or non-ground functional terms (e.g. f(a), g(X)).
- 2.
For ordinary \(\varPi \), these are Gelfond & Lifschitz’s answer sets.
- 3.
The external atom
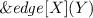 is intended to return the neighbors Y of X in a fixed finite graph, thus \(\varPi \) computes the nodes which are reachable from a given start node s.
is intended to return the neighbors Y of X in a fixed finite graph, thus \(\varPi \) computes the nodes which are reachable from a given start node s. - 4.
- 5.
To see that this is always possible, let \( runTM (m, i)\) be a function which maps the definition of a turing machine m and an input string i to the tape content after the machine encoded by m under input i terminates. Then any function \(f(\mathbf{x})\) can be defined as \( runTM (m_f, i)\), where i encodes arguments \(\mathbf{x}\) and \(m_f\) is a turing machine which computes f.
References
Alviano, M., Calimeri, F., Ianni, G., Faber, W., Leone, N.: Function symbols in ASP: overview and perspectives 31 (2011)
Balduccini, M.: ASP with non-herbrand partial functions: a language and system for practical use. TPLP 13(4–5), 547–561 (2013)
Bartholomew, M., Lee, J.: Stable models of formulas with intensional functions. In: Proceedings of International Conference on Principles of Knowledge Representation and Reasoning KR, pp. 2–12 (2012)
Bartholomew, M., Lee, J.: Functional stable model semantics and answer set programming modulo theories. In: Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, IJCAI 2013, pp. 718–724. AAAI Press (2013)
Brewka, G., Roelofsen, F., Serafini, L.: Contextual default reasoning. In: Proceedings of the Twentieth International Joint Conference on Artificial Intelligence (IJCAI 2007), January 6–12, 2007, Hyderabad, India (2007)
Burstall, R.: Christopher strachey-understanding programming languages. Higher-Order Symbolic Comput. 13(1), 51–55 (2000)
Cabalar, P.: Functional answer set programming. CoRR abs/1006.3678. http://arxiv.org/abs/1006.3678(2010)
Calimeri, F., Cozza, S., Ianni, G.: External sources of knowledge and value invention in logic programming. Ann. Math. Artif. Intell. 50(3–4), 333–361 (2007)
Dantsin, E., Eiter, T., Gottlob, G., Voronkov, A.: Complexity and expressive power of logic programming. ACM Comput. Surv. 33(3), 374–425 (2001)
Eiter, Thomas, Fink, Michael, Krennwallner, Thomas, Redl, Christoph: hex-programs with existential quantification. In: Hanus, Michael, Rocha, Ricardo (eds.) WLP 2013. LNCS (LNAI), vol. 8439, pp. 99–117. Springer, Cham (2014). doi:10.1007/978-3-319-08909-6_7
Eiter, T., Fink, M., Krennwallner, T., Redl, C.: Domain expansion for ASP-programs with external sources. Artif. Intell. 233, 84–121 (2016)
Eiter, T., Ianni, G., Schindlauer, R., Tompits, H.: A uniform integration of higher-order reasoning and external evaluations in answer-set programming. In: IJCAI, pp. 90–96. Professional Book Center (2005)
Faber, W., Leone, N., Pfeifer, G.: Semantics and complexity of recursive aggregates in answer set programming. Artif. Intell. 175(1), 278–298 (2011)
Gamma, E., Helm, R., Johnson, R., Vlissides, J.: Design Patterns: Elements of Reusable Object-oriented Software. Addison-Wesley Longman Publishing Co. Inc., Boston (1995)
Gebser, M., Kaminski, R., König, A., Schaub, T.: Advances in gringo series 3. In: Delgrande, J.P., Faber, W. (eds.) LPNMR 2011. LNCS (LNAI), vol. 6645, pp. 345–351. Springer, Heidelberg (2011). doi:10.1007/978-3-642-20895-9_39
Gebser, M., Kaufmann, B., Kaminski, R., Ostrowski, M., Schaub, T., Schneider, M.: Potassco: the potsdam answer set solving collection. AI Commun. 24(2), 107–124 (2011)
Gebser, M., Schaub, T., Thiele, S.: GrinGo: a new grounder for answer set programming. In: Baral, C., Brewka, G., Schlipf, J. (eds.) LPNMR 2007. LNCS (LNAI), vol. 4483, pp. 266–271. Springer, Heidelberg (2007). doi:10.1007/978-3-540-72200-7_24
Gelfond, M., Lifschitz, V.: Classical negation in logic programs and disjunctive databases. New Gener. Comput. 9(3–4), 365–386 (1991)
Greco, S., Molinaro, C., Trubitsyna, I.: Bounded programs: A new decidable class of logic programs with function symbols. In: Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence (IJCAI 2013), pp. 926–931. AAAI Press (2013)
Hanus, M.: Multi-paradigm declarative languages. In: Dahl, V., Niemelä, I. (eds.) ICLP 2007. LNCS, vol. 4670, pp. 45–75. Springer, Berlin (2007). doi:10.1007/978-3-540-74610-2_5
Hanus, M.: The integration of functions into logic programming: From theory to practice. J. Logic Program. 1920, Supplement 1, 583–628 , special Issue: Ten Years of Logic Programming (1994)
Leone, N., Pfeifer, G., Faber, W., Eiter, T., Gottlob, G., Perri, S., Scarcello, F.: The DLV system for knowledge representation and reasoning. ACM TOCL 7(3), 499–562 (2006)
Lierler, Y., Lifschitz, V.: One more decidable class of finitely ground programs. In: Hill, P.M., Warren, D.S. (eds.) ICLP 2009. LNCS, vol. 5649, pp. 489–493. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02846-5_40
Lifschitz, V.: Logic programs with intensional functions. In: Proceedings of International Conference on Principles of Knowledge Representation and Reasoning (KR) (2012)
Lin, F., Wang, Y.: Answer set programming with functions. In: Brewka, G., Lang, J. (eds.) Proceedings of the Eleventh International Conference on Principles of Knowledge Representation and Reasoning, KR 2008, Sydney, Australia, September 16–19, 2008, pp. 454–465. AAAI Press (2008)
Pearce, D., Valverde, A.: Towards a first order equilibrium logic for nonmonotonic reasoning. In: Alferes, J.J., Leite, J. (eds.) JELIA 2004. LNCS (LNAI), vol. 3229, pp. 147–160. Springer, Berlin (2004). doi:10.1007/978-3-540-30227-8_15
Ross, K.A.: On negation in HiLog. J. Logic Program. 18(1), 206–215 (1994)
Schönfinkel, M.: Über die bausteine der mathematischen logik. Math. Ann. 92, 305–316 (1924)
Syrjänen, T.: Omega-restricted logic programs. In: Eiter, T., Faber, W., Truszczyński, M. (eds.) LPNMR 2001. LNCS (LNAI), vol. 2173, pp. 267–280. Springer, Berlin (2001). doi:10.1007/3-540-45402-0_20
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Redl, C. (2017). Extending Answer Set Programs with Interpreted Functions as First-Class Citizens. In: Lierler, Y., Taha, W. (eds) Practical Aspects of Declarative Languages. PADL 2017. Lecture Notes in Computer Science(), vol 10137. Springer, Cham. https://doi.org/10.1007/978-3-319-51676-9_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-51676-9_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-51675-2
Online ISBN: 978-3-319-51676-9
eBook Packages: Computer ScienceComputer Science (R0)





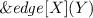 is intended to return the neighbors Y of X in a fixed finite graph, thus
is intended to return the neighbors Y of X in a fixed finite graph, thus