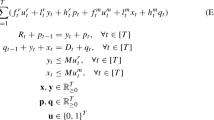Economic Lot-Sizing Problem with Remanufacturing Option: Complexity and Algorithms

Abstract

In a single item dynamic lot-sizing problem, we are given a time horizon and demand for a single item in every time period. The problem seeks a solution that determines how much to produce and carry at each time period, so that we will incur the least amount of production and inventory cost. When the remanufacturing option is included, the input comprises of number of returned products at each time period that can be potentially remanufactured to satisfy the demands, where remanufacturing and inventory costs are applicable. For this problem, we first show that it cannot have a fully polynomial time approximation scheme (FPTAS). We then provide a pseudo-polynomial algorithm to solve the problem and show how this algorithm can be adapted to solve it in polynomial time, when we make certain realistic assumptions on the cost structure. We finally give a computational study for the capacitated version of the problem and provide some valid inequalities and computational results that indicate that they significantly improve the lower bound for a certain class of instances.

1 Introduction

Remanufacturing is the process of recovering used products by repairing and replacing worn out components so that a product is created at the same quality level as a newly manufactured product saving tonnes of landfill every year by providing an environmentally friendlier alternative to classical manufacturing. It also offers industries the potential to significantly save money by exploiting used product inventories and reusing many precious raw materials that are becoming increasingly scarcer. With this motivation, we study the single item production planning problem over a finite horizon with the option of remanufacturing. Like in classical lot-sizing problem, the problem is defined over a finite planning horizon, where demand in each time period is provided as input. With the remanufacturing option, the demand can be satisfied either by manufacturing new items or remanufacturing returned items, which are also provided as input to the problem. The problem consists of separate inventory costs for carrying remanufactured items and manufactured items (sometimes referred to as serviceable inventory), and there is also a cost incurred for manufacturing or remanufacturing.

The classical lot-sizing problem was introduced in [17] by Wagner and Whitin, with a dynamic program that can solve the uncapacitated problem in polynomial time. Various variants of it have been thoroughly studied over the last 6 decades, see [1] for a recent review. Later, the capacitated version was introduced and the problem was shown to be NP-hard, see [6]. A dynamic program was provided in [5] which runs in polynomial time for unary encoding. A fully polynomial time approximation scheme (FPTAS) was provided in [9]. The problem with remanufacturing option was first studied in [8] and proved as NP-hard in [15]. A dynamic program with polynomial running time was provided for a special case of when the cost involved are time invariant and there is a joint set-up cost involved for both manufacturing and remanufacturing [14]. A polynomial time algorithm was provided when all costs are linear by solving it as a flow problem [8]. Since then, very little progress has been made for polynomial special cases.

We first show in Sect. 2 that the general case of this problem cannot have an FPTAS unless P=NP. We refer the reader to [7] for concepts about NP-hardness and [16] for concepts about FPTAS. We then provide a straightforward dynamic program for the general case that runs in pseudopolynomial time in Sect. 3. We use this dynamic program as an ingredient to design an algorithm that runs in polynomial time to solve a special case, where the inventory cost of the returned items is at least as much as the inventory cost of the manufactured items. In addition, we assume that the concave costs involved in manufacturing has a fixed cost and variable cost component. We also assume that the costs are time invariant. The algorithm and the proof would work for time varying costs but they need to increase over time. No other assumptions are required for the polynomial solvability of this special case. Finally, in Sect. 4 we study the effects of two families of valid inequalities for the capacitated version of the problem. These are based on the well known flow cover cuts and they are NP-hard to separate in general. We show that a class of polynomially separable cases of these cuts are quite effective to close the gaps down for many instances. We test them on several instances that were generated to have a gap. Creating these instances are of interest, which have substantial gaps and hence are of concern to improve performance on such instances, whereas instances with small gaps will be handled effectively by standard optimization packages.

In the single item economic lot-sizing problem with remanufacturing option (ELSR), we are given a time horizon T. For each time period $t=1\dots T$, we are given a demand $D_t$, and the amount of returned products $R_t$ that is available for remanufacturing. W.l.o.g., we assume that manufacturing and remanufacturing can be both completed for an item in a single period. We also define the following cost functions for each time period $t=1\dots T$: (1) manufacturing cost $f^m_t:T\rightarrow \mathbb {R}_{\ge 0}$, (2) remanufacturing cost $f^r_t:T\rightarrow \mathbb {R}_{\ge 0}$, (3) holding cost of manufactured items $h^m_t:T\rightarrow \mathbb {R}_{\ge 0}$, and (4) holding cost of returned items $h^r_t:T\rightarrow \mathbb {R}_{\ge 0}$. We will assume that cost could be time variant but we have a linear inventory cost and the concave cost structure associated with remanufacturing and manufacturing involves in a fixed cost and linear variable cost component, i.e., $f^i_t(x) = f^i_t + l^i_t(x)$, when $x>0$ and 0 otherwise, for $i={r,m}$. $f^r_t, f^m_t (l^r_t, l^m_t)$ are the fixed costs (variable costs) incurred in period t for remanufacturing and manufacturing respectively. We slightly abuse the notation here to denote both the fixed cost component and the function by the same notation, but this is easy to distinguish from the context. In each time period, we have the option to remanufacture the returned item, manufacture the item new, or use serviceable inventory from previous period to satisfy the demand. The problem aims to generate a production plan that details the amount of products to be manufactured $p^m_t$, remanufactured $p^r_t$, the returned items carried in inventory $q^r_t$, and manufactured items carried in the inventory $q^m_t$, for each time period $t=1,\dots , T$ such that the demand is met in each time period and we minimize the total cost incurred.

2 Complexity

The problem is known to be NP-hard in general [15]. We extend the reduction provided in [15] to show the following theorem.

Theorem 1

ELSR does not have FPTAS unless P=NP.

Proof

We will show this through a reduction from a variation of the partition problem, wherein we are given 2n integer $a_1, a_2, \dots , a_{2n}$ such that $\sum _{i=1}^{2n}a_i = 2A$ and for all $i=1, \dots , 2n$, we have $\frac{A}{n+1}< a_i < \frac{A}{n-1}$. We can also assume $a_i \ge 2, i=1,\dots , 2n$. We are asked the question, whether there is a subset of these integers that add to A. Even with this restriction, the partition problem is NP-hard (see [10]). Also note that, if there exists a subset that adds up to exactly A, then such a subset must have exactly n items due to the assumption we made on the integers.

In our reduction, we first take the time horizon $T=2n$ and the demand for each time period $i=1,\dots , T=2n$ as $a_i$. We incur a fixed cost of 1 for both manufacturing and remanufacturing. While the remanufacturing does not incur a variable cost, manufacturing incurs a variable cost of $\frac{k}{n}$ for some constant k. The inventory cost of the manufactured items is some big M and for returned items is 0. The amount of returns in period 1 is $R_1=A$ and there are no returns for all other time periods, $R_i=0, i=2,\dots , 2n$. If there is a solution to the partition problem, then it is easy to see that the optimal solution to ELSR is less than $2n+k$. Otherwise, the optimal solution to ELSR is at least $2n+k+\frac{k}{n}$. In order to see this case, note that all subsets of n items either add up to at least $A+1$ or at most $A-1$. If we choose to use the A returned products to satisfy a subset of n demands that add up to $A+1$ or more, then we need to manufacture for the remaining n periods and at least in one of the n periods in which we used remanufactured goods to satisfy demands (as they could only satisfy a total demand of A). In this case, we incur a cost of at least $2n+k+\frac{k}{n}+1$. In the event we use the remanufactured goods to satisfy some n items that add up to $A-1$ or less, then the remaining n items that add up to $A+1$ or more needs to come from manufacturing in all n periods (in addition to the possibly remanufacturing of the residual return goods). In this case, we incur a cost of at least $2n+k+\frac{k}{n}$. This also rules out an FPTAS for the problem, since we can choose $\epsilon =\frac{k}{n(2n+k)}$ and an algorithm that runs in $O(f(n,\frac{1}{\epsilon }))$, $f(n,\frac{1}{\epsilon })$ being a polynomial function in n and $\frac{1}{\epsilon }$, to obtain an $(1+\epsilon )$-approximation for the ELSR can then distinguish YES and NO instances of the partition problem in polynomial time.    $\square$

3 Dynamic Program for the General Case

We now provide a dynamic program that runs in pseudopolynomial time to solve the general case exactly. This is an extension of Wagner and Whitin’s solution that incorporates the remanfacturing option, and we present it here as we will be needing it as an ingredient of our special case. We define the following function $W_t(p,q)$ as the minimum cost of obtaining an inventory level of p for the returned products and q for the manufactured products at the end of period t, such that all demands are met for the periods $i=0,\dots ,t$ either through manufacturing new items or remanufacturing returns. We define for $t=1,\dots , T$, $\mathcal {D}_t = \sum _{i=1}^t D_i$ and $\mathcal {R}_t = \sum _{i=1}^t R_i$. We will now do a forward recursion. It is easy to compute the value for $W_1(p,q)$, $p=0,\dots R_1$, $q=0,\dots , \mathcal {D}_T-\mathcal {D}_1$. For a specific value of p and q, there is exactly one way of obtaining the solution, so it is easy to compute $W_1(p,q)$ for all possible values of p and q. For infeasible solutions, we set $W_1(p,q) = \infty$. Then, the recursive function is:

The size of the state space of the problem is $T\cdot \mathcal {D}_T\cdot \mathcal {R}_T$, making the above algorithm pseudopolynomial in running time.

Theorem 2

$W_t(p,q)$ is the optimal value of the ELSR problem for periods $1,\dots , t$, when we need p (q) as the return (manufacturing) inventory level at the end of time period t

The proof is omitted as it is a straightforward extension from Wagner and Whitin [17] for the dynamic lot-sizing problem. We will provide it in the full version of the paper. As a consequence of Theorem 2, we get the following result.

Corollary 3

$\max _{p,q} W_T(p,q)$ is the optimal solution to ELSR.

3.1 Dynamic Program for the Special Case: Return Inventory Cost Is Higher Than Serviceable Inventory Cost

We now investigate the special case where $h^r(p) \ge h^m(p), \text {for all } p\in \mathbb {R}_{\ge 0}$. This is a reasonable assumption in practice, where the value of the returned products depreciate faster than a newly manufactured product and in terms of storage space, there is no difference between a returned or a manufactured product. Note that we also omitted the time index as we are assuming the costs are time invariant. If the cost are time variant, the algorithm requires that cost (both set up and variable costs) increases over time, and all arguments in the proof remain valid. In practice, this assumption is also realistic. For this special case, we now provide a dynamic program that runs in polynomial time. The following three lemmas help us reduce the state space for this special case. Remember the possible values of p and q in our function $W_t(p,q)$ are $0,\dots , \mathcal {R}_t$ and $0,\dots , \mathcal {D}_T - \mathcal {D}_t$ respectively. Let $t^*$ be the last time period in an optimal solution where we use the returned products to satisfy demand and for all $t > t^*$ we only manufacture new items or use inventory of serviceable goods to satisfy the demands and let $(\mathbf {p^*},\mathbf {q^*})$ be the corresponding optimal solution. We define the following notation for compactness: $(a-b)^+ := \max \{a-b,0\}$.

Lemma 1

For the optimal solution $\mathbf {p^*}, \mathbf {q^*}$, let us say we have $\tilde{R}_t$ of returned goods available for some time period $t<t^*$, then there is an optimal solution (by possibly re-writing the solution $\mathbf {p^*}, \mathbf {q^*}$ from time t and onwards) in which the amount of remanufactured items in time t will only be from the set $\{0, \tilde{R}_t\}$. If such a choice of return inventory is not possible, then we can create a new optimal solution with t being the last remanufactured period.

Proof is provided in Appendix A

Lemma 2

For each time period $t< t^*$, there exists an optimal solution for ELSR where the possible inventory level of the returned products right after period t takes a value only from the set $\{0, R_t, \bigcup _{i=1}^t \{\mathcal {R}_t - \mathcal {R}_i\}\}$, where $t^*$ is the last time period of remanufacturing in that optimal solution.

Proof Sketch:

The proof can be easily obtained through induction by invoking Lemma 1 and the induction hypothesis.    $\square$

An alternative way of interpreting the above lemma is that whenever we choose to remanufacture at time t, we remanufacture all return inventory available or nothing. This fact also helps us bound the serviceable goods inventory level up until a certain point. Just like we guess the last time period of remanufacturing, we will also make a guess on the last time period of manufacturing before time $t^*$ in an optimal solution and we shall denote it by $\ell ^*$. We can now bound the state space of the serviceable goods inventory level for all time period $t\le \ell ^*$, where $\ell ^*\le t^*$.

Lemma 3

There exists an optimal solution, where the inventory level of the manufactured goods in time period $t< \ell ^*$ is in the set $\{0, \bigcup _{i=t+1}^T \{\sum _{k=t+1}^iD_k\},$ $\bigcup _{i=t+1}^{\ell ^*}\bigcup _{j=t+1}^i \{(\sum _{k=t+1}^{i} D_k - \sum _{k=t+1}^jR_k)^+\}, \bigcup _{i=1}^t\{(\sum _{k=1}^iR_k - \mathcal {D}_t)^+\}\}$.

Proof provided in Appendix B.

Now that we have bounded the size of the state space for all our time periods before $t^*$, we are ready to provide our algorithm. Since we can make all possible guesses for our $\ell ^*$ and $t^*$, we will be providing the algorithm assuming that we made the correct guess. We just need to repeat the algorithm for all possible guesses and pick the guess with the cheapest solution.

Definition 4

(Uncapacitated minimum concave cost flow problem (UMCCF)). We are given a directed network G(V, A) and a demand function $d:V\rightarrow \mathbb {Q}$, such that $\sum _{i\in V}d_i = 0$ and a concave cost function $c:A\rightarrow \mathbb {Q}_+$. Find a set of assignment of flows $f:A\rightarrow \mathbb {Q}_+$, such that for each node $i\in V$, we have $\sum _{(i,j)\in A}f_{ij} + d_i = \sum _{(j,i)\in A}f_{ji}$ and $\sum _{(i,j)\in A}c_{ij}(f_{ij})$ is minimised.

For the UMCCF problem defined on a planar graph, a send-and-split (SAS) dynamic program was provided in [4] which runs in a time which is exponential in the number of distinct faces in which the terminal (source and supply) nodes lie. If the number of distinct faces on which the terminal nodes lie is bounded, then the algorithm has a polynomial time complexity.

Algorithm DP-SAS

• Run the dynamic program for the general case provided in Sect. 3 until $\ell ^*$ using the reduced state space.

• Set up a minimum concave cost flow for planar problem from time period $\ell ^*$ and onwards, where all the demand nodes lie on exactly two different faces and solve the problem for all possible input inventory levels at $\ell ^*$ (to solve this problem in polytime use the SAS algorithm in [4], where the algorithm runs in a time that is an exponential in the number of distinct faces on which all the terminal nodes are lying).

The Algorithm DP-SAS has to guess the values of $\ell ^*$ and $t^*$ and for every possible guess, all possible inventory levels entering period $\ell ^*$ are enumerated. For each such level, we set up a minumum concave cost flow problem by first creating two source nodes, one for manufactured products and one for return products, with the corresponding inventory levels as their surplus flow values and the demand and return values occuring after time $\ell ^*$ are taken as the rest of terminal nodes (acting as sink and source nodes respectively). Since we know from assumption that there is no manufacturing between periods $\ell ^*$ and $t^*$ and there is no remanufacturing after $t^*$, all terminal nodes lie on at most three distinct faces. This along with Lemmas 2 and 3 guarantees polynomial running time of DP-SAS. We would like to point out that this is a highly impractical algorithm as we are running the SAS algorithm (which runs in a time that is a cubic function of T) for every possible guess of $\ell ^*$ and $t^*$ and for all possible inventory levels for the corresponding guesses. We are mainly interested in the answering the question of tractability. Designing a faster algorithm or improving upon the above algorithm to solve this special case will be a good research question for the future. We will now focus on a more practical exact algorithm for solving the general version of the problem in the following section.

4 Valid Inequalities and Numerical Computation

In this section, we consider a more general variation of the problem, wherein we are given a capacity restriction of $\mathcal {C}_j$ on how much we can manufacture in each time period $j=1,\dots , T$. For this general version, we give an integer programming formulation and provide two families of valid inequalities and demonstrate the strength of these inequalities on some test instances. The inequalities are based on the popular flow-cover cuts introduced in [12], which in turn can be viewed as a generalisation of Dicuts introduced in [13] for uncapacitated fixed charge flow problems. We follow the same line of Carnes and Shmoys [3], where they introduce these inequalities for capacitated single item dynamic lot sizing problem and show how these inequalities help in bounding the gap. In this work, we also show how to tighten these inequalities. We will show the inequalities’ validity and the special case where the separation time is polynomial. In the general case, the separation problem is NP-hard, see [12]. We perform the numerical computation only for the family of inequalities where the separation time is polynomial and we will show through numerical computations that these are enough to close most of the gap.

We will cast the whole problem as an uncapacitated fixed charge flow problem and in order to balance the supply and demand, we will increase the planning horizon by 1 and this last time period will have a demand of $\mathcal {R}_T = \sum _{i=1}^Tr_i$. We will first give the following MIP formulation that will solve the ELSR. The decision variables are:

• $x^i_{jk}$: The percentage of $d_k$ satisfied by returns from i that was remanufactured in j. Note by this definition, for $x^i_{jk} > 0$, we need $i\le j\le k$.

• $y_{jk}$: The percentage of $d_k$ satisfied by the order that was manufactured in period k. Again, we need $j\le k$ for $y_{jk} > 0$

• $u_j$: Binary variable indicating whether we remanufactured in period j

• $v_j$: Binary variable indicating whether we manufactured in period j

We will re-write the cost functions in a more convenient format for our model: $g^r_{i,jk}(x):=\sum _{t=i}^{j}h^r_j(x) + \sum _{t=j}^{k}h^m_t(x) + l^r_j(x), g^m_{jk}(x):=\sum _{t=j}^{k}h^m_t(x) + l^m_j(x)$

$$\begin{aligned} \mathcal {P}_1: \min \sum _{j=1}^{T}f^r_ju_j + \sum _{j=1}^{T}f^m_jv_j + \sum _{k=1}^{T}\sum _{j=1}^{k}\sum _{i=1}^{j} g^r_{i,jk}d_kx^i_{jk} + \sum _{k=1}^{T}\sum _{j=1}^{k}g^m_{jk}d_ky_{jk} \end{aligned}$$

$$\begin{aligned} \sum _{j=1}^{k}\sum _{i=1}^{j} x^i_{jk} + \sum _{j=1}^{k}y_{jk}&\ge 1, \quad \quad \forall k \in [T]\\ \sum _{k=1}^{T}\sum _{j=i}^{k}d_kx^i_{jk}&\le r_i, \quad \quad \forall i\in [T]\\ \sum _{k=j}^{T}d_ky_{jk}&\le \mathcal {C}_j, \quad \quad \forall j\in [T]\\ \sum _{i=1}^j x^i_{jk}&\le u_j, \quad \quad \forall k\in [T], j=1,\dots , k\\ y_{jk}&\le v_j, \quad \quad \forall k\in [T], j=1,\dots , k\\ \mathbf {x}, \mathbf {y}&\ge 0\\ \mathbf {u}, \mathbf {v}&\in \{0,1\}^T \end{aligned}$$

For the subsets of return, demand and manufacturing periods $A, B, C\subseteq [T]$ respectively, we define d(A, B, C) as the demand in B that cannot be satisfied by just the returns in A and the manufacturing capacity provided in periods in C. This demand, d(A, B, C), needs to be satisfied by either manufacturing in the periods $\bar{C}=[T]\backslash C$ or by using the returns in $\bar{A}=[T]\backslash A$. The value of d(A, B, C) can be determined by solving the following LP.

For $j\in [T]$, we define $w^r_j(A,B,C)$ as the maximum amount of d(A, B, C) that could be satisfied by returns in $\bar{A}$, if they are allowed to be remanufactured only during j. We calculate this value by setting up a suitable LP similar to LP-U. For each $j\notin C$, we define $w^m_j(A,B,C) := d(A,B,C) - d(A,B,C\cup \{j\})$ which denotes the decrease in unsatisfiable demand in B by C if j were to be added to C. Let $\mathcal {T}_C$ be the set of all 2-tuple sets that partitions $[T]\backslash C$ for some set C and and let $\mathcal {T}$, be the set of all 2-tuple sets that partitions [T]. Let $\{T_1^m, T_2^m\}\in \mathcal {T}_C$ and $\{T_1^r, T_2^r\} \in \mathcal {T}$. Now consider the following inequality.

$$\begin{aligned}&\begin{aligned} \sum _{k\in B}\sum _{j\in T_1^r}\sum _{i\notin A}^{j}d_kx^i_{jk} + \sum _{j\in T_2^r}w^r_j(A,B,C) u_j + \sum _{k\in B}\sum _{j\in T_1^m}d_ky_{jk} \qquad \qquad \qquad \qquad \\ + \sum _{j\in T_2^m}w^m_j(A,B,C) v_j \ge d(A,B,C), \forall (T_1^r, T_2^r)\in \mathcal {T}, (T_1^m, T_2^m)\in \mathcal {T}_C, B\subseteq [T] \end{aligned} \end{aligned}$$

(1)

For a fixed A, B and C it is pretty straightforward to realise that the separation problem is polynomially solvable. Note that, even for a fixed A, B and C we have exponentially many constraints, as we need to enumerate all the partitions of [T]. For a fixed A, B and C, and a given LP solution $\mathbf {\hat{x}}, \mathbf {\hat{u}},\mathbf {\hat{y}},\mathbf {\hat{v}}$, the partition could be determined in the following way

• If $\sum _{k\in B}\sum _{i\notin A}^{j}d_k\hat{x}^i_{jk} \ge w_j^r(A,B,C)\hat{u}_j$ then $j\in T_2^r$ otherwise $j\in T_1^r$.

• Similarly, if $\sum _{k\in B}d_k\hat{y}_{jk} \ge w_j^m(A,B,C)\hat{v}_j$ then $j\in T_2^m$ otherwise $j\in T_1^m$.

Valid inequalities of type 1 are not very strong. We illustrate this through the following example.

Example 5

We have uniform capacities $\mathcal {C}$ and our fixed sets are as follows: $A =\{1,\dots ,t\} ,B=\{1,\dots ,t\},C=\emptyset$, for some t.

In Example 5, it is clear that $d(A,B,C) \ge \max (\mathcal {D}_t - \mathcal {R}_t,0)$. Our inequality 1 for this example will be

$$\begin{aligned} \mathcal {C}\sum _{i=1}^tu_i \ge d(A,B,C) \end{aligned}$$

This gives us a straight forward mechanism to tighten it. We can divide by $\mathcal {C}$ and round down the right hand side to obtain the valid inquality:

$$\begin{aligned} \sum _{i=1}^tu_i \ge \Bigl \lfloor \frac{d(A,B,C)}{\mathcal {C}}\Bigr \rfloor \end{aligned}$$

Drawing on this, from inequalities 1 we derive MIR inequalities. We briefly describe MIR inqualities here. For the set $\{(x,y)\in \mathbb {R}\times \mathbb {Z}: x + cy \ge b, x \ge 0 \}$, it is easy to see that $x + fy \ge f\lceil \frac{b}{c}\rceil$ is a valid inequality, where $f = b -c\lfloor \frac{b}{c}\rfloor$ (see [11] for more details).

The next set of inequalities are quite similar to the flow cut inequalities but are given with respect to the returned products. Since the flows are balanced in our network, we can reverse all arc orientations and take the nodes with returns as the demand nodes with demands as the returns and write our flow cuts based on these as sinks. In other words, it is a generalisation of the following simple idea: For every $i\in [T]$ with $r_i>0$, we need to have either $u_i\ge 1$ or $\sum _{j\ge i}\sum _{k\ge j}x^i_{jk}d_k \ge r_i$. We then get the disjunctive inequality:

$$\begin{aligned} u_ir_i + \sum _{j\ge i}\sum _{k\ge j}x^i_{jk}d_k \ge r_i \end{aligned}$$

(2)

Once again for every partition $(T_1,T_2)$ of $\{i, i+1,\dots T\}$, we have the following inequality:

$$\begin{aligned} \sum _{i'\in T_1}u_{i'}r_i + \sum _{\begin{array}{c} j\ge i\\ j\in T_2 \end{array}}\sum _{k\ge j}x^i_{jk}d_k \ge r_i \end{aligned}$$

(3)

The validity of the above inequality is straightforward and it is easy to see that 2 is a special case of 3 with $T_1= \{i\}$.

5 Experiments

The experiments were carried out on an Intel core i5-3320 @2.6Ghz CPU with a 8GB RAM and the implementation was done in Gurobi 6.0.4 using Python API. It was difficult to directly adapt the instances available for capaciated lot sizing problem [2] to the remanufacturing setting in a way that the new instances could have large root gaps. So we randomly generated instances with special return and demand structures in order to create instances with gap. We took the manufacturing capacities to be uniform. For varying cost and demand structures we generated nine instances with 100 time periods and three instances with 200 time periods. We implemented the cover and MIR cuts from 1 and as we could see from Table 1, for the gap instances we generated, we were able to close the gap at the root when all other Gurobi cuts were turned off. The default settings of Gurobi could not solve the problem when we increased the time horizon to 200 within 1000 s that we set as a time limit for all our test runs. As one could see the new cuts proposed drastically reduced the running time for solving these gap instances. In addition to that the lower bounds were considerably improved at the root. As we moved on to larger instance (with time horizon = 200), the problem was getting increasingly harder to solve with just the default GUROBI settings.

Table 1. Gaps from test runs with Gurobi default setting and cover and MIR derived from 3

6 Conclusion and Open Problems

In this work, we studied the ELSR problem. We first provided a hardness proof that rules out FPTAS for this problem. We then provided a dynamic program with a pseudopolynomial running time to solve the general version of the problem. We later showed how this can be used to design a polynomial running time algorithm, when we make some assumptions on the cost structure. We finally performed a computational study on the capacitated version of the problem, where we introduced two families of valid inequalities and our preliminary results were promising. Our future work would include obtaining an approximation algorithm for the general version of the problem. In the negative side, although we have ruled out a possibility of FPTAS, we have no proofs for APX-hardness (see [16]) and this is still open. We are also interested in performing a more comprehensive experimental study of the capacitated version of the problem. It will be interesting to verify whether the proofs presented above could be extended to multiple items (taking the number of items to be a constant will be a good starting point) and general concave functions.

Appendices

A Proof of Lemma 1

Proof

Suppose in $(\mathbf {p}^*,\mathbf {q}^*)$, we produce something not from this set $\{0, \tilde{R}_t\}$. Hence, some intermediate return stock of $0< a < \tilde{R}_t$ is carried, which also means that we are remanufacturing at time t in the optimal solution. Since $t<t^*$, there exist a time period after t in the optimal solution where we remanufacture. Let the $\tilde{t}$ be the first time period after t, when we remanufacture in the optimal solution. We are also carrying a non-zero return inventory until this time period. If we remanufacture at least a in time $\tilde{t}$, then we could have remanufactured this a in time t and carried a units of manufactured inventory until time $\tilde{t}$ with no additional cost, since return inventory cost is higher than manufactured inventory cost. If we produced less than a in time $\tilde{t}$, say $\tilde{a}$, then we could have produced $\tilde{a}$ in time t and produced nothing in time $\tilde{t}$ and continue with our argument. If $\tilde{t} = t^*$ and $\tilde{a} < a$, then we would have new optimal solution with t being the last time period of remanufacturing.    $\square$

B Proof of Lemma 3

Proof

We prove this lemma again through induction. For $t=1$, the lemma’s claim is that the inventory level of serviceable goods after time $t=1$ will belong to the set $\{0, \bigcup _{i=2}^T \{\sum _{k=2}^iD_k\}, \bigcup _{i=2}^{\ell ^*}\bigcup _{j=2}^i\{(\sum _{k=2}^{i}D_k - \sum _{k=2}^{j}R_k)^+\}, (R_1-D_1)^+ \}$. In order to show this, we do a case analysis:

• Case 1 Manufacturing takes place at $t=1$ : In this case, either remanufacturing does not take place or it does take place and we have $R_1 < D_1$, otherwise we could manufacture everything we manufactured in time period 1 in time period 2 and get a cheaper solution by saving on the inventory cost. Let us take k, where $1<k\le \ell ^*$, as the first time period after time $t=1$ when we manufacture again. Now the demand for all the intermediate periods $\sum _{i=2}^{k-1}D_i$ needs to come from either the manufactured goods in period 1 or the return products from periods 1 to $k-1$. From Lemma 2, we know that the only possible return inventory levels between the time periods 2 to $k-1$ are $\{0, \bigcup _{i=2}^{k-1} \{\mathcal {R}_{i} - R_1\}\}$ and we know from lemma 1 that at any of these time periods, we either remanufacture all available inventory or none of them. The remaining demand then needs to be manufactured at time period 1. This has to be true for all values of $k=2\dots \ell ^*$. So we get the claim.

• Case 2 Manufacturing does not take place at $t=1$ : This would mean that $R_1 \ge D_1$, otherwise, we would not have a feasible solution and the possible inventory levels in this case is $(R_1-D_1)^+$.

In order to see that the lemma is true, we invoke the induction hypothesis and do a similar case analysis as above.    $\square$