A Residual Based Method for Fitting PAR Models Using Fourier Representation of Periodic Coefficients

Abstract

In this paper we present a preliminary simulation study of a method for estimating the Fourier coefficients of the periodic parameters of a periodic autoregressive (PAR) sequence. For motivational and comparative purposes, we first examine the estimation of Fourier coefficients of a periodic function added to white noise. The method is based on the numerical minimization of mean squared residuals, and permits the fitting of PAR models when the period T equals the observation size N. For this paper, algorithms and simulations were coded in MATLAB, but an implementation will be available in the R package, perARMA.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

There exist many natural random processes in which the probability structure has a periodic rhythm, which, in the strict sense means that the probability law is invariant under shifts of length T. To be precise, a process $X_t(\omega ) : \varOmega \longrightarrow \mathbf{C} \text{ or } \mathbf{R}$ is called periodically stationary with period T if for every n, collection of times $t_1,t_2,...,t_n$ in $\mathbf{Z}$ or $\mathbf{R}$, collection of Borel sets $A_1,A_2,...,A_n$ of $\mathbf{C} \text{ or } \mathbf{R}$,

$$\begin{aligned}&Pr[X_{t_1+T}\in A_1,X_{t_2+T}\in A_2, ... ,X_{t_n+T}\in A_n]\nonumber \\&\ =Pr[X_{t_1}\in A_1,X_{t_2}\in A_2, ... ,X_{t_n}\in A_n]. \end{aligned}$$

(1)

and there are no smaller values of $T>0$ for which (1) holds. Synonyms for periodically stationary include periodically non-stationary, cyclostationary (think of cyclically stationary [1]), processes with periodic structure [6], and a few others. If $T=1$, the process is strictly stationary.

When the process is of second order, $X_{t} \in L_2(\varOmega ,{\mathscr {F}},P)$ with $t\in \mathbf{Z}$, it is called periodically correlated [2] (PC), or wide-sense cyclostationary with period T if

$$\begin{aligned} m(t)= & {} E\{X_{t}\}=m(t+T) \forall t, \text{ and } \end{aligned}$$

(2)

$$\begin{aligned} R(s,t)= & {} E\{ X_{s} \overline{X_{t}} \} =R(s+T,t+T) \forall s,t \in \mathbf{Z} \end{aligned}$$

(3)

and there are no smaller values of $T>0$ for which (2) and (3) hold. If $T=1$, the process is weakly (or wide-sense) stationary.

A second order stochastic sequence $X_t$ is called PARMA (p, q) with period T if it satisfies, for all $t\in \mathbf{Z}$,

$$\begin{aligned} \sum _{j=0}^{p}\phi _j(t)X_{t-j}= \sum _{k=1}^{q}\theta _k(t)\xi _{t-k}+\sigma (t) \varepsilon _{t} \end{aligned}$$

(4)

where $\varepsilon _{t}$ is a real valued orthogonal process and real parameters, $\phi _j(t)=\phi _j(t+T), \theta _k(t)=\theta _k(t+T)$ and $\sigma (t)=\sigma (t+T)$ for every appropriate j, k. Sometimes we write $\theta _0(t)=\sigma (t)$. Under certain constraints of the parameters, expressed by (8) below, these sequences are PC.

Here we will concentrate on the special case of periodic autoregressive (PAR) sequences, for which

$$\begin{aligned} \sum _{j=0}^{p}\phi _j(t)X_{t-j}=\sigma (t) \varepsilon _{t} \quad t\in \mathbf{Z}, \end{aligned}$$

(5)

where $\varepsilon _{t}$ is an orthogonal process, $\phi _0(t)\equiv 1$, $\phi _j(t)=\phi _j(t+T)$, and $\sigma (t)=\sigma (t+T)$ for every appropriate j. Although Pagano [8] initiated the recent notation and stream of effort on PAR sequences, it is clear that Hannan [3] was aware of them.

Essential information may be obtained by blocking $X_t$ into vectors $\mathbf{X}_n$ of length T as prescribed by Gladyshev [2]; then (5) becomes

$$\begin{aligned} L \mathbf{X}_n - \sum _{j=1}^{p'} U_j \mathbf{X}_{n-j} = \varGamma \mathbf{\varepsilon }_n \end{aligned}$$

(6)

where L has the form

$$\begin{aligned} L = \left[ \begin{array}{lllll} 1 &{} 0 &{} 0 &{} \dots &{} 0 \\ - \phi _{1}(1) &{} 1 &{} 0 &{} \dots &{} 0 \\ - \phi _{2}(2) &{} -\phi _{1}(2)&{} 1 &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ -\phi _{T-1}(T-1) &{} -\phi _{T-2}(T-1) &{} -\phi _{T-3}(T-1) &{} \dots &{} 1 \end{array} \right] , \end{aligned}$$

(7)

$$ [U_j]_{nn'} = \phi _{jT +n-n'}(n), $$

and $\mathbf{\varepsilon }_n=[\varepsilon _{nT}, \varepsilon _{nT+1}, \dots \varepsilon _{nT+T-1}]'$. The matrix $\varGamma$ is similarly arranged as L except the diagonal is $\{\sigma (0),\sigma (1),\dots , \sigma (T-1)\}$ and the condition for $X_t$ to be PC is identical to the condition for the vector sequence $\mathbf{X}_n$ to be stationary, namely that

$$\begin{aligned} \det \, \left[ L - \sum _{j=1}^{p'} U_j \lambda ^j \right] \ne 0,\quad |\lambda | \le 1 \end{aligned}$$

(8)

The condition (8) was expressed first by Pagano [8] for PAR, and then by Vecchia [9] for general PARMA.

Of course the vector sequence $\mathbf{X}_n$ could also be modeled by a vector AR, (VAR) model, but we note that the number of real autoregressive parameters for a general VAR(p) is on the order of $pT^2$ because the autoregressive coefficients are $T \times T$ matrices. But for PAR(p) the number is on the order of pT, which can still be sizable when compared to the total length of the series available. See Pagano [8, p. 1316]. For a full PARMA given by (4) the parameter count is seen to be $(p+q+1)T$. An alternative parameterization of a PARMA system (see Jones and Breslford [6]) can sometimes substantially reduce the number of parameters via representing the periodically varying parameters by Fourier series. In the case of PAR we have

$$\begin{aligned} \phi _j^{A_j}(t)= & {} a_{j,1} + \sum _{n=1}^{[T/2]} a_{j,2n} \cos (2 \pi n t /T)+a_{j,2n+1} \sin (2 \pi n t /T) \end{aligned}$$

(9)

for $t=0,1,\dots ,T-1, j=1,\dots ,p$. The inverse for the $a_{j,n}$ coefficients is given by

$$\begin{aligned} a_{j,1}= & {} \frac{1}{T} \sum _{t=0}^{T-1} \phi _j(t) \\ a_{j,2n}= & {} \frac{2}{T} \sum _{t=0}^{T-1} \phi _j(t) \cos (2 \pi n t /T) \nonumber \\ a_{j,2n+1}= & {} \frac{2}{T} \sum _{t=0}^{T-1} \phi _j(t) \sin (2 \pi n t /T) \nonumber \end{aligned}$$

(10)

for $n=2,\dots , [T/2], j=1,\dots ,p$. We also denote

$$\begin{aligned} A_j =\{a_{j,1}, a_{j,2},a_{j,3}, \dots , a_{j,2*[T/2]+1} \}' \end{aligned}$$

(11)

to be a column vector.

When estimating the natural PAR coefficients $\{\phi _j(t), j=1,2,\dots ,p, t=0,1,\dots ,T-1$ or their Fourier coefficients, $\{A_j, j=1,2, \dots ,p\}$, there is always an issue of the length of the sample N relative to the period T. The two important cases are (1) $N {>}{>} T$ and (2) $N=T$. In the case $N {>}{>} T$, the usual method for estimating the coefficients is through the Yule-Walker equations and the existence of multiple periods allows the sample covariance to be estimated and used to solve for the unknown coefficients. In the case of $N=T$, although the covariance of the sequence cannot be estimated in the usual way, the Fourier coefficients can still be successfully estimated via ordinary least squares (OLS) when the number of coefficients is small relative to N. In this note, for the purpose of background, we will briefly review the usual method for $N {>}{>} T$ and then, for $N=T$, present a simulation study that illustrates the effectiveness of the OLS method. We also include, for the purpose of motivation and comparison, results from application of the method to the estimation of Fourier coefficients of a periodic function added to white noise.

The application of this idea to full PARMA models is of interest but not so straightforward because of the way that the moving average parameters appear in (4). Approaches to this problem are currently under study.

2 Determination of PAR Coefficients by Yule Walker Method

The Yule-Walker method, which is based on minimizing mean square error of a linear predictor, gives an important way for finding the coefficients $\{ \phi _j(t)=\phi _j(t+T), j=1,\dots ,p \}$.

For some fixed t, the linear predictor of $X_{t}$, based on $\{X_{t-p},\dots ,X_{t-1}\}$, that minimizes the MS error is given by the orthogonal projection of $X_{t}$ onto ${\mathscr {M}}(t-1;p)=\mathrm{sp}\{X_{s},s\in \{t-p,\dots ,t-1\}\}$. We denote

$$ \widehat{X}_{t,t-1;p} = (X_{t}|{\mathscr {M}}(t-1;p)),\quad \text{ and } \text{ set } \quad \widehat{X}_{t,t-1;0}=0. $$

Specializing to real sequences we then need to determine the coefficients $\alpha _{j,p}^{(t)}$ in

$$ \widehat{X}_{t,t-1;p} = \sum _{j=1}^{p} \alpha _{j,p}^{(t)} X_{t-j}. $$

The normal equations arising from the orthogonal projection are

$$ E\{[X_{t} - \widehat{X}_{t,t-1;p}]X_{s} \} = 0,\quad s=t-p,\dots ,t-1 $$

or in matrix form

$$ \left[ \begin{array}{c} R(t,t-1)\\ \vdots \\ R(t,t-p) \end{array} \right] = \left[ \begin{array}{ccc} R(t-1,t-1) &{} \cdots &{} R(t-p,t-1)\\ R(t-1,t-2) &{} \cdots &{} R(t-p,t-2)\\ \vdots &{} \vdots &{} \vdots \\ R(t,t-p) &{} \cdots &{} R(t-p,t-p) \end{array} \right] \left[ \begin{array}{c} \alpha _{1,p}^{(t)}\\ \alpha _{2,p}^{(t)}\\ \vdots \\ \alpha _{p,p}^{(t)} \end{array} \right] $$

and in a shorter notation

$$\begin{aligned} \mathbf{r}_{{t,t-1:t-p}} = \mathbf{R}_{t-1,p} \varvec{\alpha }_p^{(t)}. \end{aligned}$$

(12)

Any $\varvec{\alpha }_{p}^{(t)} = [\alpha _{1,p}^{(t)} \alpha _{2,p}^{(t)} \dots \alpha _{p,p}^{(t)}]'$ that solves (12) (the normal equations) implements the projection. If $\mathbf{R}_{t-1,p}$ is invertible, the solution is unique but if not, then any pseudo-inverse still yields a predictor that minimizes MS error. Other results using this notation may be found in [4, 5].

Since for PC-T processes the covariances are invariant (see (3)) under shifts of length T, then the prediction coefficients will be periodic in t with period T. So for a sample of length KT, there are multiple occurrences (order of K) of products $X_{t_1+kT} X_{t_2+kT}$ from which we estimate the covariances $\mathbf{r}_{t,t-1:t-p}$ and $\mathbf{R}_{t-1,p}$ appearing in (12). Specifically,

$$\begin{aligned} \widehat{R}_K(t_1,t_2)=\frac{1}{K} \sum _{k=0}^{K-1}[X_{t_1+kT}-\widehat{m}_{t_1,N}][X_{t_2+kT}-\widehat{m}_{t_2,N}] \end{aligned}$$

(13)

is the estimator for some entry $R(t_1,t_2)$.

Then the estimator $\widehat{\varvec{\alpha }}_p^{(t)}$ is obtained by solving $\widehat{\mathbf{r}}_{t,t-1:t-p} = \widehat{\mathbf{R}}_{t-1,p} \widehat{\varvec{\alpha }}_p^{(t)}$ and estimates for the Fourier coefficients $A_j$ are obtained via (11). But to estimate $R(t_1,t_2)$ in this manner requires K to be of nontrivial size, some say at least 40. Here we seek a methodology to estimate the $A_j$ when the number of periods K available in the sample is small, say $K=1$.

3 OLS Fit for Periodic Function with Additive Noise

In order to develop some intuition for the PAR estimation problem, we first examine the simpler case of estimating the Fourier coefficients of a periodic function added to white noise. Given a trajectory of observations $\{X_0,X_2, \dots ,X_{N-1}\}$, we wish to minimize

$$\begin{aligned} Q(\mathbf{A}) = \sum _{t=1}^N \left[ X_t - \left\{ a_{1} + \sum _{n=1}^{[T/2]} a_{2n} \cos (2 \pi n t /T)+a_{2n+1} \sin (2 \pi n t /T) \right\} \right] ^2 \end{aligned}$$

(14)

where $\{a_1,a_2,...\}= \mathbf{A}$. Although there is a closed form solution due to the mutual orthogonality of the set of sines and cosines, we do the minimization numerically to prepare for the application to PAR, for which there is no closed form solution.

To see the idea in very simple example, suppose we wish to fit just the $\cos (2 \pi t /T)$ term to $X_t$ using ordinary least squares (OLS). The OLS estimate for $a_2$ is well known to be $\hat{a_2}=\frac{2}{T} \sum _{t=0}^{T-1} X_t \cos (2 \pi t /T)$ and more generally

$$\begin{aligned} \hat{a}_{2n} = \frac{2}{T} \sum _{t=0}^{T-1} X_t \cos (2 \pi n t /T) \quad \hat{a}_{2n+1} = \frac{2}{T} \sum _{t=0}^{T-1} X_t \sin (2 \pi n t /T). \end{aligned}$$

(15)

If $X_t = \zeta _t + f_t$ for $t\in \{0,1,\dots , N-1\}$, where $\zeta _t$ is Gaussian white noise with zero mean and variance $\sigma _{noise}^2$, and $f_t=A \cos (2 \pi t/T)$, with $T=N$, then it is easy to see that $\hat{a}_{2n}$ and $\hat{a}_{2n+1}$ are Gaussian and that

$$\begin{aligned} E\{\hat{a}_2\} = A, \quad \quad E\{\hat{a}_3\} = 0, \quad \quad \mathrm{Var}\;\{ \hat{a}_2\} = \mathrm{Var}\;\{ \hat{a}_3\} = \frac{\sigma _{noise}^2}{T} \end{aligned}$$

(16)

and

$$\begin{aligned} E \{ \hat{a}_2 \hat{a}_3 \}= & {} \frac{4}{T^2} \sum _{t=0}^{T-1} \sum _{t'=0}^{T-1} \cos (2 \pi t /T) \sin (2 \pi t' /T) E\{Z_t Z_{t'}\} \nonumber \\= & {} \frac{4}{T^2} \sum _{t=0}^{T-1} \cos (2 \pi t /T) \sin (2 \pi t /T) = 0. \end{aligned}$$

(17)

Simulated series of $X_t$ for $T=N=1024$, $\sigma _{noise}=1$ and $A=0, 0.2, 0.4,1.0$ were produced; note the coefficients of the Fourier series in (14) are therefore $a_1=0, a_2=A$ and $a_j=0, j\ge 3$.

Fig. 1

Top panel red is true signal $f_t= A \cos (2 \pi t/T)$ with $A=1$, blue is signal plus noise, green is estimated signal where $\hat{A}=0.947$ is determined by minimizing $Q(\mathbf{A})$ in (14). Middle panel is residual series $Z_t = X_t - \hat{A} \cos (2 \pi t/T)$; bottom is FFT of $Z_t$

These simulated series were processed by a MATLAB script that implements the minimization with respect to $\mathbf{A}$ of $Q(\mathbf{A})$, where the single trajectory $\{X_0,X_2, \dots ,X_{N-1}\}$ is treated as fixed. Figure 1 (top panel) shows the signal $f_t=A \cos (2 \pi t/T)$ with $A=1$ in red, the sum $X_t$ in blue and the estimated signal $\hat{f}_t = \hat{A} \cos (2 \pi t/T)$ in green. Although both are present, the difference between the red and green curves is nearly imperceptible on the scale used.

The middle panel of Fig. 1 is the residual $Z_t$ of the OLS fit and the bottom panel is the sample Fourier transform (computed via FFT) of the residual, showing no clear residual periodic component.

Some questions that we can address by simulation: (1) Sample distribution of parameter estimates; (2) Variance of estimates as function of $N=T$; (3) Variance of estimates as function of number of frequencies searched.

Figures 2 and 3 are the sample histograms of $\hat{a}_2$ and $\hat{a}_3$ when the true values are $a_2=0.2$ and $a_3=0.0$; in each, $\sigma _{noise}=1$, $N=T=4096$. These histograms were produced by $NSAMP=500$ replicates of the simulation-estimation process. In both of these histograms the p-value of a Lilliefors test for normality were both $\ge 0.5$, indicating no evidence for rejection of normality. The Lilliefors test is a Kolmogorov-Smirnov type of test for normality in which the null is normal with parameters estimated from the data [7]; thus a large $p_L$ indicates the normality of the sample distribution cannot be rejected.

The sample variances were 0.023 and 0.022, whereas the values computed via (16) were 0.0221.

Fig. 2

Estimates $\hat{a}_2$ with $a_2=0.2$, $N=T=4096$, $\sigma _{noise}=1$, $\hat{\mu }_2=0.199$, $\hat{\sigma }_2=0.023$

Fig. 3

Estimates $\hat{a}_3$ with $a_2=0$, $N=T=4096$, $\sigma _{noise}=1$, $\hat{\mu }_3=0.001$ $\hat{\sigma }_3=0.022$

For each parameter, the empirical dependence of $\hat{\sigma }$ on $N=T$ can be seen by the least squares fit of a straight line, $y= m x + b$, to the pairs $(N, \hat{\sigma })$, where both N and $\hat{\sigma }$ are transformed to a $\log$ scale, so the expected $T^{- 1/2}$ dependence becomes $m=-1/2$.

Fig. 4

Estimating $a_2$ where $\sigma _{noise}=1$, $a_2=A=0.4$, slope $=-0.512$

Fig. 5

Estimating $a_3$ where $\sigma _{noise}=1$, $a_2=A=0.4$, slope $=-0.483$

Figures 4 and 5 illustrate this fitting for parameters $\{a_2,a_3\}$, where for each parameter the values $A=0.4$, $N=\{512,1024,2048,4096\}$ are used. The resulting slope estimates are $m=\{-0.512,-0.483\}$, where blue lines connect the observed data and the red lines are the least squares fit to the pairs $(N, \hat{\sigma })$.

In order to show the variability of parameter estimates when parameter values are zero, we set parameters $a_1$ through $a_{17}$ to be active whereas only $a_2=A=0.4$ was nonzero. Figure 6 shows the boxplots, based on 500 replicates, of all 17 parameters estimated. Box vertical boundaries are 25th and 75th percentiles and red line is median. The ability to perceive non-nullity of parameters is visually clear. In the next section we use the t-test for testing for this non-nullity.

Fig. 6

Active parameters are $\{a_1,a_2,\dots ,a_{17}\}$ with $A=0.4$, $N=4096$. Boxplots of parameter estimates are based on 500 replicates

4 OLS fit of a Fourier Series Parametrization of a PAR Model

For a PAR model as in (5), we designate the following estimating procedure as parmsef. First we minimize the objective function

$$\begin{aligned} Q(\mathbf{A}) = \frac{1}{N-p} \sum _{t=p+1}^N \left[ X_{t} - \sum _{j=1}^{p}\phi ^{\mathbf{A}}_{j}(t)X_{t-j} \right] ^2 \end{aligned}$$

(18)

where

$$ \phi ^{\mathbf{A}}_j(t)= a_{j,1} + \sum _{n=1}^{[T/2]} a_{j,2} \cos (2 \pi n t /T)+a_{j,2n+1} \sin (2 \pi n t /T) $$

and we set $N=T$.

The OLS estimate of $\mathbf{A}$ is the value of $\mathbf{A}$ that minimizes $Q(\mathbf{A})$ for $\mathbf{A}\in \mathbf{S}_1$, the parameter search space, defined as $\mathbf{S}_1= \mathrm{sp}\{e_j\in \mathbf{R}^N : j\in I_{\mathbf{A}}\}$ where $I_{\mathbf{A}}$ is the set of indexes identifying the active $\mathbf{A}$ parameters. If $\mathbf{A}^*$ minimizes the mean square residuals Q, then denoting $\hat{Z}_t$ as the residual sequence $\hat{Z}_t = X_t - \sum _{j=1}^{p}\phi _j^{A_j^*}(t)X_{t-j}$, we then determine the OLS estimate of $\sigma (t)$ by minimization of

$$\begin{aligned} Q_{\sigma }(\mathbf{B}) = \frac{1}{N-p} \sum _{t=p+1}^N \left[ \hat{Z}^2_t - \sigma ^2_B(t) \right] ^2, \end{aligned}$$

(19)

using

$$\begin{aligned} \sigma _B(t)= \sum _{n_j\in J_B} b_{2n_j} \cos (2 \pi n_j t /T)+b_{2n_j+1} \sin (2 \pi n_j t /T). \end{aligned}$$

(20)

The minimization is with respect to the active parameters $b_{n_j}$ in the collection $B =\{b_{0},b_{1}, b_{2},b_{3}, \dots , b_{2*[T/2]+1} \}$.

To exercise this program we simulated a PAR(2) by specifying the coefficients $\phi _1(t)$ and $\phi _2(t)$, shown in Fig. 7 to be

$$\begin{aligned} \phi _1(t)= & {} 1.1 + 0.6 \cos 2 \pi t / 4096 \end{aligned}$$

(21)

$$\begin{aligned} \phi _2(t)= & {} -0.3450 - 0.33 \cos 2 \pi t / 4096 -0.045 \cos 4 \pi t/4096 \end{aligned}$$

(22)

and $\sigma _B(t) = 1$.

Fig. 7

$\phi _1(t)$ and $\phi _2(t)$ given in (22) for PAR2a run1, $N=4096$

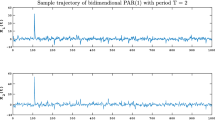
Figure 8 is a simulated series of $N=T=4096$ samples using $\phi _1(t)$ and $\phi _2(t)$ given in (22) and illustrated in Fig. 7. Note the higher amplitudes and lower frequency fluctuations at the beginning and end of the series in comparison to the middle section.

Fig. 8

Sample series using $\phi _1(t)$ and $\phi _2(t)$ given in (22) and illustrated in this figure with $N=4096$

Table 1 Sample $\mu$ and $\sigma$ with $N=T=4096$ for selected Fourier coefficients estimated by parmsef. Estimates are based on $NSAMP=100$ replicates

In the first experiment with the parmsef algorithm we set the seven autoregressive parameters shown in Table 1 to be active where the true values, the sample mean and standard deviations and the Lilliefors p-value, $p_L$, are also given in the table.

The sample distributions for all seven of the estimated $a_{jk}$ parameters are found to be consistent with the normal; six of these are shown in Fig. 9a–f. Additionally, but not shown here, the sample distribution for the first few b parameters from (20) are consistent with normal and with sample variances similar to those of the a parameters. Finally, for the estimates of each parameter, we include the t-score and the p-value of the t-test for $\mu =0$ based on $NSAMP=100$ replicates. Although these tests correctly differentiate the null from the nonnull parameters, we note that in the usual time series analysis, there is only one sample available on which one can base a test.

Fig. 9

Sample distributions of parameter estimates with $N=T=4096$ for selected Fourier coefficients estimated by parmsef. Estimates are based on $NSAMP=100$ replicates

As in Figs. 4 and 5, for each estimated parameter the dependence of $\hat{\sigma }$ on the series length $T=N$ can be seen by fitting a straight line to the $(N, \hat{\sigma })$ as we did in Sect. 3 for the OLS fit to a periodic function with additive noise. Values of $\hat{\sigma }$ were determined for $N=T=(512,1024,2048,4096)$, and this fitting is illustrated in Fig. 10a, b for parameters $a_{11}$ and $a_{14}$, producing values $m= -0.524,-0.508$ in the two cases; the observed data are in blue and and the red line is the result of the OLS straight line fit. The empirical dependence on N is slightly steeper than the expected $m=-1/2$.

Fig. 10

OLS fit (red) of $y=m x + b$ to $\hat{\sigma }$ (blue) as function of $N=T=(512,1024,2048,4096)$ using log10 scales

As a check that the fit has successfully explained the correlation structure in the simulated series, the empirical ACF and PACF were computed for the residual $\hat{Z}_t$ of the fit, resulting in the plots of Fig. 11. Both ACF and PACF are consistent with uncorrelated noise.

Fig. 11

PAR2a run1 $N=4096$, ACF, PACF of PARMSEF residuals from one realization

Finally, to again see the effect of more coefficients with null values we made a run in which parameters $\{a_{11},\dots ,a_{19},a_{21},\dots ,a_{28}\}$ (a total of 17) were estimated, although only 5 had nonzero true values. Figure 12 illustrates the ability to visually perceive the non zero values among the 17 from a sample of 100 simulations.

For each parameter, Table 2 presents true values and estimated means and standard deviations; in addition, the p-value of the Lilliefors test, $p_L$, t-scores and p-values for t-tests for $\mu =0$ are given. As in Table 1, the t-tests correctly differentiate the null from the nonnull parameters, but the more important issue, not addressed here, is the ability of these tests to detect non null parameters from only one sample. Methods for accomplishing this may be based on (1) computed parameter variances (2) estimates of parameter variances based on bootstrapping or simulation.

Fig. 12

Boxplots for PAR2a run1, $N=T=1024$. Active parameters are $\{a_{11},\dots ,a_{19},a_{21},\dots ,a_{28}\}$ (17 total), all null except $a_{11}=1.1, a_{12}=0.6, a_{21}=-0.345, a_{22}=-0.33, a_{24}=-0.045$. Boxplots of parameter estimates are based on 100 replicates

Table 2 Sample $\mu$ and $\sigma$ for 17 selected Fourier coefficients estimated by parmsef. $NSAMP=100$, $N=T=1024$

5 Conclusions

We demonstrated the use of an OLS minimization to estimate the Fourier coefficients of the periodic parameters in a periodic autoregressive model. This method is shown to be effective even when the sample size N is small relative to the period T, say $N=T$. Simulations show that the empirical distributions of parameter estimates are typically normal and standard errors diminish as $N^{-1/2}$ as expected. Topics for future research include (1) improvement of computational methods (2) direct (parametric) computation of estimator standard errors to facilitate the identification of important Fourier coefficients (3) use of simulation or bootstrapping to characterize empirical distributions of parameter estimates (4) extension to PARMA.