Abstract
Partial order reduction covers a range of techniques based on eliminating unnecessary transitions when generating a state space. On the other hand, abstractions replace sets of states of a system with abstract representatives in order to create a smaller state space. This article explores how stubborn sets and abstraction can be combined. We provide examples to provide intuition and expand on some recent results. We provide a classification of abstractions and give some novel results on what is needed to combine abstraction and partial order reduction in a sound way.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The term partial order reduction refers to methods that combat state explosion by eliminating unnecessary transitions. This article focuses on stubborn sets [20]. The theory as presented here, mostly applies to also ample [17] and persistent [9] sets. We use the term “stubborn set method” or “partial order reduction” to mean any method that attempts to reduce the size of a state space by exploring some subset of enabled transitions in each state of a state.
The term abstraction [3] refers to methods that eliminate some features of a system, by mapping the states of a to a smaller set. The goal of abstraction is to preserve counterexamples to specifications while bringing down the complexity of model checking. Abstractions can be thought of as equivalence relations over states and an abstract state space is generated by expanding the relevant transitions that are enabled in the equivalence class. In this sense abstraction includes also methods such as symmetry [5]. Abstractions have been combined with partial order reduction methods both in the early literature and more recently. Significant synergistic benefits between abstraction and reduction was gained with a relaxed zone abstraction of timed automata [11]. In [1], partial order reduction was combined with an abstraction that replaces bisimilar states with a common representative. We discuss the result in this article.
We take the view in this article that transitions of systems are inherently deterministic, i.e., each transition has a unique outcome. We use the term firing for the execution of a single transition. Abstraction may then result in nondeterminism, because an abstraction may not distinguish between two states from which a given transition is fired, while still differentiating between the states that result when the transition is fired.
The interpretation of the transitions from a semantic standpoint is done by associating transitions with actions. Several transitions may be associated with she same action, and this gives rise to the concept of operational (non) determinism, which refers to whether the external behavior of the system is deterministic. The relationship between operational determinism and abstraction is a complicated one, and we provide some insights on the issue in this article.
This article is organized so that we first explore a general theory of transition systems in Sect. 2, which gives the ground theory and semantic models, and also some results regarding determinism. Section 3 defines abstractions and abstract state spaces, and we prove that general abstractions behave monotonously only with linear time semantic models that are not significantly stronger than traces and divergence traces. Then, a state-of-the art version of stubborn sets for preservation of safety properties and some divergence properties are given in Sect. 4. We also discuss some static relations of transitions that can be used for the computation of stubborn sets.
Section 5 provides results about how stubborn sets can be combined with abstraction. We provide a few theorems for certain classes of abstractions, to show how relations for computing the stubborn sets generalize for the abstract state spaces. We also provide some examples that show that the results do not apply for abstractions in general.
The last section provides some concluding remarks and outlines future work.
2 Theoretical Preliminaries
We consider a system where transitions operate on a collection of n variables with domains \(X_1, \ldots , X_n\). The domains will in most cases be numerable, but this need not be the case in general. For example, in the case of timed automata, clocks can assume non-negative real values. We denote the set of syntactically possible states by \(X = X_1 \times \cdots \times X_n\).
A transition is a pair (g, e), where \(g: X \rightarrow \{ true , false \}\) is called a guard and \(e: X \rightarrow X\) is called an effect. The set of transitions of the system is denoted with \(\mathcal T\).
The initial value of a system is denoted \(\hat{x} \in X\). We call the tuple \((X,\mathcal T,\hat{x})\) a system description, or simply a system.
The execution semantics of a system are defined over labeled transition systems (LTSs).
Definition 1 (LTS-unfolding)
An LTS is a 4-tuple \((S, \mathcal T, \varDelta , \hat{s})\), where S is a set of states, \(\varDelta \subseteq S \times \mathcal T\times S\) is a set of semantic transitions, and \(\hat{s}\in S\) is the initial state.
Given a system \(M = (X,\mathcal T, \hat{x})\), the LTS-unfolding of the system M is given as \(L = (S, \mathcal T, \varDelta , \hat{s})\) where
-
\(\hat{s}= \hat{x}\).
-
\(\varDelta \) and S are defined as the minimal sets such that
-
1.
\(\hat{x} \in S\), and
-
2.
whenever \((g,e) = t\) and \(t \in \mathcal T\), \(x \in S\) and \(g(x) = true \), then \(e(x) \in S\) and \((x, t, e(x)) \in \varDelta \).
-
1.
We refer to the LTS-unfolding of the system as the concrete state space of M.
Given an LTS, we define the following notation for convenience. We write \(s \xrightarrow {t} s'\), when \((s,t,s') \in \varDelta \). \(s \xrightarrow {t}\) means that \(\exists s': s \xrightarrow {t} s'\).  means that \(s \xrightarrow {t}\) does not hold. For a sequence \(t_1 t_2 \cdots t_n \in \mathcal T^*\), \(s \xrightarrow {t_1 \cdots t_n} s'\) means that \(\exists s_0, \ldots , s_n\) such that \(s = s_0 \wedge s' = s_n\) and, for \(0 < i \le n\), \(s_{i-1} \xrightarrow {t_i} s_{i}\). When we write \(s_0 \xrightarrow {t_1 \cdots t_n} s_n\), we let \(s_i\) for \(0 < i \le n\), denote the state such that \(s_0 \xrightarrow {t_1 \cdots t_i} s_i\). The set \( en (s) = \{t \in \mathcal T| s \xrightarrow {t}\}\) refers to transitions enabled at s and \( dis (s) = \mathcal T{\setminus } en (s)\) refers to actions disabled at s.
means that \(s \xrightarrow {t}\) does not hold. For a sequence \(t_1 t_2 \cdots t_n \in \mathcal T^*\), \(s \xrightarrow {t_1 \cdots t_n} s'\) means that \(\exists s_0, \ldots , s_n\) such that \(s = s_0 \wedge s' = s_n\) and, for \(0 < i \le n\), \(s_{i-1} \xrightarrow {t_i} s_{i}\). When we write \(s_0 \xrightarrow {t_1 \cdots t_n} s_n\), we let \(s_i\) for \(0 < i \le n\), denote the state such that \(s_0 \xrightarrow {t_1 \cdots t_i} s_i\). The set \( en (s) = \{t \in \mathcal T| s \xrightarrow {t}\}\) refers to transitions enabled at s and \( dis (s) = \mathcal T{\setminus } en (s)\) refers to actions disabled at s.
Because an effect of a transition is a function, a concrete state space is always deterministic, i.e., if \(s \xrightarrow {t} s'\) and \(s \xrightarrow {t} s''\), then \(s' = s''\).
The properties of the system are determined as behaviours interpreted over a set of symbols \(\varSigma \), called actions or events. We assume that a mapping \(l: \mathcal T\rightarrow \varSigma \cup \{\epsilon \}\) is given and fixed, and extended to \(\varSigma ^*\) in the usual manner by concatenating, i.e., for \(l(t_1 \cdots t_n) = l(t_1)l(t_2)\cdots l(t_n)\), and \(\epsilon \) denotes the empty string. We write  when there are transitions \(t_1, \ldots , t_n\) such that \(s \xrightarrow {t_1 \cdots t_n} s'\) \(l(t_1 \cdots t_n) = \sigma \).
when there are transitions \(t_1, \ldots , t_n\) such that \(s \xrightarrow {t_1 \cdots t_n} s'\) \(l(t_1 \cdots t_n) = \sigma \).
In keeping with tradition, when there is some \(t \in \mathcal T\) such that \(l(t) = a\) and \(s \xrightarrow {t} s'\), we also write \(s \xrightarrow {a} s'\), except when \(a = \epsilon \), when we write \(s \xrightarrow {\tau } s'\). We refer to such transitions as \(\tau \)-transitions or invisible transitions. We write \(\sigma \le \rho \) if \(\sigma \) is a prefix of \(\rho \) and \(\sigma < \rho \) if it is a proper prefix.
A semantic model is an equivalence or pre-order relation for systems or LTSs. For the purpose of this article, we consider semantics over LTSs. Two systems are considered equivalent if and only if their concrete state spaces are equivalent.
There are several semantic models which can be considered, we shall consider only a few most relevant. Note that we restrict this study to linear time properties. The sets of traces, divergence traces, failures, and stable failures of an LTS are defined as:
-
\(\mathsf {Tr}(L)\,{=}\)
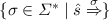
-
\(\mathsf {Divtr}(L)\,=\)

-
\(\mathsf {Mindiv}(L)\,{=}\) \(\{\sigma \in \mathsf {Divtr}(L) \mid \forall \rho < \sigma : \rho \notin \mathsf {Divtr}(L)\}\)
-
\(\mathsf {Fail}(L)\,{=}\)

-
\(\mathsf {Sfail}(L)\,{=}\)

-
\(\mathsf {CSP}(L)\,{=}\) \(\mathsf {Sfail}(L) \cup \{(\sigma , X) \mid \exists \rho : \rho \le \sigma \wedge \rho \in \mathsf {Divtr}(L) \wedge X \in 2^\varSigma \}\)
The \(\mathsf {CSP}\)-set is known as the failures-divergences-model, which is named like this as it is commonly associated with the process-algebra CSP [18]. It preserves \(\mathsf {Sfail}\) up to minimal divergence traces, and all divergence traces are extended with maximal behaviour in terms of \(\mathsf {Sfail}\). It is also worth to mention the so called CFFD-equivalence [24], which preserves infinite traces, \(\mathsf {Sfail}\), and \(\mathsf {Divtr}\). It also preserves, under suitable interpretation, all linear temporal logic properties of a system. A comprehensive survey of different semantic models and epistemological considerations behind them can be found in [26].
Let \(L_1\) and \(L_2\) be LTSs. We write \(L_1 \sqsubseteq _{\mathsf {Tr}} L_2\) if and only if \(\mathsf {Tr}(L_1) \subseteq (L_2)\). For the other semantic sets \(L_1 \sqsubseteq _{X} L_2\) is defined analogously. We also write \(L_1 \sqsubseteq _{X,Y} L_2\) to mean \(L_1 \sqsubseteq _{X} L_2 \wedge L_1 \sqsubseteq _{Y} L_2\) If \(L_1 \sqsubseteq _{X} L_2\) and \(L_2 \sqsubseteq _{X} L_1\), we say that \(L_1\) and \(L_2\) are X-equivalent, and write \(L_1 \equiv _X L_2\). We also write \(M_1 \sqsubseteq _{X} M_2\) if and only \(L_1 \sqsubseteq _{X} L_2\), where \(L_1\) and \(L_2\) are concrete state spaces of \(M_1\) and \(M_2\). We abuse the notation slightly by writing  and \(s \sqsubseteq _{X} s'\) for states analogously.
and \(s \sqsubseteq _{X} s'\) for states analogously.
We distinguish between determinism of the transition system, and operational determinism, i.e. determinism from the point of view of the actions it performs. Operational determinism, also known as determinacy [12, 16] is defined as follows.
Definition 2
An LTS \(L = (S, \mathcal T, \varDelta , \hat{s})\) is operationally deterministic if and only if for all traces \(\sigma \), if  and
and  , then
, then
-
1.
For each \(a \in \varSigma \),
 if and only if
if and only if  , and
, and -
2.
\(s_1 \xrightarrow {\tau ^\omega }\) if and only if \(s_2 \xrightarrow {\tau ^\omega }\).
Except for the treatment of divergences, all the semantic equivalences between trace + divergence trace equivalence and divergence sensitive branching bisimulation collapse into one equivalence for operationally deterministic LTSs [6, 12].
The following theorem is evident.
Theorem 1
For every LTS L, there exists an operationally deterministic \(L_D\) such that \(L \equiv _{\mathsf {Tr},\mathsf {Divtr}} L_D\).
For trace equivalence the theorem is well-known, and for finite LTSs a simple variant of the block-splitting algorithm produces exactly the equivalent LTS. For divergence traces, it is sufficient to store a local \(\tau \)-loop in diverging states.
We provide a significant strengthening of [12, Corollary 1]. The following lemma applies in the absence of divergences.
Lemma 1
Assume there are no divergences and \(L_1 \equiv _{\mathsf {Fail}} L_2\). Then \(L_1\) is operationally deterministic if and only if \(L_2\) is.
Proof
Let  in \(L_1\). Now, there must be a state \(s_2\) of \(L_2\) such that
in \(L_1\). Now, there must be a state \(s_2\) of \(L_2\) such that  , due to trace equivalence, which is implied by \(\mathsf {Fail}\)-equivalence. Assume that \(L_1\) is operationally deterministic and denote by
, due to trace equivalence, which is implied by \(\mathsf {Fail}\)-equivalence. Assume that \(L_1\) is operationally deterministic and denote by  and
and  . Firstly, assume \(a \notin F_1\). If
. Firstly, assume \(a \notin F_1\). If  , \(F_2 \ne F_1\), which contradicts \(\mathsf {Fail}\)-equivalence. Secondly, assume \(a \in F_1\). Then \(\sigma a\) is not a trace of \(L_1\) because \(L_1\) is operationally deterministic, so that \(a \in F_2\) must also hold. This implies \(F_2\) must be the same for every such state and hence \(L_2\) is operationally deterministic. \(\square \)
, \(F_2 \ne F_1\), which contradicts \(\mathsf {Fail}\)-equivalence. Secondly, assume \(a \in F_1\). Then \(\sigma a\) is not a trace of \(L_1\) because \(L_1\) is operationally deterministic, so that \(a \in F_2\) must also hold. This implies \(F_2\) must be the same for every such state and hence \(L_2\) is operationally deterministic. \(\square \)
Theorem 2
Let \(L_1 \equiv _{\mathsf {Divtr},\mathsf {Sfail}} L_2\). Then \(L_1\) is operationally deterministic if and only if \(L_2\) is.
Proof
Assume \(L_1\) is operationally deterministic. Let  in \(L_1\) and
in \(L_1\) and  in \(L_2\). If \(s_1\) is not diverging, \(s_2\) cannot be diverging either due to \(\mathsf {Divtr}\)-equivalence. Lemma 1 guarantees then that \(s_1\) and \(s_2\) must agree on failures.
in \(L_2\). If \(s_1\) is not diverging, \(s_2\) cannot be diverging either due to \(\mathsf {Divtr}\)-equivalence. Lemma 1 guarantees then that \(s_1\) and \(s_2\) must agree on failures.
If \(s_1\) is diverging, then \(\sigma \in \mathsf {Divtr}(L_1)\), and \((\sigma ,X) \notin \mathsf {Sfail}(L_1)\) for any X. Thus \(s_2\) must also be diverging, or there would be \((\sigma , X) \in \mathsf {Sfail}(L_2)\) for some X, which would contradict equivalence. \(\square \)
Theorem 2 is strong enough for the purpose of this article, but we conjecture that a stronger theorem would hold. In process-algebra terms, with a reasonable set of operators, if \(\equiv _P\) is a “reasonable” congruence and \(L_1 \equiv _P L_2\) for any nondeterministic \(L_1\) and \(L_2\), then P is not stronger than \(\mathsf {Tr},\mathsf {Divtr}\). We leave the exact formulation of “reasonable” and research of the theory for future research.
The failures/divergences theory associated with CSP considers divergence as chaos, or maximally nondeterministic behaviour. Neither Theorem 1 nor 2 holds for \(\mathsf {CSP}\)-equivalence, the counterexample to the latter is shown in Fig. 1. An operationally deterministic LTS may be \(\mathsf {CSP}\)-equivalent with a nondeterministic one. It should be noted, however, that the interpretation of operational determinism we use is different from the one usually associated with CSP, as it is customary to assume that diverging processes are not deterministic in the context of CSP.
A system is specified in terms of some semantic model P by giving a set \(\mathcal L\), or, alternatively, an LTS that has the requires semantics. We say that the system M satisfies the specification if \(P(L) \subseteq \mathcal L\) where L is the concrete state space of M. If M does not satisfy the specification, then there exists some behaviour that is not in \(\mathcal L\). For example, if we specify in terms of traces, then  such that \(\sigma \notin \mathcal L\). The execution \(\hat{s}\xrightarrow {t_1 \cdots t_n} s\) such that \(l(t_1 \cdots t_n) = \sigma \) is called a (concrete) counterexample. Similarly, a counterexample with respect to \(\mathsf {Divtr}\) or \(\mathsf {Sfail}\) is execution of L that diverges or has a stable failure not specified by \(\mathcal L\).
such that \(\sigma \notin \mathcal L\). The execution \(\hat{s}\xrightarrow {t_1 \cdots t_n} s\) such that \(l(t_1 \cdots t_n) = \sigma \) is called a (concrete) counterexample. Similarly, a counterexample with respect to \(\mathsf {Divtr}\) or \(\mathsf {Sfail}\) is execution of L that diverges or has a stable failure not specified by \(\mathcal L\).
3 Abstraction
Definition 3
Let \(M = (X,\mathcal T, \hat{x})\) be a system and \(X'\) be any set. An abstraction of the system \(\alpha \) is a mapping \(\alpha : X \rightarrow X'\), and an abstract unfolding or \(\alpha \)-unfolding of M is the LTS \(L^\alpha = (S^\alpha ,\mathcal T, \varDelta ^\alpha , \hat{s}^\alpha )\), which is the minimal LTS satisfying
-
1.
\(S^\alpha \subseteq X'\).
-
2.
\(\hat{s}^\alpha = \alpha (\hat{x}) \in S^\alpha \).
-
3.
\((x_1,t,x_2) \in \varDelta ^\alpha \) only if \(x_1 \in S^\alpha \), and \(\exists x, y \in X: \alpha (x) = x_1\) and \(g(x) = true \), \(y = e(x)\) and \(\alpha (y) = x_2\).
-
4.
If \(x_1 \in S^\alpha \), \(\exists x, y \in X: \alpha (x) = x_1\) and \(g(x) = true \), \(y = e(x)\) and \(\alpha (y) = x_2\), and \(x_2 \ne x_1\) or \(l(t) \in \varSigma \), then \((x_1,t,x_2) \in \varDelta ^\alpha \).
We refer to the \(\alpha \)-unfolding as an abstract state space. Please note that as per the definition, \(L^\alpha \) is not required to preserve such \(\tau \)-transitions of L that firing the transition results in the same abstract state, though it is allowed to do so.
We use otherwise the same notation for abstract state spaces, but to avoid confusion we write \(\xrightarrow {t}_\alpha \) and  for transitions and executions. An abstract unfolding gives rise to a different semantic sets than the concrete unfolding. For example, if \(\mathcal L\) is a specification in terms of traces and given an abstraction \(\alpha \), an abstract counterexample is an execution \(\hat{s}^\alpha \xrightarrow {t_1 \cdots t_n}_\alpha \) such that \(l(t_1 \cdots t_n) \notin \mathcal L\).
for transitions and executions. An abstract unfolding gives rise to a different semantic sets than the concrete unfolding. For example, if \(\mathcal L\) is a specification in terms of traces and given an abstraction \(\alpha \), an abstract counterexample is an execution \(\hat{s}^\alpha \xrightarrow {t_1 \cdots t_n}_\alpha \) such that \(l(t_1 \cdots t_n) \notin \mathcal L\).
If \(\alpha \) is the identity mapping on X, then \(L^\alpha \) is simply the unfolding of the system. Each \(\alpha \) with range \(X'\) induces an equivalence relation for the states of the concrete state space, such that \(s, s'\in S\) are equivalent if \(\alpha (s) = \alpha (s')\). We denote by \(X_\alpha = \{[s]_\alpha \mid s \in S\}\) where \([s]_\alpha = \{x \in X: \alpha (x) = \alpha (s)\}\). We mostly use this notation and write \([s]_\alpha \) for the states of \(L^\alpha \).
If \(\alpha _1\) and \(\alpha _2\) are abstractions, we write \(\alpha _1 \prec \alpha _2\) iff for every \(s \in X\) we have \([s]_{\alpha _1} \subseteq [s]_{\alpha _2}\). We say in such a case that \(\alpha _1\) is a refinement of \(\alpha _2\), and \(\alpha _2\) is said to be coarser than \(\alpha _1\). The identity mapping on X is a refinement of every abstraction, and a mapping that maps the whole of X into a single element set is the coarsest possible abstraction.
It is possible that the abstract unfolding is nondeterministic: if there are two states u, v such that \(\alpha (u) = \alpha (v)\), and \((u,t,w_1)\) and \((v,t,w_2)\) are two (concrete) transitions, it may still be that \(\alpha (w_1) \ne \alpha (w_2)\). To complicate matters further, it may be that \(\alpha _1 \prec \alpha _2\) such that \(L^{\alpha _1}\) is nondeterministic and \(L^{\alpha _2}\) is deterministic. Consider Fig. 2. The fist LTS is a concrete state space, and we have two abstractions, \(\alpha _1 \prec \alpha _2\). \(L^{\alpha _1}\) is nondeterministic, while \(L^{\alpha _2}\) is deterministic.
We give here some properties of abstractions that can be used firstly, to overcome the limitation imposed by Theorem 3, and secondly, to deduce some important properties later when we combine abstractions with reductions.
Definition 4
Let \(M = (X, \mathcal T, \hat{x})\), where \(X = X_1 \times \cdots \times X_n\). Let \(\mathcal A\) be a collection of abstractions for M We say that \(\mathcal A\)
-
respects divergences if and only if for every \(\alpha \in \mathcal A\), \([s]_\alpha \xrightarrow {\tau }_\alpha [s]_\alpha \) implies that there is some \(s' \in [s]_\alpha \) such that \(s' \xrightarrow {\tau ^\omega }\),
-
preserves divergences if and only if for every \(\alpha \in \mathcal A\) if there are \(s_0, \ldots , s_{n-1} \in [s]_\alpha \) and \(s_0 \xrightarrow {\tau } s_1 \xrightarrow {\tau } \cdots \xrightarrow {\tau } s_{n-1} \xrightarrow {\tau } s_0\), then \([s]_\alpha \xrightarrow {\tau }_\alpha [s]_\alpha \),
-
is monotonous with respect to the semantic model P if and only if for every \(\alpha _1, \alpha _2 \in \mathcal A\), if \(\alpha _1 \prec \alpha _2\), then \(L^{\alpha _1} \sqsubseteq _{P} L^{\alpha _2}\),
-
preserves the semantic model P if and only if for every \(\alpha \in \mathcal A\), \(s \in S\) \(\alpha (s) \equiv _{P}~s\),
-
respects the semantic model P if and only if for every \(\alpha \in \mathcal A\), \(s_1, s_2 \in S\), \(s_1 \sqsubseteq _{P} \alpha (s_1)\).
-
is a collection of 1-simulations if and only if for every \(\alpha \in \mathcal A\), \(s_1,s_2,s_3 \in S\), and \(t \in \mathcal T\), if \(s_1 \xrightarrow {t} s_2\), \(\alpha (s_1) = \alpha (s_3)\) and \(s_3 \xrightarrow {t}\), then there exists \(s_4 \in S\) such that \(s_3 \xrightarrow {t} s_4\) and \(\alpha (s_3) = \alpha (s_4)\),
-
preserves (operational) determinism if and only if for every \(\alpha _1, \alpha _2 \in \mathcal A\) such that \(\alpha _1 \prec \alpha _2\), \(L^{\alpha _2}\) is (operationally) deterministic if \(L^{\alpha _1}\) is (operationally) deterministic,
-
respects enabling if and only if, for every \(\alpha \in \mathcal A\), if \([s]_\alpha = [s']_\alpha \), then \( en (s) = en (s')\),
-
\(\mathcal A\) respects stability if and only if, for every \(\alpha \in \mathcal A\), if \([s]_\alpha = [s']_\alpha \), then either (1) neither s, \(s'\) or \([s]_\alpha \) is stable, or (2) there exist stable states \(s_1, s_1' \in [s]_\alpha \) such that
 ,
,  and \( en (s_1) = en (s_1') = en ([s]_\alpha )\),
and \( en (s_1) = en (s_1') = en ([s]_\alpha )\), -
separable if and only if, for every \(\alpha \in \mathcal A\) where \(\alpha : X \rightarrow X'\), \(X' = X'_1 \times \cdots X'_n\), and there exists \(\alpha _1, \ldots \alpha _n\), \(\alpha _i: X_i \rightarrow X_i'\) for \(i = 1,\ldots ,n\), such that for \(x = (x_1, \ldots , x_n) \in X\), \(\alpha (x) = (\alpha _1(x_1), \ldots , \alpha _n(x_n))\).
From these definitions, the following proposition is self-evident.
Proposition 1
An arbitrary collection of abstractions is monotonous with respect to \(\mathsf {Tr}\). If it preserves divergences, it is also monotonous with respect to \(\mathsf {Divtr}\).
As a corollary, every concrete counterexample to \(\mathsf {Tr}\) or \(\mathsf {Divtr}\) specification has a corresponding abstract counterexample regardless of abstraction. Proposition 1 is the main reason why we adopt the trace model as our canonical model, as other semantic models are less robust with respect to abstraction.
Theorem 3
Assume P is a semantic model that preserves \(\mathsf {Fail}\). There exists a family of abstractions \(\mathcal A\) such that \(\mathcal A\) preserves divergences, and there are \(\alpha _1, \alpha _2 \in \mathcal A\), \(\alpha _1 \prec \alpha _2\) and some L such that \(L^{\alpha _1} \not \sqsubseteq _{P} L^{\alpha _1}\).
Proof
Theorem 2 and the example in Fig. 2 prove this. \(\square \)
Theorem 3 together with Theorem 2 mean that except for \(\mathsf {Tr}\) and \(\mathsf {Divtr}\), abstraction in general is not guaranteed to preserve counterexamples.
Proposition 2
If \(\mathcal A\) is a collection of 1-simulations that preserves and respects divergences and respects stability, then \(\mathcal A\) preserves operational determinism.
Proof
Assume L is operationally deterministic. Then there exists a D-relation as described in [12, Definition 8] on the states of L. Denote this D-relation with \(\sim \). It is simple to show that if \(\alpha \) is a 1-simulation that preserves and respects divergences and stability, then \(\alpha (s_1) = \alpha (s_2)\) implies \(s_1 \sim s_2\). \(\square \)
Theorem 4
Assume \(\mathcal A\) respects stability and preserves divergences. Then \(\mathcal A\) is monotonous with respect to \(\mathsf {CSP}\).
Proof
Let \(\alpha , \beta \in \mathcal A\) and \(\mathcal A\) respects stability, and \(\alpha \prec \beta \). Let \((\sigma , A) \in \mathsf {Sfail}(L^\alpha )\). Then there is a stable state \([s]_\alpha \) such that  , and \(A \cap en (s) = \emptyset \). Then
, and \(A \cap en (s) = \emptyset \). Then  holds, and either \([s]_\beta \) is diverging or it is stable and \( en ([s]_\beta ) = en ([s]_\alpha )\), so that \((\sigma ,A) \in \mathsf {Sfail}(L^\beta )\) \(\square \)
holds, and either \([s]_\beta \) is diverging or it is stable and \( en ([s]_\beta ) = en ([s]_\alpha )\), so that \((\sigma ,A) \in \mathsf {Sfail}(L^\beta )\) \(\square \)
Example 1
Consider the mapping h(s) which returns a representative of s in the equivalence class under a strong bisimulation relation. The quotient \(L^h\) where \(S^h = \{h(s) \mid s \in S\}\) and \(\varDelta ^h\) is \(\varDelta \) restricted to \(S^h\). \(L^h\) is strongly bisimilar to L. When \(\mathcal A\) consists of strong bisimulations the abstractions preserve virtually all reasonable semantic models. Such abstractions were used in [1].
Example 2
In Predicate abstraction, a set of predicates over states is defined, and an abstract state consists of the set of states which agree on the truth value of all predicates. Predicate abstraction is used for example in the so-called CEGAR approach [2]. Predicate abstraction is not separable or monotonous in general, nor does it respect enabling or stability.
The abstractions described in [2], however, do result in \(\mathcal A\) that respects enabledness, because the coarsest abstraction h has the property that for every guard g, \(h(s) = h(s')\) if and only if \(g(s) = g(s')\).
Example 3
Data abstraction or value abstraction is a general term for abstractions that replace the set of values of a variable with a smaller set. Data abstractions are easily expanded into separable sets of abstractions, where each variable is abstracted separately.
4 Stubborn Set Reductions
4.1 State-of-the Art for Finite Traces
In this section we start with definition of stubborn sets that is as such applicable to any LTSs.
Definition 5 (Reduced LTS)
Given an LTS \((S, \mathcal T, \varDelta , \hat{s})\), a function \(T: S \mapsto 2^{\mathcal T}\) is a reduction function. We define the reduced LTS of L by T, as \(L_T = (S_T,\mathcal T, \varDelta _T, \hat{s})\), where \(S_T\) and \(\varDelta _T\) are minimal subsets of S and \(\varDelta \), respectively, that satisfy the following conditions:
-
\(\hat{s}\in S_T\), and
-
if \(s \in S_T\), \(s \xrightarrow {t} s'\) and \(t \in T(s)\), then \(s' \in S_T\) and \((s,t,s') \in \varDelta _T\).
By definition, a reduced LTS is a sub-LTS of the original LTS. For the remainder of this section we shall refer to \(L_T\) an L as the reduced and full LTSs, respectively. The properties preserved in the reduction depend on the properties of the reduction function. The term stubborn set in this article is a collective term for the sets produced by reduction functions. We describe the stubborn set reduction functions by giving various conditions.
Such conditions can be given towards one of two goals. The first goal, adopted in most of the literature on partial order reduction, is to provide a set of conditions sufficient for preserving the semantics of the system in the fullest. In the case of traces, this would mean that the reduced LTS should be trace-equivalent to the original. That is, the reduced LTS should satisfy \(\mathsf {Tr}(L) = \mathsf {Tr}(L_T)\). We will explore such conditions in what follows, but they will be of secondary importance.
The second goal, one which we shall be primarily aiming for, is the preservation of the existence of a counterexample. For example, with traces, given a specification \(\mathcal L\), the reduction should satisfy \(\mathsf {Tr}(L) \cap \mathcal L\ne \emptyset \) if and only if \(\mathsf {Tr}(L_T) \cap \mathcal L\ne \emptyset \).
We introduce the conditions incrementally to make them more understandable. The first two (or their equivalents in the case for abstract state spaces) are common to all versions. We also give a third condition, which is more restrictive, but it is used in practical analysis. Every condition is given for a state s.
- D1. :
-
For every \(t \in T(s)\) and \(t_1, \ldots , t_k \notin T(s)\), if \(s \xrightarrow {t_1 \cdots t_k t} s'\), then \(s \xrightarrow {t t_1 \cdots t_k} s'\).
- N. :
-
There exists \(t \in T(s)\) such that for every \(t_1, \ldots , t_k \notin T(s)\), if \(s \xrightarrow {t_1 \cdots t_k}\) and \(s \xrightarrow {t} s'\), then \(s' \xrightarrow {t_1 \cdots t_k}\). Such a transition is called a neutral transition.
- D2. :
-
For every \(t \in T(s)\) and every \(t_1, \ldots , t_k \notin T(s)\), if \(s \xrightarrow {t}\), then \(s'\xrightarrow {t_1 \cdots t_k t}\).
The classical stubborn sets are defined using \(\mathbf {D1}\) and \(\mathbf {D2}\); \(\mathbf {D1}\) and \(\mathbf {D2}\) clearly imply \(\mathbf {N}\). We give our theoretical treatment for \(\mathbf {N}\) as it theoretically has the potential to overcome the optimality result of [22]. The conditions above are not sufficient for preservation of properties such as traces. This stems from two issues. The first one is that they allow the reduction to ignore permutations of transitions in such a way that the order of symbols in the trace is not preserved.
The trace-preserving version requires the concept of visible transition. A transition t is visible if and only if \(l(t) \ne \epsilon \), i.e., if its occurrence in an execution has an effect on the trace.
- V. :
-
If there is some visible transition \(t \in T(s)\) such that \(t \in en (s)\), then T(s) contains all visible transitions, including the disabled ones.
But for preserving counterexamples, we do not need to be quite as strict. Assume  and \(\sigma \rho \notin \mathcal L\). Let \(u_1, \ldots , u_n \in \mathcal T\) such that \(\rho = l(u_1 \cdots u_n)\). We define the following conditions:
and \(\sigma \rho \notin \mathcal L\). Let \(u_1, \ldots , u_n \in \mathcal T\) such that \(\rho = l(u_1 \cdots u_n)\). We define the following conditions:
- Va. :
-
If \(u_i \in T(s)\) for some i and \(u_j \notin T(s)\) for \(1 \le j < i\), then for some prefix of \(\rho ' \le l(u_i u_1 \cdots u_{i-1} u_{i+1} \cdots u_n)\), \(\sigma \rho ' \notin \mathcal L\).
- Vb. :
-
If \(u_i \notin T(s)\) for each i, then there is a neutral transition \(t \in T(s)\) such that for some prefix \(\rho ' \le l(t u_1 \cdots \cdots u_n)\), \(\sigma \rho ' \notin \mathcal L\).
Verbally, the condition \(\mathbf {Va}\) states that if we take a transition that is a part of a counterexample, then commuting the said transition to the front of the execution will also result in a counterexample. \(\mathbf {Vb}\) states that if we explore a neutral transition and ignore transitions remaining of a counterexample, we can still continue and find a counterexample. Note that \(\mathbf {V}\) trivially implies \(\mathbf {Va}\) by forcing all visible transitions in the stubborn set and \(\mathbf {Vb}\) is implied when the stubborn set contains only \(\tau \)-transitions.
We still need to solve the so-called ignoring problem, where neutral transitions are taken indefinitely. Such a scenario is possible if the system contains, for example, a cycle consisting of neutral transitions. To ensure progress, the literature suggests rather crude rules such as those requiring that the stubborn set contains all transitions if a cycle is closed. We forgo such rules for a more nuanced approach.
We need to define the set of interesting transitions at a state s. If we set out to preserve all traces, the set of interesting transitions will be the set of visible transitions in every state. When we set out to preserve only the existence of counterexamples, we can choose the set of interesting transitions in several ways, as long as it has the property that all possible ways of completing a counterexample will contain at least one interesting transition.
We say that a set U of transitions is interesting at state s for every relevant execution  there is some \(1 \le i \le n\) such that \(t_i \in U\). Note that “relevant execution” may mean one of several things. If the reduction must preserve all traces, then \(U = \{t \mid l(t) \in \varSigma \}\), the set of visible transitions must be interesting. If it must preserve counterexamples of some type, then the set must guarantee that every counterexample that visits s, requires the firing of at least one interesting transition at s.
there is some \(1 \le i \le n\) such that \(t_i \in U\). Note that “relevant execution” may mean one of several things. If the reduction must preserve all traces, then \(U = \{t \mid l(t) \in \varSigma \}\), the set of visible transitions must be interesting. If it must preserve counterexamples of some type, then the set must guarantee that every counterexample that visits s, requires the firing of at least one interesting transition at s.
We say that a set \(W \subseteq \mathcal T\) is closed under enabling at state s, if for every \(t \in W\), \(s \xrightarrow {t_1 \cdots t_n t}\) implies that either \(s \xrightarrow {t}\) or \(t_i \in W\) for some \(1 \le i \le n\).
- S. :
-
There exists a set W that is closed under enabling at s and contains all interesting transitions, and for every \(u \in W \cap en (s)\) there exists a sequence \(s \xrightarrow {t_1 \cdots t_n} s'\) of neutral transitions such that \(u \in T(s')\).
The proof of the following theorem was given in [13].
Theorem 5
Let \(\mathcal L\) be a trace specification. If T is a reduction function that satisfies conditions \(\mathbf {D1}\), \(\mathbf {N}\), \(\mathbf {Va}\), \(\mathbf {Vb}\), and \(\mathbf {S}\). Then \(L_T\) has a trace \(\sigma \notin \mathcal L\) if and only if L some trace \(\rho \notin \mathcal L\).
Proof
If \(L_T\) has an illegal trace, then L trivially has an illegal trace, because all traces of \(L_T\) are traces of L. The other direction is by induction on the unexplored part of an illegal trace. Let s be a state of \(L_T\). The situation where  and \(\sigma \notin \mathcal L\) is the trivial base case. Let \(\sigma \rho \notin \mathcal L\) be some trace of \(L_T\) and let
and \(\sigma \notin \mathcal L\) is the trivial base case. Let \(\sigma \rho \notin \mathcal L\) be some trace of \(L_T\) and let  be such that
be such that  . Let \(u_1, \ldots , u_n \in \mathcal T\) be transitions such that \(s \xrightarrow {u_1 \cdots u_n}\) and \(l(u_1 \cdots u_n) = \rho \).
. Let \(u_1, \ldots , u_n \in \mathcal T\) be transitions such that \(s \xrightarrow {u_1 \cdots u_n}\) and \(l(u_1 \cdots u_n) = \rho \).
Firstly, assume \(u_i \in T(s)\) for some \(1 \le i \le n\), and without loss of generality, assume i is chosen as the minimal such i. Let \(s_i\) be such that \(s \xrightarrow {u_1 \cdots u_i} s_i\) and Now, \(\mathbf {D1}\) guarantees that \(u_i\) must be enabled and that \(s \xrightarrow {u_i u_1 \cdots u_{i-1}} s_i\). Then \(s \xrightarrow {u_i}_T s'\) holds for some state. \(\mathbf {Va}\) then guarantees that some prefix of \(s' \xrightarrow {u_1 \cdots u_{i-1} u_{i+1} \cdots u_n}\) completes the illegal trace, and we have an inductive step.
Secondly, assume that \(t_i \notin T(s)\) for every \(1 \le i \le n\). Then \(\mathbf {N}\) guarantees there is a neutral transition \(t \in T\) such that \(s \xrightarrow {t}_T s'\) and \(s' \xrightarrow {u_1 \cdots u_n}\). \(\mathbf {Vb}\) then guarantees that some prefix of \(l(t u_1 \cdots u_n)\) will complete the illegal trace, so that \(\sigma l(t) \rho ' \notin \mathcal L\), where \(\rho '\) is some prefix of \(\rho \). If the prefix is shorter than \(\rho \), this constitutes an inductive step.
If \(\rho = \rho '\), we need to employ \(\mathbf {S}\). Note that because \(s \xrightarrow {u_1 \cdots u_n}\) completes an illegal trace, it is guaranteed that \(u_i\) is interesting in s for some \(1 \le i \le n\). Let \(u_k\) be interesting. Let W be the set stipulated by \(\mathbf {S}\) that is closed under enabling. Because it W is closed under enabling, then some \(u_i \in W\) such that \(u_i\) is enabled at s and \(i < k\). Then there exists \(s_0 \xrightarrow {t_1}_T s_1 \xrightarrow {t_2}_T \cdots \xrightarrow {t_m}_T s_m\) of neutral transitions such that \(s_0 = s\) and \(u_i \in T(s_m)\). \(\mathbf {N}\) guarantees that in each of these states \(s_l\), as long as \(u_j \notin T(s_l)\) for \(1 \le j \le n\), \(s_{l+1} \xrightarrow {u_1 \cdots u_n}\) holds, and \(\mathbf {Vb}\) guarantees some prefix \(u_1 \cdots u_n\) of completes the illegal trace from \(s_{l+1}\). If \(u_j \in T(s_l)\) for some \(1 \le j \le n\) and \(1 \le l < m\), the first inductive case materializes. At the latest in \(s_m\) this happens, because \(u_i \in T(s_m)\). \(\square \)
4.2 Stable Failures, Divergences, and Branching Time
The condition \(\mathbf {S}\), \(\mathbf {Va}\) and \(\mathbf {Vb}\) are sufficient for finite counterexamples, but not in general for infinite traces; we cannot just extend \(\mathbf {Va}\) to infinite traces. Consider the language over \(\varSigma = \{a,b\}\) that contains all infinite traces such that either a or b (but not both) can appear infinitely many times. Counterexamples consist of infinite sequences where both a and b appear infinitely many times. Consider Fig. 3(a). We label the transitions directly with elements of \(\varSigma \). \(\mathbf {Va}\) and \(\mathbf {Vb}\) are satisfied by exploring only a in the initial state, because if \(\rho \) is an infinite counterexample of any kind, then \(a \rho \) is also. This holds no matter how many finite steps we have taken, both a and b are needed to complete counterexamples, i.e., every counterexample contains at least an a-transition, so that \(\{a\}\) is interesting and it is immediately chosen as the stubborn set. It is also neutral with respect to b. \(\mathbf {V}\) would be sufficient with \(\mathbf {S}\) to preserve traces, and this implies for finite systems that infinite traces are preserved.
Consider then Fig. 3(b) and the requirement that \(\mathsf {Divtr}\subseteq \{\epsilon \}\). Counterexamples to this include any divergences after any visible transitions. In the initial state \(\{\tau _1, \tau _2\}\) is a stubborn set that satisfies \(\mathbf {V}\) in addition to all the conditions in Theorem 5. Because \(a \tau _1^\omega \) is a counterexample, \(\tau _1\) is interesting because it is needed before any counterexample is finished. \(\tau _2\) is neutral, as \(\xrightarrow {a}\) is the only execution consisting of transitions that are not in the stubborn set, and it is preserved.
The best conditions for preserving all divergence traces all require conditions such as the following. It has recently been discussed in [23].
- L. :
-
For every visible transition t, every infinite execution \(s_0 \xrightarrow {t_1}_T s_1 \xrightarrow {t_2}_T \cdots \) in the reduced state space contains a state \(s_i\) such that \(t \in T(s_i)\).
For finite state spaces, this is called a cycle condition because all infinite executions are cyclic. We shall not explore their use in this article.
For \(\mathsf {CSP}\)-semantics the problem in Fig. 3 does not manifest, because \(\mathsf {CSP}\) does not require us to preserve all divergences, only minimal ones, which then are extended with otherwise maximal behaviour. The traditional stubborn sets as described, for example, in [21, 23], require the conditions \(\mathbf {V}\) and a condition called \(\mathbf {I}\), which unfortunately loses its meaning when we use the condition \(\mathbf {N}\).
- IN. :
-
T(s) contains either a neutral \(\tau \)-transition or all \(\tau \)-transitions.
Lemma 2
If T is a reduction function that satisfies \(\mathbf {D1}\), \(\mathbf {N}\) and \(\mathbf {IN}\) in every state of \(L_T\), and if \(s \xrightarrow {\tau ^\omega }\), then \(s \xrightarrow {\tau ^\omega }_T\).
Proof
Let s be a state of \(L_T\) and let \(s \xrightarrow {t_1 t_2 \cdots }\) be a diverging execution starting from s. If none of \(t_i\) is in T(s), then \(\mathbf {IN}\) guarantees there is a neutral \(\tau \)-transition t and \(s'\) such that \(s \xrightarrow {t}_T s'\) and \(s' \xrightarrow {t_1 t_2 \cdots }\). On the other hand, if \(t_i \in T(s)\) for some i, we choose the minimal i such that this holds. then let \(s \xrightarrow {t_1 t_2 \cdots t_i} s_i\). \(\mathbf {D1}\) guarantees that \(s \xrightarrow {t_i}_T s'\) for some \(s'\) such that \(s' \xrightarrow {t_1 t_2 \cdots t_{i-1} t_{i+1} \cdots }\).
This gives an infinite sequence of \(\tau \)-transitions in \(L_T\) whenever a state is diverging. \(\square \)
Unfortunately \(\mathbf {D1}\), \(\mathbf {N}\) and \(\mathbf {IN}\) are not enough, even with \(\mathbf {V}\), to preserve stable failures, as is witnessed by Fig. 4, but \(\mathbf {D1}\), \(\mathbf {D2}\), \(\mathbf {V}\) and \(\mathbf {IN}\) are. In the presence of \(\mathbf {D2}\) all transitions are neutral, so \(\mathbf {IN}\) is equivalent to \(\mathbf {I}\). Various solutions that use conditions more restrictive than \(\mathbf {N}\) have been used in practice with good empirical results when preserving traces or \(\mathsf {CSP}\) [8, 14].
For completeness we restate the important results that are well-known about preservation of the semantic models discussed earlier, as well as one for branching properties. We need two further conditions.
- D0. :
-
\( en (s) \cap T(s) = \emptyset \) if and only if \( en (s) = \emptyset \).
- B. :
-
\( en (s) \subseteq T(s)\) or \(T(s) \cap en (s)\) contains a single invisible transition.
Theorem 6
Assume T satisfies \(\mathbf {D1}\) at every state of \(L_T\). Then the following hold:
-
1.
If T satisfies \(\mathbf {D0}\) and \(\mathbf {D2}\) at every state of \(L_T\), then \(L_T\) contains all reachable states s of L such that \( en (s) = \emptyset \).
-
2.
If all visible transitions are interesting and T satisfies \(\mathbf {N}\), \(\mathbf {IN}\), and \(\mathbf {V}\) at every state of \(L_T\), then \(L_T \equiv _{\mathsf {Mindiv}} L\).
-
3.
If all visible transitions are interesting and T satisfies \(\mathbf {D2}\), \(\mathbf {S}\), \(\mathbf {IN}\), and \(\mathbf {V}\) at every state of \(L_T\), then \(L_T \equiv _{\mathsf {CSP}} L\).
-
4.
If all visible transitions are interesting and T satisfies \(\mathbf {D0}\), \(\mathbf {D2}\), \(\mathbf {V}\), and \(\mathbf {L}\) at every state of \(L_T\), then \(L_T \equiv _{\mathsf {Sfail},\mathsf {Divtr}} L\).
-
5.
If L is deterministic and T(s) satisfies \(\mathbf {D2}\), \(\mathbf {V}\), \(\mathbf {B}\), and \(\mathbf {S}\) in every state of \(L_T\), then \(L_T\) is branching bisimilar to L.
Mostly the theorem was proven in [21], albeit with a slightly different set of rules which, nevertheless, for deterministic transition systems are implied by the given conditions. The second statement of the theorem is novel, and follows from Lemma 2.
4.3 Considerations for Computing Stubborn Sets
Various methods for actually computing stubborn sets as defined in the earlier parts of this section have been proposed. Most commonly they include a form of dependency relation, or dependency graph, such as in [8, 10, 14]. Several authors discuss strategies based on shared variables and they range from forbidding changes of variables [4] to more nuanced approaches such as using write-up sets [19], analysis of guards [15]. It was proven in [22] that the classic stubborn sets are optimal in a model-theoretic sense with respect to symmetric dependency relations such as those used in [7]. We discuss some relations that can be defined by the rather coarse level of analysis [7], based on so-called effect sets. Unfortunately, these sets do not make it possible to employ the theoretical benefits afforded by the use of condition \(\mathbf {N}\) instead of \(\mathbf {D2}\).
Definition 6
Let L be an LTS. We define the following relations.
-
A left dependency relation \(\leadsto \) over \(\mathcal T\) is any relation such that if either \(t \leadsto u\) or for every state s, if \(s \xrightarrow {ut} s_2\) then there is a state \(s_3\) such that \(s_1 \xrightarrow {u} s_3\) and \(s_3 \xrightarrow {t} s_2\). We write \(t \not \leadsto u\) when \(t \leadsto u\) does not hold.
-
A dependency relation \(\leftrightharpoons \) over \(\mathcal T\) is any relation such that if either \(t \leftrightharpoons u\) or for every state s, if \(s \xrightarrow {u} s_1\) and \(s\xrightarrow {t} s_2\) then there is a state \(s_3\) such that \(s_1 \xrightarrow {t} s_3\) and \(s_2 \xrightarrow {u} s_3\). We write \(t \not \leftrightharpoons u\) when \(t \leftrightharpoons u\) does not hold.
The following lemma is given for the left-dependency and dependency relations
Lemma 3
Let \(s_0, s_n \in S\), \(t, t_1, \ldots , t_n \in \mathcal T\) and \(s_0 \xrightarrow {t_1 \cdots t_n} s_n\)
-
If \(t \not \leadsto t_i\) for \(1 \le i \le n\), and \(s_n \xrightarrow {t} s_n'\) for some \(s_n'\) then there is a state \(s_0'\) such that \(s_0 \xrightarrow {t} s_0'\) and \(s_0' \xrightarrow {t_1 \cdots t_n} s_n'\).
-
If \(t \not \leftrightharpoons t_i\) for \(1 \le i \le n\), and \(s_0 \xrightarrow {t}\) then \(s_n \xrightarrow {t}\).
Recall that a guard is a binary function \(X \rightarrow \{ true , false \}\). Recall that transitions are of the form (g, e), where g is a guard.
Definition 7
Let G be a set of guards. A guard relation for state s is a relation \(\hookrightarrow \) over \(\mathcal T\times G \cup G \times \mathcal T\) that has the following properties.
-
1.
If \(t = (g,e) \in \mathcal T\) and \(g(s) = false \), then \(t \hookrightarrow g_i\) if \(g_i \in G\) such that \(g_i(s) = false \) and for all \(x \in X\), \(g(x) = true \) implies \(g_i(x) = true \).
-
2.
If \(g \in G\) and \(g(s) = false \), then \(g \hookrightarrow t\) if \(t \in \mathcal T\) and there exists some states \(s_1\) and \(s_2\) such that \(s_1 \xrightarrow {t} s_2\), \(g(s_1) = false \) and \(g(s_2) = true \).
The following lemma is useful in calculation of stubborn sets:
Lemma 4
Let \(U \subseteq \mathcal T\) be a set of transitions and G be a set of guards. The set U is closed under enabling at state s if there exists a guard relation \(\hookrightarrow \) for s and a subset \(G' \subseteq G\) such that
-
1.
For every \(t \in dis (s) \cup U\), there is some \(g \in G'\) such that \(t \hookrightarrow g\).
-
2.
For every \(g \in G'\) and \(t \in \mathcal T\), if \(g \hookrightarrow t\) then \(t \in U\).
Lemma 4 was proven, for example, in [14]. Lemmas 3 and 4 are useful in the computation of stubborn sets; We do not go into details about particular algorithms, they have been discussed in [7, 8, 10, 15, 22, 25] to name a few. We give the theorem that the computation of stubborn sets is based on.
Theorem 7
Let \(\leftrightharpoons \) be a dependency relation and \(\hookrightarrow \) be a guard relation for s. The set T(s) satisfies \(\mathbf {D1}\) and \(\mathbf {D2}\) if there exists a set of guards G such that
-
1.
For every \(t \in T(s) \cap en (s)\) and \(u \in \mathcal T\), if \(t \leftrightharpoons u\) then \(u \in T(s)\).
-
2.
For every \(t \in T(s) \cap dis (s)\), there exists some \(g \in G\) such that \(t \hookrightarrow g\).
-
3.
For every \(g \in G\) and \(t \in \mathcal T\), if \(g \hookrightarrow t\) then \(t \in T(s)\).
Recall that \(X = X_1 \times \cdots \times X_n\). Let \(x = (x_1, \ldots , x_n)\) and \(y = (y_1, \ldots , y_n)\). We write \(\delta (x,y) = \{i \mid x_i \ne y_i\}\) Given a transition \(t = (g,e)\) we define the effect sets as:
-
The guard set of t as \( Gd (t) = \{i \mid \exists x,y \in X: \delta (x,y) = i \wedge g(x) \ne g(y)\}\),
-
the write set of t as \( Wr (t) = \{i \mid \exists x \in X: i \in \delta (x,e(x)\}\), and
-
the read set of t as \( Rr (t) = \{i \mid \exists x,y \in X: \delta (x,y) = i \wedge \exists j \in Wr (t): j \in \delta (e(x),e(y))\}\).
The union of these sets, \( Vr (t) = Gd (t) \cup Wr (t) \cup Rr (t)\) is called variable set of t. Intuitively, the guard set consists of variables whose value has an effect on the guard, the write set is the set of variables whose value is subject to change when the transition is fired, and the read set is the set of variables whose value has an effect on the resulting state, i.e. if a variable in a read set changes its value, then firing the transition will result in some change in some variable in the write set.
Given \(t_1, t_2 \in \mathcal T\), if we define the relation \(\leftrightharpoons ^G\) so that \(t_1 \not \leftrightharpoons ^G t_2\) implies \( Wr (t_1) \cap Vr (t_2) = Wr (t_2) \cap Vr (t_1) = \emptyset \), then this will result in a dependency relation. It is also a left dependency relation.
We can define \(\hookrightarrow ^G\) using the guard of each transition, or, if the guard is given as a conjunction of clauses, for example so that \(g = g_1 \wedge \cdots \wedge g_k\), we can use the conjuncts in G and have \(g_i \hookrightarrow ^G t\) if \( Wr (t)\) contains some variable appearing in \(g_i\), for example.
5 Stubborn Sets and Abstraction
As we saw in Sect. 3, abstraction may lead to nondeterminism. We also saw in Sect. 4 that the state-of-the art stubborn sets do not preserve all counterexamples if transitions may be nondeterministic. In this section we discuss some problems with combining stubborn sets and abstractions. We discuss the results of [1], and show that the approach applies only to a narrow class of abstractions.
The proof of Theorem 5 does not require the system is deterministic, but abstraction nevertheless gives rise problem. Consider the following hypothesis: given an abstraction \(\alpha \), the set U satisfies \(\mathbf {N}\) at that state \([s]_\alpha \) in \(L^\alpha \) if for every state \(s' \in [s]_\alpha \), U satisfies \(\mathbf {N}\) in L. Figure 5(a) and (b) demonstrate a counterexample to the hypothesis; abstractions do not in general satisfy this property. The transition \(\tau _1\) is neutral in all the states of the equivalence class (indicated by the gray states).
Firstly we note that we could define a dependency relation \(\leftrightharpoons ^\alpha \) for the transitions of \(L^\alpha \) directly, analogously to Definition 6. Then Theorem 6 would hold for all other parts, except part 5 which assumes transitions are deterministic, and this is not true for \(L^\alpha \) in general. The following lemma is trivial, but we state it in any case.
Lemma 5
If \(\alpha \) is separable, then the relations \(\leftrightharpoons ^G\) and \(\hookrightarrow ^G\) are dependency and guard relations for \(L^\alpha \).
This lemma is important in practice, as it applies to several methods that are used in practice. For example in [4], the analysis is carried out using this type of dependency. Thus, all linear time stubborn set methods based on these relations are in fact robust with respect to separable abstractions.
Definition 8
Let \(\alpha \) be an abstraction. The relation \(\leftrightharpoons _\alpha \) over \(\mathcal T\) is an abstract dependency relation, or \(\alpha \) -dependency, if for every s, if \(t,u \in en (s)\) either \(t \leftrightharpoons _\alpha u\) or the following hold:
-
1.
For for every \(s'\) such that \(s \xrightarrow {t} s'\) we have \(s' \xrightarrow {u}\) (and symmetrically for u), and
-
2.
For every state \(s_1\) such that \(s \xrightarrow {tu} s_1\) there is a state \(s_2\) such that \(s \xrightarrow {ut} s_2\) and \([s_1]_\alpha = [s_2]_\alpha \) (and symmetrically).
Lemma 6
Assume \(\mathcal A\) respects enabledness and \(\alpha \in \mathcal A\). For every \(t_1, \ldots , t_n\) such that \(t_i \not \leftrightharpoons _\alpha t\) for \(1 \le i \le n\), if \([s]_\alpha \xrightarrow {t_1 \cdots t_n}_\alpha [s_n]_\alpha \) and \([s]_\alpha \xrightarrow {t} [s']_\alpha \), then there is a state \([s_n']_\alpha \) such that \([s']_\alpha \xrightarrow {t_1 \cdots t_n}_\alpha [s_n']_\alpha \) and \([s_n]_\alpha \xrightarrow {t}_\alpha [s_n]'\).
Furthermore, if \(\mathcal A\) is a collection of 1-simulations, then for every \([s_n']_\alpha \) such that \([s_n]_\alpha \xrightarrow {t}_\alpha [s_n']_\alpha \), \([s]_\alpha \xrightarrow {t t_1 \cdots t_n}_\alpha [s_n']_\alpha \) holds.
Proof
We prove the claims by induction. If \(n = 0\), both claims holds trivially. Assume as inductive hypothesis that the first claim holds for \(n-1\). Let \([s_0]_\alpha \xrightarrow {t_1 \cdots t_n}_\alpha [s_n]_\alpha \) and \([s_0]_\alpha \xrightarrow {t}_\alpha [s_0']_\alpha \). By inductive hypothesis we have \([s_0']_\alpha \xrightarrow {t_1 \cdots t_{n-1}}_\alpha [s_{n-1}']_\alpha \) and \([s_{n-1}]_\alpha \xrightarrow {t}_\alpha [s_{n-1}']_\alpha \). Let \(s_{n-1}\) be one of the states in \([s_{n-1}]_\alpha \) such that \(s_{n-1} \xrightarrow {t} s_{n-1}'\).
Because \(\alpha \) respects enabledness, \(s_{n-1} \xrightarrow {t_n} s_{n}\) for some state \(s_n\). And because \(\leftrightharpoons _\alpha \) is an \(\alpha \)-dependency relation, we must have \(s_{n} \xrightarrow {t} s_{n}'\) for some state \(s_{n}'\) and \(s_{n-1}' \xrightarrow {t_{n}} s_{n}^*\) for some state \(s_{n}^* \in [s_{n}']_\alpha \).
Hence \([s_{n-1}]_\alpha \xrightarrow {t_{n} t}_\alpha [s_{n}']_\alpha \) and \([s_{n-1}']_\alpha \xrightarrow {t_{n}}_\alpha [s_{n}]'_\alpha \), finishing the inductive step for the first part of the lemma.
Assume then that \(\alpha \) is a 1-simulation and the second claim holds for \(n-1\). Let \([s_n]_\alpha \xrightarrow {t}_\alpha [s_n']_\alpha \). Then, for every state \(s_n \in [s_n]_\alpha \) there exists some state \(s_n' \in [s_n']_\alpha \) such that \(s_n \xrightarrow {t} s_{n}'\). For at least one of them we have \(s_{n-1} \xrightarrow {t_n} s_n \xrightarrow {t} s_n'\), and again, \(s_{n-1} \xrightarrow {t} s_{n-1}'\) because \(\alpha \) respects enabledness. And because of \(\alpha \)-dependency, we have some state \(s_n^* \in [s_n']_\alpha \) such that \(s_{n-1}' \xrightarrow {t_n} s_n^*\), finishing the inductive step for the second part of the lemma. \(\square \)
Definition 9
Let \(\alpha \) be an abstraction. Let G be a set of of Boolean functions \(\alpha (X) \rightarrow \{ true , false \}\). The relation \(\hookrightarrow _\alpha \) over \(\mathcal T\times G \cup G \times \mathcal T\) is an abstract guard relation for \([s]_\alpha \) if
-
1.
For every \(t \in dis _\alpha ([s]_\alpha )\) there exists a guard \(g \in G\) such that \(g([s]_\alpha ) = false \) and \(t \hookrightarrow _\alpha g\).
-
2.
For every state \(g \in G\) and \(t \in \mathcal T\), if there is some states \(s', s''\) such that \(s' \xrightarrow {t} s''\), \(g([s']_\alpha ) = false \) and \(g([s'']_\alpha ) = true \) then \(g \hookrightarrow _\alpha t\).
Theorem 8
Assume \(\mathcal A\) is a collection of 1-simulations and that it respects enabledness. Let \(\alpha \in \mathcal A\). Let \([s]_\alpha \) be an abstract state. Then the set U satisfies \(\mathbf {D1}\) and \(\mathbf {D2}\) if there exist some abstract guard relation \(\hookrightarrow _\alpha \), a set of guards G, and an abstract dependency relation \(\leftrightharpoons _\alpha \) such that
-
1.
For every \(t \in en _\alpha ([s]_\alpha )\) and \(u \in \mathcal T\), if \(t \in U\) and \(t \leftrightharpoons _\alpha u\) then \(u \in U\).
-
2.
For every \(t \in dis _\alpha ([s]_\alpha )\) there is some \(g \in G\) such that \(t \hookrightarrow _\alpha g\) and for every \([s']_\alpha \).
-
3.
For every \(g \in G\) and \(t \in \mathcal T\), if \(g \hookrightarrow _\alpha t\), then \(t \in U\).
Proof
Because Definition 9 is strictly analogous to Definition 7 and Lemma 4 applies, we skip the proof that U will be closed under enabling. Lemma 6 applied to the first condition proves \(\mathbf {D2}\). Because \(\alpha \) is a 1-simulation, Lemma 6 guarantees that also \(\mathbf {D1}\) holds. \(\square \)
The restriction that \(\mathcal A\) must respect both enabledness and determinism is a severe one. The result of [1] merits discussion in light of the weakness of the above theorem. The result of using \(\alpha \)-dependency when \(\alpha \) is a strong bisimulation is sound, because two states cannot be strongly bisimilar unless they have the same enabled transitions. It does not hold, however, for weaker equivalences. Consider Fig. 6(a). The grey states are branching bisimilar, but not strongly bisimilar. \(\alpha \)-dependency would declare the transitions labeled a and \(\tau _2\) as independent regardless of what happens after they are fired, because they are not enabled together. In fact, simple as it is, Fig. 6(a) leaves little hope for developing a method that is based on dependencies significantly less restrictive than those that consider the whole equivalence class, i.e., dependency in Definition 6 applied to the whole abstract state space.
The counterexample to abstractions that are not 1-simulations is given in Fig. 6(b). The abstraction equates the gray states in the figure. We can then define an abstract dependency relation that declares a and b independent. c and b are likewise independent. The set \(\{a\}\) would satisfy the conditions of Theorem 8 under this abstraction. The abstraction also respects enabledness. In the state that follows the execution of a, \(\{c\}\) is a set that likewise satisfies the conditions of the theorem, and the execution of d is missed. The example leaves open the possibility that forbids possibly nondeterministic transitions (such as c) from being stubborn.
6 Discussion and Future Work
As this article is to appear in a collection to honor professor Bill Roscoe, I break the convention and write in first person. I do so out of respect for the community and the person, as I hope to explain in a more personal manner what has been written here. I also wish to express my gratitude and sense of honor to have been invited to write this article.
The main theorem in [11] states that for timed automata, relaxing zone abstractions and applying an abstract dependency very similar to the one in Theorem 8 will preserve the existence of counterexamples. In fact, it not only does this, but sometimes it is able to reduce away abstract counterexamples that are spurious. When I started writing this article, I started with a hypothesis stronger than Theorem 8, one that would replicate the same powerful results.
A series of counterexamples, given in the previous sections, emerged while I was trying to prove a similar result, and in the end, the result was not significantly stronger than the main theorem of [1]. Instead of this article providing groundbreaking results as I had hoped, it thus is more of a document of how such a result does not hold for the abstract dependency relation as defined here. I hope that a careful analysis of the counterexamples to weaker hypothesis might prove fruitful in the pursuit of a more general theorem, one that may still be out there. I am still haunted by the intuition that there is a hidden diamond amid the ashes of this failed theorem.
For other parts, the results in this article are mostly re-stated facts that have been known separately with a couple of minor improvements to existing results. I hope my analysis may serve as a starting point for a more careful analysis of properties of abstractions and how they combine with the myriad other methods.
For future work, there are two important avenues. Firstly, the classification of abstractions is in its own right an important topic, and this rather truncated treatment merely scratches the surface. Results pertaining to preservation of determinism and monotony with respect to semantic models is something that we plan to pursue further.
Secondly, the combination of stubborn set methods with abstractions. There are probably good reasons why the relaxed zone abstraction combine in a synergistic manner with stubborn sets but abstractions labeled transition systems in general do not. Understanding of the said reasons may lead to powerful methods, or at least understanding, in the never ending battle against state explosion. The guard relation, for example, was simply lifted verbatim to abstract state spaces. It remains a possibility that some version of such a relation might be the key to unlock a more powerful theory.
References
Bošnački, D., Scheffer, M.: Partial order reduction and symmetry with multiple representatives. In: Havelund, K., Holzmann, G., Joshi, R. (eds.) NFM 2015. LNCS, vol. 9058, pp. 97–111. Springer, Heidelberg (2015). doi:10.1007/978-3-319-17524-9_8
Clarke, E., Grumberg, O., Jha, S., Lu, Y., Veith, H.: Counterexample-guided abstraction refinement. In: Emerson, E.A., Sistla, A.P. (eds.) CAV 2000. LNCS, vol. 1855, pp. 154–169. Springer, Heidelberg (2000). doi:10.1007/10722167_15
Clarke, E.M., Grumberg, O., Long, D.E.: Model checking and abstraction. ACM Trans. Programm. Lang. Syst. (TOPLAS) 16(5), 1512–1542 (1994)
Clarke, E.M., Grumberg, O., Peled, D.: Model Checking. MIT press, Cambridge (1999)
Emerson, E.A., Sistla, A.P.: Symmetry and model checking. In: Courcoubetis, C. (ed.) CAV 1993. LNCS, vol. 697, pp. 463–478. Springer, Heidelberg (1993). doi:10.1007/3-540-56922-7_38
Engelfriet, J.: Determinancy \(\rightarrow \) (observation equivalence = trace equivalence). Theor. Comput. Sci. 36, 21–25 (1985)
Geldenhuys, J., Hansen, H., Valmari, A.: Exploring the scope for partial order reduction. In: Liu, Z., Ravn, A.P. (eds.) ATVA 2009. LNCS, vol. 5799, pp. 39–53. Springer, Heidelberg (2009). doi:10.1007/978-3-642-04761-9_4
Gibson-Robinson, T., Hansen, H., Roscoe, A.W., Wang, X.: Practical partial order reduction for CSP. In: Havelund, K., Holzmann, G., Joshi, R. (eds.) NFM 2015. LNCS, vol. 9058, pp. 188–203. Springer, Heidelberg (2015). doi:10.1007/978-3-319-17524-9_14
Godefroid, P. (ed.): Partial-Order Methods for the Verification of Concurrent Systems. LNCS, vol. 1032. Springer, Heidelberg (1996). doi:10.1007/3-540-60761-7
Hansen, H., Kwiatkowska, M., Qu, H.: Partial order reduction for model checking Markov decision processes under unconditional fairness. In: Quantitative Evaluation of Systems (QEST 2011), pp. 203–212. IEEE (2011)
Hansen, H., Lin, S.-W., Liu, Y., Nguyen, T.K., Sun, J.: Diamonds are a girl’s best friend: partial order reduction for timed automata with abstractions. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 391–406. Springer, Heidelberg (2014). doi:10.1007/978-3-319-08867-9_26
Hansen, H., Valmari, A.: Operational determinism and fast algorithms. In: Baier, C., Hermanns, H. (eds.) CONCUR 2006. LNCS, vol. 4137, pp. 188–202. Springer, Heidelberg (2006). doi:10.1007/11817949_13
Hansen, H., Valmari, A.: Safety property-driven stubborn sets. In: Larsen, K.G., Potapov, I., Srba, J. (eds.) RP 2016. LNCS, vol. 9899, pp. 90–103. Springer, Heidelberg (2016). doi:10.1007/978-3-319-45994-3_7
Hansen, H., Wang, X.: Compositional analysis for weak stubborn sets. In: 2011 11th International Conference on Application of Concurrency to System Design (ACSD), pp. 36–43. IEEE (2011)
Laarman, A., Pater, E., van de Pol, J., Hansen, H.: Guard-based partial-order reduction. Int. J. Softw. Tools Technol. Transfer 18(4), 427–448 (2016)
Milner, R. (ed.): A Calculus of Communicating Systems. LNCS, vol. 92. Springer, Heidelberg (1980). doi:10.1007/3-540-10235-3
Peled, D.: All from one, one for all: on model checking using representatives. In: Courcoubetis, C. (ed.) CAV 1993. LNCS, vol. 697, pp. 409–423. Springer, Heidelberg (1993). doi:10.1007/3-540-56922-7_34
Roscoe, A.W.: The Theory and Practice of Concurrency. Prentice-Hall, Upper Saddle River (1997)
Valmari, A.: A stubborn attack on state explosion. In: Clarke, E.M., Kurshan, R.P. (eds.) CAV 1990. LNCS, vol. 531, pp. 156–165. Springer, Heidelberg (1991). doi:10.1007/BFb0023729
Valmari, A.: Stubborn sets for reduced state space generation. In: Rozenberg, G. (ed.) ICATPN 1989. LNCS, vol. 483, pp. 491–515. Springer, Heidelberg (1991). doi:10.1007/3-540-53863-1_36
Valmari, A.: Stubborn set methods for process algebras. In: Proceedings of the DIMACS Workshop on Partial Order Methods in Verification (1997)
Valmari, A., Hansen, H.: Can stubborn sets be optimal? Fundamenta Informaticae 113(3–4), 377–397 (2011)
Valmari, A., Hansen, H.: Stubborn set intuition explained. In: International Workshop on Petri Nets and Software Engineering 2016, pp. 213–232 (2016)
Valmari, A., Tienari, M.: Compositional failure-based semantic models for basic lotos. Formal Aspects Comput. 7(4), 440–468 (1995)
Valmari, A., Vogler, W.: Fair testing and stubborn sets. In: Bošnački, D., Wijs, A. (eds.) SPIN 2016. LNCS, vol. 9641, pp. 225–243. Springer, Heidelberg (2016). doi:10.1007/978-3-319-32582-8_16
Glabbeek, R.J.: The linear time — branching time spectrum II. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 66–81. Springer, Heidelberg (1993). doi:10.1007/3-540-57208-2_6
Acknowledgements
I wish to thank the editors for inviting me to submit an article, Antti Valmari for pioneering the field and his eagerness to discuss the topic after all these years, Xu Wang for discussions we have had over the years about the merits and pitfalls of various approaches, and Dragan Bosnacki for providing some insights on the matter. I am grateful to Bill Roscoe, for asking me one instrumental question about partial order reduction years ago. Answering that question led me to write a few articles, and, in a way, also this one.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Hansen, H. (2017). Abstractions for Transition Systems with Applications to Stubborn Sets. In: Gibson-Robinson, T., Hopcroft, P., Lazić, R. (eds) Concurrency, Security, and Puzzles. Lecture Notes in Computer Science(), vol 10160. Springer, Cham. https://doi.org/10.1007/978-3-319-51046-0_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-51046-0_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-51045-3
Online ISBN: 978-3-319-51046-0
eBook Packages: Computer ScienceComputer Science (R0)





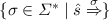



 if and only if
if and only if  , and
, and

 ,
,  and
and 


