Load Balancing Congestion Games and Their Asymptotic Behavior

Abstract

A central question in routing games has been to establish conditions for the uniqueness of the equilibrium, either in terms of network topology or in terms of costs. This question is well understood in two classes of routing games. The first is the non-atomic routing introduced by Wardrop on 1952 in the context of road traffic in which each player (car) is infinitesimally small; a single car has a negligible impact on the congestion. Each car wishes to minimize its expected delay. Under arbitrary topology, such games are known to have a convex potential and thus a unique equilibrium. The second framework is splitable atomic games: there are finitely many players, each controlling the route of a population of individuals (let them be cars in road traffic or packets in the communication networks). In this paper, we study two other frameworks of routing games in which each of several players has an integer number of connections (which are population of packets) to route and where there is a constraint that a connection cannot be split. Through a particular game with a simple three link topology, we identify various novel and surprising properties of games within these frameworks. We show in particular that equilibria are non unique even in the potential game setting of Rosenthal with strictly convex link costs. We further show that non-symmetric equilibria arise in symmetric networks.

1 Introduction

A central question in routing games has been to establish conditions for the uniqueness of the equilibria, either in terms of the network topology or in terms of the costs. A survey on these issues is given in [1].

The question of uniqueness of equilibria has been studied in two different frameworks. The first, which we call F1, is the non-atomic routing introduced by Wardrop on 1952 in the context of road traffic in which each player (car) is infinitesimally small; a single car has a negligible impact on the congestion. Each car wishes to minimize its expected delay. Under arbitrary topology, such games are known to have a convex potential and thus have a unique equilibrium [2]. The second framework, denoted by F2, is splitable atomic games. There are finitely many players, each controlling the route of a population of individuals. This type of games have already been studied in the context of road traffic by Haurie and Marcotte [3] but have become central in the telecom community to model routing decisions of Internet Service Providers that can decide how to split the traffic of their subscribers among various routes so as to minimize network congestion [4].

In this paper we study properties of equilibria in two other frameworks of routing games which exhibit surprising behavior. The first, which we call F3, known as congestion games [5], consists of atomic players with non splitable traffic: each player has to decide on the path to be followed by for its traffic and cannot split the traffic among various paths. This is a non-splitable framework. We further introduce a new semi-splitable framework, denoted by F4, in which each of several players has an integer number of connections to route. It can choose different routes for different connections but there is a constraint that the traffic of a connection cannot be split. In the case where each player controls the route of a single connection and all connections have the same size, this reduces to the congestion game of Rosenthal [5].

We consider in this paper routing games with additive costs (i.e. the cost of a path equals to the sum of costs of the links over the path) and the cost of a link is assumed to be convex increasing in the total flow in the link. The main goal of this paper is to study a particular symmetric game of this type in a simple topology consisting of three nodes and three links. We focus both on the uniqueness issue as well as on other properties of the equilibria.

This game has already been studied within the two frameworks F1 -F2 that we mentioned above. In both frameworks it was shown [6] to have a unique equilibrium. Our first finding is that in frameworks F3 and F4 there is a multitude of equilibria. The price of stability is thus different than the price of anarchy and we compute both. We show the uniqueness of the equilibrium in the limit as the number of players N grows to infinity extending known results [3] from framework F2 to the new frameworks. In framework F2 uniqueness is in fact achieved not only for the limiting games but also for all N large enough. We show that this is not the case for F3 -F4: for any finite N there may be several equilibria. We finally show a surprising property of F4 that exhibits non symmetric equilibria in our symmetric network example while under F1, F2 and F3 there are no asymmetric equilibria.

The structure of the paper is as follows. We first introduce the model and the notations used in the while study, we then move on to the properties of frameworks F3 (Sect. 3) and F4 (Sect. 4) before concluding the paper. All proofs of the theorems and propositions of the paper are available on ArXiv [7].

2 Model and Notations

We shall use throughout the term atomic game to denote situations in which decisions of a player have an impact on other players’ utility. It is non-atomic when players are infinitesimally small and are viewed like a fluid of players, such that a single player has a negligible impact on the utility of other players.

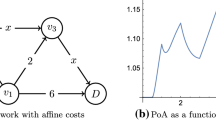
We consider a system of three nodes (A, B and C) with two incoming traffic sources (respectively from node A and B) and an exit node C. There are a total of N connections originating from each one of the sources. Each connection can either be sent directly to node C or rerouted via the remaining node. The system is illustrated in Fig. 1.

Fig. 1

Physical system

This model has been used to model load balancing issues in computer networks, see [6] and references therein. Jobs arrive to two computing centers represented by nodes A and B. A job can be processed locally at the node where it arrives or it may be forwarded to the other node incurring further communication delay. The costs of links [AC] and [BC] represent the processing delays of jobs processed at nodes A and B respectively. Once processed, the jobs leave the system. A connection is a collection of jobs with similar characteristics (e.g. belonging to the same application).

We introduce the following notations:

• A link between two nodes, say A and B, is denoted by [AB]. Our considered system has three links [AB], [BC] and [AC].

• A route is simply referred by a sequence of nodes. Hence, the system has four connections: two originating from node A (route AC and ABC) and two originating from node B (route BC and BAC).

Further, in the following, n _AC , n _BC , n _ABC and n _BAC will refer to the number of connections routed via the different routes while n[AC], n[BC] and n[AB] will refer to the number of connections on each subsequent link. By conservation law, we have:

$$\displaystyle{n_{AC}+n_{ABC} = n_{BC}+n_{BAC} = N\quad \text{and }\quad \left \{\begin{array}{l} n[AC] = n_{AC} + n_{BAC}, \\ n[BC] = n_{ABC} + n_{BC}, \\ n[AB] = n_{BAC} + n_{ABC}. \end{array} \right.}$$

For each route r, we also define the fraction (among N) of flow using it, i.e. f _r  = n _r ∕N. The conservation law becomes f _AC + f _ABC  = f _BC + f _BAC  = 1.

Finally, the performance measure considered in this work is the cost (delay) of connections experienced on their route. We consider a simple model in which the cost is additive (i.e. the cost of a connection on a route is simply taken as the sum of delays experienced by the connection over the links that constitute this route). We further assume that the costs on each link are linear with coefficient a∕N on link [AB] and coefficient b∕N on link [AC] and [BC], i.e.

$$\displaystyle\begin{array}{rcl} & \left \{\begin{array}{ll} C_{[AB]} = \frac{a} {N}n[AB] = a(f_{BAC} + f_{ABC}), \\ C_{[AC]} = \frac{b} {N}n[AC] = b(f_{BAC} + f_{AC}), \\ C_{[BC]} = \frac{b} {N}n[BC] = b(f_{BC} + f_{ABC}). \end{array} \right. & {}\\ & \text{and then }\begin{array}{@{}llll@{}} C_{AB} = C_{[AB]},\;&C_{ABC} = C_{[AB]} + C_{[BC]},\;&C_{BC} = C_{[BC]}\; & C_{BAC} = C_{[AB]} + C_{[AC]}.\end{array}& {}\\ \end{array}$$

We restrict our study to the (pure) Nash equilibria and give the equilibria in terms of the corresponding flows marked by a star. By conservation law, the equilibria is uniquely determined by the specification of f _ABC ^∗ and f _BAC ^∗ (or equivalently n _ABC ^∗ and n _BAC ^∗).

We recall that in this paper, we consider two types of decision models. In the first (F3 ), the decision is taken at the connection level (Sect. 3), i.e. each connection has its own decision maker that seeks to minimize the connection’s cost, and the connection cannot be split into different routes. In the second (F4 ), (Sect. 4) each one of the two source nodes decides on the routing of all the connections originating there. Each connection of a given source node (either A or B) can be routed independently but a connection cannot be split into different route. We hence refer to F4 this semi-splitable framework. Note that the two-approaches (F3 and F4 ) coincide when there is only N = 1 connection at each source, which we also detail later.

3 Atomic Non-Splitable Case and Its Non-Atomic Limit (F3 Framework)

We consider here the case where each connection belongs to an individual user acting selfishly. We first show that for fixed parameters, the game may have several equilibria, all of which are symmetric for any number of players. The number of distinct equilibria can be made arbitrary large by an appropriate choice of the parameters a and b, and for any choice of a and b, there exists N ₀ such that the number of equilibria remain constant for all N ≥ N ₀. We then show properties of the limiting game obtained as the number of of players increases to infinity.

3.1 Non-Uniqueness of the Equilibrium

Theorem 1

The set of pure Nash equilibria of the game are the points satisfying $n_{BAC}^{{\ast}} = n_{ ABC}^{{\ast}}\leq \frac{b} {2a}$ .

Corollary 1

For $N \geq N_{0} = \lceil \frac{b} {2a}\rceil$ , there exists exactly b∕2a + 1 Nash equilibria in pure strategies.

3.2 The Potential and Asymptotic Uniqueness

When the number of players N grows to infinity, the limiting game becomes a non-atomic game with a potential [8]

$$\displaystyle{F_{\infty }(f_{ABC},f_{BAC}) = b(f_{ABC} - f_{BAC})^{2} + \frac{a} {2}\left (f_{ABC} + f_{BAC}\right )^{2}.}$$

Indeed, recall that the potential g is unique up to an additive constant and that it satisfies

$$\displaystyle{\left \{\begin{array}{@{}l@{}l@{}l@{}} \frac{\partial g} {\partial f_{AC}} &\mathop{ =}\limits^{ def}C_{AC} = b(f_{AC} + f_{BAC}) \\ \frac{\partial g} {\partial f_{ABC}}&\mathop{ =}\limits^{ def}C_{ABC} = a(f_{ABC} + f_{BAC}) + b(f_{ABC} + f_{BC}) \\ \frac{\partial g} {\partial f_{BC}} &\mathop{ =}\limits^{ def}C_{BC} = b(f_{BC} + f_{ABC}) \\ \frac{\partial g} {\partial f_{BAC}}&\mathop{ =}\limits^{ def}C_{BAC} = a(f_{ABC} + f_{BAC}) + b(f_{BAC} + f_{AC}).\end{array} \right.}$$

One can check that the function

$$\displaystyle{\begin{array}{@{}l@{}l@{}} g(&f_{AC},f_{ABC},f_{BC},f_{BAC}) = \frac{a} {2} (f_{ABC} + f_{BAC})^{2} + \frac{b} {2}((f_{AC} + f_{BAC})^{2} + (f_{ BC} + f_{ABC})^{2}) \end{array}}$$

readily satisfies these conditions. Then g can be rewritten as

$$\displaystyle{\begin{array}{@{}l@{}l@{}} g(f_{ABC},f_{BAC}) = \frac{a} {2} (f_{ABC} + f_{BAC})^{2} + \frac{b} {2}(1 + (f_{ABC} - f_{BAC})^{2}). \end{array} }$$

As the potential is unique up to an additive constant, we consider F _∞  = g − b. Id∕2.

Proposition 1

The non-atomic game has a unique Nash equilibrium, which is f _ABC ^∗ = f _BAC ^∗ = 0.

To show the uniqueness of the equilibrium in the limiting game, we made use of the fact that the limiting game has a potential which is convex. Yet, not only the limiting game has a convex potential, but also the original one, as we conclude from next theorem, whose proof is a direct application of [5].

Theorem 2

For any finite number of players, the game is a potential game [9] with the potential function:

$$\displaystyle{ \begin{array}{@{}l@{}l@{}} F(f_{ABC}&,f_{BAC}) = bN(f_{ABC} - f_{BAC})^{2} + \frac{aN} {2} \left (f_{ABC} + f_{BAC}\right )\left (f_{ABC} + f_{BAC} + 1/N\right ). \end{array} }$$

(1)

Note that unlike the framework of non-atomic games, the fact that the game has a convex potential does not imply uniqueness. The reason for that is that in congestion games, the action space over which the potential is minimized is not a convex set (due to the non-splitable nature) so that it may have several local minima, each corresponding to another equilibrium, whereas a for a convex function over the Euclidean space, there is a unique local minimum which is also a global minimum of the function (and thus an equilibrium of the game).

3.3 Efficiency

Theorem 3

In the non-atomic setting, the only Nash equilibrium is also the social optimum (i.e. the point minimizing the sum of costs of all players) of the system.

Since the game possesses several equilibria, we can expect the PoA (Price of Anarchy - the largest ratio between the sum of costs at an equilibrium and the sum of costs at the social optimum) and PoS (Price of Stability - the smallest corresponding ratio) to be different.

Theorem 4

The price of stability is 1 and the price of anarchy is $1 + \frac{b} {2aN^{2}}$ .

We make the following observations:

• (i) In the splitable atomic games studied in [6] the PoA was shown to be greater than one for sufficiently small number of players (smaller than some threshold), and was 1 for all large enough number of players (larger than the same threshold). Here for any number of players, the PoS is 1 and the PoA is greater than 1.

• (ii) The PoA decreases in N and tends to 1 as N tends to infinity, the case of splitable games.

• (iii) We have shown that the PoA is unbounded: for any real value K and any number of players one can choose the cost parameters a and b so that the PoA exceeds K. This corresponds to what was observed in splitable games [6] and contrast with the non-atomic setting of single commodity flows (i.e. when there is only one source node instead of two), and arbitrary topology networks where the PoA equals 4/3 [10].

4 Atomic Semi-Splitable Case and Its Splitable Limit (F4 Framework)

The game can be expressed as a 2-player matrix game where each player (i.e. each source node A and B) has N + 1 possible actions, for each of the N + 1 possible values of f _ABC and f _BAC respectively. The utility for player A is

$$\displaystyle{ \begin{array}{@{}l@{}l@{}} U_{A}(f_{ABC},f_{BAC})& = f_{AC}C_{AC} + f_{ABC}C_{ABC} \\ & = b - bf_{ABC} + bf_{BAC} + (a - 2b)f_{ABC}f_{BAC} + (a + 2b)f_{ABC}^{2}. \end{array} }$$

(2)

Similarly, for player B:

$$\displaystyle{ \begin{array}{@{}l@{}l@{}} U_{B}(f_{ABC},f_{BAC})& = f_{BC}C_{BC} + f_{BAC}C_{BAC} \\ & = b - bf_{BAC} + bf_{ABC} + (a - 2b)f_{BAC}f_{ABC} + (a + 2b)f_{BAC}^{2}\end{array} }$$

(3)

Note that

$$\displaystyle\begin{array}{rcl} & \frac{\partial U_{A}} {\partial f_{ABC}} = -b + (a - 2b)f_{BAC} + 2(a + 2b)f_{ABC} & {}\\ & \text{and}\hspace{3.0pt} \frac{\partial U_{B}} {\partial f_{BAC}} = -b + (a - 2b)f_{ABC} + 2(a + 2b)f_{BAC}.& {}\\ \end{array}$$

Hence $\frac{\partial ^{2}U_{A}} {\partial f_{ABC}^{2}} = 2(a + 2b) = \frac{\partial ^{2}U_{B}} {\partial f_{BAC}^{2}}$. Therefore, both u _A : f _ABC ↦ U _A (f _ABC , f _BAC ) and u _B : f _BAC ↦ U _B (f _ABC , f _BAC ) are (strictly) convex functions. This means that for each action of one player, there would be a unique best response to the second player if its action space was the interval (0, 1). Hence, for the limit case (when N → ∞), the best response is unique. In contrast, for any finite value of N, there are either 1 or 2 possible best responses which are the discrete optima of functions u _A : f _ABC ↦ U _A (f _ABC , f _BAC ) and u _B : f _BAC ↦ U _B (f _ABC , f _BAC ). We will however show that in the finite case, there may be up to 2 × 2 = 4 Nash equilibria while in the limit case the equilibrium is always unique.

4.1 Efficiency

Note that the total cost of the players is

$$\displaystyle{\begin{array}{@{}l@{}l} \varSigma (f_{ABC},f_{BAC})& = U_{A}(f_{ABC},f_{BAC}) + U_{B}(f_{ABC},f_{BAC}) \\ & = 2b + 2(a - 2b)f_{ABC}f_{BAC} + (a + 2b)(f_{ABC}^{2} + f_{BAC}^{2}) \\ & = 2b + a(f_{ABC} + f_{BAC})^{2} + 2b(f_{ABC} - f_{BAC})^{2} \geq 2b.\end{array} }$$

Further, note that Σ = 2(F _∞ + b). Hence Σ is strictly convex. Also Σ(0, 0) = 2b. Therefore (0, 0) is the (unique) social optimum of the system. Yet, for sufficiently large N (that is, as soon as we add enough flexibility in the players’ strategies), this is not a Nash equilibrium, as stated in the following theorem:

Theorem 5

The point (f _ABC ,f _BAC ) = (0,0) is a Nash equilibrium if and only if $N \leq \frac{a} {b} + 2$ .

Also, we can bound the total cost by:

$$\displaystyle{\begin{array}{@{}l@{}l} \varSigma (f_{ABC},f_{BAC})& = 2b + 2(a - 2b)f_{ABC}f_{BAC} + (a + 2b)(f_{ABC}^{2} + f_{BAC}^{2}) \\ & \leq 2b + (a - 2b)(f_{ABC}^{2} + f_{BAC}^{2}) + (a + 2b)(f_{ABC}^{2} + f_{BAC}^{2}) \\ & \leq 2b + 2a(f_{ABC}^{2} + f_{BAC}^{2}) \\ & \leq 2b + 4a\end{array} }$$

This bound is attained at Σ(1, 1) = 2b + 2(a − 2b) + 2(a + 2b) = 4a + 2b. Yet, it is not obtained at the Nash equilibrium for sufficiently large values of N:

Theorem 6

(1,1) is a Nash equilibrium if and only if $N \leq \frac{2b + a} {3a + b}$ .

Therefore, for $N \geq \max (\frac{a} {b} + 2, \frac{2b+a} {3a+b})$ the Nash equilibria are neither optimal nor worse-case strategies of the game.

4.2 Case N = 1

In case of N = 1 (one flow arrives at each source node and there are thus two players) the two approach coincides: the atomic non-splitable case (F3 ) is also a semi-splitable atomic game (F4 ). f _ABC and f _BAC take values in {{0}, {1}}. From Eqs. (2) and (3), the matrix game can be written

$$\displaystyle{\left (\begin{array}{r@{\,,\,}lr@{\,,\,}l} (b\,,\,&b) & (2b\,,\,&a + 2b)\\ (a + 2b\,,\, &2b) &(2a + b\,,\, &2a + b) \end{array} \right )}$$

and the potential of Eq. (1) becomes

$$\displaystyle{\left (\begin{array}{cc} 0 &a + b\\ a + b & 3a \end{array} \right ).}$$

Then, assuming that either a or b is non null, we get that (0, 0) is always a Nash equilibrium and that (1, 1) is a Nash equilibrium if and only if 3a ≤ a + b, i.e. 2a < b.

We next consider any integer N and identify another surprising feature of the equilibrium. We show that depending on the sign of a − 2b, non-symmetric equilibria arise in our symmetric game. In all frameworks other than the semi-splitable games there are only symmetric equilibria in this game. We shall show however that in the limit (as N grows to infinity), the limiting game has a single equilibrium.

4.3 Case a − 2b < 0

In this case, there may be multiple equilibria. Note that due to the shape of U _A and U _B the cost matrices of the game are transpose of each other. Therefore in the following, we shall only give matrix U _A . We have the following theorem:

Theorem 7

All Nash equilibria are symmetrical, i.e. f _ABC ^∗ = f _BAC ^∗ .

The proof is given in the Arxiv version [7], as well as an illustrative example.

4.4 Case a = 2b (with a > 0)

When a = 2b, we shall show that some non-symmetrical equilibria exists.

Theorem 8

If a = 2b, there are exactly either 1 or 4 Nash equilibria. For any N, let $\overline{N} = \lfloor \frac{N} {8} \rfloor$.

• If N mod 8 = 4, there are 4 equilibria (n _ABC ^∗ ,n _BAC ^∗ ), which are $(\overline{N},\overline{N})$ , $(\overline{N} + 1,\overline{N})$ , $(\overline{N},\overline{N} + 1)$ and $(\overline{N} + 1,\overline{N} + 1)$ .

• Otherwise, there is a unique equilibrium, which is $(\overline{N},\overline{N})$ if N mod 8 < 4 or $(\overline{N} + 1,\overline{N} + 1)$ if N mod 8 > 4.

4.5 Case a − 2b > 0

Theorem 9

If a − 2b > 0, there are exactly either 1, 2 or 3 Nash equilibria.

Let $\alpha = \frac{a + 2b} {3a + 2b}$ , $\beta = \frac{2a} {3a + 2b}$ and $\gamma = \frac{b} {3a + 2b}$ .

Define further $\widetilde{N} = \lfloor N\gamma \rfloor$ and $z(N) = N\gamma -\widetilde{ N}$ . The equilibria are of the form

• Either $(\widetilde{N},\widetilde{N})$ , $(\widetilde{N} + 1,\widetilde{N})$ , $(\widetilde{N},\widetilde{N} + 1)$ if N is such that z(N) = α (mode 3-A in Fig.  2)

  Fig. 2

  

  Different modes according to different values of N

• Or $(\widetilde{N} + 1,\widetilde{N} + 1)$ , $(\widetilde{N} + 1,\widetilde{N})$ , $(\widetilde{N},\widetilde{N} + 1)$ if N is such that z(N) = β (mode 3-B)

• Or $(\widetilde{N},\widetilde{N} + 1)$ , $(\widetilde{N} + 1,\widetilde{N})$ if N is such that α < z(N) < β (mode 2)

• Or $(\widetilde{N},\widetilde{N})$ if N is such that β < z(N) < α + 1 (mode 1).

The proof is given in the Arxiv version [7], as well as an illustrative example.

4.6 Limit Case: Perfectly Splitable Sessions

We focus here in the limit case where N → +∞.

Theorem 10

There exists a unique Nash equilibrium and it is such that

$$\displaystyle{f_{BAC}^{{\ast}} = f_{ ABC}^{{\ast}} = \frac{b} {3a + 2b}.}$$

Recall that the optimum sum (social optimum) is given by (0, 0) and that the worse case is given by (1, 1). Hence, regardless of the values of a and b, at the limit case, we observe that there is a unique Nash equilibrium, that is symmetrical, and is neither optimal (as opposed to F3 ), nor the worst case scenario. The price of anarchy is then:

$$\displaystyle{PoA = PoS = \frac{2b + 2f_{ABC}^{{\ast}^{2} }a} {2b} = 1 + \frac{ab} {(3a + 2b)^{2}}.}$$

5 Conclusions

We revisited in this paper a load balancing problem within a non-cooperative routing game framework. This model had already received much attention in the past within some classical frameworks (the Wardrop equilibrium analysis and the atomic splitable routing game framework). We studied this game under other frameworks - the non splitable atomic game (known as congestion game) as well as a the semi-splitable framework. We have identified many surprising features of equilibria in both frameworks. We showed that unlike the previously studied frameworks, there is no uniqueness of equilibrium, and non-symmetric equilibria may appear (depending on the parameters). For each of the frameworks we identified the different equilibria and provided some of their properties. We also provided an efficiency analysis in terms of price of anarchy and price of stability. In the future we plan to investigate more general cost structures and topologies.