Stochastic Model Predictive Control for Water Transport Networks with Demand Forecast Uncertainty

Abstract

Two formulations of the stochastic model predictive control (SMPC) problem for the control of large-scale drinking-water networks are presented in this chapter. The first approach, named chance-constrained MPC, makes use of the assumption that the uncertain future water demands follow some known continuous probability distribution while at the same time, certain risk (probability) for the state constraints to be violated is allocated. The second approach, named tree-based MPC, does not require any assumptions on the probability distribution of the demand estimates, but brings about a complexity that is harder to handle by conventional computational tools and calls for more elaborate algorithms and the possible utilization of sophisticated devices.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

One of the challenges in water system management is the existence of different sources of uncertainty. The availability of historical data allows to accurately predict the behaviour of the system disturbances over large horizons, but still a meaningful degree of uncertainty is present. In previous chapters, the use of MPC to tackle the complex multi-variable interactions and large-scale nature of drinking-water network control is proposed. There are several examples of MPC applied to water systems in the literature, see, e.g., [2, 7, 10, 16, 29, 30] and references therein.

In a DWN, the main management purpose is the achievement of the highest level of consumer satisfaction and service quality in line with the prevailing regulatory framework, while making best use of available resources. Hence, networks must be reliable and resilient while being subject to constraints and to continuously varying conditions with both deterministic and probabilistic nature. Customer behaviour determines the transport and storage operations within the network, and flow demands can vary in both the long and the short term, often presenting time-based patterns in some applications. Therefore, a better understanding and forecasting of demands will improve both modelling and control of DWNs.

While Chaps. 12 and 13 deal with the uncertainty in the classical way of feed-forward action, this chapter focuses on the way that uncertainty can be faced by using stochastic-based approaches. The simplest way to do this is by ignoring the explicit influence of disturbances or using their expected value as done in the previous chapters. However, dealing with the demand uncertainty explicitly in the control model is expected to produce more robust control strategies. In [12], a reliability-based MPC was proposed to handle demand uncertainty by means of a (heuristic) safety stock allocation policy, which takes into account the short-term demand predictions but without propagating uncertainty along the prediction horizon. As discussed in [5], alternative approaches of MPC for stochastic systems are based on min-max MPC, tube-based MPC and stochastic MPC. The first two consider disturbances to be unmeasured but bounded in a predefined set. The control strategies are conservative, because they consider worst-case demand deviations from their expected value, limiting the control performance. On the other hand, stochastic MPC considers a more realistic description of uncertainty, which leads to less conservative control approaches at the expense of a more complex modelling of the disturbances. The stochastic approach is a mature theory in the field of optimization [3], but a renewed attention has been given to the stochastic programming techniques as powerful tools for control design (see, e.g., [4] and references therein).

From the wide range of stochastic MPC methods, this chapter specializes on scenario tree-based MPC (TB-MPC) and chance-constrained MPC (CC-MPC). Regarding TB-MPC, see, e.g., [17, 24], uncertainty is addressed by considering simultaneously a set of possible disturbance scenarios modelled as a rooted tree, which branches along the prediction horizon. On the other hand, CC-MPC [28] is a stochastic control strategy that describes robustness in terms of probabilistic (chance) constraints, which require that the probability of violation of any operational requirement or physical constraint is below a prescribed value, representing the notion of reliability or risk of the system. By setting this value properly, the operator/user can trade conservatism against performance. Relevant works that address the CC-MPC approach in water systems can be found in [8, 22] and references therein. Therefore, this chapter is focused on the design and assessment of CC-MPC and TB-MPC controllers for the operational management of transport water networks, which may be described using only flow equations, discussing their advantages and weaknesses in the sense of applicability and performance. The particular case study is related to the Barcelona DWN described in [19] and presented in Chap. 2.

Problem Formulation

Consider the MPC problem associated with the flow control problem in a DWN (see [20]). In general, a DWN consists in a set of water storage (dynamic) nodes, pipe junction (static) nodes, source nodes and sink nodes, which are interconnected in such a way that the water can be transported from source nodes to sink nodes when demanded. In order to derive a control-oriented model, define the state vector $\mathbf{x} \in \mathbb {R}^{n_x}$ to represent the storage at dynamic nodes. Similarly, define the vector $\mathbf{u} \in \mathbb {R}^{n_u}$ of controlled inputs as the collection of the flow rate through the actuators of the network, and the vector $\mathbf{d} \in \mathbb {R}^{n_d}$ of uncontrolled inputs (demands) as the collection of flow rate required by the consumers at sink nodes. Following flow/mass balance principles, a discrete-time model based on linear difference-algebraic equations can be formulated for a given DWN as follows:

where $k\in \mathbb {Z}_+$ is the current time instant and $\mathbf {A}$, $\mathbf {B}$, $\mathbf {B}_d$, $\mathbf {E}_u$ and $\mathbf {E}_d$ are matrices of compatible dimensions dictated by the network topology. Specifically, (14.1a) represents the balance at dynamic nodes while (14.1b) represents the balance at static nodes. The system is subject to state and input constraints considered here in the form of convex polyhedra defined as follows:

$$\begin{aligned} \mathbf {x}(k)\in \mathcal {X}&:=\{\mathbf {x}\in \mathbb {R}^{n_x}\mid \mathbf {G} \mathbf {x} \le \mathbf {g}\} ,\end{aligned}$$

(14.2a)

$$\begin{aligned} \mathbf {u}(k)\in \mathcal {U}&:=\{\mathbf {u}\in \mathbb {R}^{n_u}\mid \mathbf {H}\mathbf {u} \le \mathbf {h}\}, \end{aligned}$$

(14.2b)

for all k, where $\mathbf {G}\in \mathbb {R}^{r_{x}\times n_x}$, $\mathbf {g}\in \mathbb {R}^{r_x}$, $\mathbf {H}\in \mathbb {R}^{r_{u}\times n_u}$ and $\mathbf {h}\in \mathbb {R}^{r_u}$ are matrices/vectors collecting the system constraints, being $r_{x}\in \mathbb {Z}_+$ and $r_{u}\in \mathbb {Z}_+$ the number of state and input constraints, respectively.

Regarding the operation of the generalized flow-based networks, the following assumptions are considered in this chapter.

Assumption 14.1

The pair (A, B) is controllable and (14.1b) is reachable,¹ i.e., $m\le n_u$ with $\mathrm {rank}(E_u)=m$.

Assumption 14.2

The states in $\mathbf {x}$ and the demands in $\mathbf {d}$ are measured at any time instant $k\in \mathbb {Z}_{+}$. Future demands $d(k+i)$ are unknown for all $i\in \mathbb {Z}_+$ but forecasted information of their first two moments (i.e., expected value and variance) is available for a given prediction horizon $H_p\in \mathbb {Z}_{\ge 1}$.

Assumption 14.3

The realization of demands at any time instant $k\in \mathbb {Z}_+$ can be decomposed as

$$\begin{aligned} \mathbf {d}(k) = {\bar{\mathbf{d}}}(k) + \mathbf{e}(k), \end{aligned}$$

(14.3)

where ${\bar{\mathbf{d}}} \in \mathbb {R}^{n_d}$ is the vector of expected disturbances, and $\mathbf{e} \in \mathbb {R}^{n_d}$ is the vector of forecasting errors with non-stationary uncertainty and a known (or approximated) quasi-concave probability distribution $\mathcal {D}(0,\Sigma (e_{(j)}(k))$. The stochastic nature of each jth row of ${\mathbf{d}}_{(k)}$ is described by $\mathbf{d}_{(j)}(k)\sim \mathcal {D}_{i}({\bar{\mathbf{d}}}_{(j)}(k),\Sigma (\mathbf{e}_{(j)}(k))$, where ${\bar{\mathbf{d}}}_{(j)}$ denotes its mean, and $\Sigma (\mathbf{e}_{(j)}(k)$ its variance.

Notice in (14.1b) that a subset of controlled flows are directly related with a subset of uncontrolled flows. Hence, it is clear that $\mathbf {u}$ does not take values in $\mathbb {R}^{n_u}$ but in a linear variety. This latter observation, in addition to Assumptions 14.1 and 14.2, can be exploited to develop an affine parametrization of control variables in terms of a minimum set of disturbances as shown in [12, Appendix A], mapping control problems to an input space with a smaller decision vector and with less computational burden due to the elimination of the equality constraints. Thus, the system (14.1) can be rewritten as follows:

$$\begin{aligned} \mathbf {x}(k+1)=\mathbf {A}\mathbf {x}(k)+ {\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}(k) + {\tilde{\mathbf {B}}}_d \mathbf {d}(k), \end{aligned}$$

(14.4)

and the input constraint (14.2b) replaced with a time-varying restricted set defined as follows:

$$\begin{aligned} \tilde{\mathcal {U}}(k) :=\{{\tilde{\mathbf {u}}}\in \mathbb {R}^{n_u-m}\,\vert \, \mathbf {H}{\tilde{\mathbf {P}}} {\tilde{\mathbf {M}}}_1{\tilde{\mathbf {u}}} \le \mathbf {h}-\mathbf {H}{\tilde{\mathbf {P}}} {\tilde{\mathbf {M}}}_2 \mathbf {d}(k)\}. \end{aligned}$$

(14.5)

Being $\tilde{B} = B \tilde{P} \tilde{M}_1$, $\tilde{B}_d = B \tilde{P} \tilde{M}_2 + B_d$, where $\tilde{P}$, $\tilde{M}_1$ and $\tilde{M}_2$ a control parametritzation matrices ([12], Appendix A). The control goal is considered here as to minimize a convex (possibly multi-objective) stage cost $J (k,\mathbf {x},{\tilde{\mathbf {u}}}): \mathbb {Z}_+\times \mathcal {X} \times \tilde{\mathcal {U}}(k) \rightarrow \mathbb {R}_+$, which might bear any functional relationship to the economics of the system operation. Let $\mathbf {x}(k)\in \mathcal {X}$ be the current state, and let $\mathbf {d}(k)$ be the disturbances. The sequence of disturbances should be known over the considered prediction horizon $H_p$. The first element of this sequence is measured, while the rest of the elements are estimates of future disturbances computed by an exogenous forecasting system and available at each time instant $k\in \mathbb {Z}_+$. Hence, the MPC controller design is based on the solution of the following finite horizon optimization problem (FHOP):

$$\begin{aligned}&\min _{\tilde{\mathbf {u}}(k)=\{\tilde{u}(k+i\vert k)\}_{i\in \mathbb {Z}_{[0,H_p-1]}}}\,\sum _{i=0}^{H_p-1} J(k+i,x(k+i\vert k),\tilde{u}(k+i\vert k)),\quad&\end{aligned}$$

(14.6a)

$$\begin{aligned}&{\text {subject to:}}\nonumber \\&\mathbf {x}^j(k+i+1\vert k)=\mathbf {A}\mathbf {x}^j(k+i\vert k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}^j(k+i\vert k)+{\tilde{\mathbf {B}}}_d \mathbf {d}(k+i),&\forall i\in \mathbb {Z}_{[0,H_p-1]}\end{aligned}$$

(14.6b)

$$\begin{aligned}&\mathbf {x}(k+i\vert k) \in \mathcal {X},&\forall i\in \mathbb {Z}_{[1,H_p]} \end{aligned}$$

(14.6c)

$$\begin{aligned}&{\tilde{\mathbf {u}}}(k+i\vert k) \in \tilde{\mathcal {U}}(k+i),&\forall i\in \mathbb {Z}_{[0,H_p-1]}\end{aligned}$$

(14.6d)

$$\begin{aligned}&\mathbf {x}(k\vert k)=x(k),&\end{aligned}$$

(14.6e)

Assuming that (14.6) is feasible, i.e., there exists a non-empty solution given by the optimal sequence of control inputs $\tilde{\mathbf {u}}_k^\star =\{\tilde{u}^\star (k+i\vert k)\}_{i\in \mathbb {Z}_{[0,H_p-1]}}$, then the receding horizon philosophy commands to apply the control action

$$\begin{aligned} \mathbf {u}(k) :={\tilde{\mathbf {u}}}^*(k\vert k), \end{aligned}$$

(14.7)

and disregards the rest of the sequence of the predicted manipulated variables. At the next time instant k, the FHOP (14.6) is solved again using the current measurements of states and disturbances and the most recent forecast of these latter over the next future horizon.

Due to the stochastic nature of future disturbances, the prediction model (14.6b) involves exogenous additive uncertainty, which might cause that the compliance of state constraints for a given control input cannot be ensured. Therefore, uncertainty has to be represented in such a way that their effect on present decision-making can properly be taken into account. To do so, stochastic modelling based on data analysis, probability distributions, disturbance scenarios, among others, and the use of stochastic programming may allow to establish a trade-off between robustness and performance. In the sequel, two stochastic MPC strategies are proposed for their application to network flow control.

Chance-Constrained MPC

Since the optimal solution to (14.6) does not always imply feasibility of the real system, it is appropriate to relax the original constraints in (14.6c) with probabilistic statements in the form of the so-called chance constraints . In this way, the state constraints are required to be satisfied with a predefined probability to manage the reliability of the system. Considering the form of the state constraint set $\mathcal {X}$, there are two types of chance constraints according to the definitions below.

Definition 14.1

(Joint chance constraint) A (linear) state joint chance constraint is of the form

$$\begin{aligned} \mathbb {P}[\mathbf {G}_{(j)}\mathbf {x}\le \mathbf {g}_{(j)}\, , \, \forall j\in \mathbb {Z}_{[1,r_x]}]\ge 1-\delta _{\mathbf {x}}, \end{aligned}$$

(14.8)

where $\mathbb {P}$ denotes the probability operator, $\delta _{\mathbf {x}}\in (0,1)$ is the risk acceptability level of constraint violation for the states, and $\mathbf {G}_{(j)}$ and $\mathbf {g}_{(j)}$ denote the jth row of $\mathbf {G}$ and $\mathbf {g}$, respectively. This requires that all rows j have to be jointly fulfilled with the probability $1-\delta _{\mathbf {x}}$.

Definition 14.2

(Individual chance constraint) A (linear) state individual chance constraint is of the form

$$\begin{aligned} \mathbb {P}[\mathbf {G}_{(j)}\mathbf {x}\le \mathbf {g}_{(j)}]\ge 1-\delta _{\mathbf {x},j}, \quad \forall j\in \mathbb {Z}_{[1,r_x]}, \end{aligned}$$

(14.9)

which requires that each jth row of the inequality has to be fulfilled individually with the respective probability $1-\delta _{\mathbf {x},j}$, where $\delta _{\mathbf {x},j}\in (0,1)$.

Both forms of constraints are useful to measure risks; hence, their selection depends on the application. All chance-constrained models require prior knowledge of the acceptable risk $\delta _\mathbf {x}$ associated with the constraints. A lower risk acceptability implies a harder constraint. This chapter is concerned with the use of joint chance constraints since they can express better the management of the overall reliability in a DWN. In general, joint chance constraints lack from analytic expressions due to the involved multivariate probability distribution. Nevertheless, sampling-based methods, numeric integration and convex analytic approximations exists (see, e.g., [3] and references therein). Here, (14.8) is approximated following the results in [18, 23] by upper bounding the joint constraint and assuming a uniform distribution of the joint risk among a set of individual chance constraints that are later transformed into equivalent deterministic constraints under Assumption 14.4.

Assumption 14.4

Each demand in $\mathbf {d}\in \mathbb {R}^{n_d}$ follows a log-concave univariate distribution, which stochastic description is known.

Given the dynamic model in (14.4), the stochastic nature of the demand vector $\mathbf {d}$ makes the state vector $\mathbf {x}\in \mathbb {R}^{n_x}$ to be also a stochastic variable. Then, let the cumulative distribution function of the constraint be denoted as follows:

$$\begin{aligned} F _{\mathbf {Gx}}(\mathbf {g}) :=\mathbb {P}\left[ \left\{ \mathbf {G}_{(1)}\mathbf {x}\le \mathbf {g}_{(1)},\ldots , \mathbf {G}_{(r_x)}\mathbf {x}\le \mathbf {g}_{(r_x)}\right\} \right] . \end{aligned}$$

(14.10)

Defining the events $C_{j} := \left\{ \mathbf {G}_{(j)}\mathbf {x}\le \mathbf {g}_{(j)} \right\}$ for all $j \in \mathbb {Z}_{[1,r_x]}$, and denoting their complements as $C_{j}^c :=\left\{ \mathbf {G}_{(j)}\mathbf {x} > \mathbf {g}_{(j)}\right\}$, then it follows that

$$\begin{aligned} F_{\mathbf {Gx}}(\mathbf {g})&=\mathbb {P}\left[ C_{1}\cap \cdots \cap C_{r_x}\right] \end{aligned}$$

(14.11a)

$$\begin{aligned}&=\mathbb {P}\left[ (C_{1}^c\cup \cdots \cup {C}_{r_x}^c)^{c}\right] \end{aligned}$$

(14.11b)

$$\begin{aligned}&=1-\mathbb {P}\left[ (C_{1}^c\cup \cdots \cup C_{r_x}^c)\right] \ge 1-\delta _{\mathbf {x}} . \end{aligned}$$

(14.11c)

Taking advantage of the union bound, the Boole’s inequality allows to bound the probability of the second term in the left-hand side of (14.11c), stating that for a countable set of events, the probability that at least one event happens is not higher than the sum of the individual probabilities [23]. This yields

$$\begin{aligned} \mathbb {P}\left[ \bigcup _{j=1}^{r_x} C_{j}^c\right] \le \sum _{j=1}^{r_x}\mathbb {P}\left[ C_{j}^c\right] . \end{aligned}$$

(14.12)

Applying (14.12) to the inequality in (14.11c), it follows that

$$\begin{aligned} \sum _{j=1}^{r_x}\mathbb {P}\left[ C_{j}^{c}\right] \le \delta _{x} \Leftrightarrow \sum _{j=1}^{r_x}\left( 1-\mathbb {P}\left[ C_{j}\right] \right) \le \delta _{\mathbf {x}}. \end{aligned}$$

(14.13)

At this point, a set of constraints arise from the previous result as sufficient conditions to enforce the joint chance constraint (14.8), by allocating the joint risk $\delta _{x}$ in separate individual risks denoted by $\delta _{\mathbf {x},j}$, $j\in \mathbb {Z}_{[1,r_x]}$. These constraints are as follows:

$$\begin{aligned}&{\mathbb {P}}\left[ C_{j}\right] \ge 1-\delta _{\mathbf {x},j}, \quad \forall j \in {\mathbb {Z}}_{[1,r_x]},\end{aligned}$$

(14.14)

$$\begin{aligned}&\sum _{j=1}^{r_x}\delta _{\mathbf {x},j}\le \delta _{\mathbf {x}},\end{aligned}$$

(14.15)

$$\begin{aligned}&0 \le \delta _{\mathbf {x},j}\le 1, \end{aligned}$$

(14.16)

where (14.14) forms the set of $r_{x}$ resultant individual chance constraints, which bounds the probability that each inequality of the receding horizon problem may fail; and (14.15) and (14.16) are conditions imposed to bound the new single risks in such a way that the joint risk bound is not violated. Any solution that satisfies the above constraints is guaranteed to satisfy (14.8). As done in [18], assigning, for example, a fixed and equal value of risk to each individual constraint, i.e., $\delta _{\mathbf {x},j}=\delta _\mathbf {x} \slash r_x$ for all $j\in \mathbb {Z}_{[1,r_x]}$, then (14.15) and (14.16) are satisfied.

Remark 14.1

The single risks $\delta _{\mathbf {x},j}$, $j\in \mathbb {Z}_{[1,r_x]}$, might be considered as new decision variables to be optimized, see, e.g., [21]. This should improve the performance but at the cost of more computational burden due to the greater complexity and dimensionality of the optimization task. Therefore, as generalized flow-based networks are often large-scale systems, the uniform risk allocation policy is adopted to avoid overloading of the optimization problem.   $\lozenge$

After decomposing the joint constraints into a set of individual constraints, the deterministic equivalent of each separate constraint may be used given that the probabilistic statements are not suitable for algebraic solution. Such deterministic equivalents might be obtained following the results in [6]. Assuming a known (or approximated) quasi-concave probabilistic distribution function for the effect of the stochastic disturbance in the dynamic model (14.4), it follows that

$$\begin{aligned} {\mathbb {P}}\left[ \mathbf {G}_{(j)}\mathbf {x}(k+1)\le \mathbf {g}_{(j)}\right] \ge 1-\delta _{\mathbf {x},j}&\Leftrightarrow F_{\mathbf {G}_{(j)}{\tilde{\mathbf {B}}}_d \mathbf {d}(k)}(\mathbf {g}_{(j)}-\mathbf {G}_{(j)}(\mathbf {A}\mathbf {x}(k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}(k))\ge 1-\delta _{\mathbf {x},j}\nonumber \\&\Leftrightarrow \mathbf {G}_{(j)}(\mathbf {A}\mathbf {x}(k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}(k)\le \mathbf {g}_{(j)}-F_{\mathbf {G}_{(j)}{\tilde{\mathbf {B}}}_d \mathbf {d}(k)}^{-1}(1-\delta _{\mathbf {x},j}), \end{aligned}$$

(14.17)

for all $j\in {\mathbb {Z}}_{[1,r_x]}$, where $F_{\mathbf {G}_{(j)}{\tilde{\mathbf {B}}}_d \mathbf {d}(k)}(\cdot )$ and $F_{\mathbf {G}_{(j)}{\tilde{\mathbf {B}}}_d \mathbf {d}(k)}^{-1}(\cdot )$ are the cumulative distribution and the left-quantile function of $\mathbf {G}_{(j)}{\tilde{\mathbf {B}}}_d \mathbf {d}(k)$, respectively. Hence, the original state constraint set $\mathcal {X}$ is contracted by the effect of the $r_x$ deterministic equivalents in (14.17) and replaced by the stochastic feasibility set given by

$$\begin{aligned} \mathcal {X}_{s,k} := \{ \mathbf {x}(k)\in {\mathbb {R}}^{n_x}\mid&\exists {\tilde{\mathbf {u}}}(k)\in \bar{\mathcal {U}}(k),\text { such that} \\&\mathbf {G}_{(j)}(\mathbf {A}\mathbf {x}(k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}(k)\le \mathbf {g}_{(j)}-F_{\mathbf {G}_{(j)}{\tilde{\mathbf {B}}}_d \mathbf {d}(k)}^{-1}(1-\delta _{\mathbf {x},j}), \, \forall j\in {\mathbb {Z}}_{[1,r_x]} \}, \end{aligned}$$

for all $k\in {\mathbb {Z}}_+$. From convexity of $\mathbf {G}_{(j)}\mathbf {x}(k+1)\le \mathbf {g}_{(j)}$ and Assumption 14.4, it follows that the set $\mathcal {X}_{s,k}$ is convex when non-empty for all $\delta _{\mathbf {x},j} \in (0,1)$ in most distribution functions [14]. For some particular distributions, e.g., Gaussian, convexity is retain for $\delta _{\mathbf {x},j} \in (0,0.5].$

In this way, the reformulated predictive controller solves the following deterministic equivalent optimization problem for the expectation ${\mathbb {E}}[\cdot ]$ of the cost function in (14.6a):

$$\begin{aligned} {}&\min _{\tilde{\mathbf{u}}(k)}\sum _{i=0}^{H_p-1} {\mathbb {E}}[J(k+i,\mathbf {x}(k+i\vert k),{\tilde{\mathbf{u}}}(k+i\vert k))],&\end{aligned}$$

(14.18a)

$$\begin{aligned}&\text {subject to:}\nonumber \\&\mathbf{x}(k+i+1\vert k)=\mathbf{A}{} \mathbf{x}(k+i\vert k)+{\tilde{\mathbf{B}}}{\tilde{\mathbf{u}}}(k+i\vert k)+{\tilde{\mathbf{B}}}_d {\bar{\mathbf{d}}}(k+i),&\forall i\in {\mathbb {Z}}_{[0,H_p-1]},\end{aligned}$$

(14.18b)

$$\begin{aligned}&\mathbf{G}_{(j)}(\mathbf{A}{} \mathbf{x}(k+i\vert k)+{\tilde{\mathbf{B}}}{\tilde{\mathbf{u}}}(k+i\vert k))\le \mathbf{g}_{(j)}-{z}_{k,j}(\delta _\mathbf{x}),\quad&\forall i\in {\mathbb {Z}}_{[0,H_p-1]},\;\forall j\in {\mathbb {Z}}_{[1,r_x]},\end{aligned}$$

(14.18c)

$$\begin{aligned}&{\tilde{\mathbf{u}}}(k+i\vert k) \in \tilde{\mathcal {U}}(k+i),&\forall i\in {\mathbb {Z}}_{[0,H_p-1]},\end{aligned}$$

(14.18d)

$$\begin{aligned}&\mathbf{x}(k\vert k)=\mathbf{x}(k),&\end{aligned}$$

(14.18e)

where $\tilde{\mathbf{u}}_k=\{{\tilde{\mathbf{u}}}(k+i\vert k)\}_{i\in {\mathbb {Z}}_{[0,H_p-1]}}$ is the sequence of controlled flows, ${\bar{\mathbf{d}}}(k+i)$ is the expected future demands computed at time instant $k\in {\mathbb {Z}}_+$ for i-steps ahead, $i\in {\mathbb {Z}}_{[0,H_p-1]}$, $n_c\in {\mathbb {Z}}_{\ge 1}$ is the number of total individual state constraints along the prediction horizon, i.e., $n_c=r_x H_p$ and $z_{k,j}(\delta _\mathbf {x}) := F_{\mathbf{G}_{(j)}{\tilde{\mathbf{B}}}_d \mathbf{d}(k+i)}^{-1}\left( 1-\frac{\delta _{\mathbf {x}}}{n_c}\right)$. Since $n_c$ depends not only on the number of state constraints $r_x$ but also on the value of $H_p$, the decomposition of the original joint chance constraint within the MPC algorithm could lead to a large number of constraints. This fact reinforces the use of a fixed risk distribution policy for generalized flow-based network control problems, in order to avoid the addition of a large number of new decision variables to be optimized.

Remark 14.2

It turns out that most (not all) probability distribution functions used in different applications, e.g., uniform, Gaussian, logistic, Chi-squared, Gamma, Beta, log-normal, Weibull, Dirichlet, and Wishart, among others, share the property of being log-concave. Then, their corresponding quantile function can be computed offline for a given risk acceptability level and used within the MPC convex optimization problem.   $\lozenge$

Tree-Based MPC

The deterministic equivalent CC-MPC proposed before might be still conservative if the probabilistic distributions of the stochastic variables are not well characterized or do not lie in a log-concave form. Therefore, this section presents the TB-MPC strategy that relies on scenario trees to approximate the original problem, dropping Assumption 14.4. The approach followed by the TB-MPC is based on modelling the possible scenarios of the disturbances as a rooted tree (see Fig. 14.1 right). This means that all the scenarios start from the same measured disturbance value. From that point, the scenarios must remain equal until the point in which they diverge from each other, which is called a bifurcation point. Each node of the tree has a unique parent and can have many children. The total number of children at the last stage corresponds to the total number of scenarios. The probability of a scenario is the product of probabilities of each node in that scenario.

Notice that before a bifurcation point, the evolution followed by the disturbance cannot be anticipated because different evolutions are possible. For this reason, the controller has to calculate control actions that are valid for all the scenarios in the branch. Once the bifurcation point has been reached, the uncertainty is solved and the controller can calculate specific control actions for the scenarios in each of the new branches. Hence, the outcome of TB-MPC is not a single sequence of control actions, but a tree with the same structure of that of the disturbances. As in standard MPC, only the first element of this tree is applied (the root) and the problem is repeated in a receding horizon fashion.

In generalized flow-based networks, the uncertainty is generally introduced by the unpredictable behaviour of consumers. Therefore, a proper demand modelling is required to achieve an acceptable supply service level. For the case study considered in this chapter, the reader is referred to [26], where the authors presented a detailed comparison of different forecasting models. Once a model is selected, it has to be calibrated and then used to generate a large number of possible demand scenarios by Monte Carlo sampling for a given prediction horizon $H_p\in {\mathbb {Z}}_{\ge 1}$. For the CC-MPC approach, the mean demand path is used, while for the TB-MPC approach, a set of scenarios is selected. The size of this set is here computed following the bound proposed in [27], which takes into account the desired risk acceptability level. A large number of scenarios might improve the robustness of the TB-MPC approach but at the cost of additional computational burden and economic performance losses. Hence, a trade-off must be achieved between performance and computational burden. To this end, a representative subset of scenarios may be chosen using scenario reduction algorithms. In this chapter, the backward reduction algorithm proposed in [13] is used to reduce a specified initial fan of $N_s\in {\mathbb {Z}}_{\ge 1}$ equally probable scenarios into a rooted tree of $N_r<<N_s$ scenarios, where $N_r$ is the number of considered scenarios while $N_s$ is the total number of scenarios (see Fig. 14.1).

Fig. 14.1

Reduction of a disturbance fan (left) of equally probable scenarios into a rooted scenario tree (right)

The easiest way to understand the optimization problem that has to be solved in TB-MPC is to solve as many instances of Problem (14.6) as the number $N_r$ of considered scenarios, but formally it is a multi-stage stochastic programme and solved as a big optimization for all the scenarios. Due to the increasing uncertainty, it is necessary to include non-anticipativity constraints [25] in the MPC formulation so that the calculated input sequence is always ready to face any possible future bifurcation in the tree. More specifically, if $\mathbf {d}_k^a=\{d^a(k\vert k),d^a(k+1\vert k),\ldots ,d^a(k+N\vert k)\}$ and $\mathbf {d}_k^b=\{d^b(k\vert k),d^b(k+1\vert k),\ldots ,d^b(k+N\vert k)\}$ are two disturbance sequences corresponding respectively to certain forecast scenarios $a,b\in {\mathbb {Z}}_{[1,N_r]}$, then the non-anticipativity constraint ${\tilde{\mathbf {u}}}^a(k+i\vert k)={\tilde{\mathbf {u}}}^b(k+i\vert k)$ has to be satisfied for any $i\in {\mathbb {Z}}_{[0,H_p]}$ whenever $d^a(k+i\vert k)=d^b(k+i\vert k)$ in order to guarantee that for all $j\in {\mathbb {Z}}_{[1,N_r]}$ the input sequences $\tilde{\mathbf {u}}^j=\{\tilde{u}^j(k+i\vert k)\}_{i\in \mathbb {Z}_{[0,H_p-1]}}$ form a tree with the same structure of that of the disturbances.

In this way, the TB-MPC controller has to solve the following optimization problem at each time instant $k\in {\mathbb {Z}}_+$, accounting for the $N_r$ demand scenarios, each with probability $p_j\in (0,1]$ satisfying $\sum _{j=1}^{N_r} p_j=1$:

$$\begin{aligned}&\min _{\tilde{\mathbf {u}}_k^j}\,\sum _{j=1}^{N_r}p_j\left( \sum _{i=0}^{H_p-1} J(k+i,\mathbf {x}(k+i\vert k),{\tilde{\mathbf {u}}}(k+i\vert k))\right) ,&\end{aligned}$$

(14.19a)

$$\begin{aligned}&\text {subject to:}\nonumber \\&\mathbf {x}^j(k+i+1\vert k)=\mathbf {A}\mathbf {x}^j(k+i\vert k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}^j(k+i\vert k)+{\tilde{\mathbf {B}}}_d \mathbf {d}^j(k+i),&\forall i\in {\mathbb {Z}}_{[0,H_p-1]}, \forall j\in {\mathbb {Z}}_{[1,N_r]},\end{aligned}$$

(14.19b)

$$\begin{aligned}&\mathbf {x}^j(k+i+1\vert k) \in \mathcal {X},&\forall i\in {\mathbb {Z}}_{[0,H_p-1]},\forall j\in {\mathbb {Z}}_{[1,N_r]}, \end{aligned}$$

(14.19c)

$$\begin{aligned}&{\tilde{\mathbf {u}}}^j(k+i\vert k) \in \tilde{\mathcal {U}}^j(k+i),&\forall i\in {\mathbb {Z}}_{[0,H_p-1]},\forall j\in \mathbb {Z}_{[1,N_r]},\end{aligned}$$

(14.19d)

$$\begin{aligned}&\mathbf {x}^J(k\vert k)=\mathbf {x}(k),\quad \mathbf {d}^{j}(k\vert k)=\mathbf {d}(k),\qquad \forall j\in \mathbb {Z}_{[1,N_r]},\end{aligned}$$

(14.19e)

$$\begin{aligned}&{\tilde{\mathbf {u}}}^{a}(k+i\vert k)={\tilde{\mathbf {u}}}^{b}(k+i\vert k)\;\text { if }\; \mathbf {d}^{a}(k+i\vert k)=d^{b}(k+i\vert k),&\forall i\in \mathbb {Z}_{[0,H_p-1]}, \forall a,b \in \mathbb {Z}_{[1,N_r]}, \end{aligned}$$

(14.19f)

where $\tilde{\mathcal {U}}^j(k+i) :=\{{\tilde{\mathbf {u}}}^j\in \mathbb {R}^{n_u-m}\,\vert \, \mathbf {H}{\tilde{\mathbf {P}}} {\tilde{\mathbf {M}}}_1{\tilde{\mathbf {u}}}^j \le \mathbf {h}-\mathbf {H}{\tilde{\mathbf {P}}} {\tilde{\mathbf {M}}}_2 \mathbf {d}^j(k+i)\}.$

Remark 14.3

The number of scenarios used to build the rooted tree should be determined regarding the computational capacity and the probability of risk that the manager is willing to accept.   $\lozenge$

Numerical Results

In this section, the performance of the proposed stochastic MPC approaches is assessed with a case study consisting in a large-scale real system reported in [19], specifically the Barcelona WTN already described in Sect. 2.3 in Chap. 2. The general role of this system is the spatial and temporal reallocation of water resources from both superficial (i.e., rivers) and underground water sources (i.e., wells) to distribution nodes located all over the city. The directed graph of this network can be obtained from the layout shown in Fig. 2.2 of Chap. 2, and its model in the form of (14.1) can be derived by setting the state $\mathbf {x}(k)\in \mathbb {R}^{63}$ as the volume (in m$^3$) of water stored in tanks at time instant k, the control input $\mathbf {u}(k)\in \mathbb {R}^{114}$ as the flow rate through all network actuators (expressed in m$^3/$s) and the measured disturbance $\mathbf {d}(k)\in \mathbb {R}^{88}$ as the flow rate of customer demands (expressed in m$^3/$s). This network is currently managed by Aguas de Barcelona that manages the drinking-water transport and distribution in Barcelona (Spain), and it supplies potable water to the Metropolitan Area of Barcelona (Catalunya, Spain). The main control task for the managers is to economically optimize the network flows while satisfying customer demands. These demands are characterized by patterns of water usage and can be forecasted by different methods (see, e.g., [1, 26]).

The operational goals in the management of the Barcelona DWN are of three kinds, economic, safety and smoothness, and are respectively stated as follows (see Chap. 12. for the mathematical formulation):

• 1. To provide a reliable water supply in the most economic way, minimizing water production and transport costs.

• 2. To guarantee the availability of enough water in each reservoir to satisfy its underlying demand, keeping a safety stock to face uncertainties and avoid stock-outs.

• 3. To operate the DWN under smooth control actions.

Fig. 14.2

Barcelona DWN small subsystem layout

Performance Comparison on a Small-Scale System

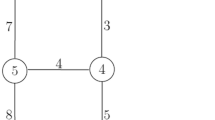
To analyse via simulation the computational burden of each proposed controller, a small portion/subsystem of the complete network is used (see Fig. 14.2 and [9] for details). The DWN is considered as a stochastic constrained system subject to deterministic hard constraints on the control inputs and linear joint chance constraints on the states. The source of uncertainty in the system is assumed to be the forecasting error of the water demands. The stochastic control problem of the DWN is stated as follows:

$$\begin{aligned}&\min _{\tilde{\mathbf {u}}_{k}}\,\sum _{i=0}^{H_p-1} \mathbb {E}\left[ \lambda _1 J_{E}(k+i,\mathbf {x}(k+i\vert k),{\tilde{\mathbf {u}}}(k+i\vert k)) + \lambda _2 J_{\Delta }(\Delta {\tilde{\mathbf {u}}}(k+i\vert k)) \right] ,\end{aligned}$$

(14.20a)

$$\begin{aligned}&{\text {subject to:}} \nonumber \\&\mathbf {x}(k+i+1\vert k)=\mathbf {A}\mathbf {x}(k+i\vert k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}(k+i\vert k)+{\tilde{\mathbf {B}}}_{d} \mathbf {d}(k+i\vert k), \end{aligned}$$

(14.20b)

$$\begin{aligned}&\mathbb {P}\left[ \mathbf {x}(k+i+1\vert k)\ge \mathbf {x}^{\mathrm {min}}\right] \ge 1-\frac{\delta _{\mathbf {x}}}{2},\end{aligned}$$

(14.20c)

$$\begin{aligned}&\mathbb {P}\left[ \mathbf {x}(k+i+1\vert k)\le \mathbf {x}^{\mathrm {max}}\right] \ge 1-\frac{\delta _{\mathbf {x}}}{2},\end{aligned}$$

(14.20d)

$$\begin{aligned}&\mathbb {P}\left[ \mathbf {x}(k+i+1\vert k)\ge \mathbf {d}_{\mathrm {net}}(k+i+1\vert k)\right] \ge 1-\delta _{s}, \end{aligned}$$

(14.20e)

$$\begin{aligned}&{\tilde{\mathbf {u}}}(k+i\vert k)\in \tilde{\mathcal {U}}(k+i),\end{aligned}$$

(14.20f)

$$\begin{aligned}&\mathbf{d}_{\text {net}}(k+i+1\vert k)=-({\tilde{\mathbf{B}}}_{\mathrm{out}} ({\tilde{\mathbf{P}}} {\tilde{\mathbf{M}}}_1{\tilde{\mathbf{u}}} (k+i\vert k)+{\tilde{\mathbf{P}}} {\tilde{\mathbf{M}}}_2 \mathbf{d} (k+i\vert k))+{\tilde{\mathbf{B}}}_{d} \mathbf{d}(k+i+1\vert k)),\end{aligned}$$

(14.20g)

$$\begin{aligned}&\Delta {\tilde{\mathbf {u}}}(k+i\vert k) = {\tilde{\mathbf {u}}}(k+i\vert k) - {\tilde{\mathbf {u}}}(k+i-1\vert k),\end{aligned}$$

(14.20h)

$$\begin{aligned}&(\mathbf {x}(k\vert k),{\tilde{\mathbf {u}}}(k-1\vert k)) = (\mathbf {x}(k),{\tilde{\mathbf {u}}}(k-1)), \end{aligned}$$

(14.20i)

for all $i\in \mathbb {Z}_{[0,H_p-1]}$, where $J_{E}(k+i,\mathbf {x}(k+i\vert k),{\tilde{\mathbf {u}}}(k+i\vert k)) := c_{u,k+i}^{\top } W_{e}\, {\tilde{\mathbf {u}}}(k)\Delta t$ captures the economic costs with $c_{u,k+i}\in \mathbb {R}^{n_u}$ being a known periodically time-varying price of electric tariff, and $J_{\Delta }(\Delta {\tilde{\mathbf {u}}}(k+i\vert k)) := \Vert {\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_1 \Delta {\tilde{\mathbf {u}}}(k+i\vert k)+{\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_2\Delta \mathbf {d}(k+i\vert k)\Vert _{W_{\Delta {\tilde{\mathbf {u}}}}}^2$ is a control move suppression term aiming to enforce a smooth operation. Moreover, $\delta _{\mathbf {x}},\delta _{s}\in (0,1)$, are the accepted maximum risk levels for the state constraints and the safety constraint (14.20e), respectively. The objectives are traded-off with the scalar weights $\lambda _1,\lambda _2\in \mathbb {R}_+$, while the elements of the decision vector are prioritized by the weighting matrices $W_e, W_{\Delta {\tilde{\mathbf {u}}}}\in \mathbb {S}_{++}^m$. The service reliability goal (i.e., demand satisfaction) is enforced by the constraints (14.20e) and (14.20g). In this latter constraint, $\mathbf {d}_{\mathrm {net}}(k+i+1\vert k)\in \mathbb {R}^{n_d}$ is a vector of net demands above which is desired to keep the reservoirs to avoid stock-outs. The ${\tilde{\mathbf {B}}}_{\mathrm {out}}({\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_1{\tilde{\mathbf {u}}}(k+i\vert k)+{\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_2 \mathbf {d}(k+i\vert k))$ component represents the current prediction step endogenous demand, i.e., the outflow of the tanks caused by water requirements from neighbouring tanks or nodes, and the ${\tilde{\mathbf {B}}}_{d} \mathbf {d}(k+i+1\vert k)$ component denotes the exogenous (customer) demands of tanks for the next prediction step. In the dynamic model (14.4) of the DWN, randomness is directly described by the uncertainty of customer demands, which can be estimated from historical data. In order to solve the above DWN control problem, a tractable safe approximation is derived following Sect. 14.3. The joint chance constraints (14.20c)–(14.20e) are transformed into deterministic equivalent constraints as shown in [11, Appendix B] for the particular case of Gaussian distributions.

The optimization problem associated with the deterministic equivalent CC-MPC for the selected application is stated as follows for a given sequence of forecasted demands denoted by $\bar{\mathbf {d}}_k=\{\mathbf {{d}}(k+i\vert k)\}_{i\in \mathbb {Z}_{[0,H_p-1]}}$:

$$\begin{aligned}&\min _{\tilde{\mathbf {u}}_{k},\varvec{\xi }_k}\,\sum _{i=0}^{H_p-1} \mathbb {E}\left[ \lambda _1 J_{E}(k+i,{\bar{\mathbf {x}}}(k+i\vert k),{\tilde{\mathbf {u}}}(k+i\vert k)) + \lambda _2 J_{\Delta }(\Delta {\tilde{\mathbf {u}}}(k+i\vert k)) + \lambda _3 J_{S}(\varvec{\xi }(k+i\vert k))\right] , \end{aligned}$$

(14.21a)

$$\begin{aligned}&{\text {subject to:}}\nonumber \\&{\bar{\mathbf {x}}}(k+i+1\vert k)=\mathbf {A}{\bar{\mathbf {x}}}(k+i\vert k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}(k+i\vert k)+{\tilde{\mathbf {B}}}_{d} {\bar{\mathbf {d}}}(k+i\vert k),\end{aligned}$$

(14.21b)

$$\begin{aligned}&{\bar{\mathbf {x}}}_{(j)}(k+i+1\vert k)\ge \mathbf {x}^{\mathrm {min}}_{(j)}+\Phi ^{-1}\left( 1-\frac{\delta _{\mathbf {x}}}{2n_x H_p}\right) {\Sigma _{x_{(j)}}(k+i+1\vert k)^{1/2}}, \end{aligned}$$

(14.21c)

$$\begin{aligned}&{\bar{\mathbf {x}}}_{(j)}(k+i+1\vert k)\le \mathbf {x}^{\mathrm {max}}_{(j)}-\Phi ^{-1}\left( 1-\frac{\delta _{\mathbf {x}}}{2n_x H_p}\right) {\Sigma _{x_{(j)}}(k+i+1\vert k)^{1/2}}, \end{aligned}$$

(14.21d)

$$\begin{aligned}&{\bar{\mathbf {x}}}_{(j)}(k+i+1\vert k)\ge {\bar{\mathbf {d}}}_{\mathrm {net}(j)}(k+i+1\vert k)+\Phi ^{-1}\left( 1-\frac{\delta _{s}}{n_x H_p}\right) {\Sigma _{{d}_{\mathrm {net}(j)}}(k+i+1\vert k)^{1/2}} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \quad \qquad \qquad -\varvec{\xi }_{(j)}(k+i\vert k),\end{aligned}$$

(14.21e)

$$\begin{aligned}&\varvec{\xi }(k+i\vert k)\ge 0,\end{aligned}$$

(14.21f)

$$\begin{aligned}&{\tilde{\mathbf {u}}}(k+i\vert k)\in \tilde{\mathcal {U}}(k+i),\end{aligned}$$

(14.21g)

$$\begin{aligned}&{\bar{\mathbf {d}}}_{\mathrm {net}}(k+i+1\vert k)=-({\tilde{\mathbf {B}}}_{\mathrm {out}}\left( {\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_1{\tilde{\mathbf {u}}}(k+i\vert k)+{\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_2 {\bar{\mathbf {d}}}(k+i\vert k)\right) +{\tilde{\mathbf {B}}}_{d} {\bar{\mathbf {d}}}(k+i+1\vert k)),\end{aligned}$$

(14.21h)

$$\begin{aligned}&\Delta {\tilde{\mathbf {u}}}(k+i\vert k) = {\tilde{\mathbf {u}}}(k+i\vert k) - {\tilde{\mathbf {u}}}(k+i-1\vert k),\end{aligned}$$

(14.21i)

$$\begin{aligned}&({\bar{\mathbf {x}}}(k\vert k),{\tilde{\mathbf {u}}}(k-1\vert k)) = (\mathbf {x}(k),{\tilde{\mathbf {u}}}(k-1)), \end{aligned}$$

(14.21j)

for all $i\in \mathbb {Z}_{[0,N-1]}$ and all $j\in \mathbb {Z}_{[1,n]}$, where $\tilde{\mathbf {u}}_k=\{{\tilde{\mathbf {u}}}(k+i\vert k)\}$ and $\varvec{\xi }_k=\{\varvec{\xi }(k+i\vert k)\}$ are the decision variables. The vectors ${\bar{\mathbf {x}}}$ and ${\bar{\mathbf {d}}}$ denote the mean of the random state and demand variables, respectively. Moreover, $\Phi ^{-1}$ is the left-quantile function of the Gaussian distribution, and ${\bar{\mathbf {x}}}_{(j)}$ and $\Sigma _{x_{(j)}}$ denote, respectively, the mean and variance of the jth row of the state vector. Notice that Problem (14.21) includes the additional objective $J_{S}(\varvec{\xi }(k+i\vert k)) := \Vert \varvec{\xi }(k+i\vert k)\Vert _{W_s}^2$ with $\mathbf {W}_s\succ 0$, and the additional constraint (14.21f), which are related to the safety operational goal. These elements appear due to the safety deterministic equivalent soft constraint (14.21e) introduced with the slack decision variable $\varvec{\xi }\in \mathbb {R}^{n_x}$ to allow the trade-off between safety, economic, and smoothness objectives. Constraints (14.21c) and (14.21d) can be softened in the same way to guarantee recursive feasibility of the optimization problem if uncertainty is too large. For a strongly feasible stochastic MPC approach using closed-loop predictions by means of an affine disturbance parametrization of the control inputs, the reader is referred to [15]. The enforcement of the chance constraints enhances the robustness of the MPC controller by causing an optimal back-off from the nominal deterministic constraints as a risk averse mechanism to face the non-stationary uncertainty involved in the prediction model of the MPC. The states are forced to move away from their limits before the disturbances have chance to cause constraint violation. The $\Phi ^{-1}(\cdot )$ terms represent safety factors for each constraint, and specially in (14.21e), it denotes the optimal safety stock of storage tanks. Problem 14.18 may be casted as a second-order cone programming problem. However, state uncertainty is a function of the disturbances only and is not a function of the decision variables of the optimization problem. Therefore, the variance terms in each deterministic equivalent can be forecasted prior to the solution of the optimization problem to include them as known parameters in the MPC formulation. This simplification results in a set of linear constraints, and the optimization remains as a quadratic programming (QP) problem, which can be efficiently solved.

The optimization problem associated with the scenario tree-based MPC approach is stated as follows for all $i\in \mathbb {Z}_{[0,H_p-1]}$ and all $j\in \mathbb {Z}_{[1,N_r]}$:

$$\begin{aligned}&\min _{\tilde{\mathbf {u}}_k^j,\varvec{\xi }_k^j}\,\sum _{j=1}^{N_r}p_j\sum _{i=0}^{H_p-1} \lambda _1 J_{E}(k+i,\mathbf {x}^j(k+i\vert k),{\tilde{\mathbf {u}}}^j(k+i\vert k)) + \lambda _2 J_{\Delta }(\Delta {\tilde{\mathbf {u}}}^j(k+i\vert k)) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad + \lambda _3 J_{S}(\varvec{\xi }^j(k+i\vert k)),\end{aligned}$$

(14.22a)

$$\begin{aligned}&{\text {subject to:}} \nonumber \\&\mathbf {x}^j(k+i+1\vert k)=\mathbf {A}\mathbf {x}^j(k+i\vert k)+{\tilde{\mathbf {B}}}{\tilde{\mathbf {u}}}^j(k+i\vert k)+{\tilde{\mathbf {B}}}_d \mathbf {d}^j(k+i\vert k),\end{aligned}$$

(14.22b)

$$\begin{aligned}&(\mathbf {x}^j (k+i+1\vert k), {\tilde{\mathbf {u}}}^j(k+i\vert k), \varvec{\xi }^j(k+i\vert k))\in \mathcal {X}\times \tilde{\mathcal {U}}^j(k+i)\times \mathcal {R}_+^{n_u},\end{aligned}$$

(14.22c)

$$\begin{aligned}&\mathbf {x}^j(k+i+1\vert k)\ge \mathbf {d}^j_{\text {net}}(k+i+1|k) - \varvec{\xi }^j(k+i\vert k),\end{aligned}$$

(14.22d)

$$\begin{aligned}&\mathbf {d}_{\mathrm {net}}(k+i+1\vert k)^j=-({\tilde{\mathbf {B}}}_{\mathrm {out}}\left( {\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_1{\tilde{\mathbf {u}}}^j(k+i\vert k)+{\tilde{\mathbf {P}}}{\tilde{\mathbf {M}}}_2 \mathbf {d}^j(k+i\vert k)\right) +{\tilde{\mathbf {B}}}_{d} \mathbf {d}^j_{\text {net}}(k+i+1|k),\end{aligned}$$

(14.22e)

$$\begin{aligned}&\Delta {\tilde{\mathbf {u}}}^j(k+i\vert k) = {\tilde{\mathbf {u}}}^j(k+i\vert k) - {\tilde{\mathbf {u}}}^j(k+i-1\vert k),\end{aligned}$$

(14.22f)

$$\begin{aligned}&(\mathbf {x}^j(k\vert k)\mathrm{X},{\tilde{\mathbf {u}}}^j(k-1\vert k),\mathbf {d}^{j}(k\vert k)) = (\mathbf {x}(k),{\tilde{\mathbf {u}}}(k-1),\mathbf {d}(k),\end{aligned}$$

(14.22g)

$$\begin{aligned}&{\tilde{\mathbf {u}}}^{a}(k+i\vert k)={\tilde{\mathbf {u}}}^{b}(k+i\vert k)\;\text { if }\; \mathbf {d}^{a}(k+i\vert k)=\mathbf {d}^{b}(k+i\vert k)\quad \forall a,b \in \mathbb {Z}_{[1,N_r]}. \end{aligned}$$

(14.22h)

Table 14.1 Assessment of the CC-MPC and TB-MPC applied to the sector model of the DWN case study

Table 14.1 summarizes the results of applying the deterministic equivalent CC-MPC and the TB-MPC to the aforementioned small example. Simulations have been carried out over a time period of eight days, i.e., $n_s=192$ hours, with a sampling time of 1 hour. Applied demand scenarios were taken from historical data of the Barcelona DWN. The weights of the multi-objective cost function are $\lambda _1=100$, $\lambda _2=1$ and $\lambda _3=10$. The prediction horizon is selected as $H_p=24$ h due to the periodicity of demands. The key performance indicators used to assess the aforementioned controllers are defined as follows:

$$\begin{aligned}&\text {KPI}_1 \triangleq \frac{24}{n_s+1}\sum _{k=0}^{n_s}\gamma _1 J_{E}(k,\mathbf {x}(k),{\tilde{\mathbf {u}}}(k) + \lambda _2 J_{\Delta }(\Delta {\tilde{\mathbf {u}}}(k)) + \lambda _3 J_{S}(\varvec{\xi }(k)),\end{aligned}$$

(14.23a)

$$\begin{aligned}&\text {KPI}_2 \triangleq \vert \left\{ k\in \mathbb {Z}_1^{n_s} \;\vert \; \mathbf {x}(k) < -\mathbf {B}_d \mathbf {d}(k) \right\} \vert ,\end{aligned}$$

(14.23b)

$$\begin{aligned}&\text {KPI}_3 \triangleq \sum _{k=1}^{n_s}\sum _{i=1}^{n_x}\max \{0,-\mathbf {B}_{d(i)} \mathbf {d}(k) -\mathbf {x}(k(i))\},\end{aligned}$$

(14.23c)

$$\begin{aligned}&\text {KPI}_4 \triangleq \frac{1}{n_s}\sum _{k=1}^{n_s} t(k), \end{aligned}$$

(14.23d)

where KPI$_1$ is the average daily multi-objective cost, KPI$_2$ is the number of time instants where the stored water goes below the demanded volume (for this, $\vert \cdot \vert$ denotes the cardinal of a set of elements), KPI$_3$ is the accumulated volume of water demand that was not satisfied over the simulation horizon, and KPI$_4$ is the average time in seconds required to solve the MPC problem at each time instant $k\in \mathbb {Z}_{[0,n_s]}$. For the CC-MPC approach, the effect of considering different levels of joint risk acceptability was analysed using $\delta _{\mathbf {x}}=\{0.3, 0.2, 0.1, 0.01, 0.001\}$ and $\delta _s=\delta _{\mathbf {x}}$. Regarding the TB-MPC approach, different sizes for the initial set of scenarios were considered, i.e., $N_s =\{19, 28, 59,599,5999\}$. The size of this initial set was computed following the bound proposed in [27] taking into account the risk levels involved in the chance constraints. This initial set was reduced later by a factor of 0.25, 0.50 and 0.75 to obtain different rooted trees with $N_r$ scenarios.

As shown in Table 14.1, the different CC-MPC scenarios highlight that reliability and control performance are conflicting objectives; that is, the inclusion of safety mechanisms in the controller increases the reliability of the DWN in terms of demand satisfaction, but also the cost of its operation. The main advantage of the CC-MPC is its formal methodology, which leads to obtain optimal safety constraints that tackle uncertainties and allow to achieve a specified global service level in the DWN. Moreover, the deterministic equivalent CC-MPC robustness is achieved with a low computational burden given that the only extra load (compared with a nominal formulation) is the computation of the stochastic characteristics of disturbances propagated in the prediction horizon. In this way, the deterministic equivalent CC-MPC approach is suitable for real-time control (RTC) of large-scale DWNs. Regarding the TB-MPC approach, numeric results show that considering higher $N_s$ increments the stage cost while reducing the volume of unsatisfied water demand. Nevertheless, this latter observation is not applicable for the different $N_r$ cases within a same $N_s$. This might be influenced by the quality of the information that remains after the scenario generation and reduction algorithms that affect the robustness of the approach and will be subject of further research. The main drawback of the TB-MPC approach is the solution of the average time and the computational burden. In this case study, the implementation for all cases taking $N_s=\{599,5999\}$ was not possible due to memory issues. Hence, some simplification assumptions as those used in [17] or parallel computing techniques might be useful.

Performance Assessment of CC-MPC on a Large-Scale System

The previous results showed that both CC-MPC and TB-MPC have similar performance under high levels of risk acceptability. Nevertheless, when requiring small risk levels ($\delta _{\mathbf {x}} < 0.1$), CC-MPC retains tractability of the FHOP with low complexity, while the TB-MPC suffers the curse of dimensionality. Therefore, in the following, only the performance of the CC-MPC approach is assessed on the full model of the Barcelona DWN. The tuning of the controller parameters is the same as in the previous simulations. In order to further evaluate the proposed CC-MPC scheme, results are compared with the certainty-equivalent MPC approach proposed in [19], which assumes predictions of demands as certain. In these simulations, the CE-MPC strategy has been set up to allow the volume of water in tanks to decrease until the predicted volume of future net demands, which is set as a hard constraint but ignoring the influence of uncertainty. Contrary, the CC-MPC strategy considers and propagates the uncertainty of forecasted demands explicitly in the MPC design and, as a consequence, involves a robust handling of constraints. Again, to analyse the effect of the risk level ($\delta _{\mathbf {x}}$) in this CC-MPC strategy when considering large-scale systems, different scenarios have been simulated for acceptable joint risks of 50, 40, 30, 20, 10, 5 and 1%.

Table 14.2 presents the numeric assessment of the aforementioned controllers through different key performance indicators (KPIs), which are defined as follows:

$$\begin{aligned}&\mathrm {KPI}_{E} := \frac{1}{n_s+1}\sum _{k=0}^{n_s} c_{u,k}^{\top } {\tilde{\mathbf {u}}}(k) \Delta t,\end{aligned}$$

(14.24a)

$$\begin{aligned}&\mathrm {KPI}_{\Delta U} := \frac{1}{n_s+1}\sum _{i=1}^{n_u} \sum _{k=0}^{n_s} \left( \Delta {\tilde{\mathbf {u}}}_{(i)}(k)\right) ^{2},\end{aligned}$$

(14.24b)

$$\begin{aligned}&\mathrm {KPI}_{S} := \sum _{i=1}^{n_x} \sum _{k=0}^{n_s}\max \left\{ 0,s_{(i)}(k)-\mathbf {x}_{(i)}(k)\right\} ,\end{aligned}$$

(14.24c)

$$\begin{aligned}&\mathrm {KPI}_{D} := \sum _{i=1}^{n_x} \sum _{k=0}^{n_s}\max \left\{ 0,\mathbf {d}_{\mathrm {net}(i)}(k) - \mathbf {x}_{(i)}(k)\right\} ,\end{aligned}$$

(14.24d)

$$\begin{aligned}&\mathrm {KPI}_{R} := \frac{\sum _{i=1}^{n_x} \sum _{k=1}^{n_s}s_{(i)}(k)}{\sum _{i=1}^{n_x} \sum _{k=1}^{n_s} \mathbf {x}_{(i)}(k)}\times 100\%,\end{aligned}$$

(14.24e)

$$\begin{aligned}&\mathrm {KPI}_{O} := t_{\mathrm {opt}}(k), \end{aligned}$$

(14.24f)

Table 14.2 Comparison of the MPC strategies applied to the Barcelona DWN

Fig. 14.3

Comparison of the robustness in the management of water storage in a sample of tanks of the Barcelona DWN. (Blue circle) CC-MPC$_{1\%}$, (black diamond) CC-MPC$_{20\%}$, (red square) CC-MPC$_{50\%}$, (solid green) CE-MPC, (dashed red) net demand

where KPI$_{E}$ is the average economic performance of the DWN operation, KPI$_{\Delta U}$ measures the smoothness of the control actions, KPI$_{S}$ is the amount of water used from safety stocks, KPI$_{D}$ is the volume of water demand that is not satisfied over the simulation period, KPI$_{R}$ is the average percentage of safety volume that is contained in the real water volume, and KPI$_{O}$ determines the difficulty to solve the optimization tasks involved in each strategy accounting $t_{\mathrm {opt}}(k)$ as the average time that takes to solve the corresponding MPC optimization problem. The CE-MPC has been tuned with a safety stock for each tank equal to its net exogenous demand, i.e., $s(k)=d_{\mathrm {net}}(k)$. Therefore, the KPI$_S$ results equal to the KPI$_D$ as should be expected given their definitions. In the case of the CC-MPC, s(k) is equal to the right hand of (14.21e). Regarding the comparison of the KPI$_S$ between the CE-MPC and the CC-MPC, the results present greater values for the CC-MPC cases. This trend is also an expected behaviour given that reducing the risk probability generates a larger back-off of the demand satisfaction constraint; that is, more safety stock is stored to address demand uncertainty. This latter fact, in addition with the tuning of the multi-objective cost function, leads to higher KPI$_S$ (but lower or null KPI$_D$) if this is required by the real demand scenario in order to guarantee a service level. It can be observed that the CE-MPC is the cheapest control strategy (lower KPI$_E$) but the less reliable one given that the certainty equivalence assumption leads to unsatisfying demands (higher KPI$_{D}$), especially when the water volume in the tank is close to the expected demand. Thus, the CE-MPC performance represents a strategy for the supply of drinking water with a higher risk of failure. The different CC-MPC scenarios (those of varying the risk acceptability level) have shown that reliability and economic performance are conflicting objectives that have to reach a trade-off; that is, the inclusion of safety mechanisms in the controller increases the reliability of the DWN in terms of demand satisfaction (see Fig. 14.3), but also the economic cost of its operation. The main advantage of the CC-MPC is its formal methodology that leads to obtain optimal dynamic constraints that tackle uncertainties with a minimum cost to achieve also a global service level of the DWN. Table 14.2 shows a smooth degradation of the economic performance under the CC-MPC when varying the risk within a wide range of acceptability levels. Therefore, the CC-MPC approach addressed in this chapter is a suitable mean to compute the proper amount of safety and the proper control actions to assure a desired service level. Notice that the computational burden (KPI$_{O}$) of the CC-MPC is similar to the CE-MPC given that the complexity of the optimization problem is not altered; that is, the number of constraints and decision variables remain the same. The only extra load that might be added is the computation of the variance of the disturbances propagated in the prediction horizon. Consequently, the CC-MPC approach is suitable for RTC of the Barcelona DWN.

Table 14.3 Comparison of daily average economic costs of MPC strategies

Table 14.3 discloses details of the average production and operational costs related to each strategy. Comparing the CE-MPC controller with the CC-MPC$_{@5\%}$ controller (requiring a reliability of $95\%$), it can be noticed that the dynamic safety stocks resulting within the stochastic approach might lead to an increase in the operational cost, especially in the electric cost, mainly due to the extra amount of water that is needed to be moved through the network and allocated in tanks to guarantee that the water supply will be feasible with a certain probability for future disturbance realizations.

Table 14.4 Conservatism of the deterministic equivalent CC-MPC

The conservatism of reformulating the stochastic CC-MPC problem into the tractable deterministic equivalent in (14.21) has been studied in [12]. Table 14.4 shows the conservatism related to approximate constraints (14.20c), (14.20d) and (14.20e), considering different levels of maximum joint risk. It can be observed that conservatism increases when the risk level increases but remains almost constant despite the variation in the number of individual constraints. Hence, the goodness of the approximation using Boole’s inequality is not affected, neither by the number of decision variables nor by the prediction horizon. Therefore, the addressed approach is advantageous to be applied to any other DWNs or general flow networks.

Conclusions

In this chapter, two stochastic control approaches have been assessed to deal with the management of generalized flow-based networks. Both the CC-MPC and the TB-MPC approaches focused on robust economic performance under additive disturbances (unbounded and stationary or non-stationary) and avoid relying on heuristic fixed safety volumes such as those used in the CE-MPC or the RB-MPC schemes proposed in Chaps. 12 and 13, what is traduced in better economic performance. According to the results obtained with the considered case study, both techniques showed a relatively similar performance. However, it seems clear that CC-MPC is more appropriate when requiring a low probability of constraint violation, since the use of TB-MPC demands the inclusion of a higher number of scenarios, which may be an issue for the application of the latter to large-scale networks. The analytical approximation of joint chance constraints based on their decomposition into individual chance constraints, these latter bounded by means of the Boole’s inequality, has shown to be suitable for large networks regarding that the conservatism involved is not affected neither by the number of the inequalities nor by the prediction horizon of the MPC. The level of resultant back-off is variable and depends on the volatility of the forecasted demand at each prediction step and the suitability of the probabilistic distribution used to model uncertainty. The fact of unbounded disturbances in the system precludes the guarantee of robust feasibility with these schemes. Hence, the approaches proposed in this chapter are based on a service-level guarantee and a probabilistic feasibility. The case study shows that the CC-MPC is suitable for the operational guidance of large-scale networks due to its robustness, flexibility, modest computational requirements, and ability to include risk considerations directly in the decision-making process. Even when the CC-MPC increased the operational costs by around $2.5\%$, it allowed to improve the service reliability by more than $90\%$ when compared with a CE-MPC setting.

Future research will be directed to incorporate parametric uncertainty and unmeasured disturbances in the model. In addition, future work should include a more detailed study regarding the number of scenarios contained in the tree. Likewise, distributed computation could be used in order to relieve the scaling problems of TB-MPC when the number of scenarios is too high. Moreover, it is of interest to extend the results and develop decentralized/distributed stochastic MPC controllers for large-scale complex flow networks.