1 Introduction

The massive amount of data available in the financial markets, also free downloadable, allows us to strategically process and to convert them into useful information about the future trend of the prices of one or more assets.

Hu et al. [5] identify three different analysis methods: technical, fundamental and blending. The main aim of Technical Analysis (TA) is to compute technical indicators using the time series of stock prices and volumes and, starting from these indicators, to generate a Buy, Hold or Sell (BHS) signal [8]. On the other hand, Fundamental Analysis generates trading rules when the stock is undervalued or overvalued with respect to its fundamental value. The last analysis, the Blending one, combines both of them.

As underlined by Wu et al. [11], to elaborate a set of profitable trading rules we have to forecast the direction of the asset prices, so an effective information extraction is needed.

In this work, we consider the formulation of a trading system (TS) from the perspective of TA, so that the analysis of the patterns of price and/or of volume sequences can enables us to generate trading rules [3]. The literature on TA has proposed several indicators, to each of which is associated a trading rule generating BHS signal. The indicators, and consequently the signals generated, depend on some parameters, the most important of which is the time-window width. Thus, the selection of the time-window width is crucial. According to the latest state of our knowledge, there is not an estimation methodology for these parameters, furthermore the rule of thumb used by many practitioners appears to us inappropriate and risky. The BHS signals generated by an indicator results in profits or losses. So, we need a procedure to select the time-window widths in a such way to maximize the profit or to minimize the losses. According to this, we look for an optimization algorithm allowing the estimation of the time-window widths.

Several Authors, [1, 5, 9, 12], present interesting applications of evolutionary optimization approaches implemented in the trading framework. For instance, the Ant Colony Optimization (ACO), as well as Particle Swarm Optimization (PSO), that maximizes/minimizes a fitness function by mimicking the behaviour of a group of insects or animals. Moreover, designing a TS based on several indicators, we have to consider possible conflicting BHS signals, so we have also to tackle the issue of combining these signals. It follows that there are two aspects to face when we examine this problem. On one hand we have to determine the parameter values (that is the time-window widths), on the other we have to combine the different signals in a single one.

In this paper we focus on the first problem, since the combination of the signals can be solved considering the simple unweighted sum of each signal. In particular, in this paper we propose a TS based on four indicators: two momentum indicators, typically used for trend detection, such as the Exponential Moving Average (EMA) and the Bollinger Bands (BB), and two oscillator indicators such as the Relative Strength Index (RSI) and the Moving Average Convergence/Divergence (MACD). All these indices depend on the time-window widths that we can specify using the swarm intelligence approach.

The paper is organized as follows. The next section will introduce the methodology we will use. In Sect. 3 we will show some in-sample and out-of-sample results of the implemented methodology. In the last section we will give some final remarks.

2 Methodology

As we said in the previous section, effective TA tools settings are crucial to reach good performance by a TS. Nevertheless, the evidence is that many trading practitioners follow a rule of thumb, meaning that parameters have a default. For example, several financial web-sites, like for instance finance.yahoo.com or, in an Italian context, borsaitaliana.it, provide indicators and oscillators with identical or very similar settings. In order to improve the performances of TA indicators, we propose a more objective method to optimize their parameter settings. In particular, we use a metaheuristic known as Particle Swarm Optimization (PSO) to estimate the best time-window widths. The use of this solver is justified by the complexity of the involved optimization problem for which the exact solution methods could be extremely time-consuming for practical purposes.

In the next subsection we will describe the adopted TS. Then, we will introduce the optimization problem. At last, in Sect. 2.3, the PSO and its specific implementation will be presented in the considered context.

2.1 A Simple TS

As previously highlighted, we propose a combination of four classical and widely used indicators, two momentum indicators and two oscillators, to define our TS. The main aim of this work is to verify if using PSO allow us to improve the performance in terms of rate of return with respect to the same TS with default settings of the indicators. The involved TA indicators are: Exponential Moving Average (EMA), Bollinger Bands (BB), Moving Average Convergence/Divergence (MACD), and Relative Strength Index (RSI). For the description of such indicators we refer to [7].

For each indicator we define a decisional rule that provides a trading signal. More precisely the signal may be: “ − 1”, namely “Sell or stay short in the market”; “0”, namely “Stay out from the market”; “ + 1”, namely “Buy or stay long in the market”. The four trading signals are then aggregated in order to obtain a single signal. As far as the four decisional rules are concerned, let us specify as trading period the discrete time interval t = 1, …, T > 1, and let us assume that at time t = 1 each of the four trading signals is equal to 0. From t = 2 to t = T, the four decisional rules are:

  • the one based on EMA, with EMA f (⋅ ) a fast EMA and EMA s (⋅ ) a slow EMA:

    $$\displaystyle{signal_{EMA}(t) = \left \{\begin{array}{@{}l@{\quad }l@{}} -1\mbox{ if }EMA_{f}(t) <EMA_{s}(t) \wedge EMA_{f}(t - 1) \geq EMA_{s}(t - 1) \quad \\ +1\mbox{ if }EMA_{f}(t)> EMA_{s}(t) \wedge EMA_{f}(t - 1) \leq EMA_{s}(t - 1);\quad \\ signal_{EMA}(t - 1)\mbox{ otherwise} \quad \end{array} \right.}$$

  • the one based on RSI:

    $$\displaystyle{signal_{RSI}(t) = \left \{\begin{array}{@{}l@{\quad }l@{}} -1\mbox{ if }RSI(t)> 70 \wedge RSI(t - 1) \leq 70 \quad \\ +1\mbox{ if }RSI(t) <30 \wedge RSI(t - 1) \geq 30;\quad \\ signal_{RSI}(t - 1)\mbox{ otherwise} \quad \end{array} \right.}$$

  • the one based on MACD, where DL(⋅ ) and SL(⋅ ) are respectively the so-called differential line and signal line:

    $$\displaystyle{signal_{MACD}(t) = \left \{\begin{array}{@{}l@{\quad }l@{}} -1\mbox{ if }DL(t) <SL_{sl}(t) \wedge DL(t - 1) \geq SL_{sl}(t - 1) \quad \\ +1\mbox{ if }DL(t)> SL_{sl}(t) \wedge DL(t - 1) \leq SL_{sl}(t - 1);\quad \\ signal_{MACD}(t - 1)\mbox{ otherwise} \quad \end{array} \right.}$$

  • the one based on BB, where P(⋅ ) is the price of the considered financial asset, BB L (⋅ ) and BB U (⋅ ) are respectively the lower band and the upper band:

    $$\displaystyle{signal_{BB}(t) = \left \{\begin{array}{@{}l@{\quad }l@{}} -1\mbox{ if }P(t) <BB_{U}(t) \wedge P(t - 1) \geq BB_{U}(t - 1)\quad \\ +1\mbox{ if }P(t)> BB_{L}(t) \wedge P(t - 1) \leq BB_{L}(t - 1).\quad \\ signal_{BB}(t - 1)\mbox{ otherwise} \quad \end{array} \right.}$$

We must keep in mind that any decisional rule will depends on the values of the indicators which, in their turn, will depends on a given parametrization. In the following, we will denote by w the vector of the following parameters: w f and w s are the time-window widths related to the fast EMA and to the slow EMA, respectively; w RSI is the time-window width related to RSI; w MACD, 1, w MACD, 2 and w sl are the three time-window widths related to MACD; w LB and w UB are the two time-window widths related to BB.

To define only one operational trading signal, we propose to aggregate the trading signals in the following way:

$$\displaystyle{signal(t) = \mbox{ sign}(signal_{EMA}(t)+signal_{RSI}(t)+signal_{MACD}(t)+signal_{BB}(t))\mbox{,}}$$

where sign(⋅ ) is the signum function.

Note that if three or four out of four decisional rules give the same trading signal then the single operational trading signal is equal to it. Moreover, it is easy to prove that if two decisional rules provide the same trading signal and the other two decisional rules provide different trading signals, also between them, then the single operational trading signal is equal to the one of the two former decisional rules.

2.2 The Optimization Problem

In this paper we measure the performance of a TS in a quite simple way, although there are other ways to do this. An intuitive measure is the net capital at the end of the trading period, C(T), where “net” means that we explicitly take into accounts of the transaction costs. In detail, let δ be the transaction costs expressed in percentage; we define the net rate of return, e(t), obtained by the TS from t − 1 to t, as follows:

$$\displaystyle{e(t) = signal(t - 1)\ln \left ( \frac{P(t)} {P(t - 1)}\right ) -\delta \left \vert signal(t) - signal(t - 1)\right \vert \mbox{, }t = 2,\ldots,T,}$$

and, fixing C(1), the equity line produced by the TS is:

$$\displaystyle{C(t) = C(t - 1)[1 + e(t)]\mbox{, }t = 2,\ldots,T\mbox{.}}$$

At this stage, we can formulate the constrained optimization problem as:

$$\displaystyle{ \begin{array}{cl} \max _{\begin{array}{c} \mathbf{w} \end{array} }&C(T) \\ \mbox{ s.t.} &\left \{\begin{array}{@{}l@{\quad }l@{}} w_{EMA_{f}} <w_{EMA_{s}} \quad \\ w_{sl} <w_{MACD,1} <w_{MACD,2} \quad \\ w_{EMA_{f}},w_{EMA_{s}},w_{RSI},w_{sl},w_{MACD,1},w_{MACD,2},w_{BB} \in \mathbb{N}^{+}\quad \end{array} \right. \end{array} \!\!\!\!\!\!\!\!. }$$
(1)

This constrained maximization problem is “complex” because the objective function C(⋅ ) is nonlinear a non differentiable, moreover it is formulated in terms of variables that must assume integer values. So, as underlined above, we need to use as a solver a metaheuristic like PSO.

2.3 Particle Swarm Optimization

PSO is an iterative metaheuristic for the solution of global unconstrained continuous optimization problems [6, 10], that may be adapted for solving also constrained ones. The basic idea of PSO is to mimic the social behaviour of swarm of bees or of flocks of birds cooperating for searching for food. For this purpose, each particle, or member, of the swarm moves in the search area. The direction and the velocity of the movement depend on its best position reached so far, and on the exchanges of information with the neighboring particles in the swarm. The behaviour of each particle allows to the whole swarm to converge towards the best global position. From a mathematical point of view, the paradigm of a flying swarm may be formulated as follows: given an optimization problem, each particle of the swarm represents a possible solution; its starting position x j 1 and starting velocity v j 1 are randomly assigned, so determining its initial direction and velocity of movement.

Let us consider the global unconstrained optimization problem \(\min _{\mathbf{x}\in \mathbb{R}^{d}}f(\mathbf{x}),\) where \(f: \mathbb{R}^{d}\mapsto \mathbb{R}\) is the objective function. Suppose to solve it using PSO and considering M particles. At the k-th iteration of the algorithm, three vectors are associated to the j-th particle, with j = 1, …, M:

  • the position \(\mathbf{x}_{j}^{k} \in \mathbb{R}^{d}\);

  • the velocity \(\mathbf{v}_{j}^{k} \in \mathbb{R}^{d}\);

  • the best position visited so far \(\mathbf{p}_{j} \in \mathbb{R}^{d}\).

Moreover, pbest j = f(p j ) is the value of the objective function in position p j , while p g and gbest are respectively the best position reached by the swarm and the value of the objective function in such a position.

The steps of the algorithm are the following:

  1. 1.

    Randomly assign the starting position x  1 j and the starting velocity v  1 j for j = 1, …, M.

  2. 2.

    Set pbest j = +∞ for j = 1, …, M, set gbest = +∞, and set k = 1.

  3. 3.

    Evaluate f(x j k) for j = 1, …, M.

  4. 4.

    If f(x j k) < pbest j then set p j = x j k and pbest j = f(x j k) for j = 1, …, M.

  5. 5.

    If f(x j k) < gbest then set p g = x j k and gbest j = f(x j k) for j = 1, …, M.

  6. 6.

    Update position and velocity of the j-th particle for j = 1, …, M as:

    $$\displaystyle\begin{array}{rcl} \mathbf{v}_{j}^{k+1}& =& w^{k+1}\mathbf{v}_{ j}^{k} + \mathbf{U}_{\phi _{ 1}} \otimes (\mathbf{p}_{j} -\mathbf{x}_{j}^{k}) + \mathbf{U}_{\phi _{ 2}} \otimes (\mathbf{p}_{g} -\mathbf{x}_{j}^{k}) {}\end{array}$$
    (2)
    $$\displaystyle\begin{array}{rcl} \mathbf{x}_{j}^{k+1}& =& \mathbf{x}_{ j}^{k} + \mathbf{v}_{ j}^{k+1} {}\end{array}$$
    (3)

    where \(\mathbf{U}_{\phi _{1}},\mathbf{U}_{\phi _{2}} \in \mathbb{R}^{d}\) and their components are uniformly randomly distributed in [0, ϕ 1] and [0, ϕ 2] respectively, and denoting ⊗ the component-wise product.

  7. 7.

    If a convergence criterion is not satisfied then set k = k + 1 and go to step 3.

The values of ϕ 1 and ϕ 2 strongly affect the strength of the attractive forces towards the personal and the swarm best positions explored so far by the particles. Thus, in order to get the convergence of the swarm, they have to be set carefully in accordance with the value of the inertia weight w k. The parameter w k generally decreases linearly with the number of steps, as:

$$\displaystyle{w^{k} = w_{ max} + \frac{w_{min} - w_{max}} {K} k}$$

where K is usually the maximum number of iterations allowed. The values for w max and w min are typically 0. 9 and 0. 4.

We previously said that our optimization problem is a constrained integer one and, for this reason, we have to adapt the standard PSO algorithm to deal with these peculiarities.

As concern the presence of integer variables, we apply the approach suggested in [7] and ≪ [e]ach particle of the swarm [is] truncated to the closest integer, after the determination of its new position [by (3)] ≫ [7, p. 1584]. As pointed out in [7] ≪ [t]he truncation of real values to integers seems not to affect significantly the performance of the method, as the experimental results indicate. Moreover, PSO outperforms the [Branch and Bound] technique for most test problems ≫ [7, p. 1583]. So, with this approach we can manage the constraints \(w_{EMA_{f}}\), \(w_{EMA_{s}}\), w RSI , w sl , w MACD, 1, w MACD, 2, \(w_{BB} \in \mathbb{N}^{+}\) of our optimization problem.

As regards the other constraints, different strategies are proposed in literature. In this paper we use PSO as a tool for the solution of unconstrained optimization problems according to its original aim, so we have to reformulated our problem into an unconstrained one. To this purpose, we use an approach described in [4] and recently applied in the financial context [2]. Such an approach uses a nondifferentiable ℓ 1 penalty function to reformulated our problem into an unconstrained one and is known as exact penalty method. The term “exact” refers to the correspondence between the minimizers of the original constrained problem and the minimizers of the unconstrained (penalized) one.

Let ε be the penalty parameter, then the reformulated version of our optimization problem is:

$$\displaystyle{ \begin{array}{cc} \max _{\mathbf{w}}& C(T) -\frac{1} {\epsilon } \Big[\max \{0,w_{EMA_{f}} - w_{EMA_{s}}\} +\max \{ 0,w_{sl} \\ & - w_{MACD,1}\} +\max \{ 0,w_{MACD,1} - w_{MACD,2}\}\Big].\\ \end{array} }$$
(4)

A correct choice of the value of the penalty parameter ensures the correspondence between the solutions of the original constrained problem and of the reformulated unconstrained one. Note that in the (4), the constraints \(w_{EMA_{f}}\), \(w_{EMA_{s}}\), w RSI , w sl , w MACD, 1, w MACD, 2, \(w_{BB} \in \mathbb{N}^{+}\) do not appear as they are taken into account by the truncation of real values described above.

3 Applications

As stated above, in this paper we want to study the performances of a simple TS based on indicators coming from TA, finding the optimal values of the time-window widths associated to such indicators by using PSO.

To assess the actual improvement of the applied procedure, we have carried out both an in-sample and an out-of-sample analysis. In particular, we have determined the optimized parameter values of the considered TS solving the optimization problem (4) by the version of the PSO described in Sect. 2.3.

We have considered time series of eight stocks in the period from January 2, 2001 to June 30, 2016 (3932 prices). More specifically, we have tested the TS on the following stocks: BUZZI UNICEM S.p.A. (BU), ENEL S.p.A. (EE), ENI S.p.A. (EI), Generali S.p.A. (GE), INTESA SANPAOLO S.p.A. (IS), LUXOTTICA GROUP S.p.A. (LG), STMICROELECTRONICS S.p.A. (ST) and TELECOM ITALIA S.p.A. (TI). We have choosen the stocks considering their importance in the Italian stock market. In fact, all of them are components of the Italian stock index FTSE MIB and they represent some meaningful sectors of the Italian economy.

We have performed the in-sample analysis in the period going from June 2, 2001 to June 30, 2016 (3880 pricesFootnote 1), whereas the out-of-sample analysis has been carried out in the period from November 1, 2011 to June 30, 2016 (1180 prices), using the period from January 2, 2001 to October 31, 2011 (2752 prices) to evaluate the optimal values of the time-window widths.

All the applications have used δ = 0. 15% (percentage transaction cost currently applied by several Italian brokerage companies) and C(1) = 100.

As regards the PSO algorithm, we have used the following setting: M = 10 as number of particles; K = 100 as maximum number of iterations; ϕ 1 = ϕ 2 = 1. 49618 as coefficients; ε = 0. 0001 as penalty parameter. The first two values have been determined by a trial-and error procedure, the last three values are commonly suggested in the literature. Considering that the methodology proposed in Sect. 2.3 is stochastic in reason of the random initialization (of both position and velocity of the particles) and of the random disturbance in the updating equation of the velocity (see step 6 of the algorithm presented in Sect. 2.3), we have applied 100 times our methodology to each stock, then we have calculated the mean values and other statistics.

As far as the TS with standard setting is concerned, following the relevant professional literature, we have used the following values for the parameters: \(w_{EMA_{f}} = 12\), \(w_{EMA_{s}} = 26\), w RSI = 26, w sl = 9, w MACD, 1 = 12, w MACD, 2 = 26 and w BB = 26.

3.1 In-Sample Analysis

The in-sample performances achieved by the two TSs (with default and optimized settings) for the eight stocks are presented in Table 1. More specifically, in column 2 we report the annualized rate of return performed by the TS with standard setting (r); in columns 3 and 4 we respectively report the average annualized rate of return performed by the TS with optimized parameter values (\(\overline{r}\)) and the associated standard deviation (s r ); column 5 shows the 95% confidence interval calculated using \(\overline{r}\) and s r ([⋅ , ⋅ ]95%, r ); in columns 6 and 7 we have the minimum of r (r min) and the maximum of r (r max), respectively, over the 100 applications of our methodology; in column 8 and 9 we respectively report the average percentages of times in which, during the trading period, the value of the equity line produced by the TS with optimized parameter values has been greater than, and not less than, the value of the equity line produced by the TS with standard setting (\(\overline{\%>}\) and \(\overline{\% \geq }\)).

Table 1 In-sample performances achieved by the various TSs
Full size table

We point out that all the annualized rates of return achieved by the TS with standard setting are negative, whereas all the average annualized rates of return performed by the TS with optimized parameter values are far greater than the former ones and are all positive. It indicates that also in the case of simple TA-based TS, like the one considered in this paper, the parameters optimization can play an important role. Then, no average annualized rate of return achieved by the TS with standard setting belongs to the 95% confidence interval calculated using \(\overline{r}\) and s r . This indicates that, for all the investigated stocks, \(\overline{r}\) is statistically different from r at the 5% significance level. Moreover, note also that, with the only exception of the stock asset ST, all rs are lower than the corresponding r min (r mins are in column 6), which means that the worst results obtained with optimized parameters is generally better than those obtained with standard settings.

All the previous remarks concern with the performances achieved by the various TSs in the final time instant t = T of the trading period, that is June 30, 2016. But the results in column 8 and 9 well put in evidence that for very large part of the trading period (never lower than 74.97%) the TSs with optimized parameter values perform better than the TS with standard setting.

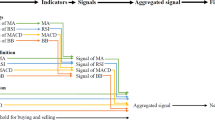
As example, in Fig. 1 we show the in-sample performance related to the stock asset TI. In particular, on the top, the closing price time series is shown; in the second panel, the operational trading signal is reported; on the bottom, the time series of the gross equity line produced by the TS with optimized parameter values (dotted curve), of the net equity line produced by the same TS (bold curve), and of the net equity line produced by the TS with standard setting (continuous curve) are shown.

Fig. 1
figure 1

In-sample performance related to the stock asset TI. Data to the left of the vertical line are related to the first 52 prices used for calculating the starting values of indicators and oscillators

Full size image

3.2 Out-of-Sample Analysis

In Table 2 we present the out-of-sample performances attained by the various TSs. Its columns are the same of those of Table 1.

Table 2 Out-of-sample performances achieved by the various TSs
Full size table

Similarly to what highlighted by the in-sample analysis, even in the out-of-sample one all the annualized rates of return achieved by the TS with standard setting (column 2) are negative and all the average annualized rates of return performed by the TS with optimized parameter values (column 3) are greater than the former. But conversely, now all \(\overline{r}\) s are negative. It indicates that the parameter optimization play a positive role also in the out-of-sample applications, although its importance is significantly diminished with respect to the in-sample ones. As a further confirmation of such an importance reduction, note that now all the annualized rates of return achieved by the TS with standard setting (column 2) belong to the 95% confidence intervals calculated using \(\overline{r}\) and s r (column 5), and that each r is greater than the corresponding r min (r mins are in column 6). This may suggest that in the out-of-sample applications the standard setting does not appear so far from the optimal setting.

We recall that all the previous remarks concern with the performances obtained by the various TSs in the final time instant t = T, that is June 30, 2016. But the results in column 8 and 9 point out that, with the only exception of the stock asset GE, for large part of the trading period the TSs with optimized parameter values perform better than the TS with standard setting.

As example, in Fig. 2 we show the out-of-sample performances related to the stock asset TI. Its panels are the same of those of Fig. 1.

Fig. 2
figure 2

Out-of-sample performances related to the stock asset IS. Data to the right of the vertical line are related to the out-of-sample period

Full size image

4 Conclusions

In this paper we have considered a simple TS based on four indicators, two momentum and two oscillators, coming from TA. Instead of using a rule of thumb to select the time-window widths, we have proposed to apply an adapted version of PSO in order to determine the optimal values of these parameters. The results we have obtained, summarized in Table 1 for the in-sample analysis and in Table 2 for the out-of-sample analysis, show that parameter optimization can play an important role as the results of our proposal, expressed in terms of annualized rate of return, are always better than the classical TA-based ones.

Another advantage of the procedure is that the parameter setting may vary according to the stock, so avoiding the use of the same parameter values in possible different contexts.

Our future goals are: to check the proposed technique with different price time series coming from other financial markets; to improve our methodology in order to anticipate the market signals using observational data; to generalize the proposed procedure in order to generate trading rule.