Abstract
Almost all the available strong designated verifier signature (SDVS) schemes are either insecure or inefficient for practical implementation. Hence, an efficient and secure SDVS algorithm is desired. In this paper, we propose an efficient strong designated verifier signature on identity-based setting, we call it ID-SDVS scheme. The proposed scheme is strong existentially unforgeable against adaptive chosen message and adaptive chosen identity attack under standard assumptions, the hardness of the decisional and computational Bilinear Diffie-Hellman Problem (BDHP). Though the unverifiability by a non-designated verifier and the strongness are essential security properties of a SDVS, the proofs for these properties are not provided in most of the literature on SDVS we reviewed. We provide the proofs of unverifiability and of strongness of the proposed scheme. Moreover, we show that the proposed scheme is significantly more efficient in the view of computation and operation time than the existing similar schemes.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Strong designated verifier signature
- Identity-based cryptography
- Bilinear Diffie-Hellman problem
- Provable security
1 Introduction
Digital signature is a widely accepted tool for authentication in cryptography. The general definition of digital signature in public key cryptography allows any user in public to verify the authentication of the signature. However, in many situations, like proposal of construction bidding, licensing software, electronic voting etc., the signers may desire to sign a document for a particular receiver with control over the verification of their signatures. In these applications, the signed message may include crucial information between the signer and the verifier.
For such scenarios, Chaum et al. [3] introduced the undeniable signature which allows a signer to have a control over the signature with the property that verification of a signature requires the participation of the signer. But a practical issue with such a signature is that the signer’s presence for verification requires the signer to be online all the time. To overcome this complication, Jakobsson et al. [7] proposed the concept of designated verifier signature (DVS), that transforms Chaum’s scheme [2] into non-interactive verification using a designated verifier proof. Their scheme allows the signer to convince the validity of a statement to a particular verifier without allowing any third party to verify the validity of that signature.
Saeednia et al. [14] pointed out that given a DVS, anybody can make sure that there are only two potential signers. Hence, if the signatures may be captured on the line before arriving at the designated verifier, then one can identify the signer, since it is now sure that the verifier did not produce the signature. To overcome this issue, they extended the notion of DVS with a property of strongness which requires that to a third party, who is none of the signer or designated verifier, the DVS from a signer A to a designated verifier B, is indistinguishable from a DVS from any other signer C to some other verifier D. They call such a signature strong designated verifier signature (SDVS).
1.1 Related Work
In 2004, Susilo et al. [15] proposed the first identity-based strong designated verifier signature (ID-SDVS). Unforgeability of their scheme is based on the Bilinear Diffie-Hellman (BDH) assumption. In 2006, Huang et al. [6] proposed a short ID-SDVS scheme based on Diffie-Hellman key exchange protocol. The security of their scheme relies on the Gap Bilinear Diffie-Hellman (GBDH) assumption. Computation cost of the former scheme is more than double of the latter one. However, the scheme in [6] is not strongly unforgeable since the signature of a message always remains the same and a replay attack is always possible and cannot be trivially avoided. Later, in 2008, Zhang et al. [16] proposed another ID-SDVS scheme that is claimed to be non-delegatable, but in 2009, Kang et al. [9] pointed out security flaws in [16] against the strongness property of SDVS scheme. They observed that in [16], an outsider who eavesdrops an old signature and can obtain some information that is to be used for the verification of subsequent signatures. It has also been explained in [9], that how the property of strongness in [16] does not fulfil their claim. In [9], they also proposed another ID-SDVS scheme and an identity-based designated verifier proxy signature (ID-DVPS). However, in 2010, Lee et al. [11] showed that the scheme in [9] is universally forgeable. In 2009, Kang et al. [10] proposed another ID-SDVS scheme which is more efficient than that in [9]. However, this construction was also shown to be universally forgeable in [5].
1.2 Applications
The strong designated verifier signature has crucial applications in various real world scenarios including the following:
-
1.
Licensing software: Software companies use digitally signed keys as their software license so that these keys can only be used by the person who has purchased the product. The strong designated verifier signature on keys protects illegal distribution of the software.
-
2.
Electronic voting: In electronic voting schemes, a voting center is required to ensure that a vote has been counted in the final tally or not. The verification of the center’s signature on the receipt is one way of doing so. But it should also be taken in account that the voters must not have the ability to convince a third party the nature of their votes they have casted. This may cause some gain or threats by the parties depending upon the nature of the vote. To fulfil this requirement in electronic voting schemes, the center’s signature should be a strong designated verifier signature.
1.3 Our Contribution
In this paper, we propose an efficient identity-based strong designated verifier signature (ID-SDVS) scheme using bilinear pairing. Proposed scheme is existentially unforgeable (resp. unverifiable) against adaptive chosen message and adaptive chosen identity attack under the computational (resp. decisional) Bilinear Diffie-Hellman (BDH) assumption in the random oracle model. We also provide a proof for the strongness property of the proposed scheme. We reviewed the existing ID-SDVS schemes including [5, 6, 8–11, 15, 16] and noticed that most of the papers on ID-SDVS were missing the full proofs of security which we tabulate in Table 1. Moreover, we show that the proposed scheme is upto 120 % more efficient in the sense of computation and operation time than these schemes.
1.4 Outline of the Paper
The rest of this paper is organized as follows. In Sect. 2, we introduce some related mathematical definitions, problems and assumptions. In Sect. 3, we present the formal definition of an identity-based strong designated verifier signature scheme and a formal security model for it. The proposed signature scheme is presented in Sect. 4. In Sect. 5 we analyze the security of the proposed scheme and in Sect. 6 we do an efficiency comparison with the state-of-art. Finally, in Sect. 7 we conclude our work.
2 Preliminaries
A probabilistic polynomial time (PPT) algorithm is a probabilistic/randomized algorithm that runs in time polynomial in the length of input. We denote by \(y \leftarrow A(x)\) the operation of running a randomized or deterministic algorithm A(x) and storing the output to the variable y. If X is a set, then  denotes the operation of choosing an element v of X according to the uniform random distribution on X. We say that a given function \(f: N \rightarrow [0,1]\) is negligible in n if \(f(n) < 1/p(n)\) for any polynomial p for sufficiently large n. For a group G and \(g\in G\), we write \(G=\langle g \rangle \) if g is a generator of G.
denotes the operation of choosing an element v of X according to the uniform random distribution on X. We say that a given function \(f: N \rightarrow [0,1]\) is negligible in n if \(f(n) < 1/p(n)\) for any polynomial p for sufficiently large n. For a group G and \(g\in G\), we write \(G=\langle g \rangle \) if g is a generator of G.
Definition 1 (Bilinear Map)
Let \(G_{1}\) be an additive cyclic group with generator P and \(G_{2}\) be a multiplicative cyclic group. Let both the groups are of the same prime order q. Then a map \(e: G_1\times G_1\rightarrow G_2\) is called a cryptographic bilinear map if it satisfies the following properties.
-
Bilinearity: For all \(a, b \in \mathbb {Z}_q^*\), \(e(aP, bP) = e(P,P)^{ab}\), or equivalently, for all \(Q,R,S \in G_{1}\), \(e(Q+R,S)=e(Q,S)e(R,S)\) and \(e(Q,R+S)=e(Q,R)e(Q,S)\).
-
Non-degeneracy: There exists \(Q,R \in G_{1}\) such that \(e(Q,R)\ne 1\). Note that since \(G_{1}\) and \(G_{2}\) are groups of prime order, this condition is equivalent to the condition \(g:=e(P,P) \ne 1\), which again is equivalent to the condition that \(g:=e(P,P)\) is a generator of \(G_{2}\).
-
Computability: There exists an efficient algorithm to compute \(e(Q,R)\in G_2\) for all \(Q,R \in G_{1}\).
Definition 2
A bilinear map parameter generator \(\mathfrak {B}\) is a PPT algorithm that takes as input security parameter \(\lambda \) and outputs a tuple
where q, \(G_{1}\), \(G_{2}\), e, P and g are as in Definition 1.
Definition 3 (Bilinear Diffie-Hellman Problem)
Given a security parameter \(\lambda \), let \(\langle q,e: G_1 \times G_1 \rightarrow G_2, P, g \rangle \leftarrow \mathfrak {B}(\lambda )\). Let \(BDH: G_1 \times G_1 \times G_1 \rightarrow G_2\) be a map defined by
The bilinear Diffie-Hellman problem (BDHP) is to evaluate BDH(X, Y, Z) given  . (Without the knowledge of \(x,y,z\in \mathbb {Z}_q\) — obtaining \(x\in \mathbb {Z}_q\), given \(P,X\in G_1\) is solving the discrete logarithm problem (DLP)).
. (Without the knowledge of \(x,y,z\in \mathbb {Z}_q\) — obtaining \(x\in \mathbb {Z}_q\), given \(P,X\in G_1\) is solving the discrete logarithm problem (DLP)).
Definition 4
A BDHP parameter generator \(\mathfrak {C}\) is a PPT algorithm that takes as input security parameter \(\lambda \) and outputs a tuple
where q, \(G_{1}\), \(G_{2}\), e, P, g, X, Y and Z are as in Definition 3.
Definition 5 (Bilinear Diffie-Hellman Assumption)
Given a security parameter \(\lambda \), let \(\langle q, e: G_1 \times G_1 \rightarrow G_2, P,g, X,Y,Z \rangle \leftarrow \mathfrak {C}(\lambda )\). The bilinear Diffie-Hellman assumption (BDHA) states that for any PPT algorithm \(\mathcal {A}\) which attempts to solve BDHP, its advantage
is negligible in \(\lambda \).
Definition 6 (Decisional Bilinear Diffie-Hellman Problem)
Given a security parameter \(\lambda \), let \(\langle q, e: G_1 \times G_1 \rightarrow G_2, P,g, X,Y,Z \rangle \leftarrow \mathfrak {C}(\lambda )\). Let  . The decisional bilinear Diffie-Hellman problem (DBDHP) is to decide if
. The decisional bilinear Diffie-Hellman problem (DBDHP) is to decide if
That is, if \(X = xP, Y = yP, Z = zP\), for some \(x,y,z\in \mathbb {Z}_q\), then the DBDHP is to decide if
(Without the knowledge of \(x,y,z\in \mathbb {Z}_q\) — obtaining \(x\in \mathbb {Z}_q\), given \(P,X\in G_1\) is solving the discrete logarithm problem (DLP)).
Definition 7
A DBDHP parameter generator \(\mathfrak {D}\) is a PPT algorithm that takes as input security parameter \(\lambda \) and outputs a tuple
where q, \(G_{1}\), \(G_{2}\), e, P, g, X, Y, Z and \(\omega \) are as in Definition 6.
Definition 8 (Decisional Bilinear Diffie-Hellman Assumption)
Given a security parameter \(\lambda \), let \(\langle q, e: G_1 \times G_1 \rightarrow G_2, P,g, X,Y,Z, \omega \rangle \leftarrow \mathfrak {D}(\lambda )\). The bilinear Diffie-Hellman assumption (DBDHA) states that, for any PPT algorithm \(\mathcal {A}\) which attempts to solve DBDHP, its advantage
is negligible in \(\lambda \).
3 Identity-Based Strong Designated Verifier Signature
In this section we present the formal definition of an identity-based strong designated verifier signature (ID-SDVS) and formalize a security model for it.
3.1 Identity-Based Strong Designated Verifier Signature
In an ID-SDVS scheme, a signer with identity \(\mathsf {ID}_{\!\mathcal {S}}\) intends to send a signed message to a designated verifier with identity \(\mathsf {ID}_{\!\mathcal {V}}\) such that no one other than the designated verifier can verify the signature. An ID-SDVS scheme is consists of the following five algorithms:
-
1.
\( params \leftarrow Setup (\lambda )\): An algorithm run by the private key generator (PKG) which takes as input a security parameter \(\lambda \) and outputs the public parameters params and a master secret s of the system. In all the algorithms from here onward, params will be considered as an implicit input.
-
2.
\((Q_{\mathsf {ID}}, S_{\mathsf {ID}})\leftarrow Key Extract (\mathsf {ID})\): An algorithm run by the (PKG) which takes input identity \(\mathsf {ID}\) and outputs its public and private key pair \((Q_{\mathsf {ID}}, S_{\mathsf {ID}})\).
-
3.
\(\sigma \leftarrow DVSign (S_{\mathsf {ID}_{\!\mathcal {S}}}, Q_{\mathsf {ID}_{\!\mathcal {V}}}, m)\): A probabilistic algorithm run by the signer that takes as input the signer’s secret key \(S_{\mathsf {ID}_{\!\mathcal {S}}}\), the designated verifier’s public key \(Q_{\mathsf {ID}_{\!\mathcal {V}}}\) and a message m to generate a signature \(\sigma \).
-
4.
\(b\leftarrow DVVer (S_{\mathsf {ID}_{\!\mathcal {V}}}, Q_{\mathsf {ID}_{\!\mathcal {S}}}, m, \sigma )\): A deterministic algorithm run by the verifier that takes the verifier’s secret key \(S_{\mathsf {ID}_{\!\mathcal {V}}}\), the signer’s public key \(Q_{\mathsf {ID}_{\!\mathcal {S}}}\), a message m and a signature \(\sigma \), and returns a bit \(b\) which is \(1\) if the signature is valid and \(0\) if invalid.
-
5.
\(\widehat{\sigma } \leftarrow DVTrans (S_{\mathsf {ID}_{\!\mathcal {V}}}, Q_{\mathsf {ID}_{\!\mathcal {S}}}, m)\): A deterministic algorithm run by the verifier that takes the verifier’s secret key \(S_{\mathsf {ID}_{\!\mathcal {V}}}\), and the signer’s public key \(Q_{\mathsf {ID}_{\!\mathcal {S}}}\) and a message m to generate a signature \(\widehat{\sigma }\).
3.2 Security Model for Identity-Based Strong Designated Verifier Signature
An ID-SDVS scheme must satisfy the following security properties.
-
1.
Correctness : If the signature \(\sigma \) on a message m is correctly computed by a signer \(\mathsf {ID}_{\!\mathcal {S}}\), then the designated verifier \(\mathsf {ID}_{\!\mathcal {V}}\) must be able to verify the correctness of the message-signature pair \((m, \sigma )\). That is,
$$\begin{aligned} Prob[1\leftarrow DVVer (S_{\mathsf {ID}_{\!\mathcal {V}}},Q_{\mathsf {ID}_{\!\mathcal {S}}},m, DVSign (S_{\mathsf {ID}_{\!\mathcal {S}}}, Q_{\mathsf {ID}_{\!\mathcal {V}}}, m))] = 1 \end{aligned}$$ -
2.
Unforgeability : It is computationally infeasible to construct a valid ID-SDVS signature without the knowledge of the private key of either the signer or the designated verifier. We define below strong existential unforgeability against an adaptive chosen message and adaptive chosen identities attack.
Definition 9 (Unforgeability)
An ID-SDVS scheme is said to be strong existential unforgeable against adaptive chosen message and adaptive chosen identities attack if for any security parameter \(\lambda \), no probabilistic polynomial time adversary \(\mathcal {A}(q_{H_1},q_{H_2},q_{E},q_{S},q_{V},\varepsilon _{\mathcal {A}}(\lambda ),t)\) which runs in time t has a non-negligible advantage
against the challenger \(\mathcal {B}\) in the following game:
-
1.
Setup: The challenger \(\mathcal {B}\) generates the system’s public parameter \( params \) for security parameter \(\lambda \).
-
2.
Query Phase:
-
The adversary \(\mathcal {A}\) may request upto \(q_{H_1}\) hash queries on its adaptively chosen identities and upto \(q_{H_2}\) hash queries on its adaptively chosen messages and obtain responses from \(\mathcal {B}\) acting as a random oracle.
-
\(\mathcal {A}\) may request upto \(q_{E}\) key extraction queries on its adaptively chosen identities and obtain the corresponding private keys.
-
\(\mathcal {A}\) may request upto \(q_{S}\) signature queries on its adaptively chosen messages and adaptively chosen identities for the signer and the designated verifier and obtain a valid strong designated verifier signature.
-
\(\mathcal {A}\) may request upto \(q_{V}\) verification queries on signatures on its adaptively chosen messages m and adaptively chosen identities for the signer and the designated verifier and obtain the verification result \(1\) if it is valid and \(0\) if invalid.
-
-
3.
Output: Finally, \(\mathcal {A}\) outputs a (message, signature) pair \((m^*, \sigma ^*)\) for identities \(\mathsf {ID}_{\!\mathcal {S}}^*\) of the signer and \(\mathsf {ID}_{\!\mathcal {V}}^*\) of the designated verifier such that:
-
\(\mathcal {A}\) has never submitted \(\mathsf {ID}_{\!\mathcal {S}}^*\) or \(\mathsf {ID}_{\!\mathcal {V}}^*\) during the key extraction queries.
-
\(\sigma ^*\) was never given as a response to a signature query on the message \(m^*\) with the signer’s identity \(\mathsf {ID}_{\!\mathcal {S}}^*\), and the designated verifier’s identity \(\mathsf {ID}_{\!\mathcal {V}}^*\);
-
\(\sigma ^*\) is a valid signature on the message \(m^*\) from a signer with identity \(\mathsf {ID}_{\!\mathcal {S}}^*\), for a designated verifier with identity \(\mathsf {ID}_{\!\mathcal {V}}^*\).
-
-
3.
Unverifiability : It is computationally infeasible to verify the validity of an ID-SDVS without the knowledge of the private key of either the signer or the designated verifier. We define below existential designated unverifiability against an adaptive chosen message and adaptive chosen identities attack.
Definition 10 (Unverifiability)
An ID-SDVS scheme is said to be existential designated unverifiable against adaptive chosen message and adaptive chosen identities attack if for any security parameter \(\lambda \), no probabilistic polynomial time adversary \(\mathcal {A}(q_{H_1},q_{H_2},q_{E},q_{S},q_{V},\varepsilon _{\mathcal {A}}(\lambda ),t)\) which runs in time t has a non-negligible advantage
against the challenger \(\mathcal {B}\)’s response \(\sigma ^*\) in the following game:
-
1.
Setup: Similar to the unforgeability game in Definition 9.
-
2.
Query Phase 1: Similar to the unforgeability game in Definition 9.
-
3.
Challenge: At some point, \(\mathcal {A}\) outputs a message \(m^*\) and identities \(\mathsf {ID}_{\!\mathcal {S}}^*\) of the signer and \(\mathsf {ID}_{\!\mathcal {V}}^*\) of the designated verifier on which it wishes to be challenged such that \(\mathcal {A}\) has never submitted \(\mathsf {ID}_{\!\mathcal {S}}^*\) or \(\mathsf {ID}_{\!\mathcal {V}}^*\) during the key extraction queries. The challenger \(\mathcal {B}\) responds with a “signature” \(\sigma ^*\) and challenges \(\mathcal {A}\) to verify if it is valid or not.
-
4.
Query Phase 2: \(\mathcal {A}\) continues its queries as in Query Phase 1 with an additional restriction that now it cannot submit a verification query on \(\sigma ^*\).
-
5.
Output: Finally, \(\mathcal {A}\) outputs its guessed bit \(b^*\) which is \(1\) if the signature is valid and \(0\) if invalid.
-
4.
Non-transferability : Given a signature \(\sigma \) on message m, it is infeasible for any PPT adversary \(\mathcal {A}\) to decide whether \(\sigma \) was produced by the signer or by the designated verifier, even if \(\mathcal {A}\) is also given the private keys of the signer and the designated verifier. In other words, it is impossible for the designated verifier to prove to an outsider that the signature is actually generated by the signer.
Definition 11 (Non-transferability)
An ID-SDVS scheme is said to be non-transferable if the signature generated by the signer is computationally indistinguishable from that generated by the designated verifier, that is,
-
5.
Strongness : Let \(\sigma \leftarrow DVSign (S_{\mathsf {ID}_{\!\mathcal {S}}}, Q_{\mathsf {ID}_{\!\mathcal {V}}}, m)\) be a signature on a message m from a signer \(\mathcal {S}\) to a designated verifier \(\mathcal {V}\). Strongness requires that \(\sigma \) could have been produced by any other third party \(\mathcal {S}^{*}\) other than \(\mathcal {S}\) for some designated verifier \(\mathcal {V}^{*}\) other than \(\mathcal {V}\).
Definition 12 (Strongness)
An ID-SDVS scheme is said to be strong designated if given \(\sigma \leftarrow DVSign (S_{\mathsf {ID}_{\!\mathcal {S}}}, Q_{\mathsf {ID}_{\!\mathcal {V}}}, m)\), anyone, say \(\mathcal {V}^*\), other than the designated verifier \(\mathcal {V}\) can produce identically distributed transcripts that are indistinguishable from those of \(\sigma \) from someone, say \(\mathcal {S}^*\), except the signer \(\mathcal {S}\). That is,
4 Proposed Scheme
We present here our efficient and secure ID-SDVS. As described in Sect. 3, the proposed scheme consists of the following algorithms: Setup, Key Extract, Designated Signature, Designated Verification and Transcript Simulation.
-
Setup: In the setup phase, PKG on input security parameter \(\lambda \), generates the system’s master secret key \(s \in \mathbb {Z}_{q}^{*}\) and the system’s public parameters params = \((1^{\lambda }, G_{1}, G_{2}, q, e, H_{1}, H_{2}, P, P_{\!\! pub })\), where \(G_{1}\) is an additive cyclic group of prime order q with generator P, \(G_{2}\) is a multiplicative cyclic group of prime order q, and \(H_{1} : \{0, 1\}^{*} \longrightarrow G_{1}\), \(H_{2} : \{0, 1\}^{*} \times G_{1} \longrightarrow \mathbb {Z}_{q}^{*}\) are two cryptographic secure hash functions, and \(P_{pub} = sP \in G_{1}\) is system’s public key, \(e: G_{1} \times G_{1} \longrightarrow G_{2}\) is a bilinear map as defined in Sect. 2.
-
Key Extract: For a user with identity \(\mathsf {ID}_{i} \in \{0, 1\}^{*}\), the PKG computes its public key as \(Q_{\mathsf {ID}_{i}} = H_{1}(\mathsf {ID}_{i}) \in G_{1}\) and corresponding private key as \(S_{\mathsf {ID}_{i}} = sQ_{\mathsf {ID}_{i}} \in G_{1}\).
-
Designated Signature: To sign a message \(m \in \{0, 1\}^{*}\) which can be verified by a designated verifier \(\mathcal {V}\), the signer \(\mathcal {S}\) chooses a random
 and computes
and computes-
–
\(U= rP\in G_{1}\);
-
–
\(h = H_{2}(m, U) \in \mathbb {Z}_{q}^{*}\);
-
–
\(V = rP_{\!\! pub }+ hS_{\mathsf {ID}_{\!\mathcal {S}}}\in G_{1}\);
-
–
\(\sigma = e(V, Q_{\mathsf {ID}_{\!\mathcal {V}}})\).
The strong designated verifier signature on message m is \((U, \sigma ) \in G_{1} \times G_{2}\).
-
–
-
Designated Verification: On receiving a message m and a signature \((U, \sigma )\), a verifier first computes \(h = H_{2}(m, U) \in \mathbb {Z}_{q}^{*}\) and accepts the signature if and only if the following equality holds:
$$ \sigma = e( U + hQ_{\mathsf {ID}_{\!\mathcal {S}}}, S_{\mathsf {ID}_{\!\mathcal {V}}}) \,. $$ -
Transcript Simulation: The designated verifier \(\mathcal {V}\) can produce the signature \(\widehat{\sigma }\) intended for itself, by performing the following: chooses an integer
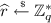 and computes
and computes-
–
\(\widehat{U}= \widehat{r}P \in G_{1}\);
-
–
\(\widehat{h} = H_{2}(m, \widehat{U}) \in \mathbb {Z}_{q}^{*}\);
-
–
\(\widehat{V} = \widehat{r}P + \widehat{h}Q_{\mathsf {ID}_{\!\mathcal {S}}}\in G_{1}\); and
-
–
\(\widehat{\sigma } = e(\widehat{V}, S_{\mathsf {ID}_{\!\mathcal {V}}})\).
-
–
5 Analysis of the Proposed Scheme
5.1 Correctness of the Proposed Scheme
The correctness of the scheme follows since if \((U,\sigma )\) is a correctly generated signature on a message m from a signer with identity \(\mathsf {ID}_{\!\mathcal {S}}\) for a designated verifier with identity \(\mathsf {ID}_{\!\mathcal {V}}\), then
5.2 Unforgeability
We now prove that the proposed ID-SDVS is unforgeable. That is, any third party other than the signer and the designated verifier, cannot forge a valid signature on an adaptively chosen message from an adaptively chosen signer’s identity for an adaptively chosen designated verifier’s identity with non-negligible probability. We show that if there exists a probabilistic polynomial time (PPT) adaptive chosen message and adaptive chosen identity algorithm which can produce a forgery for the proposed ID-SDVS then there exists another PPT algorithm which can use the forgery to solve the BDHP. In particular, we prove the following theorem:
Theorem 1
Given a security parameter \(\lambda \), if there exists a PPT adversary \(\mathcal {A}(q_{H_1},q_{H_2},q_{E},q_{S},q_{V},\varepsilon _{\mathcal {A}}(\lambda ),t)\) which breaks the unforgeability of the proposed ID-SDVS scheme in time t with success probability \(\varepsilon _{\mathcal {A}}(\lambda )\), then there exists a PPT adversary \(\mathcal {B}(\varepsilon _{\mathcal {B}}(\lambda ),t')\) which solves BDHP with success probability at least
in time at most
where \(S_{G_1}\) (resp. \(S_{G_2}\)) is the time taken for one scalar multiplication in \(G_1\) (resp. \(G_2\)), \(O_{G_1}\) (resp. \(O_{G_2}\)) is the time taken for one group operation in \(G_1\) (resp. \(G_2\)), and \(P_e\) is the time taken for one pairing computation.
Proof: Let for a security parameter \(\lambda \), \(\mathcal {B}\) is challenged to solve the BDHP for
where \(G_1\) is an additive cyclic group of prime order q with generator P, \(G_2\) is a multiplicative cyclic group of prime order q with generator e(P, P), and \(e: G_1 \times G_1 \rightarrow G_2\) is a cryptographic bilinear map as described in Sect. 2.  are unknown to \(\mathcal {B}\). The goal of \(\mathcal {B}\) is to solve BDHP by computing \(e(P,P)^{abc} \in G_2\) using \(\mathcal {A}\), the adversary who claims to forge the proposed ID-SDVS scheme. \(\mathcal {B}\) simulates the security game for unforgeability with \(\mathcal {A}\) as follows.
are unknown to \(\mathcal {B}\). The goal of \(\mathcal {B}\) is to solve BDHP by computing \(e(P,P)^{abc} \in G_2\) using \(\mathcal {A}\), the adversary who claims to forge the proposed ID-SDVS scheme. \(\mathcal {B}\) simulates the security game for unforgeability with \(\mathcal {A}\) as follows.
-
Setup: \(\mathcal {B}\) generates the system’s public parameter
$$ params = \langle q,e: G_1 \times G_1 \rightarrow G_2,P,P_{\!\! pub }:=cP,H_1,H_2 \rangle $$for security parameter \(\lambda \) where the hash functions \(H_1\) and \(H_2\) behave as random oracles and responds to \(\mathcal {A}\)’s queries as below.
-
\(H_{1}\) -queries: To respond to the \(H_1\) queries, \(\mathcal {B}\) maintains a list
$$L_{H_1}=\{( \mathsf {ID}_{i} \in \{0,\!1\}^*, r_i \in \mathbb {Z}_q^*, R_i \in G_1 )_{i=1}^{q_{H_1}}\}$$which is initially empty. \(\mathcal {B}\) randomly chooses two indices \(\alpha ,\beta \in [1,q_{H_1}]\) and sets \(i=0\). When \(\mathcal {A}\) makes an \(H_{1}\)-query for an identity \(\mathsf {ID}\in \{0,\!1\}^{*}\), \(\mathcal {B}\) proceeds as follows.
-
1.
If the query \(\mathsf {ID}\) already appears in \(L_{H_{1}}\) in some tuple \((\mathsf {ID}_{i}, r_i, R_i)\) then \(\mathcal {B}\) responds to \(\mathcal {A}\) with \(H_{1}(\mathsf {ID}) = R_i \in G_1\);
-
2.
otherwise \(\mathcal {B}\) sets \(i=i+1\) and
-
– if \(i = \alpha \), \(\mathcal {B}\) sets \(r_i = \perp \) and \(R_i = aP\);
-
– if \(i = \beta \), \(\mathcal {B}\) sets \(r_i = \perp \) and \(R_i = bP\);
-
– if \(i\ne \alpha ,\beta \), \(\mathcal {B}\) chooses
 and sets \(R_i = r_i P\);
and sets \(R_i = r_i P\);
-
-
3.
Finally \(\mathcal {B}\) adds the tuple \((\mathsf {ID}_{i}:=\mathsf {ID}, r_i, R_i)\) to \(L_{H_1}\) and responds to \(\mathcal {A}\) with \(H_{1}(\mathsf {ID}) = R_{i}\).
-
1.
-
\(H_{2}\) -queries: To respond to the \(H_2\) queries, \(\mathcal {B}\) maintains a list
$$\begin{aligned} L_{H_2}=\{( (m,U) \in \{0,\!1\}^* \times G_1, h \in \mathbb {Z}_q^* ) \} \end{aligned}$$which is initially empty. When \(\mathcal {A}\) queries the oracle \(H_{2}\) on (m, U), \(\mathcal {B}\) responds as follows.
-
1.
If the query (m, U) already appears in \(L_{H_2}\) in some tuple (m, U, h) then \(\mathcal {B}\) responds with \(H_{2}(m, U) = h \in \mathbb {Z}_{q}^{*}\).
-
2.
Otherwise \(\mathcal {B}\) picks a random \(h \in \mathbb {Z}_{q}^{*}\) and adds the tuple (m, U, h) to \(L_{H_2}\) and responds to \(\mathcal {A}\) with \(H_{2}(m, U) = h\).
-
1.
-
Key extraction queries: When \(\mathcal {A}\) makes a private key query on identity \(\mathsf {ID}\), \(\mathcal {B}\) proceeds as follows.
-
1.
Runs the above algorithm for responding to \(H_{1}\)-query for identity \(\mathsf {ID}\) and obtains \(H_{1}(\mathsf {ID}) = R_i\).
-
2.
If \(i=\alpha \text { or }\beta \), \(\mathcal {B}\) reports failure and halts.
-
3.
If \(i\ne \alpha ,\beta \), \(\mathcal {B}\) responds to \(\mathcal {A}\) with the private key \(S_{\mathsf {ID}} := r_{i} P_{\!\! pub }\) on the identity \(\mathsf {ID}\).
It can be verified that the provided private key \(S_{\mathsf {ID}} = r_{i}P_{\!\! pub }\) is a valid private key for the user with identity \(\mathsf {ID}_{i}:=\mathsf {ID}\) since
$$ r_{i}P_{\!\! pub }= r_{i} cP = c r_{i} P = c H_{1}(\mathsf {ID}) \,. $$Note that \(\mathcal {B}\) aborts the security game during a key extraction query with probability \(\frac{2}{q_{H_{1}}}\).
-
1.
-
Signature queries: To respond to the signature queries, \(\mathcal {B}\) maintains a list
$$L_{S}=\{( m_\ell \!\in \! \{0,\!1\}^*\!, {\mathsf {ID}_{\!\mathcal {S}}}_{\ell } \!\in \! \{0,\!1\}^*\!, {\mathsf {ID}_{\!\mathcal {V}}}_{\ell } \!\in \! \{0,\!1\}^*\!, x_\ell \!\in \! \mathbb {Z}_q^*, U_\ell \!\in \! G_1, \sigma _\ell \!\in \! G_2 )_{\ell =1}^{q_{S}}\}$$which is initially empty with \(\ell =0\). When \(\mathcal {A}\) queries the signature on a message m from a signer with identity \(\mathsf {ID}_{\!\mathcal {S}}\) for a designated verifier with identity \(\mathsf {ID}_{\!\mathcal {V}}\), \(\mathcal {B}\) proceeds as follows.
-
1.
If the query \((m,\mathsf {ID}_{\!\mathcal {S}},\mathsf {ID}_{\!\mathcal {V}})\) already appears in \(L_{S}\) in some tuple \((m_\ell ,{\mathsf {ID}_{\!\mathcal {S}}}_{\ell },{\mathsf {ID}_{\!\mathcal {V}}}_{\ell },x_\ell ,U_\ell ,\sigma _\ell )\) then \(\mathcal {B}\) responds to \(\mathcal {A}\) with the signature \((U_\ell , \sigma _\ell )\).
-
2.
Otherwise \(\mathcal {B}\) sets \(\ell =\ell +1\) and runs the above algorithm for responding to \(H_{1}\)-query for identities \(\mathsf {ID}_{\!\mathcal {S}}\) and \(\mathsf {ID}_{\!\mathcal {V}}\) and obtains \(Q_{\mathsf {ID}_{\!\mathcal {S}}} = H_{1}(\mathsf {ID}_{\!\mathcal {S}}) = R_i\) and \(Q_{\mathsf {ID}_{\!\mathcal {V}}} = H_{1}(\mathsf {ID}_{\!\mathcal {V}}) = R_j\).
-
3.
If \(\{i,j\}=\{\alpha ,\beta \}\), \(\mathcal {B}\) reports failure and halts.
-
4.
If \(i\ne \alpha ,\beta \), \(\mathcal {B}\) computes the private key for \(\mathsf {ID}_{\!\mathcal {S}}\), \(S_{\mathsf {ID}_{\!\mathcal {S}}} = r_{i}P_{\!\! pub }\), and proceeds as follows.
-
– randomly chooses \(x_{\ell } \in \mathbb {Z}_{q}^{*}\);
-
– sets \(U_{\ell }= x_{\ell }P \in G_{1}\);
-
– runs the \(H_{2}\)-query algorithm to obtain \(h_{\ell } = H_{2}(m, U_{\ell }) \in \mathbb {Z}_{q}^{*}\);
-
– sets \(V_{\ell } = x_{\ell }P_{\!\! pub }+ h_{\ell } S_{\mathsf {ID}_{\!\mathcal {S}}} \in G_{1}\);
-
– computes \(\sigma _{\ell } = e(V_{\ell }, Q_{\mathsf {ID}_{\!\mathcal {V}}})\).
-
-
5.
Otherwise if \(j\ne \alpha ,\beta \), \(\mathcal {B}\) computes the private key for \(\mathsf {ID}_{\!\mathcal {V}}\), \(S_{\mathsf {ID}_{\!\mathcal {V}}} = r_{j}P_{\!\! pub }\), and proceeds as follows.
-
– randomly chooses \(x_{\ell } \in \mathbb {Z}_{q}^{*}\);
-
– sets \(U_{\ell }= x_{\ell }P \in G_{1}\);
-
– runs the \(H_{2}\)-query algorithm to obtain \(h_{\ell } = H_{2}(m, U_{\ell }) \in \mathbb {Z}_{q}^{*}\);
-
– sets \(V_{\ell } = x_{\ell }P + h_{\ell } Q_{\mathsf {ID}_{\!\mathcal {S}}} \in G_{1}\);
-
– computes \(\sigma _{\ell } = e(V_{\ell }, S_{\mathsf {ID}_{\!\mathcal {V}}})\).
-
-
6.
Finally \(\mathcal {B}\) adds the tuple \((m_\ell , {\mathsf {ID}_{\!\mathcal {S}}}_{\ell }, {\mathsf {ID}_{\!\mathcal {V}}}_{\ell }, x_\ell , U_\ell , \sigma _\ell )\) to \(L_{S}\) and responds to \(\mathcal {A}\) with the signature \((U_\ell , \sigma _\ell )\).
Note that \(\mathcal {B}\) aborts the security game during a signature query with probability \(\frac{2}{q_{H_1}(q_{H_1}-1)}\).
-
1.
-
Verification queries: When \(\mathcal {A}\) makes a verification query on the signature \((U,\sigma )\) on a message m from a signer with identity \(\mathsf {ID}_{\!\mathcal {S}}\) for a designated verifier with identity \(\mathsf {ID}_{\!\mathcal {V}}\), \(\mathcal {B}\) proceeds as follows.
-
1.
\(\mathcal {B}\) runs the above algorithm for responding to \(H_{1}\)-query for identities \(\mathsf {ID}_{\!\mathcal {S}}\) and \(\mathsf {ID}_{\!\mathcal {V}}\) and obtains \(H_{1}(\mathsf {ID}_{\!\mathcal {S}}) = R_i\) and \(H_{1}(\mathsf {ID}_{\!\mathcal {V}}) = R_j\).
-
2.
If \(j\in \{\alpha ,\beta \}\), \(\mathcal {B}\) reports failure and halts.
-
3.
If \(j\ne \alpha ,\beta \), then \(\mathcal {B}\) computes \(\mathsf {ID}_{\!\mathcal {V}}\)’s private key, \(S_{\mathsf {ID}_{\!\mathcal {V}}} = r_{j}P_{\!\! pub }\), and proceeds as in the verification of the proposed scheme and responds to \(\mathcal {A}\) accordingly.
Note that \(\mathcal {B}\) aborts the security game during a verification query with probability \(\frac{2}{q_{H_1}}\).
-
1.
-
Output: After \(\mathcal {A}\) has made its queries, it finally outputs a valid signature \((U^*, \sigma ^*)\) on a message \(m^*\) from a signer with identity \(\mathsf {ID}_{\!\mathcal {S}}^{*}\) for a designated verifier with identity \(\mathsf {ID}_{\!\mathcal {V}}^{*}\) with a non-negligible probability \(\varepsilon _{\mathcal {A}}(\lambda )\) such that:
-
– \(\mathcal {A}\) has never submitted \(\mathsf {ID}_{\!\mathcal {S}}^*\) or \(\mathsf {ID}_{\!\mathcal {V}}^*\) during the key extraction queries;
-
– \((U^*, \sigma ^*)\) was never given as a response to a signature query on the message \(m^*\) with the signer’s identity \(\mathsf {ID}_{\!\mathcal {S}}^*\), and the designated verifier’s identity \(\mathsf {ID}_{\!\mathcal {V}}^*\); and
-
– \(\sigma ^{*} = e(U^{*} + h^{*}Q_{\mathsf {ID}_{\!\mathcal {S}}}^{*}, S_{\mathsf {ID}_{\!\mathcal {V}}}^{*})\).
-
If \(\mathcal {A}\) did not make \(H_1\)-query for the identities \(\mathsf {ID}_{\!\mathcal {S}}^{*}\) and \(\mathsf {ID}_{\!\mathcal {V}}^{*}\), then the probability that verification equality holds is less than \(1/q^2\). Thus, with probability greater than \(1-1/q^2\), both the public keys were computed using \(H_1\)-oracle and there exist indices \(i,j \in [1,q_{H_1}]\) such that \(\mathsf {ID}_{\!\mathcal {S}}^{*}=\mathsf {ID}_{i}\) and \(\mathsf {ID}_{\!\mathcal {V}}^{*}=\mathsf {ID}_{j}\). If \(\{i,j\} \ne \{\alpha ,\beta \}\), then \(\mathcal {B}\) reports failure and terminates.
Solution to BDHP: Otherwise, as in the forking lemma [13], \(\mathcal {B}\) repeats the game with the same random tape for \(x_{\ell }\) but with different choices of a random set for \(H_{2}\)-queries to obtain another forgery \((U^{*}, \sigma ')\) on the message \(m^{*}\) with \(h'\) such that \(h^{*} \ne h'\) and \(\sigma ^{*} \ne \sigma '\). Then,
Let \((h^{*} - h')^{-1} \mod q = \hat{h}\). Then, from the above equation, \(\mathcal {B}\) solves the BDHP by computing
Probability calculation: If \(\mathcal {B}\) does not abort during the simulation then \(\mathcal {A}\)’s view is identical to its view in the real attack. The responses to \(H_{1}\)-queries and \(H_{2}\)-queries are as in the real attack, since each response is uniformly and independently distributed in \(G_{1}\) and \(\mathbb {Z}_{q}^{*}\) respectively. The key extraction, signature and verification queries are answered as in the real attack.
The probability that \(\mathcal {B}\) does not abort during the simulation is
The probability that \(\mathcal {A}\) did \(H_1\)-query for the identities \(\mathsf {ID}_{\!\mathcal {S}}^{*}\) and \(\mathsf {ID}_{\!\mathcal {V}}^{*}\) and that \(\{\mathsf {ID}_{\!\mathcal {S}}^{*},\mathsf {ID}_{\!\mathcal {V}}^{*}\}=\{\mathsf {ID}_{\alpha },\mathsf {ID}_{\beta }\}\) is
Clearly \(\mathcal {B}\)’s advantage \(\varepsilon _{\mathcal {B}}(\lambda )\) for solving the BDHP, that is, the total probability that \(\mathcal {B}\) succeeds to solve BDHP, is the product of \(\mathcal {A}\)’s advantage \(\varepsilon _{\mathcal {A}}(\lambda )\) of forging the proposed ID-SDVS and the above two probabilities. Hence
Time calculation: It can be observed that running time of the algorithm \(\mathcal {B}\) is same as that of \(\mathcal {A}\) plus time taken to respond to the hash queries, key extraction queries, signature queries and verification queries, \(q_{H_1}+q_{H_2}+q_{E}+q_{S}+q_{V}\). Hence the maximum running time required by \(\mathcal {B}\) to solve the BDHP is
as \(\mathcal {B}\) requires to compute one scalar multiplication in \(G_1\) to respond to \(H_1\) hash query, one scalar multiplication in \(G_1\) to respond to key extraction query, three scalar multiplications in \(G_1\) to respond to signature query, one scalar multiplication in \(G_1\) to respond to verification query; one pairing computation to respond to signature query, one pairing computation to respond to verification query, one group operation in \(G_1\) to respond to signature query, and, one group operation in \(G_2\) and one scalar multiplication in \(G_2\) to output a solution of BDHP.
5.3 Unverifiability
We now prove that the proposed ID-SDVS is strongly designated. That is, any third party other than the signer and the designated verifier, cannot verify the validity of a signature from a signer for a designated verifier with non-negligible probability. We show that if there exists a PPT adaptive chosen message and adaptive chosen identity algorithm which can verify the proposed ID-SDVS, then there exists another PPT algorithm which can use the earlier algorithm to solve the DBDHP. In particular, we prove the following theorem:
Theorem 2
Given a security parameter \(\lambda \), if there exists a PPT adversary \(\mathcal {A}(q_{H_1},q_{H_2},q_{E},q_{S},q_{V},\varepsilon _{\mathcal {A}}(\lambda ),t)\) which breaks the designated unverifiability of the proposed ID-SDVS scheme in time t with success probability \(\varepsilon _{\mathcal {A}}(\lambda )\), then there exists a PPT adversary \(\mathcal {B}(\varepsilon _{\mathcal {B}}(\lambda ),t')\) which solves DBDHP with success probability at least
in time at most
where \(S_{G_1}\), \(S_{G_2}\), \(O_{G_1}\), \(O_{G_2}\) and \(P_{e}\) are as defined in Theorem 1.
Proof: Let for a security parameter \(\lambda \), \(\mathcal {B}\) is challenged to solve the DBDHP for
where \(G_1\) is an additive cyclic group of prime order q with generator P, \(G_2\) is a multiplicative cyclic group of prime order q with generator e(P, P), and \(e: G_1 \times G_1 \rightarrow G_2\) is a cryptographic bilinear map as described in Sect. 2 and  .
.  are unknown to \(\mathcal {B}\). The goal of \(\mathcal {B}\) is to solve DBDHP by verifying if \(e(P,P)^{abc}=\omega \) using \(\mathcal {A}\), the adversary who claims to forge the proposed ID-SDVS scheme.
are unknown to \(\mathcal {B}\). The goal of \(\mathcal {B}\) is to solve DBDHP by verifying if \(e(P,P)^{abc}=\omega \) using \(\mathcal {A}\), the adversary who claims to forge the proposed ID-SDVS scheme.
\(\mathcal {B}\) simulates the security game for strongness with \(\mathcal {A}\) by doing the Setup and by responding the \(H_{1}\) -queries, \(H_{2}\) -queries, Key extraction queries, Signature queries and Verification queries as in the security game for unforgeability.
Output: After \(\mathcal {A}\) has made its queries, it finally outputs a message \(m^*\), an identity \(\mathsf {ID}_{\!\mathcal {S}}^{*}\) of a signer and an identity \(\mathsf {ID}_{\!\mathcal {V}}^{*}\) of a designated verifier on which it wishes to be challenged.
If \(\mathcal {A}\) did not make \(H_1\)-query for the identities \(\mathsf {ID}_{\!\mathcal {S}}^{*}\) and \(\mathsf {ID}_{\!\mathcal {V}}^{*}\), then the probability that verification equality holds is less than \(1/q^2\). Thus, with probability greater than \(1-1/q^2\), both the public keys were computed using \(H_1\)-oracle and there exist indices \(i,j \in [1,q_{H_1}]\) such that \(\mathsf {ID}_{\!\mathcal {S}}^{*}=\mathsf {ID}_{i}\) and \(\mathsf {ID}_{\!\mathcal {V}}^{*}=\mathsf {ID}_{j}\). If \(\{i,j\} \ne \{\alpha ,\beta \}\), then \(\mathcal {B}\) reports failure and terminates.
Solution to DBDHP: Otherwise, \(\mathcal {B}\)
-
chooses a random
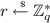 ;
; -
sets \(U = rP\);
-
sets \(h = H_2(m^{*},U)\);
-
sets \(\sigma = e(bP,cP)^{r} \omega ^{h}\);
and challenges \(\mathcal {A}\) to verify the validity of the signature \((U,\sigma )\).
Then, the verification holds if and only if each of the following holds

Then, from the above equation, \(\mathcal {B}\) solves the DBDHP by simply returning the response of \(\mathcal {A}\) to the strongness challenge.
Probability calculation: If \(\mathcal {B}\) does not abort during the simulation then \(\mathcal {A}\)’s view is identical to its view in the real attack. The responses to \(H_{1}\)-queries and \(H_{2}\)-queries are as in the real attack, since each response is uniformly and independently distributed in \(G_{1}\) and \(\mathbb {Z}_{q}^{*}\) respectively. The key extraction, signature and verification queries are answered as in the real attack.
The probability that \(\mathcal {B}\) does not abort during the simulation is
The probability that \(\mathcal {A}\) did \(H_1\)-query for the identities \(\mathsf {ID}_{\!\mathcal {S}}^{*}\) and \(\mathsf {ID}_{\!\mathcal {V}}^{*}\) and that \(\mathsf {ID}_{\!\mathcal {S}}^{*}=\mathsf {ID}_{\alpha }\) and \(\mathsf {ID}_{\!\mathcal {V}}^{*}=\mathsf {ID}_{\beta }\) is
Clearly \(\mathcal {B}\)’s advantage \(\varepsilon _{\mathcal {B}}(\lambda )\) for solving the DBDHP, that is, the total probability that \(\mathcal {B}\) succeeds to solve DBDHP, is the product of \(\mathcal {A}\)’s advantage \(\varepsilon _{\mathcal {A}}(\lambda )\) of breaking the strongness of the proposed ID-SDVS and the above two probabilities. Hence
Time calculation: It can be observed that running time of the algorithm \(\mathcal {B}\) is same as that of \(\mathcal {A}\) plus time taken to respond to the hash queries, key extraction queries, signature queries and verification queries, that is, \(q_{H_1}+q_{H_2}+q_{E}+q_{S}+q_{V}\). Hence the maximum running time required by \(\mathcal {B}\) to solve the DBDHP is
since during the query phase, \(\mathcal {B}\) requires to compute the same operations as in the security game for unforgeability and additionally, one scalar multiplication in \(G_1\), one scalar multiplication in \(G_2\) and one pairing computation to output a solution of DBDHP.
5.4 Non-transferability
The proposed scheme achieves the property of non-transferability as defined in Sect. 3. For this, we show that the transcripts simulated by the designated verifier are indistinguishable from the signatures that he receives from the signer. In the proposed scheme it can be observed that it is hard to distinguish the signature \((U, \sigma )\) on a message m by the signer from the signature \((\widehat{U}, \widehat{\sigma })\) on the message m by the designated verifier, that is, the distributions

are identical.
5.5 Strongness
The proposed scheme also achieves the property of strongness as defined in Sect. 3. Let \(\sigma \leftarrow DVSign (S_{\mathsf {ID}_{\!\mathcal {S}}}, Q_{\mathsf {ID}_{\!\mathcal {V}}}, m)\). Then \(\sigma \leftarrow DVTrans (S_{\mathsf {ID}_{\!\mathcal {V}}^{*}}, Q_{\mathsf {ID}_{\!\mathcal {S}}^{*}}, m)\) (where \(Q_{\mathsf {ID}_{\!\mathcal {S}}^{*}}\) and \(S_{\mathsf {ID}_{\!\mathcal {V}}^{*}}\) are defined as in the following) since

6 Comparative Analysis
Here, we compare our scheme with similar existing ID-SDVS schemes [8, 11, 15] and show that our scheme is more efficient in the sense of computation and operation time than these schemes.
For the computation of operation time in pairing-based scheme, to achieve the 1024-bit RSA level security, Tate pairing defined over the supersingular elliptic curve \(E=F_p : y^2=x^3+x\) with embedding degree 2 was used, where q is a 160-bit Solinas prime \(q=2^{159}+2^{17}+1\) and p a 512-bit prime satisfying \(p+ 1=12qr\), using MIRACL [12], a standard cryptographic library, and the hardware platform is a PIV 3 GHZ processor with 512 M bytes memory and the Windows XP operating system. For computation of operation time, we refer to [4] where the operation time for various cryptographic operations have been obtained. The OT(Operation Time) for one scalar multiplication is 6.38 ms, for one exponentiation in \(G_2\) it is 5.31 ms, for one map-to-point hash function it is 3.04 ms and for one pairing computation it is 20.04 ms. Other operations are omitted in the following analysis since their computation cost is trivial, such as the cost of an inverse operation over \(Z_{q}^{*}\) takes only 0.03 ms and one general hash function takes less than 0.001 ms which are negligible with compare to the time taken by the other operations.
To evaluate the total operation time in the efficiency comparison tables, we use the method from [1, 4]. In each of the two phases: signature generation and verification, we compare the total number of scalar multiplications (SM), exponentiations (E), map-to-point hash functions (H), bilinear pairings (P) and the consequent operation time (OT) (Table 2).
7 Conclusion
In this paper, we have proposed a strong designated verifier signature scheme on the identity-based setting. Our scheme is strong existentially unforgeable against adaptive chosen message and adaptive chosen identity attack under standard assumptions, the hardness of the computational and decisional Bilinear Diffie-Hellman problems. We also provide a proof for the strongness property of our scheme. Moreover, we do an efficiency comparison of our scheme with the existing similar schemes. In the view of computational cost and operation time our scheme is significantly more efficient than the existing schemes. The scheme is suitable for the environments in which less computational cost with strong security is required.
References
Cao, X., Kou, W., Xiaoni, D.: A pairing-free identity-based authenticated key agreement protocol with minimal message exchanges. Inf. Sci. 180(15), 2895–2903 (2010)
Chaum, D.: Zero-knowledge undeniable signatures (extended abstract). In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 458–464. Springer, Heidelberg (1991). doi:10.1007/3-540-46877-3_41
Chaum, D., Antwerpen, H.: Undeniable signatures. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 212–216. Springer, Heidelberg (1990). doi:10.1007/0-387-34805-0_20
Debiao, H., Jianhua, C., Jin, H.: An identity-based proxy signature schemes without bilinear pairings. Ann. Telecommun. 66(11–12), 657–662 (2011)
Du, H., Wen, Q.: Attack on Kang et al.’s identity-based strong designated verifier signature scheme. IACR Cryptology ePrint Archive, 2008:297 (2008)
Huang, X., Susilo, W., Mu, Y., Zhang, F.: Short (identity-based) strong designated verifier signature schemes. In: Chen, K., Deng, R., Lai, X., Zhou, J. (eds.) ISPEC 2006. LNCS, vol. 3903, pp. 214–225. Springer, Heidelberg (2006). doi:10.1007/11689522_20
Jakobsson, M., Sako, K., Impagliazzo, R.: Designated verifier proofs and their applications. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 143–154. Springer, Heidelberg (1996). doi:10.1007/3-540-68339-9_13
Kancharla, P.K., Gummadidala, S., Saxena, A.: Identity based strong designated verifier signature scheme. Informatica 18(2), 239–252 (2007)
Kang, B., Boyd, C., Dawson, E.: Identity-based strong designated verifier signature schemes: attacks and new construction. Comput. Electr. Eng. 35(1), 49–53 (2009)
Kang, B., Boyd, C., Dawson, E.D.: A novel identity-based strong designated verifier signature scheme. J. Syst. Softw. 82(2), 270–273 (2009)
Lee, J.-S., Chang, J.H., Lee, D.H.: Forgery attacks on Kang et al.’s identity-based strong designated verifier signature scheme and its improvement with security proof. Comput. Electr. Eng. 36(5), 948–954 (2010)
MIRACL. Multiprecision integer and rational arithmetic cryptographic library. http://certivox.org/display/EXT/MIRACL
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13(3), 361–396 (2000)
Saeednia, S., Kremer, S., Markowitch, O.: An efficient strong designated verifier signature scheme. In: Lim, J.-I., Lee, D.-H. (eds.) ICISC 2003. LNCS, vol. 2971, pp. 40–54. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24691-6_4
Susilo, W., Zhang, F., Mu, Y.: Identity-based strong designated verifier signature schemes. In: Wang, H., Pieprzyk, J., Varadharajan, V. (eds.) ACISP 2004. LNCS, vol. 3108, pp. 313–324. Springer, Heidelberg (2004). doi:10.1007/978-3-540-27800-9_27
Zhang, J., Mao, J.: A novel ID-based designated verifier signature scheme. Inf. Sci. 178(3), 766–773 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Sharma, N., Sahu, R.A., Saraswat, V., Sharma, B.K. (2016). Adaptively Secure Strong Designated Signature. In: Dunkelman, O., Sanadhya, S. (eds) Progress in Cryptology – INDOCRYPT 2016. INDOCRYPT 2016. Lecture Notes in Computer Science(), vol 10095. Springer, Cham. https://doi.org/10.1007/978-3-319-49890-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-49890-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-49889-8
Online ISBN: 978-3-319-49890-4
eBook Packages: Computer ScienceComputer Science (R0)




 and computes
and computes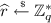 and computes
and computes and sets
and sets 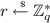 ;
;