Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 The Embedded Model Equations

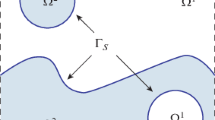
Let Ω 1(t) be a fluid domain immersed in an infinite exterior fluid Ω 2(t), Γ t be the free boundary separating both domains, and Ω D be a fixed domain that should contain the free boundary for all t ∈ [0, T]. The level set/extended potential flow model, [3, 4], may be then written as:

$$\displaystyle\begin{array}{rcl} \mathbf{u}& =& \nabla \phi \;\;\mbox{ in}\;\;\varOmega _{1}(t){}\end{array}$$
(1)
$$\displaystyle\begin{array}{rcl} \varDelta \phi & =& 0\;\;\mbox{ in}\;\;\varOmega _{1}(t){}\end{array}$$
(2)
$$\displaystyle\begin{array}{rcl} \varPsi _{t} + \mathbf{u}_{\text{ext}} \cdot \nabla \varPsi & =& 0\;\mbox{ in}\;\varOmega _{D}{}\end{array}$$
(3)
$$\displaystyle\begin{array}{rcl} G_{t} + \mathbf{u}_{\text{ext}} \cdot \nabla G& =& f_{\mbox{ ext}}\;\mbox{ in}\;\varOmega _{D}.{}\end{array}$$
(4)

Here, ϕ is the velocity potential, u the velocity field, Ψ the level set function, G the extended potential function, f accounts for the surface forces, and the subscript “ext” refers to the extended quantities off the front into Ω D . This hydrodynamic problem can be coupled with any other exterior problem on Ω 2(t). In particular, assuming a uniform electric field E in Ω 2(t), acting in the direction of the z axis and E = 0 in Ω 1(t) (perfect conductor fluid) then:

$$\displaystyle\begin{array}{rcl} \mathbf{E}& =& -\nabla U\;\;\mbox{ in}\;\;\varOmega _{2}(t){}\end{array}$$
(5)
$$\displaystyle\begin{array}{rcl} \varDelta U& =& 0\;\;\mbox{ in}\;\;\varOmega _{2}(t){}\end{array}$$
(6)
$$\displaystyle\begin{array}{rcl} U& =& U_{0}\;\;\mbox{ on}\;\varGamma _{t}{}\end{array}$$
(7)
$$\displaystyle\begin{array}{rcl} U& =& -E_{\infty }z\;\;\mbox{ at the far field},{}\end{array}$$
(8)

where U is the electric potential and E ∞ is the electric field intensity.

2 Numerical Approximation

The semidiscretization in time of the model equations is:

$$\displaystyle\begin{array}{rcl} \mathbf{u}^{n}& =& \nabla \phi ^{n}\;\;\mbox{ in}\;\;\varOmega _{ 1}(t_{n}){}\end{array}$$
(9)
$$\displaystyle\begin{array}{rcl} \varDelta \phi ^{n}(r,z)& =& 0\;\;\mbox{ in}\;\;\varOmega _{ 1}(t_{n}){}\end{array}$$
(10)
$$\displaystyle\begin{array}{rcl} \frac{\varPsi ^{n+1} -\varPsi ^{n}} {\varDelta t} & =& -\mathbf{u}_{\text{ext}}^{n} \cdot \nabla \varPsi ^{n}\;\;\mbox{ in}\;\;\varOmega _{ D}{}\end{array}$$
(11)
$$\displaystyle\begin{array}{rcl} \frac{G^{n+1} - G^{n}} {\varDelta t} & =& -\mathbf{u}_{\text{ext}}^{n} \cdot \nabla G^{n} + f_{\mbox{ ext}}^{\,n}\;\;\mbox{ in}\;\;\varOmega _{ D},{}\end{array}$$
(12)
$$\displaystyle\begin{array}{rcl} \varDelta U^{\,n}(r,z)& =& 0\;\;\mbox{ in}\;\;\varOmega _{ 2}(t_{n}){}\end{array}$$
(13)

where a first order explicit scheme has been applied. For the space discretization of Eqs. (11) and (12) a first order or second order upwind scheme can be used. The approximation of (10) and (13) is crucial in this numerical method, as it provides the velocity to advance the free boundary and also the velocity potential evolution within this front. We have coupled the following solvers for the interior and exterior Laplace equations:

  • For 2D and 3D axisymmetric geometries a Galerkin boundary integral solution is established, where the boundary element method with linear elements have been used to approximate the integral equations, see [6, 8].

  • For the fully 3D approximation a non conforming Nitsche finite element method has been used together with stabilization techniques of the bilinear forms, as the jump stabilization or the ghost penalty stabilization, see [1, 2, 9].

3 Numerical Results

Several physical scenarios can be simulated using the assumptions and the numerical method presented here. In the case of pure hydrodynamic problems, Eqs. (1)–(4), results for the wave breaking phenomena in a 2D geometry have been presented in [3], where splitting of the fluid domain was not considered. The first simulation involving computations through singular events was presented in [4], where the pinch-off of an infinite fluid jet and subsequent cascade of drop formation was reproduced in a seamless 3D axi-symmetric computation. In Fig. 1 we present the comparison of the satellite break up simulation with laboratory photographs. The interaction of two inviscid fluids of different densities was studied in [5]. The only parameter in the non-dimensional model is the fluid density ratio and simulations of the breaking up transition patterns from air bubbles to water droplets have been computed. When electrical forces acting on the free surface are also considered, Eqs. (1)–(8), the flow gets even more interesting: a charged water droplet will elongate until Taylor cones are formed, from which fine filaments will be ejected from both drop tips. As soon as the drop losses enough charge, it will recoil and oscillate back to equilibrium. In Fig. 2 we show also a comparison between computed profiles on top and Laboratory experiments on bottom at corresponding times. See [7].

Fig. 1
figure 1

Satellite drop breaking up, computed profiles (a) and Laboratory photographs (b), see [10]. Reproduced from [4] with permission from Elsevier

Full size image
Fig. 2
figure 2

Laboratory snapshots at indicated times of the evolution of a surface charged super-cooled water droplet, reprinted figure with permission from E. Giglio, D. Duft and T. Leisner, Phys. Rev. E, 77, 036319 (2008). Copyright (2008) by the American Physical Society (bottom); and computed profiles at times 80, 101. 2, 108. 1, 108. 5, 109. 8, 112. 1, 124. 2, 133. 4, 138, 142, 154. 1 μs (top)

Full size image