Simulating Stochastic Dynamic Interactions with Spatial Information and Flux

Abstract

We present a conservative extension to rule based modeling languages with constructs for component attributes and functions that modify these attributes; the language has a stochastic semantics, and it is equipped with flux analysis. We show that the constructs of this language, called $\mathsf {M}$, bring an ease especially in modeling biological systems, where spatial information is of essence. We discuss the language on models from molecular biology such as membrane diffusion systems, and actin polymerization networks, as well as models from ecology, where spatial behavior of animals as in bird flocks and fish schools are studied.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The recent advances in systems and synthetic biology are now giving rise to an increased integration of modeling languages. The capabilities that these technologies offer make it possible to model, simulate and analyze biological phenomena with the aim of complementing and accelerating the investigations in life sciences. The compact constructs of such languages for expressing various phenomena, as they are considered in different areas of biology, speed up the modeling process. As a result, specialized domain-specific languages contribute to investigations on a great variety of phenomena from molecular biology [1, 5, 10, 15, 16], pharmacology [12], ecology [4, 8, 9], and others, e.g., [11].

Among many mathematical and computational formalisms used to model biological systems, probably the most common representation schemes are those that are based on chemical reaction networks (CRN). The formalism of CRN is quite convenient as it finds deterministic and stochastic interpretations in terms of simulations. While the deterministic simulations are easily performed as numeric solutions of ordinary differential equation systems, the discrete stochastic simulations, which we consider here, are commonly performed by resorting to the Gillespie algorithm [6]. This algorithm and its many variations provide the semantics for the rule based languages, commonly used in many systems biology applications with results that provide insights to biological questions. In a nut shell, the rule based languages such as BNG and Kappa [1, 5, 15] provide compact representations for CRNs. This, in return, makes it possible for these languages to express biological system models with only few rules, in contrast to many, sometimes even infinite number of reactions of simple CRN representations.

Here, we introduce a modeling language, called $\mathsf {M}$, that extends some of the more common notations that are in use in rule based languages with the gain of an increased expressive power. $\mathsf {M}$ extends the constructs of the rule based languages with those for encoding attributes of model components and functions that modify these attributes. These encodings become instrumental, for example, for implementing spatial information and arbitrary constraints on model dynamics that account for the encoded information. Our implementation of the simulation engine conservatively extends the Gillespie algorithm to accommodate these features for the models that employ them. Moreover, the simulation algorithm makes use of the analysis methods, introduced in [13], for quantifying the stochastic fluxes due to the continuous time Markov chain semantics. The constructs that we introduce bring an ease to the modeling and analysis of certain phenomena that are more challenging in standard rule based languages. However, some of these constructs can be implemented by not-so-straight-forward encodings in stochastic Pi-calculus, that is, $\mathsf {SPiM}$ [2, 10, 14, 16].

In the following, we introduce the syntax and semantics of $\mathsf {M}$, and discuss its properties as a modeling language. We illustrate its features on a number of example models with varying detail and structure of model components. In particular, we present how simple CRN models and rule based models are accommodated, and how flux analysis can be easily applied to these models. We illustrate how geometric information can be encoded to capture classes of models from biology and ecology such as those for protein diffusions on membranes, and movements of animals as in bird flocks or fish schools. We show how the geometric information can be used to render movies that reflect the emerging geometric structures in molecular biology as in actin dynamics.¹

2 Syntax

Each $\mathsf {M}$ model consists of a set of rules, a description of the initial state, and a number of directives that specify the kind of data to be output at the end of a simulation. These directives determine the data to be recorded besides the time series resulting from the simulation. This is because simulations with these models can generate different kinds of information such as the evolution of the species in space with respect to their coordinates, stochastic fluxes at arbitrary time intervals, or the evolution of other species parameters defined below.

The rules for the interactions are defined with the grammar in Fig. 1, where the curly brackets denote the optional components. Here, $\mathsf {Name}$, $\mathsf {Species}$, x, y, z, $v_1$, ..., $v_k$, Site, and Bond are strings. $\mathsf {f_x}$, $\mathsf {f_y}$, and $\mathsf {f_z}$ as well as $\mathsf {Rate}$ and $\mathsf {Exp}$ are functions with type float on any subset of all the variables in the rule. $\mathsf {f_1}$, ..., $\mathsf {f_k}$ are also functions on any subset of the variables in the rule, however with types $\mathsf {Type_1}$, ..., $\mathsf {Type_k}$, respectively. If the $\mathsf {Rate}$ value is not given for a rule, it is assigned a default value of 1.0. $\mathsf {Sites}$ is associative and commutative, so the order of the $\mathsf {Site}$ expressions does not matter.

Fig. 1.

The grammar that defines the rules of language $\mathsf {M}$.

The definition of the rules above extends the standard definition of the chemical reaction networks (CRN), and also rule based languages such as BNG [1], Kappa [5], or others [15]. It is immediate that any chemical reaction of a CRN can be written as a rule of the above form that does not involve any $\mathsf {CoordinateVariables}$, $\mathsf {Variables}$, $\mathsf {Sites}$ or $\mathsf {Condition}$ expressions. Similarly, any BNG rule can be mapped to a rule with $\mathsf {Sites}$ and $\mathsf {Variables}$ as defined above, and modifications on complexes can be modeled by using the associative and commutative ‘.’ construct in $\mathsf {Reactant}$ and $\mathsf {Product}$ primitives. These permit a number of common modeling expressions, including BNG style rules; in particular, the following are valid in language $\mathsf {M}$:

• 1. Reactions (that create or destroy molecules), e.g., $\texttt {A} \; \texttt {+} \; \texttt {B} \texttt { -> } \texttt {C;}$

• 2. Rules for forming a bond, e.g., $\texttt {A(b)} \; \texttt {+} \; \texttt {B(a)} \texttt { -> } \texttt {A(b!0).B(a!0);}$

• 3. Rules for breaking a bond, e.g., $\texttt {A(b!0).B(a!0)} \texttt { -> } \texttt {A(b)} \; \texttt {+} \; \texttt {B(a);}$

• 4. Rules for changing a component state, e.g., $\texttt {X(x)} \texttt { -> } \texttt {X(x\texttt {+}1);}$

Besides these expressions that are common to other modeling languages, the definition above permits other constructs, in particular:

• 5. Variables and functions on species coordinates, and conditions on their interactions, e.g., to model two species that exchange their locations if they are less than 2 units apart from each other:

  $$ \texttt {A(c(x,y))} \;\texttt {+} \texttt {B(c(p,q))} \texttt { -> } \texttt {A(c(p,q))} \texttt {+} \;\texttt {B(c(x,y))} \; \texttt {if} \; \texttt {(x-p)}^\texttt {2} \texttt {+} \texttt {(y-q)}^\texttt {2}{} \texttt { < 4;} $$

• 6. Other variables and functions on species, and conditions on their interactions to model various attributes of species, e.g., to model state changes given as modifications of arguments under specific conditions:

  $$ \texttt {A(p,r)} \texttt { -> } \texttt {A(p*2,"very-high")} \; \; \texttt {if} \;\; \texttt {p} > \texttt {10} \;\; \texttt { \& \& } \;\; \texttt {r} = \texttt {"high";} $$

In any model, these constructs can be combined and used together to express arbitrarily complex phenomena including conditional complexation and decomplexation, and positioning in space with respect to species interactions.

The initial state at the beginning of a simulation is defined by the grammar below, which is used to describe the species that are present at time zero.

Here, $\mathsf {Quantity}$ is an integer. $\mathsf {c_x}$, $\mathsf {c_y}$, and $\mathsf {c_z}$ are real numbers. $\mathsf {c_1},\ldots , \mathsf {c_k}$ are constants with types that agree with those in reactant and product definitions in the rules. These constructs are used to specify the state of the system at time zero, which is then modified by the rules at each simulation step.

The modifications performed by the rules are recorded in a number of log files as state updates according to the directives of the model. Each of these log files contain various aspects of the simulation trace, including the time series of the model species. These directives are given by the following grammar:

Here, $\mathsf {t_x}$, $\mathsf {t_y}$, and $\mathsf {t_z}$ vary over real numbers and variables. $\mathsf {t_1},\ldots , \mathsf {t_k}$ vary over constants and variables with types that agree with those in reactant and product definitions in the rules. These constructs are used to specify the species and complexes, the time-series of which are recorded. If a coordinate or parameter is specified with a variable instead of a constant, then all the species that match that expression are counted. The instructions ‘directive coordinates’ and ‘directive parameters’, respectively, write to separate files the modifications on species coordinates and species parameters by individual rule instances. This way, for example, the movement of species in space as a result of the stochastic simulation dynamics can be plotted as a movie. If ‘directive flux’ is included in the model, then the initial state and the rules will be annotated off-line by the preprocessing engine with respect to the algorithm described in [13]. In this respect, the monitoring of the stochastic fluxes during simulation does not require any syntactic notation in the modeling language. The flux information is then written to a separate file.

Given a model with the syntax above, the pre-processing engine performs a number of syntactic checks on the input model. These are as follows.

• 1. All the occurrences of the same species in different rules and initial conditions agree with each other in terms of their arguments, their arity and their types. For example, for a species A, the language does not permit two occurrences with A(1.0,"free") and A("free",1.0), as one of them has a parameter with type float as the first argument and the other with type string.

• 2. All the occurrences of all the species in different rules and initial conditions agree with each other in terms of the arity of their coordinates. For example, given two species A and B, the language does not permit two occurrences with A(c(1.0)) and B(c(3.0,1.0)), as one of them has a coordinate with one dimension whereas the other has two dimensions. However, species without any coordinate parameter are permitted in the presence of others with coordinates. These coordinate-free species are then to be interpreted as "freely diffusing". (However, as it is explained below, the coordinate parameters do not have any effect on the simulation dynamics, unless they are specified to affect it by means of conditions or rate functions.)

• 3. Any $\mathsf {Bond}$ expression is permitted to occur at maximum two $\mathsf {Site}$ expressions in any $\mathsf {Reactants}$, $\mathsf {Products}$, or $\mathsf {Species}$ expression.

• 4. The variable occurrences in any $\mathsf {Reactant}$ expression is a superset of those in the $\mathsf {Product}$, $\mathsf {Rate}$ and $\mathsf {Condition}$ expression of the same rule.

• 5. The $\mathsf {Species}$ expressions in the initial conditions are subset of those that occur in the $\mathsf {Reactants}$ and $\mathsf {Products}$ expressions.

3 Semantics and Implementation

The models of language $\mathsf {M}$ that do not include any species parameters are CRN models. Thus, it is immediate that the continuous time Markov chain (CTMC) interpretation of CRNs, given by the Gillespie algorithm [6], provides a semantics for simulations with these models. Similarly, rule-based models are implemented by resorting to the CTMC semantics; this is done by generating the chemical reactions from the rules at every state when they become applicable. This way, a rule based model can be used to simulate a system that would potentially require an infinite number of reactions as a simple CRN. Examples to such models include polymerization models [2, 3].

The semantics of language $\mathsf {M}$ extends the CTMC semantics of the rule based languages to those models that include species coordinates and other parameters and functions that operate on these parameters under given conditions. This is done by considering any two species or any two complexes distinct if they differ in terms of any of their parameters. As a result of this, species and complexes at any state of the simulation that are modified by the rules are grouped with respect to their bonds as in rule based models, and also with respect to their parameters. For identifying and comparing the individual species and complexes, we employ a canonical form for the complexes given by the ‘.’ construct. Because any syntactic expression A.B or B.A refer to the same complex, imposing a pre-defined lexicographic order on these entities provides a canonical form.

Following the standard CTMC semantics of the CRN with respect to the Gillespie algorithm, the propensity of each rule is computed in the usual way, whereby the rate of the rule is multiplied by the number n of possible combinations in the current state that match the $\mathsf {Reactants}$. If a rule has a $\mathsf {Condition}$, only those matches that satisfy the $\mathsf {Condition}$ are considered; as the number of such combinations is $m \le n$, the propensity is computed by using m instead of n. Then, as the rule to be applied is selected by the standard procedure of the Gillespie algorithm, an instance of $\mathsf {Reactants}$ is randomly picked from m combinations, and the rule is applied to this instance. Although this procedure is linear-time, considering the individual differences of the species with respect to their parameters introduces an overhead to the simulation, which can be avoided for the models that do not involve parameters such as pure CRN models. This is done by inspecting the model automatically with respect to the constructs that it employs, and by automatically simplifying the data structures and procedures according to the level of complexity introduced by these constructs.

According to the algorithm in [13], the fluxes are computed by labeling each species with a unique id, which is a natural number assigned to each species during the creation of that species. If the flux directive is set in the model description, the simulation engine performs this labeling to produce the simulation trajectory with respect to the definitions in [13]. Fluxes are collected during the simulation in terms of the flow of species between rules. The flux algorithm conservatively extends the Gillespie algorithm, and thereby constructs several data structures, which reveal a variety of statistics about resource creation and consumption during the simulation. This information is logged into a file to be used to quantify the causal interdependence and relative importance of the reactions at arbitrary time intervals. As it is the case for complexes and parameters of species, computation of fluxes introduces a computational overhead due to the tracking of individuals. However, this overhead becomes relevant only if the fluxes are being monitored during simulation.

Fig. 2.

$\mathsf {M}$ implementation of a CRN that models an oscillator, and a time-series of it.

4 Example Models

In the following, we present a number of models with varying expressivity to illustrate the constructs above in use. While the individual models are valid in isolation, the concepts they use can be combined for incrementally richer models.

Simple CRNs and Rule Based (BNG-Style) Models

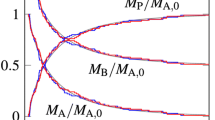
CRN models as in [12] are implemented with the common notation. For a simple example, consider the oscillator model in $\mathsf {M}$, depicted in Fig. 2 together with a time-series plot. Here, the rates are set to 1.0 by default.

Fig. 3.

Schematic EGFR model. EGFR forms a dimer with another EGFR, and thereby facilitates the binding of its ligand EGF. The ligand bound EGFR has a higher phosphorylation affinity of its tyrosin residues. The phosphorylated residues then become binding sites for other proteins. The phosphorylated sites Y1068 or Y1086 become available for the binding of the protein Grb2, whereas phosphorylated Y1045 is a binding site for Cbl. Cbl and Grb2 bind each other, independent from their binding to EGFR.

Fig. 4.

A model that implements the dynamics depicted in Fig. 3.

Let us now consider a more complex model that would require hundreds of reactions as a CRN model, however can be modeled with few rules in $\mathsf {M}$ as in other rule based languages. We consider the Epidermal Growth Factor Receptor (EGFR), as depicted in Fig. 3. In the model in Fig. 4, for simplicity we use default rates, which can be easily replaced with the actual kinetic rates by using the ‘$\texttt {with} \; \mathsf {Rate}$’ construct. We also omit the reverse rules for simplicity. Here, Rule 1 states that two EGFR form a dimer, no matter what the state of their other binding sites are. Rule 2 states that an EGFR binds to its ligand if it is part of a dimer. Rule 3 states that Y1045 on EGFR (p1) gets phosphorylated if it is not already phosphorylated. Rule 4 states that one of Y1068 or Y1086 on EGFR (p2) gets phosphorylated if both of them are not already phosphorylated. Rule 5 states that EGFR binds to Cbl if the Y1045 on EGFR (p1) is phosphorylated. Rule 6 states that EGFR binds to Grb2 if at least one of Y1068 or Y1086 on EGFR (p2) is phosphorylated. Rule 7 states that Cbl and Grb2 bind, no matter what the state of their other binding sites are.

Stochastic Flux Analysis

Thanks to the automatic annotation of the model species, if ‘directive flux’ is included in the model, flux information is automatically generated and written in a separate file with respect to the algorithm in [13]. For example, the oscillator model in Fig. 2 produces the fluxes depicted in Fig. 5 at three distinct non-steady-state intervals, denoted within the square brackets, where respectively A, B and C increase. Here the fluxes quantify the amount of resources that flow between the reactions within these intervals.

Fig. 5.

Flux configurations of the simulation with the oscillator network depicted in Fig. 2, for different time intervals, where the species $\textsf {A}$, $\textsf {B}$ and $\textsf {C}$ increase.

Models with Space and Geometric Information

The constructs of language $\mathsf {M}$ permit the definition of the dynamic behavior of the species to depend on the geometric state or the spatial constraints. In this setting, species can alter their position in space with respect to arbitrary functions defined on their parameters or the parameters of the species they interact with. For a simple example, we consider a class of models that are commonly used, for example, to study the behavior of diffusing proteins on membranes [7]. A diffusion model on a two dimensional grid, where a particle moves either north or east, is given by the two rules below.

Another class of models that we consider here as an example is individual based models in ecology [4] that are used for simulating the spatial behavior of animals in groups as in fish schools or bird flocks. The birds in a migrating flock of birds, for instance, adjust their distances with their neighbors by synchronizing on few simple rules [8, 9, 17]. This gives rise to the emergent behavior known as flocking. Although there are much more refined characterizations, the most basic form of flocking behavior is modeled by three simple principles:

• 1. Separation, that is, avoid crowding neighbors.

• 2. Alignment, that is, steer towards average heading of neighbors.

• 3. Cohesion, steer towards average position of neighbors.

The constructs of $\mathsf {M}$ permit describing these principles as model rules with arbitrary level of detail or precision. To illustrate this, let us take a simpler setting on the two-dimensional plane, whereby all the birds move in the same direction along the x-axis, and each bird synchronizes with its neighbors. Among other rules that describe the movement of the birds, the rules below provide a simple implementation of these three principles. However, models with arbitrary detail can be similarly accommodated as well as rules with greater control.

Fig. 6.

Graphical representation of the formation of a polymer, consisting of three monomers, that is, a trimer. Af denotes the monomer that is freely diffusing, whereas Al and Ar, respectively, denote the monomers that are bound on the left and bound on the right to other monomers. Ab denotes a monomer that is bound to other monomers on both sides. The trimer then consists of the chain of Ar, Ab, and Al.

Another class of models that are more than challenging for simple CRNs is polymerization models as these models would require an infinite number of CRN reactions to capture unbounded polymerization [3]. The situation gets even more complicated when the polymers have rich structures as it is the case for actin [2], where each monomer in a polymer can have a number of states depending on being bound to ADP, ADP-P$_i$ or ATP or other actin binding proteins. The following $\mathsf {M}$ model illustrates how polymerization can be modeled by two rules.

Here, Rule 1 states that two free monomers bind to form a dimer, and Rule 2 states that a free monomer binds to the right-end of a filament, and thereby becomes the new end-most monomer of the filament. The important point to observe in this model is how the coordinate information is updated, that is, each free monomer gets a coordinate information when it binds to an existing filament. This concept, which is here illustrated for one dimensional space, can be easily generalized for models in two or three dimensions. In particular, the images depicted in Fig. 7 are obtained from the screen shots of movies generated by stochastic simulation on actin polymerization models by applying theses ideas [2].² These models are constructed by encoding the geometric information as coordinate parameters and the dynamics as functions that alter this information.

Fig. 7.

Example screen shots captured from the movies generated by stochastic simulations with actin models that contain encodings of geometric information. The image on the left is from a 2D simulation where the filaments branch, however they do not rotate along the growth axis. The image on the right is obtained from a model that contains the 3D encoding of the branching as well as the helical rotations.

The actin filaments in Fig. 6 are polymers of monomers that grow along an axis [2, 14]. As in the polymer model implementation above, the free actin do not have coordinate parameters, because they are assumed to be free in the cytosol. However, all the bound actin monomers are equipped with a coordinate parameter. When a free monomer binds to a filament, the free monomer evolves to a bound state, while receiving the coordinate information from the filament that it binds to. When branching filaments are considered, we adopt this idea to include the rotation of the filaments with respect to the axis of growth. This is because the angle between a mother actin filament and a daughter filament is measured as 70 degrees. Moreover, actin filaments have a helical shape with a rotating structure, repeating every 13 subunits. In order to model these rotations, we equip each rule with a function that implements a rotation matrix on the coordinates with respect to the growth vector of its filament axis. In this setting, due to the inclusion of ‘directive coordinates’, as the simulation evolves simulation steps are recorded in a separate file with respect to the emerging coordinate dynamics. This information is then used, for example, to render movies that reflect the dynamics emerging from the species interactions.

5 Discussion

We have introduced a modeling language that extends common rule based languages with constructs for encoding species attributes, and functions that modify them, as well as features for stochastic flux analysis. The example models above should provide a flavor of the possible applications that make use of spatial information as well as flux analysis.

For the models that makes use of all the constructs of language $\mathsf {M}$, the simulation algorithm results in reduction in efficiency in comparison to, for example, pure CRN models. This overhead is due to the increase in the information monitored and modified within the data structures during simulation. However, our design of the simulation algorithm inspects the constructs that are used in the model, and enables certain data structures only if they are required for the model in use. In this respect, ‘pure’ models that do not exploit $\mathsf {M}$ features can be easily exported to other platforms that provide the fastest algorithm for the task.

Future work includes the implementation of a modeling platform that integrates all the components of $\mathsf {M}$, and incrementally extends it with various dynamic and static analysis methods available in the literature.