Abstract
Automatic reasoning tools play an important role when developing provably correct software. Both main approaches, program verification and program synthesis employ automated reasoning tools, more specifically, automated theorem provers. Besides classical logic, non-classical logics are particularly relevant in this field. This chapter presents calculi to automate theorem proving in classical and some important non-classical logics, namely first-order intuitionistic and first-order modal logics. These calculi are based on the connection method, which permits a goal-oriented and, hence, a more efficient proof search. The connection calculi for these non-classical logics extend the calculus for classical logic in an elegant and uniform way by adding so-called prefixes to atomic formulae. The leanCoP theorem prover is a very compact PROLOG implementation of the connection calculus for classical logics. We present details of the implementation and describe some basic techniques to improve its efficiency. leanCoP is adapted to non-classical logics by integrating a prefix unification algorithm, which depends on the specific logic. This results in leading theorem provers for the aforementioned non-classical logics.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Information Technology (IT) has been penetrating literally all areas of our society. The essential building blocks of IT are algorithms coded in hardware or software. The tools for hardware design as well as for software production have become impressively powerful indeed. Their outcomes are engineering constructs of an unprecedented complexity. The correctness of these systems to a certain degree is guaranteed by ingenious and automated test methods.
While we all use systems of this kind on a daily basis, we tend to ignore their actual degree of complexity, for which reason we want to remind ourselves at this point that, for instance, actual operating systems or computing platforms today comprise hundreds of millions of lines of code (loc). The applications running on top of these platforms add to this order of magnitude in (extensional) complexity even further. How far can we trust systems this large and complex?
Unfortunately, experience shows in fact that any of these systems is full of (semantic and syntactic) bugs. Occasionally, these bugs have consequences which are embarrassing at the very least, occasionally extremely costly and sometimes even the cause for injury or death to people. Reference [1] lists five most embarrassing software bugs including the well-known Pentium FDIV bug and the disintegration of the $655-million Mars Climate Orbiter (in 1998). Further disasters caused by bugs were the crash of Ariane 5 (1996) and of an Airbus A400M Atlas cargo plane on a test flight with four people killed (2015, see [2]). Apparently, there is no guarantee for preventing a future disaster due to a bug killing many more people and causing further huge damages.
There is a second major aspect to this downside of current IT. Despite an enormous methodological improvement of the processes producing hardware and software, software projects that are large, complicated, poorly specified, or involve unfamiliar aspects, are still vulnerable to large, unanticipated problems, often leading to spectacular and costly failures (e.g. [3]). Generally, the software projects failure rate is much too high still and extensive delays are commonplace, with huge and costly consequences for the industry.
Has theory a remedy in store for these two deplorable aspects of IT? In principle, it has. In fact there are two major perspective routes for ending up with more reliable systems to begin with, known as verification and synthesis. The idea behind verification is to let a verifier check the correctness of a system against its specification. While this is possible in theory, it has remained an illusion to expect larger software projects to produce as a by-product a complete system specification, needed by the verifier. Just imagine the challenge to fully specify an operating system with hundreds of millions of loc in order to understand why, in practice and for large systems, this will remain an illusion. Smaller systems, however, have been fully and successfully verified already [26, 30, 36, 43].
Program synthesis follows the more direct route towards producing correct software. It starts from the project requirements presented in some informal way which are assumed to be transformed somehow, possibly aided with system support, into a precise specification in some formal language. The resulting formal code then in turn is automatically synthesized into an efficiently executable code which is correct under the proviso that the specification as well as the synthesizer both are correct. The problem with this approach in general — and apart from the difficulties involved in the transformation just described — is the extreme intellectual challenge involved in automating (and verifying) the synthesis step. To a limited extent though, synthesis has already been quite successful. Namely, the techniques used in hardware production are to a significant extent exactly of this nature. Similarly, popular techniques in software production such as model-driven engineering (or model-driven software development), the use of domain specific languages or modelling languages (such as UML), and so forth do already feature automatic synthesis aspects to some limited extent. Also, logical programming languages such as PROLOG have substantially narrowed the gap between a formal system specification and its executable code written in such a language, laying part of the synthesis burden on the program interpreter or compiler. However, while all these approaches may be seen as major steps towards more reliable systems, the route towards the ultimate synthesis vision has remained a truly challenging one.
To sum up so far, given the utmost importance of IT and at the same time the severe problems with IT systems, we are still faced with the challenge to find a way out of this urging dilemma since neither the practical solutions found so far nor the two theoretically possible routes have brought a satisfactory solution as yet. Hence the old vision of building Provably Correct Systems (ProCoS) has by far not lost its attractions and has remained extremely relevant.
A crucial component in both verification and synthesis is a theorem prover for some logic [12, 20, 24, 58]. This is why Automated Deduction (AD) or Automated Theorem Proving (ATP) lies at the heart of the ProCoS vision. The field of ATP has in fact made remarkable progresses in the last decades and the resulting systems are in use in numerous applications, including verification and synthesis. Yet, the problem underlying ATP seems so hard that we will have to go still a long way to reach the next higher level of performance (see Sect. 6 in this chapter as well as [16]). This is true even for a popular logic such as classical first-order logic (fol), let alone more involved logics. In the context of programming, logics other than fol are deemed necessary though. In fact, in the formal specification of an IT system, which typically is dynamic by nature, fol seems to be rather inconvenient for this purpose since it allows to represent transitions in time in an indirect way only. Non-classical or higher-order logics along with corresponding theorem provers are deemed more convenient for this purpose. Unfortunately, ATP in non-classical logics has not received the same level of attention as the one in classical fol. In part, the contributions reported in the present chapter are an attempt to make up for this neglect.
Concretely, we present a number of theorem provers for various logics some of which are outperforming any of its competitors internationally. They all belong to the family of provers uniformly designed on the basis of the leanCoP (lean Connection Prover) technology, originally developed for classical fol and following a separate and unique line of research in ATP (see Sect. 5). In fact, since theorem provers are themselves software systems which should be correct as well according to our ProCoS vision, these provers are based on a mathematically precise formalism serving as their specification. From this formal specification it is only a rather small step to the actual code written in PROLOG. The correctness proof for this step is rather straightforward in each case [51]. In other words, our provers themselves are provably correct systems as desired.
True, our provers are small systems indeed (comprising a few dozens of loc only), hence the term “lean”. They are so by intention. Competitive provers with similar performance in comparison sometimes feature hundreds of thousands loc, serving exactly the same purpose. In other words, the comparable intensional complexity of an algorithm can be represented in a vast variety of different extensional complexities. The lean extensional complexity version is accessible to formal correctness proofs while the huge one is not. This is one of the reasons why we opt for the lean approach. It is thereby understood that an optimization of the PROLOG code into some low-level code could of course be followed once the PROLOG code has settled to a stable one, whereby the optimizer should consist of verified code as well, of course. These explanations of our approach demonstrate that, apart from presenting tools in this chapter relevant for the ProCoS vision, these themselves at the same time may be seen as a model for how to follow this kind of an approach towards a provably correct software of high intensive complexity, possibly extended to high extensive complexity thereafter.
The chapter is organized as follows. Section 2 introduces basic concepts and the matrix characterization of logical validity. Section 3 presents the clausal and the non-clausal connection calculus for classical logic and some basic optimization techniques. In Sect. 4 connection calculi for first-order intuitionistic and first-order modal logics are introduced. Section 5 describes compact PROLOG implementations that are based on the presented connection calculi. In Sect. 6 we give a brief history of the line of research in ATP to which this chapter contributes. In addition we outline there some of the steps which are expected to be taken along this line in the future. Section 7 concludes with a summary and a brief outlook on further research.
2 Preliminaries
This section provides a brief overview of classical and non-classical logics, and presents the matrix characterization of logical validity, which is the basis for the connection calculi presented in Sects. 3 and 4.
2.1 Classical Logic
The reader is assumed to be familiar with the language of classical first-order logic, see, e.g., [8, 54, 62]. In this chapter the letters P is used to denote predicate symbols, f to denote function symbols and x, X to denote variables. Terms are denoted by t and are built from functions, constants and variables.
An atomic formula, denoted by A, is built from predicate symbols and terms. The connectives \(\lnot \), \(\wedge \), \(\vee \), \(\Rightarrow \) denote negation, conjunction, disjunction and implication, respectively. A (first-order) formula, denoted by F, G, H, consists of atomic formulae, the connectives and the existential and universal quantifiers, denoted by \(\forall \) and \(\exists \), respectively. A literal L has the form A or \(\lnot A\). The complement \({\overline{L}}\) of a literal L is A if L is of the form \(\lnot A\), and \(\lnot L\) otherwise. A formula in clausal form has the form \(\exists x_1\ldots \exists x_n (C_1 \vee \ldots \vee C_n)\), where each \(C_i\) is a clause. For classical logic, every formula F can be translated into an equivalent formula \(F'\) in clausal form.
2.2 Non-Classical Logics
Intuitionistic logic [23] and modal logics [9] are popular non-classical logics. Intuitionistic and classical logic share the same syntax, i.e. formulae in both logics use the same connectives and quantifiers, but their semantics is different. For example, the formula
is valid in classical logic, but not in intuitionistic logic. This property holds for all formulae of the form \(P \vee \lnot P\) for any proposition P. In classical logic this formula is valid as P or \(\lnot P\) is true whether P is true or not true. The semantics of intuitionistic logic requires a proof for P or for \(\lnot P\). As this property neither holds for P nor for \(\lnot P\), the formula is not valid in intuitionistic logic. For this reason intuitionistic logic is also called constructive logic. Every formula that is valid in intuitionistic logic is also valid in classical logic, but not vice versa.
Modal logics extend the language of classical logic by the modal operators \(\Box \) and \(\Diamond \) representing necessarily and possibly, respectively. For example, the proposition “if Plato is necessarily a man, then Plato is possibly a man” can be represented by the modal formula
The Kripke semantics of the (standard) modal logics is defined by a set of worlds and a binary accessibility relation between these worlds. In each single world the classical semantics applies to the classical connectives, whereas the modal operators \(\Box \) and \(\Diamond \) are interpreted with respect to accessible worlds. There is a broad range of different modal logics and the properties of the accessibility relation specify the particular modal logic. Thus, the validity of a formula depends on the chosen modal logic. For example, the modal formula 2 is valid in all (standard) modal logics.
2.3 Matrix Characterisation
The general questioning in ATP is to provide an answer to the question as to whether a given formula \(F'\) is a logical consequence of a given set of formulae \(\{F_1,F_2,\ldots ,F_n\}\). According to the deduction theorem, this problem can be reduced to the problem of determining whether the formula \(F_1 \wedge F_2 \wedge \ldots \wedge F_n \Rightarrow F'\) is valid.
The matrix characterization of logical validity considers the formula to be in a certain form, often clausal form. More formally, a matrix of a formula consists of its clauses \(\{C_1,\ldots ,C_n\}\), in which each clause is a set of literals \(\{L_1,\ldots ,L_m\}\). The notion of multiplicity is used to encode the number of clause copies used in a connection proof. It is a function \(\mu \,{:}\,M\,{\rightarrow }\,I\!\! N\) that assigns each clause in M a natural number specifying how many copies of this clause are considered in a proof. In the copy of a clause C all variables in C are replaced by new variables. \(M^{\mu }\) is the matrix that includes these clause copies. Clause copies correspond to applications of the contraction rule in the sequent calculus [29]. In the graphical representation of a matrix, its clauses are arranged horizontally, while the literals of each clause are arranged vertically. The polarity 0 or 1 is used to represent negation in a matrix, i.e. literals of the form A and \(\lnot A\) are represented by \(A^0\) and \(A^1\), respectively,
Then, a connection is a set \(\{A^0, A^1\}\) of literals with the same predicate symbol but different polarities. A term substitution \(\sigma \) assigns terms to variables that occur in the literals of a given formula. A connection \(\{L_1,L_2\}\) with \(\sigma (L_1)\,{=}\,\sigma ({\overline{L_2}})\) is called \(\sigma \) -complementary. It corresponds to a closed branch in the tableau calculus [31] or an axiom in the sequent calculus [29].
For example, the formula
has the equivalent clausal form
and its matrix is
which has the graphical representation

A path through a matrix \(M\,{=}\,\{C_1,{\ldots },C_n\}\) is a set of literals that contains one literal from each clause \(C_i\,{\in }\,M\), i.e. a set \(\cup _{i=1}^{n} \{L'_i\}\) with \(L'_i\,{\in }\, C_i\). Then, the matrix characterization [15] states that a formula F is (classically) valid iff (if and only if) there exists (1) a multiplicity \(\mu \), (2) a term substitution \(\sigma \), and (3) a set of connections S, such that every path through its matrix \(M^{\mu }\) (attached with the multiplicity \(\mu \)) contains a \(\sigma \)-complementary connection \(\{L_1,L_2\}\in S\).
For example, in order to make \(\{{\textit{man(X)}}^0,{\textit{man(Plato)}}^1\}\) a \(\sigma \)-complementary connection, the variable X needs to be substituted by Plato, i.e. \(\sigma (X)\,{=}\,{\textit{Plato}}\). Then every path through the matrix 5 (with multiplicity \(\mu (C_i)\,{=}\,1\)) contains a \(\sigma \)-complementary connection and, hence, formula 3 is (classically) valid.
All these notions can be generalized to the non-clausal form case where the clauses of matrices are not just sets of literals, but may rather contain general matrices as elements as well (see Sect. 3.3). For the following characterization we assume that the term matrix characterization refers to this general case.
Any proof method that is based on the matrix characterization and operates in a connection-oriented way is called a connection method. The specific calculus of a connection method is called a connection calculus. In other words, the connection method denotes a general approach comprising many different connection calculi. This general terminology is similar to resolution. We talk of a resolution method, or simply of resolution, whenever the proof rule of resolution is involved somehow. Also in this case resolution denotes a general approach comprising many different specific resolution calculi (like, for instance, linear resolution).
3 Connection Calculi for Classical Logic
Connection calculi are a well-known basis to automate formal reasoning in classical first-order logic. Among these are the calculi introduced in [13,14,15], the connection tableau calculus [38], and the model elimination calculus [40]. Proof search in the connection calculus is guided by connections \(\{A^0,A^1\}\), hence, it is more goal-oriented compared to the proof search in sequent or tableau calculi.
First, this section introduces a formal clausal connection calculus for classical logic. Afterwards the technique of restricted backtracking is introduced that reduces the search space in connection calculi significantly. Finally, a generalization of the connection calculus to non-causal formulae is presented.
3.1 The Basic Calculus
The connection calculus for classical logic to be introduced now is based on the matrix characterization of logical validity presented in Sect. 2.3. It uses a connection-driven search strategy in order to calculate an appropriate set of connections S. In each step of a derivation in the connection calculus a connection is identified and only paths that do not contain this connection are investigated afterwards. If every path contains a (\(\sigma \)-complementary) connection, the proof search succeeds and the given formula is valid. A connection proof can be illustrated within the graphical matrix representation. For example, the proof of matrix 5 consists of two inferences, which identify two connections:

In contrast to sequent calculi, connection calculi permit a more goal-oriented proof search. This leads to a significantly smaller search space and, thus, to a more efficient proof search.
A formal description of the calculus was given by Otten and Bibel [51]. The axiom and the rules of this formal clausal connection calculus are given in Fig. 1. The words of the calculus are tuples of the form “C, M, Path”, where M is a matrix, C and Path are sets of literals or \(\varepsilon \); C is the subgoal clause, Path is the active path, and \(\sigma \) is a rigid term substitution. A clausal connection proof of a matrix M is a clausal connection proof of \(\varepsilon ,M,\varepsilon \).
For example,

is a proof of matrix 5, termed \(M'\), in the clausal connection calculus with the term substitution \(\sigma (X')\,{=}\,{\textit{Plato}}\), in which a copy of the second clause was made. In order to prove that Plato as well as Socrates are mortal, another copy of the second clause \(\{{\textit{man(X)}}^0,\) \({\textit{mortal(X)}}^1\}\) would be needed, using the new variable \(X''\) and \(\sigma (X'')\,{=}\,{\textit{Socrates}}\).
The presented clausal connection calculus is correct and complete, i.e. a formula is valid in classical logic iff there is a clausal connection proof of its matrix M [15]. The proof is based on the matrix characterization for classical logic.
Proof search in the clausal connection calculus is carried out by applying the rules of the calculus in an analytic way, i.e. from bottom to top, starting with \(\varepsilon ,M,\varepsilon \), in which M is the matrix of the given formula. At first a start clause is selected. Afterwards, connections are successively identified by applying reduction and extension rules in order to make sure that all paths through the matrix contain a \(\sigma \)-complementary connection. This process is guided by the active path, a subset of a path through M. During the proof search, backtracking might be required, i.e. alternative rules or rule instances have to be considered if the chosen rule or rule instance does not lead to a proof. This might happen when choosing the clause \(C_1\) in the start and extension rules or the literal \(L_2\) in the reduction and extension rules. The term substitution \(\sigma \) is calculated step by step by one of the well-known term unification algorithms (see, e.g. [57]) whenever a reduction or extension rule is applied.
3.2 Restricted Backtracking
In contrast to saturation-based calculi, such as resolution [57] or instance-based methods [37], standard connection calculi are not proof confluent, i.e. a significant amount of backtracking is necessary during the proof search. Backtracking is required if there is more than one rule instance applicable (see Sect. 3.1). Confluent connection calculi that have been developed so far [10, 15] have not shown an improved performance, as these calculi lose the strict goal-oriented proof search.
The idea of restricted backtracking is to cut off any alternative connections once a literal from the subgoal clause has been solved [46]. A literal L is called solved if it is the literal \(L_1\) of a reduction or extension rule application (see Fig. 1) and in the case of the extension rule, there is also a proof for the left premise. A solved literal in the connection calculus corresponds to a closed branch in the tableau calculus.
For example, starting the proof search with the first clause of the following matrix

the first possible connection to the literal \({\textit{man(X)}}^1\) in the second clause does not solve the literal \({\textit{man(X)}}^0\), as the literal \({\textit{martian(X)}}^1\) cannot be solved. But \({\textit{man(X)}}^0\) can be solved by the second alternative connection to \({\textit{man(Socrates)}}^1\) in the third clause, i.e.

In case of backtracking, the third alternative connection to the literal \({\textit{man(Plato)}}^1\) in the fourth clause would be considered. Restricted backtracking cuts off this third and all following alternative connections for the literal \({\textit{man(X)}}^0\).
The potential of this approach to significantly reduce the search space becomes clear, if connection proofs for first-order formulae are analysed in a statistical way [46]. To this end the 1256 connection proofs for formulae in version 3.7.0 of the TPTP problem library [66] that are found by the automated theorem prover leanCoP are considered. It can be observed that the first connection (or rule application) that solves a literal is often the same one used in the final proof. This applies to 89% of all solved literals used within the found connection proofs. In this case, backtracking that occurs afterwards can be cut off without effecting a successful proof search, hence, it is called non-essential backtracking. Backtracking with alternative connections that occur before the literal is solved is still necessary and, hence, called essential backtracking. In the above matrix the alternative connection to the third clause is considered essential backtracking as the connection to the second clause does not solve the literal \({\textit{man(X)}}^0\). However, the alternative connection to the fourth clause is non-essential backtracking.
Even though most literals within the connection proofs can be solved by performing only essential backtracking, a significant amount of non-essential backtracking occurs during the actual proof search. Restricted backtracking cuts off this non-essential backtracking [46]. As this reduces the search space significantly, the approach turns out to be very successful in practice. For example, for the formula AGT016+2 of the TPTP problem library [66], which contains more than 1000 clauses, the standard proof search requires 84 s using 312,831 inference steps. With restricted backtracking the proof search requires only 0.3 s, using 427 inference steps. Proofs are not only found faster, but many new proofs are obtained. A similar technique can also be used to restrict backtracking when selecting the start clause \(C_1\) within the application of the start rule. Restricted backtracking preserves correctness of the connection calculus, as the search space is only pruned. However, completeness is lost, as can be seen by the example matrix shown above. Namely, non-essential backtracking would solve \({\textit{man(X)}}^0\) with a connection to the fourth clause and the resulting substitution of X by \({\textit{Plato}}\) would allow to solve the second literal (by connecting it to the fifth clause) as well.
3.3 Non-clausal Calculus
Clausal connection calculi, such as the ones presented in Sect. 3.1, require the input formula in disjunctive normal (or clausal) form. Formulae that are not in clausal form have to be translated into this form. The standard transformation translates a first-order formula F into clausal form by applying the distributivity laws. In the worst case, the size of the resulting formula grows exponentially with respect to the size of the original formula F. This increases the search space significantly. Even a definitional translation [52] that introduces definitions for subformulae introduces a significant overhead for the proof search [46]. Furthermore, both clausal form translations modify the structure of the original formula F.
A non-clausal connection calculus [47] that works directly on the structure of the original formula does not have these disadvantages. Existing non-clausal approaches [7, 15, 32] work only on ground formulae. For first-order formulae, copies of subformulae are added iteratively, which introduces a huge redundancy into the proof search. For a more efficient proof search, clauses have to be added dynamically during the proof search, similar to the approach used for copying clauses in clausal connection calculi. To this end, the clausal connection calculus is generalized and its rules are carefully extended.
The non-clausal matrix \(M(F^{pol})\) of a formula F with polarity pol is a set of clauses, in which a clause is a set of literals and (sub-)matrices, and is defined inductively according to Table 1 [47]. In this table \(G[x\backslash t]\) denotes the formula G in which all free occurrences of x are replaced by t. \(x^*\) is a new variable, \(t^*\) is the Skolem term \(f^*(x_1,\ldots ,x_n)\) in which \(f^*\) is a new function symbol and \(x_1,\ldots ,x_n\) are the free variables in \(\forall x G\) or \(\exists x G\). The non-clausal matrix of a formula F is the matrix \(M(F^0)\). In the graphical representation its clauses are arranged horizontally, literals and (sub-)matrices of its clauses are arranged vertically.
For example, the formula
has the (simplified) non-clausal matrix
The definition of paths through a non-clausal matrix can be generalized in a straightforward way. All other concepts used for clausal matrices, e.g. the definitions of connections and term substitutions, remain unchanged.
For example, the non-clausal connection proof of matrix 7 using the substitution \(\sigma (X)\,{=}\,{\textit{Plato}}\) is illustrated in its graphical (non-clausal) matrix

The formal non-clausal connection calculus [47] has the same axiom, start rule, and reduction rule as the clausal connection calculus. The extension rule is restricted to so-called extension clauses and a decomposition rule that splits subgoal clauses into their subclauses is added. A clause C in a matrix M is an extension clause of M with respect to a set of literals Path iff
-
a.
C contains a literal of Path, or
-
b.
C is \(\alpha \)-related to all literals of Path occurring in M and if C has a parent clause, it contains a literal of Path.
A clause C is \(\alpha \) -related to a literal L iff it occurs besides L in the graphical matrix representation. For example, in the given matrix, \({\textit{man(Plato)}}^1\) is only \(\alpha \)-related to \({\textit{man(X)}}^0\), \({\textit{mortal(X)}}^1\), and \({\textit{mortal(Plato)}}^0\). The parent clause of a clause C in a matrix M is a clause \(C'\,{=}\,\{M_1,\ldots ,M_n\}\) in M such that \(C\in M_i\) for some \(1\,{\le }\, i\,{\le }\, n\). See [47] for the full description of the formal non-clausal connection calculus.
The non-clausal connection calculus for classical logic is correct and complete. The correctness proof is based on the non-clausal matrix characterization, completeness is proved by an embedding into the clausal connection calculus.
The proof search in the non-clausal connection calculus is carried out in the same way as in the clausal connection calculus. On formulae in clausal form, the non-clausal connection calculus behaves just like the clausal connection calculus. If the matrices that are used in the non-clausal connection calculus are slightly modified, the start and the reduction rule are subsumed by the decomposition and the extension rule, respectively [47]. Optimization techniques, such as positive start clauses, regularity, and restricted backtracking, can be used in the non-clausal connection calculus as well. Furthermore, the non-clausal calculus can be extended to non-classical logics in the same way as the clausal connection calculus (see Sect. 4).
4 Connection Calculi for Non-classical Logics
By using the notion of prefixes the connection calculus for classical logics can be extended to intuitionistic logic and several modal logics.
4.1 Intuitionistic Logic
Every formula F that is valid in intuitionistic logic is also valid in classical logic. The opposite direction does not hold. Hence, the three rules

of the sequent calculus for intuitionistic logic [29] differ from the ones for classical logic. In all three rules the set of formulae \(\varDelta \) does not occur in the sequent of the premises anymore. During the proof search these rules are applied from bottom to top and the formulae in \(\varDelta \) are removed from the sequent. As these formulae might be necessary to complete the proof, the application of these rules need to be controlled. To this end, a prefix is assigned to every subformula G of a given formula F. A prefix is a string, i.e. a sequence of characters over an alphabet \({\varPhi }\cup \varPsi \), in which \(\varPhi \) is a set of prefix variables and \(\varPsi \) is a set of prefix constants. Prefix constants and variables represent applications of the rules \({\lnot }{\textit{-right}}\), \({\Rightarrow }{\textit{-right}}\), \({\forall }{\textit{-right}}\), and \({\lnot }{\textit{-left}}\), \({\Rightarrow }{\textit{-left}}\), \({\forall }{\textit{-left}}\), respectively [69, 70]. Then, the prefix p of a subformula G, denoted \(G\,{:}\,p\), specifies the sequence of these rules that have to be applied (analytically) to obtain G in the sequent. In order to preserve two atomic formulae that form an axiom in the intuitionistic sequent calculus, their prefixes need to unify. This is done by an intuitionistic substitution \(\sigma _J\) that maps elements of \(\varPhi \) to strings over \(\varPhi \cup \varPsi \).
In the matrix characterization for intuitionistic logic it is additionally required that the prefixes of the literals in every connection unify under \(\sigma _J\) [70]. For a combined substitution \(\sigma \,{:=}\) \((\sigma _Q,\sigma _J)\), a connection \(\{L_1\,{:}\,p_1,L_2\,{:}\,p_2\}\) is \(\sigma \) -complementary iff \(\sigma _Q(L_1)\,{=}\,\sigma _Q({\overline{L_2}})\) and \(\sigma _J(p_1)\,{=}\) \(\sigma _J(p_2)\). An additional interaction condition on \(\sigma \) ensures that \(\sigma _Q\) and \(\sigma _J\) are mutually consistent [70].
For intuitionistic logic there exists no equivalent clausal form for a given formula F and the original matrix characterization for intuitionistic logic does not use a clausal form. In order to adapt the existing clausal connection calculus for classical logic, Wallen’s original matrix characterization has to be modified. To this end, the skolemization technique, originally used to eliminate eigenvariables in classical logic, is extended and also used for prefix constants in intuitionistic logic [44]. This allows the specification of a clausal matrix characterization, in which clause copies can simply be made by renaming all term and prefix variables [44]. Furthermore, there is no need for an explicit irreflexivity test of the reduction ordering. Instead, this test is realized by the occurs check during the term and prefix unification. For classical logic this close relationship between the reduction ordering and skolemization was first pointed out by Bibel [15]. For the extended skolemization, the same Skolem function symbol is used for instances of the same subformula, a technique that is similar to the liberalized \(\delta ^+\) -rule in classical tableau calculi [31].
The following description gives a formal definition of a prefixed clausal matrix for intuitionistic logic and the extended skolemization. The prefixed matrix \(M(F^{pol}{:}p)\) of a prefixed formula \(F^{pol}{:}p\) is a set of prefixed clauses, in which pol is a polarity and p is a prefix, and is defined inductively according to Table 2 [44]. In this table it is \(M_G\,{\cup _{\beta }}\, M_H\) \(\,{:=}\,\) \(\{C_G\,{\cup }\, C_H \;|\; C_G\,{\in }\, M_G,\) \(C_H\,{\in }\, M_H\}\). \(x^*\) is a new term variable, \(t^*\) is the Skolem term \(f^*(x_1,\ldots ,x_n)\) in which \(f^*\) is a new function symbol and \(x_1,\ldots ,x_n\) are all free term and prefix variables in \((\forall x G)^0\,{:}\,p\) or \((\exists x G)^1\,{:}\,p\). \(V^*\) is a new prefix variable, \(a^*\) is a prefix constant of the form \(f^*(x_1,\ldots ,x_n)\) in which \(f^*\) is a new function symbol and \(x_1,\ldots ,x_n\) are all free term and prefix variables in \(A^0\,{:}\,p\), \((\lnot G)^0\,{:}\,p\), \((G{\Rightarrow } H)^0\,{:}\,p\), or \((\forall x G)^0\,{:}\,p\). The intuitionistic matrix M(F) of a formula F is the prefixed matrix \(M(F^0\,{:}\,\varepsilon )\), in which \(\varepsilon \) is the empty string.
For example, the intuitionistic matrix of the formula
is
in which \(a_1\), \(a_2(X)\), \(a_3\) are prefix constants, and \(V_1\), \(V_2\), \(V_3\) are prefix variables. Then,

is a graphical intuitionistic connection proof of matrix 9 with \(\sigma _Q(X)={\textit{Plato}}\), \(\sigma _J(V_1)=a_2(Plato)\), \(\sigma _J(V_2)=\varepsilon \), and \(\sigma _J(V_3)=a_3\), where \(\varepsilon \) is the empty string.
The intuitionistic matrix of the formula
is
There is no substitution \(\sigma _J\) with \(\sigma _J(a_1)\,{=}\,\sigma _J(a_2)\) and no connection proof of this matrix. Hence, formula 10 is not valid in intuitionistic logic.
The formal clausal connection calculus for intuitionistic logic [44] is shown in Fig. 2. It is an extension of the clausal connection calculus for classical logic, in which a prefix is added to each literal and an additional intuitionistic substitution is used to identify \(\sigma \)-complementary connections. An intuitionistic connection proof of the matrix M is a proof of \(\varepsilon ,M,\varepsilon \). The clausal connection calculus for intuitionistic logic is correct and complete, i.e. a formula F is valid in intuitionistic logic iff there is an intuitionistic connection proof of its intuitionistic matrix M(F).
The intuitionistic substitution \(\sigma _J\) is calculated by a prefix unification algorithm [44]. For a given set of prefix equations \(\{p_1\,{=}\,q_1, \ldots , p_n\,{=}\,q_n\}\), an appropriate substitution \(\sigma _J\) is a unifier such that \(\sigma _J(p_i)\,{=}\,\) \(\sigma _J(q_i)\) for all \(1\,{\le }\,i\,{\le }\,n\). General algorithms for string unification exist, but the following unification algorithm is more efficient, as it takes the prefix property of all prefixes \(p_1,p_2,\ldots \) into account: for two prefixes \(p_i\,{=}\,u_1 X w_1\) and \(p_j\,{=}\,u_2 X w_2\) with \(X\,{\in }\,\varPhi \cup \varPsi \) the property \(u_1\,{=}\,u_2\) holds. This reflects the fact that prefixes correspond to sequences of connectives and quantifiers within the same formula.
The prefix unification for the prefixes equation {\(p\,{=}\,q\}\) is carried out by applying the rewriting rules in Fig. 3. It is \(V,\bar{V},V'\,{\in }\,\varPhi \) with \(V\,{\ne }\,\bar{V}\), \(V'\) is a new prefix variable, \(a,b\,{\in }\,\varPsi \), \(X\,{\in }\,\varPhi \,{\cup }\,\varPsi \), and \(u,w,z\,{\in }\) \((\varPhi \,{\cup }\,\varPsi )^*\). For rule 10 the restriction \((*)\) \(u\,{=}\,\varepsilon \) or \(w\,{\ne }\,\varepsilon \) or \(X\,{\in }\,\varPsi \) applies. \(\sigma _J(V)\,{=}\,u\) is written \(\{V\backslash u\}\).
The unification starts with the tuple \((\{p\,{=}\,\varepsilon |q\},\{\})\). The application of a rewriting rule \(E \rightarrow E',\tau \) replaces the tuple \((E,\sigma _J)\) by the tuple \((E',\tau (\sigma _J))\). E and \(E'\) are prefix equations, \(\sigma _J\) and \(\tau \) are (intuitionistic) substitutions. The unification terminates when the tuple \((\{\},{\sigma _J})\) is derived. In this case, \(\sigma _J\) represents a most general unifier. Rules can be applied non-deterministically and lead to a minimal set of most general unifiers. In the worst-case, the number of unifiers grows exponentially with the length of the prefixes p and q. To solve a set of prefix equations \(\bar{E}=\{p_1\,{=}\,p_1,\ldots ,q_n\,{=}\,t_q\}\), the equations in \(\bar{E}\) are solved one after the other and each calculated unifier is applied to the remaining prefix equations in \(\bar{E}\).
For example, for the prefix equation \(\{a_1 V_2 V_3\,{=}\,a_1 a_3\}\), there are the two possible derivations \(\{a_1 V_2 V_3\,{=}\,\varepsilon |a_1 a_3\},\{\}\!\mathop {\longrightarrow }\limits ^{\text{3. }} \{V_2 V_3\,{=}\,\varepsilon |a_3\},\{\}\mathop {\longrightarrow }\limits ^{\text{6. }} \{V_3 \,{=}\,\varepsilon |a_3\},\) \(\{V_2\backslash \varepsilon \}\) \(\mathop {\longrightarrow }\limits ^{\text{10. }} \{V_3 \,{=}\,a_3|\varepsilon \},\{V_2\backslash \varepsilon \}\mathop {\longrightarrow }\limits ^{\text{5. }} \{\varepsilon \,{=}\,\varepsilon |\varepsilon \},\{V_2\backslash \varepsilon ,V_3\backslash a_3\} \) and \( \{a_1 V_2 V_3\,{=}\varepsilon |a_1 a_3\},\{\}\mathop {\longrightarrow }\limits ^{\text{3. }} \{V_2 V_3\,{=}\,\varepsilon |a_3\},\!\{\}\mathop {\longrightarrow }\limits ^{\text{10. }} \{V_2 V_3\,{=}\,a_3|\varepsilon \},\!\{\}\mathop {\longrightarrow }\limits ^{\text{5. }} \{V_3\,{=}\,\varepsilon |\varepsilon \},\!\{V_2\backslash a_3\}\!\mathop {\longrightarrow }\limits ^{\text{5. }} \{\varepsilon \,{=}\,\varepsilon |\varepsilon \},\) \(\{V_2\backslash a_3,V_3\backslash \varepsilon \} \), yielding the most general unifiers \(\{V_2\backslash \varepsilon ,V_3\backslash a_3\}\) and \(\{V_2\backslash a_3,V_3\backslash \varepsilon \}\).
4.2 Modal Logics
For modal logic the classical sequent calculus is extended by rules for the modal operators \(\Box \) and \(\Diamond \). For example, the additional modal rules of the modal sequent calculus [70] for the modal logic T are

with \(\varGamma _{(\Box )}:=\{ G \,|\, \Box G\in \varGamma \}\) and \(\varDelta _{(\Diamond )}:=\{ G \,| \Diamond G\in \varDelta \}\). When the rules \(\Box {\textit{-right}}\) or \(\Diamond {\textit{-left}}\) are applied from bottom to top during the proof search, all formulae that are not of the form \(\Box G\) or \(\Diamond G\), respectively, are deleted from the sets \(\varGamma _{(\Box )}\) and \(\varDelta _{(\Diamond )}\) in the premise. As these formulae might be necessary to complete the proof, the application of the modal rules need to be controlled. Again, a prefix is assigned to every subformula G of a given formula F. This prefix is a string over an alphabet \({\nu }\cup \varPi \), in which \(\nu \) is a set of prefix variables and \(\varPi \) is a set of prefix constants. Prefix variables and constants represent applications of the rules \(\Box {\textit{-left}}\) or \(\Diamond {\textit{-right}}\), and \(\Box {\textit{-right}}\) or \(\Diamond {\textit{-left}}\), respectively [69, 70].
Proof-theoretically, a prefix of a subformula G captures the modal context of G and specifies the sequence of modal rules that have to be applied analytically in order to obtain G in the sequent. Semantically, a prefix denotes a specific world in a model [27, 70]. Prefixes of literals that form an axiom in the sequent calculus need to denote the same world, hence, they need to unify under a modal substitution \(\sigma _M\) that maps elements of \(\nu \) to strings over \(\nu \cup \varPi \). A connection \(\{L_1\,{:}\,p_1,L_2\,{:}\,p_2\}\) is \(\sigma \) -complementary for a combined substitution \(\sigma \,{:=}\,(\sigma _Q,\sigma _M)\) iff \(\sigma _Q(L_1)\,{=}\,\sigma _Q({\overline{L_2}})\) and \(\sigma _M(p_1)\,{=}\,\sigma _M(p_2)\). An additional domain condition specifies if constant, cumulative, or varying domains are considered [70].
The skolemization technique is extended to modal logic by introducing a Skolem term also for the prefix constants [48]. This integrates the irreflexivity test into the term and prefix unification. The prefixed matrix \(M(F^{pol}{:}p)\) of a prefixed formula \(F^{pol}{:}p\) is a set of prefixed clauses, in which pol is a polarity and p is a prefix, and is defined inductively according to the Table 3 [48]. The definitions of \(\cup _{\beta }\), \(x^*\), and \(t^*\) are identical to the ones used for intuitionistic logic. \(V^*\) is a new prefix variable, \(a^*\) is a prefix constant of the form \(f^*(x_1,\ldots ,x_n)\), in which \(f^*\) is a new function symbol and \(x_1,\ldots ,x_n\) are all free term and prefix variables in \((\Box G)^0\,{:}\,p\) or \((\Diamond G)^1\,{:}\,p\). The modal matrix M(F) of a modal formula F is the prefixed matrix \(M(F^0\,{:}\,\varepsilon )\), in which \(\varepsilon \) is the empty string.
For example, the modal matrix of the formula
is
in which \(V_1\) and \(V_2\) are prefix variables. Then,

is a graphical modal connection proof of matrix 13 with \(\sigma _M(V_1)\,{=}\,V_2\).
The core of the formal clausal connection calculus for modal logic [21, 48] is identical to the one for intuitionistic logic given in Fig. 2. The only difference to the intuitionistic calculus is the definition of the prefixes and the prefix unification algorithm. The clausal connection calculus for modal logic is correct and complete.
A prefix unification algorithm [48] is used to calculate the modal substitution \(\sigma _M\). Depending on the modal logic, the accessibility condition has to be respected when calculating this substitution: for all \(V\in \nu \): \(|\sigma _M(V)|\,{=}\,1\) for the modal logic D, \(|\sigma _M(V)|\,\le \,1\) for the modal logic T; there is no restriction for the modal logics S4 and S5. The prefix unification for D is a simple pattern matching, for S4 the prefix unification for intuitionistic logic can be used, for S5 only the last character of each prefix (or \(\varepsilon \) if the prefix is empty) has to be unified. The prefix unification for T is specified by the rewriting rules given in Fig. 4 (with \(\bar{V}\,{\ne }\,X\)), which are applied in the same way as the ones for intuitionistic logic (see Sect. 4.1).
5 Implementing Connection Calculi
Several automated theorem provers for classical logic that are based on clausal connection calculi have been implemented so far, such as KoMeT [18], METEOR [5], PTTP [64], and SETHEO [39]. Because of their complexity, it would be a difficult — if not impossible — task to adapt these implementations to the non-classical connection calculi described in Sect. 4.
At first, this section presents a very compact PROLOG implementation of the clausal connection calculus for classical logic. Afterwards, this implementation is extended to intuitionistic and modal logics.
5.1 Classical Logic
leanCoP is an automated theorem prover for classical first-order logic [45, 46, 51]. It is a very compact PROLOG implementation of the clausal connection calculus described in Sect. 3.1. leanCoP 1.0 [51] essentially implements the basic clausal connection calculus shown in Fig. 1. The source code of the core prover is given in Fig. 5 (sound unification has to be used). PROLOG lists are used to represent sets and PROLOG terms are used to represent atomic formulae. PROLOG variables represent term variables, and “-” is used to mark literals that have polarity 1. For example, the matrix
is represented by the PROLOG list
[[-man(plato)],[man(X),-mortal(X)],[mortal(plato)]] .
The prover is invoked by calling the predicate prove(M,I), in which M is a matrix and I is a positive number. The predicate succeeds only if there is a connection proof for the matrix M, in which the size of the active path is smaller than I. The proof search starts by applying the start rule implemented in the first two lines. As a first optimization technique, the clause \(C_1\) in the start rule of Fig. 1 can be restricted to positive clauses, i.e. clauses that contain only literals with polarity 0 [51]. For the above example this would be the clause \(\{{\textit{mortal(Plato)}}^0\}\). Afterwards, reduction and extension rules are repeatedly applied. These rules are implemented in the last four lines by the PROLOG predicate prove(C,M,P,I), in which C is the subgoal clause, M is the matrix, P is the active path, and I is the path limit. The path limit is used to perform iterative deepening on the size of the active path, which is necessary for completeness. When the extension rule is applied, the proof search continues with the left premise before the right premise is considered. The axiom is implemented in the third line. The term substitution \(\sigma \) is stored implicitly by PROLOG.
leanCoP 1.0 already shows an impressive performance and proves some formulae not proven by more complex automated theorem provers [51]. As clause copies are restricted to ground clauses, leanCoP is also a decision procedure for determining the validity of propositional formulae.
leanCoP 2.0 integrates additional optimization techniques into the basic connection calculus [45, 46]. The source code of the core prover is shown in Fig. 6. Lean PROLOG technology is a technique that stores the clauses of the matrix in PROLOG’s database. It integrates the main advantage of the ”PROLOG technology” approach [64] into leanCoP by using PROLOG’s fast indexing mechanism to quickly find connections. A controlled iterative deepening stops the proof search if the current path limit for the size of the active path is not exceeded (line 4). This yields a decision procedure for ground formulae and also allows for refuting some (not valid) first-order formulae. The regularity condition [38] restricts the proof search such that no literal occurs more than once in the active path (lines 6–7). The lemmata technique [38] reuses the subproof of a literal in order to solve the same literal on other branches (line 7). Restricted backtracking [46] cuts off alternative connections once the application of the reduction or extension rule has successfully solved a literal (line 11; see also Sect. 3.2). Backtracking over alternative start clauses can be cut off as well. A definitional clausal form translation is used in a preprocessing step to translate arbitrary first-order formulae into an equivalent clausal form by introducing definitions for certain subformulae [46]. Furthermore, leanCoP 2.0 uses a fixed strategy scheduling, i.e. the PROLOG core prover is consecutively invoked by a shell script with different strategies [45, 46]. See [46] for a more detailed explanation of the source code.
The core prover in Fig. 6 is invoked with prove(1,S), where S is a strategy (see [45] for details) and the start limit for the size of the active path is 1. The predicate succeeds if there is a connection proof for the clauses stored in PROLOG’s database. The full source code of the prover and the definitional clausal form translation are available on the leanCoP website at http://www.leancop.de.
The additional techniques improve the performance of leanCoP significantly, in particular for formulae containing many axioms [46]. Of the (non-clausal) formulae in the TPTP v3.7.0 problem library, leanCoP 2.0 proves (within 600 s) about 50% more formulae than leanCoP 1.0, about as many formulae as Prover9 [41], and about 30% less formulae than E [61]. The new definitional clausal form translation performs significantly better than those of E, SPASS, and TPTP [46].
nanoCoP [50] implements the non-clausal calculus described in Sect. 3.3. It proves more problems from the TPTP library than the core prover of leanCoP for both, the standard and the definitional translation into clausal form. Furthermore, the returned non-clausal proofs are on average about 30% shorter than the clausal proofs of leanCoP.
5.2 Intuitionistic Logic
ileanCoP is a prover for first-order intuitionistic logic [44, 45]. It is a compact PROLOG implementation of the clausal connection calculus for intuitionistic logic described in Sect. 4.1. ileanCoP extends the classical connection prover leanCoP by
-
a.
prefixes that are added to the literals in the matrix in a preprocessing step,
-
b.
a set of prefix equations that are collected during the proof search,
-
c.
a set of term variables together with their prefixes in order to check the interaction condition, and
-
d.
an additional prefix unification algorithm that unifies the prefixes of the literals in each connection.
The source code of the ileanCoP 1.2 core prover is shown in Fig. 7. The underlined code was added to the classical prover leanCoP 2.0; no other modifications were made. Prefixes are represented by PROLOG lists, e.g. the prefix \(a_1 V_2 V_3\) is represented by the list [a1,V2,V3]. For example, the intuitionistic matrix
is represented by the PROLOG list

In a preprocessing step the clauses of the intuitionistic matrix are written into PROLOG’s database. Then, the prover is invoked with prove(1,S), where S is a strategy (see [45] for details) and the start limit for the size of the active path is 1. The predicate succeeds if there is an intuitionistic connection proof for the clauses stored in PROLOG’s database.
First, ileanCoP performs a classical proof search, which uses only a weak prefix unification (line 11 and line 12). After a classical proof is found, the prefixes of the literals in each connection are unified and the interaction condition is checked. To this end, the two predicates prefix_unify and check_addco are invoked (line 4). They implement the rewriting rules shown in Fig. 3 and require another 26 lines of PROLOG code. If the prefix unification or the interaction condition fails, the search for alternative connections continues via backtracking. The substitutions \(\sigma _Q\) and \(\sigma _J\) are stored implicitly by PROLOG. The full source code is available on the ileanCoP website at http://www.leancop.de/ileancop.
Version 1.0 of ileanCoP is based on leanCoP 1.0 and implements only the basic calculus [44]. In ileanCoP 1.2 all additional optimization techniques used for classical logic described in Sect. 5.1 are integrated as well [45]. To this end, some of these techniques are adapted to the intuitionistic approach using prefixes. This includes regularity, lemmata, and the definitional clausal form translation. Other techniques, such as the lean PROLOG technology and restricted backtracking, can be applied directly without any modifications.
ileanCoP 1.2 proves significantly more formulae of the TPTP problem library and the ILTP problem library [55] than any other automated theorem prover for first-order intuitionistic logic [45]. Of the (non-clausal) formulae of the TPTP v3.3.0 problem library it proves (within 600 s) between 250 and 700% more formulae than the intuitionistic provers JProver, ileanTAP, ft, and ileanSeP [45]. It solves about 50% more formulae than ileanCoP 1.0, and proves significantly more formulae than Imogen [42]. Of the formulae of the TPTP v3.7.0 problem library, ileanCoP 1.2 proves a higher number of problems of certain problem classes than some classical provers [46], even though these classes contain formulae that are valid in classical but not in intuitionistic logic.
5.3 Modal Logics
MleanCoP is a prover for several first-order modal logics [48, 49]. It is a compact PROLOG implementation of the clausal connection calculi for modal logics, as described in Sect. 4.2. The source code of the MleanCoP 1.2 core prover is identical to the source code of ileanCoP 1.2 shown in Fig. 7. PROLOG lists are used to represent sets and prefixes. For example, the modal matrix
is represented by the PROLOG list
[[-man(plato):[V1]],[man(plato):[V2]] .
In a preprocessing step, the clauses of the modal matrix are written into PROLOG’s database. First, MleanCoP performs a classical proof search using a weak prefix unification. After a classical proof is found, the prefixes of the literals in each connection are unified and the domain condition is checked. This is done by the two predicates prefix_unify and domain_cond. Depending on the chosen modal logic, the prefix unification algorithm has to respect different accessibility conditions. For example, for the modal logic T, the rewriting rules shown in Fig. 3 are used. For the modal logic S4, the code of the prefix unification for intuitionistic logic can be used. For D and S5, the prefix unification is a simple pattern matching. If the prefix unification or the domain condition fails, the search for alternative connections continues via backtracking. The substitutions \(\sigma _Q\) and \(\sigma _M\) are stored implicitly by PROLOG. The full source code is available on the MleanCoP website at http://www.leancop.de/mleancop.
As MleanCoP 1.2 is based on leanCoP 2.0, all additional optimization techniques used for classical logic described in Sect. 5.1 are integrated into this implementation as well [48]. This includes the lean PROLOG technology, regularity, lemmata, the definitional clausal form translation, and restricted backtracking. MleanCoP supports the constant, cumulative, and varying domain variants of the first-order modal logics D, T, S4, and S5.
MleanCoP 1.2 proves more formulae from the QMLTP v1.1 problem library [56] than any other prover for first-order modal logic, such as the provers LEO-II, Satallax, MleanSeP, or MleanTAP [21]. For the modal logic D, MleanCoP 1.2 proves (within 600 s) between 35 and 120% more problems than any of the other provers; for the modal logic T, between 25 and 85% more problems; for the modal logic S4, between 30 and 100% more problems, and for the modal logic S5, between 40 and 110% more problems. MleanCoP is also able to refute a large number of modal formulae that are not valid.
Version 1.3 of MleanCoP [49] contains additional enhancements, such as the support for heterogeneous multimodal logics, the output of a compact modal connection proof, support for the modal TPTP input syntax [56] and an improved strategy scheduling.
6 A Brief History and Perspectives
One of the fundamental achievements of logic is the discovery that truth can be demonstrated in a purely syntactic way. This means that any statement, represented as a formula F in some language, can be shown to be valid by purely syntactical means. All known methods for such a demonstration use syntactic rules of roughly the kind \(F_1\Rightarrow F_2\) and some termination criterion which, applied to a formula in the chain of demonstration, specifies whether the respective line in this chain can successfully stop at the point of the formula’s occurrence.
When the idea of testing the validity of formulae in a mechanical way came up in the beginning of the last century, the most obvious way of choosing appropriate rules of this kind was to inverse the rules of the formal logical systems then known for deriving valid formulae. Even if the logic is restricted to fol, its formulae are rather complex syntactic constructs as are the rules of those systems. Hence this approach led to a rather complicated solution first realized by Prawitz [53] (for more historical details concerning the beginnings of ATP see Sect. 2 in [17]).
The problem with this solution was tractability — tractability from the point of view of human researchers and system developers, that is. Hence some kind of simplification was called for. It was Herbrand who first succeeded in reducing the problem of determining the validity of fol formulae to propositional ones [34]. This reduction is known as Herbrand’s Theorem. Since propositional logic is much easier to handle for human researchers this opened a line of research additionally characterized as a confluent saturation method based on the resolution rule along with unification which to some extent hides first-order features.
When the second author, abbreviated as WB in the following, entered the field of ATP around 1970 as a trained logician, the Prawitz line was out of date and the Herbrand-resolution line was highly in vogue. This observation took him by surprise as expressed at the beginning of his first publication in ATP [11]: “In the field of theorem proving in first-order logic almost all work is based on Herbrand’s theorem. This is a surprising fact since from a logical point of view the most natural way ... .” Hence, for nearly a decade he tried to further develop the Prawitz line and at the same time to study the virtues and disadvantages of both lines in a comparative way, in order to reach a rational decision which line to follow in the future.
In the course of this research and after several publications WB, like Prawitz and others, realized that a core of ATP lies in the connection structure of the given formula (or of the set of clauses resulting from it), independent of which line of research is pursued. With this insight different approaches to ATP could be developed and analysed from a common viewpoint as demonstrated in the paper [13]. The paper was completed in 1978, published as “Bericht 79” in January 1979 and as a journal article in 1981 (submitted 1979). It already contains all the basic notions underlying the matrix characterization of logical validity, provides the basis for the connection method (CM) and features a number of different results.
In 1979 WB attended CADE-4 where Peter Andrews presented his paper [6] later published as [7]. This independently taken approach turned out to be very closely related to the one taken in the CM while using a different terminology (mating instead of spanning set of connections, etc.). It cites one of WB’s papers while WB had not been aware of Andrews’ work before this talk. Therefore, it is not yet cited in the report version of 1979, but then of course in the journal version [13]. Andrews’ future work focussed more on higher-order logic while WB’s work in ATP continued the line taken so far, producing [14] as well as the book [15] among numerous other publications including ones with several co-authors. It eventually resulted in the system SETHEO [39]. SETHEO in 1996 won first-place at the first international competition among theorem provers, the CADE ATP System Competition or CASC.
There is a close relative to the Prawitz line which we might call the Beth line, today known under the term tableaux (see e.g. [28]). The team realizing the implementation of SETHEO featured two members who by education were committed to thinking in terms of tableaux rather than of the CM. Hence, SETHEO was influenced by the CM and some of its features but cannot be called a proper CM-prover. The prover  [18] may be regarded a more authentical product in this respect; but its main developer unfortunately soon left the field thus terminating its development towards an internationally competitive system. Hence, the leanCoP prover family discussed in this chapter has become the first long-term project on the very basis of the CM.
[18] may be regarded a more authentical product in this respect; but its main developer unfortunately soon left the field thus terminating its development towards an internationally competitive system. Hence, the leanCoP prover family discussed in this chapter has become the first long-term project on the very basis of the CM.
Most researchers in ATP are still committed to the resolution approach in ATP. In fact, the two most successful systems in terms of the CASC competition are based on resolution. On first sight, this seems to be a good reason to regard resolution superior to its competitors. But the argument is not really convincing if a closer look is taken, as we will try to show now.
The high performance of resolution systems is to a large extent due to the following two reasons. First of all, resolution was designed intentionally as a machine-oriented inference rule which could be implemented relatively easily and in a way so that an extremely massive amount of inferences can be performed in a short time. Due to the resulting successes of those implementations many systems have been developed on its basis. So, secondly, sheer numbers of investments have made the systems ever more powerful. Winning a CASC competition may well be a consequence of these two peculiarities and does not necessarily say something in sufficient detail about the ultimate potential of the underlying proof method.
In fact, resolution in principle does suffer from serious inherent drawbacks. It operates on sets of clauses resulting from the original formula F to be proved. The formula is built from axioms, theorems, lemmas and the assertions and has exactly in this respect an information-rich structure, from which human mathematicians draw heavily as they search for a proof of the assertions. This structure is totally destroyed in the resolution context. In order to cope with this deficiency to some extent, strategies like set-of-support have been developed. While they are surely useful to some extent, they do not bring back in full the rich information contained in the original structure of F. Hence resolution inferences in present systems to a large extent are carried out in a rather blind way, a disadvantage compensated by brute force and sheer power due to the two peculiarities mentioned. But for proving truly hard theorems brute force does and will not suffice. Even Alan Robinson, the hero in ATP who has laid the basis for the resolution line, in his more recent work has convincingly argued into the same direction [59] but so far has largely remained unnoticed by the huge community of his followers who keep sticking exclusively to his earlier work.
For all these reasons we continue to be deeply convinced that, in contrast, the research path pursued on the basis of the matrix characterization and the CM in the long term will yield much better results. Let us therefore summarize here its ultimate vision of a future proof method which is based on Theorem 10.4 in [15]. The idea is to elaborate within F a deductively sufficient skeleton (cf. Definition 10.2 in [15]) which is characterized exclusively by the very syntactic items occurring in F and some relations defined for them (like the pairing relation defining connections, etc.). This goal has already been achieved by leanCoP for formulae in skolemized clausal form, and by nanoCoP for arbitrary formulae in skolemized (non-clausal) form, as discussed in Sect. 5 of the present chapter. The particular feature of splitting by need (Sect. 10 in [15]) has been studied extensively in [4, 33], but without focussing on an effective proof search guided by connections. There is the additional feature of integrating an alternative for skolemization, discussed in Sect. 8 of [15] (and in fact already introduced in Sect. 4 of [11]). It would not only preserve a given formula in its truly original structure but would also make the translation back to a more readable sequent proof significantly easier. Despite these advantages, this alternative for skolemization is widely unknown in the community.
Altogether a comprehensive calculus combining all these results along with a corresponding implementation is still missing because the way towards it is a truly hard one. Once it will be available additional strategies for guiding the proof search through the information given by the structural elements in F (axioms, theorems, etc.) may be explored for the first time within a competitive system. This will be possible since the calculus keeps the given formula in its original structure completely unchanged. This also opens a way to consider the realization and inclusion of Robinson’s recent ideas referenced just before.
The line of research described here is unique and pursued so far by only a very few researchers worldwide. The reason for the lack of popularity also lies in the fact that the technical details are extremely challenging for anyone. There is a relationship with tableaux in that both lines originate from related formal systems of fol. But in contrast to tableaux which redundantly expand F to numerous subformulae according to the tableau rules, in our approach F is left completely untouched, instead accumulating information about its structure in the skeleton. Hence the Beth-line in terms of performance in principle cannot compete with our much more compact approach. But tableaux are much easier for humans to work with, thus explaining their continuing popularity.
The skeleton identified after a successful proof search represents a set of possible derivations in the underlying formal system of fol and in this sense is an extremely condensed abstraction from such a set of derivations. Any derivation of this set may easily be rolled out as soon as the skeleton has been found (see Corollary 10.6 in [15]). In this manner proofs become accessible to human understanding after they have been discovered by machine.
At some point in the last century people believed that resolution had an advantage in terms of complexity in the limit in comparison with our approach. But in the book [25] it has been shown that this in fact is not the case (see its Theorem 4.4.1), provided that one avoids repeating one and the same part of a connection proof redundantly over and over again. This is another feature which has to be cared for in a future system following our approach. For further aspects concerning such a future system see also [16, 19].
7 Conclusion
Formal reasoning in classical and non-classical logics is a fundamental technique when developing provably correct software. Over the last decades, the implementation of proof calculi has made considerable advances and automated theorem provers are nowadays used in industrial applications. But whereas the development of efficient ATP systems for classical logic has made significant progress (See e.g. [60]), the development of ATP systems for many important non-classical logics is still in its infancy. This is in particular true for first-order intuitionistic logic and first-order modal logics. Whereas the time complexity of determining whether a given propositional formula F is valid in classical logic is co- NP -complete [22], it is already PSPACE -complete [63] for intuitionistic or the (standard) modal logics (except for the modal logic S5, which is co- NP-complete [70]). Proof search in these non-classical logics is considerably more difficult than for first-order classical logic and, hence, only a few implementations of ATP systems for these logics exist to date.
This chapter provides a summary of research work on proof calculi and efficient implementations for classical and non-classical logics that has been carried out during the last ten years. All these calculi and implementations are based on the connection method. In particular, they are based on the matrix characterization of logical validity and operate in a goal-oriented connection-driven manner. As a result of this research work, three efficient automated theorem provers for first-order classical, first-order intuitionistic, and first-order modal logic are now available. All implemented ATP systems are elegant and very compact implementations based on uniform clausal connection calculi for classical, intuitionistic, and modal logics. Different non-classical logics are specified by prefixes in the clausal matrix and additional prefix unification algorithms. The minimal PROLOG source code of the core theorem provers consists of between only 11 and 16 lines.
leanCoP is one of the strongest theorem provers for first-order classical logic. It has won several prizes at CASC, the yearly competition for fully automated ATP systems, such as the “Best Newcomer” award (leanCoP 2.0) [65] and the SUMO reasoning prize (leanCoP-SInE) [67] and was winner of the first arithmetic division (leanCoP-\(\Omega \)) [68]. It is currently the most efficient theorem prover based on a connection calculus. leanCoP includes well-known techniques, such as regularity, lemmata, and some novel optimization techniques, such as lean PROLOG technology, an optimized definitional clausal form translation, and restricted backtracking. The definitional clausal form translation works significantly better than other well-known translations [46]. Restricted backtracking reduces the search space in connection calculi significantly, in particular for formulae containing many axioms. Indeed, restricted backtracking turned out to be the single most effective technique for pruning the search space in connection calculi.
The clausal connection calculus for classical logics was adapted to first-order intuitionistic logic and several first-order modal logics. To this end, an intuitionistic matrix and a modal matrix were defined, which add prefixes to the clausal matrix. The skolemization technique is extended to prefixes, hence, clause copies are made by simply renaming all term and prefix variables. The additionally required prefix unification algorithm is specified by a small set of rewriting rules and depends on the particular logic. ileanCoP extends leanCoP to first-order intuitionistic logic by adding prefixes to literals and integrating an intuitionistic prefix unification algorithm. It is currently the most efficient automated theorem prover for first-order intuitionistic logic. MleanCoP extends leanCoP to the first-order modal logics D, T, S4, and S5. To this end the definition of prefixes and the prefix unification algorithm is modified and adapted, whereas the core prover already used for ileanCoP remains unchanged. Experimental results indicate that the performance of MleanCoP is better than that of any other existing theorem prover for first-order modal logic.
In summary, the use of an additional prefix unification during the proof search for non-classical logics resembles the use of term unification in first-order logic:
By capturing the intuitionistic and modal contents of formulae in prefixes, most optimization techniques, such as the definitional clausal form translation and restricted backtracking, can be used for intuitionistic and modal logic as well.
The non-clausal connection calculus is a generalization of the clausal connection calculus. To this end, a formal definition of non-clausal matrices is given, the extension rule is slightly modified and a decomposition rule is added. In contrast to existing approaches, clause copies are added carefully and dynamically during the proof search. The non-clausal connection calculus combines the advantages of more natural (non-clausal) sequent or tableau calculi with the goal-oriented property of connection calculi. The non-clausal connection calculus is implemented in the compact PROLOG theorem prover nanoCoP. nanoCoP not only returns more natural non-clausal proofs, but the proofs are also significantly shorter.
To sum up, the presented research work has provided sufficient evidence to support the assertion that connection calculi are a solid basis for efficiently automating formal reasoning in classical and non-classical logics. They have been implemented carefully in a very compact and elegant way. Whereas the resulting performance is similar or even superior to that of existing — significantly more complex — ATP systems, the correctness of the concise code of the core provers can be checked much more easily. Hence, such implementations can not only serve as tools for constructing provably correct software, but they themselves follow an approach that ensures that they are provably correct software. An observation that was made 25 years ago by Hoare [35]:
I conclude that there are two ways of constructing a software design: One way is to make it so simple that there are obviously no deficiencies and the other way is to make it so complicated that there are no obvious deficiencies. The first method is far more difficult.
References
http://www.scientificamerican.com/article/pogue-5-most-embarrassing-software-bugs-in-history/. Accessed 15 June 2016
https://en.wikipedia.org/wiki/2015_Seville_Airbus_A400M_Atlas_crash. Accessed 15 June 2016
https://en.wikipedia.org/wiki/List_of_failed_and_overbudget_custom_software_projects. Accessed 15 June 2016
Antonsen, R., Waaler, A.: Liberalized variable splitting. J. Autom. Reason. 38, 3–30 (2007)
Astrachan, O., Loveland, D.: METEORs: high performance theorem provers using model elimination. In: Bledsoe, W., Boyer, S. (eds.) Automated Reasoning: Essays in Honor of Woody Bledsoe, pp. 31–60. Kluwer, Amsterdam (1991)
Andrews, P.B.: General matings. In: Joyner, W.H. (ed.) Fourth Workshop on Automated Deduction, pp. 19–25 (1979)
Andrews, P.B.: Theorem proving via general matings. J. ACM 28, 193–214 (1981)
Barwise, J.: An introduction to first-order logic. In: Barwise, J. (ed.) Handbook of Mathematical Logic, pp. 5–46. North-Holland, Amsterdam (1977)
Blackburn, P., van Bentham, J., Wolter, F.: Handbook of Modal Logic. Elsevier, Amsterdam (2006)
Baumgartner, P., Eisinger, N., Furbach, U.: A confluent connection calculus. In: Hölldobler, S. (ed.) Intellectics and Computational Logic. Applied Logic Series 19, pp. 3–26. Kluwer, Dordrecht (2000)
Bibel, W.: An approach to a systematic theorem proving procedure in first-order logic. Computing 12, 43–55 (1974)
Bibel, W.: Syntax-directed, semantics-supported program synthesis. Artificial Intelligence 14, 243–261 (1980)
Bibel, W.: On matrices with connections. J. ACM 28, 633–645 (1981)
Bibel, W.: Matings in matrices. Commun. ACM 26, 844–852 (1983)
Bibel, W.: Automated Theorem Proving, 2nd edn. Vieweg, Braunschweig (1987)
Bibel, W.: Research perspectives for logic and deduction. In: Stock, O., Schaerf, M. (eds.) Reasoning. Action, and Interaction in AI Theories and Systems - Essays dedicated to Luigia Carlucci Aiello, LNAI 4155, pp. 25–43. Springer, Berlin (2006)
Bibel, W.: Early history and perspectives of automated deduction. In: Hertzberg, J., Beetz, M., Englert, R. (eds.) KI 2007. LNAI 4667, pp. 2–18. Springer, Berlin (2007)
Bibel, W., Brüning, S., Egly, U., Rath, T.:
 In: Bundy, A. (ed.) CADE-12. LNAI 814, pp. 783–787. Springer, Heidelberg (1994)
In: Bundy, A. (ed.) CADE-12. LNAI 814, pp. 783–787. Springer, Heidelberg (1994)Bibel, W., Otten, J.: From schütte’s formal system to modern automated deduction. In: Kahle, R., Rathjen, M. (eds.), The Legacy of Kurt Schütte. Springer, London, to appear
Brandt, C., Otten, J., Kreitz, C., Bibel, W.: Specifying and verifying organizational security properties in first-order logic. In: Siegler, S., Wasser, N. (eds.) Verification, Induction, Termination Analysis. LNAI 6463, pp. 38–53. Springer, Heidelberg (2010)
Benzmüller, C., Otten, J., Raths, T.: Implementing and evaluating provers for first-order modal logics. In: De Raedt, L., et al. (eds.) 20th European Conference on Artificial Intelligence (ECAI 2012), pp. 163–168. IOS Press, Amsterdam (2012)
Cook, S.A.: The complexity of theorem-proving procedures. In: Proceedings of the 3rd Annual ACM Symposium on the Theory of Computing, pp. 151–158. ACM, New York (1971)
van Dalen, D.: Intuitionistic logic. In: Goble, L. (ed.) The Blackwell Guide to Philosophical Logic, pp. 224–257. Blackwell, Oxford (2001)
Deville, Y.: Logic Programming, Systematic Program Development. Addison-Wesley, Wokingham (1990)
Eder, E.: Relative Complexities of First Order Calculi. Vieweg, Braunschweig (1992)
Fisher, K.: HACMS: high assurance cyber military systems. In: Proceedings of the 2012 ACM Conference on High Integrity Language Technoloby, pp. 51–52. ACM, New York (2012)
Fitting, M.: Proof Methods for Modal and Intuitionistic Logic. D. Reidel, Dordrecht (1983)
Fitting, M.: First-Order Logic and Automated Theorem Proving, 2nd edn. Springer, Heidelberg (1996)
Gentzen, G.: Untersuchungen über das logische Schließen. Math. Z. 39(176–210), 405–431 (1935)
Goel, S., Hunt, W.A., Kaufmann, M.: Engineering a formal, executable x86 ISA simulator for software verification. In: Bowen, J.P., Hinchey, M., Olderog, E.-R. (eds.) Provably Correct Systems. Springer, London (2016)
Hähnle, R.: Tableaux and related methods. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, pp. 100–178. Elsevier, Amsterdam (2001)
Hähnle, R., Murray, N.V., Rosenthal, E.: Linearity and regularity with negation normal form. Theor. Comput. Sci. 328, 325–354 (2004)
Hansen, C.: A Variable Splitting Theorem Prover. University of Oslo (2012)
Herbrand, J.J.: Recherches sur la théorie de la démonstration. Travaux Soc. Sciences et Lettres Varsovie, Cl. 3 Mathem. Phys. (1930)
Hoare, C.A.R.: The emperor’s old clothes. Commun. ACM 24, 75–83 (1981)
Klein, G., Elphinstone, K., Heiser, G., Adronick, J., Cock, D., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolanski, R., Norrish, M., Sewell, T., Tuch, H., Winwood, S.: SeL4: formal verification of an OS kernel. In: Proceedings of the 22nd ACM SIGOPS, pp. 207–220. ACM, New York (2009)
Lee, S.-J., Plaisted, D.: Eliminating duplicates with the hyper-linking strategy. J. Autom. Reason. 9, 25–42 (1992)
Letz, R., Stenz, G.: Model elimination and connection Tableau procedures. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, pp. 2015–2114. Elsevier, Amsterdam (2001)
Letz, R., Schumann, J., Bayerl, S., Bibel, W.: SETHEO: a high-performance theorem prover. J. Autom. Reason. 8, 183–212 (1992)
Loveland, D.: Mechanical theorem proving by model elimination. J. ACM 15, 236–251 (1968)
McCune, W.: Release of Prover9. Mile High Conference on Quasigroups, Loops and Nonassociative Systems. Technical report, Denver (2005)
McLaughlin, S., Pfenning, F.: Efficient intuitionistic theorem proving with the polarized inverse method. In: Schmidt, R.A. (ed.) CADE-22. LNCS 5663, pp. 230–244. Springer, Heidelberg (2009)
Moore, J.S.: Computing verified machine address bounds during symbolic simulation of code. In: Bowen, J.P., Hinchey, M., Olderog, E.-R. (eds.) Provably Correct Systems. Springer, London (2016)
Otten, J.: Clausal connection-based theorem proving in intuitionistic first-order logic. In: Beckert, B. (ed.) TABLEAUX 2005. LNAI 3702, pp. 245–261. Springer, Heidelberg (2005)
Otten, J.: \({{ leanCoP}}\) 2.0 and \({{ ileanCoP}}\) 1.2: high performance lean theorem proving in classical and intuitionistic logic. In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS 5195, pp. 283–291. Springer, Heidelberg (2008)
Otten, J.: Restricting backtracking in connection calculi. AI Commun. 23, 159–182 (2010)
Otten, J.: A Non-clausal Connection Calculus. In: Brünnler, K., Metcalfe, G. (eds.) TABLEAUX 2011. LNAI 6793, pp. 226–241. Springer, Heidelberg (2011)
Otten, J.: Implementing connection calculi for first-order modal logics. In: Ternovska, E., Korovin, K., Schulz, S. (eds.), 9th International Workshop on the Implementation of Logics (IWIL 2012), EPiC, EasyChair, vol. 22, pp. 18–32 (2012)
Otten, J.: \({{ MleanCoP}}\): a connection prover for first-order modal logic. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNAI 8562, pp. 269–276. Springer, Heidelberg (2014)
Otten, J.: \({{ nanoCoP}}\): a non-clausal connection prover. In: Olivetti, N., Tiwari, A. (eds.) IJCAR 2016, LNAI 9706. Springer, Heidelberg (2016)
Otten, J., Bibel, W.: \({{ leanCoP}}\): lean connection-based theorem proving. J. Symb. Comput. 36, 139–161 (2003)
Plaisted, D., Greenbaum, S.: A structure-preserving clause form translation. J. Symb. Comput. 2, 293–304 (1986)
Prawitz, D.: A proof procedure with matrix reduction. In: Laudet, M., et al. (eds.) Symposium on Automatic Demonstration. Lecture Notes in Mathem, pp. 207–214. Springer, Berlin (1970)
Rautenberg, W.: A Concise Introduction to Mathematical Logic. Springer, Heidelberg (2010)
Raths, T., Otten, J., Kreitz, C.: The ILTP problem library for intuitionistic logic. J. Autom. Reason. 38, 261–271 (2007)
Raths, T., Otten, J.: The QMLTP problem library for first-order modal logics. In: Gramlich, B., et al. (eds.) IJCAR 2012. LNAI 7364, pp. 454–461. Springer, Heidelberg (2012)
Robinson, J.A.: A machine-oriented logic based on the resolution principle. J. ACM 12, 23–41 (1965)
Ray, S.: Scalable Techniques for Formal Verification. Springer, Heidelberg (2010)
Robinson, J.A.: Proof \(=\) guarantee \(+\) explanation. In: Hölldobler, S. (ed.) Intellectics and Computational Logic. Applied Logic Series 19, pp. 277–294. Kluwer, Dordrecht (2000)
Robinson, J.A., Voronkov, A.: Handbook of Automated Reasoning. Elsevier, Amsterdam (2001)
Schulz, S.: E - a brainiac theorem prover. AI Commun. 15, 111–126 (2002)
Smullyan, R.M.: First-Order Logic. Springer, Heidelberg (1968)
Statman, R.: Intuitionistic propositional logic is polynomial-space complete. Theoret. Comput. Sci. 9, 67–72 (1979)
Stickel, M.: A Prolog technology theorem prover: implementation by an extended Prolog compiler. J. Autom. Reason. 4, 353–380 (1988)
Sutcliffe, G.: The CADE-21 automated theorem proving system competition. AI Commun. 21, 71–81 (2008)
Sutcliffe, G.: The TPTP problem library and associated infrastructure: the FOF and CNF parts, v3.5.0. J. Autom. Reason. 43, 337–362 (2009)
Sutcliffe, G.: The CADE-22 automated theorem proving system competition - CASC-22. AI Commun. 23, 47–59 (2010)
Sutcliffe, G.: The 5th IJCAR automated theorem proving system competition - CASC-J5. AI Commun. 24, 75–89 (2011)
Waaler, A.: Connections in nonclassical logics. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, pp. 1487–1578. Elsevier, Amsterdam (2001)
Wallen, L.A.: Automated Deduction in Nonclassical Logics. MIT Press, Cambridge (1990)
Acknowledgements
We would like to thank several anonymous referees for their constructive comments which were helpful to improve the text. Our thanks are also due to the editors Jonathan Bowen, Michael Hinchey and Ernst-Ruediger Olderog for the organization of the ProCoS Workshop in 2015, for compiling this volume and for inviting us to both projects.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Otten, J., Bibel, W. (2017). Advances in Connection-Based Automated Theorem Proving. In: Hinchey, M., Bowen, J., Olderog, ER. (eds) Provably Correct Systems. NASA Monographs in Systems and Software Engineering. Springer, Cham. https://doi.org/10.1007/978-3-319-48628-4_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-48628-4_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-48627-7
Online ISBN: 978-3-319-48628-4
eBook Packages: Computer ScienceComputer Science (R0)


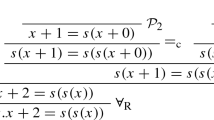









 In: Bundy, A. (ed.) CADE-12. LNAI 814, pp. 783–787. Springer, Heidelberg (1994)
In: Bundy, A. (ed.) CADE-12. LNAI 814, pp. 783–787. Springer, Heidelberg (1994)