Keywords

1 Introduction

Piezoelectric devices are nowadays broadly spread and commonly adopted in various industrial fields. In the last years, bimorph piezoelectric systems are gathering great attention by scholars and technicians as interesting actuators, able to perform mechanical motion or, in particular, vibration [1–8].

In 2005, Zhou et al. [9] presented semi-analytic approach for the evaluation of the eigenfrequencies of a piezoelectric bimorph based on an improved first-order shear deformation theory (FSDT) beam model.

In 2013, Borboni and Faglia [10] described how uncertainties on the knowledge of mechanical, piezoelectric or electric parameters reflect on the first vibration mode of a simply supported piezoelectric bimorph. Nevertheless, good practice for finest machine design would require a thorough awareness of the non-ideal responses of the system until the fifth vibration mode: for this reason, the present paper aims to investigate the previous models to the fifth vibration mode, thanks to a stochastic evaluation of the free vibrations of the piezoelectric bimorph.

2 Model Definition

The basic system is composed of two piezoelectric layers, mechanically connected, and is constrained by simple supports; the layers are also electrically connected thanks to a parallel arrangement for the electric circuit and the Timoshenko theory [11] is applied in order to study the beam deformation.

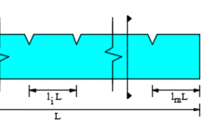
According to this theory, the beam deformation can be properly analyzed in a planar space, since the deflection can be reduced to a two-dimensional movement. Referring to Fig. 1, a beam l long and having two layers h thick each, performs a movement in the x 1 Ox 3 plane, and the neutral axis of the beam overlaps the x 1 axis in the undeformed configuration. The selection of the Timoshenko theory implicates that: (i) displacement u of the axis points only depends by the linear x 1 variable, (ii) consecutive segments, normal to the neutral axis, remain consecutive after the deformation, and (iii) segments normal to the neutral axis in undeformed configuration do not strictly remain normal to the axis under deflection, indeed they could perform an additional Ψ rotation around the axis itself, as a consequence of the shear strain.

Fig. 1
figure 1

Simply supported piezoelectric bimorph

Full size image

Under the effect of mechanical and/or electric actions, the beam deflects as presented in Fig. 1: in the deformed configuration, the bender presents for each section a w displacement along the x 3 direction and a Ψ rotation around x 2 .

Under the hypotheses of small deflection and plane stress state, the equilibrium equations along the ith direction (i = 1, 3) for an infinitesimal portion of the beam are described by Eq. (1), according to the definitions introduced by Eqs. (2)–(4), where σ and τ are components of the stress tensor is the stress tensor, f is a body force, ρ is the mass density of the bar, \( \bar{c} \) and are \( \bar{e} \) the components of the stiffness and piezoelectric matrix, ε and γ are the components of the strain tensor and E are the components of the electric field.

$$ \frac{{\partial \sigma_{xi} }}{\partial xi} + \frac{{\partial \tau_{x1x3} }}{\partial x1} + f_{xi} = \rho \frac{{\partial^{2} u_{xi} }}{{\partial t^{2} }} $$
(1)
$$ \sigma_{x3} = \bar{c}_{13} \varepsilon_{x1} + \bar{c}_{33} \varepsilon_{x3} - ( -1)^{r} \bar{e}_{31} E_{x3} $$
(2)
$$ \sigma_{x1} = \bar{c}_{11} \varepsilon_{x1} + \bar{c}_{13} \varepsilon_{x3} - ( -1)^{r} \bar{e}_{31} E_{x3} $$
(3)
$$ \tau_{x1x3} = \bar{c}_{55} \gamma_{x1x3} - ( -1)^{r} \bar{e}_{15} E_{x1} $$
(4)

Since no external electrical charge is applied to the beam, the divergence and Gauss theorems led to Eq (5), where the components of the electric displacement matrix D x3 and D x1 are defined according to Eqs. (6) and (7), where \( \bar{\varepsilon } \) are the components of the dielectric matrix.

$$ \frac{{\partial D_{x1} }}{\partial x1} + \frac{{\partial D_{x3} }}{\partial x3} = 0 $$
(5)
$$ D_{x3} = ( - 1)^{r} \left( {\bar{e}_{31} \varepsilon_{x1} + \bar{e}_{33} \varepsilon_{x3} } \right) + \bar{\varepsilon }_{33} E_{x3} $$
(6)
$$ D_{x1} = ( - 1)^{r} \left( {\bar{e}_{15} \gamma_{x1x3} } \right) + \bar{\varepsilon }_{11} E_{x1} $$
(7)

Moreover, Eqs. (8)–(12) describe the relation of kinematics with displacement and electric potential ϕ.

$$ \varepsilon_{x1} = \frac{{\partial u_{x1} }}{\partial x1} $$
(8)
$$ \varepsilon_{x3} = \frac{{\partial u_{x3} }}{\partial x3} $$
(9)
$$ \gamma_{x1x3} = \frac{{\partial u_{x1} }}{\partial x3} + \frac{{\partial u_{x3} }}{\partial x1} $$
(10)
$$ E_{x1} = - \frac{\partial \phi }{\partial x1} $$
(11)
$$ E_{x3} = - \frac{\partial \phi }{\partial x3} $$
(12)

Finally, according to the first-order shear deformation theory, the final mechanical displacement can be presented as in Eqs. (13) and (14); merging those definitions with the previous relations, the final Eqs. (15) and (16) can be obtained, where w and ψ are the translation and rotation of a cross section.

$$ u_{x3} \left( {x1,x3,t} \right) = w\left( {x1,t} \right) $$
(13)
$$ u_{x1} \left( {x1,x3,t} \right) = - x3\uppsi\left( {{\text{x}}1,{\text{t}}} \right) $$
(14)
$$ \varepsilon_{x1} = - x3\frac{\partial \uppsi }{\partial x1} $$
(15)
$$ \gamma_{x1x3} = - \uppsi + \frac{\partial w}{\partial x1} $$
(16)

Under the further hypothesis of parallel electric configuration, Eqs. (17)–(21) can be written to approximate Eqs. (1) and (2), where m and p are the applied torque and force, Mx and Qx are the bending moment and the shear force.

$$ \frac{{\partial M_{x1} }}{\partial x1} - Q_{x1} - \mathop \smallint \limits_{ - h}^{h} \rho z\frac{{\partial^{2} u_{x1} }}{{\partial t^{2} }}dx3 = m $$
(17)
$$ - \frac{{\partial Q_{x} 1}}{\partial x1} + \mathop \smallint \limits_{ - h}^{h} \rho \frac{{\partial^{2} u_{x3} }}{{\partial t^{2} }}dx3 = p $$
(18)
$$ \mathop \smallint \limits_{0}^{h} \left( {\frac{{\partial D_{x1} }}{\partial x1} + \frac{{\partial D_{x3} }}{\partial x3}} \right)dx3 = 0\quad o\quad \mathop \smallint \limits_{ - h}^{0} \left( {\frac{{\partial D_{x1} }}{\partial x1} + \frac{{\partial D_{x3} }}{\partial x3}} \right)dx3 = 0 $$
(19)
$$ M_{x1} = \mathop \smallint \limits_{ - h}^{0} x3\sigma_{x1} dx3 + \mathop \smallint \limits_{0}^{h} x3\sigma_{x1} dx3 $$
(20)
$$ Q_{x1} = \mathop \smallint \limits_{ - h}^{0} \tau_{x1x3} dx3 + \mathop \smallint \limits_{0}^{h} \tau_{x1x3} dx3 $$
(21)

The initial conditions are then described by Eqs. (22)–(24), and expanding in Fourier series, the solving system in Eq. (25) can be defined: Eqs. (26)–(35) collect the definition of the A matrix coefficients, where b are the components of a parameter matrix opportunely dependent on the shear coefficient k and on different parameters of the model, as shown in [9]

$$ w|_{x1 = 0,l} = 0 $$
(22)
$$ \sigma_{x1} |_{x1 = 0,l} = 0 $$
(23)
$$ \varPhi |_{x1 = 0,l} = 0 $$
(24)
$$ \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {a_{22} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {a_{33} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {W_{n} } \\ {\varPsi_{n} } \\ {\Phi _{n} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {a_{14} V_{n} } \\ {P_{n} + a_{24} V_{n} } \\ {a_{34} V_{n} } \\ \end{array} } \right) $$
(25)
$$ a_{12} = - b_{21} (\frac{n\pi }{l})^{2} - b_{12} + b_{41} \omega_{n}^{2} $$
(26)
$$ a_{13} = \left( {b_{22} - b_{13} } \right)\frac{n\pi }{l} $$
(27)
$$ a_{21} = b_{11} (\frac{n\pi }{l})^{2} - b_{42} \omega_{n}^{2} $$
(28)
$$ a_{22} = b_{12} \frac{n\pi }{l} $$
(29)
$$ a_{23} = b_{13} (\frac{n\pi }{l})^{2} $$
(30)
$$ a_{31} = - b_{31} (\frac{n\pi }{l})^{2} $$
(31)
$$ a_{32} = - b_{32} \frac{n\pi }{l} $$
(32)
$$ a_{33} = - b_{33} (\frac{n\pi }{l})^{2} + b_{35} $$
(33)
$$ a_{24} = - b_{14} (\frac{n\pi }{l})^{2} $$
(34)
$$ a_{34} = - b_{34} (\frac{n\pi }{l})^{2} $$
(35)

The determinant of the system in Eq. (25) solved for the nth value allows to define the nth eigenvalue.

3 Stochastic Approach

In order to obtain comparable results, the same stochastic approach introduced by Borboni and Faglia in 2013 [10] has been adopted in the sensitivity analysis of the variable parameters collected in the Z vector: the mechanical stiffness C, and the piezoelectric parameters e and ε.

Once defined µ ij the nominal value of the ijth element of Z, and Δ Z the maximum allowed error (i.e. the maximum implemented variation of the parameter), the variance ζ can be described as Eqs. (36) and (37) present.

$$ \delta_{ij} \left( {z_{ij} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{{2\mu_{ij}\Delta _{z} }},} & {\mu_{ij} \left( {1 -\Delta _{z} } \right) \le z_{ij} \le \mu_{ij} \left( {1 +\Delta _{z} } \right)} \\ {0,} & { elsewhere} \\ \end{array} } \right. $$
(36)
$$ 3\varsigma_{ij}^{2} = \mu_{ij}^{2}\Delta _{z}^{2} $$
(37)

The aims of the work is to test the sensitivity of the model, in terms of ability to quantify the natural frequencies of the system, to parametric errors. The numerical simulations are performed for: five values of the geometric ratio λ, five values of the shear coefficient k, five values of the maximum error Δ Input and four types of error conditions, as shown in Table 1. Each test is statistically repeated 1000 times, according to (36) and (37), for each natural frequency from the 1st to the 5th.

Table 1 PZT-5A: nominal values of the main material property
Full size table

Table 1 collects the testing conditions of the stochastic simulations.

4 Numerical Results and Discussion

Numerical evaluation have been performed under the hypothesis of PZT-5A; the main characteristics of this material are collected in Table 2.

Table 2 PZT-5A: nominal values of the main material property
Full size table

The main result is that the influence of the electric and piezoelectric error on the frequency evaluation is limited, less than 0.5 %, whereas the mechanical parameters are predominant. Although the shear coefficient is an important parameter, when its value is chosen within the range proposed by Cowper [11], the error produced on the frequency evaluation is limited. The error on the geometric ratio λ is relevant starting from the 2nd frequency and the instability of the model increases with increasing vibrational modes (Fig. 2).

Fig. 2
figure 2

Δω with respect to λ. The results of mechanical (diamond), piezoelectric (square), electric (triangle) and all (dot) parameters variations are presented, under the hypotheses of 1 % input error and k = 5/6. The first diagram on the top left is the 1st vibration mode, the consequent diagrams are associated to increasing vibration modes

Full size image

5 Conclusions

The problem of the computation of the natural frequencies for the 1st–5th modes of a simply supported piezoelectric bimorph beam was investigated in presence of evaluation errors in mechanical, piezoelectric and electric parameters. The analysis was performed on a PZT-5A device. Under some limitations, we can conclude that: the effect of the errors on mechanical stiffness is predominant with respect to the piezoelectric and electric errors. The correlation between mechanical errors and natural frequencies can be represented with simple empirical expressions. These results was known for the first vibration mode and this work extends the previous result to the 1st–5th vibration modes. We must also observe that the model is stable for the first modes, where the effect of the errors on the parameters and of the number of tests is limited on the natural frequencies. Increasing the number of modes the model becomes more and more unstable and its ability to predict the vibrational frequencies of the devices becomes really dependent on the ability to estimate, particularly its mechanical parameters. Thus a superficial analysis is not sufficient and a deep mechanical analysis of the device is necessary to accurately predict high order vibrational behavior of the device.