Abstract
Symbolic execution is a software analysis technique that has been used with success in the past years in program testing and verification. A main bottleneck of symbolic execution is the path explosion problem: the number of paths in a symbolic execution tree is exponential in the number of static branches of the executed program. Here we put forward an abstraction-based framework for state merging in symbolic execution. We show that it subsumes existing approaches and prove soundness. The method was implemented in the verification system KeY. Our empirical evaluation shows that reductions in proof size of up to 80 % are possible by state merging when applied to complex verification problems; new proofs become feasible that were out of reach so far.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Symbolic execution [7, 20] is a classic program analysis technique that was used with considerable success in the past years, for example, in program testing [8] and program verification [4]. One of the main bottlenecks of symbolic execution is the path explosion problem [8]. It stems from the fact that symbolic execution must explore all symbolic paths of a program to achieve high coverage (in testing), respectively, soundness (in verification). As a consequence, the number of paths from the root to the leaves in a symbolic execution tree is usually exponential in the number of static branches of the executed program.
Various strategies are in use to mitigate path explosion, including subsumption [3, 9], method contracts [5] and value summaries [23]. The last two allow one to perform symbolic execution per method: different symbolic execution paths are merged into the postcondition of a contract or a value summary (a conditional execution state over guard expressions). Summaries are computed on the fly and bottom-up, while contracts characterize all possible behaviors and must at least partially be written by hand. Unfortunately, even the use of rich contracts (instead of inlining) is insufficient to deal with complex problems [15].
A seemingly obvious technique to alleviate state explosion in symbolic execution trees consists of merging the states resulting from a symbolic execution step that caused a split (e.g., guard evaluation, statements that can throw exceptions, polymorphic method calls). After all, graph-based data structures are standard in model checking for the exploration of symbolic state spaces [10], as well as in other static software analyses. Indeed, several state merging variants were suggested for symbolic execution [18, 21, 23], but there are problems:
-
(1)
State merging does not come for free, but creates considerable overhead: states must be merged, graph data structures are more complex than trees, path conditions as well as summaries tend to grow fast and must be simplified. Eager state merging can make things worse [18], therefore, it has to be carefully controlled. Simplification of intermediate expressions with the help of automated deduction is indispensable.
-
(2)
All mentioned approaches assume that merged states are identical to corresponding unmerged states, possibly up to the differences encoded in value summaries. This is insufficient to merge large numbers of different behaviors.
In the present paper we address both issues. Regarding the second, we observe that instead of encoding merged states precisely into a conditional state, one might also abstract from the precise value of a variable. This results in a loss of precision, but reduces complexity. For example, consider symbolic execution of “if (b) x = 1 else x = 2;” in state \(\sigma \). Precise state merging would result in a state identical to \(\sigma \) except the value of x is “\(\text {x}\mapsto (1,~\text {if}~\sigma (b)= true )\,|\,x\mapsto (2,~\text {if }\sigma (b)= false )\)”. This does not avoid path explosion, it only delays it. Now, assume that we define an abstract domain A for the possible values of x, where \(\alpha (\text {x})\) is the abstraction of x and A is an upper semilattice \(\sqcup \). For example, A might be the sign lattice \(\{\bot ,-,0,+,\top \}\). Then the merged state can be over-approximated by the partially abstract state that is identical to \(\sigma \) except \(\text {x}\mapsto +\). Path explosion is avoided. We lost precision about the exact value of x, but for many analyses this is acceptable provided that the abstract lattice is suitably chosen.
Based on the theory of symbolic execution with abstract interpretation [6], in the present paper we put forward a general lattice-based framework for state merging in symbolic execution where a family of abstract lattices is defined by formulas of a program logic. Our framework preserves soundness of verification and we show that it subsumes earlier approaches to state merging [18, 21, 23].
Regarding issue (1) above, as a second contribution, we improved automation by implementing suitable proof macros for KeY as well as an extension of the Java Modeling Language (JML)Footnote 1 which allows software engineers to annotate Java source code with instructions on when to perform state merges.
We implemented the framework in the state-of-art verification system KeY [5], where contracts are available to mitigate state explosion. Since the latter must be partially written by hand, state merging is a complementary technique that promises a high degree of automation. We confirmed the usefulness of our approach empirically with an extensive evaluation: Results for small to medium sized programs are, as expected, mixed, because of the overhead of state merging. The strength of symbolic execution with state merging emerges when applied to complex verification problems like the TimSort implementation in the Java standard library [15], where we observe reductions in proof size of up to 80 %. Additionally, some proofs become feasible that were elusive before.
We continue with Sect. 2, which provides sufficient theoretical background to make the paper self-contained. Section 3 sets up our abstract lattice model. Section 4 defines the actual merge rules, states a soundness theorem and briefly mentions implementation issues. Section 5 contains the empirical evaluation, Sect. 6 lessons learned as well as future work, and Sect. 7 related work plus a brief conclusion.
2 Background
We formalize our theory in the program logic JavaDL [5], but the approach is easily adaptable to any program logic with an explicit notion of symbolic state.
2.1 Program Logic and Calculus
Our framework is realized in JavaDL, a sorted first-order dynamic logic [19] for sequential deterministic Java programs. For the sake of presentation, we restrict ourselves to a simplified JavaDL variant (simple imperative Java programs over primitive types \(\mathbf{int}\), \(\mathbf{boolean}\)) and only give the essential definitions. The actual implementation is based on KeY which covers most sequential Java features: inheritance, dynamic dispatch, reference types, recursive methods, exceptions, and strings. Not covered are generic types (which are translated away), floating point types and lambda expressions. We refer the reader to [5] for a full account.
JavaDL extends sorted first-order logic by two modalities to express partial and total correctness of programs. For space reasons, we restrict ourselves to the former, the box modality \([\cdot ]{\cdot }\). Its first argument is a program (more precisely, an executable sequence of Java statements); the second argument can be any JavaDL formula, possibly containing further modal operators. Given a program p and a JavaDL formula \(\varphi \), the informal meaning of the formula \(\left[ p\right] \varphi \) is: if the program p terminates then the formula \(\varphi \) holds in the final state.
The syntax of terms and formulas is standard except for a few extra cases like modalities, conditional terms/formulas (Example 1) as well as updates. The set of all programs is \( Prg \); the set of all program variables is denoted by \(\mathsf {PV}\). Updates represent state changes: an elementary update has the form  with \(\mathrm{l}\in \mathsf {PV}\) and t a term of a type compatible with \(\mathrm{l}\). Informally, an update has the same meaning as an assignment, where the program variable on the left-hand side is assigned the value of the right-hand side. Elementary updates are combined to parallel updates
with \(\mathrm{l}\in \mathsf {PV}\) and t a term of a type compatible with \(\mathrm{l}\). Informally, an update has the same meaning as an assignment, where the program variable on the left-hand side is assigned the value of the right-hand side. Elementary updates are combined to parallel updates  which represent simultaneous assignments. In case of a clash where the same variable \(\mathrm{l}\) is assigned different values in a parallel update, the syntactically later assignment wins. The set of all updates is \(\mathrm {Upd}_{}\), \( skip \) is the “empty update”. Updates U can be applied to terms t, written
which represent simultaneous assignments. In case of a clash where the same variable \(\mathrm{l}\) is assigned different values in a parallel update, the syntactically later assignment wins. The set of all updates is \(\mathrm {Upd}_{}\), \( skip \) is the “empty update”. Updates U can be applied to terms t, written  , and formulas \(\varphi \), written
, and formulas \(\varphi \), written  . We give the non-standard cases of the inductive definitions of terms and formulas:
. We give the non-standard cases of the inductive definitions of terms and formulas:
Definition 1
(Terms). Let \(\varphi \) denote a formula, \(t_1\), \(t_2\) are terms of type \(T_1\) and \(T_2\) and U an update, then (i)  is a term of type \(T_1\) (ii) \(\mathsf {if}\left( \varphi \right) \mathsf {then}\left( t_1\right) \mathsf {else}\left( t_2\right) \) is a term of type T where T is the least common supertype of \(T_1\) and \(T_2\). The set of all terms is denoted by \(\mathrm {Trm}^{}\).
is a term of type \(T_1\) (ii) \(\mathsf {if}\left( \varphi \right) \mathsf {then}\left( t_1\right) \mathsf {else}\left( t_2\right) \) is a term of type T where T is the least common supertype of \(T_1\) and \(T_2\). The set of all terms is denoted by \(\mathrm {Trm}^{}\).
Definition 2
(Formulas). Let \(\varphi , \psi _1,\psi _2\) denote formulas, U an update and p a program, then each of (i) \(\left[ p\right] {\varphi }\) (ii)  and (iii)
and (iii)  is a formula. For open formulas with free variables
is a formula. For open formulas with free variables  we use the notation
we use the notation  to make their occurrence explicit. The set of all formulas is denoted by \(\mathrm {Fml}\).
to make their occurrence explicit. The set of all formulas is denoted by \(\mathrm {Fml}\).
Example 1
Let \(\mathrm{i}, \mathrm{j}\) be program variables and x, y logic variables, all of sort int.
-
The formula
 uses a parallel update to exchange the values of \(\mathrm{i}\) and \(\mathrm{j}\).
uses a parallel update to exchange the values of \(\mathrm{i}\) and \(\mathrm{j}\). -
The formula \(\mathrm{i}>\mathrm{j} \rightarrow {[\mathrm{i}=\mathrm{i}-\mathrm{j};]}\mathrm{i}>0\) expresses that if program \([\mathrm{i}=\mathrm{i}-\mathrm{j};]\) is executed in a state where the value of i is greater than the value of j and it terminates, then in its final state \(\mathrm{i}\) is positive.
-
\(\mathsf {if}\left( \mathrm{i}>\mathrm{j}\right) \mathsf {then}\left( \mathrm{i}\right) \mathsf {else}\left( \mathrm{j}\right) \ge 0\) means that the maximum of \(\mathrm{i}\) and \(\mathrm{j}\) is positive.
Formulas are evaluated in first-order structures with a non-empty domain \( D\) and an interpretation function \(I\) giving meaning to sort, function and predicate symbols. To reason about programs, we extend this to Kripke structures \(K = \left( D, I,S,\rho \right) \). The values of program variables depend on the current program state and cannot be evaluated by the static interpretation function \(I\). Instead they are assigned values by Kripke states \(\sigma \!:\!\mathsf {PV}\rightarrow D\in S\). The state transition function \(\rho \!:\! Prg \rightarrow (S\rightarrow 2^{S})\) captures the program semantics (here: Java’s semantics [14]).Footnote 2
As our programs are deterministic, the value of \(\rho (p)(\sigma )\) (for any program p and state \(\sigma \)) is either the empty set (p does not terminate when started in state \(\sigma \)) or a singleton. Formulas and terms are assigned meaning by an evaluation function \( val \left( K,\sigma ,\beta ;\cdot \right) \), parametric in a Kripke structure \(K\), a state \(\sigma \) and a variable assignment \(\beta \). The evaluation function assigns terms a value in their domain and formulas one of the truth values \( tt \), \( ff \). Figure 1 shows some inductive definition cases. For expressions without free logic variables, we write \( val \left( K,\sigma ;\cdot \right) \); for sets of closed formulas \(C\), we write \( val \left( K,\sigma ;C\right) \) meaning \( val \left( K,\sigma ;\bigwedge _{\varphi \in C}\varphi \right) \).
A sequent calculus [12], [5, Chap. 3] is used to prove the validity of JavaDL formulas. The rules for the first-order logic connectives are standard, those for programs follow the symbolic execution paradigm. Formulas with programs are transformed into pure first-order formulas by symbolically executing the programs in a forward manner and thereby computing the weakest precondition. Each execution step transforms or eliminates the first statement until the program is eliminated. We write \(\vdash \varphi \) if a formula \(\varphi \) is provable using the calculus.
2.2 Symbolic Execution
We explain how the notions and concepts introduced in the standard literature [7] relate to our logic-based setting. Symbolic Execution (SE) of a program results in a Symbolic Execution Tree (SET) consisting of SE states, i.e., triples  with (1) an update U, the symbolic state, capturing the changes made to program variables in the course of the execution, (2) the path condition \(C\), a set of closed formulas comprising the decisions leading to this particular SE path as well as additional preconditions, and (3) the program counter \(\varphi \), a closed formula, typically containing the remaining program to be executed as well as the postcondition to prove.
with (1) an update U, the symbolic state, capturing the changes made to program variables in the course of the execution, (2) the path condition \(C\), a set of closed formulas comprising the decisions leading to this particular SE path as well as additional preconditions, and (3) the program counter \(\varphi \), a closed formula, typically containing the remaining program to be executed as well as the postcondition to prove.
Please note that we generalize the usual notion of a program counter, which is normally only a pointer to a statement in the executed program. In our setting, a program counter may be an arbitrary closed formula. This generalization facilitates reasoning about the validity of SE states.
Definition 3
(Validity of SE States). An SE state  is called valid iff for all Kripke structures \(K\) and states \(\sigma \) either \( val \left( K,\sigma ;C\right) = ff \) or
is called valid iff for all Kripke structures \(K\) and states \(\sigma \) either \( val \left( K,\sigma ;C\right) = ff \) or  holds. We write \( valid \left( s\right) \).
holds. We write \( valid \left( s\right) \).
Consider an SE state  . Intuitively, if the path condition C does not hold in s, then the state is unreachable and trivially valid. Otherwise, all final state(s) reached when executing p in state
. Intuitively, if the path condition C does not hold in s, then the state is unreachable and trivially valid. Otherwise, all final state(s) reached when executing p in state  must satisfy \(\varphi \).
must satisfy \(\varphi \).
SET transitions are constrained by a rule-based SE transition relation \(\delta : 2^{ SEStates _{}} \rightarrow 2^{ SEStates _{}}\), where \( SEStates _{}\) is the set of all SE states. Again, this is a generalization of traditional SE, since the result of applying \(\delta \) does not have to be a singleton. Based on Definition 3, we introduce a soundness notion for \(\delta \).
Definition 4
(Soundness of Symbolic Execution). An SE transition relation \(\delta : 2^{ SEStates _{}} \rightarrow 2^{ SEStates _{}}\) is called sound iff for each input-output pair \(\left( I,O\right) \in \delta \) it is the case that \(\bigwedge _{o\in {}O} valid \left( o\right) \implies \bigwedge _{i\in {}I} valid \left( i\right) \).
The intuition behind the above definition is that, whenever one input state is not valid, also at least one output state must not be valid. Otherwise, it would be possible to derive an invalid property about a program.
2.3 Running Example

The program in Listing 1 is our running example. It computes the absolute difference (distance) between two positive numbers. Aiming to prove that the result is never negative, we start with the SE state below as initial SE state (the return value is assigned to the global program variable “result”):
The SE state \((U,C,\varphi )\) given above is valid iff for any Kripke state \(\sigma \) satisfying the path condition C, whenever we execute the program if (y<x) ... ; in \(\sigma \), then in the reached final state the value of program variable \(\mathrm{result}\) is non-negative.
We explain how the SET for the example is constructed by stepwise symbolic execution: Symbolic execution of the first statement (by applying the appropriate calculus rule) splits the SET into the following two new intermediate states:
On each branch, either the body of the then-branch or the else-branch has to be executed, followed by the remaining program. The remaining program is just a single assignment statement here, but could be arbitrarily complex in general. In addition, the path condition in each branch has been extended by the conjunct \(\mathrm{y}<\mathrm{x}\) and its negation, respectively. Continuing symbolic execution on the first branch results in the state

The motivation for state merging becomes very clear now: on each branch the same remaining program has to be executed.
3 The General Lattice Model
Symbolic Execution can be cast as abstract interpretation [11]. Each SE state describes a potentially infinite set of concrete states. As abstract interpretation demands a complete semilattice with join operation, partial order, least and top element, we define a concretization function from SE states to concrete states as well as a partial order relation between SE states.
Definition 5
(Concrete Execution States). A concrete execution state is a pair \(\left( \sigma ,\varphi \right) \) of a Kripke state \(\sigma \) and a formula \(\varphi \) (the program counter).
A concrete execution state for a given program counter assigns to each program variable a concrete value of the universe. We define the semantics of SE states by stipulating a concretization function from SE states to concrete states based on the evaluation function \( val \left( K,\sigma ;\cdot \right) \) (\(\beta \) is not needed as formulas are closed).
Definition 6
(Concretization Function). Let  be an SE state. The concretization function \( concr \) maps s to the set of concrete states
be an SE state. The concretization function \( concr \) maps s to the set of concrete states

The set of concrete states for a symbolic state s contains all pairs of Kripke states \(\sigma '\) and the program counter such that \(\sigma '\) can be reached via some state \(\sigma \) satisfying s’s path condition in some Kripke structure. So the set \( concr \left( s\right) \) contains exactly the concrete states that are described by the SE state s. Consider, for instance, the SE state  : The set of concretizations for this state consists of all pairs \(\left( \sigma ,\varphi \right) \), where \(\sigma \) is any function mapping the program variable \(\mathrm{x}\) to a strictly positive integer.
: The set of concretizations for this state consists of all pairs \(\left( \sigma ,\varphi \right) \), where \(\sigma \) is any function mapping the program variable \(\mathrm{x}\) to a strictly positive integer.
Based on Definition 6, we define a weakening relation expressing that one symbolic execution state describes more concrete states than another one.
Definition 7
(Weakening Relation). Let \(s_{1}\), \(s_{2}\) be two SE states. State \(s_{2}\) is weaker than (a weakening of) \(s_{1}\) (written: \(s_{1}\lesssim s_{2}\)) iff \( concr \left( s_{1}\right) \subseteq concr \left( s_{2}\right) \).
Given a state \(s_1\) with satisfiable path condition, Definitions 6 and 7 imply that a state \(s_{2}\) can only be weaker than \(s_1\) if both have syntactically the same program counter. States with unsatisfiable path condition have an empty set of concretizations and hence are stronger than any other state.
Consider the SE states  and
and  . The set of concretizations of \(s_2\) contains all concrete states of \(s_1\) and additionally all concrete states that map \(\mathrm{x}\) to zero, hence \(s_2\) is a weakening of \(s_1\) (\(s_1\lesssim s_2\)).
. The set of concretizations of \(s_2\) contains all concrete states of \(s_1\) and additionally all concrete states that map \(\mathrm{x}\) to zero, hence \(s_2\) is a weakening of \(s_1\) (\(s_1\lesssim s_2\)).
Consider the SE state  . Although \(s_{1}\) and \(s_{3}\) are syntactically different, all Kripke models coincide on the value of \(\mathrm{x}\) and we would actually prefer to consider them as equal. Hence, we define an extensional equality \(s_{1}\mathop {=}\limits ^{ concr }s_{2}:\Leftrightarrow concr \left( s_{1}\right) = concr \left( s_{2}\right) \) stating that symbolic execution states are equal iff they evaluate to the same set of concrete execution states. Using \(\mathop {=}\limits ^{ concr }\) as equality, we can state the following lemma:
. Although \(s_{1}\) and \(s_{3}\) are syntactically different, all Kripke models coincide on the value of \(\mathrm{x}\) and we would actually prefer to consider them as equal. Hence, we define an extensional equality \(s_{1}\mathop {=}\limits ^{ concr }s_{2}:\Leftrightarrow concr \left( s_{1}\right) = concr \left( s_{2}\right) \) stating that symbolic execution states are equal iff they evaluate to the same set of concrete execution states. Using \(\mathop {=}\limits ^{ concr }\) as equality, we can state the following lemma:
Lemma 1
The weakening relation \(\lesssim \) is a partial order relation.
The core of our formal framework is a family of join-semilattices parametric in a join operation. The partial order induced by the join operation is constrained by the semantic weakening relation, see Definition 7.
Definition 8
(Induced Join-Semilattice of States). Let \(\varphi \in \mathrm {Fml}\) be a closed formula. The carrier set \(S_{\varphi }\) for \(\varphi \) is defined as

A join-semilattice of SE states is a structure \(\left( S_{\varphi },\dot{\sqcup }\right) \) over \(S_{\varphi }\) with operator \(\dot{\sqcup }\) s.t. the semilattice properties (based on \(\mathop {=}\limits ^{ concr }\)) (SEL1)–(SEL3) hold for all \(a,b,c\in S_{\varphi }\):

Furthermore, we require that the partial order relation \(\preceq \) on \(S_{\varphi }\) defined as
satisfies (SEL4) and (SEL5)Footnote 3 for  and
and  :
:

We call  the induced family of join-semilattices for \(\dot{\sqcup }\).
the induced family of join-semilattices for \(\dot{\sqcup }\).
We term (SEL4) correctness since it enables, together with (SEL5), to prove the correctness of our state merging rule (Theorem 1 below). The conservativity property (SEL5) imposes restrictions on merge operations that introduce Skolem constants (thus extending the signature), such as the abstraction technique introduced in Sect. 4.3. Property (SEL5) enforces that the path condition of a merged state is divisible into (1) a formula C without new constants which is implied by the states that are merged (for example, the disjunction of the path conditions of the merged states) and (2) a formula  providing restrictions on the values of the new constants. In addition (3) it must be possible in every structure to assign values to the new constants such that
providing restrictions on the values of the new constants. In addition (3) it must be possible in every structure to assign values to the new constants such that  holds. This is achieved by proving
holds. This is achieved by proving  in the unextended signature of the merged states.
in the unextended signature of the merged states.  may be seen as a (generalized) defining axiom [24] for the
may be seen as a (generalized) defining axiom [24] for the  : we only demand the existence condition
: we only demand the existence condition  and explicitly forgo the uniqueness condition to facilitate abstraction. In summary, (SEL5) allows only “conservative” extensions to a merged path condition. An example for a formula
and explicitly forgo the uniqueness condition to facilitate abstraction. In summary, (SEL5) allows only “conservative” extensions to a merged path condition. An example for a formula  is \(c > 0\), where c is a constant introduced in the merging step. Example 2 (Sect. 4.2) shows a fragment of a join-semilattice induced by a join operation based on the \(\mathsf {if}\left( \cdot \right) \mathsf {then}\left( \cdot \right) \mathsf {else}\left( \cdot \right) \) operator.
is \(c > 0\), where c is a constant introduced in the merging step. Example 2 (Sect. 4.2) shows a fragment of a join-semilattice induced by a join operation based on the \(\mathsf {if}\left( \cdot \right) \mathsf {then}\left( \cdot \right) \mathsf {else}\left( \cdot \right) \) operator.
4 State Merging Techniques
We instantiate our framework with two join operations: the If-Then-Else (ITE) technique, a “classic” of state merging for symbolic execution (e.g., [18, 21, 23]) with full precision; and an abstraction-based technique which trades efficiency with potential loss of precision. To simplify specification of the join operations, we define a pattern that can be instantiated with specific merging techniques.
4.1 A State Merging Pattern
Definition 9
Given two SE states  , \(j=1,2\), with program variables \(\mathrm{x}_{1},\dots ,\mathrm{x}_{n}\in \mathrm {PV}\) of type T occurring in the
, \(j=1,2\), with program variables \(\mathrm{x}_{1},\dots ,\mathrm{x}_{n}\in \mathrm {PV}\) of type T occurring in the  . A merge technique \(M\) defines two functions \(\mathsf {joinVal}\left( s_1,s_2;\mathrm{x},c_{\mathrm{x}}\right) \) and \(\mathsf {constraints}\left( s_1,s_2;\mathrm{x},c_{\mathrm{x}}\right) \) mapping \(s_1\), \(s_2\), program variable \( \mathrm{x} \) and a fresh (for \(\mathrm{x}\)) Skolem constant \( c_{\mathrm{x}} \) to a closed term and a JavaDL formula, respectively. The join operation \(\dot{\sqcup }_M\) is defined by
. A merge technique \(M\) defines two functions \(\mathsf {joinVal}\left( s_1,s_2;\mathrm{x},c_{\mathrm{x}}\right) \) and \(\mathsf {constraints}\left( s_1,s_2;\mathrm{x},c_{\mathrm{x}}\right) \) mapping \(s_1\), \(s_2\), program variable \( \mathrm{x} \) and a fresh (for \(\mathrm{x}\)) Skolem constant \( c_{\mathrm{x}} \) to a closed term and a JavaDL formula, respectively. The join operation \(\dot{\sqcup }_M\) is defined by

where  . To define the terms \(t_i\), let
. To define the terms \(t_i\), let  be fresh Skolem constants of suitable types. Then
be fresh Skolem constants of suitable types. Then

Define  where
where
Condition  holds if
holds if  is evaluated identically in either state and is defined as
is evaluated identically in either state and is defined as

where P is a fresh (for  ) predicate symbol.
) predicate symbol.
The provability relation “\(\vdash \)” in \(\left( \star \right) \) is undecidable, but it can be safely approximated in practice. For example, a prover may simply return “unprovable” after exceeding a fixed time limit. This way soundness is maintained at the cost of completeness due to overapproximation in some situations. The update application of  to \(\left( \bigwedge C_{i}^{ abs }\right) \) allows to take into account relations between values of program variables changed by the merge (e.g., the merge by predicate abstraction for the dist example in Sect. 5). Otherwise, only relations between constants and values before the merge would be reflected.
to \(\left( \bigwedge C_{i}^{ abs }\right) \) allows to take into account relations between values of program variables changed by the merge (e.g., the merge by predicate abstraction for the dist example in Sect. 5). Otherwise, only relations between constants and values before the merge would be reflected.
4.2 The If-Then-Else Technique
Definition 10
(If-Then-Else Merge). Given two SE states  , \(j=1,2\), the join operation \(\dot{\sqcup }_{ ite }\) is defined by
, \(j=1,2\), the join operation \(\dot{\sqcup }_{ ite }\) is defined by

The definition can be generalized by allowing a distinguishing formula for the first argument of the \(\mathsf {if}\left( \cdot \right) \mathsf {then}\left( \cdot \right) \mathsf {else}\left( \cdot \right) \) term instead of \(\bigwedge C_{1}\). It suffices to find a set of sub-conjuncts of \(C_{1}\) whose negation implies \(C_{2}\). Often one can simply choose the guard of the conditional statement which caused the SET to branch.
Proposition 1
The “If-Then-Else Merge” technique induces a family of join-semilattices of SE states, i.e., the operation \(\dot{\sqcup }_{ ite }\) and its associated partial order relation \(\preceq \) satisfy axioms (SEL1)–(SEL5) of Definition 8.
Example 2
Figure 2 depicts a fragment of the join-semilattice \(\left( S_{\varphi },\dot{\sqcup }_{ ite }\right) \) induced by \(\dot{\sqcup }_{ ite }\) for Listing 1. The two states at the bottom of the figure correspond to the outcome of the execution until the end of the if block, where \(\varGamma \) represents a common set of preconditions. Since the values for both \(\mathrm{\_x}\) and \(\mathrm{\_y}\) differ in those states, the If-Then-Else construction is applied. The differing formulas in the path conditions, \(\mathrm{y}<\mathrm{x}\) and \(\mathrm{y}\ge \mathrm{x}\), vanish in the path condition of the merged state since their disjunction can be simplified to \(\mathsf {true}\).
4.3 Abstract Weakening and Predicate Abstraction
Our General Lattice Framework, along with the state merging technique proposed below, at least partially closes the gap between symbolic execution and abstract interpretation [11] by facilitating merges based on abstract domain lattices. We first define the notion of abstract domain elements.
Definition 11
(Abstract Domain Element). An Abstract Domain Element is a function \( defAx :\mathrm {Trm}^{}\rightarrow \mathrm {Fml}\) mapping terms to closed formulas.
Intuitively, an abstract domain element models an infinite set of defining axioms for JavaDL terms. If an axiom is true for a given term, then this term is described by the corresponding abstract domain element. This rather technical, syntactic definition is beneficial for the application in branch merging and allows for a straightforward embedding of predicate abstraction [16]. However, in contrast to predicate abstraction we allow infinite domains.
Definition 12
(Abstract Domain Lattice). An Abstract Domain Lattice is a join-semilattice \(\mathcal {A}_{T}=\left( A_{T},\sqcup \right) \) with the induced partial order relation \(\sqsubseteq \) for a countable set \(A_{T}\) of abstract domain elements accepting terms of some fixed type T as arguments. We impose the following requirements on \(A_{T}\) and \(\sqsubseteq \):
-
(1)
\(A_{T}\) includes two elements with \(\bot \left( t\right) =\mathsf {false}\), \(\top \left( t\right) =\mathsf {true}\) for any \(t\in \mathrm {Trm}^{}\).
-
(2)
For \(a,b\in A_{T}\) with \(a\sqsubseteq b\), \(\mathbin {\vdash }a\left( t\right) \rightarrow b\left( t\right) \) holds for any term t of type T.
-
(3)
For all \(a\in A_{T}\) except for \(\bot \), it holds that \(\vdash \exists v;a\left( v\right) \).
Example 3 below illustrates the above definitions in the context of predicate abstraction. As usual, we have a bottom and a top element, where the bottom element is the only one that is not satisfiable. Furthermore, for each lattice element a that is more concrete than an element b (\(a\sqsubseteq b\)), also the defining axiom of a has to be stronger than that of b. Now we are in a position to generalize the “If-Then-Else Merge” technique: instead of using conditional terms for the result of \(\mathsf {joinVal}\left( s_1,s_2;\mathrm{x},c_{\mathrm{x}}\right) \) as in Definition 10, we compute a sound abstraction of the SE states to be merged. Technically, we employ the symbols \(c_{\mathrm{x}}\) and constrain them by defining axioms computed from a suitable join in the join semi-lattice.
Definition 13
(Abstract Weakening Merge Method). Let \(\mathcal {A}_{T}=\left( A_{T},\sqcup \right) \) be an abstract domain lattice. Given two SE states  , \(j=1,2\), the join operation \( \dot{\sqcup }_{ abstr }\) is defined by
, \(j=1,2\), the join operation \( \dot{\sqcup }_{ abstr }\) is defined by

where, for \(k\in 1,2\), \( defAx _{k}\in A_{T}\) are abstract domain elements such that  is provable and there is no element \( defAx _{k}'\in A_{T}\) with \( defAx _{k}'\ne defAx _{k}\) and \( defAx _{k}'\sqsubseteq defAx _{k}\).
is provable and there is no element \( defAx _{k}'\in A_{T}\) with \( defAx _{k}'\ne defAx _{k}\) and \( defAx _{k}'\sqsubseteq defAx _{k}\).
The constraints on \( defAx _{k}\) state that they must be contained in the abstract domain lattice. There is not necessarily a unique element such that  is provable. Any element for which there is no strictly smaller one suffices. For countable abstract lattices with an enumerable linearization, the functions \( defAx _{k}\) are computable, in particular, for finite domains an enumeration is obtained by topological sorting. For the sign analysis domain, one enumeration is \(\bot ,-,0,+,\top \). Generally, infinite domains should support widening [11] to ensure that suitable abstractions can be computed.
is provable. Any element for which there is no strictly smaller one suffices. For countable abstract lattices with an enumerable linearization, the functions \( defAx _{k}\) are computable, in particular, for finite domains an enumeration is obtained by topological sorting. For the sign analysis domain, one enumeration is \(\bot ,-,0,+,\top \). Generally, infinite domains should support widening [11] to ensure that suitable abstractions can be computed.
In Definition 13 we consider lattices with a uniform type. It is possible to use different lattices for different types in the merge technique. When no lattice is specified for some type, If-Then-Else merges are used as fallback. Depending on the situation, it may also be appropriate to define multiple lattices for the same type (see Example 3 and Fig. 3 for a concrete example for \(\dot{\sqcup }_{ abstr }\)).
Proposition 2
The abstract weakening merge method induces a family of join-semilattices of SE states, i.e. the operation \(\dot{\sqcup }_{ abstr }\) and its associated partial order relation \(\preceq \) satisfy the axioms (SEL1)–(SEL5) of Definition 8.
Abstract domain for Example 3
Predicate abstraction [16] is an instance of abstract weakening where the domain elements are constructed from combinations of a given finite set of unary predicates. The following example defines a domain for predicate abstraction that captures relations between program variables.
Example 3
(Predicate Abstraction as Abstract Domain). Consider Listing 1. To prove that the result is non-negative, we need after the merge (line 7) the fact that the value of y is not smaller than the value of x. To capture this relation among the variables, we choose as abstraction predicates \(v\ge \mathtt {x}\) and \(v\ge 0\), where v is a placeholder for the input term. The resulting abstract domain is built from the conjunctions of all subsets of those predicates, see Fig. 3.
State Merging with Join-Semilattices. The following theorem establishes the correctness of state merges with induced join-semilattices in the course of symbolic execution. We omit the proof for space reasons, and refer the reader to [22].
Theorem 1
(Correctness of Merging with Induced Join-Semilattices). Let \(\varphi \in \mathrm {Fml}\) be a formula and \(\mathbb {L}_{\varphi }\) an induced join-semilattice for a join operation \(\dot{\sqcup }\). Then, merging two SE states  , \(i=1,2\), to a state
, \(i=1,2\), to a state  is sound, i.e. if \(s^*\) is valid, then both \(s_1\) and \(s_2\) are valid.
is sound, i.e. if \(s^*\) is valid, then both \(s_1\) and \(s_2\) are valid.
Example 4
(Continuation of Example 3 ). After symbolic execution of the conditional statement, we are left with two states that have identical program counters. So we can merge them using the abstraction predicates of Example 3 and end up in a single (valid) SE state as shown in Fig. 4.
5 Evaluation

To assess the efficacy of our state merging methods, we implemented them in the KeY verification system and applied them on a micro benchmark suite consisting of four Java programs. We also present the results of a highly complex case study on the TimSort method [15], which has been redone using our implementation.
5.1 Micro Benchmarks
Our micro benchmarks comprise the dist method \(({\rightarrow }\) Listing 1), method abs \(({\rightarrow }\) Listing 2) computing the absolute of a given integer parameter, method gcd \(({\rightarrow }\) Listing 4) computing the Greatest Common Divisor (GCD) of two integers, and method posSum computing the absolute of the sum of two positive integers \(({\rightarrow }\) Listing 3). In the dist example, the SE states after the execution of the if statement are suitable for merging. For abs, where the proof goal is to show that the result is positive, we use state merging after the execution of the if block before Line 5. In the case of gcd, we aim to prove that the returned result is actually the GCD of the input; state merging techniques are applied after Lines 2 and 3. Method posSum demonstrates the application of state merging for a while loop. Our goal is to prove that the returned result is the absolute of the sum of the inputs. To render the SET finite, we constrain the value of \( \mathrm{x} \) by the upper bound 5. Thus, the loop is unwound five times during SE, giving the opportunity of four merges before the call to the method abs in Line 3.
For each example, we compare the number of rule applications in a proof without merging to the corresponding number in a proof containing merge rule applications on the basis of the If-Then-Else as well as the predicate abstraction technique. Results are shown in Table 1. In the last column, the predicates used for abstraction are listed; v is a placeholder for an input term of type \(\mathtt {int}\). The choice for abs induces a standard abstract domain for sign analysis of integers; in the other cases, the predicates are tailored to the specific situations.
The result for dist demonstrates that If-Then-Else merging can even increase the proof size when states are merged close to the end of SE. Merging with predicate abstraction was beneficial in all cases. However, If-Then-Else merging is easy to automate, whereas it is a harder problem to automatically infer abstraction predicates. Furthermore, the TimSort case study affirms that If-Then-Else merges can substantially decrease the sizes of larger proofs.
5.2 TimSort
In 2015, de Gouw et al. [15] discovered a bug in the TimSort implementation of the JDK library, Java’s default sorting routine. The bug triggered, under certain circumstances, an uncaught exception. The authors fixed the bug and proved its absence as well as that of any other uncaught exception. An extended journal version of [15] is currently under preparation, where all verification proofs are being redone using the state merging approach presented in this paper. De Gouw et al. kindly allowed us to include their current results as part of our evaluation.Footnote 4 Table 2 provides a comparison of the proof sizes with and without merging. It shows that the proof sizes improved significantly for most proofs. All merges used, if not stated otherwise, the If-Then-Else technique and thus required no expert knowledge. In particular, state merging allowed to verify the method mergeHi which was out of reach in [15] due to the path explosion problem.
For ensuresCapacity, where merging with If-Then-Else actually increased the proof size, we created a new proof using a merge based on predicate abstraction. The resulting proof size is 15 % smaller compared to the version without merging and even 25 % smaller than the proof with If-Then-Else based merging.
6 Lessons Learned and Future Work
The proposed state merging approach transforms an SET into a connected and rooted Directed Acyclic Graph (DAG). Changing the underlying data structures in a complex verification system such as KeY would be a substantial undertaking. We implemented a different solution by adding the new merge node as a child to only one of the parents and linking the second parent to it. Our implementation ensures that, if the subtree below a merge node is closed (or the merge node is pruned away), then the linked node is also closed (or “unlinked”).
It is important to automate state merging as much as possible, in particular for less complex verification tasks that are otherwise fully automatic. To help this, we extended the specification language JML with the annotation \({ /*@} \,{ merge\_proc <join\_operator> @*/}\). It is placed in front of a Java block after which the merge is supposed to happen. For certain join operators, for example the If-Then-Else join operator, this requires much less expert knowledge than the definition of a block contract, i.e. an annotation of a block of statements with pre- and postconditions, as an alternative way of tackling path explosion.
In our experiments, we discovered that state merging with the If-Then-Else technique is most beneficial when applied in situations where (1) a substantial amount of code remains to be executed, and thus a lot of repetition can be avoided, and (2) the difference between the states to be merged is as small as possible. “Difference” means the number of variables attaining different values in the symbolic states and the number of different formulas in the path conditions.
Predicate abstraction-based state merging is applicable to a wider range of constellations. However, to come up with suitable predicates requires a certain amount of expertise. An unsuitable choice of abstraction predicates can cause the unfeasibility of the proof goal, because abstraction loses precision. At this time, to merge states with predicate abstraction is comparable in difficulty to writing block contracts. Nevertheless, we think that state merging is more suitable for automation, because it can be performed on-the-fly during the proof process. Future work will aim at integrating heuristic approaches to improve the performance of If-Then-Else state merging [21] as well as methods developed for specification generation to automatically infer abstraction predicates [17, 25].
7 Related Work and Conclusion
Existing work on state merging in symbolic execution employs If-Then-Else based techniques [2, 18, 21, 23] or addresses the automatic generation of loop invariants by the means of abstraction [6, 25]. Kuznetsov et al. [21] try to assess the “cost-benefit ratio” of If-Then-Else based merges by heuristically trading off the reduction of states against the complexity of the resulting expressions. Bubel et al. [6] use value abstraction and Weiß et al. [25] use predicate abstraction for merging states in the course of the automatic generation of loop invariants.
In contrast to previous work, our approach is not limited to a particular state merging technique. We devised a general lattice-based framework for join operations and proved soundness of a state merging rule for join operations conforming to our framework. The two most popular state merging techniques in the literature, If-Then-Else and predicate abstraction, are instances of our framework. Our implementation is based on the state-of-the-art verification system KeY [1]. It has been extensively evaluated with the highly complex TimSort case study and it was demonstrated that significant improvements can be gained. This led to proofs that were out of reach before.
Notes
- 1.
- 2.
Our notion of Kripke structure is derived from that commonly used in modal logic [13] and slightly differs from the one often used in model checking. E.g., we require no fixed set of initial states, and the labeling function is given implicitly by the interpretation and Kripke state which is natural for imperative programs. There is no essential difference, however.
- 3.
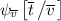 denotes the substitution of the terms \({\overline{t}}\) for the free variables \({\overline{v}}\) in \(\psi _{{\overline{v}}}\).
denotes the substitution of the terms \({\overline{t}}\) for the free variables \({\overline{v}}\) in \(\psi _{{\overline{v}}}\). - 4.
Available at http://www.key-project.org/timsort/stats.html.
References
Ahrendt, W., et al.: The KeY platform for verification and analysis of Java programs. In: Giannakopoulou, D., Kroening, D. (eds.) VSTTE 2014. LNCS, vol. 8471, pp. 55–71. Springer, Heidelberg (2014)
Anand, S., Godefroid, P., Tillmann, N.: Demand-driven compositional symbolic execution. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 367–381. Springer, Heidelberg (2008)
Anand, S., Păsăreanu, C.S., Visser, W.: Symbolic execution with abstract subsumption checking. In: Valmari, A. (ed.) SPIN 2006. LNCS, vol. 3925, pp. 163–181. Springer, Heidelberg (2006)
Beckert, B., Hähnle, R.: Reasoning and verification. IEEE Intell. Syst. 29(1), 20–29 (2014)
Beckert, B., Hähnle, R. (eds.): Verification of Object-Oriented Software: The KeY Approach. Springer, Berlin (2006)
Bubel, R., Hähnle, R., Weiß, B.: Abstract interpretation of symbolic execution with explicit state updates. In: Boer, F.S., Bonsangue, M.M., Madelaine, E. (eds.) FMCO 2008. LNCS, vol. 5751, pp. 247–277. Springer, Heidelberg (2009)
Burstall, R.M.: Program proving as hand simulation with a little induction. In: Information Processing, pp. 308–312. Elsevier (1974)
Cadar, C., Sen, K.: Symbolic execution for software testing: three decades later. Commun. ACM 56(2), 82–90 (2013)
Chu, D.-H., Jaffar, J., Murali, V.: Lazy symbolic execution for enhanced learning. In: Bonakdarpour, B., Smolka, S.A. (eds.) RV 2014. LNCS, vol. 8734, pp. 323–339. Springer, Heidelberg (2014)
Clarke, E.M., Grumberg, O., et al.: Model Checking. The MIT Press, Cambridge (1999)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: 4th Symposium of POPL, pp. 238–252. ACM Press, January 1977
Fitting, M.C.: First-Order Logic and Automated Theorem Proving, 2nd edn. Springer, Berlin (1996)
Fitting, M.C., Mendelsohn, R.: First-Order Modal Logic. Kluwer, Dordrecht (1998)
Gosling, J., Joy, B., et al.: The Java (TM) Language Specification, 3rd edn. Addison-Wesley Professional, Wokingham (2005). http://psc.informatik.uni-jena.de/languages/Java/javaspec-3.pdf
de Gouw, S., Rot, J., de Boer, F.S., Bubel, R., Hähnle, R.: OpenJDK’s Java.utils.Collection.sort() is broken: the good, the bad and the worst case. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 273–289. Springer, Heidelberg (2015)
Graf, S., Saidi, H.: Construction of abstract state graphs with PVS. In: Grumberg, O. (ed.) CAV 1997. LNCS, vol. 1254, pp. 72–83. Springer, Heidelberg (1997)
Hähnle, R., Wasser, N., et al.: Array abstraction with symbolic pivots. In: Ábrahám, E., Bonsangue, M., et al. (eds.) Theory and Practice of Formal Methods. LNCS, vol. 9660, pp. 104–121. Springer, Berlin (2016)
Hansen, T., Schachte, P., Søndergaard, H.: State joining and splitting for the symbolic execution of binaries. In: Bensalem, S., Peled, D.A. (eds.) RV 2009. LNCS, vol. 5779, pp. 76–92. Springer, Heidelberg (2009)
Harel, D., Tiuryn, J., et al.: Dynamic Logic. MIT Press, Cambridge (2000)
King, J.C.: Symbolic execution and program testing. Commun. ACM 19(7), 385–394 (1976)
Kuznetsov, V., Kinder, J., et al.: Efficient state merging in symbolic execution. In: Proceedings of the 33rd Conference on PLDI, pp. 193–204. ACM (2012)
Scheurer, D.: From trees to DAGs: a general lattice model for symbolic execution. Master’s thesis, Technische Universität Darmstadt (2015). http://tinyurl.com/Trees2DAGs
Sen, K., Necula, G., et al.: MultiSE: multi-path symbolic execution using value summaries. In: 10th Joint Meeting on Foundations of Software Engineering, pp. 842–853. ACM (2015)
Shoenfield, J.R.: Mathematical Logic. Addison-Wesley, Wokingham (1967)
Weiß, B.: Predicate abstraction in a program logic calculus. In: Leuschel, M., Wehrheim, H. (eds.) IFM 2009. LNCS, vol. 5423, pp. 136–150. Springer, Heidelberg (2009)
Acknowledgment
We would like to thank the authors of [15] for the permission to quote data from the extended journal version of their paper under preparation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Scheurer, D., Hähnle, R., Bubel, R. (2016). A General Lattice Model for Merging Symbolic Execution Branches. In: Ogata, K., Lawford, M., Liu, S. (eds) Formal Methods and Software Engineering. ICFEM 2016. Lecture Notes in Computer Science(), vol 10009. Springer, Cham. https://doi.org/10.1007/978-3-319-47846-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-47846-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47845-6
Online ISBN: 978-3-319-47846-3
eBook Packages: Computer ScienceComputer Science (R0)





 uses a parallel update to exchange the values of
uses a parallel update to exchange the values of 



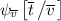 denotes the substitution of the terms
denotes the substitution of the terms