Batch and Online Mixture Learning: A Review with Extensions

Abstract

This paper addresses the problem of learning online finite statistical mixtures of regular exponential families. We first start by reviewing concisely the gradient-based and stochastic gradient-based optimization methods and their generalizations. We then focuses on two stochastic versions of the celebrated Expectation-Maximization (EM) algorithm: Titterington’s second-order stochastic gradient EM and Cappé and Moulines’ online EM. Depending on which step of EM is approximated, the possible constraints on the mixture parameters may be violated. A justification of these approaches as well as ready-to-use formulas for mixtures of regular exponential families are provided. Finally, to illustrate our study, some experimental comparisons on univariate normal mixtures are provided.

1 Introduction

Mixture models $f(x; \theta )$ are a powerful and flexible tool to approximate any unknown smooth probability density function $\pi$ as a finite convex combination of parametric density functions $g_{j}(x;\theta _{j})$:

$$\begin{aligned} \pi (x) \approx f(x; \theta ) = \sum _{j=1}^{K} w_{j} g_{j}(x;\theta _{j}), \text{ with } w_{j} > 0 \text{ and } \sum _{j=1}^{K} w_{j} = 1, \end{aligned}$$

(1)

where $K\in \mathbb {N}$ denotes the number of components of the mixture. Fitting such a kind of semi-parametric model amounts to find a “good” candidate within a parametric family of distributions $\mathcal {F}_\theta$ defined by a set of parameters $\theta$. Among all those distributions, the closest candidate in $\mathcal {F}_\theta$ to $\pi$ will be denoted $f^*$ (related to the approximation error). Figure 1 depicts the case of a density of a continuous random variable modeled as a mixture of three univariate normal components.

Fig. 1

Approximating an unknown distribution $\pi$ (black curve) with a mixture distribution $f(x; \theta )$ (blue curve) of three normal component distributions ($K=3$, dashed magenta curves) (color figure online)

This mixture learning task received much attention in the literature since it is a core operation for both theoretical purposes, and it is widely used in many applications. Classically, one may distinguish two main approaches:

• 1. Maximum Likelihood Estimation (MLE), and

• 2. Bayesian Learning.

While the former approach gives a point estimate of mixture parameters, the latter considers the posterior distribution of the parameters given a prior distribution on them. In this work, we restrict ourselves to the MLE approach since it is by far the most popular approach.

Consider a random sample $\chi =\{x_{i}\}_{i=1}^{N}$ of N independent and identically distributed (iid) observations from $\pi$. Under this assumption, the joint probability of set $\chi$ regarding a particular value for $\theta$ is simply $f(\chi ; \theta )=\prod _i f(x_i; \theta )$. Viewing $\chi$ as a fixed set and $\theta$ as a parameter vector, the maximum likelihood estimator (MLE) $\hat{\theta }^{(N)}$ is defined as the maximizer of the likelihood, or equivalently of the average log-likelihood:

$$\begin{aligned} \bar{l}(\theta ; \chi ) = N^{-1} \sum _{i=1}^{N} \log f(x_{i};\theta ) = N^{-1} \sum _{i=1}^{N} \log \left( \sum _{j=1}^{K} w_{j} g_{j} (x_{i};\theta _{j})\right) . \end{aligned}$$

(2)

In the remainder of this chapter, we will discuss the case when sample $\chi$ is not fully known in a whole. That is, we shall consider that the observations $x_{i}$ are available one after another (e.g. in the data stream model, useful for dealing with very large data sets). Thus online methods differ from batch methods, and ideally aim to get same convergence and efficiency properties as batch ones while having a single pass over the full dataset. This topic receives increasing attention due to the recent challenges associated to massive datasets.

2 Online Learning with Gradient-Based Methods

In this section, we recall the basics of gradient-based optimization and of stochastic approximation. Most of the content below comes from the paper (Bottou 1998; Amari 1997; Bottou and Bousquet 2011).

2.1 Gradient-Based Optimization

The maximization of $\bar{l}$ takes the form of a sum-minimization problem (M-estimation):

$$C_N(\theta ) = N^{-1}\sum _{i=1}^N C(x_i, \theta )$$

for the loss function $C(x, \theta ) = -\log f(x; \theta )$. The empirical risk $C_N(\theta )$ evaluated on sample $\chi$ of size N is an approximation of the expected risk

$$C(\theta ) = \mathbb {E}_{\pi }[C(x, \theta )]. $$

The iterative minimization of the empirical risk with a batch gradient descent (GD) takes the following form:

$\underline{\text {At }\text {iteration }t}$:

$$\begin{aligned} \boxed {\hat{\theta }^{(t+1)} = \hat{\theta }^{(t)} - \alpha ^{(t)} R^{-1}(\hat{\theta }^{(t)}) \underbrace{N^{-1} \sum _{i=1}^{N} \nabla _{\theta } C(x_i,\hat{\theta }^{(t)})}_{\nabla C_N(\hat{\theta }^{(t)})}} \end{aligned}$$

(3)

where $\hat{\theta }^{(t)}$ is the parameter estimates, $\alpha ^{(t)}$ is the learning rate, and positive definite matrix $R\succ 0$ a rescaling matrix. When R is chosen as the identity matrix, this amounts to ordinary first-order gradient ascent. For $R=\nabla ^2 C_N$ chosen as the hessian matrix of $C_N$, this defines the Newton–Raphson method for finding extrema. Since naïve versions of these methods involve costly operations at each iteration (computation of gradients, hessians for all observations and a matrix inversion), quasi-newton methods (e.g., L-BGFS) which approximate the inverse of hessians are generally preferred.

When the parameter space $\varTheta$ is a Riemannian manifold with tensor metric G, the direction of the steepest descent at $\theta$ is given by the natural gradient (Amari 1997, 1998, 2016):

$$\begin{aligned} \tilde{\nabla }_{\theta } C_N(\theta ) \mathop {=}\limits ^{\cdot }G^{-1}(\theta ) \nabla _{\theta } C_N(\theta ) \end{aligned}$$

(4)

So, picking $R(\hat{\theta }^{(t)})$ as $G(\hat{\theta }^{(t)})$ defines the natural gradient descent method (Amari 1998).

In information geometry, a D-dimensional parametric exponential or mixture family has a dually flat structure (Amari 2016) induced by a convex potential function F with a canonical divergence a Bregman divergence (with convex generator defined modulo an affine term). The convex function induced two dual coordinate systems $\theta$ and $\eta$ such that $\eta =\nabla F(\theta )$ and $\theta =\nabla F^*(\eta )$, where $F^*$ is the Legendre convex conjugate (Amari 2016). In a dually flat space, the dual basis vectors $e^i=\partial _i=\frac{\partial }{\partial \eta _i}$ and $e_j=\partial ^j=\frac{\partial }{\partial \theta ^j}$ are orthogonal since ${\langle e^i,e_j \rangle }=\delta _j^i$ (with $\delta _j^i=1$ iff $i=j$, and 0 otherwise). We can define a mixed coordinate system (Amari 2016, p. 144) $\xi$ by choosing the first k components from the $\theta$-coordinate system and the $D-k$ remaining coordinates from the $\eta$-coordinate system. Then then Riemannian metric G in this mixed coordinate system has a block-diagonal structure by construction:

$$ G= \left[ \begin{array}{cc}g_{ij} &{} 0 \\ 0 &{} g^{lm} \end{array}\right] , $$

where $g_{ij}={\langle e_i,e_j \rangle }$ and $g^{lm}={\langle e^l,e^m \rangle }$.

It follows that when $D=2$, the mixed coordinate systems always ensure a diagonal Riemannian (Fisher information) matrix (see Miura (2011) for an example of such parameter orthogonalization). Computing the inverse $G^{-1}$ of a diagonal matrix $G=\mathrm {diag}(a_{11}, \ldots ,a_{DD})$ is fast since $G^{-1}=\mathrm {diag}(a_{11}^{-1},\ldots ,a_{DD}^{-1})$, and the gradient-based optimization efficient. However,

Note that the ordinary gradient is obtained for $G=I$ (the identity matrix), and it makes sense to consider this natural gradient updating rule since $\Delta ^{(t+1)}=\theta ^{(t+1)}-\theta ^{(t)}$ is a contravariant vector and $\nabla l$ is a covariant derivative. Therefore in the natural gradient, the factor $G^{-1}$ converts a covariant to contravariant vector (Amari 1997).

2.2 Stochastic Gradient Descent Methods

While batch methods have good convergence properties (linear or quadratic), their costs in time and memory is prohibitive when the sample size increases. During the last decade, stochastic methods for optimization (especially those based on GD) have been proven to be very effective in the situation.

Following the seminal work of Robbins and Monro (1951), the observations $\nabla _{\theta } C(x_1, \theta )$, $\nabla _{\theta } C(x_2, \theta ), \ldots$ can be considered as “noise corrupted” ones of $\nabla _{\theta } C(\theta )$ for which a root $\theta ^*$ is searched. Under the assumptions that learning rates $\alpha ^{(t)}$ satisfy $\sum _{t\ge 0}\alpha ^{(t)} =\infty$ (diverge) and $\sum _{t\ge 0}{\alpha ^{(t)}}^2 < \infty$ (converge), they proved that the sequence $\hat{\theta }^{(0)}, \hat{\theta }^{(1)}, \ldots$ in Eq. 5 converges almost surely to $\theta ^*$. This method is referred in the literature as the Stochastic Gradient Descent (SGD):

$\underline{\text {At } \text {iteration }t}$:

$$\begin{aligned} \boxed {\hat{\theta }^{(t+1)} = \hat{\theta }^{(t)} - \alpha ^{(t)} R(\hat{\theta }^{(t)})^{-1} \nabla _{\theta } C(x_{t},\hat{\theta }^{(t)})} \end{aligned}$$

(5)

Again, if the parameter space has a non-Euclidean Riemannian structure, it is preferable to use the stochastic natural gradient descent (SNGD).

$\underline{\text {At } \text {iteration }t}$:

$$\begin{aligned} \boxed {\hat{\theta }^{(t+1)} = \hat{\theta }^{(t)} - \alpha ^{(t)} \tilde{\nabla }_{\theta } C(x_{t},\hat{\theta }^{(t)})} \end{aligned}$$

(6)

One strength of the natural gradient descent for online learning besides its invariance under reparameterization is that is it provably Fisher efficient (Amari 1997, 2016), meaning that it meets asymptotically the Cramér-Rao lower bound Amari (2016).

There exist many extensions to this algorithm. In the sequel, we report some old and new heuristics:

(Minibatch SGD):

In order the reduce the variance in the parameter update, the gradient of C may be estimated from a limited sample $B_{t}$ (a.k.a. mini-batch, see Sculley 2010). Since this mini-batch is created at each iteration (successive picks in the stream or through the sampling without replacement from $\chi$), the resulting estimate is also a noisy observation of $\nabla _{\theta } C(\hat{\theta }^{(t)})$.

$\underline{\text {At } \text {iteration }t}$:

$$\begin{aligned} \boxed {\hat{\theta }^{(t+1)} = \hat{\theta }^{(t)} - \alpha ^{(t)} |B_{t}|^{-1}\sum _{x \in B_{t}} \nabla _{\theta } C(x,\hat{\theta }^{(t)}) } \end{aligned}$$

(7)

(Momentum SGD):

Another strategy for regularizing the parameter update consists in doing a convex combination between the previous update and the gradient.¹

$\underline{\text {At } \text {iteration }t}$:

$$\begin{aligned} \boxed {\begin{aligned} \Delta ^{(t+1)}&= \epsilon ^{(t)}\Delta ^{(t)} - \alpha ^{(t)} \nabla _{\theta } C(x_t,\hat{\theta }^{(t)})\\ \hat{\theta }^{(t+1)}&= \hat{\theta }^{(t)} +\Delta ^{(t+1)} \end{aligned}} \end{aligned}$$

(8)

Doing such modification enforces velocity vector $\Delta$ to accumulate directions of steepest descent. Momentum coefficient $\epsilon ^{(t)}$ is an additional hyper-parameter which has to be set in [0, 1]. A popular setting of $\epsilon$ consists in taking it around 0.5 in the warmup phase (initial learning) then to increase it towards 0.9 simultaneously to the iterations to enforce the stability of the update.

Better methods have been proposed when a sequence of gradients or parameters over iterations is used. This leads the following heuristics:

(Average SGD):

Polyak–Ruppert averaging Polyak and Juditsky (1992) refers to a post-processing method where a second sequence $\bar{\theta }^{(0)}, \bar{\theta }^{(1)}, \ldots$ is generated by averaging estimates after $t_0$ iterations:

$$\begin{aligned} \bar{\theta }^{(t)} = {\left\{ \begin{array}{ll} \hat{\theta }^{(t)} &{} t \le t_0,\\ \frac{1}{t-t_0} \sum _{t'=t_0+1}^t \hat{\theta }^{(t')} &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(9)

In practice, recursive reformulations are always preferable since it avoids a significant memory cost.

$\underline{\text {At } \text {iteration }t}$:

$$\begin{aligned} \boxed {\begin{aligned} \hat{\theta }^{(t+1)}&= \hat{\theta }^{(t)} - \alpha ^{(t)} R(\hat{\theta }^{(t)})^{-1} \nabla _{\theta } C(x_{t},\hat{\theta }^{(t)})\\ \bar{\theta }^{(t+1)}&= \left( (t-t_0)~\bar{\theta }^{(t)} + \hat{\theta }^{(t+1)}\right) / (t-t_0+1) \text{ if } t > t_0 \end{aligned}} \end{aligned}$$

(10)

There are many policies for setting $\alpha ^{(t)}$. The original proposition in Robbins and Monro (1951) is to pick $\alpha ^{(t)} = t^{-1}$ which meets the requirements mentioned before. Nowadays, a classical setting is $\alpha ^{(t)} = \alpha ^{(0)}(1 + C t)^{-1}$ where $\alpha ^{(0)}$ and C are prescribed constants. Because the convergence of the optimization depends strongly on these constants, several authors suggest to re-evaluate them periodically using a small validation dataset (different from the training set).

(Adam):

This method (named after adaptive moment estimation) is a first-order method which use estimates of first and second moments of the gradient with respect to each parameter to estimate.

$\underline{\text {At } \text {iteration }t}$:

(11)

The first two steps consist in estimating moments of the gradient using exponential moving averages (the symbol $^{\circ j}$ denotes the Hadamard power) then correct their biases. The biais correction are mandatory since the $m_1$ and $m_2$ are initialized as 0’s vectors. Note that the learning rate is adapted for each parameter independently. One of the most appealing property of this method is that the magnitudes of parameter updates are invariant to rescaling of the gradient and are controlled by hyperparameter $\alpha$ (the term $\hat{m}_1 / \left( \sqrt{\hat{m}_2} + \epsilon \right)$ is unitless).

2.3 From Batch Learning to Online Learning

Observe that the previous methods (except Minibatch SGD) which do not need to remember previous observations are suitable for on-the-fly processing: the iteration number t becomes the observation number N. In such a case, since the examples are randomly drawn from the ground truth distribution $\pi$, the expected risk $C(\theta )$ is directly minimized. Note that the same methods applied to $\chi$, a sample from $\pi$, lead to the minimization of $\mathbb {E}_{\pi _N}[C(x, \theta )]$ over an empirical distribution $\pi _N$ with distribution:

$$ \pi _N(x) = \frac{1}{N} \sum _{i=1}^N \delta _{x_i}(x), $$

where $\delta _x$ is the Dirac measure.

In order to prevent overfitting, the empirical risk is classically replaced by a regularized risk where a $L_1$ or $L_2$ penalty term is added. From the implementation perspective, a fixed dataset $\chi$ may be processed seamlessly as a data stream using function generators of modern programming languages (e.g. Python). Such kind of functions is able to yield an observation on demand by repeating infinitely $\chi$ (with shuffle). Also, let us mention that the parallelization of optimization techniques remains a very active research field leading to sophisticated hardware and software architectures.

3 Online Mixture Modelling

Before dealing with mixtures of multiple components, the simpler special case of a single component mixture is first discussed below.

3.1 Online Learning with a Single Component

Consider the case when $f = g_1$ is a (regular) exponential family (EF), that is f may be decomposed as

$$\begin{aligned} f(x;\theta ) = \exp \left\{ \langle \theta ,s(x)\rangle + k(x) - F(\theta )\right\} \end{aligned}$$

(12)

where $\theta$, s, k, F are respectively the natural parameters, the sufficient statistics, the carrier measure, the log-partition function (see Nielsen and Garcia (2009) for further definitions). Most common distributions (but not the uniform, heavy-tailed Student t-, and Cauchy distributions) are regular exponential families: Gaussian, Dirichlet, Multinomial (including the categorical distribution), von Mises-Fisher, Wishart, Rayleigh, etc.

In case of EF, the loss function $C(x,\theta )$ takes the following expression:

$$\begin{aligned} C(x, \theta ) = -\log f(x; \theta ) = - \langle \theta ,s(x) \rangle - k(x) + F(\theta ) \end{aligned}$$

(13)

The MLE $\hat{\theta }^{(N)}$ is given analytically by differentiating $C_N(\theta )$ with respect to $\theta$:

$$\begin{aligned} \nabla F(\hat{\theta }^{(N)}) = \frac{1}{N} \sum _{i=1}^{N} s(x_i) \longrightarrow \hat{\theta }^{(N)} = (\nabla F)^{-1} \left( \frac{1}{N} \sum _{i=1}^{N} s(x_i)\right) \end{aligned}$$

(14)

The functional reciprocal $(\nabla F)^{-1}$ of $\nabla F$ is generally available in an explicit formula for most (but not all) EF. It corresponds to the gradient of the dual Legendre convex conjugate (Nielsen and Garcia 2009): $(\nabla F)^{-1}=\nabla F^*$. The Fisher information matrix $I(\theta )$ of a regular exponential family is the Hessian of the log-normalizer:

$$ I(\theta )=-E_\theta [\nabla ^2\log f(x;\theta )]=\nabla ^2 F(\theta )\succ 0, $$

a positive-definite matrix for all $\theta \in \varTheta$, where $\varTheta$ denotes the natural parameter space. When switching to the online case, it is interesting to get an exact expression of the MLE by a recursive formulation of the average of the sufficient statistics. For that, it suffices to keep the sum of the previous sufficient statistics and update as:

$$\begin{aligned}&\hat{\theta }^{(N+1)} =&(\nabla F)^{-1} \left( \frac{\{\sum _{i=1}^{N} s(x_{i})\} + s(x_{N+1})}{N+1}\right) \end{aligned}$$

(15)

$$\begin{aligned} \text{ or } \text{ equivalently }&(\nabla F)^{-1} \left( \frac{N\nabla F(\hat{\theta }^{(N)}) + s(x_{N+1})}{N+1}\right) \end{aligned}$$

(16)

The recursion in Eq. 5 appears more clearly when this formula is written in the Expectation parameter space H (Nielsen and Garcia 2009). Let $\eta =\nabla F(\theta )$. The recursive computation of the exact MLE is then given by²:

$$\begin{aligned} \hat{\eta }^{(N+1)} = \hat{\eta }^{(N)} + \{N+1\}^{-1} (s(x_{N+1}) - \hat{\eta }^{(N)}) \text{ and } \hat{\eta }^{(0)}=0. \end{aligned}$$

(17)

It is of interest to compare this expression to the one given by the SGD update (Eq. 5) on natural parameter space $\varTheta$:

$$\begin{aligned} \hat{\theta }^{(N+1)} = \hat{\theta }^{(N)} + \alpha ^{(N+1)} \left( s(x_{N+1}) - \nabla _{\theta } F (\hat{\theta }^{(N)})\right) \end{aligned}$$

(18)

For the same optimization but in the expectation space H, recall the bijection between exponential families and Bregman divergences (Banerjee et al. 2005):

$$\begin{aligned} \log f(x; \eta ) = -B_{F^*}(s(x) : \eta ) +F^*(s(x)) + k(x), \end{aligned}$$

(19)

where $B_{F^*}$ is the Bregman divergence associated with $F^*$, the convex conjugate of F. It follows that maximizing the loss function $C(\eta ) = \mathbb {E}_{\pi }[-\log f(x;\eta )]$ leads to the following computation:

$$\begin{aligned} - \nabla _{\eta } \log f(x; \eta )&= \nabla _{\eta } B_{F^*}(s(x) : \eta ) \nonumber \\&= - \nabla _{\eta } F^*(\eta ) - \nabla _{\eta } \langle s(x) - \eta , \nabla _{\eta } F^*(\eta ) \rangle \nonumber \\&= - H(F^*)(\eta ) (s(x) - \eta ) \end{aligned}$$

(20)

where $H(F^*)(\eta )$ is the hessian of $F^*$ at observed point $\eta$. Thus, the minimization of $C(\eta )$ with the stochastic gradient descent on H takes the following form:

$$\begin{aligned} \hat{\eta }^{(N+1)} = \hat{\eta }^{(N)} + \alpha ^{(N+1)} H(F^*)(\hat{\eta }^{(N)}) (s(x_{N+1}) - \hat{\eta }^{(N)}) \end{aligned}$$

(21)

Section 4 of this chapter gives an empirical comparison of Eqs. 17, 18 and 21.

To conclude this part, recall that for a regular exponential family, the natural parameter space $\varTheta$ is an open convex space, and F is strictly convex and differentiable function. It follows that f is a log-concave function and that $-\log f$ is a convex function. Since we consider data stream of many different observations, we are not concerned by the problem of existence of the MLE (see Bogdan and Bogdan (2000) for a rigorous treatment of that point) in Algorithm 1.

When f does not belong to an exponential family, its mathematical properties have to be studied (especially convexity, convex relaxations, etc) and numerical methods are often required (see previous section or Shalev-Shwartz 2011).

3.2 Batch Mixture Learning with Multiple Components

Before carrying on with details of online mixture learning methods, let us first recall the basics of Expectation-Maximization algorithm (EM) in the next subsection.

Batch mixture learning with EM For $K>1$, the direct maximization of $\bar{l}$ is a difficult problem since $\log f$ is the logarithm of the sum of multiple terms (${-}\log f$ is no more convex). However it can be made easier if we know the component, let say $z_{i}$, which have generated $x_{i}$. This mechanism, called data augmentation, amounts to introduce a latent (unobservable) random variable.

Let $Z_{i}$ be a categorical random variable over $1,\ldots ,K$ whose parameters are $\{w_{j}\}_{j}$, that is, $Z_{i} \sim \mathrm {Cat}_{K}(\{w_{j}\}_{j})$. Also, assuming that $X_{i}|Z_{i}=j \sim g_{j}(\cdot ;\theta _{j})$, the unconditional mixture distribution f in Eq. 1 is recovered by marginalizing their joint density p over $Z_{i}$ (i.e. $f (x) = \sum _z p(x,z)$). Obviously, $Z_{i}$ is a latent (unobservable) variable so that the realizations $x_{i}$ of $X_{i}$ (resp. $(x_{i},z_{i})$ of $(X_{i}, Z_{i})$) is often viewed as an incomplete (resp. complete) data observation. Alternatively, we may consider that $Z_{i}$ is a random vector $[Z_{i,1}, Z_{i,2}, \ldots , Z_{i,k}]$ where $Z_{i,j}=1$ iff. $X_{i}$ arises from the j-th component of the mixture and 0 otherwise. Thus, $Z_1,\ldots ,Z_{N}$ are unconditionally distributed according to the multinomial law $\mathcal {M}_{K}(1,\{{w}_{j}\}_{j})$ which is an exponential family.

Similarly to Eq. 2, the average complete log-likelihood function can be written as:

$$\begin{aligned} \bar{l}_c(\theta ; \chi _{c})= & {} N^{-1} \sum _{i=1}^{N} \log p(x_i,z_i;\theta ) = N^{-1} \sum _{i=1}^{N} \log \prod _{j=1}^{K} \left( w_{j} g_j (x_{i};\theta _{j})\right) ^{z_{i,j}} \nonumber \\= & {} N^{-1} \sum _{i=1}^{N} \sum _{j=1}^{K} z_{i,j} \log (w_{j} g_j (x_{i};\theta _{j})) \end{aligned}$$

(22)

where $\chi _{c}=\{(x_{i}, z_{i})\}_{i=1}^{N}$, is the set of complete data observations.

Here comes the EM algorithm (cf. Algorithm 2) which optimizes $\bar{l}(\theta ; \chi )$ (proofs in Dempster et al. 1977; Robbins and Monro 1951; Titterington 1984; Amari 1997, 1998, 2016; Miura 2011; Cappé and Moulines 2009; Neal and Hinton 1999) by repeating two steps until convergence:

• Compute the conditional expectation of missing values

  $$\begin{aligned} \mathcal {Q}(\theta ;\hat{\theta }^{(t)}, \chi )&:= \mathbb {E}_{\hat{\theta }^{(t)}}[\bar{l}_c(\theta ; \chi _{c}) |\chi ]\\&= N^{-1} \sum _{i=1}^{N} \sum _{j=1}^{K} \mathbb {E}_{\hat{\theta }^{(t)}}[Z_{i,j}|X_{i}=x_{i}] \log (w_{j} g_j (x_{i};\theta _{j})) \end{aligned}$$

• Maximize $\mathcal {Q}(\theta ;\hat{\theta }^{(t)}, \chi )$ over $\theta$.

Remark that while $\hat{w}_{j}^{(t+1)}$ is always known in closed-form whatever the chosen $g_j$, $\hat{\theta }_{j}^{(t+1)}$ are obtained by component-wise specific optimization involving all observations. More generally, the improvement of $\bar{l}(\theta ; \chi )$ is guaranteed whatever the increase of $\mathcal {Q}$ is in the M-Step. This leads to the Generalized EM algorithm (GEM) when partial maximization (i.e., not necessarily global optimization) is performed.

Batch mixture learning with EM and EF Consider now the case when all the $g_j$’s are exponential families (EF, e.g. gaussians densities or generalized gaussians densities). The joint density p(x, z) may be decomposed as follows:

$$\begin{aligned} \log p(x,z;\theta )&= \sum _{j=1}^K [z=j] \{\log (w_j) + \log g_j(x;\theta _j)\}\\&= \sum _{j=1}^K [z=j] \{\log (w_j) + \langle \theta _j, s_j(x) \rangle + k_j(x) - F_j(\theta _j)\}\\&= \sum _{j=1}^K \left\langle \begin{pmatrix} [z=j] \\ [z=j]~s_j(x)\end{pmatrix}, \begin{pmatrix}\log w_j - F_j (\theta _j)\\ \theta _j\end{pmatrix} \right\rangle + \sum _{j=1}^K [z=j]~k_j(x)\\&= \langle s(x,z), \theta _c \rangle + \sum _{j=1}^K [z=j]~k_j(x) \end{aligned}$$

where $[z=j]$ denotes the Iverson’s bracket,

$$\begin{aligned} s(x,z):= & {} ([z=1], [z=1]~s_1(x),&\ldots ,&[z=K], [z=K]~s_K(x))^T\end{aligned}$$

(25)

$$\begin{aligned} \theta _c:= & {} (\log w_1-F_1(\theta _1),\theta _1,&\ldots ,&\log w_K-F_K (\theta _K),\theta _K)^T \end{aligned}$$

(26)

Note that notation $\theta _c$ may be considered as ambiguous but in the paper the subscript j always refers to component-specific parameters. One can then recognize the form of an exponential family. Then, it follows very simple expressions for $\bar{l}_c$ and $\mathcal {Q}$:

$$\begin{aligned} \bar{l}_c(\theta ; \chi _{c}) = N^{-1} \sum _{i=1}^{N} \langle s(x_i,z_i), \theta _c \rangle + N^{-1} \sum _{i=1}^{N} \sum _{j=1}^K z_{i,j} ~k_j(x_i) \end{aligned}$$

(27)

$$\begin{aligned} \nonumber \mathcal {Q}(\theta ;\hat{\theta }^{(t)}, \chi ) =&N^{-1} \sum _{i=1}^{N} \langle \mathbb {E}_{\hat{\theta }^{(t)}}\left[ s(X_i,Z_i)|X_{i}=x_{i}\right] , \theta _c \rangle + \\&N^{-1} \sum _{i=1}^{N} \sum _{j=1}^K \mathbb {E}_{\hat{\theta }^{(t)}}\left[ Z_{i,j}|X_{i}=x_{i}\right] ~k_j(x_i) \end{aligned}$$

(28)

Since the second term is irrelevant (i.e., a constant) to the maximization $\mathcal {Q}$, the EM algorithm for such distributions can be reformulated with sufficient statistics for complete data. The E-Step amounts to compute the vector $\hat{S}^{(t)}$, the empirical average of the conditional expectation of sufficient statistics for complete data (see Eq. 30). The M-Step consists in finding the value $\theta _c$ which maximizes the inner product with $\hat{S}^{(t)}$ (see Eq. 31). If this mapping is denoted by $\theta ^\dagger : H \mapsto \varTheta$, the EM algorithm for the mixture of EF can be written in one recurring formula:

$$\begin{aligned} \hat{S}^{(t+1)} = N^{-1}\sum _{i=1}^{N}\mathbb {E}_{\theta ^\dagger (\hat{S}^{(t)})}[s(X_i,Z_{i})|X_{i}=x_{i}] \end{aligned}$$

(29)

where initial values $\hat{S}^{(0)}$ is given by $\hat{\theta }^{(0)}$ and Eq. 26.

3.3 Online Mixture Learning with Multiple Components

The case of online mixture learning is discussed in the following. It is now more appropriate to denote $\hat{\theta }^{(N)}$ the current parameter estimate instead of $\hat{\theta }^{(t)}$.

Titterington’s algorithm The first online algorithm, due to Titterington (1984), corresponds to the direct optimization of $\mathcal {Q}(\theta ;\hat{\theta }^{(N)}, \chi )$ using a second-order stochastic gradient ascent:

$$\begin{aligned} \boxed {\hat{\theta }^{(N+1)}= \hat{\theta }^{(N)} + \alpha ^{(N+1)} I^{-1}_{c}(\hat{\theta }^{(N)}) \nabla _{\theta } \log f(x_{N+1}; \hat{\theta }^{(N)}) } \end{aligned}$$

(32)

where $\{\alpha ^{(N+1)}\}$ is a decreasing sequence of positive step sizes ($\alpha ^{(N+1)}= N^{-1}$ in the original paper) and the hessian $\nabla ^2\mathcal {Q}$ of $\mathcal {Q}$ is approximated by the Fisher Information matrix $I_{c}$ for the complete data:

$$ I_{c}(\hat{\theta }^{(N)})=-\mathbb {E}_{\hat{\theta }^{(N)}}\left[ H(\log p(x,z;\theta ))\right] , $$

where H denotes the hessian operator $\nabla ^2$.

The justification of this recursion relies on the Fisher’s identity (see discussion in Dempster et al. 1977) for finite mixture models: for any value $\theta '$ for mixture parameters,

$$\begin{aligned} \nabla _{\theta } \log f(x;\theta ')&= {f(x;\theta ')}^{-1} \nabla _{\theta }f(x;\theta ')= {f(x;\theta ')}^{-1} \sum _{z} \nabla _{\theta } p(x,z;\theta ') \nonumber \\&= {f(x;\theta ')}^{-1} \sum _{z} \left\{ p(x,z;\theta ') \nabla _{\theta } \log p(x,z;\theta ') \right\} \nonumber \\&= \sum _{z} \left\{ h(z|x; \theta ') \nabla _{\theta } \log p(x,z;\theta ') \right\} \nonumber \\&= \mathbb {E}_{\theta '}[\nabla _{\theta } \log p(X,Z;\theta ')|X=x] \end{aligned}$$

(33)

where $h(z|x;\theta )$ is the conditional density of z given x.

It follows that the gradient of $\mathcal {Q}$ at $\hat{\theta }^{(N)}$ (see Eq. 28) has a particular form especially when the model for the complete data is an exponential family:

$$\begin{aligned} \nabla _{\theta } \mathcal {Q}(\hat{\theta }^{(N)};\hat{\theta }^{(N)}, \chi )&= N^{-1} \sum _{i=1}^N \mathbb {E}_{\hat{\theta }^{(N)}}[\nabla _{\theta } \log p(X_i,Z_i;\hat{\theta }^{(N)})|X_i=x_i]\\&= N^{-1} \sum _{i=1}^N \nabla _{\theta } \log f(x_i;\hat{\theta }^{(N)}) \end{aligned}$$

In order to incorporate the constraint on weight components ($\sum _{j=1}^K w_j = 1$), the last component weight $w_K$ is removed from the parameters to be optimized and set to $w_K = 1 - \sum _{j=1}^{K-1} w_j$. Thus, if the $\theta$-coordinate system is considered and parameters are ordered as $\theta = (w_1, \ldots , w_{K-1}, \theta _1, \ldots , \theta _{K})$, we are able to further describe this algorithm for mixtures of exponential families (MEFs):

$$\begin{aligned} \text{ For } j=1,\ldots ,K-1~~~ \frac{\partial \log f(x_{N+1};\hat{\theta }^{(N)})}{\partial w_j}&= \frac{g_j(x_{N+1};\hat{\theta }_j^{(N)})- g_K(x_{N+1};\hat{\theta }_K^{(N)})}{f(x_{N+1};\hat{\theta }^{(N)})}\end{aligned}$$

(34)

$$\begin{aligned} \text{ For } j=1,\ldots ,K~~~ \frac{\partial \log f(x_{N+1};\hat{\theta }^{(N)})}{\partial \theta _j}&= \hat{z}_{N+1,j}^{(N)} \left( s_j(x_{N+1}) - \nabla _{\theta _j} F_j(\hat{\theta }_j^{(N)})\right) \end{aligned}$$

(35)

where $\hat{z}_{N+1,j}^{(N)} = w_j g_j(x_{N+1};\hat{\theta }_j^{(N)}) / f(x_{N+1};\hat{\theta }^{(N)})$.

Due to the chosen parametrization, the hessian of $\log p$ is a block diagonal matrix where the hessians $H(F_j)$ of all the $F_j$ appear. It follows that the information matrix $I_c$ is easier to compute:

$$\begin{aligned} I_c (\theta ) = block diag&\left( \begin{pmatrix} diag(w_1^{-1}, \ldots ,w_{K-1}^{-1}) - \frac{\mathbf {\large 1}_{K-1} {}^t\mathbf {\large 1}_{K-1}}{w_K} \end{pmatrix},\right. \nonumber \\&~~\left. \begin{matrix} w_1 H(F_1)(\theta _1), \ldots , w_K H(F_K)(\theta _K) \end{matrix}\right) \end{aligned}$$

(36)

The inverse of first block matrix is given by the Sherman-Morrison identity (see formula 160 in Petersen and Pedersen 2012). By plugging these results in Eq. 32, the update equations for a generic MEF are:

$\underline{\text {For } \text {a } \text {new } \text {observation } x_{N+1}}$,

This recursive procedure does not necessarily take into account the constraints on the $\theta _j$’s (e.g. $\theta _j >0$ for a mixture of Rayleigh distributions).

Online EM In a recent paper, Cappé and Moulines (2009) proposed to replace the E-Step by a stochastic approximation and leave the M-step unchanged. Here are the key ideas of their approach in the case of mixture of EFs.

When considering an infinite number of observations, the EM update given by an empirical average in Eq. 29 can be defined by the mapping $\mathcal {T} : H \mapsto H$ as follows:

$$\begin{aligned} \mathcal {T}(S) = {\mathbb {E}}_{\pi } \left[ {\mathbb {E}}_{\theta ^{\dagger }(S)} [s(X,Z)|X]\right] \end{aligned}$$

(39)

Thus, the sequence $\hat{S}^{(0)}, \hat{S}^{(1)}, \hat{S}^{(2)}, \ldots$ converges to the sequence $\hat{S}^{(0)}, \mathcal {T}(\hat{S}^{(0)}), \mathcal {T}(\mathcal {T}(\hat{S}^{(0)})), \ldots$ which depends only on $\hat{S}^{(0)}$. Finding the limit of this sequence amounts to find a fixed point of $\mathcal {T}$ or equivalently to look for a root of the function $C : H \mapsto H$:

$$\begin{aligned} C(S) = \mathcal {T}(S) - S = \mathbb {E}_{\pi } \left[ \mathbb {E}_{\theta ^\dagger (S)} [s(X,Z)|X] - S\right] \end{aligned}$$

(40)

According again to the framework of Robbins-Monro, one can get the solution by iterating :

$$\begin{aligned} \tilde{S}^{(N+1)} = \tilde{S}^{(N)} + \alpha ^{(N+1)} \left( \mathbb {E}_{\theta ^\dagger (\tilde{S}^{(N)})} [s(x_{N+1}, z_{N+1}) | x_{N+1}] - \tilde{S}^{(N)}\right) \end{aligned}$$

(41)

The initial value for parameters $\hat{\theta }^{(0)}$ is transformed $\tilde{S}^{(0)}$ by Eq. 31. Obviously, this formula is comparable to the one for $K=1$ (see Eq. 17).

This approach guarantees that parameter constraints are automatically respected solving a known problem for Titterington’s approach. The authors have proved that two algorithms are asymptotically equivalent. The link between the two approaches will be discussed later on.

4 Experiments

4.1 Online Learning for a Gaussian Distribution

The aim of this first experiment is to test several methods of optimization for the simple case of the online learning of a single univariate gaussian distribution. This experiment may appear to be unnecessary since a recursive formulation for the MLE is known from Eq. 17. Hence, many properties of previous optimization methods can be exhibited from this case. This distribution is an exponential family for which the canonical decomposition is recalled in Appendix 6.1. In particular, Eqs. 54, 58 and 66 are needed for the different update formulas 17, 18 and 21.

The experiment consists in the recursive estimation of the parameters on an univariate gaussian $\mathcal {N}(\mu =1, \sigma ^2=4)$ from a continuous stream of its realizations. The dataset of size 60,000 is splitted on two parts, one for training (1/3) and the other for the validation (2/3). Two criteria are used to evaluate the estimates $(\hat{\mu }^{(N)}, \hat{\sigma }^{2(N)})$: the average log-likelihood on training and testing datasets, the Kullback–Leibler (KL) divergence (see. Eq. 68) between true parameters values and their estimates.

Fig. 2

Recursive estimation with exact formula: parameters estimates (top) - Average log-likelihood/KL divergence (bottom) w.r.t. the number of observations (color figure online)

Fig. 3

Recursive estimation with SGD on source space (left), natural space (middle), expectation space (right) with same initialization and different $\alpha ^{(N+1)}$

The results of the recursive estimation with exact formula are reported on Fig. 2. As expected, since the variance of the MLE for a N-sample is $\{NI(\lambda )\}^{-1}$ (see Eq. 69), a convergence is achieved quite quickly. This method does not depend on a particular initialization and one can remark that the average log-likelihood does not necessarily increase after incorporating a new observation. This property is common to many recursive methods. On the right side, one may notice that green and blue curves are very similar, but the shift between them shows the training error is an optimistically biased criterion.

Figure 3 shows the estimates of $\mu$ and $\sigma ^2$ through the iterations with various settings (space, fixed learning rate) but same initialization. We can immediately see that the speed convergence of SGD methods is highly dependent on the learning rate. For some good values (e.g. $\alpha =0.0316$ for SGD on source parameters), the online method is quite competitive with recursive estimation. When, the learning rate is too low, parameter update and therefore the convergence is very slow. In contrast, when $\alpha$ is too large, the estimates oscillate around the global maximum. During these optimizations, the updates can lead to estimates that are outside the domain of admissible values for them. To cope with that, several strategies can be implemented: reject the update, project onto the set of admissibles values, Uzawa’s method (Boyd and Vandenberghe 2004), etc.

Remark that the SGD on H seems to be less stable. Figure 4 shows the average log-likelihood over 100 runs at different steps of the SGD on $\Lambda$ and on H for a fixed learning rate or when it decreases after each iterations ($\alpha ^{(N+1)} = n^{-0.85}$). The two algorithms seem to have more or less a similar behavior. Note that adapting the learning rate yields very good estimates in few iterations (black stroke indicates the median value) which are competitive over the exact MLE (cf. Fig. 2). However, this strategy seems to be too aggressive when the $\theta ^{(0)}$ is far from the global optimum.

Fig. 4

Average log-likelihood over 100 runs with SGD on source space and on expectation space ($\alpha ^{(N+1)} = 0.0316$ or $\alpha ^{(N+1)} = n^{-0.85}$)

4.2 Online Learning for a Mixture of Gaussian Distributions

In this part, we focus on the online learning for a mixture of gaussian distributions. Firstly, consider the expression of Titterington’s recursive EM for this case. By plugging several formulas of the appendix in Eq. 38, the following update equations are obtained:

$\underline{\text {For } \text {a } \text {new } \text {observation } x_{N+1}}$,

Estimate $\hat{z}_{N+1,j}^{(N)}$ and $\hat{w}_j^{(N+1)}$ using Eq. 38.

$$\begin{aligned} \boxed {\begin{aligned} \hat{\theta }_j^{(N+1)} = \hat{\theta }_j^{(N)} + \alpha ^{(N+1)}\frac{2\hat{z}_{N+1,j}^{(N)}}{\hat{w}_j^{(N+1)}}&\begin{pmatrix} \hat{\theta }_{1_j}^{2(N)} + \hat{\theta }^{(N)}_{2_j} &{} &{} \hat{\theta }_{1_j}^{(N)}\hat{\theta }^{(N)}_{2_j}\\ \hat{\theta }^{(N)}_{1_j}\hat{\theta }^{(N)}_{2_j} &{} &{}\hat{\theta }_{2_j}^{2(N)} \end{pmatrix}\\&\begin{pmatrix} x_{N+1} - \frac{\hat{\theta }_{1_j}^{(N)}}{2\hat{\theta }_{2_j}^{(N)}}\\ -x_{N+1}^2 + \frac{\hat{\theta }_{1_j}^{2(N)}}{4\hat{\theta }_{2_j}^{2(N)}} + \frac{1}{2\hat{\theta }_{2_j}^{(N)}} \end{pmatrix} \end{aligned}} \end{aligned}$$

(42)

This latter expression appears to be quite complicated. If this algorithm is applied on $\lambda =(\mu ,\sigma ^2)$-coordinates, the matrix $I_c$ is almost diagonal:

$$\begin{aligned} I_c (\lambda ) = block diag&\left( \begin{pmatrix} diag(w_1^{-1}, \ldots ,w_{K-1}^{-1}) - \frac{\mathbf {\large 1}_{K-1} {}^t\mathbf {\large 1}_{K-1}}{w_K} \end{pmatrix},\right. \nonumber \\&~~\left. \begin{matrix} w_1 I(\lambda _1), \ldots , w_K I(\lambda _K)\end{matrix} \right) \end{aligned}$$

(43)

where I represents in this case the Fisher information matrix on $\lambda$ for the gaussian distribution (see Eq. 69). With this parametrization, the score vector given by Eq. 35 is partially composed by the following expressions:

$$\begin{aligned} \text{ For } j=1,\ldots ,K~~~ \frac{\partial \log f(x_{N+1};\hat{\lambda }^{(N)})}{\partial \mu _j}&= \hat{z}_{N+1,j}^{(N)} \frac{x_{N+1} -\hat{\mu }_j^{(N)}}{\hat{\sigma }_j^{2(N)}}\end{aligned}$$

(44)

$$\begin{aligned} \frac{\partial \log f(x_{N+1};\hat{\lambda }^{(N)})}{\partial \sigma ^2_j}&= \hat{z}_{N+1,j}^{(N)} \frac{(x_{N+1} -\hat{\mu }_j^{(N)})^2 - \hat{\sigma }_j^{2(N)}}{\hat{\sigma }_j^{4(N)}} \end{aligned}$$

(45)

After few simplifications, the update equations in this coordinates system are:

Note the estimation of weight components remains unchanged.

In order to compare Titterington’s algorithm with online EM, consider its formulation in the $\eta$-coordinates system. Recall that for a regular exponential family $g_j$:

$$\begin{aligned} \nabla _{\eta _j} \log g_j(x; \eta _j) = H(F_j^*)(\eta _j) (s_j(x) - \eta _j) \end{aligned}$$

(48)

Moreover, since the matrix $I_c(\eta )$ is

$$\begin{aligned} I_c (\eta ) = block diag&\left( \begin{pmatrix} diag(w_1^{-1}, \ldots ,w_{K-1}^{-1}) - \frac{\mathbf {\large 1}_{K-1} {}^t\mathbf {\large 1}_{K-1}}{w_K} \end{pmatrix},\right. \nonumber \\&~~\left. \begin{matrix} w_1 H(F_1^*)(\eta _1), \ldots , w_K H(F_K^*)(\eta _K) \end{matrix}\right) , \end{aligned}$$

(49)

the recursion no longer requires to invert a matrix:

$$\begin{aligned} \boxed {\hat{\eta }_j^{(N+1)} = \hat{\eta }_j^{(N)} + \alpha ^{(N+1)}\frac{\hat{z}_{N+1,j}^{(N)} }{\hat{w}_j^{(N)} } \left( s_j(x_{N+1}) - \hat{\eta }_j^{(N)} \right) } \end{aligned}$$

(50)

Unfortunately, for all the above methods, the constraints on parameters ($\sigma _j^2 > 0$) have to be checked beforehand in order to accept the parameters update. Looking at equations Eqs. 31 and 41, we can conclude that the online EM differs in the way components parameters are updated:

$$\begin{aligned} \hat{\eta }_j^{(N+1)} = \frac{\hat{w}_j^{(N)}}{\hat{w}_j^{(N+1)}} \hat{\eta }_j^{(N)} + \alpha ^{(N+1)} \left( \frac{\hat{z}_{N+1,j}^{(N)}}{\hat{w}_j^{(N+1)}} s_j(x_{N+1}) - \frac{\hat{w}_j^{(N)}}{\hat{w}_j^{(N+1)}} \hat{\eta }_j^{(N)} \right) \end{aligned}$$

(51)

For more details about the convergence of these algorithms, the interested reader is referred to Cappé and Moulines (2009) for further information.

To illustrate these algorithms, two experiments on synthetic datasets are provided (see Fig. 5). Their respective parameters are:

Dataset 1 : ${\small (w_1=0.5,\mu _1=0,\sigma _1^2=1), (w_2=0.5,\mu _2=4, \sigma _2^2=4)}$

Dataset 2 : ${\small (w_1 = 0.25, \mu _1=0.25, \sigma _1^2=0.15), (w_2=0.65, \mu _2=-1, \sigma _2^2=0.4)}$

         ${\small (w_3 = 0.1, \mu _3=-0.5, \sigma _3^2=0.6)}$

All the methods were initialized with same parameters values coming from the k-means algorithm.

Fig. 5

Synthetic datasets

Fig. 6

Average log-likelihood and Kullback–Leibler for all estimators

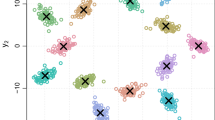
The policy for the learning rate is also identical: $\alpha ^{(N)} = \left( \frac{1}{N_0+N}\right) ^{0.7}$ where $N_0$ is the number of observations used for k-means. The criteria used to evaluated the results are the average log-likelihood and the Kullback–Liebler divergence (KL). Since there is no closed form to evaluate this divergence, we rely on numerical integration which is reasonably fast and accurate in 1d. Figure 6 reports the results of all estimators on the two datasets. Additionally, Figs. 7 and 8 illustrates the best estimates KL resulting components.

Fig. 7

Dataset 1: Best estimates w.r.t. to KL divergence

Fig. 8

Dataset 2: Best estimates w.r.t. to KL divergence

As expected, since the dataset 1 contains two relatively separated components, the estimation converges very quickly for all methods except for the Recursive EM on $\theta$-coordinates. For this experiment, we observe that most of the first updates are rejected due to the constraints on parameters ($\theta _2> 0 \equiv \sigma ^2 > 0$). Later in the recursion, the learning rate has decreased and the updates do not violate the constraints. Undoubtedly, and as also observed in first experiment, the choice of the learning rate policy should be different on natural parameter space. Also, one can observe that some methods are trapped in different local minima even if their initialization are the same (see Fig. 7). For dataset 2, we remark the constraints prevents some updates for Recursive EM on natural and expectation parameters. Despite this, the mixture estimate is very good (see Recursive EM(natural) on Fig. 8).

As a conclusion of these experiments, Recursive EM on $\eta$-coordinates and online EM do not require the computation and the inversion of matrix. This is a very appealing property especially when the components have a more complicated parametric distribution (e.g. Wishart distributions Saint-Jean and Nielsen 2014). But in practice, this provides only easier to implement methods and does not guarantee better estimates. Since online EM makes a stochastic approximation of the E-Step of EM, the constraints on parameters are automatically guaranteed by the maximization step which is particularly efficient for exponential families.

5 Conclusion

This paper addresses the problem of online learning of finite statistical mixtures with a special focus on distribution components belonging to the exponential families. Many details to compare Recursive EM and online EM from the practical point of view are given. The presented methods are fast since they require only one pass over the data stream. However, there is still room for improvement, especially for the Recursive EM method which is roughly a classical second-order stochastic gradient ascent. More recent optimization methods are described in the paper and leads to overcome the difficulty to choose an adequate policy for the learning rate. We might have also mentioned the incremental EM by Neal and Hinton (1999) which shares many properties with the online EM (partial E-Step). Further speed increase may be achieved by using distributed computing on a cluster of machines by aggregating partial sums of sufficient statistics (see Liu and Ihler 2014) since the statistical estimation is a decomposable problem.

Appendices

Appendices

Univariate Gaussian Distribution as an Exponential Family

Canonical Decomposition and ${\varvec{F}}$

$$\begin{aligned} f(x;\mu ,\sigma ^{2})&= \frac{1}{(2 \pi \sigma ^{2})^{1/2}}\exp \left\{ -\frac{(x - \mu )^{2}}{2\sigma ^{2}} \right\} \\&= \exp \left\{ -\frac{1}{2\sigma ^{2}} (x^{2} - 2 x \mu + \mu ^{2}) - \frac{1}{2} \log \left( 2 \pi \sigma ^{2}\right) \right\} \\&= \exp \left\{ \langle \frac{1}{2\sigma ^{2}}, -x^{2} \rangle + \langle \frac{\mu }{\sigma ^{2}}, x \rangle - \frac{\mu ^{2}}{2\sigma ^{2}} - \frac{1}{2} \log \left( 2 \pi \sigma ^{2}\right) \right\} \\ \end{aligned}$$

In the sequel, the vector of source parameters is denoted $\lambda =(\mu , \sigma ^2)$. One may recognize the canonical form of an exponential family

$$f(x;\theta ) = \exp \left\{ <\theta ,s(x)> +\, k(x) - F(\theta )\right\} $$

by setting $\theta = (\theta _1,\theta _2)$ with

$$\begin{aligned} \theta _{1}&= \frac{\mu }{\sigma ^{2}} \Longleftrightarrow \mu = \frac{\theta _{1}}{2\theta _{2}}\end{aligned}$$

(52)

$$\begin{aligned} \theta _{2}&= \frac{1}{2\sigma ^{2}} \Longleftrightarrow \sigma ^{2} = \frac{1}{2\theta _{2}} \end{aligned}$$

(53)

$$\begin{aligned} s(x)&=(x,-x^{2}) \end{aligned}$$

(54)

$$\begin{aligned} k(x)&= 0 \end{aligned}$$

(55)

$$\begin{aligned} f(x; \theta _{1}, \theta _{2})&= \exp \left\{ \langle \theta _{2}, -x^{2} \rangle + \langle \theta _{1}, x \rangle - \frac{1}{2} \frac{(\theta _{1}/2\theta _{2})^{2}}{1/2\theta _{2}} - \frac{1}{2} \log (2\pi /2\theta _{2})\right\} \\&= \exp \left\{ \langle \theta _{2}, -x^{2} \rangle + \langle \theta _{1}, x \rangle - \frac{\theta _{1}^{2}}{4\theta _{2}} - \frac{1}{2} \log (\pi ) + \frac{1}{2} \log \theta _{2}\right\} \end{aligned}$$

with the log normalizer F as

$$\begin{aligned} F(\theta _{1}, \theta _{2}) = \frac{\theta _{1}^{2}}{4\theta _{2}} + \frac{1}{2} \log (\pi ) - \frac{1}{2} \log \theta _{2} \end{aligned}$$

(56)

1.1 Gradient of the Log-Normalizer

The gradient of the log-normalizer is given by:

$$\begin{aligned} \frac{\partial F}{\partial \theta _{1}}(\theta _{1}, \theta _{2})&= \frac{\theta _{1}}{2\theta _{2}} \end{aligned}$$

(57)

$$\begin{aligned} \frac{\partial F}{\partial \theta _{2}}(\theta _{1},\theta _{2})&= -\frac{\theta _{1}^{2}}{4\theta _{2}^{2}} - \frac{1}{2\theta _{2}} \end{aligned}$$

(58)

In order to get the dual coordinate system $\eta =(\eta _{1}, \eta _{2})$, the following set of equations has to be inverted:

$$\begin{aligned} \eta _{1}&= \frac{\theta _{1}}{2\theta _{2}} \end{aligned}$$

(59)

$$\begin{aligned} \eta _{2}&= -\frac{\theta _{1}^{2}}{4\theta _{2}^{2}} - \frac{1}{2\theta _{2}} \end{aligned}$$

(60)

By plugging the first equation into the second one, it follows:

$$\begin{aligned} \eta _{2} = - \eta _{1}^{2} - \frac{1}{2\theta _{2}} \Longleftrightarrow&\theta _{2} = -\frac{1}{2(\eta _{1}^{2} + \eta _{2})}&= \frac{\partial F^*}{\partial \eta _{2}}(\eta _{1},\eta _{2}) \end{aligned}$$

(61)

$$\begin{aligned}&\theta _{1} = 2 \theta _{2} \eta _{1} = - \frac{\eta _{1}}{(\eta _{1}^{2} + \eta _{2})}&= \frac{\partial F^*}{\partial \eta _{1}}(\eta _{1},\eta _{2}) \end{aligned}$$

(62)

Formulas are even simpler regarding the source parameters since we know that

$$\begin{aligned} \eta _{1} = \mathbb {E}[X] = \mu\Longleftrightarrow & {} \mu = \eta _{1} \end{aligned}$$

(63)

$$\begin{aligned} \eta _{2} = \mathbb {E}[-X^2] = -\left\{ \mu ^2 + \sigma ^2\right\}\Longleftrightarrow & {} \sigma ^2 = - \left\{ \eta _{1}^2 + \eta _{2}\right\} \end{aligned}$$

(64)

In order to compute $F^{*}$, we simply have to reuse our previous results in

$$F^{*}(H) = \langle (\nabla F)^{-1} (H), H \rangle - F ( (\nabla F)^{-1} (H))$$

and obtain the following expression

The hessians H(F), $H(F^*)$ of respectively F and $F^*$ are

$$\begin{aligned} H(F)(\theta _1, \theta _2) = \begin{pmatrix} \frac{1}{2 \theta _2} &{} -\frac{\theta _1}{2 \theta _2^2}\\ -\frac{\theta _1}{2 \theta _2^2} &{} \frac{\theta _1^2 + \theta _2}{2 \theta _2^3} \end{pmatrix} \end{aligned}$$

(65)

$$\begin{aligned} H(F^*)(\eta _1, \eta _2) = \begin{pmatrix} \frac{\eta _1^2 - \eta _2}{(\eta _1^2 + \eta _2)^2} &{} \frac{\eta _1}{(\eta _1^2 + \eta _2)^2}\\ \frac{\eta _1}{(\eta _1^2 + \eta _2)^2} &{} \frac{1}{2(\eta _1^2 + \eta _2)^2} \end{pmatrix} \end{aligned}$$

(66)

Since the univariate normal distribution is an exponential family, the Kullback–Leibler divergence is a Bregman divergence for $F^*$ on expectation parameters:

$$\begin{aligned} KL(\mathcal {N}(\mu _{p},\sigma ^2_{p}) || \mathcal {N}(\mu _{q},\sigma ^2_{q}))&= B_{F^*}(\eta _p : \eta _q) \\&= F^*(\eta _p) - F^*(\eta _q) - \langle \eta _p - \eta _q, \nabla F^* (\eta _q) \rangle \end{aligned}$$

After calculations, it follows:

$$\begin{aligned} B_F^*(\eta _p : \eta _q) = \frac{1}{2} \left( \log \left( \frac{\eta _{1_q}^{2} + \eta _{2_q}}{\eta _{1_p}^{2} + \eta _{2_p}}\right) + \frac{2(\eta _{1_p} - \eta _{1_q})\eta _{1_q}}{(\eta _{1_q}^{2} + \eta _{2_q})} + \frac{\eta _{2_p} - \eta _{2_q}}{(\eta _{1_q}^{2} + \eta _{2_q})} \right) \end{aligned}$$

(67)

A simple rewrite of it with the source parameters leads to the known closed form:

$$\begin{aligned} \frac{1}{2} \left( \log \left( \frac{\eta _{1_q}^{2} + \eta _{2_q}}{\eta _{1_p}^{2} + \eta _{2_p}}\right) + \frac{2(\eta _{1_p} - \eta _{1_q})\eta _{1_q}}{(\eta _{1_q}^{2} + \eta _{2_q})} + \frac{\eta _{2_p} - \eta _{2_q}}{(\eta _{1_q}^{2} + \eta _{2_q})} \right)&= \nonumber \\ \frac{1}{2} \left( \log \left( \frac{\eta _{1_q}^{2} + \eta _{2_q}}{\eta _{1_p}^{2} + \eta _{2_p}}\right) + \frac{(\eta _{1_p}^2 + \eta _{2_p}) - (\eta _{1_p}-\eta _{1_q})^2 - (\eta _{1_q}^2 + \eta _{2_q})}{(\eta _{1_q}^{2} + \eta _{2_q})} \right)&= \nonumber \\ \frac{1}{2} \left( \log \left( \frac{\sigma _q^{2}}{\sigma _p^{2}}\right) + \frac{\sigma _p^{2}}{\sigma _q^{2}} + \frac{(\mu _p-\mu _q)^2}{\sigma _q^{2}} -1 \right) \end{aligned}$$

(68)

The Fisher information matrix $I(\lambda )$ is obtained by computing the expectation of the product of Fisher score and its transposition:

$$\begin{aligned} I(\lambda )&\mathop {=}\limits ^{def} \mathbb {E}\left[ \nabla _\lambda \log f(x;\lambda ) . \nabla _\lambda \log f(x;\lambda )^T\right] \nonumber \\&= \mathbb {E}\left[ \begin{pmatrix} \frac{x-\mu }{\sigma ^2}\\ \frac{(x-\mu )^2 - \sigma ^2}{2\sigma ^4}\end{pmatrix}. \begin{pmatrix} \frac{x-\mu }{\sigma ^2} \frac{(x-\mu )^2 - \sigma ^2}{2\sigma ^4}\end{pmatrix}\right] \nonumber \\&=\begin{pmatrix} \frac{1}{\sigma ^2} &{} 0 \\ 0 &{} \frac{1}{2\sigma ^4}\end{pmatrix}. \end{aligned}$$

(69)

By change in coordinates or direct computation, the Fisher information matrix is also:

$$\begin{aligned} I(\theta ) = H(F)(\theta ) = \begin{pmatrix}\frac{1}{2\theta _2} &{} -\frac{\theta _1}{2\theta _2^2}\\ -\frac{\theta _1}{2\theta _2^2} &{} \frac{\theta _1^2 + \theta _2}{2\theta _2^3}\end{pmatrix} \text{ and } I(\eta ) = \frac{1}{(\eta _1^2 + \eta _2)^2} \begin{pmatrix} (\eta _1^2 - \eta _2) &{} \eta _1\\ \eta _1 &{} \frac{1}{2}\end{pmatrix} \end{aligned}$$

(70)

1.2 Multivariate Gaussian Distribution as an Exponential Family

Canonical Decomposition and ${\varvec{F}}$

$$\begin{aligned} f(x;\mu ,\varSigma )&= \frac{1}{(2 \pi )^{d / 2} |\varSigma |^{1/2}}\exp \left\{ -\frac{ {}^t (x - \mu ) \varSigma ^{-1} (x - \mu )}{2} \right\} \\&= \exp \left\{ -\frac{ {}^tx\varSigma ^{-1}x - {}^t\mu \varSigma ^{-1}x - {}^tx\varSigma ^{-1}\mu + {}^t\mu \varSigma ^{-1}\mu }{2} - \log \left( (2 \pi )^{d / 2} |\varSigma |^{1/2}\right) \right\} \\&= \exp \left\{ -\frac{tr({}^tx\varSigma ^{-1}x) - \langle {}^t\varSigma ^{-1} \mu , x \rangle -\langle x, \varSigma ^{-1}\mu \rangle + \langle {}^t\varSigma ^{-1}\mu , \varSigma \varSigma ^{-1} \mu \rangle }{2} - \log \left( \pi ^{d / 2} |2\varSigma |^{1/2}\right) \right\} \end{aligned}$$

Due to the cyclic property of the trace and to the symmetry of $\varSigma ^{-1}$, it follows:

$$\begin{aligned} f(x;\mu ,\varSigma )&= \exp \left\{ tr\left( ^t\left( \frac{1}{2}\varSigma ^{-1}\right) (-x{}^tx)\right) + \langle \varSigma ^{-1} \mu , x \rangle - \frac{1}{2} \langle \varSigma ^{-1}\mu , \varSigma \varSigma ^{-1} \mu \rangle - \frac{d}{2} \log (\pi ) - \frac{1}{2} \log |2\varSigma |\right\} \\&= \exp \left\{ \langle \frac{1}{2}\varSigma ^{-1}, -x{}^tx \rangle _{F} + \langle \varSigma ^{-1} \mu , x \rangle - \frac{1}{4} {}^t(\varSigma ^{-1}\mu ) 2\varSigma (\varSigma ^{-1}\mu ) - \frac{d}{2} \log (\pi ) - \frac{1}{2} \log |2\varSigma | \right\} \\ \end{aligned}$$

where $\langle \cdot , \cdot \rangle _{F}$ is the Frobenius scalar product. One may recognize the canonical form of an exponential family

$$f(x;\varTheta ) = \exp \left\{ <\varTheta ,t(x)> + k(x) - F(\varTheta )\right\} $$

by setting:

$$\varTheta = (\theta _{1}, \theta _2)$$

$$\begin{aligned} \theta _1&= \varSigma ^{-1}\mu \Longleftrightarrow \mu = \frac{1}{2}\theta _2^{-1} \theta _1\end{aligned}$$

(71)

$$\begin{aligned} \theta _2&= \frac{1}{2}\varSigma ^{-1} \Longleftrightarrow \varSigma = \frac{1}{2}\theta _2^{-1} \end{aligned}$$

(72)

$$\begin{aligned} t(x)&=(x,-x{}^tx)\end{aligned}$$

(73)

$$\begin{aligned} k(x)&= 0 \end{aligned}$$

(74)

$$\begin{aligned} f(x; \theta _1, \theta _2) = \exp \left\{ \langle \theta _2, -x{}^tx \rangle _{F} + \langle \theta _1, x \rangle - \frac{1}{4} {}^t\theta _1 \theta _2^{-1} \theta _1 - \frac{d}{2} \log (\pi ) + \frac{1}{2} \log |\theta _2| \right\} \nonumber \\ \end{aligned}$$

(75)

with the log normalizer F:

$$\begin{aligned} F(\theta _1, \theta _2) = \frac{1}{4} {}^t\theta _1 \theta _2^{-1} \theta _1 + \frac{d}{2} \log (\pi ) - \frac{1}{2} \log |\theta _2| \end{aligned}$$

(76)

1.3 Gradient of the Log-Normalizer

By applying the following formulas from the matrix cookbook (Petersen and Pedersen 2012)

identity 57:

$$ \frac{\partial \log |X|}{\partial X} = ({}^tX)^{-1} = {}^t(X^{-1}) $$

identity 61:

$$\frac{\partial {}^ta X^{-1} b}{\partial X} = - {}^tX^{-1} a {}^tb X^{-1} $$

identity 81:

$$\frac{\partial {}^tx B x}{\partial x} = (B + {}^tB)x $$

the gradient of the log-normalizer is given by:

$$\begin{aligned} \frac{\partial F}{\partial \theta _1}(\theta _1,\theta _2)&= \frac{1}{4} (\theta _2^{-1}+ {}^{t}\theta _2^{-1}) \theta _1 = \frac{1}{2} \theta _2^{-1} \theta _1 \end{aligned}$$

(77)

$$\begin{aligned} \frac{\partial F}{\partial \theta _2}(\theta _1,\theta _2)&= - \frac{1}{4} {}^t\theta _2^{-1} \theta _1 {}^t\theta _1 \theta _2^{-1} - \frac{1}{2} {}^t\theta _2^{-1} = - \left( \frac{1}{2} \theta _2^{-1} \theta _1\right) ^t\left( \frac{1}{2} \theta _2^{-1} \theta _1\right) - \frac{1}{2} \theta _2^{-1} \end{aligned}$$

(78)

In order to emphasize the coherence of these formulas, recall that the gradient of the log-normalizer corresponds the expectation of the sufficient statistics:

$$\begin{aligned} \mathbb {E}[x]&= \mu\equiv & {} ~\frac{1}{2}\theta _2^{-1} \theta _1\end{aligned}$$

(79)

$$\begin{aligned} \mathbb {E}[-x{}^tx]&= -\mathbb {E}[x{}^tx] = -\mu {}^{t}\mu - \varSigma\equiv & {} - \left( \frac{1}{2}\theta _2^{-1} \theta _1\right) ^t\left( \frac{1}{2}\theta _2^{-1} \theta _1\right) - \frac{1}{2}\theta _2^{-1} \end{aligned}$$

(80)

Last equation comes from the expansion of $\mathbb {E}[(x - \mu ) {}^t(x - \mu )]$.

1.4 Convex Conjugate G of F and Its Gradient

In order to get the dual coordinate system $H=(\eta _1, \eta _2)$, the following set of equations has to be inverted:

$$\begin{aligned} \eta _1&=\frac{1}{2} \theta _2^{-1} \theta _1 \end{aligned}$$

(81)

$$\begin{aligned} \eta _2&= -\left( \frac{1}{2}\theta _2^{-1} \theta _1\right) ^t\left( \frac{1}{2}\theta _2^{-1} \theta _1\right) - \frac{1}{2}\theta _2^{-1} \end{aligned}$$

(82)

By plugging the first equation into the second one, it follows

$$\begin{aligned} \eta _2 = - \eta _1 {}^t\eta _1 - \frac{1}{2}\theta _2^{-1} \Longleftrightarrow \theta _2= \frac{1}{2}(-\eta _1 {}^t\eta _1 -\eta _2)^{-1} = \frac{\partial G}{\partial \eta _2}(\eta _1,\eta _2) \end{aligned}$$

(83)

and

$$\begin{aligned} \theta _1 = 2 \theta _2\eta _1= (- \eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1 = \frac{\partial G}{\partial \eta _1}(\eta _1,\eta _2) \end{aligned}$$

(84)

Formulas are even simpler regarding the source parameters since we know from Eqs. 79 and 80 that

$$\begin{aligned} \eta _1 = \mu\Longleftrightarrow & {} \mu = \eta _1 \end{aligned}$$

(85)

$$\begin{aligned} \eta _2= -\mu {}^{t}\mu - \varSigma\Longleftrightarrow & {} \varSigma = - \eta _1 {}^t\eta _1 - \eta _2 \end{aligned}$$

(86)

In order to compute $G := F^{*}$, we simply have to reuse our previous results in

$$G(H) = \langle (\nabla F)^{-1} (H), H \rangle - F ( (\nabla F)^{-1} (H))$$

and obtain the following expression

$$\begin{aligned} G(\eta _1, \eta _2)&= \langle (-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1, \eta _1 \rangle + \langle \frac{1}{2} (- \eta _1 {}^t\eta _1 - \eta _2)^{-1}, \eta _2 \rangle _{F}\\&- \frac{1}{4} {}^t((-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1) 2(-\eta _1 {}^t\eta _1 - \eta _2) (-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1 \\&- \frac{d}{2} \log (\pi ) + \frac{1}{2} \log |\frac{1}{2} (-\eta _1 {}^t\eta _1 - \eta _2)^{-1}|\\&= {}^t \eta _1 (-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1 +\frac{1}{2} tr({}^{t}(-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _2)\\&- \frac{1}{2} {}^t\eta _1{}^t(-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1\\&- \frac{d}{2} \log (\pi ) + \frac{1}{2} \log |(2(-\eta _1 {}^t\eta _1 - \eta _2))^{-1}|\\&= \frac{1}{2} {}^t \eta _1 (- \eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1 +\frac{1}{2} tr((-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _2)\\&- \frac{d}{2} \log (\pi ) - \frac{1}{2} \log |2(-\eta _1 {}^t\eta _1 - \eta _2)|\\&= \frac{1}{2} \left( tr((- \eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _1 {}^t \eta _1 ) +tr((-\eta _1 {}^t\eta _1 - \eta _2)^{-1} \eta _2)\right) \\&- \frac{d}{2} \log (\pi ) - \frac{1}{2} \log |2(-\eta _1 {}^t\eta _1 - \eta _2)|\\&= - \frac{1}{2} tr((- \eta _1 {}^t\eta _1 - \eta _2)^{-1} (- \eta _1 {}^t \eta _1 - \eta _2)) - \frac{d}{2} \log (\pi )\nonumber \\&- \frac{1}{2} \log |2(-\eta _1 {}^t\eta _1 - \eta _2)|\\&= - \frac{1}{2} tr(I_{d}) - \frac{d}{2} \log (\pi ) - \frac{1}{2} \log |2(-\eta _1 {}^t\eta _1 - \eta _2)|\\&= - \frac{d}{2} \log (e\pi ) - \frac{1}{2} \log |2(-\eta _1 {}^t\eta _1 - \eta _2)|\\ \end{aligned}$$

Let us rewrite this expression with source parameters:

$$\begin{aligned} G(\mu , \varSigma ) = - \frac{d}{2} \log (e\pi ) - \frac{1}{2} \log |2\varSigma |\ \end{aligned}$$

(87)

1.5 Kullback–Leibler Divergence

First recall that the Kullback–Leibler divergence between two p.d.f. p and q is

$$ KL(p || q) = \int p(x) \log \frac{p(x)}{q(x)} dx$$

For two multivariate normal distributions, it is known in closed form

$$\begin{aligned} KL(\mathcal {N}(\mu _{p},\varSigma _{p}) || \mathcal {N}(\mu _{q},\varSigma _{q})) = \frac{1}{2}\left( \log \left( \frac{|\varSigma _{q}|}{|\varSigma _{p}|}\right) + tr(\varSigma _{q}^{-1}\varSigma _{p}) + {}^{t}(\mu _{q}-\mu _{p})\varSigma _{q}^{-1}(\mu _{q}-\mu _{p}) - d\right) \end{aligned}$$

(88)

Since the multivariate normal distribution is an E.F., the same result must be obtained using the bregman divergence for G on expectation parameters $H_{p}$ and $H_{q}$:

$$KL(\mathcal {N}(\mu _{p},\varSigma _{p}) || \mathcal {N}(\mu _{q},\varSigma _{q})) = B_G(H_p || H_q) = G(H_{p}) - G(H_{q}) - \langle H_{p} - H_{q}, \nabla G (H_{q}) \rangle $$

$$\begin{aligned} G(H_{p}) - G(H_{q})&= - \frac{d}{2} \log (e\pi ) - \frac{1}{2} \log |-2(\eta _{1_{p}} {}^t\eta _{1_{p}} + \eta _{2_{p}})| \\&+ \frac{d}{2} \log (e\pi ) + \frac{1}{2} \log |-2(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})| \\&= \frac{1}{2} \log \frac{|-(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})|}{|-(\eta _{1_{p}} {}^t\eta _{1_{p}} + \eta _{2_{p}})|}\\ - \langle H_{p} - H_{q}, \nabla G (H_{q}) \rangle&= - \langle \eta _{1_{p}} - \eta _{1_{q}}, - (\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1} \eta _{1_{q}} \rangle \\&- tr\left( ^{t} (\eta _{2_{p}} - \eta _{2_{q}}) \left( -\frac{1}{2} (\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1}\right) \right) \\&= {}^t \eta _{1_{p}} (\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1} \eta _{1_{q}} - {}^t \eta _{1_{q}} (\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1} \eta _{1_{q}} \\&- \frac{1}{2} tr({}^{t} \eta _{2_{p}} (-(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1})) + \frac{1}{2} tr({}^{t}\eta _{2_{q}} (-(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1}))\\ \end{aligned}$$

In order to go further, we can express these two formulas using $\mu$ and $\varSigma ^{-1} = (-\eta _1 {}^t\eta _1 - \eta _2)^{-1} = -(\eta _1 {}^t\eta _1 + \eta _2)^{-1}$ (cf. Eq. 86):

$$\begin{aligned} \frac{1}{2} \log \frac{|-(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})|}{|-(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})|}&= \frac{1}{2} \log \frac{|\varSigma _q|}{|\varSigma _p|} \end{aligned}$$

$$\begin{aligned} {}^t \eta _{1_{p}} (\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1} \eta _{1_{q}}&= -{}^t \mu _{p} \varSigma _{q}^{-1} \mu _{q}\\ - {}^t \eta _{1_{q}} (\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1} \eta _{1_{q}}&= {}^t \mu _{q} \varSigma _{q}^{-1} \mu _{q} \end{aligned}$$

$$\begin{aligned} - \frac{1}{2} tr({}^{t} \eta _{2_{p}} (-(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1}))&= \frac{1}{2} tr((\mu _{p}{}^{t}\mu _{p} + \varSigma _{p}) \varSigma _{q}^{-1})\\&= \frac{1}{2} tr(\mu _{p}{}^{t}\mu _{p}\varSigma _{q}^{-1}) + \frac{1}{2} tr(\varSigma _{p}\varSigma _{q}^{-1})\\&= \frac{1}{2} {}^{t}\mu _{p}\varSigma _{q}^{-1}\mu _{p} + \frac{1}{2} tr(\varSigma _{q}^{-1}\varSigma _{p})\\ + \frac{1}{2} tr({}^{t}\eta _{2_{q}} (-(\eta _{1_{q}} {}^t\eta _{1_{q}} + \eta _{2_{q}})^{-1}))&= - \frac{1}{2} tr((\mu _{q}{}^{t}\mu _{q} + \varSigma _{q}) \varSigma _{q}^{-1})\\&= - \frac{1}{2} tr(\mu _{q}{}^{t}\mu _{q}\varSigma _{q}^{-1}) - \frac{1}{2} tr(\varSigma _{q}\varSigma _{q}^{-1})\\&= - \frac{1}{2} {}^{t}\mu _{q}\varSigma _{q}^{-1}\mu _{q} - \frac{1}{2} d \end{aligned}$$

By summing up of these terms, the standard formula for KL divergence is recovered:

$$\begin{aligned} KL(\mathcal {N}(\mu _{p},\varSigma _{p})&|| \mathcal {N}(\mu _{q},\varSigma _{q})) = \frac{1}{2} \log \frac{|\varSigma _q|}{|\varSigma _p|} -{}^t \mu _{p} \varSigma _{q}^{-1} \mu _{q} +{}^t \mu _{q} \varSigma _{q}^{-1} \mu _{q} + \\&\frac{1}{2} {}^{t}\mu _{p}\varSigma _{q}^{-1}\mu _{p} + \frac{1}{2} tr(\varSigma _{q}^{-1}\varSigma _{p}) - \frac{1}{2} {}^{t}\mu _{q}\varSigma _{q}^{-1}\mu _{q} - \frac{1}{2} d\\ =&\frac{1}{2} \left( \log \frac{|\varSigma _q|}{|\varSigma _p|} + tr(\varSigma _{q}^{-1}\varSigma _{p}) - d~-\right. \\&\left. \left\{ 2{}^t \mu _{p} \varSigma _{q}^{-1} \mu _{q} - 2 {}^t \mu _{q} \varSigma _{q}^{-1} \mu _{q} - ^{t}\mu _{p}\varSigma _{q}^{-1}\mu _{p} + {}^{t}\mu _{q}\varSigma _{q}^{-1}\mu _{q}\right\} \right) \\ =&\frac{1}{2}\left( \log \frac{|\varSigma _q|}{|\varSigma _p|} + tr(\varSigma _{q}^{-1}\varSigma _{p}) - {}^t (\mu _{p} - \mu _{q}) \varSigma _{q}^{-1} (\mu _{p} - \mu _{q}) - d \right) \end{aligned}$$