Abstract
Probabilistic databases accommodate well the requirements of modern applications that produce large volumes of uncertain data from a variety of sources. We propose an expressive class of probabilistic keys which empowers users to specify lower and upper bounds on the marginal probabilities by which keys should hold in a data set of acceptable quality. Indeed, the bounds help organizations balance the consistency and completeness targets for their data quality. For this purpose, algorithms are established for an agile schema- and data-driven acquisition of the right lower and upper bounds in a given application domain, and for reasoning about these keys. The efficiency of our acquisition framework is demonstrated theoretically and experimentally.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Background. Keys allow us to understand the structure and semantics of data. In relational databases, a key is a set of attributes that holds on a relation if no two different tuples in the relation have matching values on all the attributes of the key. The ability of keys to uniquely identify entities makes them invaluable in data processing and applications.
Motivation. Relational databases target applications with certain data, such as accounting and payroll. Modern applications, such as data integration and financial risk assessment produce large volumes of uncertain data from a variety of sources. For instance, RFID (radio frequency identification) can track movements of endangered species of animals, such as the Japanese Serow in central Honshu. Here it is sensible to apply probabilistic databases. Table 1 shows two probabilistic relations (p-relation), which are probability distributions over a finite set of possible worlds, each being a relation.
In requirements acquisition the goal is to specify all keys that apply to the application domain, and those keys only. This goal addresses the consistency and completeness dimensions of data quality. Here, consistency means to specify all meaningful keys in order to prevent the occurrence of inconsistent data, while completeness means not to specify any meaningless keys in order to capture any potential meaningful database instance. This situation is exemplified in Fig. 1.
In probabilistic databases, one may speak of a key when it holds in all possible worlds. That is to say that a key holds with marginal probability one, which means that the probabilities of the worlds in which the key holds add up to one. Due to the veracity of probabilistic data and the variety of sources the data originate from, one must not expect to satisfy the completeness criteria with this definition. Neither does such definition make sensible use of probabilities, as one would expect for probabilistic data. In our example, neither \(r_1\) nor \(r_2\) satisfy any non-trivial key with marginal probability one: The key \(k\{\textit{rfid},\textit{time}\}\) has marginal probability 0.75 in both \(r_1\) and \(r_2\), while \(k\{\textit{time},\textit{zone}\}\) has marginal probability 0.65 in \(r_1\) and marginal probability 0.75 in \(r_2\).
We propose keys with probabilistic intervals, or p-keys for short, which stipulate lower and upper bounds on the marginal probability by which a traditional key holds on probabilistic data. For example, we may specify the p-keys \(k\{\textit{rfid},\textit{time}\}\in (0.75,1)\) and \(k\{\textit{time},\textit{zone}\}\in (0.65,0.75)\). In particular, the ability to stipulate lower and upper bounds on the marginal probability of keys is useful for probabilistic data. The p-key \(k\{\textit{time},\textit{zone}\}\in (0.65,0.75)\) reflects our observations that different serows may occur at the same time in the same zone at least with probability 0.25 and at most with probability 0.35. Our main motivation for p-keys is their ability to balance the consistency and completeness targets for the quality of probabilistic data. Consistency means that for each key the specified lower (upper) bound on its marginal probability is not too high (low), and completeness means that for each key the specified lower (upper) bound is not too low (high). Once the bounds have been consolidated, p-keys can be utilized to control these data quality dimensions during updates. When new data arrives, p-keys can help detect anomalous patterns of data in the form of p-key violations. That is, automated warnings can be issued whenever data would not meet a desired lower or upper bound of some p-key. In a different showcase, p-keys can be used to infer probabilities that query answers are (non-)unique. In our example, we may wonder about the chance that different serows are in the same zone at the same time, indicating potential mating behavior. We may ask

P-keys enable us to derive a minimum (maximum) probability of 0.65 (0.75) that a unique answer is returned, because different serows are in zone z2 at 2pm at least with probability 0.25 and at most with probability 0.35. These bounds can be inferred without accessing any data at all, only requiring that \(k\{\textit{time},\textit{zone}\}\) has a marginal probability between 0.65 and 0.75 on the given data.
Contributions. Our contributions can be summarized as follows. Modeling: We propose p-keys \(kX\in (p,q)\) as a natural class of integrity constraints over uncertain data. Their main use is to help organizations balance consistency and completeness targets for the quality of their data, and to quantify bounds on the probability for (non-)unique query answers. Reasoning: While sets of p-keys can be unsatisfiable, we establish an efficient algorithm to decide satisfiability. The implication problem is to decide for a given set \(\varSigma \cup \{\varphi \}\) of p-keys, whether every p-relation that satisfies all elements of \(\varSigma \) also satisfies \(\varphi \). We characterize the implication problem of satisfiable sets of p-keys by a finite set of Horn rules, and a linear time decision algorithm. This enables organizations to reduce the overhead of managing p-keys to a minimal level necessary. Summarization: For the schema-driven acquisition of the right probabilistic intervals, we show how to perfectly summarize any given satisfiable set of p-keys as an Armstrong PC-base. An Armstrong PC-base consists of two PC-tables: One that satisfies every key with the exact marginal probability that is the perceived best lower bound for the domain, and one that is the perceived best upper bound. Any flaws with these perceptions are explicitly pointed out: Either as unreasonably high lower bounds, or unreasonably low upper bounds. For example, Table 2 shows an Armstrong PC-base for the p-keys shown in Fig. 2. In the CD table, the W column of a tuple shows the identifiers of possible worlds to which the tuple belongs. The P-table shows the probability distribution on the possible worlds. The first PC-table represents the p-relation \(r_1\) and the second PC-table represents the p-relation \(r_2\) from Table 1. While all p-keys that are implied by this p-key set are satisfied by both PC-tables, every non-implied p-key is violated by at least one PC-table. For example, the implied p-key \(k\{\textit{time,zone}\}\in (0.6,0.8)\) is satisfied by the p-relations the tables represent, while the non-implied p-key \(k\{\textit{time,zone}\}\in (0.7,0.75)\) is violated by \(r_1\).
P-key profile of Table 2
Discovery: For the data-driven acquisition of p-keys we compute the probabilistic interval of any key as the smallest and largest marginal probabilities across all given PC-tables. For example, given the two PC-tables in Table 2, our algorithm would discover the profile of p-keys in Fig. 2. Experiments: Experiments show that our algorithms are efficient and scale linearly in our acquisition framework.
Organization. We discuss related work in Sect. 2. P-keys are introduced in Sect. 3. Computational problems are characterized in Sect. 4. The schema- and data-driven acquisition of p-keys is developed in Sect. 5. Experiment results are presented in Sect. 6. We conclude in Sect. 7.
2 Related Work
Poor data quality inhibits the transformation of data into value [23]. P-keys provide a well-founded, yet simple approach to balance the consistency and completeness targets for the quality of data. Keys are fundamental to most data models [3, 6, 9, 12, 15, 25, 26]. P-keys subsume keys from traditional relations [1, 2], covered by the special case where p-relations consist of one possible world only. There is substantial work on the discovery of “approximate” constraints, see [4, 16, 20] for recent surveys. Approximate means that not all tuples satisfy the given constraint, but exceptions are tolerable. P-keys are not approximate since they are either satisfied or violated by the given p-relation. Future work will investigate approximate p-keys. Possibilistic keys [11] are attributed some degree of certainty saying to which tuples they apply. Possibility theory is a qualitative approach, while probability theory is a quantitative approach to uncertainty. P-keys complements the qualitative approach to possibilistic keys from [11]. Keys with probabilistic intervals extend our own work on keys with lower bounds only [3]. The extension causes significant differences. Keys with intervals are more expressive as upper bounds smaller than 1 can be specified, addressing better any consistency and completeness targets. Sets of keys with intervals may not be satisfiable by any p-relation, while every set of keys with only lower bounds is satisfiable. While implication and inference problems become more complex for intervals, we succeed in establishing linear time algorithms. While keys with only lower bounds enjoy representations by a single Armstrong PC-table, keys with intervals require generally two PC-tables. This is an interesting novelty for Armstrong databases for which more than one database instance have not been considered in previous research. We also generalize the discovery problem for keys with intervals to a collection of input instances, while only single input instances were considered in [3] for keys with lower bounds.
3 Keys with Probabilistic Intervals
We introduce our notion of keys with probabilistic intervals after some preliminaries on probabilistic databases.
A relation schema is a finite set R of attributes A. Each attribute A is associated with a domain \(\textit{dom}(A)\) of values. A tuple t over R is a function that assigns to each attribute A of R an element t(A) from the domain \(\textit{dom}(A)\). A relation over R is a finite set of tuples over R. Relations over R are also called possible worlds of R here. An expression kX over R with \(X\subseteq R\) is called a key. A key kX is said to hold in a possible world W of R, denoted by  , if and only if there no two tuples \(t_1,t_2\in W\) such that \(t_1\not =t_2\) and \(t_1(X)=t_2(X)\). A probabilistic relation (p-relation) over R is a pair \(r=(\mathcal {W},P)\) of a finite non-empty set \(\mathcal {W}\) of possible worlds over R and a probability distribution \(P:\mathcal {W}\rightarrow (0,1]\) such that \(\sum _{W\in \mathcal {W}}P(W)=1\) holds. Table 1 shows two p-relations over relation schema Tracking = {rfid,time,zone}. World \(W_2\) of \(r_1\), for example, satisfies the keys \(k\{\textit{rfid},\textit{time}\}\) and \(k\{\textit{zone},\textit{time}\}\), but violates the key \(k\{\textit{rfid},\textit{zone}\}\). The marginal probability \(m_{X,r}\) of a key kX in the p-relation r is the sum of the probabilities of those possible worlds in r which satisfy kX. We will now introduce the central notion of a key with probabilistic intervals.
, if and only if there no two tuples \(t_1,t_2\in W\) such that \(t_1\not =t_2\) and \(t_1(X)=t_2(X)\). A probabilistic relation (p-relation) over R is a pair \(r=(\mathcal {W},P)\) of a finite non-empty set \(\mathcal {W}\) of possible worlds over R and a probability distribution \(P:\mathcal {W}\rightarrow (0,1]\) such that \(\sum _{W\in \mathcal {W}}P(W)=1\) holds. Table 1 shows two p-relations over relation schema Tracking = {rfid,time,zone}. World \(W_2\) of \(r_1\), for example, satisfies the keys \(k\{\textit{rfid},\textit{time}\}\) and \(k\{\textit{zone},\textit{time}\}\), but violates the key \(k\{\textit{rfid},\textit{zone}\}\). The marginal probability \(m_{X,r}\) of a key kX in the p-relation r is the sum of the probabilities of those possible worlds in r which satisfy kX. We will now introduce the central notion of a key with probabilistic intervals.
Definition 1
A key with probabilistic intervals, or p-key for short, over relation schema R is an expression \(kX\in (l,u)\) where \(X\subseteq R\), \(l,u\in [0,1]\), and \(l\le u\). The p-key \(kX\in (l,u)\) over R is satisfied by, or said to hold in, the p-relation r over R if and only if the marginal probability \(m_{X,r}\) of kX in r falls into the interval (l, u), that is, \(l\le m_{X,r}\le u\).
In our running example over relation schema Tracking, the p-relation \(r_2\) from Table 1 satisfies the p-keys \(k\{\textit{rfid},\textit{time}\}\in (0.7,0.75)\) and \(k\{\textit{time},\textit{zone}\}\in (0.3,0.8)\), but violates the p-keys \(k\{\textit{rfid},\textit{time}\}\in (0.7,0.7)\) and \(k\{\textit{time},\textit{zone}\}\in (0.3,0.65)\). The reasons are that \(m_{\{\textit{rfid},\textit{time}\},r_2}=m_{\{\textit{time},\textit{zone}\},r_2}=0.75\).
It is useful to separate a p-key into one key that stipulates the lower bound and one key that stipulates the upper bound. This allows users to focus on one bound at a time, but also allows us to gain a better understanding of their interaction. A key with lower bound, or l-key, is of the form \(kX\in (l,1)\), and we write \(kX_{\ge l}\). A key with upper bound, or u-key, is of the form \(kX\in (0,u)\), and written as \(kX_{\le u}\). For example, the p-key \(k\{\textit{time},\textit{zone}\}\in (0.65,0.75)\) can be rewritten as the l-key \(k\{\textit{time},\textit{zone}\}_{\ge 0.65}\) and the u-key \(k\{\textit{time},\textit{zone}\}_{\le 0.75}\). It follows directly that a p-relation satisfies a p-key iff it satisfies the corresponding l-key and u-key. L-keys were studied in [3]. First, we will study u-keys, and then combine them with l-keys.
4 Reasoning Tools
When using sets of p-keys to enforce the consistency and completeness targets on the quality of data, their overhead must be reduced to a minimal level necessary. In practice, this requires us to reason about p-keys efficiently. We will now establish tools to reason about the interaction of p-keys. This will help us identify efficiently (i) if a given set of p-keys is consistent, and (ii) the most concise interval by which a given key is implied from a given set of p-keys. This helps optimize query and update efficiency, but is also essential for developing our acquisition framework later.
4.1 Computational Problems
Let \(\varSigma \cup \{\varphi \}\) denote a set of constraints over relation schema R. We say that \(\varSigma \) is satisfiable, if there is some p-relation over R that satisfies all elements of \(\varSigma \); and say that \(\varSigma \) is unsatisfiable otherwise. We say \(\varSigma \) implies \(\varphi \), denoted by  , if every p-relation r over R that satisfies \(\varSigma \), also satisfies \(\varphi \). We use
, if every p-relation r over R that satisfies \(\varSigma \), also satisfies \(\varphi \). We use  to denote the semantic closure of \(\varSigma \). Let \(\mathcal {C}\) denote a class of constraints. The \(\mathcal {C}\)-satisfiability problem is to decide for a given relation schema R and a given set \(\varSigma \) of constraints in \(\mathcal {C}\) over R, whether \(\varSigma \) is satisfiable. The \(\mathcal {C}\)-implication problem is to decide for a given relation schema R and a given satisfiable set \(\varSigma \cup \{\varphi \}\) of constraints in \(\mathcal {C}\) over R, whether \(\varSigma \) implies \(\varphi \). If \(\mathcal {C}\) denotes the class of p-keys, then the \(\mathcal {C}\)-inference problem is to compute for a given relation schema R, a given satisfiable set \(\varSigma \) of p-keys, and a given key kX over R the largest probability l and the smallest probability u such that \(\varSigma \) implies \(kX\in (l,u)\). We will characterize the computational problems for u-keys first. Subsequently, we then show how to combine these results with our previous findings on l-keys to characterize the computational problems for p-keys.
to denote the semantic closure of \(\varSigma \). Let \(\mathcal {C}\) denote a class of constraints. The \(\mathcal {C}\)-satisfiability problem is to decide for a given relation schema R and a given set \(\varSigma \) of constraints in \(\mathcal {C}\) over R, whether \(\varSigma \) is satisfiable. The \(\mathcal {C}\)-implication problem is to decide for a given relation schema R and a given satisfiable set \(\varSigma \cup \{\varphi \}\) of constraints in \(\mathcal {C}\) over R, whether \(\varSigma \) implies \(\varphi \). If \(\mathcal {C}\) denotes the class of p-keys, then the \(\mathcal {C}\)-inference problem is to compute for a given relation schema R, a given satisfiable set \(\varSigma \) of p-keys, and a given key kX over R the largest probability l and the smallest probability u such that \(\varSigma \) implies \(kX\in (l,u)\). We will characterize the computational problems for u-keys first. Subsequently, we then show how to combine these results with our previous findings on l-keys to characterize the computational problems for p-keys.
4.2 Keys with Upper Bounds
Satisfiability. Unsatisfiability is strong evidence that a set of keys has been over-specified. While every set of l-keys is satisfiable, this is not the case for every set of u-keys. However, satisfiable sets are easy to characterize for u-keys: Unsatisfiability can only originate from stipulating an upper bound smaller than one for the trivial key kR.
Proposition 1
A set \(\varSigma \) of u-keys over relation schema R is satisfiable if and only if \(\varSigma \) does not contain a u-key of the form \(kR_{\le u}\) where \(u<1\). The satisfiability problem for u-keys can thus be decided with one scan over the input. \(\square \)
Axioms. We determine the semantic closure by applying inference rules of the form \(\frac{\text {premise}}{\text {conclusion}}\). For a set \(\mathfrak {R}\) of inference rules let \(\varSigma \vdash _\mathfrak {R}\varphi \) denote the inference of \(\varphi \) from \(\varSigma \) by \(\mathfrak {R}\). That is, there is some sequence \(\sigma _1,\ldots ,\sigma _n\) such that \(\sigma _n=\varphi \) and every \(\sigma _i\) is an element of \(\varSigma \) or is the conclusion that results from an application of an inference rule in \(\mathfrak {R}\) to some premises in \(\{\sigma _1,\ldots ,\sigma _{i-1}\}\). Let \(\varSigma ^+_\mathfrak {R}=\{\varphi \,:\,\varSigma \vdash _{\mathfrak {R}}\varphi \}\) be the syntactic closure of \(\varSigma \) under inferences by \(\mathfrak {R}\). \(\mathfrak {R}\) is sound (complete) if for every satisfiable set \(\varSigma \) over every R we have \(\varSigma ^+_\mathfrak {R}\subseteq \varSigma ^*\) (\(\varSigma ^*\subseteq \varSigma ^+_\mathfrak {R}\)). The (finite) set \(\mathfrak {R}\) is a (finite) axiomatization if \(\mathfrak {R}\) is both sound and complete. The set \(\mathfrak {U}\) of inference rules from Table 3 forms a finite axiomatization for the implication of u-keys. Here, R denotes the underlying relation schema, X and Y form attribute subsets of R, and p, q as well as \(p+q\) are probabilities.
Theorem 1
\(\mathfrak {U}\) forms a finite axiomatization for u-keys. \(\square \)
It is worth pointing out the soundness of the rules. The maximum rule \(\mathcal {M}\) holds trivially, because every marginal probability can at most be one. For the fragment rule \(\mathcal {F}\) assume that the marginal probability of kX exceeds p. Since every world that satisfies kX must also satisfy kXY, the marginal probability of kXY exceeds p, too. Finally, for the relax rule \(\mathcal {R}\) assume that the marginal probability of kX exceeds \(p+q\). Then the marginal probability of kX exceeds p, for sure. Some examples illustrate the use of the inference rule for reasoning about u-keys.
For example, \(\varSigma =\{k\{\textit{rfid,time}\}_{\le 0.75}\}\) implies \(\varphi =k\{\textit{time}\}_{\le 0.8}\), but not \(\varphi '=k\{\textit{time}\}_{\le 0.2}\). Indeed, \(\varphi \) can be inferred from \(\varSigma \) by applying \(\mathcal {F}\) to \(k\{\textit{rfid,time}\}_{\le 0.75}\) to infer \(k\{\textit{time}\}_{\le 0.75}\), and applying \(\mathcal {R}\) to \(k\{\textit{time}\}_{\ge 0.75}\) to infer \(\varphi \).
If a p-relation satisfies a set \(\varSigma \) of p-keys, then it also satisfies every p-key \(\varphi \) implied by \(\varSigma \). Consequently, it is redundant to verify that a given p-relation satisfies an implied p-key. In particular, the larger the given p-relation, the more time we save by avoiding such redundant validation checks.
Algorithms. In practice, the semantic closure \(\varSigma ^*\) of a finite set \(\varSigma \) is infinite and even though it can be represented finitely, it is often unnecessary to determine all implied constraints. In fact, the implication problem has input \(\varSigma \cup \{\varphi \}\) and the question is if \(\varSigma \) implies \(\varphi \). Computing \(\varSigma ^*\) and checking if \(\varphi \in \varSigma ^*\) is not feasible. We will now establish a linear-time algorithm for computing the smallest probability u, such that \(kX_{\le u}\) is implied by \(\varSigma \). The following theorem allows us to reduce the implication problem for u-keys to a single scan of the input.
Theorem 2
Let \(\varSigma \cup \{kX_{\le u}\}\) denote a satisfiable set of u-keys over relation schema R. Then \(\varSigma \) implies \(kX_{\le u}\) if and only if (i) \(u=1\) or (ii) there is some \(kZ_{\le q}\in \varSigma \) such that \(X\subseteq Z\) and \(q\le u\). \(\square \)
Based on Theorem 2, Algorithm 1 returns for a given satisfiable set \(\varSigma \) of u-keys and a given key kX over R, the smallest probability u such that \(kX_{\le u}\) is implied by \(\varSigma \). Starting with \(u=1\), the algorithm scans all input keys \(kZ_{\le q}\) and sets u to q whenever q is smaller than the current u and X is contained in Z. We use |S| to denote the total number of attributes that occur in set S.
Corollary 1
On input \((R,\varSigma ,kX)\), Algorithm 1 returns in \(\mathcal {O}(|\varSigma |+|R|)\) time the minimum probability u with which \(kX_{\le u}\) is implied by \(\varSigma \). \(\square \)
Given \(R,\varSigma ,kX_{\le p}\) as an input to the implication problem for u-keys, Algorithm 1 computes  and we return an affirmative answer iff \(u\le p\). Hence, the implication problem is linear time decidable in the input.
and we return an affirmative answer iff \(u\le p\). Hence, the implication problem is linear time decidable in the input.
Corollary 2
The implication problem of u-keys is decidable in linear time. \(\square \)
Given \(\varSigma =\{k\{\textit{rfid,time}\}_{\le 0.75}\}\) and \(k\{\textit{time}\}\), Algorithm 1 returns \(u=0.75\). For \(\varphi '=k\{\textit{time}\}_{\le 0.2}\), we conclude that \(\varSigma \) does not imply \(\varphi '\) as \(u>0.2\).

4.3 Keys with Probabilistic Intervals
We will now study p-keys as the combination of l-keys and u-keys. That is, we think of every set \(\varSigma \) of p-keys as the union of the set \(\varSigma _l:=\{kX_{\le p}\mid kX\in (p,q)\in \varSigma \}\) of l-keys and the set \(\varSigma _u:=\{kX_{\ge q}\mid kX\in (p,q)\in \varSigma \}\) of u-keys.
Satisfiability. While satisfiability for l-keys can be decided in constant time [3], and satisfiability for u-keys requires one scan over the input, the satisfiability problem for p-keys requires two scans over the input.
Proposition 2
A set \(\varSigma \) of p-keys over relation schema R is satisfiable if and only if \(\varSigma _l\cup \varSigma _u\cup \{kR_{\ge 1}\}\) does not contain \(kX_{\ge p}\), \(kXY_{\le q}\) such that \(p>q\). The satisfiability problem for p-keys is decidable with two scans over the input. \(\square \)
The set \(\varSigma =\{k\{\textit{rfid}\}\in (0.75,0.75), k\{\textit{rfid,time}\}\in (0.6,0.7)\}\) is unsatisfiable.
No interaction. We reduce the remaining computational problems for p-keys to those of u-keys and l-keys. This is possible since we can show that every satisfiable set of p-keys does not exhibit any interaction between its l-keys and u-keys. Formally, u-keys and l-keys do not interact if and only if for every relation schema R, every satisfiable set \(\varSigma \) of p-keys, every l-key \(kX_{\ge p}\) and every u-key \(kY_{\ge u}\) over R, the following two conditions hold:
-
 if and only if
if and only if 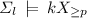 ,
, -
 if and only if
if and only if  .
.
In other words, the non-interaction between u-keys and l-keys enables us to reduce the implication problem for p-keys to the implication problems for u-keys and l-keys. That is, a p-key \(kX\in (p,q)\) is implied by a satisfiable set \(\varSigma \) of p-keys if and only if i) \(kX_{\ge p}\) is implied by \(\varSigma _l\), and ii) \(kX_{\le q}\) is implied by \(\varSigma _u\).
Theorem 3
U-keys and l-keys do not interact.
Proof (Sketch)
The non-trivial direction is to show the following: if  , then
, then  . If
. If  , then any Armstrong p-relation for \(\varSigma _l\) satisfies \(\varSigma _l\) and violates \(kX_{\ge p}\). Since \(\varSigma _u\cup \varSigma _l\) is satisfiable, it follows that the Armstrong p-relation for \(\varSigma _l\) also satisfies \(\varSigma _u\). Consequently,
, then any Armstrong p-relation for \(\varSigma _l\) satisfies \(\varSigma _l\) and violates \(kX_{\ge p}\). Since \(\varSigma _u\cup \varSigma _l\) is satisfiable, it follows that the Armstrong p-relation for \(\varSigma _l\) also satisfies \(\varSigma _u\). Consequently,  . The arguments works similarly when we know that
. The arguments works similarly when we know that  . We can create an Armstrong p-relation for \(\varSigma _u\), which must also satisfy \(\varSigma _l\) because \(\varSigma _u\cup \varSigma _l\) is satisfiable. \(\square \)
. We can create an Armstrong p-relation for \(\varSigma _u\), which must also satisfy \(\varSigma _l\) because \(\varSigma _u\cup \varSigma _l\) is satisfiable. \(\square \)
Theorem 3 allows us to reduce the implication and inference problems for p-keys to the implication and inference problems for l-keys and u-keys. As a first consequence, combining our axiomatizations for u-keys and l-keys yields an axiomatization for p-keys.
Corollary 3
Axiomatization \(\mathfrak {U}\) for u-keys from Theorem 1 together with axiomatization \(\mathfrak {P}\) for l-keys from [3] form a finite axiomatization for p-keys. \(\square \)
As a second consequence, we can also combine our inference algorithms for u-keys and l-keys to obtain an efficient inference algorithm for p-keys.
Corollary 4
Given relation schema R, a satisfiable set \(\varSigma \) of p-keys, and a key kX over R, we can return in \(\mathcal {O}(|\varSigma |+|R|)\) time the maximum probability l and the minimum probability u such that \(kX\in (l,u)\) is implied by \(\varSigma \). \(\square \)
Thirdly, the implication problem of p-keys can be decided efficiently.
Corollary 5
The implication problem of p-keys is decidable in linear time. \(\square \)
To decide if \(k\{\textit{time,zone}\}\in (0.6,0.7)\) is implied by the set \(\varSigma \) of p-keys from Fig. 2, we check if \(k\{\textit{time,zone}\}_{\ge 0.6}\) is implied by \(\varSigma _l\) and if \(k\{\textit{time,zone}\}_{\le 0.7}\) is implied by \(\varSigma _u\). As the second condition fails, the p-key is not implied by \(\varSigma \).
Our results show that it takes quadratic time in the input to keep the enforcement of p-key sets to a minimal level necessary: For a given p-key set, we can remove successively all p-keys from the set that are implied by the remaining set. More validation time is saved the bigger the underlying p-relations grow.
5 Tools for Acquiring Probabilistic Key Intervals
The main inhibitor to the uptake of p-keys is the difficulty to determine the right interval for the marginal probabilities by which keys hold in the underlying application domain. For that purpose, analysts should communicate with domain experts. We establish two major computational tools that help analysts communicate effectively with domain experts. We follow the framework in Fig. 3. Here, analysts use our algorithm to summarize abstract sets \(\varSigma \) of p-keys in the form of some Armstrong PC-base, which is then inspected jointly with domain experts. In particular, the two PC-tables that form together the PC-base represent simultaneously for every key kX their lowest and highest marginal probabilities that quality data sets in the target domain should exhibit. Domain experts may change the PC-tables or supply new PC-tables to the analysts. For that case we establish an algorithm that discovers p-keys from sets of PC-tables. That is, the algorithm computes the lowest and highest marginal probabilities of each key across all the given PC-tables. Such profiles are also useful for query optimization, for example.
5.1 Summarizing Abstract Sets of P-Keys as Armstrong PC-bases
Our results will show that every satisfiable set \(\varSigma \) of p-keys can be summarized in the form of two PC-tables such that all given p-keys are satisfied by the two p-relations the PC-tables represent, and all those p-keys not implied by \(\varSigma \) are violated by at least one of the p-relations. This notion generalizes the concept of an Armstrong database, which is a single database instance that satisfies a constraint if and only if it is implied by the given constraint set [5]. The reason why p-keys require two database instances is simple: Each instance can only represent one marginal probability, but p-keys generally require a lower and an upper bound on the marginal probability. So, unless every given key has the same lower and upper bounds, we require two database instances. The formal definition is therefore as follows.
Definition 2
Let \(\varSigma \) be a satisfiable set of p-keys over a given relation schema R. A pair of p-relation \(r_1,r_2\) over R is Armstrong for \(\varSigma \) if and only if for all p-keys \(\varphi \) over R it holds that \(r_1\) and \(r_2\) satisfy \(\varphi \) if and only if \(\varSigma \) implies \(\varphi \).
For example, the p-relations \(r_1,r_2\) from Table 1 are Armstrong for the set \(\varSigma \) of p-keys in Fig. 2. It is worth emphasizing the effectiveness of the definition: Knowing that \(r_1,r_2\) are Armstrong for a given \(\varSigma \) enables us to reduce every instance \(\varSigma \cup \{\varphi \}\) of the implication problem to simply checking if both \(r_1\) and \(r_2\) satisfy \(\varphi \). Knowing that u-keys and l-keys do not interact, we can compute \(r_1,r_2\) such that every instance \(\varSigma \cup \{kX\}\) of the inference problem is reduced to simply computing the lower (upper) bound l (u) in \(kX\in (l,u)\) as the marginal probability \(m_{X,r_1}\) (\(m_{X,r_2}\)) of kX in \(r_1\) (\(r_2\)). For example, the \(k\{\textit{time,zone}\}\in (0.6,0.7)\) is not implied by \(\varSigma \) from Fig. 2 as the given upper bound 0.7 is smaller than the marginal probability 0.75 of \(k\{\textit{time,zone}\}\) in \(r_2\).
Instead of computing Armstrong p-relations we compute PC-tables that are more concise representations. We call these Armstrong PC-bases. Recall the following standard definition from probabilistic databases [24]. A conditional table or c-table, is a tuple \(CD = \langle r,W\rangle \), where r is a relation, and W assigns to each tuple t in r a finite set \(W_t\) of positive integers. The set of world identifiers of CD is the union of the sets \(W_t\) for all tuples t of r. Given a world identifier i of CD, the possible world associated with i is \(W_i = \{ t | t\in r \text{ and } i\in W_t\}\). The semantics of a c-table \(CD = \langle r,W\rangle \), called representation, is the set \(\mathcal {W}\) of possible worlds \(W_i\) where i denotes some world identifier of CD. A probabilistic conditional database or PC-table, is a pair \(\langle CD,P\rangle \) where CD is a c-table, and P is a probability distribution over the set of world identifiers of CD. The set of possible worlds of a PC-table \(\langle CD,P\rangle \) is the representation of CD, and the probability of each possible world \(W_i\) is defined as the probability of its world identifier. For example, the PC-tables from Table 2 form an Armstrong PC-base for the set \(\varSigma \) of p-keys from Fig. 2.
Algorithm 2 in [3] computes a single Armstrong PC-table for every given set \(\varSigma \) of l-keys. In the construction, the number of possible worlds is given by the number of distinct lower bounds that occur in \(\varSigma \). Indeed, for every given set \(\varSigma \) of l-keys over R and every \(p\in (0,1]\), \(\varSigma _p=\{kX:\exists kX_{\ge q}\in \varSigma \wedge q\ge p\}\) denotes the p-cut of \(\varSigma \). If \(\varSigma \) does not contain a p-key \(kX_{\ge p}\) where \(p=1\), an Armstrong PC-table for \(\varSigma \) is computed that contains one more possible world than the number of distinct lower bounds in \(\varSigma \). Processing the bounds in \(\varSigma \) from smallest \(p_1\) to largest \(p_n\), the algorithm computes as possible world with probability \(p_i-p_{i-1}\) a traditional Armstrong relation for the \(p_i\)-cut \(\varSigma _{p_i}\). For this purpose, the anti-keys are computed for each \(p_i\)-cut, and the set W of those worlds i is recorded for which X is an anti-key with respect to \(\varSigma _{p_i}\). The CD-table contains one tuple \(t_0\) which occurs in all worlds, and for each anti-key X another tuple \(t_j\) that occurs in all worlds for which X is an anti-key and that has matching values with \(t_0\) in exactly the columns of X.
For example, applying this construction to the lower bounds of p-keys in Fig. 2 produces the PC-table on the left of Table 2. Indeed, let \(\varSigma \) consist of \(k\{\textit{rfid},\textit{time}\}_{\ge .75}\), \(k\{\textit{rfid},\textit{zone}\}_{\ge .35}\), and \(k\{\textit{time},\textit{zone}\}_{\ge .65}\). Then \(\varSigma _{.35}\) consists of \(k\{\textit{rfid},\textit{time}\}\), \(k\{\textit{rfid},\textit{zone}\}\), and \(k\{\textit{time},\textit{zone}\}\); \(\varSigma _{.65}\) consists of \(k\{\textit{rfid},\textit{time}\}\), and \(k\{\textit{time},\textit{zone}\}\); \(\varSigma _{.75}\) consists of \(k\{\textit{rfid},\textit{time}\}\); and \(\varSigma _{1}\) is empty. The world \(W_1\) has thus probability \(p_1=0.35\), and is an Armstrong relation for \(\varSigma _{0.35}\). Here, we have the three singleton anti-keys \(\{\textit{rfid}\}\), \(\{\textit{time}\}\), and \(\{\textit{zone}\}\). \(W_1\) has four tuples, the first and second tuple have matching values on \(\{\textit{rfid}\}\), the first and third tuple have matching values on \(\{\textit{zone}\}\), and the first and fourth tuple have matching values on \(\{\textit{time}\}\). This gives us the Armstrong relation \(W_1\) of \(r_1\) shown in Table 1. The world \(W_2\) has probability \(p_2=0.3\), and is an Armstrong relation for \(\varSigma _{0.65}\). Here, we have the two anti-keys \(\{\textit{time}\}\) and \(\{\textit{rfid},\textit{zone}\}\). The world \(W_3\) has probability \(p_3=0.1\), and is an Armstrong relation for \(\varSigma _{0.75}\). Here, we have the two anti-keys \(\{\textit{rfid},\textit{zone}\}\) and \(\{\textit{time},\textit{zone}\}\). Finally, \(W_4\) has probability \(p_4=0.25\), and is an Armstrong relation for \(\varSigma _{1}\). Here, we have the three anti-keys \(\{\textit{rfid},\textit{zone}\}\), \(\{\textit{time},\textit{zone}\}\), and \(\{\textit{rfid},\textit{time}\}\). Similar to \(W_1\) it is easy to see how \(W_2\), \(W_3\), and \(W_4\) of \(r_1\) in Table 1 constitute the corresponding Armstrong relations. Finally, we simply record the identifiers of those worlds in which a tuple appears to obtain the CD-table. This results in the CD-table shown in Table 2.
The outlined algorithm can also compute an Armstrong PC-table for every satisfiable set \(\varSigma \) of u-keys. The reason is that the algorithm is independent of whether we view the given probabilities as lower or upper bounds. The only necessary change concerns the definition of \(\varSigma _p\) which becomes \(\varSigma _p=\{kX:\exists kX_{\le q}\in \varSigma \wedge q\ge p\}\) in this case. For example, applying this construction to the upper bounds of p-keys in Fig. 2 results in the PC-table on the right of Table 2.
The use of this algorithm can be taken further when we consider Theorem 3, which states that u-keys and l-keys do not interact in satisfiable sets. This means, given a satisfiable set \(\varSigma \) of p-keys, we can compute an Armstrong PC-base for \(\varSigma \) by applying Algorithm 2 of [3] to compute an Armstrong PC-table for the set \(\varSigma _l\), and by applying Algorithm 2 of [3] to compute an Armstrong PC-table for the set \(\varSigma _u\). Indeed, we obtain an Armstrong PC-base for \(\varSigma \) by simply pairing the outputs of both applications together.
Theorem 4
For every satisfiable set \(\varSigma \) of p-keys over relation schema R, applications of Algorithm 2 in [3] to \(\varSigma _l\) and \(\varSigma _u\), respectively, result in an Armstrong PC-base for \(\varSigma \) in which the total number of possible worlds coincides with the sum of the distinct non-zero lower bounds in \(\varSigma '_l\) and the distinct non-zero upper bounds in \(\varSigma '_u\). Here, \(\varSigma '_l\) (\(\varSigma '_u\)) denotes \(\varSigma _l\) (\(\varSigma _u\)) if there is some \(X\subseteq R\) such that \(kX_{\ge 1}\in \varSigma _l\) (\(kX_{\le 1}\in \varSigma _u\)), and \(\varSigma _l\cup \{kR_{\ge 1}\}\) (\(\varSigma _u\cup \{kR_{\le 1}\}\)) otherwise. \(\square \)
The PC-tables of Table 2 form an Armstrong PC-base for the set \(\varSigma \) of p-keys in Fig. 2. Indeed, the number of possible worlds in both PC-tables is 4, which is the number of distinct non-zero lower bounds in \(\varSigma \) and also the number of distinct non-zero upper bounds in \(\varSigma \). Finally, we derive some bounds on the time complexity of finding Armstrong PC-tables. Additional insight is given by our experiments in Sect. 6.
Theorem 5
The time complexity to find an Armstrong PC-base for a given set \(\varSigma \) of p-keys over relation schema R is precisely exponential in \(|\varSigma |\).
Here, precisely exponential means that there is an algorithm which requires exponential time and that there are cases in which the number of tuples in the output is exponential in the input size. Nevertheless, there are also cases where the number of tuples in some Armstrong PC-base for \(\varSigma \) over R is logarithmic in \(|\varSigma |\). Such a case is given by \(R_n=\{A_1,\ldots ,A_{2n}\}\) and \(\varSigma _n=\{ k(X_1\cdots X_n)\in (1,1): X_i\in \{A_{2i-1},A_{2i}\}\text { for }i=1,\ldots ,n\}\) with \(|\varSigma _n|=n\cdot 2^n\).
5.2 Discovery of P-Keys from Collections of PC-tables
The discovery problem of p-keys from a collection of PC-tables over a relation schema R is to determine for all \(X\subset R\), the smallest marginal probability \(l_{X,r}\) and the largest marginal probability \(u_{X,r}\) of kX across all given p-relations \(r=(\mathcal {W},P)\) represented by some given PC-table. The problem of computing the marginal probability \(m_{X,r}\) can be solved as follows: For each \(X\subset R\), initialize \(m_{X,r}\leftarrow 0\) and for all worlds \(W\in \mathcal {W}\), add the probability \(p_W\) of W to \(m_{X,r}\), if X contains some minimal key of W. The set of minimal keys of a world W is given by the set of minimal transversals over the disagree sets of W (the complements of agree sets) [21]. For example, applying this algorithm to the PC-tables from Table 2 returns the p-keys shown in Fig. 2.
6 Experiments
In this section we report on some experiments regarding the computational complexity of our algorithms for the summarization and discovery of p-keys.
Summarization. While the worst-case time complexity of generating Armstrong PC-tables is exponential, these cases occur rarely in practice and at random. In our experiment we simulated average case behavior by generating sets of keys with upper/lower bounds. For each key, the set of attributes, the associated probability, and the type (either upper or lower) were randomly selected. First, we checked whether the created set of p-keys was satisfiable. If it was, one Armstrong PC-table was computed for the set of keys with upper bounds and one for the set of keys with lower bounds. Overall, 24 % of the p-key sets created were unsatisfiable. The average sizes and times to create the Armstrong PC-tables are shown in Fig. 4. The results demonstrate that Armstrong PC-bases exhibit small sizes on average, which makes them a practical tool to acquire keys with meaningful probabilistic intervals in a joint effort with domain experts. A screenshot of our graphical user interface is shown on the left of Fig. 5.
Discovery. The right of Fig. 5 shows the discovery times of p-keys from two given PC-tables. The input size is the total number of tuples in the input. We also applied a MapReduce implementation on a single node machine with 40 processors to the “Car” data setFootnote 1 of the UCI Machine Learning Repository. We converted “Car” into a p-relation with rising numbers of possible worlds and 500 tuples in each world. Figure 6 shows that our algorithm for the discovery of p-keys scales linearly in the number of possible worlds, considering this number is relatively low in our acquisition framework.
7 Conclusion and Future Work
We introduced keys with probabilistic intervals, which stipulate lower and upper bounds on the marginal probability by which keys shall hold on large volumes of uncertain data. Keys with probabilistic intervals provide a principled, yet simple enough mechanism to control the consistency and completeness targets for the quality of an organization’s uncertain data. Similar to how lower bounds say that a key is satisfied with some minimum probability, upper bounds provide us with means to say that a key is violated with a minimum probability. Our axiomatic and algorithmic reasoning tools minimize the overhead in using the keys for data quality management and query processing. Our findings for the visualization and discovery of these keys provide effective support for the efficient acquisition of the right probabilistic intervals that apply in a given application domain.
In future research we will apply our algorithms to investigate empirically the usefulness of our framework for acquiring the right probabilistic intervals of keys in a given application domain. This will require us to extend empirical measures from certain [17] to probabilistic data. Particularly intriguing is the question whether PC-bases or their p-relations are more useful. It is also interesting to investigate probabilistic variants of other useful constraint sets, such as functional, multivalued, and inclusion dependencies [7, 8, 10, 13, 14, 18, 19]. However, we have shown that such variants are not finitely axiomatizable. In this sense, our results for p-keys are rather special. An extension that seems feasible is to add lower bounds to the probabilistic cardinality constraints from [22].
References
Abedjan, Z., Golab, L., Naumann, F.: Profiling relational data: a survey. VLDB J. 24(4), 557–581 (2015)
Beeri, C., Dowd, M., Fagin, R., Statman, R.: On the structure of Armstrong relations for functional dependencies. J. ACM 31(1), 30–46 (1984)
Brown, P., Link, S.: Probabilistic keys for data quality management. In: Zdravkovic, J., Kirikova, M., Johannesson, P. (eds.) CAiSE 2015. LNCS, vol. 9097, pp. 118–132. Springer, Heidelberg (2015). doi:10.1007/978-3-319-19069-3_8
Caruccio, L., Deufemia, V., Polese, G.: Relaxed functional dependencies - a survey of approaches. IEEE Trans. Knowl. Data Eng. 28(1), 147–165 (2016)
Fagin, R.: Horn clauses and database dependencies. J. ACM 29(4), 952–985 (1982)
Hannula, M., Kontinen, J., Link, S.: On the finite and general implication problems of independence atoms and keys. J. Comput. Syst. Sci. 82(5), 856–877 (2016)
Hartmann, S., Link, S.: Multi-valued dependencies in the presence of lists. In: Beeri, C., Deutsch, A. (eds.) Proceedings of the Twenty-third ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, Paris, France, 14–16 June 2004, pp. 330–341. ACM (2004)
Hartmann, S., Link, S.: On a problem of Fagin concerning multivalued dependencies in relational databases. Theor. Comput. Sci. 353(1–3), 53–62 (2006)
Hartmann, S., Link, S.: Efficient reasoning about a robust XML key fragment. ACM Trans. Database Syst. 34(2) (2009). Article No.10
Hartmann, S., Link, S., Schewe, K.: Functional and multivalued dependencies in nested databases generated by record and list constructor. Ann. Math. Artif. Intell. 46(1–2), 114–164 (2006)
Koehler, H., Leck, U., Link, S., Prade, H.: Logical foundations of possibilistic keys. In: Fermé, E., Leite, J. (eds.) JELIA 2014. LNCS, vol. 8761, pp. 181–195. Springer, Heidelberg (2014). doi:10.1007/978-3-319-11558-0_13
Köhler, H., Leck, U., Link, S., Zhou, X.: Possible and certain keys for SQL. VLDB J. 25(4), 571–596 (2016)
Köhler, H., Link, S.: Inclusion dependencies reloaded. In: Bailey, J., Moffat, A., Aggarwal, C.C., de Rijke, M., Kumar, R., Murdock, V., Sellis, T.K., Yu, J.X. (eds.) Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, CIKM 2015, Melbourne, VIC, Australia, 19–23 October 2015, pp. 1361–1370. ACM (2015)
Köhler, H., Link, S.: SQL schema design: foundations, normal forms, and normalization. In: Özcan, F., Koutrika, G., Madden, S. (eds.) Proceedings of the 2016 International Conference on Management of Data, SIGMOD Conference 2016, San Francisco, CA, USA, 26 June–01 July 2016, pp. 267–279. ACM (2016)
Köhler, H., Link, S., Zhou, X.: Possible and certain SQL keys. PVLDB 8(11), 1118–1129 (2015)
Köhler, H., Link, S., Zhou, X.: Discovering meaningful certain keys from incomplete and inconsistent relations. IEEE Data Eng. Bull. 39(2), 21–37 (2016)
Langeveldt, W., Link, S.: Empirical evidence for the usefulness of Armstrong relations in the acquisition of meaningful functional dependencies. Inf. Syst. 35(3), 352–374 (2010)
Link, S.: Charting the completeness frontier of inference systems for multivalued dependencies. Acta Inf. 45(7–8), 565–591 (2008)
Link, S.: Characterisations of multivalued dependency implication over undetermined universes. J. Comput. Syst. Sci. 78(4), 1026–1044 (2012)
Liu, J., Li, J., Liu, C., Chen, Y.: Discover dependencies from data - a review. IEEE Trans. Knowl. Data Eng. 24(2), 251–264 (2012)
Mannila, H., Räihä, K.J.: Algorithms for inferring functional dependencies from relations. Data Knowl. Eng. 12(1), 83–99 (1994)
Roblot, T., Link, S.: Probabilistic cardinality constraints. In: Johannesson, P., Lee, M.L., Liddle, S.W., Opdahl, A.L., López, Ó.P. (eds.) ER 2015. LNCS, vol. 9381, pp. 214–228. Springer, Heidelberg (2015). doi:10.1007/978-3-319-25264-3_16
Sadiq, S. (ed.): Handbook of Data Quality. Springer, Heidelberg (2013)
Suciu, D., Olteanu, D., Ré, C., Koch, C.: Probabilistic Databases. Synthesis Lectures on Data Management. Morgan & Claypool Publishers, San Rafael (2011)
Thalheim, B.: On semantic issues connected with keys in relational databases permitting null values. Elektronische Informationsverarbeitung und Kybernetik 25(1/2), 11–20 (1989)
Toman, D., Weddell, G.E.: On keys and functional dependencies as first-class citizens in description logics. J. Autom. Reasoning 40(2–3), 117–132 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Brown, P., Ganesan, J., Köhler, H., Link, S. (2016). Keys with Probabilistic Intervals. In: Comyn-Wattiau, I., Tanaka, K., Song, IY., Yamamoto, S., Saeki, M. (eds) Conceptual Modeling. ER 2016. Lecture Notes in Computer Science(), vol 9974. Springer, Cham. https://doi.org/10.1007/978-3-319-46397-1_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-46397-1_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46396-4
Online ISBN: 978-3-319-46397-1
eBook Packages: Computer ScienceComputer Science (R0)







 if and only if
if and only if 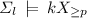 ,
, if and only if
if and only if  .
.


