Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The problem of driving an aerospace vehicle along a specified path leading to fulfilling the boundary conditions associated with the mission specifications requires defining the corrective actions aimed at compensating nonnominal flight conditions. This means that a feedback control law, or, equivalently, a closed-loop guidance algorithm, is to be defined, on the basis of the current state of the vehicle, evaluated at prescribed sampling times.

Traditionally, two different approaches to guidance exist. Adaptive algorithms compute the flight trajectory at the beginning of each guidance interval, on the basis of feasibility or optimality criteria [3, 19]. Perturbative algorithms assume a specified nominal trajectory, and define the feedback control corrections aimed at maintaining the vehicle in the proximity of the nominal path [7, 9].

Neighboring Optimal Guidance (NOG) is a perturbative guidance concept that relies on the analytical second order optimality conditions, in order to find the corrective control actions in the neighborhood of the reference trajectory. This is an optimal trajectory that satisfies the first and second-order optimality conditions. In general, the neighboring optimal path originates from a perturbed state and is associated with the minimization of the second differential of the objective function. Several time-varying gain matrices, referring to the nominal trajectory, are defined, computed offline, and stored in the onboard computer. Only a limited number of works have been devoted to studying neighboring optimal guidance [1, 4–6, 18, 21]. In particular, a thorough treatment of NOG is due to Chuang [5], who proposed a simple formula for updating the time of flight, and used a very basic strategy to evaluate the gain matrices when the time of flight exceeds its nominal value. Hull [6, 7] supplied further relevant contributions to the topic, using a vector that contains the unknown parameters to optimize and proposing an analytical formulation for the update of the time of flight, albeit only at the initial time. A common difficulty encountered in implementing the NOG consists in the fact that the gain matrices become singular while approaching the final time. As a result, the real-time correction of the time of flight can lead to numerical difficulties so relevant to cause the failure of the guidance algorithm.

This work describes and applies the recently introduced [15, 16], general-purpose variable-time-domain neighboring optimal guidance algorithm (VTD-NOG), on the basis of the general theory of NOG described in [7]. Some fundamental, original features of VTD-NOG are aimed at overcoming the main difficulties related to the use of former NOG schemes, in particular the occurrence of singularities and the lack of an efficient law for the iterative real-time update of the time of flight. This is achieved by adopting a normalized time domain, which leads to defining a novel updating law for the time of flight, a new termination criterion, and a new analytical formulation for the sweep method. Two applications are considered, for the purpose of illustrating the new guidance algorithm: (1) minimum-time-to-climb path of a Boeing 727 aircraft and (2) interception of fixed and moving targets. Specifically, perturbations arising from the imperfect knowledge of the propulsive thrust and from errors in the initial conditions are included in the dynamical modeling. In addition, atmospheric density fluctuations are modeled for application (1). Extensive Monte Carlo (MC) tests are performed, with the intent of demonstrating the effectiveness and accuracy of the variable-time-domain neighboring optimal guidance algorithm.

2 Nominal Trajectory

The nominal trajectory of aerospace vehicles is computed in the absence of any perturbation. For the purpose of applying a neighboring optimal guidance, the nominal path is required to be an optimal trajectory that minimizes a specified objective function.

In general, the spacecraft trajectory is described through the time-varying, n-dimensional state vector x(t) and controlled through the time-varying, m-dimensional control vector u(t); the dynamical evolution over the time interval [t 0, t f ] (with t 0 set to 0 and t f unspecified) depends also on the time-independent, \(\tilde{p}\)-dimensional parameter vector \(\tilde{\mathbf{a}}\). The governing state equations have the general form

$$\displaystyle{ \dot{\mathbf{x}} =\tilde{ \mathbf{f}}(\mathbf{x},\mathbf{u},\tilde{\mathbf{a}},t) }$$
(1)

and are subject to q boundary conditions

$$\displaystyle{ \boldsymbol{\psi }(\mathbf{x}_{0},\mathbf{x}_{f},\tilde{\mathbf{a}},t_{f}) = \mathbf{0} }$$
(2)

where the subscripts “0” and “f” refer to t 0 and t f . A feasible trajectory is a solution that obeys the state equations (1) and satisfies the boundary conditions (2).

The problem at hand can be reformulated by using the dimensionless normalized time τ defined as

$$\displaystyle{ \tau:= \frac{t} {t_{f}}\quad \Rightarrow \quad \tau _{0} \equiv 0 \leq \tau \leq 1 \equiv \tau _{f} }$$
(3)

Let the dot denote the derivative with respect to τ hence forward. If \(\mathbf{a}:= \left [\tilde{\mathbf{a}}\quad t_{f}\right ]^{T}\) (and \(p:=\tilde{ p} + 1\)), the state equations (1) are rewritten as

$$\displaystyle{ \dot{\mathbf{x}} = t_{f}\tilde{\mathbf{f}}(\mathbf{x},\mathbf{u},\tilde{\mathbf{a}},t_{f}\tau ) =: \mathbf{f}(\mathbf{x},\mathbf{u},\mathbf{a},\tau ) }$$
(4)

The objective functional to minimize has the following general form:

$$\displaystyle{ J =\phi (\mathbf{x}_{0},\mathbf{x}_{f},\mathbf{a}) +\int _{ 0}^{1}L\left [\mathbf{x}(\tau ),\mathbf{u}(\tau ),\mathbf{a},\tau \right ]d\tau }$$
(5)

The spacecraft trajectory optimization problem consists in identifying a feasible solution that minimizes the objective functional J, through selection of the optimal control law u ∗(t) and the optimal parameter vector a ∗, i.e.

$$\displaystyle{ \left \{\mathbf{u}^{{\ast}},\mathbf{a}^{{\ast}}\right \} =\arg \min _{\left \{\mathbf{ u},\mathbf{a}\right \}}J }$$
(6)

2.1 First-Order Necessary Conditions for a Local Extremal

In order to state the necessary conditions for optimality, a Hamiltonian H and a function of the boundary conditions Φ are defined as [7]

$$\displaystyle{ H(\mathbf{x},\mathbf{u},\mathbf{a},\boldsymbol{\lambda },\tau ):= L +\boldsymbol{\lambda } ^{T}\mathbf{f}\quad \quad \varPhi (\mathbf{x}_{ 0},\mathbf{x}_{f},\mathbf{a},\boldsymbol{\upsilon }):=\phi +\boldsymbol{\upsilon }^{T}\boldsymbol{\psi } }$$
(7)

where the time-varying, n-dimensional costate vector \(\boldsymbol{\lambda }(\tau )\) and the time-independent, q-dimensional vector \(\boldsymbol{\upsilon }\) are the adjoint variables conjugate to the state equations (4) and to the conditions (2), respectively.

In the presence of an optimal (locally minimizing) solution, the following conditions hold:

$$\displaystyle{ \mathbf{u}^{{\ast}} =\arg \min _{\mathbf{ u}}H }$$
(8)
$$\displaystyle{ \dot{\boldsymbol{\lambda }}= -\left [\frac{\partial H} {\partial \mathbf{x}} \right ]^{T} }$$
(9)
$$\displaystyle{ \boldsymbol{\lambda }_{0} = -\left [ \frac{\partial \varPhi } {\partial \mathbf{x}_{0}}\right ]^{T}\qquad \boldsymbol{\lambda }_{ f} = \left [ \frac{\partial \varPhi } {\partial \mathbf{x}_{f}}\right ]^{T} }$$
(10)
$$\displaystyle{ \left [ \frac{\partial \varPhi } {\partial \mathbf{a}}\right ]^{T} +\int _{ 0}^{1}\left [\frac{\partial H} {\partial \mathbf{a}} \right ]^{T}d\tau = \mathbf{0} }$$
(11)

For the very general Hamiltonian (7) the Pontryagin minimum principle (8) yields the control variables as functions of the adjoint variables and the state variables; the relations (9) are the adjoint (or costate) equations, together with the related boundary conditions (10); (11) is equivalent to p algebraic scalar equations. If the control u is unconstrained, then (8) implies that H is stationary with respect to u along the optimal path, i.e.

$$\displaystyle{ H_{\mathbf{u}}^{{\ast}} = \mathbf{0}^{T} }$$
(12)

Equations (8) through (11) are well established in optimal control theory (and are proven, for instance, in [7]), and allow translating the optimal control problem into a two-point boundary-value problem. Unknowns are the state x, the parameter vector a, and the adjoint variables \(\boldsymbol{\lambda }\) and \(\boldsymbol{\upsilon }\) (while the optimal control u ∗ is given by (8), as previously remarked). It is straightforward to demonstrate that the condition (11) is equivalent to

$$\displaystyle{ \boldsymbol{\mu }_{f} -\left [ \frac{\partial \varPhi } {\partial \mathbf{a}}\right ]^{T} = \mathbf{0},\quad \text{with}\quad \dot{\boldsymbol{\mu }} = -\left [\frac{\partial H} {\partial \mathbf{a}} \right ]^{T}\quad \text{and}\quad \boldsymbol{\mu }_{ 0} = \mathbf{0} }$$
(13)

where \(\boldsymbol{\mu }_{0}\) and \(\boldsymbol{\mu }_{f}\) are, respectively, the initial and final value (at τ = 1) of the time-varying (p × 1)-vector \(\boldsymbol{\mu }\).

2.2 Second-Order Sufficient Conditions for a Local Minimum

The derivation of the second-order optimality conditions involves the definition of an admissible comparison path, located in the neighborhood of the (local) nominal, optimal solution, associated with the state x ∗, costate \(\boldsymbol{\lambda }^{{\ast}}\), and control u ∗. By definition, an admissible comparison path is a feasible trajectory that satisfies the equations of motion and the boundary conditions. A neighboring optimal path is an admissible comparison trajectory that satisfies also the optimality conditions. The nonexistence of alternative neighboring optimal paths is to be proven in order to guarantee optimality of the nominal solution [7, 8].

The first second-order condition is the Clebsch-Legendre sufficient condition for a minimum [7, 8], i.e. H uu ∗ > 0 (positive definiteness of H uu ∗). In the necessary (weak) form the Hessian H uu ∗ must be positive semidefinite.

In general, a neighboring optimal path located in the proximity of the optimal solution fulfills the feasibility equations (4) and (2) and the optimality conditions (8)–(11) to first order. This means that the state and costate displacements \(\{\delta \mathbf{x},\delta \boldsymbol{\lambda }\}\) (from the optimal solution) satisfy the linear equations deriving from (4) and (9),

$$\displaystyle{ \delta \dot{\mathbf{x}} = \mathbf{f}_{\mathbf{x}}\delta \mathbf{x} + \mathbf{f}_{\mathbf{u}}\delta \mathbf{u} + \mathbf{f}_{\mathbf{a}}\delta \mathbf{a} }$$
(14)
$$\displaystyle{ \delta \dot{\boldsymbol{\lambda }}= -H_{\mathbf{x}\mathbf{x}}\delta \mathbf{x} - H_{\mathbf{x}\mathbf{u}}\delta \mathbf{u} - H_{\mathbf{x}\boldsymbol{\lambda }}\delta \boldsymbol{\lambda } - H_{\mathbf{x}\mathbf{a}}\delta \mathbf{a} }$$
(15)

in conjunction with the respective linear boundary conditions, derived from (2) and (10),

$$\displaystyle{ \boldsymbol{\psi }_{\mathbf{x}_{f}}\delta \mathbf{x}_{f} +\boldsymbol{\psi } _{\mathbf{x}_{0}}\delta \mathbf{x}_{0} +\boldsymbol{\psi } _{\mathbf{a}}\delta \mathbf{a} = \mathbf{0} }$$
(16)
$$\displaystyle{ \delta \boldsymbol{\lambda }_{0} = -\varPhi _{\mathbf{x}_{0}\mathbf{x}_{0}}\delta \mathbf{x}_{0} -\varPhi _{\mathbf{x}_{0}\mathbf{a}}\delta \mathbf{a} -\boldsymbol{\psi }_{\mathbf{x}_{0}}^{T}d\boldsymbol{\upsilon } }$$
(17)
$$\displaystyle{ \delta \boldsymbol{\lambda }_{f} =\varPhi _{\mathbf{x}_{f}\mathbf{x}_{f}}\delta \mathbf{x}_{f} +\varPhi _{\mathbf{x}_{f}\mathbf{a}}\delta \mathbf{a} +\boldsymbol{\psi }_{ \mathbf{x}_{f}}^{T}d\boldsymbol{\upsilon } }$$
(18)

The fact that the Hamiltonian is stationary with respect to u, i.e. H u ∗ = 0 T, yields

$$\displaystyle{ H_{\mathbf{u}\mathbf{x}}\delta \mathbf{x} + H_{\mathbf{u}\mathbf{u}}\delta \mathbf{u} + H_{\mathbf{u}\mathbf{a}}\delta \mathbf{a} + H_{\mathbf{x}\boldsymbol{\lambda }}\delta \boldsymbol{\lambda } = \mathbf{0} }$$
(19)

Under the assumption that the Clebsch-Legendre condition is satisfied, (19) is solved for δ u

$$\displaystyle{ \delta \mathbf{u} = -H_{\mathbf{u}\mathbf{u}}^{-1}\left (H_{\mathbf{ u}\mathbf{x}}\delta \mathbf{x} + H_{\mathbf{u}\mathbf{a}}\delta \mathbf{a} + H_{\mathbf{x}\boldsymbol{\lambda }}\delta \boldsymbol{\lambda }\right ) }$$
(20)

The parameter condition (11) is replaced by (13), leading to the following relations:

$$\displaystyle{ \delta \dot{\boldsymbol{\mu }}= -H_{\mathbf{a}\mathbf{x}}\delta \mathbf{x} - H_{\mathbf{a}\mathbf{u}}\delta \mathbf{u} - H_{\mathbf{a}\mathbf{a}}\delta \mathbf{a} - H_{\mathbf{a}\boldsymbol{\lambda }}\delta \boldsymbol{\lambda },\quad \text{with} }$$
(21)
$$\displaystyle{ \delta \boldsymbol{\mu }_{0} = \mathbf{0},\quad \delta \boldsymbol{\mu }_{f} = -\varPhi _{\mathbf{a}\mathbf{x}_{f}}\delta \mathbf{x}_{f} -\varPhi _{\mathbf{a}\mathbf{a}}\delta \mathbf{a} -\boldsymbol{\psi }_{\mathbf{a}}^{T}d\boldsymbol{\upsilon } }$$
(22)

where (22) is written under the assumption that \(\varPhi _{\mathbf{a}\mathbf{x}_{ 0}} = \mathbf{0}\), condition that is met for the problems at hand. It is relatively straightforward to recognize that solving the equation system (14)–(19) and (21)–(22) is equivalent to solving the accessory optimization problem [7, 8], which consists in minimizing the second differential d 2 J. The solution process involves the definition of the sweep variables, through the following relations:

$$\displaystyle{ \delta \boldsymbol{\lambda }= \mathbf{S}\delta \mathbf{x} + \mathbf{R}d\boldsymbol{\upsilon } + \mathbf{m}d\mathbf{a},\,\, }$$
(23)
$$\displaystyle{ \mathbf{0} = \mathbf{R}\delta \mathbf{x} + \mathbf{Q}d\boldsymbol{\upsilon } + \mathbf{n}d\mathbf{a},\,\, }$$
(24)
$$\displaystyle{ \delta \boldsymbol{\mu }= \mathbf{m}\delta \mathbf{x} + \mathbf{n}^{T}d\boldsymbol{\upsilon } +\boldsymbol{\alpha } d\mathbf{a} }$$
(25)

The matrices S, R, m, Q, n, and \(\boldsymbol{\lambda }\) must satisfy the sweep equations (not reported for the sake of conciseness), in conjunction with the respective boundary conditions (prescribed at the final time) [7, 8]. The variations \(d\boldsymbol{\upsilon }\) and d a can be solved simultaneously at τ 0 (at which \(\delta \boldsymbol{\mu }_{0} = \mathbf{0}\), cf. (22)), to yield

$$\displaystyle{ \left [\begin{array}{c} d\boldsymbol{\upsilon }\\ d\mathbf{a} \end{array} \right ] = -\mathbf{V}_{0}^{-1}\mathbf{U}_{ 0}^{T}\delta \mathbf{x}_{ 0}\quad \text{where}\quad \mathbf{U}:= \left [\mathbf{R}\,\,\,\mathbf{m}\right ]\quad \text{and}\quad \mathbf{V}:= \left [\begin{array}{c c} \mathbf{Q} &\mathbf{n} \\ \mathbf{n}^{T}& \boldsymbol{\alpha } \end{array} \right ] }$$
(26)

If (26) is used at τ 0, then \(\delta \boldsymbol{\lambda }_{0} = \left (\mathbf{S}_{0} -\mathbf{U}_{0}\mathbf{V}_{0}^{-1}\mathbf{U}_{0}^{T}\right )\delta \mathbf{x}_{0}\). Letting \(\hat{\mathbf{S}} = \mathbf{S} -\mathbf{U}\mathbf{V}^{-1}\mathbf{U}^{T}\), the same sweep equation satisfied by S turns out to hold also for \(\hat{\mathbf{S}}\), with boundary condition S → 0 as τ → τ f  ( = 1). From the previous relation on \(\delta \boldsymbol{\lambda }_{0}\) and δ x 0 one can conclude that \(\delta \boldsymbol{\lambda }_{0} \rightarrow \mathbf{0}\) as δ x 0 → 0, unless \(\hat{\mathbf{S}}\) tends to infinity at an internal time \(\bar{\tau }\,(\tau _{0} \leq \bar{\tau }<\tau _{f})\), which is referred to as conjugate point. If \(\delta \boldsymbol{\lambda }_{0} \rightarrow \mathbf{0}\) and δ x 0 → 0 then also δ u → 0. In the end, if \(\hat{\mathbf{S}} <\infty\), then no neighboring optimal path exists. This is the Jacobi condition. The use of S is not effective for the purpose of guaranteeing optimality. In fact, cases exist for which S becomes singular, while \(\hat{\mathbf{S}}\) remains finite [7, 8], and this fully justifies the use of \(\hat{\mathbf{S}}\).

It is worth remarking that, with the exception of the displacements \(\{\delta \mathbf{x},\delta \mathbf{u},\delta \mathbf{a},\ \delta \boldsymbol{\upsilon },\delta \boldsymbol{\lambda },\delta \boldsymbol{\mu },\delta \mathbf{x}_{0},\delta \mathbf{x}_{f}\}\), all the vectors and matrices reported in this section are evaluated along the nominal, optimal trajectory.

3 Variable-Time-Domain Neighboring Optimal Guidance

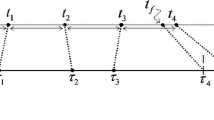
The iterative Variable-Time-Domain Neighboring Optimal Guidance (VTD-NOG) uses the optimal trajectory as the reference path, with the final intent of determining the control correction at each sampling time \(\left \{t_{k}\right \}_{k=0,\ldots,n_{S}}\). These are the times at which the displacement between the actual trajectory, associated with x, and the nominal trajectory, corresponding to x ∗, is evaluated, to yield d x k  ≡ δ x k  = x(t k ) −x k ∗(t k ). The total number of sampling times, n S , is unspecified, whereas the actual time interval between two successive sampling times is given and denoted with Δ t S , Δ t S  = t k+1 − t k . It is apparent that a fundamental ingredient needed to implement VTD-NOG is the formula for determining the overall time of flight t f (k) at time t k . This is equivalent to finding the time-to-go \(\left (t_{f}^{(k)} - t_{k}\right )\) at t k . The following subsection is focused on this issue.

3.1 Time-to-Go Updating Law and Termination Criterion

The fundamental principle that underlies the VTD-NOG scheme consists in finding the control correction δ u(τ) in the generic interval \(\left [\tau _{k},\tau _{k+1}\right ]\) such that the second differential of J is minimized,

$$\displaystyle{ \begin{array}{l} d^{2}J =\int _{ \tau _{k}}^{1}\left [\begin{array}{c} \delta \mathbf{x}\\ \delta \mathbf{u} \\ d\mathbf{a}\end{array} \right ]^{T}\left [\begin{array}{ccc} H_{\mathbf{xx}}&H_{\mathbf{xu}}&H_{\mathbf{xa}} \\ H_{\mathbf{ux}}&H_{\mathbf{uu}}&H_{\mathbf{ua}} \\ H_{\mathbf{ax}}&H_{\mathbf{au}}&H_{\mathbf{aa}} \end{array} \right ]\left [\begin{array}{c} \delta \mathbf{x}\\ \delta \mathbf{u} \\ d\mathbf{a}\end{array} \right ]d\tau \\ \qquad + \left [\begin{array}{c} d\mathbf{x}_{k} \\ d\mathbf{x}_{f} \\ d\mathbf{a} \end{array} \right ]^{T}\left [\begin{array}{ccc} \varPhi _{\mathbf{x}_{k}\mathbf{x}_{k}} &\mathbf{0}_{n\times n}&\mathbf{0}_{n\times p} \\ \mathbf{0}_{n\times n}& \varPhi _{\mathbf{x}_{f}\mathbf{x}_{f}} & \varPhi _{\mathbf{x}_{f}\mathbf{a}} \\ \mathbf{0}_{p\times n}& \varPhi _{\mathbf{a}\mathbf{x}_{f}} & \varPhi _{\mathbf{a}\mathbf{a}} \end{array} \right ]\left [\begin{array}{c} d\mathbf{x}_{k} \\ d\mathbf{x}_{f} \\ d\mathbf{a} \end{array} \right ] \end{array} }$$
(27)

while holding the first-order expansions of the state equations, the related final conditions, and the parameter condition (i.e., the second of (22)). In contrast, the first of (22) cannot be used, because in general \(\delta \boldsymbol{\mu }_{k}\neq \mathbf{0}\) at τ k . Minimizing the objective (27) is equivalent to solving the accessory optimization problem, defined in the interval \(\left [\tau _{k},1\right ]\). This means that the relations reported in Sect. 2.2 need to be extended to the generic interval \(\left [\tau _{k},1\right ]\).

Other than the linear expansion of the state and costate equations, the related boundary conditions, and the second relation of (22), also Eqs. (23)–(25), (19), and (20) remain unchanged. However, now (26) is to be evaluated at τ k and becomes

$$\displaystyle{ \left [\begin{array}{c} d\boldsymbol{\upsilon }\\ d\mathbf{a} \end{array} \right ] = -\mathbf{V}_{k}^{-1}\mathbf{U}_{ k}^{T}\delta \mathbf{x}_{ k}-\mathbf{V}_{k}^{-1}\boldsymbol{\varTheta }\delta \boldsymbol{\mu }_{ k},\quad \text{with}\quad \boldsymbol{\varTheta } = \left [\begin{array}{c} \mathbf{0}_{q\times p} \\ \mathbf{I}_{p\times p} \end{array} \right ] }$$
(28)

because \(\delta \boldsymbol{\mu }_{k}\neq \mathbf{0}\) (unlike \(\delta \boldsymbol{\mu }_{0} = \mathbf{0}\)). The latter relation supplies the corrections \(d\boldsymbol{\upsilon }\) and d a at τ k as functions of the gain matrices U and V (defined in (26)), evaluated at τ k , and \(\delta \boldsymbol{\mu }_{k}\) (coming from the numerical integration of (21) in the preceding interval \(\left [\tau _{k-1},\tau _{k}\right ]\)). Equation (28) contains the updating law of the total flight time t f , which is included as a component of a. Hence, if dt f (k) denotes the correction on t f ∗ evaluated at τ k , then t f (k) = t f ∗ + dt f (k). As the sampling interval Δ t S is specified, the general formula for τ k is

$$\displaystyle{ \tau _{k} =\sum _{ j=0}^{k-1} \frac{\varDelta t_{S}} {t_{f}^{(j)}} }$$
(29)

The overall number of intervals n S is found at the first occurrence of the following condition, associated with the termination of VTD-NOG:

$$\displaystyle{ \sum _{j=0}^{n_{S}-1} \frac{\varDelta t_{S}} {t_{f}^{(j)}} \geq \ 1\qquad \Rightarrow \qquad \tau _{n_{S}} = 1 }$$
(30)

It is worth stressing that the updating formula (28) derives directly from the natural extension of the accessory optimization problem to the time interval \(\left [\tau _{k},1\right ]\). In addition, the introduction of the normalized time τ now reveals its great utility. In fact, all the gain matrices are defined in the normalized interval [0,1] and cannot become singular. Moreover, the limiting values \(\left \{\tau _{k}\right \}_{k=0,\ldots,n_{S}-1}\) are dynamically calculated at each sampling time using (29), while the sampling instants in the actual time domain are specified and equally spaced (cf. Fig. 1). Also the termination criterion (30) has a logical, consistent definition, and corresponds to the upper bound of the interval [0,1], to which τ is constrained.

Fig. 1
figure 1

Illustrative sketch of the relations between the two time domains

Full size image

3.2 Modified Sweep Method

The definition of a neighboring optimal path requires the numerical backward integration of the sweep equations [7]. However, as previously remarked, the matrix \(\hat{\mathbf{S}}\) has practical utility, because S may become singular while \(\hat{\mathbf{S}}\) remains finite in the interval [0,1[. Therefore, a suitable integration technique is based on using the classical sweep equations in the interval \(\left [\tau _{sw},1\right ]\) (where τ sw is sufficiently close to τ f  = 1) and then switching to \(\hat{\mathbf{S}}\). However, due to (28), new relations are to be derived for \(\hat{\mathbf{S}}\) and the related matrices.

With this intent, the first step consists in combining (28) with (23)–(24), and leads to obtaining

$$\displaystyle{ \delta \boldsymbol{\lambda }= \left (\hat{\mathbf{S}} -\mathbf{W}\mathbf{m}^{T}\right )\delta \mathbf{x} -\mathbf{W}\mathbf{n}^{T}d\boldsymbol{\upsilon } -\mathbf{W}\boldsymbol{\alpha }d\mathbf{a},\quad \text{with}\quad \mathbf{W}:= \mathbf{U}\mathbf{V}^{-1}\boldsymbol{\varTheta } }$$
(31)

This relation replaces (23).

Equation (31) is to be employed repeatedly in the derivation of new sweep equations. The related analytical developments are described in full detail in [15], and lead to attaining the following modified sweep equations:

$$\displaystyle{ \dot{\hat{\mathbf{S}}} = -\hat{\mathbf{S}}\mathbf{A}+\hat{\mathbf{S}}\mathbf{B}\hat{\mathbf{S}}+\left [\hat{\mathbf{S}}\mathbf{D}\boldsymbol{\alpha }^{-1} + \mathbf{W}\mathbf{F}\boldsymbol{\alpha }^{-1} + \mathbf{E}\boldsymbol{\alpha }^{-1}\right ]\mathbf{m}^{T}-\mathbf{W}\mathbf{E}^{T}-\mathbf{W}\mathbf{D}^{T}\hat{\mathbf{S}}-\mathbf{C}-\mathbf{A}^{T}\hat{\mathbf{S}} }$$
(32)
$$\displaystyle{ \dot{\mathbf{R}}^{T} = \mathbf{R}^{T}\mathbf{B}\hat{\mathbf{S}} -\mathbf{R}^{T}\mathbf{A} -\mathbf{R}^{T}\mathbf{B}\mathbf{W}\mathbf{m}^{T} }$$
(33)
$$\displaystyle{ \dot{\mathbf{m}}^{T} = -\mathbf{m}^{T}\mathbf{A} + \mathbf{m}^{T}\mathbf{B}\hat{\mathbf{S}} -\mathbf{m}^{T}\mathbf{B}\mathbf{W}\mathbf{m}^{T} -\mathbf{E}^{T} -\mathbf{D}^{T}\hat{\mathbf{S}} + \mathbf{D}^{T}\mathbf{W}\mathbf{m}^{T} }$$
(34)
$$\displaystyle{ \dot{\mathbf{Q}} = -\mathbf{R}^{T}\mathbf{B}\mathbf{W}\mathbf{n}^{T} }$$
(35)
$$\displaystyle{ \dot{\mathbf{n}} = -\mathbf{R}^{T}\left (\mathbf{D} + \mathbf{B}\mathbf{W}\boldsymbol{\alpha }\right ) }$$
(36)
$$\displaystyle{ \dot{\boldsymbol{\alpha }}= \mathbf{D}^{T}\mathbf{W}\boldsymbol{\alpha } -\mathbf{F} -\mathbf{m}^{T}\mathbf{B}\mathbf{W}\boldsymbol{\alpha } -\mathbf{m}^{T}\mathbf{D} }$$
(37)

The gain matrices involved in the sweep method, i.e. S, \(\hat{\mathbf{S}}\), R, Q, n, m, and \(\boldsymbol{\alpha }\), can be integrated backward in two steps:

  1. 1.

    in \(\left [\tau _{sw},1\right ]\) the equations of the classical sweep method [7, 15], with the respective boundary conditions, are used.

  2. 2.

    in \(\left [0,\tau _{sw}\right ]\) (32) through (37) are used; R, Q, n, m, and \(\boldsymbol{\alpha }\) are continuous across the time τ sw , whereas \(\hat{\mathbf{S}}\) is given by \(\hat{\mathbf{S}}:= \mathbf{S} -\mathbf{U}\mathbf{V}^{-1}\mathbf{U}^{T}\); in this work, τ sw is set to 0.99.

3.3 Preliminary Offline Computations and Algorithm Structure

The implementation of VTD-NOG requires several preliminary computations that can be completed offline and stored in the onboard computer. First of all, the optimal trajectory is to be determined, together with the related state, costate, and control variables, which are assumed as the nominal ones. In the time domain τ these can be either available analytically or represented as sequences of equally spaced values, e.g. \(\mathbf{u}_{i}^{{\ast}} = \mathbf{u}^{{\ast}}(\tau _{i})\ (i = 0,\ldots,n_{D};\,\,\tau _{0} = 0\,\,\text{and}\,\,\tau _{n_{D}} = 1)\). However, in the presence of perturbations, VTD-NOG determines the control corrections δ u(τ) in each interval \(\left [\tau _{k},\tau _{k+1}\right ]\), where the values \(\left \{\tau _{k}\right \}\) never coincide with the equally spaced values \(\left \{\tau _{i}\right \}\) used for u i ∗. Hence, regardless of the number of points used to represent the control correction δ u(τ) in \(\left [\tau _{k},\tau _{k+1}\right ]\), it is apparent that a suitable interpolation is to be adopted for the control variable u ∗ (provided that no analytical expression is available). In this way, the value of u ∗ can be evaluated at any arbitrary time in the interval 0 ≤ τ ≤ 1. For the same reason also the nominal state x ∗ and costate \(\boldsymbol{\lambda }^{{\ast}}\) need to be interpolated. If a sufficiently large number of points is selected (e.g., n D  = 1001), then piecewise linear interpolation is a suitable option. The successive step is the analytical derivation of the matrices

$$\displaystyle{ \left \{\begin{array}{l} \mathbf{f}_{\mathbf{x}},\mathbf{f}_{\mathbf{u}},\mathbf{f}_{\mathbf{a}},H_{\mathbf{x}\mathbf{x}},H_{\mathbf{x}\mathbf{u}},H_{\mathbf{x}\boldsymbol{\lambda }},H_{\mathbf{x}\mathbf{a}},H_{\mathbf{u}\mathbf{x}},H_{\mathbf{u}\mathbf{u}},H_{\mathbf{u}\mathbf{a}},H_{\mathbf{u}\boldsymbol{\lambda }},H_{\mathbf{a}\mathbf{x}},H_{\mathbf{a}\mathbf{u}},H_{\mathbf{a}\mathbf{a}},H_{\mathbf{a}\boldsymbol{\lambda }},\\ \boldsymbol{\psi }_{\mathbf{x} _{f } },\boldsymbol{\psi } _{\mathbf{x} _{0 } },\boldsymbol{\psi } _{\mathbf{a} },\varPhi _{\mathbf{x} _{0 } \mathbf{x} _{0 } },\varPhi _{\mathbf{x} _{0 } \mathbf{a} },\varPhi _{\mathbf{x} _{f } \mathbf{x} _{f } },\varPhi _{\mathbf{x} _{f } \mathbf{a} },\varPhi _{\mathbf{a} \mathbf{x} _{f } },\varPhi _{\mathbf{a} \mathbf{a} } \end{array} \right \} }$$
(38)

Then, they are evaluated along the nominal trajectory and linearly interpolated, as well as A, B, C, D, E, and F, whose expressions are reported in [17]. Subsequently, the two-step backward integration of the sweep equations described in Sect. 3.2 is performed, and yields the gain matrices \(\hat{\mathbf{S}}\), R, m, Q, n, and \(\boldsymbol{\alpha }\), using also the analytic expressions of W, U, and V. The linear interpolation of all the matrices not yet interpolated concludes the preliminary computations.

On the basis of the optimal reference path, at each time τ k the VTD-NOG algorithm determines the time of flight and the control correction. More specifically, after setting the actual sampling time interval Δ t S , at each \(\tau _{k}\ \left (k = 0,\ldots,n_{S} - 1;\,\,\tau _{0} = 0\right )\) the following steps implement the feedback guidance scheme:

  1. 1.

    Evaluate δ x k .

  2. 2.

    Assume the value of \(\delta \boldsymbol{\mu }\) calculated at the end of the previous interval \(\left [\tau _{k-1},\tau _{k}\right ]\) as \(\delta \boldsymbol{\mu }_{k}\,\,(\delta \boldsymbol{\mu }_{0} = \mathbf{0})\).

  3. 3.

    Calculate the correction dt f (k) and the updated time of flight t f (k).

  4. 4.

    Calculate the limiting value τ k+1.

  5. 5.

    Evaluate \(\delta \boldsymbol{\lambda }_{k}\).

  6. 6.

    Integrate numerically the linear differential system composed of (14), (15), and (21).

  7. 7.

    Determine the control correction δ u(τ) in \(\left [\tau _{k},\tau _{k+1}\right ]\) through (20).

  8. 8.

    Points 1 through 7 are repeated after increasing k by 1, until (30) is satisfied.

Figure 2 portrays a block diagram that illustrates the feedback structure of VTD-NOG. The control and flight time corrections depend on the state displacement δ x (evaluated at specified times) through the time-varying gain matrices, computed offline and stored onboard.

Fig. 2
figure 2

Block diagram of VTD-NOG

Full size image

4 Minimum-Time-to-Climb Path of a Boeing 727 Aircraft

As a first example, the variable-time-domain neighboring optimal guidance is applied to the minimum-time ascent path of a Boeing 727 aircraft, which is a mid-size commercial jet aircraft. Its propulsive and aerodynamics characteristics are interpolated on the basis of real data, and come from [2].

4.1 Problem Definition

The aircraft motion is assumed to occur in the vertical plane. In addition, due to the low flight altitude, the flat-Earth approximation is adopted, and the gravitational force is considered constant (g = 9. 80665 m∕s2). In light of these assumptions, the equations of motion are [20]

$$\displaystyle{ z{\prime} = v\sin \gamma }$$
(39)
$$\displaystyle{ x{\prime} = v\cos \gamma }$$
(40)
$$\displaystyle{ \gamma {\prime} = -\frac{g} {v}\cos \gamma + \frac{L} {mv} + \frac{T} {mv}\sin (\alpha +\epsilon ) }$$
(41)
$$\displaystyle{ v{\prime} = -g\sin \gamma -\frac{D} {m} + \frac{T} {m}\cos (\alpha +\epsilon ) }$$
(42)
Fig. 3
figure 3

Thrust, lift, and drag forces, with the related angles

Full size image

where z, x, γ, and v denote, respectively, the altitude, range, flight path angle, and velocity of the aircraft at hand, and ′ is the derivative with respect to the actual time t; D and L represent the magnitudes of the aerodynamic drag and lift (whose direction is illustrated in Fig. 3), whereas T denotes the thrust magnitude, and m is the mass, which is assumed constant and equal to 81,647 kg. The angle ε is portrayed in Fig. 3 as well, and identifies the thrust direction with respect to the zero lift axis; α is the angle of attack. The two aerodynamic forces are functions of (1) the (dimensionless) lift and drag coefficients c L and c D , (2) the atmospheric density ρ, (3) the instantaneous velocity v, and (4) the reference surface area S, equal to 145 m2 [2], according to the following relations:

$$\displaystyle{ L = \frac{1} {2}c_{L}\rho Sv^{2}\qquad \text{and}\qquad D = \frac{1} {2}c_{D}\rho Sv^{2} }$$
(43)

Due to low altitude, the atmospheric density at sea level is used for the entire time of flight. The two coefficients c L and c D depend on the angle of attack and are interpolated in the following fashion [2]:

$$\displaystyle{ c_{L} = c_{L0} + c_{L1}\alpha + c_{L2}\left (\alpha -\alpha _{1}\right )^{2} }$$
(44)
$$\displaystyle{ c_{D} = c_{D0} + c_{D1}\alpha + c_{D2}\alpha ^{2} }$$
(45)

where the values of the constant quantities {c L0, c L1, c L2, α 1, c D0, c D1, c D2} are reported in [2]. Lastly, the thrust magnitude T depends on the instantaneous velocity, and is interpolated as well,

$$\displaystyle{ T = c_{T0} + c_{T1}v + c_{T2}v^{2} }$$
(46)

where the constant values of {c T0, c T1, c T2} are again reported in [2].

The minimum-time-to-climb problem consists in finding the optimal time history of the control angle α that minimizes the time t f needed to reach a given altitude in horizontal flight, with a prescribed velocity. This means that the objective function is simply

$$\displaystyle{ J = t_{f} }$$
(47)

(the initial time is set to 0). The final conditions are partially specified,

$$\displaystyle{ z_{f} =\bar{ z}_{f}\,(= 609.6\,\text{m}),\quad \gamma _{f} = 0\,\text{deg},\quad v_{f} =\bar{ v}_{f}\,(= 128\,\text{m}/\text{s}) }$$
(48)

whereas the initial conditions are completely known,

$$\displaystyle{ z_{0} = 0\,\text{m},\quad x_{0} = 0\,\text{m},\quad \gamma _{0} = 0\,\text{deg},\quad v_{0} = 128\,\text{m}/\text{s} }$$
(49)

As the range x does not appear in the right-hand sides of the equations of motion nor in the final conditions, x is ignorable; as a result, the state vector x is given by \(\mathbf{x} = \left [z\quad \gamma \quad v\right ]^{T}\), while the control vector u includes only α (u ≡ α). The state equations can be rewritten in terms of τ-derivatives,

$$\displaystyle{ \dot{z} = t_{f}v\sin \gamma }$$
(50)
$$\displaystyle{ \dot{\gamma }= t_{f}\left [-\frac{g} {v}\cos \gamma + \frac{L} {mv} + \frac{T} {mv}\sin (\alpha +\epsilon )\right ] }$$
(51)
$$\displaystyle{ \dot{v} = t_{f}\left [-g\sin \gamma -\frac{D} {m} + \frac{T} {m}\cos (\alpha +\epsilon )\right ] }$$
(52)

The right-hand sides of (50)–(52) form the vector f.

4.2 Optimal Trajectory

The VTD-NOG algorithm requires the preliminary determination of the optimal trajectory, which is assumed as the nominal path, together with the related optimal control, state, and costate vectors (cf. Sect. 2).

For the dynamical system at hand the Hamiltonian H and the function Φ are

$$\displaystyle{ \begin{array}{l} H =\lambda _{1}t_{f}v\sin \gamma +\lambda _{2}t_{f}\left [-\frac{g} {v}\cos \gamma + \frac{L} {mv} + \frac{T} {mv}\sin (\alpha +\epsilon )\right ]\\ \\ \quad +\lambda _{3}t_{f}\left [-g\sin \gamma -\frac{D} {m} + \frac{T} {m}\cos (\alpha +\epsilon )\right ]\end{array} }$$
(53)
$$\displaystyle{ \varPhi =\upsilon _{1}(z_{f} -\bar{ z}_{f}) +\upsilon _{2}\gamma _{f} +\upsilon _{3}(v_{f} -\bar{ v}_{f}) }$$
(54)

The adjoint equations assume the form

$$\displaystyle{ \dot{\lambda }_{1} = 0\qquad \Rightarrow \qquad \lambda _{1} =\lambda _{1,0} }$$
(55)
$$\displaystyle{ \dot{\lambda }_{2} = t_{f}\left [-\lambda _{1}v\cos \gamma -\frac{\lambda _{2}g} {v} \sin \gamma +\lambda _{3}g\cos \gamma \right ] }$$
(56)
$$\displaystyle{ \begin{array}{l} \dot{\lambda }_{3} = t_{f}\left \{-\lambda _{1}\sin \gamma - \frac{\lambda _{2}} {mv}\left [\frac{\partial T} {\partial v} \sin (\alpha +\epsilon ) + \frac{\partial L} {\partial v} -\frac{T} {v} \sin (\alpha +\epsilon ) -\frac{L} {v} \right ]\right \}\\ \\ \quad + t_{f}\left \{-\lambda _{2} \frac{g\cos \gamma } {v^{2}} -\lambda _{3}\left [-\frac{\partial D} {\partial v} + \frac{\partial T} {\partial v} \cos (\alpha +\epsilon )\right ]\right \}\end{array} }$$
(57)

The respective boundary conditions (10) do not add any further information (since the state components are completely specified at the final time), and therefore they are not reported. It is worth remarking that the derivatives of L, D, and T with respect to α and v can be easily expressed using (43)–(46) and are continuous. Moreover, the fact that H is stationary with respect to α at the optimal solution yields

$$\displaystyle{ \lambda _{2} \frac{T} {mv}\cos (\alpha +\epsilon ) + \frac{\lambda _{2}} {mv} \frac{\partial L} {\partial \alpha } - \frac{\lambda _{3}} {m} \frac{\partial D} {\partial \alpha } -\lambda _{3} \frac{T} {m}\sin (\alpha +\epsilon ) = 0 }$$
(58)

Finally, the parameter condition (11) leads to

$$\displaystyle{ \int _{0}^{1}\boldsymbol{\lambda }^{T} \frac{\partial \mathbf{f}} {\partial t_{f}}d\tau + 1 = 0 }$$
(59)

However, the parameter condition can be proven to be ignorable. As a first step, the components of \(\boldsymbol{\lambda }\) are homogeneous in the adjoint equations (55)–(57). This circumstance implies that if an optimization algorithm is capable of finding some initial value of \(\boldsymbol{\lambda }\) such that \(\boldsymbol{\lambda }_{0} = k_{\lambda }\boldsymbol{\lambda }_{0}^{{\ast}}\ (k_{\lambda }> 0)\) (where∗ denotes optimality), then the same proportionality holds between \(\boldsymbol{\lambda }\) and \(\boldsymbol{\lambda }^{{\ast}}\) at any τ. Moreover, the control u can be found through (58), which yields the same solution if \(\boldsymbol{\lambda }\) replaces \(\boldsymbol{\lambda }^{{\ast}}\). This circumstance implies that if \(\boldsymbol{\lambda }\) is proportional to \(\boldsymbol{\lambda }^{{\ast}}\) then the final conditions are fulfilled at the minimum final time t f ∗. In contrast, the parameter condition is violated, because the integral of (59) turns out to be

$$\displaystyle{ \int _{0}^{1}\boldsymbol{\lambda }^{T} \frac{\partial \mathbf{f}} {\partial t_{f}}d\tau = k_{\lambda }\int _{0}^{1}\boldsymbol{\lambda }^{{\ast}}{}^{T} \frac{\partial \mathbf{f}} {\partial t_{f}}d\tau = -k_{\lambda }\neq - 1 }$$
(60)

Therefore, provided that the proportionality condition holds, the optimal control u ∗ can be determined without considering the parameter condition, which is ignorable as an equality constraint and can be replaced by the inequality constraint

$$\displaystyle{ \int _{0}^{1}\boldsymbol{\lambda }^{T} \frac{\partial \mathbf{f}} {\partial t_{f}}d\tau <0 }$$
(61)

because k λ is an arbitrary positive constant. Once the (nonoptimal) values of the costate variables (fulfilling the proportionality condition) have been determined, the correct (optimal) values can be recovered after calculating k λ by means of (60).

In the end, the problem of determining the minimum-time-to-climb path can be reformulated as a two-point boundary-value problem, in which the unknowns are the initial values of three adjoint variables, as well as the time of flight, i.e. \(\left \{\lambda _{1,0},\lambda _{2,0},\lambda _{3,0},t_{f}\right \}\). The boundary conditions are represented by (48), accompanied by the inequality constraint (61). Once the optimal parameter set has been determined, the state and costate equations can be integrated, using (58) to express the control angle α as a function of the adjoint variables.

The optimal parameter set is determined by means of a simple implementation of swarming algorithm (PSO). This is a heuristic optimization technique, based on the use of a population of individuals (or particles). Selection of the globally optimal parameters is the result of a number of iterations, in which the individuals share their information. This optimization approach is extremely intuitive and easy-to-implement. Nevertheless, in the scientific literature several papers [10–14] prove that the use of this method is effective for solving trajectory optimization problems. A set of canonical units is employed for the problem at hand: the distance unit (DU) and time unit (TU) are

$$\displaystyle{ \text{DU} = \frac{2m} {\rho S} \quad \text{and}\quad \text{TU} = \sqrt{\frac{2m} {\rho gS}} }$$
(62)

The search space is defined by the inequalities − 1 ≤ λ k, 0 ≤ 1 and 1 TU ≤ t f  ≤ 6 TU. It is worth remarking that ignorability of the parameter condition allows defining arbitrarily the range in which the initial values of the adjoint variables are sought. Their correct values (fulfilling also the parameter condition (59)) can be recovered a posteriori, as discussed previously. PSO is used with the intent of minimizing the objective

$$\displaystyle{ \tilde{J} =\sum _{ k=1}^{3}\vert d_{ k}\vert }$$
(63)

where each term d k represents a final constraint violation. While minimization of (63) ensures feasibility, enforcement of the necessary conditions for optimality guarantees that the solution found by PSO is (at least locally) optimal.

The PSO algorithm yields a solution associated with \(\tilde{J} = 8.458 \times 10^{-7}\). The corresponding optimal time histories of the state and control components are portrayed in Figs. 4, 5, 6, and 7. From their inspection it is apparent that the minimum climbing path is composed of two phases: an initial ascent phase, up to an altitude greater than the final one, followed by a diving phase. The minimum time to climb equals 55.5 s.

Fig. 4
figure 4

727 aircraft: nominal altitude

Full size image
Fig. 5
figure 5

727 aircraft: nominal velocity

Full size image
Fig. 6
figure 6

727 aircraft: nominal flight path angle

Full size image
Fig. 7
figure 7

727 aircraft: optimal control time history

Full size image

4.3 Application of VTD-NOG

The neighboring optimal guidance algorithm proposed in this work is applied to the minimum-time-to-climb path of the Boeing 727 aircraft. Perturbations from the nominal situation are considered, in order to simulate a realistic scenario. In particular, perturbations on the initial state, thrust magnitude, and atmospheric density are taken into account. Several Monte Carlo campaigns are run, with the intent of obtaining some useful statistical information on the accuracy of the algorithm at hand, in the presence of the previously mentioned deviations, which are simulated stochastically. Monte Carlo campaigns test the guidance algorithm by running a significant number of numerical simulations. Each perturbed quantity in the initial state is associated with a Gaussian distribution, with mean value equal to the respective nominal one and with a specific σ-value, which is related to the statistical dispersion about the mean value. The σ-values are

$$\displaystyle{ \varDelta z^{(\sigma )} = 5\,\text{m},\quad \varDelta v^{(\sigma )} = 5\,\text{m/s},\quad \varDelta \gamma ^{(\sigma )} = 5\,\text{deg} }$$
(64)

In the numerical simulations the deviations from the nominal values are constrained to the intervals \(\left [0,2\varDelta \chi ^{(\sigma )}\right ]\ (\chi = z\,\,\text{or}\,\,\gamma )\) and \(\left [-2\varDelta v^{(\sigma )},2\varDelta v^{(\sigma )}\right ]\). A different approach was chosen for the perturbation of the thrust magnitude. In fact, usually the thrust magnitude exhibits small fluctuations. This time-varying behavior is modeled through a trigonometric series with random coefficients,

$$\displaystyle{ T_{pert} = T\left \{1 +\sum _{ k=1}^{5}a_{ k}\sin (2k\pi \tau ) +\sum _{ k=1}^{5}a_{ k+5}\cos (2k\pi \tau )\right \} }$$
(65)

where T pert denotes the perturbed thrust, whereas a k represents a random number with Gaussian distribution, zero mean, and standard deviation equal to 0.01. The atmospheric density fluctuations are modeled through a similar trigonometric series,

$$\displaystyle{ \rho _{pert} =\rho \left \{1 +\sum _{ k=1}^{5}b_{ k}\sin (2k\pi \tau ) +\sum _{ k=1}^{5}b_{ k+5}\cos (2k\pi \tau )\right \} }$$
(66)

where ρ pert denotes the perturbed density, whereas b k represents a random number with the same statistic properties as a k .

At the end of the algorithmic process described in Sect. 3.3, two statistical quantities are evaluated, i.e. the mean value and the standard deviation for all of the outputs of interest. The symbols \(\bar{\chi }\) and χ (σ) will denote the mean value and standard deviation of χ (χ = z or v or γ or t f ) henceforth. Five campaigns are performed, each including 100 runs. The first four campaigns (MC1 through MC4) use a sampling time Δ t S  = 2 s, whereas MC5 adopts a sampling time Δ t S  = 1 s. MC1 assumes only perturbations of the initial state. The second campaign (MC2) considers the thrust fluctuations, whereas MC3 takes into account only the atmospheric density perturbations. MC4 and MC5 include all the deviations from the nominal flight conditions (with different sampling times). Table 1 summarizes the results for the five Monte Carlo campaigns and reports the related statistics. Application of VTD-NOG to the problem of interest leads to excellent results, with modest errors on the desired final conditions. More specifically, inspection of Table 1 points out that errors on the initial conditions are corrected very effectively; however, also the remaining results exhibit modest deviations at the final time. The latter is extremely close to the optimal value, and this is an intrinsic characteristic of VTD-NOG, which employs first order expansions of the state and costate equations in the proximity of the optimal solution. As a final remark, in the presence of all of the perturbations (MC4 and MC5), decreasing the sampling time implies a reduction of the final errors. Figures 8, 9, 10, and 11 depict the perturbed state components and control angle, obtained in MC5.

Table 1 Statistics on the time of flight and the errors on altitude, velocity, and flight path angle
Full size table
Fig. 8
figure 8

727 aircraft: altitude time histories obtained in MC5

Full size image
Fig. 9
figure 9

727 aircraft: velocity time histories obtained in MC5

Full size image
Fig. 10
figure 10

727 aircraft: time histories of the flight path angle obtained in MC5

Full size image
Fig. 11
figure 11

727 aircraft: time histories of the angle of attack obtained in MC5

Full size image

5 Interception

As a second application of VTD-NOG, this section considers the interception of a target by a maneuvering vehicle in exoatmospheric flight or in the presence of negligible aerodynamic forces, e.g. an intercepting rocket operating at high altitudes. Both the pursuing vehicle and the target are modeled as point masses, in the context of a three-degree-of-freedom problem.

5.1 Problem Definition

Under the assumption that interception occurs in a sufficiently short time interval, the flat Earth approximation can be adopted again. This means that the Cartesian reference frame can be defined as follows: the x 1-axis is aligned with the local upward direction, the x 2-axis is directed eastward, and the x 3-axis is aligned with the local North direction. As a result, the Cartesian equations of motion for the intercepting rocket are

$$\displaystyle{ \dot{x}_{1} = t_{f}x_{4} }$$
(67)
$$\displaystyle{ \dot{x}_{2} = t_{f}x_{5} }$$
(68)
$$\displaystyle{ \dot{x}_{3} = t_{f}x_{6} }$$
(69)
$$\displaystyle{ \dot{x}_{4} = t_{f}(-g + a_{T}\cos u_{2}\sin u_{1}) }$$
(70)
$$\displaystyle{ \dot{x}_{5} = t_{f}a_{T}\cos u_{2}\cos u_{1} }$$
(71)
$$\displaystyle{ \dot{x}_{6} = t_{f}a_{T}\sin u_{2} }$$
(72)

where the derivatives are written with respect to τ, {x 1, x 2, x 3} are the three position coordinates, {x 4, x 5, x 6} are the corresponding velocity components, and t f represents the time of flight up to interception. The symbol g denotes the magnitude of the (constant) gravitational force at the reference altitude, whereas the thrust acceleration has magnitude a T and direction identified through the two angles u 1 and u 2. The target position is assumed as known, and therefore it is expressed by three specified functions of the dimensionless time τ,

$$\displaystyle{ x_{1}^{(T)} = f_{ 1}(\tau ),\qquad x_{2}^{(T)} = f_{ 2}(\tau ),\qquad x_{3}^{(T)} = f_{ 3}(\tau ) }$$
(73)

While the state vector contains the position and velocity components \(\left \{x_{i}\right \}_{i=1,\ldots,6}\), the control vector is u = [u 1 u 2]T, and the parameter vector a includes only t f (as in the previous application). As the time is to be minimized, the objective function is

$$\displaystyle{ J = t_{f} }$$
(74)

5.2 Optimal Trajectory

The first-order conditions for optimality are obtained after introducing the Hamiltonian H and the function of the boundary conditions Φ, according to (7)

$$\displaystyle{ \begin{array}{l} H =\lambda _{1}t_{f}x_{4} +\lambda _{2}t_{f}x_{5} +\lambda _{3}t_{f}x_{6} +\lambda _{4}t_{f}(-g + a_{T}\cos u_{2}\sin u_{1})\\ \\ \quad +\lambda _{5}t_{f}a_{T}\cos u_{2}\cos u_{1} +\lambda _{6}t_{f}a_{T}\sin u_{2} \end{array} }$$
(75)
$$\displaystyle{ \varPhi =\upsilon _{1}\left [x_{1f} - f_{1}(1)\right ] +\upsilon _{2}\left [x_{2f} - f_{2}(1)\right ] +\upsilon _{3}\left [x_{3f} - f_{3}(1)\right ] }$$
(76)

where the subscript f refers to the value of the respective variable at the final time. The adjoint equations (9) in conjunction with the respective boundary conditions (10) for λ 4 through λ 6 lead to

$$\displaystyle{ \dot{\lambda }_{1} = 0\qquad \Rightarrow \qquad \lambda _{1} =\lambda _{1,0} }$$
(77)
$$\displaystyle{ \dot{\lambda }_{2} = 0\qquad \Rightarrow \qquad \lambda _{2} =\lambda _{2,0} }$$
(78)
$$\displaystyle{ \dot{\lambda }_{3} = 0\qquad \Rightarrow \qquad \lambda _{3} =\lambda _{3,0} }$$
(79)
$$\displaystyle{ \dot{\lambda }_{4} = -\lambda _{1,0}t_{f}\qquad \Rightarrow \qquad \lambda _{4} =\lambda _{1,0}t_{f}(1-\tau ) }$$
(80)
$$\displaystyle{ \dot{\lambda }_{5} = -\lambda _{2,0}t_{f}\qquad \Rightarrow \qquad \lambda _{5} =\lambda _{2,0}t_{f}(1-\tau ) }$$
(81)
$$\displaystyle{ \dot{\lambda }_{6} = -\lambda _{3,0}t_{f}\qquad \Rightarrow \qquad \lambda _{6} =\lambda _{3,0}t_{f}(1-\tau ) }$$
(82)

where λ i, 0 denotes the (unknown) initial value of the adjoint variable λ i . Then, the Pontryagin minimum principle yields

$$\displaystyle{ u_{2} = -\arcsin \frac{\lambda _{3,0}} {\sqrt{\lambda _{1,0 }^{2 } +\lambda _{ 2,0 }^{2 } +\lambda _{ 3,0 }^{2}}} }$$
(83)
$$\displaystyle{ \sin u_{1} = - \frac{\lambda _{1,0}} {\sqrt{\lambda _{1,0 }^{2 } +\lambda _{ 2,0 }^{2}}}\qquad \text{and}\quad \cos u_{1} = - \frac{\lambda _{2,0}} {\sqrt{\lambda _{1,0 }^{2 } +\lambda _{ 2,0 }^{2}}} }$$
(84)

These relations imply that the optimal thrust direction is time-independent, regardless of the (known) target position. It is relatively straightforward to prove that for the present application the remaining necessary conditions coming from (10) are useless for the purpose of identifying the optimal solution, in the sense that they do not lead to establishing any new relation among the unknowns of the problem, i.e., \(\left \{\lambda _{1,0},\lambda _{2,0},\lambda _{3,0},t_{f}\right \}\). Also the parameter condition (11) can be proven to be ignorable, in a way similar to that used in Sect. 4.2. Moreover, as the two angles u 1 and u 2 are constant, they can be considered as the unknown quantities in place of \(\left \{\lambda _{1,0},\lambda _{2,0},\lambda _{3,0}\right \}\). Under the assumption that a T is constant, integration of (67)–(72) leads to obtaining the following explicit solution for x 1, x 2, and x 3:

$$\displaystyle{ x_{1} = x_{1,0} + x_{4,0}t_{f}\tau + \frac{1} {2}a_{T}(t_{f}\tau )^{2}\cos u_{ 2}\sin u_{1} -\frac{1} {2}g(t_{f}\tau )^{2} }$$
(85)
$$\displaystyle{ x_{2} = x_{2,0} + x_{5,0}t_{f}\tau + \frac{1} {2}a_{T}(t_{f}\tau )^{2}\cos u_{ 2}\cos u_{1} }$$
(86)
$$\displaystyle{ x_{3} = x_{3,0} + x_{6,0}t_{f}\tau + \frac{1} {2}a_{T}(t_{f}\tau )^{2}\sin u_{ 2} }$$
(87)

These expressions are evaluated at τ = 1, then they are set equal to the respective position coordinates of the target at τ = 1. From (85)–(87) one obtains the following equations:

$$\displaystyle{ \begin{array}{l} (a_{T}^{2} - g^{2})t_{f}^{4} + 4gx_{4,0}t_{f}^{3} - 4t_{f}^{2}(x_{4,0}^{2} + x_{5,0}^{2} + x_{6,0}^{2}) - 4gt_{f}^{2}\left [f_{1}(1) - x_{1,0}\right ]\\ \\ + 8x_{4,0}t_{f}\left [f_{1}(1) - x_{1,0}\right ] + 8x_{5,0}t_{f}\left [f_{2}(1) - x_{2,0}\right ] + 8x_{6,0}t_{f}\left [f_{3}(1) - x_{3,0}\right ]\\ \\ - 4\left [f_{1}(1) - x_{1,0}\right ]^{2} - 4\left [f_{2}(1) - x_{2,0}\right ]^{2} - 4\left [f_{3}(1) - x_{3,0}\right ]^{2} = 0\end{array} }$$
(88)
$$\displaystyle{ u_{2} =\arcsin \frac{2\left [f_{3}(1) - x_{3,0}\right ] - 2x_{6,0}t_{f}} {a_{T}t_{f}^{2}} }$$
(89)
$$\displaystyle{ \cos u_{1} = \frac{2\left [f_{2}(1) - x_{2,0}\right ] - 2x_{5,0}t_{f}} {a_{T}t_{f}^{2}\cos u_{2}} \quad \text{and}\quad \sin u_{1} = \frac{2\left [f_{1}(1) - x_{1,0}\right ] - 2x_{4,0}t_{f} + gt_{f}^{2}} {a_{T}t_{f}^{2}\cos u_{2}} }$$
(90)

Depending on the analytical form of f 1, f 2, and f 3, (88) can either represent a transcendental equation or simplify to a polynomial equation of fourth degree. Once (88) has been solved, calculation of the optimal thrust angles is straightforward, by means of (89) and (90).

5.3 Application of VTD-NOG

The guidance algorithm described in this work is applied to the interception problem in the presence of nonnominal flight conditions. In particular, perturbations on the initial state and oscillations of the thrust acceleration magnitude over time are modeled. Several Monte Carlo campaigns are run, with the intent of obtaining some useful statistical information on the accuracy of the algorithm at hand, in the presence of the previously mentioned deviations, which are simulated stochastically. The nominal initial position is perturbed by a random vector \(\boldsymbol{\rho }\): its magnitude ρ is associated with a Gaussian distribution, with standard deviation equal to 5 m and maximal value never exceeding 10 m, whereas the corresponding unit vector \(\hat{\rho }\) has direction uniformly distributed over a unit sphere. Similarly, the nominal initial velocity is perturbed by a random vector w: its magnitude w is associated with a Gaussian distribution, with standard deviation equal to 5 m/s and maximal value never exceeding 10 m/s, whereas the corresponding unit vector \(\hat{w}\) has direction uniformly distributed over a unit sphere. A different approach is adopted for the perturbation of the thrust acceleration. As the thrust magnitude (and the related acceleration a T ) exhibits fluctuations, the perturbed thrust acceleration is modeled through a trigonometric series,

$$\displaystyle{ a_{T,pert} = a_{T}\left \{1 +\sum _{ k=1}^{5}c_{ k}\sin (2k\pi \tau ) +\sum _{ k=1}^{5}c_{ k+5}\cos (2k\pi \tau )\right \} }$$
(91)

where a T is the nominal thrust acceleration, whereas the corresponding (time-varying) perturbed value a T, pert is actually used in the MC simulations. The coefficients \(\left \{c_{k}\right \}_{k=1,\ldots,10}\) have a random Gaussian distribution with zero mean and a standard deviation equal to 0.01. At the end of the algorithmic process described in Sect. 3.3, two statistical quantities are evaluated, i.e. the mean value and the standard deviation for all of the outputs of interest (with a notation similar to that adopted for the preceding application).

In this section, three different targets are taken into account. For each of them, four Monte Carlo campaigns have been performed, each including 100 runs. The first campaign (MC1) assumes only perturbations of the initial state. The second campaign (MC2) considers only oscillations of the thrust acceleration magnitude, while the third and fourth campaigns (MC3 and MC4) include both types of perturbations, with different sampling time intervals (Δ t S  = 1 s and Δ t S  = 0. 5 s, respectively).

Fixed Target As a first special case, a fixed target is considered. This means that the three functions f 1, f 2, and f 3 equal three prescribed values x 1 (T), x 2 (T), and x 3 (T). As a result, (88) assumes the form of a fourth degree equation; its smallest real root represents the minimum time to interception.

In the numerical example that follows, the reference altitude (needed for defining the value of g) is set to the initial altitude of the intercepting rocket, whereas a T  = 2g. The initial state of the pursuing vehicle is

$$\displaystyle{ x_{1,0} = 30\,\text{km}\quad x_{2,0} = 0\,\text{km}\quad x_{3,0} = 3\,\text{km}\quad x_{4,0} = x_{5,0} = x_{6,0} = 0.1\,\text{km/s}\quad }$$
(92)

whereas the target position is

$$\displaystyle{ x_{1}^{(T)} = 35\,\text{km}\quad x_{ 2}^{(T)} = 5\,\text{km}\quad x_{ 3}^{(T)} = 0\,\text{km} }$$
(93)

The minimum time of flight up to interception turns out to equal 30.58 s, whereas the two optimal thrust angles are u 1 ∗ = 73. 3 deg and u 2 ∗ = −41. 8 deg. Figure 12 portrays the optimal intercepting trajectory.

Application of VTD-NOG yields results associated with the statistics summarized in Table 2. They regard the miss distance d f (at the end of nonnominal paths) and the time of flight. Inspection of Table 2 reveals that VTD-NOG generates accurate results, with modest values of the miss distance, which decreases by 40 % from MC3 to MC4. Figure 13 portrays the time evolution of the corrected control angles, obtained in MC3.

Fig. 12
figure 12

Optimal interception trajectory of a fixed target

Full size image
Table 2 Fixed target: statistics on the time of flight and the miss distance
Full size table
Fig. 13
figure 13

Fixed target interception: time histories of the control angles obtained in MC3

Full size image

Falling Target The second special case assumes a target in free fall (e.g., a ballistic missile at high altitudes), with given initial conditions, denoted with \(\left \{x_{i,0}^{(T)}\right \}_{i=1,\ldots,6}\). This means that the three functions f 1, f 2, and f 3 are

$$\displaystyle{ f_{1} = x_{1,0}^{(T)}+x_{ 4,0}^{(T)}t_{ f}\tau -\frac{1} {2}g(t_{f}\tau )^{2}\qquad f_{ 2} = x_{2,0}^{(T)}+x_{ 5,0}^{(T)}t_{ f}\tau \qquad f_{3} = x_{3,0}^{(T)}+x_{ 6,0}^{(T)}t_{ f}\tau }$$
(94)

As a result, (88) assumes again the form of a fourth degree equation; its smallest real root represents the minimum time to interception.

In the numerical example that follows, the reference altitude is set to the initial altitude of the rocket, whereas a T  = 3g. The initial state of the pursuing vehicle is

$$\displaystyle{ x_{1,0} = 15\,\text{km}\quad x_{2,0} = x_{3,0} = 0\,\text{km}\quad x_{4,0} = 0\,\text{km/s}\quad x_{5,0} = x_{6,0} = 0.2\,\text{km/s} }$$
(95)

whereas the initial state of the target is given by

$$\displaystyle{ \begin{array}{l} x_{1,0}^{(T)} = 30\,\text{km}\quad x_{2,0}^{(T)} = x_{3,0}^{(T)} = 1\,\text{km} \\ x_{4,0}^{(T)} = -1\,\text{km/s}\quad x_{5,0}^{(T)} = x_{6,0}^{(T)} = 0.1\,\text{km/s}\end{array} }$$
(96)

The minimum time of flight up to interception turns out to equal 12.68 s, whereas the two optimal thrust angles are u 1 ∗ = 96. 6 deg and u 1 ∗ = −6. 5 deg.

The guidance algorithm is applied again in the presence of nonnominal flight conditions. The same Monte Carlo campaigns performed for the previous case are repeated for the application at hand. Table 3 summarizes the results for the four Monte Carlo campaigns and reports the related statistics, with regard to the miss distance (at the end of nonnominal paths) and the time of flight. It is worth remarking that decreasing the sampling time (cf. Table 3) leads again to reducing the mean miss distance. As in the previous application, the actual times of flight are extremely close to the minimal value (12.68 s).

Table 3 Falling target: statistics on the time of flight and the miss distance
Full size table

Moving Target The third special case assumes a target that describes a circular path at constant altitude (e.g., an unmanned aerial vehicle). This means that

$$\displaystyle{ f_{1} = x_{1}^{(T)}\qquad f_{ 2} = x_{2C}^{(T)} + R_{ T}\cos (\omega t_{f}\tau +\varphi )\qquad f_{3} = x_{3C}^{(T)} + R_{ T}\sin (\omega t_{f}\tau +\varphi ) }$$
(97)

where x 1 (T) denotes the target constant altitude, \(\left (x_{2C}^{(T)},x_{3C}^{(T)}\right )\) identify the center of the circular path, whereas ω and φ define, respectively, the angular rate of rotation and the initial angular position. In this case, (88) assumes the form of a transcendental equation, to be solved numerically (for instance, through the Matlab native function fsolve). However, numerical solvers need a suitable approximate guess solution to converge to a refined result. For the application at hand, this guess can be easily supplied. In fact, if the radius R T is sufficiently small, one can assume that the target is located at \(\left (x_{1}^{(T)},x_{2C}^{(T)},x_{3C}^{(T)}\right )\). In the presence of a fixed target, an analytical solution exists, and derives from solving a fourth degree equation, as already explained in Sect. 5.2. This solution is used as a guess for the moving target.

In the numerical example that follows, the reference altitude is set to the initial altitude of the rocket, whereas a T  = 3g. The initial state of the pursuing vehicle is

$$\displaystyle{ \begin{array}{l} x_{1,0} = 9\,\text{km}\quad x_{2,0} = x_{3,0} = 0\,\text{km} \\ x_{4,0} = 0.01\,\text{km/s}\quad x_{5,0} = 0.1\,\text{km/s}\quad x_{6,0} = 0\,\text{km/s} \end{array} }$$
(98)

whereas the fundamental parameters of the target are

$$\displaystyle{ x_{1}^{(T)} = 10\,\text{km}\quad x_{ 2C}^{(T)} = x_{ 3C}^{(T)} = 2\,\text{km}\quad 2\pi \omega ^{-1} = 60\,\text{s}\quad R_{ T} = 0.5\,\text{km}\quad \varphi = 0 }$$
(99)

The minimum time of flight up to interception turns out to equal 14.76 s, whereas the two optimal thrust angles are u 1 ∗ = 74. 4 deg and u 2 ∗ = 51. 5 deg.

The guidance algorithm is applied again in the presence of nonnominal flight conditions. The same Monte Carlo campaigns performed for the previous case are repeated for the application at hand. Table 4 summarizes the results for the four Monte Carlo campaigns and reports the related statistics, with regard to the miss distance (at the end of nonnominal paths) and the time of flight. It is worth remarking that decreasing the sampling time (cf. Table 4) leads again to reducing the mean miss distance.

Table 4 Moving target: statistics on the time of flight and the miss distance
Full size table

6 Concluding Remarks

This work describes and applies the recently introduced, general-purpose variable-time-domain neighboring optimal guidance algorithm. Usually, all the neighboring optimal guidance schemes require the preliminary determination of an optimal trajectory. Moreover, complex analytical developments accompany the implementation of this kind of perturbative guidance. However, the main difficulties encountered in former formulations of neighboring optimal guidance are the occurrence of singularities for the gain matrices and the challenging implementation of the updating law for the time-to-go. A fundamental original feature of the variable-time-domain neighboring optimal guidance is the use of a normalized time scale as the domain in which the nominal trajectory and the related vectors and matrices are defined. As a favorable consequence, the gain matrices remains finite for the entire time of flight and no extension of their domain is needed. Moreover, the updating formula for the time-to-go derives analytically from the natural extension of the accessory optimization problem associated with the original optimal control problem. This extension leads also to obtaining new equations for the sweep method, which provides all the time-varying gain matrices, computed offline and stored in the onboard computer. In this mathematical framework, the guidance termination criterion finds a logical, consistent definition, and corresponds to the upper bound of the interval to which the normalized time is constrained. Two applications are considered in the paper: (a) minimum-time-to-climb path of a Boeing 727 aircraft and (b) minimum-time exoatmospheric interception of fixed or moving targets. In both cases (especially for (a)), as well as in alternative applications already reported in the scientific literature [16, 17], the variable-time-domain neighboring optimal guidance yields very satisfactory results, with runtime (per simulation) never exceeding the time of flight. This means that VTD-NOG actually represents an effective, general algorithm for the real-time determination of the corrective actions aimed at maintaining an aerospace vehicle in the proximity of its optimal path.