Keywords

1 Introduction

Floods, soil erosion and landslides are the most dangerous geohazards in Slovakia and their activity is followed by great economic loss and threat to human life. Based on the research of slope deformation occurrence 5.25 % of the total land area of the Slovak Republic is affected by slope failures (Šimeková et al. 2014). According to Ministry of Environment of the Slovak Republic 45 million Euro will be invested into landslides prevention, identification, monitoring, registration and sanation in the time period between the years 2014 and 2020. Therefore, implementation of geological hazards models is essential in urban planning process for effective prevention and protection in high risk areas. In recent time, a machine learning became very popular phenomenon. Cheaper hardware allows wider ranges of companies and institutions to store and examine large datasets. This environment is very stimulating and new or upgraded machine learning techniques are developed continuously. This study is focused on the Support Vector Machines (SVMs) method and its usability in prediction modelling of landslides susceptibility in geographical information systems (GIS), which was never used before by professionals in Slovakia.

The objective of this study is to test linear, polynomial and radial basis function kernels and their inner parameters to find optimal model to create landslides susceptibility maps. For this purpose, we have built a classification problem with two classes “landslides” and “stable areas”.

Further step is training the SVMs to compute probability that unobserved data belong to landslides class. First, these models were validated by their accuracy. Subsequently, for each kernel, the model with the best result was trained to predict probability output and validated by the Receiver Operating Characteristic (ROC) curve. Finally, landslides susceptibility maps were created.

There are number of different approaches to the numerical measurement of landslide susceptibility evaluation in the current literature, including direct and indirect heuristic approaches and deterministic, probabilistic and statistical approaches (Pradhan et al. 2010). Statistical analysis models for landslide susceptibility zonnation were developed in Italy, mainly by Carrara (1983) who later modified his methodology to the GIS environment (Carrara et al. 1990) using mainly the bivariate and mutlivariate statistical analysis. More recently, new techniques have been used for landslide susceptibility mapping. New landslide susceptibility assessment methods such as artificial neural networks (Lee 2004), neuro-fuzzy (Vahidnia 2010) or (Hyun-Joo and Pradhan 2011), SVMs (Yao et al. 2008) and decision tree methods (Nefeslioglu et al. 2010) have been tried and their performance have been assessed. In Slovakia, landslide susceptibility assessment has experienced a significant step forward especially due to Pauditš (2005) and Bednárik (2011) achievements in their work (Bednarik et al. 2014) using the multivariate conditional analysis method and bivariate statistical analysis with weighting.

2 Study Area, Data and Materials

The study area is located in north-west of Slovakia overlying the districts Bytča, Kysucké Nové Mesto, Žilina, and covers a surface area of 300 km2 (20 km × 15 km). It lies between the S-JTSK coordinates of the y-axis 458,653.27–438,653.27 m and coordinates of the x-axis 1,162,115.32–1,177,115.32 m (S-JTSK is a national coordinate system in Slovakia, the corresponding coordinates of the study area in the WGS 84 are: latitude N49°18′59″ to N49°10′03″ and longitude E18°31′02″ to E18°48′28″). The mean annual rainfall in the area varies from 650 to 700 mm. The prominent rainy season is during the months of June and July. The geomorphology of the area is characterized by a rugged topography with the hills ranges varying from 292 to 817 m a.s.l. The study area is largely formed by the Javorníky and Súľov Montains and the Žilina basin. The land use in the area is dominated by forest land and urban land. The high occurrence of landslides was mainly within Javorníky mountains mapped in 1981 and 1982 (Baliak and Stríček 2012).

2.1 Landslide Conditioning Factors

Identification and mapping of a suitable set of instability factors having a relationship with slope failures require a priori knowledge of main causes of landslides and it is a domain of geologists. These instability factors include surface and bedrock lithology and structure, seismicity, slope steepness and morphology, stream evolution, groundwater conditions, climate, vegetation cover, land use and human activity (Pradhan 2013). The acquirement and availability of these thematic data is often a difficult task. A grid based digital elevation model (DEM) was used to acquire geomorphometric parameters. The DEM was provided by Geodetic and Cartographic Institute Bratislava in the version “3.5”. In this study, the calculated and extracted factors were converted to a spatial resolution of 10 × 10 m. This mapping unit was small enough to capture the spatial characteristics of landslide susceptibility and large enough to reduce computing complexity. Total four different input datasets are produced as the conditioning factors for occurrence of landslides. Slope and aspect were extracted using the DEM. The slope configuration plays an important role when considered in conjunction with a geological map. The geological map of the Slovak republic at scale 1:50,000 in the shapefile format was provided by State Geological Institute of Dionýz Štúr (Káčer et al. 2005). The last conditioning factor land use is extracted from Corine Land Cover 2006 with a spatial resolution 100 × 100 m.

In this study, geological and statistical evaluation of input conditional factors according to landslide susceptibility was not performed. The results from this evaluation are used to reclassify input parameters into the groups with similar properties causing slope failures. Reclassified input parameters are then used in further landslide susceptibility evaluation as in the case of bivariate and mutlivariate statistical analysis. According to the properties of the Support Vector Machines method it is not necessary to reclassify input parameters and they can be used directly in their untouched form. The only parameter that has to be reclassified is aspect because it contains continues values and special coded value for the flat. Values of aspect were reclassified into the categories N, NE, E, SE, S, SW, W, NW and Flat.

Input parameters were used in the following form. Geological map contains 90 distinct classes, land use contains 18 distinct classes and aspect was passed with 9 classes in the study area. The last used conditioning factor slope was used in its continuous form.

2.2 Landslide Inventory Map

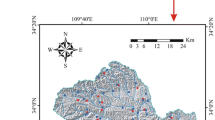
The database includes vector and raster spatial datasets using the ArcGIS software package. As a groundwork of digital layers (landslides and stable areas) serve the data from the project of Atlas of Slope Stability Maps SR at 1:50,000 (Šimeková et al. 2006), which was completed in 2006 by State Geological Institute of Dionýz Štúr. Slope deformations were identified from archival materials or mapped in the field. Data were provided in shapefile format. Landslides were extracted from zos_zosuvy_sr.shp with value of attribute STUPAKT = A (activity level = active). Stable areas were extracted from zos_8002_SR.shp. Subsequently, the landslide vector map was transformed into a grid database with a cell size of 10 × 10 m. For the study area, 72 landslides (in the range 13,464–241,044 m2) were extracted using the inventory map. The landslide inventory map was especially helpful in understanding the different conditioning factors that control slope movements. Distribution of landslides and stable areas is shown in the Fig. 1.

Fig. 1
figure 1

Location map of the study area showing landslides and stable areas from Atlas of Slope Stability Maps SR at 1:50,000 (Šimeková et al. 2006) used in training and validation

Full size image

3 Learning with Support Vector Machines

Machine learning algorithms are widely used in cases where the mapping function between input parameter(s) and output parameter(s) is complex, or even unknown. Definition of machine learning can be as following: “A computer is said to learn from experience E with respect to some test T and some performance measure P, if its performance on T, as measured by P, improves with experience E” (Mitchell 1997).

SVMs were introduced in 1995 by prof. Vladimir Naumovich Vapnik (Vapnik 1995). Since then, SVMs and their variants and extensions (also called kernel-based methods) have become one of the preeminent machine learning paradigms. Nowadays, SVMs are routinely used in wide range of areas e.g. handwriting recognition or bioinformatics.

3.1 Two-Class Support Vector Machines

In Two-Class SVMs the m-dimensional input x is mapped into l-dimensional (l · m) feature space z. Then in the feature space z the optimal separating hyperplane is found by solving the quadratic optimization problem. The optimal separating hyperplane is a boundary that separates classes with maximal generalization ability as shown in the Fig. 2.

Fig. 2
figure 2

Optimal hyperplane separating two classes with maximum margin

Full size image

Circles represent class 1 and squares are class −1. As shown in the picture (Fig. 2), there is infinite number of separating hyperplanes which separates classes 1 and −1. The separating hyperplane with maximal margin is called the optimal separating hyperplane. In this case, the separating hyperplane is given by equation:

$${\mathbf{w}}^{{\mathbf{T}}} {\mathbf{x}} + b = 0$$
(1)

where w is m-dimensional vector, b is bias term and x is m-dimensional input.

SVMs will then predict class 1 every time when w T x + b > 0, and class 2 when w T x + b < 0. Equation (1) can be converted to form:

$$y_{i} \left( {{\mathbf{w}}^{{\mathbf{T}}} {\mathbf{x}} + b} \right)\left\{ {\begin{array}{*{20}l} { \ge 1\,\,\,\,\,{\text{for}}\,{\text{every}}\,y_{i} = 1} \hfill \\ { \le - 1\,\,\,{\text{for}}\,{\text{every}}\,y_{i} = - 1} \hfill \\ \end{array} } \right.$$
(2)

where y is sample label.

From Eq. (2) it is clear that we obtain exactly the same separating hyperplane, even if all the data that satisfy the inequalities are deleted. The separating hyperplane is defined by the data that satisfy the equalities (2) and this data are called support vectors. In the Fig. 2 the support vectors are marked with filled circles and squares. Example above is linearly separable. Many times the problem can not be separated linearly and we have to admit training errors. The influence of training errors is regulated with error cost parameter C. Maximizing the margin is a problem of constrained optimization, wich can be solved by Lagrange method. Final decision function is given by:

$$f\left( {{\mathbf{x}}_{new} } \right) = {\text{sign}}\left( {\sum\limits_{i = 1}^{\# SV} {\alpha_{i} y_{i} } \left\langle {{\mathbf{x}}_{i}^{SV} ,{\mathbf{x}}_{new} } \right\rangle + b} \right)$$
(3)

where f(x new ) is decision function, #SV is number of support vectors, x SV is m-dimensional support vector input and x new is m-dimensional input of unobserved data and α is Lagrange multiplier.

3.2 Kernel Trick

Very few problems are linearly separable in the input space, and therefore SVMs does not have high generalization ability. To overcome linearly inseparable problems we map original input space into high-dimensional dot-product feature space. To map m-dimensional input feature space into l-dimensional feature space we use nonlinear vector function g(x) = (g 1 (x),…,g n (x)) T (Abe 2010). Using the Hilbert-Schmidt theory, the final solution transforms to following:

$$f\left( {{\mathbf{x}}_{new} } \right) = {\text{sign}}\left( {\sum\limits_{i = 1}^{\# SV} {\alpha_{i} y_{i} } K\left( {{\mathbf{x}}_{i}^{SV} ,{\mathbf{x}}_{new} } \right) + b} \right)$$
(4)

where \(K\left( {{\mathbf{x}}_{i}^{SV},{\mathbf{x}}_{new} } \right)\) is the kernel function or kernel.

Kernels allow us to map input space into high-dimensional (even infinite-dimensional) feature space without explicit treatment of variables.

In this study we are using three types of kernels:

  1. 1.

    Linear kernel K(x 1 ,x 2 ) = <x 1 ,x 2 >

  2. 2.

    Polynomial kernel K(x 1 ,x 2 ) = (γ <x 1 ,x 2 > + c 0 ) d

  3. 3.

    Radial basis function (RBF) K(x 1 ,x 2 ) = exp(−γ||x 1  − x 2 ||2 )

where γ is width of radial basis function, coefficent in a polynomial, d is degree of a polynomial, c 0 is additive constant in polynomial a C is influence of training errors. Detailed information about SVMs definition can be found in Abe (2010), Hamel (2009) or Cambell and Ying (2011).

4 Implementation of Support Vector Machines

In this study, the software LIBSVM v3.20 (Chang and Lin 2011) and LIBLINEAR v1.96 (Fan at el. 2008), which are widely used SVMs libraries, were used to SVMs analysis. Input environmental parameters were processed using ArcGIS. Then, MATLAB was used to transform environmental parameters into the form suitable for LIBSVM and LIBLINEAR analysis. Categorical data land use, lithology and aspect were dummy coded. Finally, all input parameters were normalized into the \(\left\langle { - 1,1} \right\rangle\) range. Therefore, four input environmental parameters, namely aspect (9 categories), geology map (90 categories), land use (18 categories) and slope (one continuous value), formed 118-dimensional input space. Landslides areas cover 35,191 pixels against 59,304 pixels covered by stable areas in the study area. These pixel sets and values of the parameters on their locations formed experimental data matrix of shape 94,495 × 118 with landslides or stable area pixels in the rows and values of the input parameters in the columns. This data was then divided into training set used to train SVMs models and validation set used to validate performance of the models with ratio 50–50 %. This size of validation sample allows to perform more complex ROC testing over more test data and is not causing decrease of the predictive performance.

The optimal set of kernel parameters was gained by grid search. Unfortunately, there is no way of how to determine the kernel parameters a priori and they must be determined experimentally. The parameters were tested in the following grid:

  • parameter C: 1, 3, 10, 30, 100, 300

  • parameter γ: 1/118 (0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100)

  • parameter c 0 : 0, 10, 30, 100

  • parameter d: 2, 3

For linear kernel there is one special parameter in LIBLINEAR library which is type of the solver. LIBLINEAR has implemented 8 types of solver [further information in Fan at el. (2008)]. This parameter will be called S: 0, 1, 2, 3, 4, 5, 6, 7.

In this case study, together 534 models were trained and tested.

5 The Validation of the Landslide Susceptibility Maps

The outputs of the SVMs models after their spatialization, are generally presented in the form of maps expressed quantitatively. Final landslides susceptibility maps are usually divided into the five susceptibility levels. On the other hand, reclassification to discreet classes causes the information loss and so the final outputs were left in the continuous form in order to produce smoother ROC curves. Primary outputs from the SVMs algorithm are predicted class labels. The probability outputs are available by transformation of sample distance to separating hyperplane, but this process is computationally costly and cannot be performed for every model during the best inner parameters search phase. The first models predictive performance was measured by parameter “Accuracy” (ACC) (Metz 1978), which was gained over the validation set (47,247 landslide grid cells that is not used in the training phase). The results of the ten best models for each kernel are shown in Tables 1, 2 and 3. Then each kernel (linear, polynomial and radial basis function) was retrained with the optimal set of inner parameters to produce probabilistic outputs. Finally, these outputs were used to validate models. The spatial effectiveness of models were checked by ROC curve. The ROC curve is a useful method of representing the quality of deterministic and probabilistic detection and forecast system (Swets 1988). The area under the ROC curve (AUC) characterizes the quality of a forecast system by describing the system’s ability to anticipate correctly the occurrence or non-occurrence of pre-defined “events”. The ROC curve plots the false positive rate (FP rate) on the x-axis and the true positive rate (TP rate) on the y-axis. It shows the trade-off between the two rates (Negnevitsky 2002). If the AUC is close to 1, the result of the validation is excellent. The predictor which is simply guessing will score 0.5 (AUC), because probability of right guess from two classes is 50 %. The results of the ROC for the best models are illustrated in the Fig. 3.

Table 1 The results of the ten best models of linear kernel
Full size table
Table 2 The results of the ten best models of polynomial kernel
Full size table
Table 3 The results of the ten best models of radial basis function kernel
Full size table
Fig. 3
figure 3

ROC plots for the susceptibility maps showing false positive rate (x-axis) vs. true positive rate (y-axis) for the best model of each kernel

Full size image

According to ROC testing, the best predictive performance was gained by polynomial kernel followed by radial basis function kernel and linear kernel. Values of AUC for each kernel point to very good prediction ability over validation set. On the other hand, only numerical results of validation are not sufficient to measure predictive performance. As we can see in the maps below (Figs. 4, 5), polynomial and linear kernels failed to generalize predictive performance on areas where there was no training data and their characteristics differ from the areas covered by the training data significantly. The most problematic region for both linear and polynomial kernel is region of city Žilina. This is caused by distribution of training data in the study area which is not homogeneous. As we can see in the Fig. 1, the most of the stable areas pixels and active landslisdes pixels that form training and validation datasets are distributed in mountainous parts of the study area. The lack of training data from areas with significantly different characteristics (e.g. from region of city Žilina) causes poor predictive performance of linear and polynomial kernels. This shortage cannot be detected by means of statistical validation and outputs need to be also visually validated.

Fig. 4
figure 4

The classification results of the study area produced by linear kernel

Full size image
Fig. 5
figure 5

The classification results of the study area produced by polynomial kernel

Full size image
Fig. 6
figure 6

The classification results of the study area produced by radial basis function kernel

Full size image

After numerical and visual validation of the classification results, the radial basis function kernel (Fig. 6) was chosen as the optimal kernel for landslides susceptibility mapping, the model’s AUC validation result is 0.974 what is only 0.006 less than the best result gained by polynomial kernel in statistical testing. Radial basis function kernel has also the best generalization ability from all kernels. Another advantage of radial basis function kernel is that the kernel has only two parameters to be set and the training time is also lower than training time of polynomial kernel with four parameters to set.

6 Conclusion

This paper presents an applicability case study of the SVMs method in landslides susceptibility mapping based on landslides recorded in districts Bytča, Kysucké Nové Mesto and Žilina. We have applied the SVMs algorithm using the LIBSVM and LIBLINEAR libraries and made a SVMs application work-flow that is as following:

  1. 1.

    Data preparation. One of the advantages of the SVMs method is the fact that there is no need to reclassify the input environmental parameters. The SVMs method is capable of using the continuous parameters such as slope steepness in the original form. The SVMs algorithm is designed for classification problems based on hundreds of input parameters. Therefore, environmental input parameters need not to be reclassified into the groups with similar properties, which prevents information loss and can be passed into the computation in the original form.

  2. 2.

    Inner parameters grid search. Support Vector Machines has various inner parameters for every kernel that need to be set correctly in order to gain the best predictive performance. Unfortunately, there is no way of choosing the parameters values a priory and values of parameters have to be search by training and testing with model’s accuracy.

  3. 3.

    Support Vector Machines retraining with the best set of parameters from grid search with probability outputs enabled.

  4. 4.

    Statistical validation over validation dataset not used in grid search and final model training.

  5. 5.

    Visual validation. Support Vector Machines algorithm is able to fit to area of interest closely and is prone to training data distribution. If the area of interest has parts with significantly different characteristics (e.g. mountainous forest and urbanized land), it is very important to ensure that the training and validation datasets are evenly distributed over all parts of study area. If this need is not met, the predictive performance will be optimized only to characteristics bounded to training data and predictions in other parts of region may not be reliable.

We have tested three types of kernels and their inner parameters. The results were first validated numerically with ROC curves over the validation set, then we produced the landslides susceptibility maps and validated them visually. From the results, we can draw following conclusions:

  1. (a)

    The results showed that the SVMs method employed in the present study gave promising results with more than 0.90 (AUC) prediction performance.

  2. (b)

    The best predictive performance 0.980 (AUC) was gained by polynomial kernel, but this kernel failed to generalize predictive performance over all study area. This type of kernel is prone to training data distribution. Another disadvantage of this kernel is more kernel parameters to be set, which means more combinations of kernel parameters to be tested in order to gain the best predictive performance.

  3. (c)

    After the visual validation of the landslides susceptibility maps, the radial basis function kernel was chosen as the optimal kernel for landslides susceptibility mapping. This kernel gained 0.974 (AUC) prediction performance. Advantages of this kernel are:

    • two parameters to be set, γ and error cost parameter C, which results to less combinations of kernel parameters to be set than in case of polynomial kernel,

    • very good generalization ability,

    • low training time.

  4. (d)

    Linear kernel scored the lowest prediction performance 0.926 (AUC). The advantages of this kernel is very low training time. The disadvantage is poor generalization ability caused by nature of linear kernel which is the simplest that does not map input space into feature space. This kernel is very effective when the problem is linearly separable or there is very large amount of input parameters which form high-dimensional input space.

  5. (e)

    Among disadvantages of the SVMs method belong computational cost and the biggest disadvantages is hard interpretation of kernels and their parameters and incapability of input parameters weights determination.

As we presented in this case study, the SVMs algorithm with radial basis function kernel gives promising results in landslides susceptibility mapping. Next we suggest further testing of the SVMs method by the professionals from geology and detailed results testing from the lithology, slope, land use and other conditioning factors points of view by the domain experts.