Hyperelasticity of Soft Tissues and Related Inverse Problems

Abstract

In this chapter, we are interested in the constitutive equations used to model macroscopically the mechanical function of soft tissues. After reviewing some basics about nonlinear finite strain constitutive relations, we present recent developments of experimental biomechanics and inverse methods aimed at quantifying constitutive parameters of soft tissues. A focus is given to in vitro characterization of hyperelastic parameters based on full-field data that can be collected with digital image correlation systems during the experimental tests. The specific use of these data for membrane-like tissues is first illustrated through the example of bulge inflation tests carried out onto pieces of aortic aneurysms. Then an inverse method, based on the principle of virtual power, is introduced to estimate regional variations of material parameters for more general applications.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

2.1 Introduction

A better understanding of many issues of human health, disease, injury, and their treatment thereof necessitates a detailed quantification of how biological cells, tissues, and organs respond to applied loads. Thus, experimental and computational mechanics can, and must, play a fundamental role in cell biology, physiology, pathophysiology, and clinical intervention. The goal of this chapter is to discuss some of the recent developments of experimental biomechanics based on the use of digital image correlation and inverse methods for quantifying the finite strain behavior of biological soft tissues in terms of nonlinear constitutive relations. After a brief review of these constitutive relations, two recent developments of the author’s experience are presented to illustrate the potential of digital image correlation and inverse methods in experimental biomechanics of soft tissues.

2.2 Basic Constitutive Equations of Soft Tissues

This section presents the theoretical background for understanding the foundations of constitutive models in soft tissues. This background is essential for the following sections and for the other chapters of this book. The presentation of this background follows the approach of a seminal paper from Millard [1].

2.2.1 Kinematics of Finite Deformation

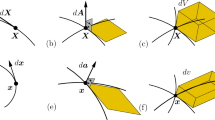
Since the early 1940s there has been enormous progress in the development of a theory of elastic materials subjected to large deformations. Significant theoretical results, many confirmed by experiments, have projected considerable light on the physical behavior of rubberlike materials such as synthetic elastomers, polymers and biological tissue, in addition to natural rubber. The mathematical theory of elasticity of materials subjected to large deformations is inherently nonlinear. The theory of elasticity of materials for which there exists an elastic potential energy function is known as hyperelasticity. Before presenting the constitutive equations for a hyperelastic solid, we begin with a sketch of the principal kinematical relations used to describe the finite deformation of a continuum and with the Cauchy stress principle and equations of kinetics. A body $B=\{P_k\}$ is a set of material points $P_k$ called particles. A reference frame is a set $\Upsilon =\{O,\mathbf {e}\}$ consisting of an origin point O and an orthonormal vector basis $\mathbf {e}$. The motion of a particle P relative to $\Upsilon$ is described by the time locus of its position vector $\mathbf x (P,t)$ relative to $\Upsilon$. This locus is the trajectory or path of P in $\Upsilon$. A typical particle P may be identified by its position vector $\mathbf {X}(P)$ in $\Upsilon$ at some reference time $t_0$. The domain $\kappa _0$ of $\mathbf {X}$, the region in Euclidian space occupied by B at time $t_0$ is called a reference configuration of B. Then, relative to $\Upsilon$ the motion of a particle P from $\kappa _0$ is described by the vector function

$$\begin{aligned} \mathbf {x}=\chi (\mathbf {X},t) \end{aligned}$$

(2.1)

The domain $\kappa$ of $\mathbf {x}$, the region in Euclidian space occupied by B at time $t_0$ is called a current configuration of B. Hence, $\mathbf {x}$ denotes the place at time t in the current configuration $\kappa$ which is occupied by the particle P whose place was X in the reference configuration of B. The velocity and acceleration of a particle P relative to $\Upsilon$ are defined by

$$\begin{aligned} \mathbf {v}(\mathbf {X},t)= {\dot{\mathbf{x}}}(\mathbf {X},t) \end{aligned}$$

(2.2)

$$\begin{aligned} \varvec{\gamma }(\mathbf {X},t)= {\dot{\mathbf{v}}}(\mathbf {X},t)= {\ddot{\mathbf{x}}}(\mathbf {X},t) \end{aligned}$$

(2.3)

We shall assume henceforward that the body is a contiguous collection of particles, we call this body a continuum. It is assumed that $\chi$ is a smooth one-to-one map of every material point of $\kappa _0 \rightarrow \kappa$ with

$$\begin{aligned} J=\det \mathbf {F} > 0, \end{aligned}$$

(2.4)

in which

$$\begin{aligned} \mathbf {F}=\partial \mathbf {x} / \partial \mathbf {X} = \varvec{\mathrm {Grad}\,}\mathbf {x} \end{aligned}$$

(2.5)

is called the deformation gradient. This tensor transforms the tangent element $\mathrm {d} \mathbf {X}$ of a material line $\mathfrak {L}_0$ in $\kappa _0$ into the tangent element $\mathrm {d} \mathbf {x}$ of its deformed image line $\mathfrak {L}$ in $\kappa$. Hence,

$$\begin{aligned} \mathrm {d} \mathbf {x} = \mathbf {F} \mathrm {d} \mathbf {X} \end{aligned}$$

(2.6)

Let $\Vert \mathrm {d} \mathbf {x}\Vert =\mathrm {d}l$ and $\Vert \mathrm {d} \mathbf {X}\Vert =\mathrm {d}L$, where l and L are the arc length parameters for $\mathfrak {L}$ and $\mathfrak {L}_0$ respectively. Then Eq. 2.6 may be written:

$$\begin{aligned} \lambda \mathbf {e} = \mathbf {F} \mathbf {E} \end{aligned}$$

(2.7)

in which $\mathbf {e} = \mathrm {d}\mathbf {x} / \mathrm {d}l$ and $\mathbf {E} = \mathrm {d}\mathbf {X} / \mathrm {d}L$ are unit vectors tangent to $\mathfrak {L}$ and $\mathfrak {L}_0$ at $\mathbf {x}$ and $\mathbf {X}$ and

$$\begin{aligned} \lambda = \mathrm {d}l / \mathrm {d}L \end{aligned}$$

(2.8)

is named the stretch, the ratio of the current length $\mathrm {d}s$ to the reference length $\mathrm {d}S$ of the material element. These lengths are commonly called the deformed and undeformed lengths, respectively. However it is not essential that the reference configuration be an undistorted reference configuration, nor one that the body actually needs to occupy at any time during its motion. It is seen that Eq. 2.7 expresses the physical result that $\mathbf {F}$ rotates $\mathbf {E}$ into the direction $\mathbf {e}$ and stretches it by an amount $0<\lambda <\infty$. This is essentially the substance of the more general and physically useful polar decomposition theorem of linear algebra applied pointwise to the nonsingular tensor $\mathbf {F}$

$$\begin{aligned} \mathbf {F}=\mathbf {R}\mathbf {U}=\mathbf {V}\mathbf {R} \end{aligned}$$

(2.9)

The proper orthogonal tensor $\mathbf {R}$ characterizes the local rigid body rotation of a material element. The positive symmetric tensors $\mathbf {U}$ and $\mathbf {V}$ describe the local deformation of the element. They are called the right and the left stretch tensors, respectively. The decomposition of the deformation gradient $\mathbf {F}$ into a pure stretch $\mathbf {U}$ at $\mathbf {X}$ followed by a rigid body rotation $\mathbf {R}$, or by the same rigid body rotation followed by a pure stretch $\mathbf {V}$ at $\mathbf {x}$ is unique. Because $\mathbf {U}$ and $\mathbf {V}$ usually are tedious to compute, it is customary to use their squares

$$\begin{aligned} \mathbf {C}=\mathbf {F}^T \mathbf {F}=\mathbf {U}^2~\text {and}~\mathbf {B}=\mathbf {F} \mathbf {F}^T =\mathbf {V}^2 \end{aligned}$$

(2.10)

The corresponding positive symmetric tensors are respectively known as the right and the left Cauchy–Green deformation tensors. It follows that $\mathbf {U}$ and $\mathbf {V}$ ($\mathbf {C}$ and $\mathbf {B}$) have the same principal values $\lambda _k$ ($\lambda _k^2$) and respective principal directions $\varvec{\mu }$ and $\varvec{\nu }$ are related by the rotation $\mathbf {R}$

$$\begin{aligned} \varvec{\nu }=\mathbf {R}.\varvec{\mu } \end{aligned}$$

(2.11)

The $\lambda _k$ are the stretches of the three principal material lines, they are called the principal stretches.

Formulae relating the respective material surface area and volume elements $\mathrm {d}a$ and $\mathrm {d}v$ in $\kappa$ to their respective reference images $\mathrm {d}A$ and $\mathrm {d}V$ in $\kappa _0$ may be easily derived by application of

$$\begin{aligned} \mathbf {n} \mathrm {d}a=J~\mathbf {F}^{-T}.\mathbf {N}\mathrm {d}A~~~\text {and}~~~\mathrm {d}v=J\mathrm {d}V \end{aligned}$$

(2.12)

where $\mathbf {n}$ is the exterior unit normal vector to $\partial \mathscr {P}$ in $\kappa$ and $\mathbf {N}$ is the exterior unit normal vector to $\partial \mathscr {P}$ in $\kappa _R$.

The previous relation shows that $\det \mathbf {F}$ is the ratio of the current (deformed) volume to the reference (undeformed) volume of a material element. Therefore the deformation is isochoric if $J=1$. It is evident on physical grounds that $0<\det \mathbf {F} <\infty$. The material time rate of the deformation of a continuum is described by the velocity gradient tensor $\mathbf {L}$

$$\begin{aligned} \mathbf {L}=\varvec{\mathrm {Grad}\,}\dot{\mathbf{x }} = {\dot{\mathbf{F}}}\mathbf {F}^{-1} \end{aligned}$$

(2.13)

The symmetric part $\mathbf {D}$ and antisymmetric part $\mathbf {W}$ of $\mathbf {L}$ are the stretching and spin tensors, respectively.

2.2.2 The Cauchy Stress Principle and the Equations of Motion

The forces that act on any part $\mathscr {P} \subset \mathscr {B}$ of a continuum $\mathscr {B}$ are of two kinds: a distribution of contact force $\mathbf {t_n}$ per unit area of the boundary $\partial \mathscr {P}$ of $\mathscr {P}$ in $\kappa$, and a distribution of body force $\mathbf {b}$ per unit volume of $\mathscr {P}$ in $\kappa$. The total force $\mathscr {F}(\mathscr {P},t)$ and the total torque $\mathscr {T}(\mathscr {P},t)$ acting on the part $\mathscr {P}$ are related to the momentum and the moment of momentum of the material points of $\mathscr {B}$ in an inertial frame $\Phi$ in accordance with Euler’s laws of motion

$$\begin{aligned} \mathscr {F}(\mathscr {P},t)= \int _{\partial \mathscr {P}} \mathbf {t_n} ~\mathrm {d}a + \int _{\mathscr {P}} \mathbf {b} ~\mathrm {d}v = \frac{\mathrm {d}}{\mathrm {d}t} \int _{\mathscr {P}} \mathbf {v} ~\mathrm {d}m \end{aligned}$$

(2.14)

$$\begin{aligned} \mathscr {T}(\mathscr {P},t)= \int _{\partial \mathscr {P}} \mathbf {x}\times \mathbf {t_n} ~\mathrm {d}a + \int _{\mathscr {P}} \mathbf {x}\times \mathbf {b} ~\mathrm {d}v = \frac{\mathrm {d}}{\mathrm {d}t} \int _{\mathscr {P}} \mathbf {x}\times \mathbf {v} ~\mathrm {d}m \end{aligned}$$

(2.15)

The moments in Eq. 2.15 are to be computed with respect to the origin in $\Phi$. Note that $\mathrm {d}m=\rho ~\mathrm {d}v$ is the material element of mass with density $\rho$ per unit volume in $\kappa$.

The principle of balance of mass requires also that $\mathrm {d}m=\rho _R~\mathrm {d}V$ where $\rho _R$ is the density of mass per unit volume V in $\kappa _R$. Therefore one finds that the respective mass densities are related by the local equation of continuity

$$\begin{aligned} \rho _R = J \rho \end{aligned}$$

(2.16)

Application of the first law of Euler to an arbitrary tetrahedral element leads to Cauchy’s stress principle

$$\begin{aligned} \mathbf {t_n} = \varvec{\sigma }. \mathbf {n} \end{aligned}$$

(2.17)

Hence the traction or stress vector $\mathbf {t_n}$ is a linear transformation of the unit normal $\mathbf {n}$ by the Cauchy stress tensor $\varvec{\sigma }$. Use of previous equations and the divergence theorem yields Cauchy first law of motion

$$\begin{aligned} \mathrm {div}\,\varvec{\sigma }+ \mathbf {b} = \rho \varvec{\gamma } \end{aligned}$$

(2.18)

The second law of Eq. 2.15 together with Eqs. 2.17 and 2.18 yields the equivalent local moment balance condition restricting the Cauchy stress $\varvec{\sigma }$ to the space of symmetric tensors

$$\begin{aligned} \varvec{\sigma }= \varvec{\sigma }^T \end{aligned}$$

(2.19)

The Cauchy stress characterizes the contact force distribution $\mathbf {t_n}$ in $\kappa$ per unit current area in $\kappa$. But this is often inconvenient in solid mechanics because the deformed configuration generally is not known a priori. Therefore, the engineering stress tensor $\mathbf {T}_R$, also known as the first Piola-Kirchhoff stress tensor, is introduced to define the contact force distribution $\mathbf {t_n}\equiv \mathbf {T}_R . \mathbf {N}$ in $\kappa$ per unit reference area in $\kappa _R$. Then for the same contact force $\mathrm {d}\mathscr {F}(\mathscr {P},t)$, we must have

$$\begin{aligned} \mathrm {d}\mathscr {F}(\mathscr {P},t) \equiv \mathbf {t_n}~\mathrm {d}a = \varvec{\sigma }.\mathbf {n}~\mathrm {d}a = \mathbf {T}_R.\mathbf {N}~\mathrm {d}A = \mathbf {t_N}~\mathrm {d}A \end{aligned}$$

(2.20)

The vector $\mathbf {t_N}$ is named the engineering stress tensor. We thus obtain the rule

$$\begin{aligned} \mathbf {T}_R = J~\varvec{\sigma }\mathbf {F}^{-T} \end{aligned}$$

(2.21)

relating the engineering and Cauchy stress tensors.

The corresponding stress principle and balance laws become

$$\begin{aligned} \mathbf {t_N} = \mathbf {T}_R . \mathbf {N} \end{aligned}$$

(2.22)

$$\begin{aligned} \mathrm{Div}\,\mathbf {T}_R + \mathbf {b}_R = \rho _R~\varvec{\gamma }_R \end{aligned}$$

(2.23)

$$\begin{aligned} \mathbf {T}_R \mathbf {F}^{T} = \mathbf {F} \mathbf {T}_R^{T} \end{aligned}$$

(2.24)

Hence the engineering stress $\mathbf {T}_R$ generally is not symmetric. Equation $\mathbf {b}_R \equiv J \mathbf {b}$ identifies the body force per unit volume in $\kappa _R$, and Div denotes the divergence operator with respect to $\mathbf {X}$ in $\kappa _R$, whereas $\mathrm {div}\,$ is with respect to $\mathbf {x}$ in $\kappa$.

Another stress tensor that will be useful is the second Piola-Kirchhoff stress defined as

$$\begin{aligned} \varvec{\pi }= \mathbf {F}^{-1} \mathbf {T}_R = J~\mathbf {F}^{-1} \varvec{\sigma }\mathbf {F}^{-T} \end{aligned}$$

(2.25)

Thus far, the deformation of a continuum and the actions that produces it have been treated separately without the mention of any special material characteristics that the body may possess. Of course the inherent constitutive nature of the material dictates its deformation response to action by forces and torques. For a specific class of materials, the specific relationship between the deformation gradient $\mathbf {F}$, the rate of deformation $\dot{\mathbf {F}}$, and the stress $\varvec{\sigma }$, $\mathbf {T}_R$ or $\varvec{\pi }$ is described by an equation known as a constitutive equation. In the next section, the principle of balance of mechanical energy will be applied to derive the constitutive equation for a special class of perfectly elastic materials called hyperelastic solids.

2.2.3 Hyperelasticity

Thermodynamics foundation The first law of thermodynamics tells that the time rate of change of the internal energy $E(\mathscr {P},t)$ for any part $\mathscr {P} \subset \mathscr {B}$ of a body $\mathscr {B}$ is balanced by the total mechanical power $W(\mathscr {P},t)$ and the total heat flux $Q(\mathscr {P},t)$.

$$\begin{aligned} \dot{E}(\mathscr {P},t) = W(\mathscr {P},t) + Q(\mathscr {P},t) \end{aligned}$$

(2.26)

The second law of thermodynamics tells that the time rate of change of entropy $\dot{S}(\mathscr {P},t)$ for any part $\mathscr {P} \subset \mathscr {B}$ of a body $\mathscr {B}$ can be decomposed into exchanges of entropy and production of entropy and that the latter can only be positive, or zero if the transformation is reversible (no dissipation). If $\Theta$ denotes temperature, exchanges of entropy at constant temperature (isotherm transformations will be assumed further) may be written such as: $Q/\Theta$. Finally, the second law of thermodynamics tells

$$\begin{aligned} \dot{S}(\mathscr {P},t) \ge \frac{Q(\mathscr {P},t)}{\Theta } \end{aligned}$$

(2.27)

$$\begin{aligned} \dot{E}(\mathscr {P},t) - \Theta \dot{S}(\mathscr {P},t) \le W(\mathscr {P},t) \end{aligned}$$

(2.28)

$\mathscr {P}$ being an arbitrary tetrahedral element, and $\varvec{\sigma }:\mathbf {D}$ being the mechanical power per unit volume, it may be written at any time t

$$\begin{aligned} \rho ( \dot{e} - \Theta \dot{s} ) \le \varvec{\sigma }:\mathbf {D} \end{aligned}$$

(2.29)

where e denotes the local specific internal energy and s denotes the local specific entropy. This equation points out that the work done by the stress would induce either an increase of the specific internal energy or a decrease of the specific entropy. In the case of elasticity, the transformation is reversible and it may be written

$$\begin{aligned} \rho ( \dot{e} - \Theta \dot{s} ) = \varvec{\sigma }:\mathbf {D} \end{aligned}$$

(2.30)

When the work done by the stress induces mostly an increase of the specific internal energy ($| \Theta \dot{s} |<< \dot{e}$), we speak of enthalpic elasticity (in an isotherm transformation, $\dot{e}=\dot{\text {h}}$ where $\text {h}$ would be the specific enthalpy). Enthalpic elasticity is the elasticity of crystals where the deformation comes mostly from a change of distances between atoms. Elastic response of the crystalline solids is due to the change of the equilibrium interatomic distances under stress and therefore, the change in the internal energy of the crystal.

When the work done by the stress induces mostly a decrease of entropy ($\dot{e}<< | \Theta \dot{s} |$), we speak of entropic elasticity. Elasticity of soft biological tissues is composed from the elastic responses of the chains crosslinked in the network sample. External stress changes the equilibrium end-to-end distance of a chain, and it thus adopts a less probable conformation, its entropy therefore decreases. Therefore, the elasticity of soft biological tissues is of purely entropic nature.

Introducing the specific free energy $\phi =e+\Theta s$, and still assuming isotherm transformations $(\dot{\Theta }=0)$, it may be written

$$\begin{aligned} \rho \dot{\phi } = \varvec{\sigma }:\mathbf {D} \end{aligned}$$

(2.31)

It is now the time to define what a hyperelastic solid is. A hyperelastic solid is a material whose specific free energy depends only on the strain. It may be written

$$\begin{aligned} \phi (\mathbf {X},t) = \phi (\mathbf {F}(\mathbf {X},t),\mathbf {X}) \end{aligned}$$

(2.32)

The $\psi =\rho \phi$ function is a strain energy density function. Then the constitutive equation for a hyperelastic solid can be written

$$\begin{aligned} \varvec{\pi }= \frac{\partial \psi }{\partial \mathbf {E}} = 2 \frac{\partial \psi }{\partial \mathbf {C}} \end{aligned}$$

(2.33)

$$\begin{aligned} \mathbf {T}_R = \frac{\partial \psi }{\partial \mathbf {F}} = \mathbf {F} \frac{\partial \psi }{\partial \mathbf {E}} = 2 \mathbf {F} \frac{\partial \psi }{\partial \mathbf {C}} \end{aligned}$$

(2.34)

$$\begin{aligned} \varvec{\sigma }= J^{-1} \frac{\partial \psi }{\partial \mathbf {F}} \mathbf {F}^T = J^{-1} \mathbf {F} \frac{\partial \psi }{\partial \mathbf {E}} \mathbf {F}^T = 2 J^{-1} \mathbf {F} \frac{\partial \psi }{\partial \mathbf {C}} \mathbf {F}^T \end{aligned}$$

(2.35)

Isotropic compressible hyperelastic solids For an isotropic solid, the strain energy function must be an isotropic scalar valued function of the principal invariants alone

$$\begin{aligned} \psi = \psi (\mathbf {C}) = \psi (\mathbf {B}) = \psi (I_1,I_2,I_3) \end{aligned}$$

(2.36)

wherein, specifically,

$$\begin{aligned} I_1 = \mathrm {tr}(\mathbf {B}) \end{aligned}$$

(2.37)

$$\begin{aligned} I_2 = \frac{1}{2} \left[ I_1^2 - \mathrm {tr}(\mathbf {B}^2) \right] \end{aligned}$$

(2.38)

$$\begin{aligned} I_3 = \mathrm {det}(\mathbf {B}) \end{aligned}$$

(2.39)

Note that Eq. 2.35 may be rewritten such as

$$\begin{aligned} \varvec{\sigma }= 2 J^{-1} \frac{\partial \psi }{\partial \mathbf {B}} \mathbf {B} \end{aligned}$$

(2.40)

Then, introducing the principal invariants

$$\begin{aligned} \varvec{\sigma }= \left( \frac{\partial \psi }{\partial J} + 2 J^{-1} \frac{\partial \psi }{\partial I_2} I_2 \right) \mathbf {1} + 2 J^{-1} \frac{\partial \psi }{\partial I_1} \mathbf {B} - 2 J^{-1} \frac{\partial \psi }{\partial I_{-1}} \mathbf {B}^{-1} \end{aligned}$$

(2.41)

where $I_{-1}=I_2/I_3=\mathrm {tr}(\mathbf {B}^{-1})$.

Isotropic hyperelastic incompressible solids The Cauchy stress on an incompressible, hyperelastic material, is determined by $\mathbf {F}$ only to within an arbitrary stress which is proportional to the identity tensor. Then the constitutive equation for an incompressible, isotropic, hyperelastic material is given by

$$\begin{aligned} \varvec{\sigma }= - p \mathbf {1} + 2 \frac{\partial \psi }{\partial I_1} \mathbf {B} - 2 \frac{\partial \psi }{\partial I_2} \mathbf {B}^{-1} \end{aligned}$$

(2.42)

where p is an undetermined scalar of $\mathbf {x}$. Note that $I_2=I_{-1}$ for an incompressible solid.

A particular type of strain energy functions may be written such as polynomials

$$\begin{aligned} \psi = \sum _{j=0}^{N_j} \sum _{i=0}^{N_i} C_{ij} (I_1 - 3)^{i} (I_2 - 3)^{j} \end{aligned}$$

(2.43)

when $N_i=3$ and $N_j=0$ it is referred to as Yeoh strain energy function, when $N_i=1$ and $N_j=1$ but $C_{11}=0$, we have the Mooney–Rivlin material. The special case when $N_i=1$ and $N_j=0$ is the neo-Hookean material.

Another particular type which is meaningful for biological tissues may be written

$$\begin{aligned} \psi = \frac{\mu _0}{2\gamma } \left[ e^{\gamma (I_1 - 3)} -1 \right] \end{aligned}$$

(2.44)

Isotropic hyperelastic nearly incompressible solids It is common for nearly incompressible hyperelastic solids to assume a perfect decoupling between purely volumetric and purely isochoric effects, and then to decompose the strain energy density function additively in two components: one depending only on volume changes and the second one independent of volume changes

$$\begin{aligned} \psi = U(J) + \bar{\psi }(\bar{I}_1,\bar{I}_2) \end{aligned}$$

(2.45)

$$\begin{aligned} \varvec{\sigma }= \left( \frac{\partial \psi }{\partial J} + 2 J^{-1} \frac{\partial \psi }{\partial I_2} I_2 \right) \mathbf {1}&\nonumber \\&+ 2 J^{-1} \frac{1}{J^{2/3}}\frac{\partial \bar{\psi } }{\partial \bar{I}_1} \mathbf {B} - 2 J^{-1} \frac{1}{J^{4/3}/J^2} \frac{\partial \bar{\psi } }{\partial \bar{I}_{2}} \mathbf {B}^{-1} \end{aligned}$$

(2.46)

where $\bar{I}_1=\mathrm {tr}({\bar{\mathbf{B}}})$, $\bar{I}_2 = \frac{1}{2} \left[ \bar{I}_1^2 - \mathrm {tr}({\bar{\mathbf{B}}}^2) \right] =\mathrm {tr}({\bar{\mathbf{B}}}^{-1})$, ${\bar{\mathbf{B}}}={\bar{\mathbf{F}}} {\bar{\mathbf{F}}}^T$ and ${\bar{\mathbf{F}}}=J^{-1/3}\mathbf {F}$.

$$\begin{aligned} \varvec{\sigma }&= \left[ \left( \frac{\partial \psi }{\partial J} + 2 J^{-1} \frac{\partial \psi }{\partial I_2} I_2 \right) + \frac{\partial \bar{\psi } }{\partial \bar{I}_1} \frac{\partial \bar{I}_1 }{\partial J } + \frac{\partial \bar{\psi } }{\partial \bar{I}_2} \frac{\partial \bar{I}_2 }{\partial J } \right] \mathbf {1} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad + 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_1} {\bar{\mathbf{B}}} - 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_{2}} {\bar{\mathbf{B}}}^{-1} \end{aligned}$$

(2.47)

$$\begin{aligned} \varvec{\sigma }&= \left[ \left( \frac{\partial \psi }{\partial J} + 2 J^{-1} \frac{\partial \psi }{\partial I_2} I_2 \right) - \frac{2}{3} J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_1} \bar{I}_1 - \frac{4}{3} J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_2} \bar{I}_2 \right] \mathbf {1} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad + 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_1} {\bar{\mathbf{B}}} - 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_{2}} {\bar{\mathbf{B}}}^{-1} \end{aligned}$$

(2.48)

$$\begin{aligned} \varvec{\sigma }&= \left[ \left( \frac{\partial \psi }{\partial J} + 2 J^{-1} \frac{\partial \psi }{\partial I_2} I_2 \right) - 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_2} \bar{I}_2 - \frac{2}{3} J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_1} \bar{I}_1 + \frac{2}{3} J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_2} \bar{I}_2 \right] \mathbf {1} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad + 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_1} {\bar{\mathbf{B}}} - 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_{2}} {\bar{\mathbf{B}}}^{-1} \end{aligned}$$

(2.49)

Finally,

$$\begin{aligned} \varvec{\sigma }&= \left[ \frac{\partial \psi }{\partial J} - \frac{2}{3} J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_1} \bar{I}_1 + \frac{2}{3} J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_2} \bar{I}_2 \right] \mathbf {1} + 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_1} {\bar{\mathbf{B}}} - 2 J^{-1} \frac{\partial \bar{\psi } }{\partial \bar{I}_{2}} {\bar{\mathbf{B}}}^{-1} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad = \frac{\partial \psi }{\partial J} \mathbf {1} + 2 J^{-1} \mathrm {Dev}\left( \frac{\partial \bar{\psi } }{\partial \bar{I}_1} {\bar{\mathbf{B}}} - \frac{\partial \bar{\psi } }{\partial \bar{I}_2} {\bar{\mathbf{B}}}^{-1} \right) \end{aligned}$$

(2.50)

where $\mathrm {Dev}$ denotes the deviatoric tensor.

The Cauchy stress is then decomposed additively into a hydrostatic component related to J and into a deviatoric component related to $\bar{I}_1$ and $\bar{I}_2$.

$$\begin{aligned} \varvec{\sigma }= - p \mathbf {1} + \mathbf {s} \end{aligned}$$

(2.51)

where $p=-\partial U/\partial J$ and

$$\begin{aligned} \mathbf {s} = 2 J^{-1} \mathrm {Dev}\left( \frac{\partial \bar{\psi } }{\partial \bar{I}_1} {\bar{\mathbf{B}}} - \frac{\partial \bar{\psi } }{\partial \bar{I}_2} {\bar{\mathbf{B}}}^{-1} \right) \end{aligned}$$

(2.52)

Common models of isotropic hyperelastic nearly incompressible solids The compressible version of a neo-Hookean material may be written

$$\begin{aligned} \psi = C_{10} (\bar{I}_1 - 3) + \frac{1}{D} (J - 1)^2 \end{aligned}$$

(2.53)

The compressible version of a Yeoh material may be written

$$\begin{aligned} \psi = \sum _{i=0}^{3} C_{i0} (\bar{I}_1 - 3)^i + \sum _{i=0}^{3} \frac{1}{D_i} (J - 1)^{2i} \end{aligned}$$

(2.54)

Another common model in compressible hyperelasticity is the Arruda Boyce model. Although its formulation is based on a thermodynamical background, it is not often used for biological tissues. The strain energy density may be written

$$\begin{aligned} \psi = \mu \sum _{i=0}^{5} \frac{C_i}{\lambda _m^{2i-2}} (\bar{I}_1^i - 3^i) + \frac{1}{D} \left[ \frac{(J^2 - 1)}{2}-\mathrm {ln}(J)\right] \end{aligned}$$

(2.55)

where: $C_1=\frac{1}{2}$, $C_2=\frac{1}{20}$, $C_3=\frac{11}{1050}$, $C_4=\frac{19}{7050}$, $C_5=\frac{51}{673750}$.

A more common model is the Ogden model, which may be written

$$\begin{aligned} \psi = \frac{2\mu }{\alpha ^2} (\lambda _1^{2\alpha }+\lambda _2^{2\alpha }+\lambda _3^{2\alpha }) + \frac{1}{D}(J^2 - 1) \end{aligned}$$

(2.56)

where $\lambda _1$, $\lambda _2$ and $\lambda _3$ are the principal stretches.

2.2.4 More Sophisticated Constitutive Models

The aim of this section is to introduce the basics for the following sections of this chapter but also for the following chapters of this book. It is not rare that soft tissues are modeled with constitutive equations including other features than the ones of isotropic hyperelasticity. The main ones are summarized hereafter.

Anisotropic hyperelastic models Soft tissues may often present anisotropic effects. The most common effect is a different stress–stretch curve when they are subjected to uniaxial tension in two different directions. Very common models permitting to represent these effects may describe the material such as a composite made of a neo-Hookean matrix in which fiber families are embedded

$$\begin{aligned} \psi = C_{10} (\bar{I}_1 - 3) + \sum _{i=1}^{N} \frac{k_{1i}}{2k_{2i}} \left[ e^{k_{2i}(\bar{\lambda }_i^2 - 1)} -1 \right] + \frac{1}{D}(J^2 - 1) \end{aligned}$$

(2.57)

where $\bar{\lambda }_i^2= \bar{\mathbf {C}}\! :\! \left( \mathbf {M_i} \!\otimes \! \mathbf {M_i} \right) =\bar{\mathbf {C}}\mathbf {M_i}.\mathbf {M_i}$.

$\mathbf {M_i}$ are vectors defining orientations of a fiber family in the reference configuration. Although motivated by microstructural information, this type of models was developed primarily to capture phenomenologically the anisotropic response of soft tissues subjected to multidirectional tensile tests, which ultimately depends on constituent fractions, fiber orientations, cross-linking, physical entanglements, and so forth.

Irreversible effects When subjected to cycled uniaxial tensile tests (or other types of testing), the loading unloading profile of biological tissues often presents an hysteresis on the first cycle. With repeated loading cycles the load-deformation curves shift to the right in a load-elongation diagram and the hysteretic effects diminish. In a load-time diagram the load-time curves shift upwards with increasing repetition number. By repeated cycling, eventually a steady state is reached at which no further change will occur unless the cycling routine is changed. In this state the tissue is said to be preconditioned. Any change of the lower or upper limits of the cycling process requires new preconditioning of the tissue. Preconditioning occurs due to internal changes in the structure of the tissue. Hysteresis, nonlinearity, relaxation and preconditioning are common properties of all soft tissues, although their observed degrees vary.

The difference between the loading and unloading response can be simulated using an isotropic damage formulation. It consists in writing the strain energy in the form of

$$\begin{aligned} \psi = ( 1-d ) \bar{\psi } + \frac{1}{D}(J^2 - 1) \end{aligned}$$

(2.58)

where $1-d$ is a reduction factor and d is a scalar damage variable defined in $0 \le d \le 1$. When $d=0$ the material is undamaged. The value $d=1$ is an upper limit in which the material is completely damaged and failure occurs. The evolution of damage may be described by a function of a maximum equivalent strain defined such as $\zeta ^m=\mathrm {max}_{t\in [-\infty ,t]}\sqrt{2\bar{\psi }(\mathbf {E}(t)}$ where $\mathbf {E}(t)$ is the Green–Lagrange strain tensor for the pseudotime t of the deformation process. The evolution of damage can be described with an exponential form

$$\begin{aligned} 1-d(\zeta ^m) = \beta +(1-\beta )\frac{1-e^{-\zeta ^m/\alpha }}{\zeta ^m/\alpha } \end{aligned}$$

(2.59)

where $\alpha$ and $\beta$ are material parameters.

Damage can also be modeled with the concept of softening hyperelasticity. In this concept, instead of having a strain energy tending to infinity when the norm of the stretch tensor tends to infinity, the stored energy is bounded [2].

More details about damage models are given in Chap. 4 of this book.

Time dependent effects The hysteresis in the stress–strain relationship may also show the viscoelastic behavior of soft biological tissue. The simplest model of viscoelasticity is the Kelvin model combining a linear spring and a dashpot. In analogy to linear viscoelasticity in small strain, we can assume an additive free energy potential with the form $\psi =\psi _0+\psi _v$ where $\psi _0$ measures the energy stored in the elastic branch (equilibrium) and $\psi _v$ measured the energy stored in the viscous branch, which progressively disappears during relaxation.

In a viscoelastic material the history of strain affects the actually observed stress. As well, loading and unloading occur on different stress–strain paths. The hysteresis of most biological tissues is assumed to show only little dependence on the strain rate within several decades of strain rate variation. This insensitivity to strain rate over several decades is not compatible with simple viscoelastic models consisting for instance of a single spring and dashpot element. With such a simple viscoelasticity approach the material model will show a maximum hysteresis loop at a certain strain rate whereas all other strain rates will show a smaller hysteresis loop. A model consisting of a discrete number of spring-dashpot elements therefore produces a discrete hysteresis spectrum with maximum dissipation at discrete strain rates. It may be written as

$$\begin{aligned} \bar{\psi } = \int _0^t \left[ \left( 1-\sum _{k=1}^N g_k(1-e^{-\frac{t-\tau }{\tau _k}}) \right) \times \frac{d \psi _0 }{d\tau } \right] d\tau \end{aligned}$$

(2.60)

where $\tau _k$ are the relaxation times and $g_k$ are the relaxation coefficients.

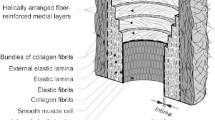
It is widely accepted that soft connective tissues are multiphasic materials. They are sometimes modeled as a mixture of two immiscible constituents: an solid hyperelastic matrix and an interstitial incompressible fluid. This type of models, sometimes called poroelastic models, can particularly describe both the stress distribution and interstitial fluid motion within the cartilage tissue under various loading conditions. Moreover the interaction between the solid and the fluid phases has been identified to be responsible for the apparent viscoelastic properties in the compression of hydrated soft tissues.

Active models It is often assumed that in the presence of an actin-myosin complex in the soft tissue, the total Cauchy stress can be split into two parts: $\varvec{\sigma }=\varvec{\sigma }_p+\varvec{\sigma }_a$, where $\varvec{\sigma }_p$ and $\varvec{\sigma }_a$ denote passive and active stress respectively. The passive stress results from the elastic deformation of the tissue and can be derived from the theory of hyperelasticity. The active stress is generated in myofibrils or in smooth muscle cells by activation and is directed parallel to the fiber orientation. Hence: $\varvec{\sigma }_a = \sigma _a \varvec{\epsilon }\otimes \varvec{\epsilon }$ where $\varvec{\epsilon }$ is the unit vector identifying the orientation. The mechanism for generating $\sigma _a$ involves internal variables.

2.2.5 Growth and Remodelling Models

Many experiments have shown that the stress field dictates, at least in part, the way in which the microstructure of soft tissues is organized. This observation leads to the concept of functional adaptation wherein it is thought that soft tissues functionally adapt so as to maintain particular mechanical metrics (e.g., stress) near target values. To accomplish this, tissues often develop regionally varying stiffness, strength, and anisotropy.

Models of growth and remodelling necessarily involve equations of reaction diffusion. There has been a trend to embed the reaction diffusion framework within tissue mechanics [3, 4]. The primary assumption is that one models volumetric growth through a growth tensor $\mathbf F _g$, which describes changes between two fictitious stress-free configurations: the original body is imagined to be fictitiously cut into small stress-free pieces, each of which is allowed to grow separately via $\mathbf F _g$, with $\det (\mathbf F _g)\ne 1$. Because these growths need not be compatible, internal forces are often needed to assemble the grown pieces, via $\mathbf F _a$, into a continuous configuration. This, in general, produces residual stresses, which are now known to exist in many soft tissues. The formulation is completed by considering elastic deformations, via $\mathbf F _a$, from the intact but residually stressed traction-free configuration to a current configuration that is induced by external mechanical loads. The initial boundary value problem is solved by introducing a constitutive relation for the stress response to the deformation $\mathbf F _e\mathbf F _a$, which is often assumed to be incompressible hyperelastic, plus a relation for the evolution of the stress-free configuration via $\mathbf F _g$. Thus, growth is assumed to occur in stress-free configurations and typically not to affect material properties.

Although the previous theory called the theory of kinematic growth yields many reasonable predictions, Humphrey and coworkers have suggested that it models consequences of growth and remodelling, not the processes by which they occur. Growth and remodelling necessarily occur in stressed, not fictitious stress-free, configurations, and they occur via the production, removal, and organization of different constituents; moreover, growth and remodelling need not restore stresses exactly to homeostatic values. Hence, Humphrey and coworkers introduced a conceptually different approach to model growth and remodelling, one that is based on tracking the turnover of individual constituents in stressed configurations (the constrained mixture model [5, 6]).

2.3 Characterization of Hyperelastic Properties Using a Bulge Inflation Test

After the introduction of basics about nonlinear finite–strain constitutive relations, we now introduce approaches of experimental biomechanics and inverse methods aimed at quantifying constitutive parameters of soft tissues.

2.3.1 Introduction

Traditional characterization of material constants in hyperelastic solids The hyperelastic constants in the strain energy density function of a material determine its mechanical response. For identifying these hyperelastic materials, simple deformation tests (consisting of six deformation models—see Fig. 2.1) can be used. It is always recommended to take the data from several modes of deformation over a wide range of strain values.

Even though the superposition of tensile or compressive hydrostatic stresses on a loaded incompressible body results in different stresses, it does not alter deformation of a material. Upon the addition of hydrostatic stresses, the following modes of deformation are found to be identical: uniaxial tension and equibiaxial compression, uniaxial compression and equiaxial tension, and planar tension and planar compression. It reduces to three independent deformation states for which we can obtain experimental data.

Fig. 2.1

Schematic representation of independent testing modes for hyperelastic materials

For each of the three independent tests, the resultant force F can be expressed analytically with respect to the applied stretch $\lambda$ using the following formulas of incompresssible hyperelasticity which are derived from the equations introduced above:

• 1. in uniaxial tension:

  $$\begin{aligned} F = 2 S_0 (\lambda -\lambda ^{-3})\left( \frac{\partial \psi }{\partial I_1} + \frac{\partial \psi }{\partial I_2} \right) \end{aligned}$$

  (2.61)

• 2. in planar tension:

  $$\begin{aligned} F = 2 S_0 (\lambda -\lambda ^{-3})\left( \lambda \frac{\partial \psi }{\partial I_1} + \frac{\partial \psi }{\partial I_2} \right) \end{aligned}$$

  (2.62)

• 3. in equibiaxial tension:

  $$\begin{aligned} F = 2 S_0 (\lambda -\lambda ^{-5})\left( \frac{\partial \psi }{\partial I_1} + \lambda ^2 \frac{\partial \psi }{\partial I_2} \right) \end{aligned}$$

  (2.63)

where $S_0$ is the initial cross-sectional area of the sample.

The identification of the material constants is achieved by a least-squares fit analysis which consists in minimizing the sum of squared discrepancies between the experimental values (if any) of F and the values predicted by the models. This yields a set of simultaneous equations which are solved for the material constants.

The identification of material constants is seldom achieved on cylindrical specimens where analytical formulas can also be derived to perform again least-squares fit analysis [7].

The bulge inflation test combined with digital image correlation As introduced previously, traditional characterization of material constants in hyperelastic solids is based on a least-squares fit analysis of F versus $\lambda$ curves. In the tests, $\lambda$ is usually measured using traditional extensometry techniques being either based on tracking the motion of the grips in the machine used to apply the deformation on the tissue, sometimes based on tracking the motion of markers or dots drawn on the tissue itself.

Recently, it has become a common practice to combine video based full-field displacement measurements experienced by tissue samples in vitro, with custom inverse methods to infer (using nonlinear regression) the best-fit material parameters and the rupture stresses and strains. These approaches offer important possibilities for fundamental mechanobiology research as they permit to quantify regional variations in properties in situ.

Here we present an illustrative example of the author’s experience where bulge inflation tests are carried out on aneurysm samples for characterizing the regional variations of hyperelastic constants across them.

2.3.2 Materials and Methods

Experimental arrangements The study deals with the characterization of aortic tissues collected on patients having an ascending thoracic aortic aneurysm (ATAA). In this reported example, an unruptured ATAA section was collected from a patient undergoing elective surgery to replace his ATAA with a graft in accordance with a protocol approved by the Institutional Review Board of the University Hospital Center of Saint–Etienne. After retrieval, the specimen was placed in saline solution and stored at 4 $^\circ$C until testing, which occurred within 48 h of the surgery. Immediately prior to testing, the ATAA was cut into a square specimen approximately 45 $\times$ 45 mm. Any fatty deposits were removed from the surface of the tissue to ensure that during mechanical testing the tissue did not slip in the clamps. An average thickness was found for the sample by measuring the thickness of the tissue at a minimum of five locations.

Fig. 2.2

Experimental setup and test sample a before testing and b after rupture

The specimen was clamped in the bulge inflation device, Fig. 2.2, so that the luminal side of the tissue faced outward. Then a speckle pattern was applied to the luminal surface using black spray paint. The sample was inflated using a piston driven at 15 mm/min to infuse water into the cavity behind the sample. During the test, the pressure was measured using a digital manometer (WIKA, DG-10). Images of the inflating specimen were collected using a commercial DIC system (GOM, 5M LT) composed of two 8-bit CCD cameras equipped with 50 mm lenses (resolution: 1624 $\times$ 1236 px). The cameras were positioned 50 cm apart at an angle of 30 $^\circ$ with an aperture of f/11. This produced a depth of field of 15.4 mm which was sufficient to capture the deformation of the tissue up to failure. Images of the deforming sample were collected every 3 kPa until the sample ruptured.

After rupture, the collected images were analyzed using the commercial correlation software ARAMIS (GOM, v. 6.2.0) to determine the three-dimensional displacement of the tissue surface. For the image analysis, a facet size of 21 px and a facet step of 5 px were chosen based on the speckle pattern dot size, distribution, and contrast. The selected parameters produced a cloud of approximately 15,000 points where the three displacement values were calculated. Details about the error quantification of the method may be found in the original paper [8].

Geometric reconstruction A deforming NURBS mesh was extracted by morphing a NURBS template to the DIC point clouds. The template was a circular domain with a diameter slightly less than that of the point cloud in the first pressure state. The NURBS surface was parameterized as a single patch containing clamped knots of 20 divisions in each parametric direction, with $22 \times 22$ control points. Since NURBS control points, in general, do not fall on the surface they describe, they cannot be directly derived from the DIC clouds. Instead, the positions of the Gauss points were obtained first using the moving least square method [9]. For each Gauss point, a set of nearest image points in the DIC point cloud were identified based on their distance to the Gauss point in the first pressure state. The radius of the neighboring region was automatically adjusted to that it contained at least six image points. The position of each Gauss point, $\mathbf {y}_g$, was computed using an affine interpolation

$$\begin{aligned} \mathbf {y}_g = \frac{\sum _{\mathbf {y} \in \Omega _g} w_j \mathbf {y}_j}{\sum _{\mathbf {y} \in \Omega _g} w_j} \end{aligned}$$

(2.64)

where $\mathbf {y}_j$ is the position vector for each image point in the neighborhood, $\Omega _g$, and $w_i$ is the weighting function taken to be the inverse of the distance from $\mathbf {y}_j$ to the Gauss point. Using the same weights calculated in the first stage, the Gauss points in every pressure stage were identified.

A global least squares problem was then formulated to compute the best-fit positions of the control points. The NURBS surface was represented as

$$\begin{aligned} \mathbf {x} = \sum _i{N_i(u_1,u_2)\mathbf {Q}_{i}} \end{aligned}$$

(2.65)

where $N_i$ are the NURBS basis functions, $\mathbf {Q}_{i}$ are the control points, and the pair of knot variables, $\left( {u}_1, {u}_2 \right)$, represent a material point. The position of a modeled Gauss point is then given by $\mathbf {x}_g = \sum _i N_i(u_{1g},u_{2g})\mathbf {Q}_{i}$. The position of the control points were obtained by minimizing a weighted sum of $\Vert \mathbf {x}_g - \mathbf {y}_g \Vert ^2$ over all Gauss points. This procedure was applied to each pressure state.

The accuracy of this reconstruction method was previously assessed and showed by [10].

Strain reconstruction Surface strains were computed in the local NURBS curvilinear coordinate system. The surface coordinates, $u_\alpha$, $\left( \alpha , \beta = 1,2\right)$ induce a set of convected basis vectors $\left( \mathbf {a}_1, \mathbf {a}_2 \right)$ where $\mathbf {a}_\alpha = \frac{\partial \mathbf {x}}{\partial \mathbf {u}_\alpha }$ and $\mathbf {x}(u_1,u_2)$ is the NURBS representation given in Eq. 2.65. The reciprocal basis $\left( \mathbf {a}^1, \mathbf {a}^2 \right)$ are computed such that $\mathbf {a}_\alpha \cdot \mathbf {a}_\beta = \delta _{\alpha \beta }$. In the reference configuration, the basis vectors are denoted by $\left( \mathbf {A}_1, \mathbf {A}_2 \right)$ and $\left( \mathbf {A}^1, \mathbf {A}^2 \right)$.

The surface deformation gradient tensor is

$$\begin{aligned} \mathbf {F} = \mathbf {a}_\alpha \otimes \mathbf {A}^\alpha \,. \end{aligned}$$

(2.66)

It then follows that the surface Cauchy–Green deformation tensor, $\mathbf {C}$, and the Green–Lagrangian strain tensor, $\mathbf {E}$, are given by

$$\begin{aligned} \mathbf {C} = \left( \mathbf {a}_\alpha \cdot \mathbf {a}_\beta \right) \mathbf {A}^\alpha \otimes \mathbf {A}^\beta \end{aligned}$$

(2.67)

$$\begin{aligned} \mathbf {E} = \frac{1}{2} \left( \mathbf {a}_\alpha \cdot \mathbf {a}_\beta - \delta _{\alpha \beta } \right) \mathbf {A}^\alpha \otimes \mathbf {A}^\beta \,. \end{aligned}$$

(2.68)

The physical components of $\mathbf {C}$ and $\mathbf {E}$ are computed by identifying a local orthonormal basis $\left( \mathbf {G}_1, \mathbf {G}_2 \right)$ that is constructed in the tangent plane spanned by $\left( \mathbf {A}_1, \mathbf {A}_2 \right)$. The physical components of the Cauchy–Green deformation tensor, $C_{\alpha \beta }$, and Green–Lagrangian strain tensor, $E_{\alpha \beta }$, are $C_{\alpha \beta } = \mathbf {G}\cdot \mathbf {C}\, \mathbf {G}$ and $E_{\alpha \beta } = \mathbf {G}\cdot \, \mathbf {E}\, \mathbf {G}$, respectively.

Wall stress reconstruction For an inverse membrane boundary value problem the deformed configurations and boundary conditions are given as inputs to the FE model and the wall stress is calculated. The balance equation that governs static equilibrium is [11, 12]

$$\begin{aligned} \frac{1}{\sqrt{\mathrm {a}}}\left( \sqrt{\mathrm {a}} t^{\alpha \beta } \mathbf {a}_\alpha \right) _{,\beta } + p \mathbf {n} = 0 \end{aligned}$$

(2.69)

where $\mathrm {a}$ is $\mathrm {det}\left( \mathbf {a}_\alpha \, \mathbf {a}_\beta \right)$, $\mathbf {t}$ is the Cauchy wall tension, p is the applied internal pressure, $\mathbf {n}$ is an outward facing unit normal, and $\left( \, \right) _{,\beta }$ indicates $\frac{\partial }{\partial \, u^\beta }$. Note that the Cauchy wall tension $\mathbf {t}$ is directly related to the Cauchy stress, $\varvec{\sigma }$, through the current thickness of the membrane, h, via $t^{\alpha \beta } = h \sigma ^{\alpha \beta } = t^{\beta \alpha }$.

The weak form of the boundary value problem reads

$$\begin{aligned} \int _\Omega t^{\alpha \beta } \mathbf {a}_\alpha . \delta \mathbf {x}_{,\beta }~\mathrm {d}a - \int _\Omega p \mathbf {n} . \delta \mathbf {x}~\mathrm {d}a = 0 , \end{aligned}$$

(2.70)

where $\delta \mathbf {x}$ is any admissible variation to the current configuration $\Omega$. The details of the FE procedure for solving Eq. 2.70 were presented in [13]. Briefly, the Cauchy wall tension is regarded as a function of the inverse deformation gradient. The weak form subsequently yields a set of nonlinear algebraic equations for the positions of control points in the reference configuration. At the same time, the tension field in the current state is determined. An auxiliary material model is needed to perform the inverse analysis. The material model influences the predicted undeformed configuration; however, due to the static determinacy of Eq. 2.69, the influence is weak [13–16]. As in a previous study [17], a neo-Hookean model was implemented. For computational efficiency, the stiffness parameter of the model was set to unrealistically high values to ensure a robust convergence.

To simulate the experimental boundary conditions the outermost edge of the specimen was fixed. This boundary condition was applied directly to the control points on the outer boundary of the mesh. Applying any displacement-based constraint in the inverse membrane analysis creates a boundary region in the solution where the stresses are inaccurate [13]. To minimize the influence of boundary effect, the outer ring of elements was excluded from further analyses. Since the influence region of each control point spans three elements in each of the two parametric directions, the outer three rings of elements were deemed to be the boundary region. By a retrospective comparison with the forward analysis reported the size of the boundary region was confirmed [18].

Material property identification Using inverse membrane analysis, the stress was calculated at every Gauss point. Combining the stress data with the local surface strains calculated from Eqs. 2.66–2.68, the stress–strain response at every Gauss point in the mesh is known. The local material properties at each Gauss point were then identified by fitting the local stress–strain response to a hyperelastic surface energy density. An anisotropic strain energy function was used, this anisotropy being implemented on the principle of Eq. 2.57. More specifically here, we used a modified form of the strain energy density proposed by Gasser, Ogden, and Holzapfel (GOH) [19] which may be written such as

$$\begin{aligned} w = \frac{\mu _1}{2} \left( \mathfrak {I}_1 - \ln {\left( \mathfrak {I}_2 \right) } -2 \right) + \frac{\mu _2}{4\gamma } \left( \mathrm {e}^{\gamma \left( \mathfrak {I}_k -1 \right) ^2} - 1\right) \end{aligned}$$

(2.71)

where $\mathfrak {I}_1 = \mathrm {tr}\, \mathbf {C}$ and $\mathfrak {I}_2 = \det \mathbf {C}$ are the principal invariants of the Cauchy–Green deformation tensor and $\mathfrak {I}_\kappa = \mathbf {C}\! :\! \left( \kappa \mathbf {1} + \left( 1 - 2\kappa \right) \mathbf {M} \!\otimes \! \mathbf {M} \right)$ is a compound invariant consisting of isotropic and anisotropic contributions.

Litteraly, Eq. 2.71 models a composite material made a matrix reinforced with fibers. In the compound invariant $\mathfrak {I}_\kappa$, the unit vector $\mathbf {M} = \cos \theta \, \mathbf {G}_1 + \sin \theta \, \mathbf {G}_2$ defines the orientation along which the tissue is stiffest while $\kappa$ characterizes the degree of anisotropy, varying from 0 to 1. When $\kappa =0$ it would model a composite with all the fibers perfectly aligned in the direction $\mathbf {M}$ and at $\kappa =1$ the fibers would be perfectly aligned in the perpendicular direction, $\mathbf {M}^\bot$. Finally, $\kappa =\frac{1}{2}$ models the case where fibers would have no preferential direction (isotropic). The parameters $\mu _1$ and $\mu _2$ are the effective stiffnesses of the matrix and fiber phases, respectively, both having dimensions of force per unit length. The parameter $\gamma$ is a nondimensional parameter that governs the tissue’s strain stiffening response.

The second Piola–Kirchhoff wall tension, $\mathbf {S}$, is written as

$$\begin{aligned} \mathbf {S}= 2\frac{\partial w}{\partial \mathfrak {I}_1} \mathbf {1} + 2\frac{\partial w}{\partial \mathfrak {I}_2}\mathfrak {I}_2 \mathbf {C}^{-1} + 2\frac{\partial w}{\partial \mathfrak {I}_\kappa } \left( \kappa \mathbf {1} + \left( 1 - 2\kappa \right) \mathbf {M} \otimes \mathbf {M} \right) \,. \end{aligned}$$

(2.72)

Substituting Eq. 2.71 into Eq. 2.72 one finds

$$\begin{aligned} \mathbf {S}= \mu _1 \left( \mathbf {1} -\mathbf {C}^{-1} \right) + \mu _2\, \mathrm {e}^{\gamma \left( \mathfrak {I}_\kappa - 1 \right) ^2} \left( \mathfrak {I}_\kappa -1 \right) \left( \kappa \mathbf {1} + \left( 1 - 2\kappa \right) \mathbf {M} \otimes \mathbf {M} \right) \end{aligned}$$

(2.73)

noting that the second Piola-Kirchoff wall tension is related to the Cauchy wall tension via $\mathbf {t} = \frac{1}{\sqrt{\mathfrak {I}_2}}\,\mathbf {F\, \mathbf {S}\, F}^{\mathrm {T}}$.

The values of the model parameters $\mu _1$, $\mu _2$, $\gamma$, $\kappa$, and $\theta$ were determined by minimizing the sum of the squared difference between the stress computed from the inverse membrane analysis and those computed using Eq. 2.73. The nonlinear minimization was solved in Matlab (MathWorks, v. 7.14) where the model parameters were constrained such that: $\mu _1$, $\mu _2$, $\gamma > 0$, $0 \le \theta \le \frac{\pi }{2}$, and $0 \le \kappa \le 1$. Due to the boundary effect in the stress analysis the perimeter ring of elements were excluded from the material parameter identification.

2.3.3 Results

Geometric reconstruction A bulge inflation test to failure was performed on a ATAA collected from a male patient who was 55 years old. The diameter of the aneurysm as determined by pre-surgical CT scan was 55 mm. The mean thickness of the sample was 2.35 mm. The pressure and DIC data during the bulge inflation tests were used to generate a deforming NURBS mesh and identify the local stress–strain response during the bulge inflation test. Using the pointwise stress–strain data, the spatial distribution of the mechanical properties was identified.

Using the experimental DIC point cloud a deforming NURBS mesh was generated of the ATAA sample.

Fig. 2.3

Contours of the magnitude of the a wall tension (N/m) and b Green–Lagrange strain at a pressure of 117 kPa. Adapted from [8]

Local stress and strain response Fig. 2.3 shows the distributions of the magnitude of the Cauchy wall tension, $\overline{t}$, and Green–Lagrangian strain, $\overline{E}$, at an applied pressure of 117 kPa for a given ATAA sample. The distribution of wall tension and strain remained similar throughout the inflation of the specimen. In general, at each Gauss point both the normal strains and the planar shear strains were nonzero. To facilitate plotting of the local stress–strain response, the axes of principal strain were identified and the local stresses and strains were rotated into the principal strain axes. In [8], the three components of the wall tension in the principal strain axes, $\tilde{t}_{11}$, $\tilde{t}_{12}$, and $\tilde{t}_{22}$ were plotted against the principal stretches $\lambda _1$ and $\lambda _2$. As expected, the local stress–strain response showed the nonlinear stiffening behavior that is common in arteries. The shear stresses, $\tilde{t}_{12}$, were much smaller than the normal stresses, $\tilde{t}_{11}$ and $\tilde{t}_{22}$. In a small region where rupture eventually occurred, the ATAA appeared to yield. The locations of this localized yielding correspond to strain concentrations in zones where rupture initiates (Fig. 2.3b).

Fig. 2.4

a $\mu _1$ (N/mm). b $\mu _2$ (N/mm). c $\gamma$. d $\kappa$. e $\theta$ (rad). Distribution of the identified material parameters over the ATAA. Adapted from [8]

Material property identification The proposed model for the elastic behavior of the ATAA was able to fit the bulge inflation data well ($0.81< \text {R}^2 < 0.99$). Lower values of the correlation coefficient were located in the small zone where rupture eventually occurred. Excluding this region the minimum value of $\text {R}^2$ was 0.96. The experimental data (points) and model fits (lines) for three Gauss points were shown in [8].

The distributions of the material parameters are plotted in Fig. 2.4. Clearly the material parameters display a heterogeneous distribution. The parameter $\mu _1$ displayed the sharpest changes in value while the parameters $\mu _2$, $\kappa$, and $\gamma$ changed more gradually. Not surprisingly, the values of $\mu _2$ are an order of magnitude larger than $\mu _1$ reflecting the difference in stiffness between the collagen fibers and matrix. The values of $\kappa$ are approximately 0.5 in the center suggesting an isotropic organization of the collagen fibers. Towards the edges of the specimen the collagen fibers become more aligned signaling that the sample is regionally anisotropic. In Fig. 2.4e, the angle $\theta$ that defines the stiffest direction is plotted. Note that $\theta$ is defined locally relative to the horizontal meshlines. Keep in mind that when the value of $\kappa$ is approximately 0.5, there is no stiffest direction.

This pointwise method was used to identify the distribution of material properties of 10 human ATAA samples [18]. Our method was able to capture the varying levels of heterogeneity in the ATAA from regional to local. The distributions of the material properties for each patient were examined to study the inter- and intra-patient variability. Future studies on the heterogeneous properties of the ATAA would benefit from some form of local structural analysis such as histology or multi-photon microscopy. The structural data and knowledge of the spatial trends should provide the information necessary to move from merely measuring the local material properties to uncovering the links that exist between the underlying microstructure and local properties.

2.4 Characterization of Hyperelastic Material Properties Using a Tension-Inflation Test and the Virtual Fields Method

In the previous section, it was shown that in some cases which are referred to as isostatic, it may be possible to derive the stress distribution independently of the material properties of the tissues. When strain distributions are also available, stress–strain curves can be derived locally and the inverse problem turns into a semi-forward problem [20], where the material parameters can be identified directly by fitting the curves with a model.

In case of hyperstatic situations, it is not possible to derive the stress distribution independently of the material properties of the tissues. A possible solution for the identification of local material properties may still be found using the Virtual Fields Method (VFM). The VFM is one of the techniques developed to identify the parameters governing constitutive equations, the experimental data processed for this purpose being displacement or strain fields. It will be shown in this chapter that one of its main advantages is the fact that, in several cases, the sought parameters can be directly found from the measurements, without resorting to a FE software.

The VFM relies on the Principle of Virtual Power (PVP) which is written with particular virtual fields.

2.4.1 General Principle

The PVP represents in fact the weak form the local equations of equilibrium which are classically introduced in mechanics of deformable media. Assuming a quasi-static transformation (the absence of acceleration forces) and assuming the absence of body forces, the PVP can be written as follows for any domain defined by its volume $\omega (t)$ in the current configuration and by its external boundary $\partial \omega (t)$:

$$\begin{aligned} \underbrace{-\int _{\omega (t)}\varvec{\sigma }:(\varvec{\mathrm {Grad}\,}\mathbf {v}^*) d\omega }_{P_{int}^*} + \underbrace{\int _{\partial \omega (t)} \mathbf {t_n}.\mathbf {v}^* ds}_{P_{ext}^*} = 0 \end{aligned}$$

(2.74)

where $\varvec{\sigma }$ is the Cauchy stress tensor, $\mathbf {v}^*$ is a virtual velocity field defined across the volume of the solid, $\varvec{\mathrm {Grad}\,}\mathbf {v}^*$ is the gradient of $\mathbf {v}^*$, $\mathbf {t_n}$ are the tractions across the boundary (surface denoted $\partial \omega (t)$), $P_{int}^*$ is the virtual power of internal forces and $P_{ext}^*$ is the virtual power of external forces.

A very important property is in fact that the equation above is satisfied for any kinematically admissible (KA) virtual field $\mathbf {v}^{\star }$. By definition, a KA virtual field must satisfy the boundary conditions of the actual velocity field in order to cancel the contribution of the resulting forces on the portion of the boundary along which actual displacement are prescribed. It must be pointed out that this requirement is not really necessary in all cases, but this point is not discussed here for the sake of simplicity. KA virtual fields are also assumed to be $\mathcal {C}_0$ functions [21].

2.4.2 Example of Application of the Principle of Virtual Power for Membranes

The PVP may be a powerful tool to derive global or semi-local equilibrium equations which eventually appear useful for the identification of material parameters. Here we illustrate this for deriving a useful equation for a hyperelastic membrane. This is purely for the sake of giving an example, but an infinity of other equations could be derived.

Let us consider a membrane-like structure made of a hyperelastic prestressed tissue. The membrane is defined by a three-dimensional surface, namely defined by a set of points $\mathbf M (\xi _1,\xi _2)$, where $(\xi _1,\xi _2)$ are the surface parametric coordinates associated with the local basis ($\mathbf g ^1$, $\mathbf g ^2$). Vector $\mathbf g ^1$ points the direction of the maximum principal curvature and vector $\mathbf g ^2$ points the direction of the minimum principal curvature. The thickness of the membrane is named $h(\xi _1,\xi _2)$ and we denote $\kappa ^1(\xi _1,\xi _2)$ and $\kappa ^2(\xi _1,\xi _2)$ respectively the maximum and minimum principal curvatures at $(\xi _1,\xi _2)$.

There is no particular assumption related to the thickness of the membrane but it is assumed that through-thickness shear is negligible. A third coordinate $\xi _3$ is introduced along the direction normal to the surface (through-thickness coordinate), with $\xi _3=0$ at the inner surface and $\xi _3=1$ at the outer surface.

Let us consider a quadrilateral patch across the membrane surface. This patch is denoted n and we will apply the PVP on its volume. For that, the following virtual field $u^*$ is defined across the given patch n:

$$\begin{aligned} \mathbf u ^*(\xi _3)= \frac{(1/\kappa ^1_n-h)(1/\kappa ^2_n-h)(1/\kappa ^1_n+1/\kappa ^2_n-2h)}{(1/\kappa ^1_n-(1-\xi )h)(1/\kappa ^2_n-(1-\xi )h)} ~ \mathbf n _n \end{aligned}$$

(2.75)

where $1/\kappa ^1_n$ is the average radius of curvature on the outer surface along the direction of the maximum principal curvature and $1/\kappa ^2_n$ is the average radius of curvature on the outer surface along the direction of the minimum principal curvature. The radii of curvature at any position $\xi _3$ between the inner ($\xi _3=0$) and outer ($\xi _3=1$) surfaces are then $(1/\kappa ^1_n-(1-\xi _3)h)$ and $(1/\kappa ^2_n-(1-\xi _3)h)$. Vector $\mathbf n _n$ points the direction normal to the surface.

The gradient of $\mathbf u ^*$ may be written as follows:

$$\begin{aligned}&\varvec{\mathrm {Grad}\,}\mathbf u ^*(\xi _3)=\left[ \frac{(1/\kappa ^1_n-h)(1/\kappa ^2_n-h)(1/\kappa ^1_n+1/\kappa ^2_n-2h)}{(1/\kappa ^1_n-(1-\xi _3)h)^2(1/\kappa ^2_n-(1-\xi _3)h)} \right] \mathbf g ^1_n \otimes \mathbf g ^1_n \nonumber \\&\qquad \qquad + \left[ \frac{(1/\kappa ^1_n-h)(1/\kappa ^2_n-h)(1/\kappa ^1_n+1/\kappa ^2_n-2h)}{(1/\kappa ^1_n-(1-\xi _3)h)(1/\kappa ^2_n-(1-\xi _3)h)^2} \right] \mathbf g ^2_n \otimes \mathbf g ^2_n \nonumber \\&- \left[ \frac{(1/\kappa ^1_n-h)(1/\kappa ^2_n-h)(1/\kappa ^1_n+1/\kappa ^2_n-2h)}{(1/\kappa ^1_n-(1-\xi _3)h)^2(1/\kappa ^2_n-(1-\xi _3)h)}\right. \nonumber \\&\left. \qquad + \frac{(1/\kappa ^1_n-h)(1/\kappa ^2_n-h)(1/\kappa ^1_n+1/\kappa ^2_n-2h)}{(1/\kappa ^1_n-(1-\xi _3)h)(1/\kappa ^2_n-(1-\xi _3)h)^2} \right] \mathbf n _n \otimes \mathbf n _n \end{aligned}$$

(2.76)

Plugging in and evaluating the integral expression for $P_{int}^*$ (cf. Eq. 2.74)

$$\begin{aligned} P_{int}^*(t)&= -h(t) ( 1/\kappa ^1_n(t)-h(t))(1/\kappa ^2_n(t)-h(t))(1/\kappa ^1_n(t)+1/\kappa ^2_n(t)-2h(t) ) \nonumber \\&\qquad \int _0^1 \left[ \frac{\sigma _{11,n}^w(t,\xi _3)-\sigma _{33,n}^w(t,\xi _3)}{(1/\kappa ^1_n-(1-\xi _3)h)^2(1/\kappa ^2_n-(1-\xi _3)h)} \right. \nonumber \\&\quad + \left. \frac{\sigma _{22,n}^w(t,\xi _3)-\sigma _{33,n}^w(t,\xi _3)}{(1/\kappa ^1_n-(1-\xi _3)h)(1/\kappa ^2_n-(1-\xi _3)h)^2} \right] A_n(t,\xi _3) \mathrm {d} \xi _3 \end{aligned}$$

(2.77)

where $A_n(t,\xi _3)$ is the area of patch n at radial position $\xi _3$ and may be written

$$\begin{aligned} A_n(t,\xi _3) = (1/\kappa ^1_n(t)-(1-\xi _3)h(t))(1/\kappa ^2_n(t)-(1-\xi _3)h(t))\Theta _n^1(t) \Theta _n^2(t) \end{aligned}$$

(2.78)

where $\Theta _n^1$ and $\Theta _n^2$ are two angles defining the angular sector of patch n along the directions of the maximum and minimum principal curvatures, respectively. Introducing the expression of $A_n(t,\xi _3)$ into Eq. 2.77, we obtain

$$\begin{aligned}&\quad P_{int}^*(t) = -h(t) ( 1/\kappa ^1_n(t)-h(t))(1/\kappa ^2_n(t)-h(t))(1/\kappa ^1_n(t)+1/\kappa ^2_n(t)-2h(t) ) \nonumber \\&\Theta _n^1(t) \Theta _n^2(t) \int _0^1 \left[ \frac{\sigma _{11,n}^w(t,\xi _3)-\sigma _{33,n}^w(t,\xi _3)}{(1/\kappa ^1_n-(1-\xi _3)h)} + \frac{\sigma _{22,n}^w(t,\xi _3)-\sigma _{33,n}^w(t,\xi _3)}{(1/\kappa ^2_n-(1-\xi _3)h)} \right] \mathrm {d} \xi _3 \end{aligned}$$

(2.79)

Regarding the virtual work on the boundaries, shear stresses are null so only the virtual work of the internal pressure needs to be considered

$$\begin{aligned} P_{ext}^*(t) = P(t) (1/\kappa ^1_n(t)&-h(t))(1/\kappa ^2_n(t)-h(t)) \Theta _n^1(t) \Theta _n^2(t) \nonumber \\&\qquad \qquad (1/\kappa ^1_n(t)+1/\kappa ^2_n(t)-2h(t)) \end{aligned}$$

(2.80)

so combining all the equations we have

$$\begin{aligned} P(t) = h(t) \int _0^1 \left[ \frac{\sigma _{11,n}^w(t,\xi _3)-\sigma _{33,n}^w(t,\xi _3)}{(1/\kappa ^1_n-(1-\xi _3)h)} + \frac{\sigma _{22,n}^w(t,\xi _3)-\sigma _{33,n}^w(t,\xi _3)}{(1/\kappa ^2_n-(1-\xi _3)h)} \right] \mathrm {d} \xi _3 \end{aligned}$$

(2.81)

Finally the obtained equation is a generalized expression of the traditional Laplace law commonly used in biomechanics of soft tissues [22].

2.4.3 Identification of Hyperelastic Parameters Using the VFM

The principle of virtual power (PVP) has been used for the identification of material properties since 1990 through the virtual fields method (VFM), which is an inverse method based on the use of full-field deformation data [21, 23, 24]. The VFM was recently applied to the identification of uniform material properties in arterial walls [23].

The first step of the VFM consists in introducing the constitutive equations. In the case of hyperelasticity, Eq. 2.74 becomes

$$\begin{aligned} -\int _{\omega (t)}\left( J^{-1} \mathbf {F} \frac{\partial \psi }{\partial \mathbf {E}} \mathbf {F}^T \right) :(\varvec{\mathrm {Grad}\,}\mathbf {v}^*) d\omega + \int _{\partial \omega (t)} \mathbf {t_n}.\mathbf {v}^* ds = 0 \end{aligned}$$

(2.82)

This equation being satisfied for any KA virtual field, any new KA virtual field provides a new equation. The VFM relies on this property by writing Eq. 2.82 above with a set of KA virtual fields chosen a priori [25]. The number of virtual fields and their type depend on the nature of the strain energy function. Two different cases can be distinguished.

• Case #1: the strain energy density function depends linearly on the sought parameters. Writing Eq. 2.82 with as many virtual fields as unknowns leads to a system of linear equations which provides the sought parameters after inversion.

• Case #2: the strain energy density function involve nonlinear relations with respect to the constitutive parameters. In this case, identification must be performed by minimizing a cost function derived from Eq. 2.82.

Let us illustrate this with the strain energy function of Eq. 2.71. It provides a membrane constitutive equation, i.e. it yields the tension and not the Cauchy stress so the integrals will be written across a given surface $\nu (t)$ figuring a portion of the membrane

$$\begin{aligned}&-\mu _1 \int _{\nu (t)} \frac{1}{\sqrt{\mathfrak {I}_2}} \left( \mathbf {B} - \sqrt{\mathfrak {I}_2} \mathbf {1} \right) :(\varvec{\mathrm {Grad}\,}\mathbf {v}^*) d\nu \nonumber \\&\qquad \qquad -\mu _2 \kappa \int _{\nu (t)} \frac{1}{\sqrt{\mathfrak {I}_2}} \mathrm {e}^{\gamma \left( \mathfrak {I}_\kappa - 1 \right) ^2} \left( \mathfrak {I}_\kappa -1 \right) \mathbf {B} :(\varvec{\mathrm {Grad}\,}\mathbf {v}^*) d\nu \nonumber \\&-\mu _2 (1-2\kappa ) \int _{\nu (t)} \frac{1}{\sqrt{\mathfrak {I}_2}} \mathrm {e}^{\gamma \left( \mathfrak {I}_\kappa - 1 \right) ^2} \left( \mathfrak {I}_\kappa -1 \right) \left( \mathbf {F} \mathbf {M} \otimes \mathbf {M} \mathbf {F}^T \right) :(\varvec{\mathrm {Grad}\,}\mathbf {v}^*) d\nu \nonumber \\&\qquad \qquad \qquad \qquad + \int _{\nu (t)} \mathbf {t_n}.\mathbf {v}^* dl = 0 \end{aligned}$$

(2.83)

The equation may be rewritten such as

$$\begin{aligned} \mu _1 A_{ij} + \mu _2 \kappa B_{ij}(\gamma ) + \mu _2 (1-2\kappa ) C_{ij}(\gamma ,\theta ) = L_{ij} \end{aligned}$$

(2.84)

where $A_{ij}$, $B_{ij}$, $C_{ij}$ and $L_{ij}$ can be evaluated directly from the experimental measurements. Index i is for different possible choices of virtual fields and index j is for different possible stages of the experiment for which deformations and loads are measured.

Equation 2.84 is an equation of the unknown material parameters for each choice of virtual field i and at every stage j of the test. The equation is linear in $\mu _1$, $\mu _2 \kappa$ and $\mu _2 (1-2\kappa )$ but it is nonlinear in $\gamma$ and $\theta$. The solution is found by minimizing a cost function defined such as

$$\begin{aligned} \sum _i \sum _j \left( \mu _1 A_{ij} + \mu _2 \kappa B_{ij}(\gamma ) + \mu _2 (1-2\kappa ) C_{ij}(\gamma ,\theta ) - L_{ij} \right) ^2 \end{aligned}$$

(2.85)

This cost function can be minimized by the simplex method or using a genetic algorithm in case of multiple minima. The chosen virtual fields and other details about the experiments can be found in [23, 26] for applications to blood vessels.

A recent extension of the method was proposed for the inverse characterization of regional, nonlinear, anisotropic properties of the murine aorta [27]. Full-field biaxial data were collected using a panoramic-digital image correlation system and the VFM was used to estimate values of material parameters regionally for a microstructurally motivated constitutive relation. The experimental-computational approach was validated by comparing results to those from standard biaxial testing. Results for the non-diseased suprarenal abdominal aorta from apolipoprotein-E null mice revealed material heterogeneities, with significant differences between dorsal and ventral as well as between proximal and distal locations, which may arise in part due to differential perivascular support and localized branches. Overall results were validated for both a membrane and a thick-wall model that delineated medial and adventitial properties.

Whereas full-field characterization can be useful in the study of normal arteries, we submit that it will be particularly useful for studying complex lesions such as aneurysms. Indeed, many vascular disorders, including aortic aneurysms and dissections, are characterized by localized changes in wall composition and structure. Notwithstanding the importance of histopathologic changes that occur at the microstructural level, macroscopic manifestations ultimately dictate the mechanical functionality and structural integrity of the aortic wall. Understanding structure–function relationships locally is thus critical for gaining increased insight into conditions that render a tissue susceptible to disease or failure.

2.5 Conclusion

In this chapter, after a brief review of the constitutive relations commonly used for soft tissues, two recent developments of the author’s experience were presented to illustrate the potential of digital image correlation and inverse methods in experimental biomechanics of soft tissues.

The inverse problems, including the semi-forward problems [20], posed by the identification of material properties in soft biological tissues are not the simplest due to the complex microstructure of soft biological tissues, their finite range of deformation, their inter-individual variability, their anisotropy, their point-dependent nonlinear behavior, and their permanent functional adaptation to the environment. Determining the mechanical properties of such tissues has nevertheless become a field of intense research since stress analysis in the tissues has been shown to be meaningful for medical diagnosis in a number of medical applications as for instance in the context of vascular medicine, indicating the risk of rupture of an aneurysm [28] or the risk of stroke [29].

The current chapter has focused on in vitro characterization. The in vivo identification of soft tissues present other important issues. They suppose both the existence of reliable experimental facilities for inducing a mechanical stimulus (natural blood pressure variations, local external compression, shear waves [30]) and the existence of imaging devices for measuring the response of tissues (Ultrasound Imaging [31], Magnetic Resonance Imaging [32] or Optical Coherence Tomography [33]). In all these situations where some elements of the response of soft tissues subjected to mechanical stimuli are measured, the access to the mechanical parameters is never direct and inverse problems have to be posed and solved. The inverse problems posed by the in vivo identification of soft tissues will be discussed more specifically in Chaps. 5 and 6 of this book.