Symmetric Properties of the Syllogistic System Inherited from the Square of Opposition

Abstract

The logical square $\Omega$ has a simple symmetric structure that visualises the bivalent relationships of the classical quantifiers A, I, E, O. In philosophy it is perceived as a self-complete possibilistic logic. In linguistics however its modelling capability is insufficient, since intermediate quantifiers like few, half, most, etc cannot be distinguished, which makes the existential quantifier I too generic and the universal quantifier A too specific. Furthermore, the latter is a special case of the former, i.e. A ⊂ I, making the square a logic with inclusive quantifiers. The inclusive quantifiers I and O can produce redundancies in linguistic systems and are too generic to differentiate any intermediate quantifiers. The redundancy can be resolved by excluding A from I, i.e.²I = I-A, analogously E from O, i.e.²O = O-E. Although the philosophical possibility of A ⊂ I is thus lost in²I, the symmetric structure of the exclusive square $^{2}\Omega$ remains preserved. The impact of the exclusion on the traditional syllogistic system $\mathbb{S}$ with inclusive existential quantifiers is that most of its symmetric structures are obviously lost in the syllogistic system $^{2}\mathbb{S}$ with exclusive existential quantifiers too. Symmetry properties of $\mathbb{S}$ are found in the distribution of the syllogistic cases that are matched by the moods and their intersections. A syllogistic case is a distinct combination of the seven possible spaces of the Venn diagram for three sets, of which there exist 96 possible cases. Every quantifier can be represented with a fixed set of syllogistic cases and so the moods too. Therefore, the 96 cases open a universe of validity for all moods of the syllogistic system $\mathbb{S}$, as well as all fuzzy-syllogistic systems $^{\mathrm{n}}\mathbb{S}$, with n-1 intermediate quantifiers. As a by-product of the fuzzy syllogistic system and its properties, we suggest in return that the logical square of opposition can be generalised to a fuzzy-logical graph of opposition, for 2 < n.

1 Introduction

The logical square of opposition, in short the square $\Omega$, is an ancient construct of Aristotle [1] that depicts all possible relationships among the four classical quantifiers, universal, existential and their negations. It visualises the consistency of the relationships in terms of philosophical possibilities. An immediate application of the square are the well known categorical syllogisms, in all 256 possible combinations within the four syllogistic figures. We will refer to the 256 moods as the syllogistic system $\mathbb{S}$.

The square and the syllogistic system have been extensively analysed in the history of logic, however mostly separately from each other. Especially the square has become increasingly controversial in pragmatical discussions and has therefore been extended to various forms of n-polytopes [24]. However, such extensions were mostly not reflected on the syllogistic system, not until modern logic emerged in the century of Frege [12]. For instance, reduction of a syllogism, by changing an imperfect mood into a perfect one [30]. Conversion of a mood, by transposing the terms, and thus drawing another proposition from it of the same quality [22, 23]. Unfortunately, such extensions on the syllogistic system were in turn not reflected back on the square.

Initial generalisations of quantifiers were introduced in linguistics [25], at a time, where computing became popular in science, along with discussions about the possibility of artificial intelligence [37]. Cardinalities of quantifiers have forced logicians to rethink [2] about related logics, such as intermediate quantifiers, like several, few, many, most in syllogisms [31]. Fuzzifications of quantifiers [8, 40] and cardinality-based fuzzy quantifications [7, 11], have enabled approximate reasoning [40], fuzzy-logical generalisations of syllogisms [27, 41] and eventually their reflections on the square [26, 31].

In order to be able to algorithmically calculate precise truth values of syllogistic moods [18], for any fuzzy-logical generalisation of the syllogistic system, first properties and dynamics of fuzzy-moods need to be well understood, such as varying validities, symmetries and equalities. Some of them have already been discussed partially in the literature, for instance, validity of moods with classical quantifiers using diagrammatic proves [29, 36]. Such approaches are the closest to our algorithmic calculations of truth ratios for moods [18]. Further, symmetry and equality of moods analysed based on Aristotle’s heuristics and geometric properties [34], validity of moods with intermediate quantifiers using axiomatic [27] or algebraic approaches [38]. Eventually, such findings about a fuzzy syllogistic system should help in verifying the logical consistencies of the used quantifiers by using their reflections on extended versions of the square.

Promising is that most of the empirically obtained truth values for the 256 moods are close to our algorithmically calculated truth ratios [18]. For instance philosophical studies confirm that syllogistic reasoning does model human reasoning with quantified object relationships [14]. For instance in psychology, studies have compared five experimental studies that used the full set of 256 syllogisms [6, 28] about different subjects. Two settings about choosing from a list of possible conclusions for given two premisses [9, 10], two settings about specifying possible conclusions for given premisses [15], and one setting about deciding whether a given argument was valid or not [16]. It has been found that the results of these experiments were very similar and that differences in design appear to have had little effect on how human evaluate syllogisms [6].

Inference logics like modus ponens or modus tollens, are some simplified derivations from syllogisms [35]. Since they have no quantities any more, they cannot capture any fuzzy-quantified propositions. Whereas fuzzy-quantified syllogisms can formalise the whole range of linguistic quantities and thus can provide more powerful inferences. Ones the capabilities of inferencing with fuzzy-syllogistic systems $^{\mathrm{n}}\mathbb{S}$ are fully revealed, they may become a preferred tool for approximate reasoning in artificial intelligence.

After formalising the square of opposition, we provide formalisations for the syllogistic system, its properties and a fuzzy syllogistic system. Finally, we introduce a fuzzy-logical square of opposition and its generalisation, the fuzzy-logical graph of opposition.

2 Logical Square of Opposition

The square reflects symmetric relationships between quantifiers that seam to be consistent in terms of philosophical possibilities, but prove to be impractical in engineering, as some of the possibilities develop redundancies, with which distinctive decision making is not possible.

The square $\Omega$ consists of four quantifiers ψ ∈ { A, E, I, O}, two affirmative A:All and I:Some, their negations, E:All Not and O:Some Not respectively, and all possible six relationships amongst them (Fig. 1):

$$\displaystyle{\Omega =\{ (\mathrm{A},\mathrm{E},\mathrm{I},\mathrm{O})\vert \mathrm{R}_{\mathrm{sa}}(\mathrm{A},\mathrm{I}),\mathrm{R}_{\mathrm{cr}}(\mathrm{A},\mathrm{E}),\mathrm{R}_{\mathrm{cd}}(\mathrm{A},\mathrm{O}),\mathrm{R}_{\mathrm{cd}}(\mathrm{E},\mathrm{I}),\mathrm{R}_{\mathrm{sa}}(\mathrm{E},\mathrm{O}),\mathrm{R}_{\mathrm{sc}}(\mathrm{I},\mathrm{O})\}}$$

where R_sa is subaltern, R_cr is contrary, R_cd is contradictory, R_sc is subcontrary and only R_sa is unidirectional, R_cr, R_cd, R_sc are bidirectional (Fig. 1).

Fig. 1

The square of opposition $\Omega$ with Euler and Venn diagram representations of the quantifiers with all Gergonne relations [13]

Set-theoretic visualisations of the quantifiers [33] help understanding the logical cases every quantifier encapsulates and help identifying overlapping partial equalities among them (Table 1). These logical cases, to which we will refer later in the text as syllogistic cases, form the essential data for our algorithmic calculations of truth ratios for the syllogistic moods. Although Venn diagrams are more popular in the literature, because they provide a more compact representation, we prefer Euler diagram, as we can visualise every logical cases of a quantifier in a distinct diagram. Logical cases of quantifiers are sometimes referred to as states [3].

Table 1 Logical case of inclusive and exclusive quantifiers represented in Euler diagrams and space diagrams

Depending on different pragmatical considerations, the cases (c) of I and O are further separated in the literature (Table 1). Some consider them as invalid [5] and some include them as valid [39] for a given domain. Since case (c) of I is equivalent to proposition A, A becomes a special case of I. Similarly, since case (c) of O is equivalent to proposition E, E becomes a special case of O. We will refer to existential quantifiers that include the universal cases as inclusive and to those that exclude the universal cases as exclusive quantifiers.

3 Categorical Syllogisms

A categorical syllogism can be defined as a logical argument that is composed of two logical propositions for deducing a logical conclusion, where the propositions as well as the conclusion consist each of a quantified object-property relationship.

3.1 Syllogistic Propositions

In general, a proposition is a statement that can specify multiple objects and properties. Since a property itself may recursively become an object with properties, we will denote a property as well as an object. Additionally, we will use further terms interchangeably, object, propositional variable and set.

A syllogistic proposition has a fixed structure, consisting of one object and one quantifying property:

$$\displaystyle{\text{Syllogistic proposition:}\ \Phi =\mathrm{ S}\uppsi \mathrm{P}}$$

where S and P denote sets, such that S is categorised on P with ψ = { A, E, I, O}.

3.2 Syllogistic Figures

A syllogism consists of two premising propositions and one concluding proposition. The first proposition specifies a quantified relationship between the objects M and P, the second proposition between S and M, the conclusion between S and P (Table 2).

Table 2 Syllogistic figures F

Below triple is a more general definition of a categorical syllogism, without distinguishing figures:

$$\displaystyle\begin{array}{rcl} \text{Syllogistic figures:}\ (\uppsi _{1}\uppsi _{2}\uppsi _{3}\mathrm{F})& =& (\Phi _{1},\Phi _{2},\Phi _{3}) {}\\ & =& (\{\mathrm{M}\uppsi _{1}\mathrm{P},\mathrm{P}\uppsi _{1}\mathrm{M}\},\{\mathrm{S}\uppsi _{2}\mathrm{M},\mathrm{M}\uppsi _{2}\mathrm{S}\},\mathrm{S}\uppsi _{3}\mathrm{P}) {}\\ \end{array}$$

where $\Phi _{1}$ and $\Phi _{2}$ denote the first and second premising propositions and $\Phi _{3}$ denotes the concluding proposition.

Since the propositional operator ψ may have 4 values, 64 syllogistic moods are possible for every figure and 256 moods for all 4 figures in total. For instance, AAA1 constitutes the mood MAP, SAM-SAP in Fig. 1.

3.3 Syllogistic Moods and Cases

Syllogistic moods are well known as categorical syllogism, whereas syllogistic case and truth ratio are relative new concepts for syllogisms [18].

Syllogistic moods (ψ₁ψ₂ψ₃F) can be defined with the following tuple constructor:

$$\displaystyle{\text{Syllogistic mood of propositions:}\ (\uppsi _{1}\uppsi _{2}\uppsi _{3}\mathrm{F}) = (\Phi _{1}\Phi _{2}\Phi _{3}\mathrm{F},\uptau )}$$

where τ = [0, 1] denotes the truth ratio of the mood in figure F = {1, 2, 3, 4}.

For three sets, there are 7 possible distinct spaces, which can be easily identified in the Venn diagram (Table 3). From these 7 spaces, in total 128 combinations can be generated, out of which, only 96 are valid for the above quantifier restrictions (Table 1) and only these allow us to uniquely distinguish the space combinations that are matched by every mood (Table 4):

$$\displaystyle\begin{array}{rcl} \text{Distinct space combinations:}\ \Delta _{\mathrm{j}}& =& \{\updelta _{1}\updelta _{2}\updelta _{3}\updelta _{4}\updelta _{5}\updelta _{6}\updelta _{7}\vert \exists _{\mathrm{m,p,s}}\mathrm{m} \in \mathrm{ M} \wedge \mathrm{ p} \in \mathrm{ P} \wedge \mathrm{ s} \in \mathrm{ S} {}\\ & \rightarrow & \mathrm{m,p,s} \in \updelta _{1} \cup \updelta _{2} \cup \updelta _{3} \cup \updelta _{4} \cup \updelta _{5} \cup \updelta _{6} \cup \updelta _{7}\} {}\\ \end{array}$$

where $\Delta _{\mathrm{j}}$ with j = [1, 96] are all possible combinations $\Delta _{\mathrm{j}}$ of δ_i with i = [1, 7], whereby every $\Delta _{\mathrm{j}}$ is the union of distinct spaces, such that at least one element from every set M, P, S must be in the union [43]. The distinct spaces δ_i are named in (Table 3). These combinations $\Delta _{\mathrm{j}}$ are exactly all those matched by propositions and conclusions of the 256 moods. The union of all $\Delta _{\mathrm{j}}$, with j = [1, 96], is the universe of all possible truth cases of all 256 moods. Therefore we refer to these 96 combinations as syllogistic distinct cases. Every mood matches some of the cases according following rules:

$$\displaystyle{\text{Syllogistic mood of cases:}\ \uppsi _{1}\uppsi _{2}\uppsi _{3}^{\Delta } =\{ _{\mathrm{ k}=1} \cap ^{2}_{ \mathrm{j}=1} \cup ^{96}\Delta _{\mathrm{ j}} \in \Phi _{\mathrm{k}} \rightarrow \Delta _{\mathrm{j}} \in \Phi ^{\Delta }_{ \mathrm{k}}\}}$$

where $\Phi ^{\Delta }_{\mathrm{k}}$ is the set of cases, out of the universal set of all cases $\Delta _{\mathrm{j}}$, j = [1, 96], that satisfy the proposition $\Phi _{\mathrm{k}}$ on all spaces of every case $\Delta _{\mathrm{j}} =\updelta _{1}\updelta _{2}\updelta _{3}\updelta _{4}\updelta _{5}\updelta _{6}\updelta _{7}$. The cases that represent the premiss of the mood, are then calculated by intersecting the cases of the propositions $\Phi ^{\Delta }_{1} \cap \Phi ^{\Delta }_{2}$. Out of this set of premising cases $\Phi ^{\Delta }_{1} \cap \Phi ^{\Delta }_{2}$, the concluding proposition $\Phi _{3}$ determines now the true $\Lambda ^{\mathrm{t}}$ and false $\Lambda ^{\mathrm{f}}$ cases of the mood:

$$\displaystyle\begin{array}{rcl} & & \text{True syllogistic cases:}\ \Lambda ^{\mathrm{t}} = \Delta \in (\Phi ^{\Delta }_{ 1} \cap \Phi ^{\Delta }_{ 2}) \wedge \Delta \in \Phi _{3} \rightarrow \Delta _{\mathrm{j}} \in \Phi ^{\Delta }_{ 3} {}\\ & & \text{False syllogistic cases:}\ \Lambda ^{\mathrm{f}} = \Delta \in (\Phi ^{\Delta }_{ 1} \cap \Phi ^{\Delta }_{ 2}) \wedge \Delta \notin \Phi _{3} \rightarrow \Delta _{\mathrm{j}}\notin \Phi ^{\Delta }_{ 3} {}\\ \end{array}$$

where $\Lambda ^{\mathrm{t}}$ and $\Lambda ^{\mathrm{f}}$ is the set of all true and false matching cases of a particular mood, respectively. Since every quantifier ψ always matches a fixed number of syllogistic cases and any particular combination thereof in a mood $\uppsi _{1}\uppsi _{2}\uppsi _{3}^{\Delta }$ results in the equal set of cases, this set of cases remains fixed for every particular mood.

Table 3 Sample syllogistic cases $\Delta _{\mathrm{j}}$

Table 4 Sample syllogistic moods, their truth cases, truth ratios and sample interpretations

For instance, the two premisses $\Phi _{1}$ and $\Phi _{2}$ of the mood IAI4 of the syllogistic system $\mathbb{S}$, match the 10 syllogistic cases $\Phi ^{\Delta }_{3} = \Lambda ^{\mathrm{t}} =\{ \Delta _{4},\Delta _{19},\Delta _{67},\Delta _{24},\Delta _{43},\Delta _{46},\Delta _{68},\Delta _{74},\Delta _{48},\Delta _{76}\}$, which are all true for the conclusion $\Phi _{3}$ as well. Thus the mood has no false cases $\Lambda ^{\mathrm{f}} = \varnothing$ (Fig. 2).

Fig. 2

10 syllogistic cases $\Delta ^{\mathrm{j}}$ of the mood IAI4 in $\mathbb{S}$ and of^2∕1IA¹I4 in $^{2}\mathbb{S}$

3.4 Truth Ratios of a Mood

The truth ratio of a mood is calculated by relating the amounts of the two sets $\Lambda ^{\mathrm{t}}$ and $\Lambda ^{\mathrm{f}}$ with each other. Consequently the truth ratio τ becomes either more true or more false:

$$\displaystyle\begin{array}{rcl} & \text{Truth ratio:}\ \uptau \in \{\uptau ^{\mathrm{t}},\uptau ^{\mathrm{f}}\} & {}\\ & \text{More true truth ratio:}\ \uptau ^{\mathrm{t}} \in \{\vert \Delta ^{\mathrm{f}}\vert <\vert \Delta ^{\mathrm{t}}\vert \rightarrow 1 -\vert \Delta ^{\mathrm{f}}\vert /(\vert \Delta ^{\mathrm{t}}\vert + \vert \Delta ^{\mathrm{f}}\vert ) = [0.545,1]\}& {}\\ & \text{More false false ratio:}\ \uptau ^{\mathrm{f}} \in \{\vert \Delta ^{\mathrm{t}}\vert <\vert \Delta ^{\mathrm{f}}\vert \rightarrow \vert \Delta ^{\mathrm{t}}\vert /(\vert \Delta ^{\mathrm{t}}\vert + \vert \Delta ^{\mathrm{f}}\vert ) = [0,0.454]\} & {}\\ \end{array}$$

where $\vert \Lambda ^{\mathrm{t}}\vert$ and $\vert \Lambda ^{\mathrm{f}}\vert$ are the numbers of true and false syllogistic cases, respectively. A fuzzy-syllogistic mood is then defined by assigning an Aristotelian mood ψ₁ψ₂ψ₃F the structurally fixed truth ratio τ:

$$\displaystyle{\text{Fuzzy-syllogistic mood:}\ (\uppsi _{1}\uppsi _{2}\uppsi _{3}\mathrm{F},\uptau )}$$

The truth ratio identifies the degree of truth of a particular mood, which we will associate further below in fuzzy-syllogistic reasoning with generic vagueness of inferencing with that mood.

For instance, the two premisses $\Phi _{1}$ and $\Phi _{2}$ of the mood IAO3, match 10 syllogistic cases, of which nine are true for the conclusion $\Phi _{3,}\Lambda ^{\mathrm{t}} =\{ \Delta _{4},\Delta _{24},\Delta _{43},\Delta _{46},\Delta _{48},\Delta _{67},\Delta _{68},\Delta _{74},\Delta _{76}\}$ and one is false $\Lambda ^{\mathrm{f}} =\{ \Delta _{19}\}$.

4 Structural Analysis

Our objective is to analyse the whole syllogistic system $\mathbb{S}$ of 256 moods, in order to reveal pure structural properties of the system and the moods. For that purpose, we will not consider any semantic interpretations on the moods and we will not apply the elimination rules of Aristotle.

4.1 Assumptions

Following assumptions allow us to perform a pure structural analysis of the system $\mathbb{S}$:

• Classical existential quantifiers: Universal cases included in I and O (Table 1a)

• Inclusive moods: All 256 moods considered, no mood elimination rules or heuristics applied

• Horizontal propositions: Major-minor proposition hierarchy not interpreted

• Set-theoretic: No distinction between the propositional variables subject and predicate

• Syllogistic cases: 96 distinct space combinations assumed to be the universal set of all possible set-theoretic truth cases of the 256 moods

• Normalised truth values: Truth ratios of moods in τ = [0, 1]

4.2 True Syllogistic Moods

24 moods are discussed in the literature since ancient times, to be the only true ones out of the 256 moods. Based on different restrictions that can be made for the value rages of the quantifiers, different numbers of valid moods can be obtained. Accordingly the mood AAO4 is considered to be conditionally true. However, our algorithmic approach calculates the very same 24 true moods, plus AAO4, namely anasoy [18], without any additional conditions for AAO4 [19], but the above assumptions (Table 1) for all moods.

Everyone of these 25 moods matches only true cases, but no false cases (Appendix 2):

$$\displaystyle{\text{Syllogistic subsystem of true moods:}\ \mathbb{S}_{1} =\{ (\Phi _{1}\Phi _{2}\Phi _{3},\uptau )\vert \uptau = 1.0\};\vert \mathbb{S}_{1}\vert = 25}$$

The number of total cases matched by any mood in $\mathbb{S}_{1}$ varies from 1 to 11.

4.3 Properties of the Syllogistic System

The algorithmic approach [18] enables revealing various structural properties of the syllogistic system. Some of them are presented here.

4.3.1 Equality

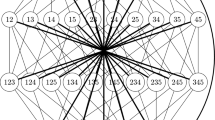
Out of the 256 moods there are 136 distinct moods, in terms of identical true and false cases matched per mood and equal truth ratios. In that sense 256 − 136 = 120 moods are redundant. For instance, the 25 true moods can be reduced to 11 distinct moods (Fig. 3). For instance, AAA1 = AAI1, AAO4 = AAI4 or EIO1 = EIO2 = EIO3 = EIO4.

Fig. 3

Set-theoretical relationships between syllogistic moods that are true in case of inclusive existential quantifiers. The inclusive syllogistic system $\mathbb{S}_{1}$ of true moods

4.3.2 Point-Symmetry

All moods are pairwise point-symmetric in terms of the syllogistic cases they match and in terms of their truth ratios.

Pairs have equal propositional quantifiers, but shifting concluding quantifiers. Almost all moods, i.e. 250, shift from O to A, in total 63 pairs, or from I to E, in total 62 pairs. Thus, the observed point-symmetry of moods is as follows:

$$\displaystyle\begin{array}{rcl} \text{Point-symmetric mood:}\ (\uppsi _{1}\uppsi _{2}\mathrm{OF}^{\Delta },\uptau _{\mathrm{ t}})& =& (\uppsi _{1}\uppsi _{2}\mathrm{AF}^{\Delta },\uptau _{\mathrm{ f}} = 1 -\uptau _{\mathrm{t}});(\uppsi _{1}\uppsi _{2}\mathrm{IF}^{\Delta },\uptau _{\mathrm{ t}}) {}\\ & =& (\uppsi _{1}\uppsi _{2}\mathrm{EF}^{\Delta },\uptau _{\mathrm{ f}} = 1 -\uptau _{\mathrm{t}}) {}\\ \end{array}$$

where $\Delta$ denotes that the moods match mutually equal cases. However, only for the following eight moods the quantifiers shift reverse, from A to O in AAA1$^{\Delta }$ = AAO1$^{\Delta }$ and from E to I in EAE1$^{\Delta }$ = EAI1$^{\Delta }$, EAE2$^{\Delta }$ = EAI2$^{\Delta }$, AEE2$^{\Delta }$ = AEI2$^{\Delta }$ and AEE4$^{\Delta }$ = AEE4$^{\Delta }$. Interesting is that these exceptional moods occur only amongst the fully true τ = 1. 0 moods.

Because of the above mood equalities, half of the 136 distinct moods, 68 moods, have 68 such point-symmetric counterparts (Appendix 2). For the 25 fully true and 25 fully false moods one can define a point-symmetric syllogistic subsystem:

$$\displaystyle\begin{array}{rcl} \text{Point-symmetric syllogistic subsystems:}\ \mathbb{S}_{1} = \mathbb{S}^{-1}_{ 0}& & {}\\ \text{Syllogistic subsystem of false moods:}\ \mathbb{S}_{0} =\{ (\Phi _{1}\Phi _{2}\Phi _{3},\uptau )\vert \uptau = 0.0\};\vert \mathbb{S}_{0}\vert = 25& & {}\\ \end{array}$$

where − 1 in the exponent denotes point-symmetry, in terms of point-symmetric moods. Equal moods in $\mathbb{S}_{1}$ have their point-symmetric counterparts in $\mathbb{S}_{0}$. Thus distinct moods in $\mathbb{S}_{0}$ are also 11.

The same symmetry exists for the remaining 206 moods in the interval (0,1), this time however without any exceptional quantifier shift (Appendix 1):

$$\displaystyle\begin{array}{rcl} \text{Point-symmetric syllogistic subsystems:}\ \mathbb{S}_{(1,0.545]}& =& \mathbb{S}^{-1}_{ [0.454,0)};\vert \mathbb{S}_{(1,0.545]}\vert {}\\ & =& \vert \mathbb{S}_{[0.454,0)}\vert = 103 {}\\ \end{array}$$

Out of the 206 moods in the range (0,1), 114 are distinct. Half of them 57 are in $\mathbb{S}_{\uptau \mathrm{t}}$ and half in $\mathbb{S}_{\uptau \mathrm{f}}$.

Interesting is that from the above subsystems, only moods in $\mathbb{S}_{1}$ are partially point-symmetric amongst each other (Fig. 3), respectively for $\mathbb{S}_{0}$. However, this partial symmetry is week, as it is observed only on the number of syllogistic cases of the moods and their relationships, but not on the distinct space combinations of the cases.

Since the truth ratio τ assigns every mood a vagueness, even before introducing fuzzy-quantifiers to the Aristotelian syllogistic system, we refer to $\mathbb{S}$ as the fuzzy-syllogistic system. Note that the truth ratio is a structural property that is constant, as long as the above assumptions hold.

4.3.3 Case Distribution

The 96 syllogistic distinct cases span the universal set, in which every mood matches a fixed number of cases. The distribution of these matches over the whole 256 moods shows interesting symmetric properties, which seam to be reflections of the above discussed symmetries.

Every mood has 0 to 65 true and 0 to 65 false distinct cases. The sum of all true and false cases matched per mood varies from 1 to 73 cases, out of the total possible 96 cases. For instance, mood AAA1 has only 1 true and 0 false case, in total 1 case, whereas mood OIA1 has 6 true and 65 false cases, in total 71 cases. Hence the truth ratio of AAA1 is τ = 1. 0, fully true, and that of OIA1 is τ = 0. 084, which is almost false.

For instance, mood OOO2 with 61 true and 11 false cases has truth ratio τ = 0. 847, which is mostly true, and its point-symmetric counterpart OOA2 with 11 true and 61 false cases has truth ratio τ = 0. 153, which is mostly false. With 72 cases in total, they match exactly 75 % of the universe.

Further details about case distributions and properties of the subsystems S_{(1, 0. 545]} and S_{[0. 454, 0)} will be provided elsewhere, since that discussion requires considerably more space.

5 Fuzzy Syllogistic System

The basic fuzzy syllogistic system consists of 256 moods that has constant truth ratios in [0, 1]. It can be further fuzzified, by introducing fuzzy-logical propositions, which can be model with fuzzy sets or fuzzy quantifications. By using fuzzy quantifiers we construct a fuzzy-quantified syllogistic system, in which some symmetric properties of the classical syllogistic system degrade, already with crisp sets. Here we discuss initial steps of an approach for gradually fuzzifying quantifiers towards a fuzzy-quantified syllogistic system and discuss the resulting fuzzy-logical square of opposition.

5.1 Fuzzy Quantification

Some of the symmetric properties of the syllogistic system are due to the inclusive existential quantifiers I and O (Table 1 logical cases a). Also, it is these cases that introduce the logical system redundancy, enable abduction of A as well as I from A and abduction of E as well as O from E, thus make the logical system undecidable on these cases. Most engineering systems cannot decide with such properties. Especially linguistic systems can decide the more effectively, the finer the quantifier granularities are adapted to semantics and pragmatics [17].

We start by fuzzifying the existential quantifiers I into²I and O into²O (Table 5):

$$\displaystyle\begin{array}{rcl} ^{2}\mathrm{I}& =& \mathrm{I} -\mathrm{ A} = \text{\textquotedblleft SOME are, but not ALL\textquotedblright } = \text{\textquotedblleft ONLYSOME are\textquotedblright };\vert ^{2}\mathrm{I}\vert = [1,\vert \mathrm{A}\vert - 1] {}\\ ^{2}\mathrm{O}& =& \mathrm{O} -\mathrm{ E} = \text{\textquotedblleft SOME are NOT, but not ALL\textquotedblright } {}\\ & =& \text{\textquotedblleft ONLYSOME are NOT\textquotedblright };\vert ^{2}\mathrm{O}\vert = [1,\vert \mathrm{A}\vert - 1] {}\\ \end{array}$$

Table 5 Logical cases of exclusive existential quantifiers represented with Euler diagrams and disjoint spaces

The value range of exclusive existential quantifiers exclude | A | , whereas inclusive quantifiers include | A | . Based on the exclusive quantifiers²I and²O, we elaborate now the smallest possible fuzzy-syllogistic system $^{\mathrm{n}}\mathbb{S}$, n = 2. The exponent n determines the granularity of distinct quantifiers, i.e. n = 2 affirmative and 2 negative. With increasing number of quantifiers 2 < n, the granularity of the total quantifier value range increases, which may be associated with further linguistic quantifiers, like, few, several, most, many (Table 6). Sometimes these are referred to as intermediate quantifiers. Since I encapsulates A, the two are not distinct. Analogously, E and O are not distinct.

Table 6 Value ranges of affirmative fuzzy quantifiers^a of n fuzzy-syllogistic systems $^{\mathrm{n}}\mathbb{S}$

Because the universal quantifiers A and E are equal in all systems $\mathbb{S}$ and $^{\mathrm{n}}\mathbb{S}$, 1 < n, we do not need to distinguish them with an exponent.

5.2 Fuzzy Syllogistic Moods

Moods²ψ₁ψ₂ψ₃F of the fuzzy-syllogistic system $^{2}\mathbb{S}$ are constructed analogously and with the same propositions ($\Phi _{1}\Phi _{2}\Phi _{3}\mathrm{F}$), but they match less truth cases and get different truth ratios τ:

$$\displaystyle{\text{Fuzzy syllogistic mood of propositions:}\ ^{2}(\uppsi _{ 1}\uppsi _{2}\uppsi _{3}\mathrm{F}) = ^{2}(\Phi _{ 1}\Phi _{2}\Phi _{3}\mathrm{F},\uptau ) \in ^{2}\mathbb{S}}$$

where²ψ = { A, E, ²I, ²O}. For instance, the mood IAI4 in $\mathbb{S}$ with inclusive existential quantifier I, becomes^2∕1IA¹I4 in $^{2}\mathbb{S}$ with the exclusive existential quantifier^2∕1I. The conclusion $\Phi _{3}$ of the mood, does not match the case $\Delta _{46}$ any more. Thus the mood has one false case $\Lambda ^{\mathrm{f}} =\{ \Delta _{46}\}$ and 9 true cases, $\Lambda ^{\mathrm{t}} =\{ \Delta _{4},\Delta _{19},\Delta _{24},\Delta _{43},\Delta _{48},\Delta _{67},\Delta _{68},\Delta _{74},\Delta _{76}\},\Phi ^{\Delta }_{3} = \Lambda ^{\mathrm{t}} \cup \Lambda ^{\mathrm{f}}$ (Fig. 2).

The fuzzy syllogistic system $^{2}\mathbb{S}$ has 11 true fuzzy syllogistic moods, of which some are equal. Thus they produce 5 distinct groups of moods (Fig. 4, Appendix 3 $^{2}\mathbb{S}_{1}$):

$$\displaystyle{\text{True:}\ ^{2}\mathbb{S}_{ 1};\vert ^{2}\mathbb{S}_{ 1}\vert = 11}$$

Fig. 4

Set-theoretical relationships between syllogistic moods that are true in case of exclusive existential quantifiers. The exclusive syllogistic system $^{2}\mathbb{S}_{1}$ of true moods

The remaining 245 moods of $^{2}\mathbb{S}$ can be categorised in terms of truth ratio ranges into further four subsystems:

• MoreTrue: $^{2}\mathbb{S}_{(1,0.5)};\vert ^{2}\mathbb{S}_{(1,0.5)}\vert = 70$

• HalfTrueHalfFalse: $^{2}\mathbb{S}_{0.5};\vert ^{2}\mathbb{S}_{0.5}\vert = 16$

• MoreFalse: $^{2}\mathbb{S}_{(0.5,0)};\vert ^{2}\mathbb{S}_{(0.5,0)}\vert = 119$

• False: $^{2}\mathbb{S}_{0};\vert ^{2}\mathbb{S}_{0}\vert = 40$

The linguistic terms that we use to express the vagueness of the subsystems may be used analogously for the subsystems of $\mathbb{S}$ [19].

5.2.1 Truth Ratio Distribution

It is interesting to observe that 16 moods that are true in $\mathbb{S}$, become false in $^{2}\mathbb{S}$ and that two moods that are false in $\mathbb{S}$ become true in $^{2}\mathbb{S}$.

OAI3 limano and IAO3 nomali are two moods that are false in $\mathbb{S}$, i.e. OAI3, $\mathrm{IAO3}\notin \mathbb{S}_{1}$, OAI3, $\mathrm{IAO3} \in \mathbb{S}_{[0,1)}$, but turn true in $^{2}\mathbb{S}$, i.e.²OAI3, $^{2}\mathrm{IAO3} \in ^{2}\mathbb{S}_{1}$ (Fig. 4, Appendix 3 $^{2}\mathbb{S}_{1}$).

Out of the 16 moods that become false in $^{2}\mathbb{S}$ (Appendix 3 $^{2}\mathbb{S}_{[0,0.89]}$), five moods,²EAO1,²EAO2,²AAI1,²AEO2,²AEO4 all turned to zero. These moods were true in $\mathbb{S}$, but turned to 100 % false, only by excluding the universal cases from the existential quantifiers, i.e. they would become true only with universal cases. In fact, if we replace in these moods²I with A and²O with E, we get EAE1, EAE2, AAA1, AEE2, AEE4, which are all true moods, found both, in $^{2}\mathbb{S}$ as well as in $\mathbb{S}$ and all have a single syllogistic case. Thus this scenario exemplifies clearly that inclusive existential quantification can turn some moods to true, whereas without universal cases the moods would remain fully false.

This observation can be generalised, such that the truth ratios of many moods with existential quantifiers decrease, whereas some increase, amongst which limano and nomali even increase to 100 % true.

5.3 Properties of the Fuzz-Quantified Syllogistic System

In general, the number of equal moods per truth ratio increases from $\mathbb{S}$ to $^{2}\mathbb{S}$, point-symmetry vanishes (Appendix 1), more moods hit a lower truth ratio and the total number of matched syllogistic cases decreases, which includes more false cases than true cases.

Every mood has 0 to 40 true and 0 to 48 false distinct cases. The sum of all true and false cases matched per mood varies from 1 to 54 cases, out of the total possible 96 cases.

For instance, the moods OOO2 = OOA2⁻¹ now become²OOO2 with 40 true and 8 false cases gets truth ratio τ = 0. 833, which is close to OOO2, and²OOA2 with 6 true and 42 false cases gets truth ratio τ = 0. 125, which is close to OOA2. With 48 cases in total, both match exactly 50 % of the universe. Most point-symmetric counterparts in $\mathbb{S}$ do not even preserve the same number of total cases in $^{2}\mathbb{S}$, like these two moods do.

5.4 Generic Fuzzy-Syllogistic Systems

We have defined the Aristotelian syllogistic system $\mathbb{S}$ as fuzzy-syllogistic, as moods have truth ratios that can be interpreted as degree of vagueness in inferencing with them. Further we have defined the fuzzy-quantified syllogistic system $^{2}\mathbb{S}$, in which the philosophically possible universal cases are excluded from the existential quantifiers. In further steps towards generic fuzzy-syllogistic systems $^{\mathrm{n}}\mathbb{S}$, 2 < n, the value range of the existential quantifiers of $^{2}\mathbb{S}$ are further partitioned, in general into n-1 partitions, each representing a fuzzy-existential quantifier (Table 6).

The systems $\mathbb{S}$ and $^{2}\mathbb{S}$ constitute the basic generic syllogistic systems, in terms of truth rations. Truth ratios are calculated from syllogistic cases and those are based on the set-theoretical logical cases (Table 1, case b and c). All fuzzy-existential quantifiers [^n∕n−1I, ^n∕1I] of $^{\mathrm{n}}\mathbb{S}$ are valid on exactly these same logical cases. Therefore, the truth ratio τ of any particular mood $^{2}(\Phi _{1}\Phi _{2}\Phi _{3}\mathrm{F},\uptau ) \in ^{2}\mathbb{S}$ is equal in the same mood with all further partitioned n-1 existential quantifiers $^{\mathrm{n}}(\Phi _{1}\Phi _{2}\Phi _{3}\mathrm{F},\uptau ) \in ^{\mathrm{n}}\mathbb{S}$.

For instance, the truth ratio τ = 0. 888 of the mood²IAI4 is equal for all moods with any further partitioned I, like^3∕2IA²I4,^3∕1IA²I4,^3∕2IA¹I4,^3∕1IA¹I4 or^6∕5IA⁵I4,^6∕4IA⁵I4,^6∕3IA⁵I4 etc.

For instance, the truth ratio τ = 1 of the mood^2∕1OA¹I3 is equal for all moods with any further partitioned O or I, like^3∕2OA²I4,^3∕1OA²I4,^3∕2OA¹I4,^3∕1OA¹I4 or^6∕5OA⁵I4,^6∕4OA⁵I4,^6∕3OA⁵I4 etc.

6 Extensions to the Square of Opposition

In order to verify the consistency of the quantifier relationships of the various fuzzy-syllogistic systems $^{\mathrm{n}}\mathbb{S}$, 1 < n, we now present extensions to the Aristotelian square of opposition $\Omega$.

6.1 Fuzzy-Logical Square of Opposition

The quantifier relationships of the fuzzy syllogistic system $^{2}\mathbb{S}$ imply the same visual structure like the original square of opposition (Fig. 1), however without universal cases in the existential quantifiers.

We will denote the fuzzy-logical square of opposition with $^{2}\Omega$ and refer to it in short as the exclusive square:

$$\displaystyle{^{2}\Omega =\{ (\mathrm{A},\mathrm{E},^{2}\mathrm{I},^{2}\mathrm{O})\vert \mathrm{R}_{\mathrm{ sa}}(\mathrm{A},^{2}\mathrm{I}),\mathrm{R}_{\mathrm{ cr}}(\mathrm{A},\mathrm{E}),\mathrm{R}_{\mathrm{cd}}(\mathrm{A},^{2}\mathrm{O}),\mathrm{R}_{\mathrm{ cd}}(\mathrm{E},^{2}\mathrm{I}),\mathrm{R}_{\mathrm{ sa}}(\mathrm{E},^{2}\mathrm{O}),\mathrm{R}_{\mathrm{ sc}}(^{2}\mathrm{I},^{2}\mathrm{O})\}}$$

where $^{2}\Omega$ has two affirmative quantifiers. In the same manner we have identified $^{2}\mathbb{S}$ as the smallest possible fuzzy syllogistic system, we identify the exclusive square $^{2}\Omega$ as the smallest possible fuzzy-logical square.

6.2 Fuzzy-Logical Graph of Opposition

For every further partition of the existential quantifiers (Table 6), we will extend the classical square analogously step-wise and eventually generalise the exclusive square $^{2}\Omega$ to a fuzzy-logical graph of opposition $^{\mathrm{n}}\Omega$.

Our first extension of $^{2}\Omega$ is $^{3}\Omega$ (Fig. 5), which verifies the logical quantifier relationships of $^{2}\mathbb{S}$. Following new relationships emerge in $^{3}\Omega$:

• Subaltern: Any existential quantifier is subaltern to the universal quantifier, so is any smaller existential quantifier to any greater one.

• Subcontrary: Any existential quantifier is subcontrary to any negative existential quantifier.

Fig. 5

3-quantified fuzzy-logical graph of opposition $^{3}\Omega$ with three fuzzy existential quantifiers and traditional relationships

The structure of $^{\mathrm{n}}\Omega$ (Fig. 6) is obtained, by simply replicating the new relationships of $^{3}\Omega$, for every further partitioning existential quantifier. The relationships are analogous to those of Buridan or Celaya [24].

Fig. 6

n-quantified fuzzy-logical graph of opposition $^{\mathrm{n}}\Omega$ with n − 1 fuzzy existential quantifiers and traditional relationships

7 Discussion

We have used the fuzzy-logical graph of opposition $^{\mathrm{n}}\Omega$ for verifying possible logical relationships between the quantifiers of the fuzzy-syllogistic systems $^{\mathrm{n}}\mathbb{S}$. Generalisations to the classical square of opposition, are not new in the literature. We shall discuss one similar approach that appears to be related to ours.

In some recent work, the validity of fuzzy syllogism have been analysed based on the concept of intermediate quantifiers and 105 moods have been heuristically identified as valid [32], structurally [27] and algebraically [38] validated and verified on a generalisation of the square of opposition [26]. For instance, fuzzy-quantified derivations of the mood AAI1, like AAT1, AAK1, AAP1 (T = most; K = many; P = almost all) are reported to be valid. However, according our truth ratio calculations that are based on the above quantifier definitions (Table 1), the mood AAI in $\mathbb{S}$ has τ = 1, but turns false in $^{2}\mathbb{S}$, i.e.²AAI1 has τ = 0. The mood turns false in $^{2}\mathbb{S}$, because the only syllogistic case of the mood is 0100101 and that is true only for the A case of the inclusive quantifier I, the very one that is excluded in²I (Table 1 logical cases a for I). As we have discussed above, this mood has τ = 0 in all systems $^{\mathrm{n}}\mathbb{S}$, 1 < n. Since the cardinalities of the fuzzy-quantifiers T, K, P are all smaller or equal than²I, i.e. T < K < P ≤ ²I, none of those moods can be true according to our calculations.

In general, according to our calculations, any mood of any system $^{\mathrm{n}}\mathbb{S}$ is true, only if it has at least one premising universal quantifier. Otherwise moods have truth ratios in τ < 1.

The same authors verify their intermediate quantifiers visually on different shapes of generalised squares of oppositions, which are all very similar to each other and partially similar with our fuzzy-logical graph of opposition $^{\mathrm{n}}\Omega$. Only few differences are worth mentioning:

• Number of quantifiers are constant at five; whereas $^{\mathrm{n}}\Omega$ has a finite number n of quantifiers.

• Contradictory and subcontrary are defined only between some specific quantifiers; whereas in $^{\mathrm{n}}\Omega$, every quantifier has either contradictory or subcontrary relations to all smaller contrapositive quantifiers, which is a derivation from the basic fuzzy-logical negation [40], e.g. ¬ ^n∕n−1O = ^n∕n−2I ∪^n∕n−3I ∪ … ∪^n∕1I.

• The quantifier Some is used; whereas Some is explicitly not used in any graph $^{\mathrm{n}}\Omega$, as Some has a historically rooted pre-defined value-range in the Aristotelian square that covers all philosophically possible values (Fig. 1).

8 Conclusion

We have analysed the classical syllogistic system $\mathbb{S}$ in terms of 96 syllogistic cases, which span the universal value range of all moods of all systems $^{\mathrm{n}}\mathbb{S}$ and in which moods match some of them either true or false. We have identified equal moods in terms of cases and truth ratios, point symmetry in terms of cases and truth ratios and the symmetric case distributions. We have presented the point symmetry of the subsystems $\mathbb{S}_{1} = \mathbb{S}^{-1}_{0}$ and $\mathbb{S}_{(1,0.545]} = \mathbb{S}^{-1}_{[0.454,0)}$. The symmetric structures are obviously not only due to the square $\Omega$, but also caused by the combinatorial ordering of the premising propositional variables.

We have discussed the properties of the smallest possible fuzzy syllogistic system $^{2}\mathbb{S}$ and revealed why the symmetric structures of $\mathbb{S}$ almost vanish in $^{2}\mathbb{S}$. We have introduced the smallest possible fuzzy syllogistic square of opposition $^{2}\Omega$ and suggested an approach for generalising it to a fuzzy-logical graph of opposition $^{\mathrm{n}}\Omega$ with 2n fuzzy quantifiers.

Currently we are testing the feasibility of the generic system $^{\mathrm{n}}\mathbb{S}$ on fuzzy-syllogistic ontologies [20] and fuzzy-syllogistic reasoning with such ontologies [21, 42].

Appendices

Appendix 1: Distinct Groups of Moods in $\mathbb{S}$ and $^{2}\mathbb{S}$?

The Aristotelian syllogistic system $\mathbb{S}$ consists of 136 distinct groups of moods, in terms of equal truth ratios (Fig. 7). One can observe the fully point-symmetric distribution of the values around τ = 0. 5. Truth ratios as well as the number of moods in the groups are symmetric.

Fig. 7

136 distinct groups of moods of $\mathbb{S}$, sorted in ascending order of truth ratio τ (inclusive logic)

The fuzzy-syllogistic system $^{2}\mathbb{S}$ consists of 70 distinct groups of moods, in terms of equal truth ratios (Fig. 8). However neither truth ratios nor the number of moods in the groups are symmetrically distributed around τ = 0. 5 any more.

Fig. 8

70 distinct groups of moods of $^{2}\mathbb{S}$, sorted in ascending order of truth ratio τ (exclusive logic)

Appendix 2: Moods with Inclusive Existential Quantifiers

In case of inclusive existential quantifiers 25 moods are 100 % true, i.e. have truth ratio τ = 1. 0, because they have only true cases t. 25 moods are 100 % false, i.e. have truth ratio τ = 0. 0, because they have only false cases f (Table 7). Some moods are equal in terms of their syllogistic cases, as they match exactly the same cases out of the possible 96 cases. For instance, AII1 has 10 cases and AII3 has the very same cases.

Table 7 In case of inclusive existential quantifiers, true moods of $\mathbb{S}_{1}$, and their point-symmetric counterparts in $\mathbb{S}_{0}$, showing numbers of true cases t and false cases f of their truth ratios τ

Everyone of the 25 true moods has a point-symmetric counterpart, in terms of the particular cases they match. For instance, AOO2 has 9 cases and AOA2 has the very same cases, but for AOO2 all cases are true, whereas for AOA2 all those cases are false.

Appendix 3: Moods with Exclusive Existential Quantifiers

In case of exclusive existential quantifiers 9 moods remain 100 % true and two^2∕1IA¹O3 and^2∕1OA¹I3 turn 100 % true. 16 moods turn false with truth ratios τ ranging in [0, 0.89] (Table 8). Some moods become equal in terms of their syllogistic cases. For instance,^2∕1IA¹I3,^2∕1OA¹O3,^2∕1IA¹O3 and^2∕1OA¹I3 reduce all to the very same 6 cases.

Table 8 In case of exclusive existential quantifiers, true moods of $^{2}\mathbb{S}_{1}$ and false turned moods in $^{2}\mathbb{S}_{[0,0.89]}$, showing numbers of true cases t and false cases f of their truth ratios τ

The syllogistic system with exclusive existential quantifiers shows considerably less symmetric properties in terms of syllogistic cases and truth ratios.