Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

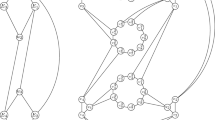
Maximum common subgraph problems arise in biology and chemistry [16, 20, 40], in computer vision [7, 9], in the analysis of source code [12], binary programs [19], and circuit designs [9], in character recognition problems [27], and in many other domains [49], both directly and as a way of measuring the similarity or difference between two graphs [5, 18, 23]. We illustrate two variants of this problem in Fig. 1—in both cases we are finding an induced subgraph and maximising the number of vertices selected, but in the second variant the common subgraph must be connected.

Fig. 1.
figure 1

A maximum common induced subgraph of the first two graphs has eight vertices, shaded. However, if we require the common subgraph to be connected, only seven vertices may be selected—one way to do this is shown in the third and fourth graphs.

Full size image

1.1 Definitions and Notation

We introduce definitions and algorithms on undirected and unlabelled graphs; the extension to general graphs is straightforward and is discussed in Sect. 2.3. An undirected graph G is defined by a finite set of vertices \({\text {V}}(G)\) and a set of undirected edges \({\text {E}}(G) \subseteq {\text {V}}(G) \times {\text {V}}(G)\), where \((u, v) \in {\text {E}}(G) \Rightarrow (v, u) \in {\text {E}}(G)\). The neighbourhood of a vertex v, written \({\text {N}}(G, v)\), is the set of vertices to which it is adjacent, so \({\text {N}}(G, v) = \{ u \in {\text {V}}(G) : (u, v) \in {\text {E}}(G) \}\). Given a graph G, two vertices \(v_s, v_e \in {\text {V}}(G)\) are connected by a path in G if there exists a sequence of vertices \((v_0, v_1, \ldots , v_k)\) such that \(v_0 = v_s\), \(v_k = v_e\), and each pair of successive vertices is connected by an edge, i.e. \(\forall i\in \{1 \ldots k \}, (v_{i-1}, v_i) \in {\text {E}}(G)\). A graph G is connected if every distinct pair of vertices is connected by a path.

The subgraph of a graph G induced by a set \(H \subseteq {\text {V}}(G)\), written G[H], is the graph with vertex set H, and with every edge in G which has both endpoints in G, i.e. \({\text {E}}(G[H]) = {\text {E}}(G) \cap ({\text {V}}(H) \times {\text {V}}(H))\). We will consider only subgraphs which are induced by some set. It is also possible to permit removing edges which are not incident to removed vertices, thus leading to partial subgraphs—we do not consider this possibility in this paper, although everything we discuss may be extended to the partial case [34, 54].

A graph G is isomorphic to another graph H if there exists a bijective function \(f : {\text {V}}(G) \rightarrow {\text {V}}(H)\) which preserves edges and non-edges, i.e. \(\forall (u, v) \in {\text {V}}(G) \times {\text {V}}(G), (u, v) \in {\text {E}}(G) \Leftrightarrow (f(u),f(v)) \in {\text {E}}(H)\). A common subgraph of two graphs G and H is a graph isomorphic to subgraphs of both G and H. A common connected subgraph is a common subgraph which is connected. A Maximum Common Subgraph, or MCS (resp. Maximum Common Connected Subgraph, or MCCS) is a common subgraph (resp. common connected subgraph) which has a maximum number of vertices.

1.2 Overview

In Sect. 2, we review existing approaches for solving the MCS problem, with a specific focus on Constraint Programming (CP)-based techniques, and on reductions of the problem to finding a maximum clique in an association graph.

Previous experimental evaluations have used simple maximum clique algorithms, or even enumeration algorithms—for example, Vismara and Valery [54] compare a modified form of the Bron-Kerbosch maximal clique enumeration algorithm [3] with a CP optimisation approach. Our experience suggests that a modern maximum clique algorithm could give many orders of magnitude improvement, due to a strong bound function which prunes the search space. Therefore, in Sect. 3, we re-evaluate the clique-based approach using a modern algorithm, and we show that it outperforms CP on labelled graphs, and that it is competitive with CP on unlabelled graphs, contradicting earlier conclusions.

Then, in Sect. 4, we consider the MCCS problem. For the CP approach, we may add a global connectedness constraint to the model. Alternatively, we may use a special branching rule [54] to grow connected subgraphs only. These two techniques may be combined, and we experimentally show that the best results are in fact obtained when combining them. When solving the MCCS problem with a clique-based approach, neither technique seems directly viable with an association graph encoding. However, we show that it is possible to adapt the combined branching and bounding rule used by modern clique algorithms to maintain connectedness during search. We compare the clique-based approach with the best CP variant for MCCS, and we show that it outperforms CP on labelled graphs, whereas it is outperformed by CP on unlabelled graphs.

2 Existing Complete Approaches for MCS

There are two main approaches for solving MCS. The first approach (described in Sect. 2.1) is based on CP, whilst the second (described in Sect. 2.2) is based on a reformulation of MCS into a maximum clique problem. Both approaches are described for undirected, unlabelled graphs; their extension to richer graphs is discussed in Sect. 2.3. Other approaches have been tried, mixed integer programming [37] and heuristics [17]; SAT encodings seem to struggle even for subgraph isomorphism [31].

2.1 Constraint Programming Models for MCS

McGregor [32] proposed a branch and bound algorithm: each branch of the search tree corresponds to the matching of two vertices, and a bounding function evaluates the number of vertices that still may be matched so that the current branch is pruned as soon as this bound becomes lower than the size of the largest known common subgraph. CP approaches may be viewed as enhancements of this branch and bound algorithm.

Vismara and Valery [54] introduced the first explicit CP model. Given two graphs G and H, this model associates a variable \(x_v\) with every vertex v of G, and the domain of this variable contains all vertices of H, plus an additional value \(\bot \): variable \(x_v\) is assigned to \(\bot \) if vertex v is not matched to any vertex of H; otherwise \(x_v\) is assigned to the vertex of H to which it is matched. Edge constraints are introduced in order to ensure that variable assignments preserve edges and non-edges between matched vertices, i.e. \(\forall u, v \in {\text {V}}(G), (x_u = \bot ) \vee (x_v = \bot ) \vee ((u, v) \in {\text {E}}(G) \Leftrightarrow (x_u, x_v) \in {\text {E}}(H))\). Difference constraints are introduced in order to ensure that each vertex of H is assigned to at most one variable, i.e. \(\forall u, v \in {\text {V}}(G)~\text {distinct,}~ (x_u = \bot ) \vee (x_v = \bot ) \vee (x_u \ne x_v)\).

This CP model was improved by Ndiaye and Solnon [34] by replacing binary difference constraints with a soft global allDifferent constraint which maximizes the number of \(x_u\) variables that are assigned to values different from \(\bot \), while ensuring they are all different when they are not assigned to \(\bot \). They find that the combination “MAC+Bound” (resp. “FC+Bound”) obtains the best results on labelled (resp. unlabelled) graphs and outperforms the two previous approaches. The combination “MAC+Bound” maintains arc consistency [41] of edge constraints, whereas the combination “FC+Bound” simply performs forward-checking on these constraints. In both combinations, the “Bound” filtering checks whether it is possible to assign distinct values to enough \(x_u\) variables to surpass the best cost found so far—it is a weaker version of GAC(softAllDiff) [36] which computes the maximum number of variables that can be assigned distinct values.

2.2 Reformulation of MCS to a Maximum Clique Problem

An alternative approach to MCS is to reduce the problem to finding a maximum clique in an association graph [2, 15, 24, 40]. An association graph (or compatibility graph, or weak modular product) of two graphs G and H is an undirected graph \(G \,\triangledown \,H\) with vertex set \({\text {V}}(G \,\triangledown \,H) = \{ (v, v') \in {\text {V}}(G) \times {\text {V}}(H) : (v, v) \in {\text {E}}(G) \Leftrightarrow (v', v') \in {\text {E}}(H)\}\)—to avoid confusing vertices of \(G \,\triangledown \,H\) with vertices of the two original graphs, we call vertices of \(G \,\triangledown \,H\) matching nodes, as each vertex \((u, u')\) of \(G \,\triangledown \,H\) denotes the matching of u with \(u'\). The edges of \(G \,\triangledown \,H\) connect matching nodes which denote compatible assignments, so two matching nodes \((u, u')\) and \((v, v')\) are adjacent if \(u \ne v\) and \(u' \ne v'\), and if they preserve both edges and non-edges, so \((u, v) \in {\text {E}}(G) \Leftrightarrow (u', v') \in {\text {E}}(H)\). We illustrate this in Fig. 2.

Fig. 2.
figure 2

A maximum common induced subgraph between the two graphs on the left has three vertices—one solution is highlighted. On the right, the association graph encoding: the highlighted clique of size three shows the same solution. The “missing” vertices correspond to assignments which are impossible due to the presence or absence of loops.

Full size image

A clique is a subgraph whose vertices are all pairwise adjacent. A clique is maximal if it is not strictly included in any other clique, and it is maximum if it is a largest clique of a given graph, with respect to the number of vertices. A clique in an association graph corresponds to a set of compatible matchings. Therefore, such a clique corresponds to a common subgraph, and a maximum clique of \(G \,\triangledown \,H\) is an MCS of G and H. It follows that any method able to find a maximum clique in a graph can be used to solve the MCS problem.

Note that the association graph is a partial subgraph of the microstructure [21] associated with the CP model of Vismara and Valery [54]: the microstructure has more matching nodes than the association graph because it has a matching node \((u,\bot )\) for each vertex u of G. Each clique of size \(\left| {\text {V}}(G)\right| \) in the microstructure corresponds to a common subgraph, the size of which is defined by the number of matching nodes that do not contain \(\bot \).

2.3 Extension to Labelled or Directed Graphs

In some applications, labels may be associated with vertices or edges. We denote \(\lambda (u)\) and \(\lambda ((u, v))\) the label of a vertex u and an edge (u, v), respectively. Where graphs are labelled, any isomorphism f must additionally preserve labels, so we require \(\lambda (f(v)) = \lambda (v)\) for any vertex v, and \(\lambda ((f(u), f(v))) = \lambda ((u, v))\) for any edge (u, v). This kind of label compatibility constraint is handled in a straightforward way in both CP and clique-based approaches to MCS. For CP, we restrict the domain of every variable \(x_u\) to vertices with compatible labels, and ensure that edge labels are preserved in edge constraints. For clique-based approaches, label compatibility is handled through the definition of the association graph, by restricting the set of matching nodes to pairs of vertices with compatible labels, and the set of matching edges to pairs of edges with compatible labels.

The extension of MCS algorithms to directed graphs, where isomorphisms must preserve directed edges, is similarly straightforward.

Labels and directed edges usually simplify the solution process, both for CP and clique-based approaches: vertex labels reduce domain sizes for CP, and the number of matching nodes in association graphs; edge labels tighten edge constraints for CP, and make the association graph sparser for clique-based approaches. It is worth noting that edge constraints do not help CP approaches to do more filtering so long as \(\bot \) remains in variable domains: every pair of variables \((x_i, x_j)\) having \(\bot \in D(x_j)\) is arc consistent, since \(\bot \) is a support for any value \(u \in D(x_i)\). However, as soon as \(\bot \) is removed from domains (i.e. when the number of variables assigned to \(\bot \) has reached the best known bound on the size of the MCS), maintaining arc consistency may filter values, and then tighter constraints increase the opportunities for filtering.

Fig. 3.
figure 3

The cumulative number of MCS instances solved in under a certain time: on the top, 33 % labelled graphs, and then unlabelled and undirected graphs. On the bottom, an instance-by-instance comparison of the clique model with the best CP model, with 33 % labelled graphs (with MAC) on the left, and unlabelled and undirected graphs (with FC) on the right.

Full size image

3 Re-evaluating the Clique Model for MCS

Previous experimental evaluations of the association graph model have used either maximal clique enumeration algorithms [22, 54] (even when the maximisation problem was being considered), or very simple maximum clique algorithms [6, 8], and so their conclusions may now be overly pessimistic. Thus we re-evaluate the approach using a modern maximum clique algorithm. Association graphs are dense, even if the input is sparse, so we will using (the single-threaded, bit-parallel version of) the maximum clique solver by McCreesh and Prosser [30], which implements Prosser’s [38] “MCSa1” variant of a series of algorithms due to Tomita et al. [51–53], using a bitset encoding due to San Segundo et al. [45, 47]. We compare this to the “FC+Bound” and “MAC+Bound” (simply referred to as FC and MAC) CP implementations of Ndiaye and Solnon [34], using smallest domain first for variable ordering, and a value ordering which prefers vertices of most similar degree. We perform our experiments on machines with Intel Xeon E5-2640 v2 CPUs and 64GBytes RAM; software was compiled using GCC 4.9, and a timeout of one hour was used.

We consider a randomly generated database [8, 42] commonly used for benchmarking maximum common subgraph problems. The dataset contains different classes of graphs: randomly connected graphs with different densities; 2D, 3D, and 4D regular and irregular meshes; regular bounded valence graphs, and irregular bounded valence graphs. For each pair of graphs, there are 3 different labellings such that the number of different labels is equal to 33 %, 50 % or 75 % of the number of vertices. In this paper, we report experiments with unlabelled graphs (labels are ignored), and with 33 % labellings (the problem becomes very easy with larger numbers of labels). For unlabelled graphs, we select the 27,500 graph pairs where the number of vertices in each graph is no more than 35; for labelled graphs, which we find less computationally challenging, we select all 81,400 graph pairs, to include graphs with up to 100 vertices.

The two plots on the top of Fig. 3 display the cumulative number of instances solved with respect to time. When graphs are labelled, the clique-based approach clearly outperforms either CP model, and MAC has a slight advantage over FC. (Recall that edge labels decrease the density of the association graph, which is typically very beneficial for clique algorithms, but do not help CP until \(\bot \) is removed from domains.) For unlabelled graphs, the three approaches are broadly comparable, and ultimately FC beats MAC, which beats the clique approach. The bottom row gives a per-instance comparison of the best CP approach with the clique approach: the heatmaps are similar to scatter plots, but due to the large number of instances, we colour each point according to the density of solutions around that point. For labelled graphs, the clique approach comes close to dominating MAC on non-trivial instances (which suggests that there is unlikely to be scope for per-instance algorithm selection here). For unlabelled graphs, there is still a broad correlation between the runtimes; the clique approach rarely wins by more than one order of magnitude, but is sometimes much worse.

A closer inspection of the data suggests that the different randomness models used to generate instances have little effect on the runtimes for either approach. However, the relative size of the solution matters, particularly for the clique algorithm: if the solution is large (i.e. the two input graphs are very similar), the clique approach finds nearly every labelled instance trivial.

4 Finding Maximum Common Connected Subgraphs

In many applications, the common subgraph must satisfy some additional constraints. This is usually handled in a straightforward way in CP, by branching rules and/or constraint propagation. In clique-based approaches, some constraints may be handled by modifying the definition of the association graph—for example, constraints on pairs of vertices that may be matched are handled by removing inconsistent pairs from \({\text {V}}(G \,\triangledown \,H)\). However, more global constraints cannot be handled by modifying the definition of the association graph.

In this paper, we focus on the connectedness constraint, which occurs in many applications [16, 22, 40, 54]. Adding the connectedness requirement makes certain special cases solvable in polynomial time, including outerplanar graphs of bounded degree [1] and trees [14], but the general case remains NP-hard. As illustrated in Fig. 1, the MCCS cannot be deduced from the MCS: we need to ensure connectedness during search. In Sect. 4.1, we show that in CP this may be done in two different ways that may be combined, and we show in Sect. 4.2 that the best results are obtained when combining them. In Sect. 4.3, we introduce a new way for ensuring connectedness in a clique-based approach. Finally, we compare CP and our clique-based approach in Sect. 4.4.

For MCCS we consider only undirected graphs (and so we treat directed edges in the inputs as being undirected). For directed graphs, there is more than one notion of connectivity, and it is not clear which should be selected—the approaches we consider extend easily to weakly connected directed graphs, but not to the strongly connected case (for which we know of no applications).

4.1 Ensuring Connectedness in CP

Vismara and Valery [54] implement the connectedness constraint by using a branching rule which selects the next variable to be assigned. Let A be the set of variables already assigned to values different from \(\bot \). The next variable to be assigned is chosen within the set of unassigned variables which are the neighbour of at least one vertex of A. When this set is empty, all remaining unassigned variables are assigned to \(\bot \). We illustrate this in Fig. 4.

Fig. 4.
figure 4

Suppose we are looking for a connected common subgraph, using the graph on the left for variables and the graph on the right (which has an isolated vertex) for values. We initially consider \(a \mapsto 1\). Our restricted branching rule requires us to select either variable b or variable c subsequently, not d or e. We try \(b \mapsto 2\), which adds d to the branchable variables, and forces \(c \mapsto \bot \). We may now only branch on d, and we try \(d \mapsto 4\). Now the only remaining variable is unbranchable, and so \(e = \bot \) is forced, even though 5 remains in its domain and does not violate any constraints.

Full size image

A more traditional CP approach would be to express connectedness as a conventional constraint. For example, CP(Graph) [13] introduces graph domain variables and enforces connectivity via the reachable constraint, ensuring that there is a path from a specified vertex to a specified set of vertices. One such constraint could be posted for each of the vertices in the graph, encoding the transitive closure of the graph. Brown et al. [4] explored the use of constraint programming in the generation of connected graphs with specified degree sequences. Two constraints were combined: the graphical constraint (a backtrackable implementation of the Havel-Hakimi algorithm), and a connectivity constraint implemented using sets of vertices, where vertex sets A and B are combined when there exists a pair of vertices \(v \in A\) and \(w \in B\) and an edge \((v,w) \in E\). Residual degree counts are maintained on components and vertices to enforce graphicality and connectivity. Prosser and Unsworth [39] proposed a connectivity constraint for connected graph generation where decision variables are edges (the search process accepts and rejects edges). The constraint employed depth first search to maintain the set of tree edges and back edges, associating path counters on these edges. The counters were then used to detect the existence of cut-edges and protects these by forcing edges.

In all these previous works, the goal was to ensure that a given set of vertices is connected. For MCCS, the problem is slightly different: we have to ensure that the number of connected vertices that may be matched (in both graphs) is greater than the size of the largest common subgraph previously found. Therefore, we introduce a new filtering algorithm to ensure connectedness consistency for MCCS. Let us consider two graphs G and H, and let D be the current domains (we suppose that \(D(x_u)\) is a singleton when \(x_u\) is assigned). Let S and T be the sets of vertices of G and H respectively which may belong to the common subgraph, i.e. \(S=\{ u\in {\text {V}}(G) : D(x_u)\ne \{\bot \}\}\), and \(T = \cup _{u\in {\text {V}}(G)} D(x_u) \setminus \{ \bot \}\). Connectedness consistency ensures that both G[S] and H[T] are connected graphs.

Connectedness consistency is ensured only once a first variable has been assigned, rather than at the root of search. Let \(x_u\) be the first assigned variable, and v the value assigned to \(x_u\). To ensure connectedness consistency, we perform a traversal of G (resp. H), starting from u (resp. v), and we initialize S (resp. T) with all visited vertices. Then, for each vertex \(v\in {\text {V}}(G) \setminus S\), we set \(x_v\) to \(\bot \), and for each \(w \in {\text {V}}(H) \setminus T\), we remove w from all domains to which it belongs.

During search, each time a variable is assigned to \(\bot \), we remove the corresponding vertex from S and perform a new traversal of G[S] starting from the initial vertex u. For each vertex \(w\in S\) that is not visited by the traversal, we remove w from S and assign \(x_w\) to \(\bot \). Also, each time a value is removed from a domain so that this value no longer belongs to any domain, we remove it from T, and perform a new traversal of H[T] starting from the initial vertex v. For each vertex w that is not visited by the traversal, we remove w from T, and remove w from all domains to which it belongs.

Finally, the two approaches for ensuring connectedness (branching and filtering) are complementary and may be combined: at each step of the search, we select the next variable to be assigned within the neighbors of A, and each time a vertex of H is removed from a domain we filter domains to ensure connectedness consistency. In the example in Fig. 4, after the first assignment, filtering alone would remove 5 from every domain but would allow branching on any remaining variable, whilst branching alone would force the next variable to be either b or c but would not immediately eliminate 5 from the domains of d and e.

Fig. 5.
figure 5

On top, the cumulative number of MCCS instances solved in under a certain time using different CP techniques, for 33 % labelled (left) and unlabelled undirected (right) graphs. Below, instance-by-instance comparisons.

Full size image

4.2 Experimental Comparison of CP Connectedness Techniques

Figure 5 compares the three approaches for ensuring connectedness in CP: by branching (Branch), by filtering (Filter), or by combining branching and filtering (Both). We show only results using the best variant for each class—that is, MAC for labelled graphs, and FC for unlabelled graphs (the other results are very similar). On labelled graphs, we see many instances which are solved very quickly by branching but not at all by filtering, and vice versa. However, combining both is rarely much worse than just doing one or the other, and is often much better, even if on average it is slightly slower. On unlabelled graphs, the three variants have rather similar performance.

4.3 Ensuring Connectedness in a Clique-Based Approach

It is not possible to determine connectedness from a raw association graph. However, we can take a maximum clique algorithm and mimic the CP branching strategy if we have access to the underlying graphs and can determine the “meaning” of the association graph vertices.

Most modern maximum clique algorithms for dense graphs use some variation of greedy graph colouring as a bound—the underlying observation is that each vertex in a clique must be given a different colour in a colouring, so if we can colour a subset of vertices using k colours then a maximum clique in this subset has at most k vertices. However, the colouring is also used as a branching heuristic: vertices are selected in reverse order from their colour classes in turn, starting with the last colour class created. Because of this coupling of branching and the bound (which is important in practice because it mimics a “smallest domain first” branching heuristic if colour classes are viewed as variables, without requiring a new bound to be calculated for every iteration [29]), if we were to select only a subset of vertices for branching at each stage inside a clique algorithm, we would lose completeness. Thus we must adapt the bound in a non-trivial way to take into account restricted branching.

figure a

In Algorithm 1 we present a novel clique-inspired algorithm which finds a maximum common connected induced subgraph via an association graph. If the additional branching restrictions are removed, the core of the algorithm is the same as the “MCSa1” clique algorithm used in the previous section (and we refer the reader to the previously cited works for implementation details on how to use bitsets and other data structures to implement the colouring stage with very low constant factors). The way we extend this algorithm for connectedness differs considerably from that of Koch [22] and Vismara and Valery [54]: these earlier approaches worked by classifying labels in the association graph based upon whether a common vertex is shared, and then constructing cliques with particular edge properties—this is harder to integrate with a strong bound function.

Our algorithm begins by building the association graph (line 4). The main part of the algorithm then works by building up candidate cliques in the \( solution \) variable, by recursive calls to the \( search \) procedure—starting from the empty set (line 5), each recursive subcall adds one vertex to \( solution \) (line 14) in such a way that \( solution \) is always a clique which corresponds to a connected common subgraph. The \( remaining \) set contains the set of vertices which are adjacent to every vertex in \( solution \), and which have not yet been accepted or rejected (and so initially it contains every vertex). The main loops in the \({\mathtt {search}}\) procedure (lines 10 and 11) have the effect of iterating over each vertex in this set in a particular order—each vertex v is selected in turn, and then a recursive call is made to consider the effects of including v in \( solution \) (line 18), followed by the next iteration where v is instead rejected. When v is accepted, we add it to the new \( solution' \) (line 14), and create a new \( remaining' \) containing only the vertices in \( remaining \) which are adjacent to v (line 17).

The \( connected \) set contains the set of matching nodes which correspond to vertices adjacent to an already-accepted vertex in the first input graph—in constraint programming terms, it is the set of assignments which could be made next which maintain connectedness. (Using only one of the two input graphs is sufficient for correctness, and has the advantage that the connectedness set may be determined by a simple lookup into a precomputed array which maps each vertex in the first input graph to a bitset.) At the top of search, this set is empty, and is not used (our first vertex selection is special, and does not care about connectedness). At subsequent depths, we may only accept vertices which are in this set, and if no such vertices remain then we return immediately (line 13). When recursing, we extend \( connected \) with the new vertices permitted by our acceptance of the branching v (line 16). Note that we are assuming that inside the main loops, we encounter every vertex in \( remaining \cap connected \) before any vertex in \( remaining \setminus connected \).

As we proceed, we keep track of the best solution we have found so far—this is stored in the \( incumbent \) variable (lines 3 and 15). We use the incumbent, together with a colour bound, to prune portions of the search space which cannot contain a better solution. The colour bound operates as follows: at each entry to the \({\mathtt {search}}\) procedure, we produce a greedy colouring of the vertices in \( remaining \) (line 9, discussed further below). This greedy colouring gives us a list of colour classes, each of which is a list of pairwise non-adjacent vertices. The two loops (lines 10 and 11) then iterate over each colour class, from last to first, and then over each vertex in that colour class, again from last to first. (Rather than actually using a list of lists and removing items, this process should be implemented using a pair of immutable flat arrays. This technique is described elsewhere [29], so we do not discuss it here.) Finally, if at any point the number of remaining colour classes plus the number of vertices currently present in \( solution \) is not strictly greater than the size of the incumbent, then we may backtrack immediately (line 12).

Fig. 6.
figure 6

Solving a maximum common connected problem using an association graph. Suppose we have already mapped vertex a to vertex 1, giving the assignments on the right. Now we have two subgraphs to colour. We need two colours for \( remaining \setminus connected \), and we place these two colour classes first in the \( colourClasses \) variable. We can also colour \( remaining \cap connected \) using two colours, since we cannot simultaneously map c to 2 and d to 3, or vice-versa. Thus \( colourClasses \) becomes a list of four colour classes. This tells us that if we hope to extend the current common subgraph by another four vertices, we must pick one assignment from each of the four colour classes (which is not actually possible, so the bound here gives an overestimate). The algorithm thus guesses \(d \mapsto 3\) as its next assignment, and if that fails, \(d \mapsto 2\), and so on; once \(b \mapsto 3\) is reached, the bound decreases by one, and if \(f \mapsto 5\) were reached we would stop due to a lack of remaining connected association nodes.

Full size image

Finally, we describe the colouring process—an example is shown in Fig. 6. In conventional clique algorithms, a simple greedy sequential colouring is used (possibly with the help of previous colourings to reduce the computational cost [35], and possibly with shortcuts taken for certain vertices [48], and possibly followed by a repair step to improve the colouring [53], or stronger bounding rules based upon MaxSAT inference [25, 26, 46]). Such colourings will not give us the required property that vertices in \( remaining \cap connected \) come last (so they are selected first by the reverse branching order). Thus we produce two greedy sequential colourings, first considering the non-branching vertices in \( remaining \setminus connected \), followed by the branching vertices, and concatenate them (line 9). This produces a valid colouring, since we do not merge any colour classes between the two stages, although it may use more colours than a single colouring would.

Fig. 7.
figure 7

The cumulative number of connected instances solved in under a certain time: on the top, 33 % labelled undirected graphs with up to 100 vertices, and then unlabelled and undirected graphs with up to 35 vertices. On the bottom, an instance-by-instance comparison of the association and CP Both approaches, with 33 % labelled graphs on the left, and unlabelled and undirected graphs on the right.

Full size image

(What if we did not guarantee that vertices in \( remaining \cap connected \) came last, and just used a conventional colouring with the branching rule? Suppose we had four vertices in \( remaining \), and produced a colouring \([[v_1, v_2], [v_3], [v_4]]\), and suppose that extending \( solution \) with \(\{ v_1, v_3, v_4 \}\) gives an optimal solution. If \(v_4\) was not \( connected \) yet, we would not branch on that subtree, and the bound could eliminate branching on \(v_3\) and \(v_1\), so we would miss the solution. Thus we cannot simply add the branching rule without also adapting the combined bound and ordering heuristic.)

Our \({\mathtt {colour}}\) procedure is a simple greedy sequential colouring. We use the bit-parallel algorithm introduced by San Segundo et al. [47], with the \(k_{ min }\) parameter set to 0, so we do not describe it here. We use a simple static degree ordering; other initial vertex orderings have been considered on general clique problems [38, 43], and it is possible that special properties of the association graph could be exploited in this step (for example, it is always possible to colour the initial association graph using \({\text {min}}(\left| {\text {V}}(G_1)\right| , \left| {\text {V}}(G_2)\right| )\) colours, but with certain vertex orderings, a greedy sequential colouring will sometimes use many more colours).

4.4 Experimental Comparison of the CP and Clique Approaches

In Fig. 7 we compare the clique-based approach to the connected problem with the two CP Both approaches. The trend is broadly similar to the unconnected problem: for labelled graphs, the clique-based approach is the clear winner, but for unlabelled graphs the clique approach lags somewhat.

The heatmaps show a more detailed picture. As before, in the unlabelled case, the association approach is almost never more than an order of magnitude better, and is often much worse. In the labelled case, however, there are now many instances where the CP approach does much better than the association approach, despite the association approach remaining much better overall.

5 Conclusion

Contradicting earlier claims in the literature, we have seen that a modern clique algorithm can perform competitively for maximum common subgraph problems, particularly when edge labels are involved. However, the best approaches for these problems is still far behind the state-of-the-art for subgraph isomorphism, where we can often scale to unlabelled graphs with thousands of vertices.

To start tackling this gap, we believe there is further scope for tailoring clique algorithms for association graphs, including specialised inference, a bound function which is aware that it is working on an association graph, and better initial vertex orderings. Treating the first branch specially may also be beneficial, since the first branch has an unusually large effect on the search space with association graphs [50].

For CP models, using a branching rule for connectedness, rather than simply as an ordering heuristic, is unconventional and does not cleanly fit into the abstractions used by toolkits. However, we saw that combining conventional filtering and the special branching rule was beneficial.

We looked only at single-threaded versions of these algorithms. Maximum clique algorithms have been extended for thread-parallel search [10, 28, 44], and in particular, work stealing strategies designed to eliminate exceptionally hard instances by forcing diversity at the top of search [30] could be beneficial in eliminating some of the rare cases where the clique algorithm is many orders of magnitude worse than the CP models. On the CP side, the focus for parallelism has been on decomposition [33], rather than fully dynamic work stealing—it would be interesting to compare these approaches.

Finally, we intend to investigate larger and more diverse sets of instances, and other variants of the problem. We have yet to investigate partial or weighted graphs. Nor have we considered strongly connected common subgraphs—this would make the branching approach impossible, and filtering would be much more complicated. From the datasets we selected, there appears to be little scope for per-instance algorithm selection, but other families of input data could lead to a different conclusion.