Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Hybrid systems can be used to model cyber-physical systems with both discrete and continuous components. Determining a low-cost strategy to control a hybrid system to complete an objective while satisfying a set of safety constraints is a common design challenge in cyber-physical systems. Further, the system dynamics are often noisy in practice due to inherent uncertainty in physical plant as well as modeling approximations. This can cause the system to violate any qualitative Boolean constraints under extreme situations which happen with very low probability. For example, an autonomous airborne vehicle might have noisy dynamics due to air drag in strong winds. Hence, only a probabilistic safety guarantee of not colliding with obstacles is possible. Furthermore, the safety constraints themselves could have uncertainty. For example, the obstacle map perceived by an autonomous vehicle could be noisy due to sensor inaccuracies or due to the presence of other mobile agents whose position is only approximately known. Several other applications such as efficient energy management of buildings and robot-assisted surgery share these characteristics due to uncertainties in process dynamics, sensor data and environment state. These uncertainties, in addition to the mixed continuous and discrete nature of multimodal hybrid systems, make the task of determining an optimal control strategy for the system extremely challenging.

In this paper, we address this challenge and present a novel approach to the synthesis of low-cost control for stochastic linear hybrid systems. We focus on hybrid systems with linear dynamics and a fixed time horizon. The synthesized controller is a discrete-time controller. Our approach uses chance constrained programming [37] to find a low-cost control strategy while satisfying probabilistic safety constraints. Directly solving the chance constrained programs using standard single-shot sampling techniques is impractical for hybrid systems due to the large dimension of the optimization problem. Further, sampling based approaches do not provide any guarantees on satisfaction of constraints, and thus, the generated system might violate probabilistic safety requirements. We split the task of synthesizing optimal control for hybrid systems into two steps. The first step uses constant control approximation and sampling over a small parameter space to determine a low-cost mode sequence and the schedule for switching between different modes in the sequence. The second step synthesizes control inputs in each mode to optimally connect the entry and exit states in each mode. The chance constrained program in the second phase is reduced to a probabilistically conservative but efficiently solvable convex program. This theoretical reduction is key to making our approach practical and scalable. The proposed approach provides a balance between efficiency and optimality (demonstrated through case-studies) while guaranteeing the satisfaction of probabilistic safety properties, and we apply it to a set of case studies from temperature control in buildings and motion planning under uncertainty for autonomous vehicles.

2 Related Work

Automated synthesis of controllers for continuous and hybrid dynamical systems has been widely studied [4, 14, 44]. Synthesis of continuous controllers and discrete switching logic controllers for noise-free hybrid systems [5, 17, 19, 27, 38] is also an active area of research. The control of stochastic systems has been extensively investigated beginning with the work of Pontryagin [33] and Bellman [7]. Its applications include optimal guidance for spacecrafts [3] and flight-simulators [6]. Probabilistic reachability of discrete-time stochastic hybrid systems has also been studied [10, 24, 34, 36]. The focus has been on the safety problem where the goal is to determine a control policy that maximizes the probability of remaining within a safe set during a finite time horizon [2]. This safe control problem is reformulated as a stochastic optimal control problem with multiplicative cost for a controlled Markov chain. Dynamic programming is then used to solve this problem. The solution to value iteration equations obtained using the dynamic programming approach cannot be written out explicitly. In practice, the safety problem is solved using approximation methods. Under appropriate continuity assumptions on the transition probabilities that characterize the stochastic hybrid systems dynamics, [1] proposes a numerical solution obtained by standard gridding scheme that asymptotically converges as the gridding scale approaches zero. The computation burden associated with this approach makes it less scalable and not applicable to realistic situations. This problem is partially alleviated in [22] where neural approximation of the value function is used to mitigate the curse of dimensionality in approximate value iteration algorithm. The goal of these techniques is not optimization of a cost function against probabilistic constraints but instead, the maximization of the probability of staying within a safety condition described by deterministic constraints.

An approximate linear programming solution to the probabilistic invariance problem for stochastic hybrid systems is proposed in [29]. In [12], the authors approximate the constraints in a feedback linearized model of an aircraft so as to make them convex, thereby enabling on-line usage of model predictive control. While we also extract a convex problem, it is based not on approximation of constraints but rather on a practical assumption on the probability bound in safety constraints. In [35], the authors propose a randomized approach to stochastic MPC, for linear systems subject to probabilistic constraints that have to be satisfied for all the disturbance realizations except with probability smaller than a given threshold. At each time step, they solve the finite-horizon chance-constrained optimization problem by first sampling a random finite number of disturbance realizations, and then replacing the probabilistic constraints with hard constraints associated with these extracted realizations only. In this work, we avoid the computationally expensive step of sampling a large number of disturbance realizations or constraints used in these approaches.

The optimization of control for satisfaction of probabilistic constraints can be naturally modeled as chance constrained programs [11, 30]. It has been used in various engineering fields that require reasoning about uncertainty such as chemical engineering [25] and artificial intelligence [41]. A detailed survey of existing literature on chance constrained programming and different approaches to solve this problem is given in [37]. Our work relies on solving the chance constrained finite-horizon control problem for the case of uncertainty modeled as Gaussian distribution and continuous dynamics in different modes of hybrid system restricted to being linear. One of the key challenge to this problem arises from evaluating an integral over a multivariate Gaussian. There is no closed form solution to this problem. A table lookup based method to evaluate this integral is possible for univariate Gaussians but the size of the table grows exponentially with the number of variables. Approximate sampling techniques [8, 25, 26] and conservative bounding methods [9, 39] have been proposed to solve this problem. While the number of samples required in sampling techniques grow exponentially with the number of Gaussian variables, the conservative approach also suffers from increased approximation error with an increase in the number of variables.

A conservative ellipsoidal set bounding approach is used to satisfy chance constraints in [39]. This approach finds a deterministic set such that the state is guaranteed to be in the set with a certain probability. An alternative approach based on Boole’s inequality is proposed in [9, 31]. Bounding approaches tend to be over-conservative such that the true probability of constraint violation is far lower than the specified allowable level. Further, these approaches have been applied only in the context of optimal control of continuous dynamical systems. A two-stage optimization approach is proposed in [32] for continuous dynamical systems. Our work uses a hybrid approach of combining sampling and convex programming to find a low cost control of hybrid systems. The sampling approach allows decomposition of hybrid control problem into a set of continuous control problems by finding the right switching points. The convex programming provides a scalable efficient solution to finding control parameters for the continuous control problem. This ensures that we achieve a good trade-off between optimization and scalability while guaranteeing satisfaction of probabilistic specifications. The use of statistical verification and optimization techniques for synthesis have also been explored in recent literature [43]. Automatic synthesis of controllers from chance-constraint signal temporal logic [18] for dynamical systems have also been proposed in literature.

3 Problem Definition

In this section, we formally define the problem of finding optimal finite time horizon control for discrete-time stochastic hybrid systems where the mode switches are controlled by a schedule. Let us consider a hybrid system consisting of m modes. A finite parametrization of such a system assuming piecewise constant control input sequence yields the following: \(x_{k+1} = A_j x_k + B_j u_k + C_j w_k\), where \( j= j_1 \ldots j_M\) denotes modes from the set \(j_i \in [1,m], x_k \in \mathcal {R}^{n_x}\) is the system state in \(n_x\) dimensions, \(u_k \in \mathcal {R}^{n_u}\) denotes the \(n_u\) control inputs and \(w_k \in \mathcal {R}^{n_w}\) denotes \(n_w\) dimensional Gaussian noise vector \(w_k \sim \mathcal {N}(0, \varSigma _w)\). M is the upper bound on the number of mode switches. Further, the control inputs lie in a convex region \(\mathcal {F}_u\), that is,

$$\begin{aligned} \mathcal {F}_u \triangleq \displaystyle \bigwedge _{i=1}^{N_g} (g_i^T u \le c_i); \;\; \displaystyle \bigwedge _k u_k \in \mathcal {F}_u \end{aligned}$$

where \(\mathcal {F}_u\) is represented as the intersection of \(N_g\) half-planes. The state variables are restricted to be in a convex safe region \(\mathcal {F}_x\) with a specified probability lower-bound. This restriction to safe region being convex can be lifted using standard branch and bound techniques [32].

$$\begin{aligned} \mathcal {F}_x \triangleq \displaystyle \bigwedge _{i=1}^{N_h} (h_i^T x \le b_i); \;\; Pr(\displaystyle \bigwedge _k x_k \in \mathcal {F}_x ) \ge 1 - \alpha _x \end{aligned}$$

where \(h_i^T x \le b_i\) is i-th linear inequality defining the convex region and the constant \(\alpha _x\) determines the probabilistic bound on violating these constraints. The dynamics in each mode of the hybrid systems is described using stochastic differential equations. The time spent in each mode is called the dwell-time of that mode. The sum of the dwell times must be equal to the fixed time horizon \(\tau \). The dwell-times, \(\hat{\tau }= \tau _1 \tau _2 \ldots \tau _M\), can also be restricted to a convex space. The synthesized control needs to be minimized with respect to a convex cost function f(x, u) over the state variables and the control inputs. Since the system is stochastic, the optimization goal is to minimize the expected cost E[f(x, u)].

The corresponding chance constrained optimization problem is as follows:

$$\begin{aligned}&\mathop {\mathbf {min}}_{m_1..m_M, u_1..u_\tau , \tau _1..\tau _M} E_{w,x_0}[ f(x_1..x_\tau ,u_1..u_{\tau -1})]\, \mathbf{{subject\, to}}&\\&(1) \; x_{k+1} = \mathbb {A}_k x_k+ \mathbb {B}_k u_k + \mathbb {C}_k w_k \text{ for } 0\le k< \tau \text{ where } \mathbb {A}_k = A_{m_j}, \mathbb {B}_k = B_{m_j}, \mathbb {C}_k= C_{m_j}&\\&\text {for}\, \sum _{i=1}^{j-1} \tau _i \le k< \sum _{i=1}^{j} \tau _i, 1<j \le M, \text { and } \mathbb {A}_k \!=\! A_{m_1}, \mathbb {B}_k \!=\! B_{m_1}, \mathbb {C}_k = C_{m_1},\! \text { for} \;0 \le k < \tau _1&\\&w \sim \mathcal {N}(0, \varSigma _w), \;\; x_0 \sim \mathcal {N}(x_0^{mean},\varSigma _{x_0}), m_1 \ldots m_j \text { is mode sequence and } \sum _i^M \tau _i = \tau&\\&(2) \; \bigwedge _{i=1}^{N_g} g_i^T u_k \le c_i \text{ and } \displaystyle \bigwedge _{i=1}^{N_l} (l_i^T \hat{\tau }\le d_i) \text { where } g_i^T, c_i, d_i \text { are given constants}.&\\&(3) \; Pr( \bigwedge _{i=1}^{N_h} h_i^T x_k \le b_i ) \ge 1 - \alpha _x \text { for all } 0 \le k \le \tau \text { where } h_i, b_i \text { are given constants}.&\end{aligned}$$

The minimization is done with respect to following parameters:

  • the sequence of modes \(m_1 \ldots m_M \),

  • the control parameters \(u_1 \ldots u_\tau \),

  • the vector of dwell-times in each mode \(\hat{\tau }= \langle \tau _1 \ldots \tau _M \rangle \).

The following observations highlight the challenges in solving the stochastic optimization problem described above.

  • Firstly, the overall system dynamics is nonlinear due to the discrete switching between different linear systems.

  • Second, the probabilistic safety constraint is not convex even when the distribution is assumed to be Gaussian. Standard sampling approach [20, 37] to solving such stochastic optimization problem requires sampling in \(O(n_x \tau m)\) dimensions to compute the multidimensional integral needed to evaluate \(Pr(\wedge _k x_k \in \mathcal {F}_x)\) even for a fixed mode sequence.

Thus, solving such a non-convex stochastic optimization problem with a large set of optimization parameters is not tractable. We address these challenges using mode-sequence discovery technique previously proposed in literature [15, 19] and a novel two-level optimization approach presented in Sect. 4. Sample average approximation is used for coarse-level exploration to determine the dwell-times of each mode. The problem of synthesizing optimal control in each mode is reduced to a convex program, which in turn can be solved efficiently.

Illustrative Example Application. We consider temperature control in two interconnected zones where the control objective is to maintain zone temperatures within a comfort range and minimize a quadratic cost function of the control inputs. Let \(C_k\) be the aggregate thermal capacitance of the k-th zone, \(R_1^a\) and \(R_2^a\) represent the thermal resistance of zone walls isolating zone air from outside, \(T_{oa}\) be the outside ambient temperature, R be the thermal resistance of the walls separating both zones, \(T_1\) and \(T_2\) be the perceived air temperature of the two zones, and \(P_1\) and \(P_2\) represent the disturbance load of the two zones induced by solar radiation, occupancy, electrical devices etc. The inputs \(u_1^h\) and \(u_2^h\) represent the two heating agents in both zones. The model of system dynamics is given by the following equations:

$$\begin{aligned} C_1 \dot{T_1} = u_1^h + \frac{T_{oa} -T_1}{R_1^a} + \frac{T_2 -T_1}{R} + P_1\\ C_2 \dot{T_2} = u_2^h + \frac{T_{oa} -T_2}{R_2^a} + \frac{T_1 -T_2}{R} + P_2 \end{aligned}$$

The system operates in four modes: \(M_1, M_2, M_3, M_4\). \(M_1\) is the mode when the zones are occupied and the heater is off, \(M_2\) is the mode when the zones are occupied and the heater is on, \(M_3\) is the mode when the zones are unoccupied and the heater is on, and \(M_4\) is the mode when the zones are unoccupied and the heater is off. We couple the heaters together to reduce the number of modes. The parameters \(P_1\) and \(P_2\) are assumed to be identical and their values are: \(P_{\{1,2\}} = P_{const} + P_{occ}\, {\texttt { in }}\, M_1, M_2\) and \(P_{\{1,2\}} = P_{const}\, {\texttt { in }}\, M_3, M_4\). The control inputs \(u_h^1\) and \(u_h^2\) are non-negative and lie in the \([0.5,8\,kW]\) range in modes \(M_2\) and \(M_3\), defined by the physical constraints when the heaters are on. The control inputs are 0 in modes \(M_1\) and \(M_4\) when the heaters are off. The parameter values are based on data gathered from Doe library building in UC Berkeley [40]. The outside temperature \(T_{oa}\) is set using the weather information at UC Berkeley and the uncertainty in prediction is Gaussian distributed with one standard deviation of \(\sigma _{T_{oa}} = 0.71 \;^{\circ } C\). The variable occupancy load \(P_{occ}\) is a Gaussian distribution with mean \(10\,kW\) and standard deviation \(0.63\,kW\). Thus, the uncertainty in this example is due to the deviation of outside temperature from the weather prediction, and the variation in occupancy load. The goal of the controller is to maintain the perceived zone temperature T between 18 and 28 degrees Celsius when the zones are unoccupied and between 21 and 25 degrees Celsius when the zones are occupied. The zones are occupied from 7 AM to 5 PM every day, and the zones are unoccupied for the remaining 14 h. The corresponding optimization problem is as follows for the mode sequence \(M_1, M_2, M_3, M_4\):

$$\begin{aligned}&\mathop {\mathbf {min}}_{u,\tau _1,\tau _2,\tau _3,\tau _4} \displaystyle \mathrm {E_{P}} [\sum _{k=0}^{\tau -1} {u_k^Tu_k}] \;\;\;\;~ \text {subject to}&\\&\text {the state } x_k = (T_1,T_2) \text { at }k\text {-th step} \text { is restricted by the dynamics equations presented}&\\&\text {earlier}, x_0 = [ 22,22], \tau _1 + \tau _2 = 10, \tau _3 + \tau _4 = 14, Pr(\displaystyle x_k \in \mathcal {F}^x) \ge 1-\alpha _x, u_k \in \mathcal {F}^u&\\&u = [u_1^h; u_2^h], w = [P_1;P_2; T_{oa}], \mathcal {F}^x = [18,28]^2 \textit{ in } M_1, M_2 \textit{ and } \mathcal {F}^x = [21,25]^2 \textit{ in}\, M_3, M_4,&\\&\mathcal {F}^u = [0.5,8]^2 \textit{in } M_2,M_3 \text { and } [0,0]^2 \textit{ in } M_1, M_4 \text { modes }&\end{aligned}$$

Param

Value

Param

Value

Param

Value

Param

Value

\(C_1\)

\(1.1e4 \; J/^{\circ }C\)

\(C_2\)

\(1.3e4 \; J/^{\circ }C\)

\(R_1\)

\(41.67 \; ^{\circ } C/W\)

\(R_2\)

\(35.71 \; ^{\circ } C/W\)

R

\(35.00 \; ^{\circ } C/W\)

\(\varDelta \)t

\(0.5 \; hr\)

\(\tau \)

48

\(\epsilon \)

\(10^{-4}\)

\(\alpha _x\)

0.05

\(\tau \)

48

\(\sigma _{T_{oa}}\)

0.71

\(u_h^1, u_h^2(on)\)

\([0.5, 8] \; kW\)

\(P_{const}\)

\(0.1\,kW\)

\(P_{occ}\)

\(\mathcal {N}(10, .6) \; kW\)

    

4 Synthesis Approach

First, we perform a high level design space exploration of control space by fixing the control input in each mode to be a constant which intuitively represents the average input. The number of optimization parameters reduce from \(O(\tau + M)\) to O(M) and since the number of modes in the switching sequence M is usually much smaller than the time horizon \(\tau \), we can now use sample average approximation techniques coupled with existing greedy techniques for finding mode sequence to solve the optimization problem in the first step. We use the entry and exit states discovered at the end of the first step to formulate decomposed chance-constrained problems for each mode of the system. We prove that these decomposed problems can be conservatively approximated as convex optimization problems, and thus, solved efficiently. Convexity ensures that any local minimum of the decomposed problems is also a global minimum. We now describe each of these two steps in detail.

figure a

4.1 Mode Sequence and Optimal Dwell Times

Mode deletion or insertion from an initial guess of mode sequence has been used in [16, 19, 21] to synthesize the mode sequence for optimal control of hybrid systems. We use a similar approach here. We adopt addition of modes proposed in [16] because it performed better experimentally that other techniques. Theoretical guarantees of this approach with requisite assumptions on the dynamics can be found in [16]. The approach begins with a mode sequence initialization which can be just the initial mode as a single-mode sequence. New modes are greedily added to the sequence if they reduce the cost. This is continued till either we reach the maximum number of modes allowed in the sequence or addition of new modes does not reduce the cost. Let \(\mathtt {fixedModeOpt}({{\varvec{m}}})\) denote the cost obtained for a given fixed mode sequence m, the mode insertion algorithm uses O(Mm) calls to the optimization routine computing \(\mathtt {fixedModeOpt}\) to find the low cost mode sequence as shown below.

In order to compute \(\mathtt {fixedModeOpt}\), we modify the chance constrained program presented in Sect. 3 by fixing the mode sequence and setting the control inputs in each mode to be a constant. The revised cost metric for schedule switched system:

$$\begin{aligned} \mathop {\mathbf {min}}\nolimits _{u^\mu _1..u^\mu _M, \tau _1..\tau _M} E_{w,x_0}[ f(x_1..x_\tau ,u_1..u_{\tau -1})] \end{aligned}$$

where \(\tau _i\) denotes the dwell-time in the i-the mode of the fixed sequence and \(u_i\) denotes the constant control input for that mode. The dimension of the optimization problem has been reduced from \(O(\tau + M)\) to O(M). We can now use sample average approximation to solve this optimization problem. This is a standard technique to solve nonlinear stochastic optimization problems. We only sketch the approach here, and details can be found in textbooks on stochastic optimization [20, 37]. The overall idea in sample average approximation is to use sampling followed by deterministic optimization. The chance constrained formulation presented earlier can be translated to the standard form:

$$\begin{aligned} \mathop {\mathbf {min}}\nolimits _{x \in X} f(x) \text{ subject } \text{ to } Pr\{ G(x,\zeta ) \le 0\} \ge 1 - \alpha \;\;\;\; [CCP] \end{aligned}$$

where \(\zeta \) are the random variables representing noise parameters and dwell time for externally controlled hybrid systems, and only noise parameters for schedule controlled systems, f is the optimization function and x includes all the variables being optimized: the control variables for externally controlled hybrid systems, and the control variables and dwell times for the schedule controlled systems. Monte Carlo sampling can be used to generate N samples \(\zeta ^1, \ldots , \zeta ^N\), and let \(\hat{q}_N(x)\) denote the proportional of samples with \(G(x,\zeta ^j) > 0\) in the sample. The sample average approximation of the chance constrained problem has the following form:

$$\begin{aligned} \mathop {\mathbf {min}}\nolimits _{x \in X} f(x) \text{ subject } \text{ to } \hat{q}_N(x) \le \epsilon \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[SAA] \end{aligned}$$

The above problem is a deterministic optimization problem which can be solved using nonlinear optimization routines in packages such as CPLEX and Gurobi. The following theorem from [23] relates the solution of this deterministic problem to the original stochastic version.

Theorem 1

[23]. The solution to sample average approximation of the chance constrained problem in Equation SAA approaches the solution of the original problem in Equation CCP with probability 1 as the number of samples (N) approaches infinity, provided the set X is compact, the cost function f is continuous and \(G(x,\cdot )\) is measurable.

Thus, sufficiently sampling the initial states and the noise parameters yields approximately optimal control parameters u and dwell times in each mode \(\tau _i\). We now describe how the synthesized control parameters and dwell times can be used to obtain the entry and exit states for each mode of the stochastic hybrid system. Since the dynamics is linear, repeated multiplication of the system matrices (described in [39]) can be used to lift the system dynamics to the following form: \(x_{k} = \mathbb A_k x_0 + \mathbb B_k \mathbb U_k + \mathbb C_k \mathbb W_k\) where \(U_k = [u_0 u_1 \ldots u_{k-1}]^T\) is obtained using the sample average approximation technique described above, \(W_k = [w_0 w_1 \ldots w_{k-1}]^T\) is the vector of Gaussian noise, and the initial state \(x_0\) is a Gaussian distribution. Hence, \(x_k\) is Gaussian with mean and variance given by: \(x^{\mu }_k = \mathbb {A}_k x^{\mu }_0 + \mathbb {B}_k \mathbb {U}_k + \mathbb {C}_k \mathbb {W}_k^{\mu }, \varSigma _{x_k} = \mathbb A_k \varSigma _{x_0} \mathbb A_k^T + \mathbb C_k \varSigma _{W_k} \mathbb C_k^T\).

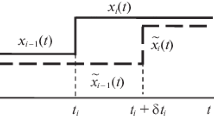
The cumulative time \(\mathcal {T}_i\) is the sum of time spent in modes upto i-th mode in the fixed mode sequence, that is, \(\mathcal {T}_i = \sum _{j=1}^i \tau _j\) for \(j \ge 1\) and \(\mathcal {T}_0 = 0\). The entry-state \(\mathtt {in}_i\) and exit-states \(\mathtt {out}_i\) for each mode i with dwell time \(\tau _i\), are: \(\mathtt {in}_i = x_{\mathcal {T}_{i-1}} \text { and } \mathtt {out}_i = x_{\mathcal {T}_{i}} \). Thus, the entry-state \(\mathtt {in}_i\) and exit-state \(\mathtt {out}_i\) are also Gaussian distributions. We denote their respective means as \(\mathtt {in}_i^\mu , \mathtt {out}_i^\mu \), and the variances as \(\varSigma _{\mathtt {in}_i}, \varSigma _{\mathtt {out}_i}\).

4.2 Mode Tuning and Optimal Control Inputs

Given the entry and exit state distributions \(\mathtt {in}_i\) and \(\mathtt {out}_i\), and the dwell time \(\tau _i\) for each mode i, the goal of second step is to find control inputs u such that the trajectory in mode i starts from \(\mathtt {in}_i\) and exits at \(\mathtt {out}_i\) with minimum cost and satisfies the probabilistic safety constraint. We define a new distance between two states \(d(x_i,x_j) = (x_i^\mu - x_j^\mu )(x_i^\mu - x_j^\mu )^T + (\varSigma _{x_i} - \varSigma _{x_j})(\varSigma _{x_i} - \varSigma _{x_j})^T\). We revise the original cost metric f by adding the distance of the state reached at the end of trajectory from the specified exit state to the cost. The revised cost metric is \(f+Md\) where the constant M is set high enough to force the end state of the trajectory to be the exit state. Both f and d are convex functions over the same domain, and hence the revised cost is also convex. We can now formulate the chance constrained problem for the second step of mode tuning. For each mode, mode tuning is done separately. The chance constrained program for a mode i is as follows:

$$\begin{aligned}&\mathop {\mathbf {min}}_{u_{\mathcal {T}_{i-1}}\ldots u_{\mathcal {T}_i-1}} E_{w,x_0}[ f(x_{\mathcal {T}_{i-1}}\ldots x_{\mathcal {T}_{i}},u_{\mathcal {T}_{i-1}} \ldots u_{\mathcal {T}_{i}-1}) + M d(x_{\mathcal {T}_{i}}, \mathtt {out}_i)]\, \mathbf{{subject\, to}}&\\&1. \; x_{k+1} = \mathbb {A}_k x_k+ \mathbb {B}_k u_k + \mathbb {C}_k w_k \; 2. \; \displaystyle \bigwedge _{i=1}^{N_g} g_i^T u_k \le c_i&\\&3. \; Pr( \displaystyle \bigwedge _{i=1}^{N_h} h_i^T x_k \le b_i ) \ge 1 - \alpha _x \text { for all } \mathcal {T}_{i-1} \le k < \mathcal {T}_{i}&\end{aligned}$$

Next, we show that the above chance constrained problem can be solved using convex programming by a conservative approximation of the probabilistic constraints as long as the violation probability bound \(\alpha _x < 0.5\), that is, the probabilistic constraint is required to be satisfied with a probability more than 0.5. This assumption is very reasonable in many applications where the system is expected to be mostly safe. In practice, the violation probability bounds \(\alpha _x\) are often close to zero.

The key challenge in solving the above chance constraint program is due to constraint (3). The probabilistic safety constraint is not convex. But we show how to approximate it as a convex constraint. Firstly, let \(y_{ik}\) denote the projection of \(x_k\) on the i-th constraint, that is, \(y_{ik} = h_i^T x_k\). A, B, C are fixed matrices for dynamics in a given mode. Since \(x_k\) is Gaussian distribution, \(y_{ik}\) is also a Gaussian distribution with the following mean and variance:

$$\begin{aligned}&y^{\mu }_{ik} = h_i^T \mathbb {A}_k x^{\mu }_0 + h_i^T\mathbb {B}_k \mathbb {U}_k + h_i^T \mathbb {C}_k \mathbb {W}_k^{\mu } = h_i^T\sum _{i=0}^{t-1}A^{t-i-1}B u_i + h_i^T A^t x_0^\mu \nonumber \\&\varSigma _{y_{ik}} = h_i^T \mathbb A_k \varSigma _{x_0} \mathbb A_k^T h_i + h_i^T \mathbb C_k \varSigma _{W_k} \mathbb C_k^T h^i = h_i^T (\sum _{i=0}^{k-1} A^i \varSigma _{x_0} (A^T)^i + A^k \varSigma _{w_k}(A^T)^k) h_i \nonumber \end{aligned}$$

Thus, the probabilistic constraint can be rewritten as:

$$\begin{aligned}&3'. \; Pr( \displaystyle \bigwedge _{i=1}^{N_h} y_{ik} \le b_i ) \ge 1 - \alpha _x \text { for all } \mathcal {T}_{i-1} \le k < \mathcal {T}_{i}&\end{aligned}$$

We can use Boole’s inequality [31] to conservatively bound the above probabilistic constraint. The probability of union of events is at most the sum of the probability of each event, that is, \(Pr( \displaystyle \bigvee _{i=1}^{N_h} y_{ik}> b_i ) \le \sum _{i=1}^{N_h} Pr( y_{ik} > b_i )\). Thus,

$$\begin{aligned}&3''. \; Pr( \displaystyle \bigwedge _{i=1}^{N_h} y_{ik} \le b_i ) \!=\! 1 - Pr( \displaystyle \bigvee _{i=1}^{N_h} y_{ik}> b_i ) \ge 1 - \sum _{i=1}^{N_h} Pr( y_{ik} > b_i ) = 1 -\! \sum _{i=1}^{N_h} ( 1- Pr( y_{ik} \le b_i ))&\end{aligned}$$

The above constraint can be now decomposed into univariate probabilistic constraints.

$$\begin{aligned}&3.1 \; Pr( y_{ik} \le b_i ) \ge 1 - \alpha _x^{ik} \text { for all } \mathcal {T}_{i-1} \le k< \mathcal {T}_{i} , 1 \le i \le N_h&\\&3.2 \; \sum _{i=1}^{N_h} \alpha _x^{ik} \le \alpha _x \text { for all } \mathcal {T}_{i-1} \le k < \mathcal {T}_{i}&\end{aligned}$$

We can show that the univariate probabilistic constraints over Gaussian variables in 3.1 is a linear constraint if the violation probability bound is smaller than 0.5.

Lemma 1

\( Pr (y_{ik} \le b_i)\le 1- \alpha _x^{ik} \) for a Gaussian variable \(y_{ik}\) and \(\alpha _x^{ik} < 0.5\) is a linear constraint.

Proof

\(y_{ik}\) is a Gaussian random variable. So,

$$ Pr (y_{ik} \le b_i)\le 1- \alpha _x^{ik} \text { iff } y_{ik}^\mu \ge \sqrt{2\varSigma _{y_{ik}}} \mathtt {erf}^{-1}(1-2\alpha _x^{ik})$$

when \(\alpha _x^{ik} < 0.5\). \(\mathtt {erf}^{-1}\) is the inverse of error function \(\mathtt {erf}\) for Gaussian distribution: \(\mathtt {erf}(x) = 2/\sqrt{\pi } \int _0^x e^{-t^2} dt.\) From Eq. 2, \(\varSigma _{y_{ik}}\) does not depend on \(u_k\). So, the right-hand side of the inequality can be computed using Maclaurin series or a look-up table beforehand. Let this value be some constant \(\delta _{ik}\). From Eq. 1, the left-hand side \(y_{ik}^\mu \) is linear in the control inputs \(u_i\). So, the probabilistic constraint is equivalent to the following linear constraint: \( h_i^T\sum _{i=0}^{t-1}A^{t-i-1}B u_i + h_i^T A^t x_0^\mu \ge \delta _{ik}\)    \(\square \)

Theorem 2

If \(\alpha _x < 0.5\), then the conservative chance-constrained formulation above can be solved as a deterministic convex program.

Proof

\(\displaystyle \sum _{i=1}^{N_h} \alpha _x^{ik} \le \alpha _x\) and \(\alpha _x^{ik}\) are probability bounds and hence, must be non-negative. Consequently, \(\alpha _x^{ik} < 0.5\) for all i, k if \(\alpha _x < 0.5\). Consequently, all constraints in (3.1) are linear constraints using Lemma 1. We can conservatively choose \(\alpha _x^{ik} = \alpha _x/N_k\) and the overall optimization problem becomes a convex optimization problem which can be optimally solved using deterministic optimization techniques.    \(\square \)

In practice correctness constraints are modelled as likely probabilistic constraints with probability at least 0.5, and hence \(\alpha _{i,j} < 0.5\).

Thus, solving a convex program yields the control inputs for each mode of the hybrid system such that the cost is minimized and the system dynamics starts from the entry state and ends in the exit state found in the first step of our approach. Although our approach uses convex programming in the second step, we can not make guarantees of global optimality for the overall control synthesized by our approach. Nonetheless, the proposed method in this section presents a more systematic alternative to existing sampling based approaches for solving a very challenging problem of designing optimal control for stochastic hybrid systems as illustrated in Sect. 5.

5 Case Studies

In this section, we present results on two other case-studies in addition to the example application presented in Sect. 3. We use quadratic costs in the case-studies and so, we can compare results obtained using the proposed method with the results obtained by using probabilistic particle control [8] for mode selection followed by linear quadratic Gaussian (LQG) control [42] to generate the control inputs for each mode. But in general, the proposed approach (CVX) can be used with any convex cost function while LQG control based approach (LQG) are applicable only when the cost is quadratic. We consider three metrics for comparison: the satisfaction of probabilistic constraints, the cost of synthesized controller and the runtime of synthesis.

5.1 Two Zone Temperature Control

In Fig. 1, we compare the quality of control obtained using our approach and that obtained directly from sampling. The comparison is done using 100 different simulation runs of the system. The proposed approach (CVX) took 476 s to solve this problem while the LQG took 927 s. The controller synthesized by CVX satisfies the probabilistic constraint with a probability of 98.9 % which is greater than required 95 %. On the other hand, the controller synthesize using LQG satisfied the probabilistic constraint with a probability of 92 %. Further, we observe that the proposed approach is able to exploit switching between the heater being on and off when the zones are occupied to produce a more efficient controller with 0.92 times the cost of controlled obtained using sample average approximation.

Fig. 1.
figure 1

System behavior: Temperature vs Time

Full size image

5.2 HVAC Control

The HVAC system is used to maintain air quality and temperature in a building. It consists of air handling units (AHUs) and variable air volume (VAV) boxes (see [28] for details). The temperature dynamics for a single zone is:

$$\begin{aligned} T_{k+1} = \sum _{q=0}^{q=2} (p_{1,q} T^{oa}_{k-q} + p_{2,q} R_{k-q}) + p_3 (T^s_k -T_k) \dot{m}_k + \sum _{q=0}^{q=2}(p_{4,q} T_{k-q} ) + p_6 + p_{occ} \end{aligned}$$

where \(T_k\) is the temperature of the zone at time k, \(\dot{m}_k\) is the supply air mass flow rate, \(T^s_k\) is the supply air temperature, \(R_k\) denotes the solar radiation intensity and \(p_{occ}\) denotes the noise due to occupancy. All parameters were taken from the model in [28]. The system dynamics can be linearized by introducing deterministic virtual inputs \(u^s_k = \dot{m}_k T^s_k\) and \(u^z_k = \dot{m}_k T_k\). The goal is to minimize power consumed by the HVAC system while ensuring temperature stays within comfortable range. The probabilistic safety property modeling the comfort constraints is the same as Sect. 3. We scale the example from just a single zone to five zones. CVX consistently outperforms LQG in terms of cost and runtime. It is probabilistically more conservative. We compare the runtime, controller cost and probability of violation obtained through 100 simulations in Fig. 3 (Fig. 2).

Fig. 2.
figure 2

Schematics of HVAC showing AHU and VAV

Full size image
Fig. 3.
figure 3

Comparison between proposed approach (CVX) and LQG for 1–5 zones

Full size image

5.3 Motion Planning

We consider motion planning for an autonomous underwater vehicle moving described in [13] with two modes: move and turn. The heading in the mode move is constant while the propeller maintains a constant speed in the mode turn. In practice, the heading and speed control are not perfect and we model the uncertainty using Gaussian distribution. The system dynamics in the two modes: move and turn, are: \(\epsilon _{1,2} = \mathcal N(0.5,0.01),\epsilon _3 = \mathcal N(0.02,0.002), 0 \le v \le 10 \text { in the mode } move; \; p_k \text { is the control input. } \epsilon _{1,2} = \mathcal N(0.2,0.01),\epsilon _3 = \mathcal N(0.01,0.002)\) \( 0 \le \omega \le 0.5 \text { in the mode } turn; \; q_k\) is the control input.

$$\begin{aligned}&\begin{pmatrix} x_{k+1} \\ y_{k+1} \\ \alpha _{k+1} \end{pmatrix} \!=\! \begin{pmatrix} x_{k} \\ y_{k} \\ \alpha _k \end{pmatrix} + \begin{pmatrix} p_k\cos \alpha _k \\ p_k\sin \alpha _k \\ 0 \end{pmatrix} + \begin{pmatrix} \epsilon _1 \cos \alpha _k \\ \epsilon _2 \sin \alpha _k \\ \epsilon _3 \end{pmatrix} , \; \begin{pmatrix} x_{k+1} \\ y_{k+1} \\ \alpha _{k+1} \end{pmatrix} \!=\! \begin{pmatrix} x_{k} \\ y_{k} \\ \alpha _k \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ q_k \end{pmatrix} + \begin{pmatrix} \epsilon _1 \\ \epsilon _2 \\ \epsilon _3 \end{pmatrix}&\end{aligned}$$

We consider two different obstacle maps shown in Fig. 4. We require that the system state is out of obstacle zone with a probability of 95 %. The trajectory synthesized by our approach is shown in blue and the one synthesized by sample average approximation is shown in red. We simulate the system 200 times to test the robustness of paths. For the first obstacle map, the trajectories synthesized by both approaches are close to each other. LQG is able to synthesize this trajectory in 38 s compared to 98 s taken by our approach. For the second obstacle map, our approach takes 115 s but LQG computes a probabilistically unsafe trajectory even after 182 s.

Fig. 4.
figure 4

Motion planning

Full size image

6 Conclusion

In this paper, we proposed a two-step approach to synthesize low-cost control for stochastic hybrid system such that it satisfies probabilistic safety properties. The first step uses sample average approximation to find switching sequence of modes and the dwell-times. The second step is used to tune the control inputs in each mode using convex programming. The experimental evaluation illustrates the effectiveness of our approach.