The Approximate Synthesis of Optimal Control for Heterogeneous Discrete Systems with Intermediate Criteria

Abstract

We consider one of the classes of hybrid systems, heterogeneous discrete systems (HDSs). The mathematical model of an HDS is a two-level model, where the lower level represents descriptions of homogeneous discrete processes at separate stages and the upper (discrete) level connects these descriptions into a single process and controls the functioning of the entire system to ensure a minimum of functionality. In addition, each homogeneous subsystem has its own goal. A method of the approximate synthesis of optimal control is constructed on the basis of Krotov-type sufficient optimality conditions obtained for such a model in two forms. A theorem on the convergence of the method with respect to a function is proved, and an illustrative example is given.

1 Introduction

The direct use of the optimal control theory’s theoretical results is associated with insurmountable difficulties regarding the solvability of practical problems in analytical form. Therefore, theoretical results have always been accompanied by the construction and development of various iterative methods. It is nearly impossible to track the many works that represent various scientific schools and areas. Therefore, generalization and analogs of Krotov’s sufficient optimality conditions [1] in two forms will be used substantially in this paper. Some insight into this field is given via an overview [2] and several publications [3,4,5].

The approach that is proposed in [6] is based on an interpretation of the abstract model of multi-step controlled processes [7] as a discrete-continuous system and extended to heterogeneous discrete systems (HDS) [8]. This method has essentially allowed the decomposition of the inhomogeneous system into homogeneous subsystems by constructing a two-level hierarchical model and generalizing optimality conditions and optimization algorithms that were developed for homogeneous systems. This refers to systems with a fixed structure that are studied within the classical theory of optimal control.

Notably, with this approach, all homogeneous subsystems are linked by a common goal and represented by a function in the model. However, each homogeneous subsystem can also have its own goal. Such a generalization of the HDS model was carried out in [11], where sufficient conditions for optimal control in two forms were obtained.

In this paper a method of approximate synthesis of optimal control is constructed, and an illustrative example is considered.

Previously, the authors proposed a more sophisticated improvement method [12] for another class of heterogeneous systems, discrete-continuous systems, that requires searching for a global extremum in control variables at both levels of the hierarchical model. For the class of heterogeneous discrete systems considered in the present paper, the derivation of its analogue is not possible due to the structural features of the discrete models and the construction of sufficient optimality conditions.

2 Heterogeneous Discrete Processes with Intermediate Criteria

Let us consider a two-level model where the lower level consists of discrete dynamic systems of homogeneous structure. A discrete model of general form appears on the top level.

$$\begin{aligned} \begin{array}{l} x(k+1)=f(k,x(k),u(k)), \\ k \in \mathbf{K}=\{k_I, k_I+1,...,k_F\},\quad u\in \mathbf{U}(k,x), \end{array} \end{aligned}$$

(1)

where k is the number of the step, x and u are respectively variables of state and control of arbitrary nature (possibly different) for different k, and $\mathbf{U}(k,x)$ is the set given for each k and x. On some subset $\mathbf{K'}\subset \mathbf{K}$, $k_F\notin \mathbf{K',}$ u(k) is interpreted as a pair $\left( u^v (k), m^d (k)\right)$, where $m^d(k)$ is a process $(x^d(k,t),u^d(k,t))$, $t\in \mathbf{T}(k,z(k))$, $m^d (k)\in \mathbf{D}^d\left( k,z(k)\right)$, and $\mathbf{D}^d$ is the set of admissible processes $m^d$, complying with the system

$$\begin{aligned} \begin{array}{l} x^d(k,t+1)= f^d\left( k,z,t,x^d(k,t),u^d (k,t)\right) , \\ t \in \mathbf{T}=\{t_I(z), t_{I}(z)+1,\dots t_F(z)\}, \end{array} \end{aligned}$$

(2)

$$ x^d\in \mathbf{X}^d(k,z,t), \quad u^d\in \mathbf{U}^d\left( k,z,t,x^d\right) , \quad z=\left( k, x, u^v \right) . $$

For this system an intermediate goal is defined on the set $\mathbf{T}$ in the form of a functional that needs to be minimized:

$$ I^k =\sum \limits _{\mathbf{T}(z)\backslash t_F(z)} f^k(t, x^d(k,t),u^d(k,t))\rightarrow \inf . $$

Here $\mathbf{X}^d(k,z,t),~ \mathbf{U}^d\left( k,z,t,x^d\right)$ are given sets for each t,  z, and $x^d$. The right-hand side operator of the 1 is the following on the set $\mathbf{K'}$:

$$ f\left( k,x, u\right) =\theta \left( z,\gamma ^d(z)\right) ,\quad \gamma ^d=\left( t _I, x^d _I,t_F, x^d _F\right) \in \mathbf{{\Gamma }}^d(k,z), $$

$$ \mathbf{{\Gamma }}^d(z)=\{\gamma ^d:t_I=\tau (k,z), t_F =\vartheta (k,z), $$

$$ x^d _I=\xi (k,z),\quad x^d_F\in \mathbf{{\Gamma }}_F^d(k,z)\}. $$

On the set $\mathbf{D}$ of the processes

$$ m=\left( x(k),u(k), x^d(k,t),u^d(k,t)\right) , $$

satisfying 1, 2, the optimal control problem on minimization of a terminal functional $I=F\left( x\left( k_F\right) \right)$ is considered. Here $k_I=0,~ k_F,~ x\left( k_I\right)$ are fixed and $x(k)\in \mathbf{X}(k)$.

3 Sufficient Optimality Conditions

The following theorems are valid [11]:

Theorem 1

Let there be a sequence of processes $\{m_s\}\subset \mathbf{D}$ and functions $\varphi ,\,~ \varphi ^d$ such that:

• (1) $R\left( k,x_s\left( k\right) ,u_s\left( k\right) \right) \rightarrow \mu \left( k\right) , \; k\in \mathbf{K}$;

• (2) $R^d\left( z_s,t,x^d_s\left( t \right) , u^d_s\left( t\right) \right) - \mu ^d\left( z_s,t \right) \rightarrow 0, \; k\in \mathbf{K'}, \; t\in \mathbf{T}\left( z_s\right)$;

• (3) $G^d\left( z_s,\gamma ^d_s\right) - l^d\left( z_s\right) \rightarrow 0, \;k\in \mathbf{K'}$;

• (4) $G\left( x_s\left( t_F\right) \right) \rightarrow l$.

Then the sequence $\{m_s\}$ is a minimizing sequence for I on the set $\mathbf{D}$.

Theorem 2

For each element $m\in \mathbf{D}$ and any functionals $\varphi ,~ \varphi ^d$ the estimate is

$$I(m)-\inf \limits _\mathbf{D}I\le \varDelta =I(m)-l.$$

Let there be two processes $m^\mathrm{I}\in \mathbf{D}$ and $m^\mathrm{II}\in \mathbf{E}$ and functionals $\varphi$ and $\varphi ^d$ such that $L\left( m^\mathrm{II}\right) < L\left( m^\mathrm{I}\right) = I\left( m^\mathrm{I}\right) ,$ and $m^\mathrm{II}\in \mathbf{D}$.

Then $I(m^\mathrm{II})<I(m^\mathrm{I})$.

Here:

$$ L=G\left( x\left( k_F\right) \right) -\sum \limits _{\mathbf{K}\backslash \mathbf{K'}\backslash k_F} R(k,x(k),u(k)) $$

$$ +\,\sum _{\mathbf{K'}}\Bigl (G^d(z)-\sum \limits _{\mathbf{T}(z)\backslash t_F }R^d(z,t, x^d(k,t),u^d(k,t))\Bigr ), $$

$$ G\left( x\right) =F\left( x( k_F)\right) +\varphi \left( k_F,x\right) -\varphi \left( k_I,x\left( k_I\right) \right) , $$

$$ R\left( k,x,u\right) =\varphi \left( k+1,f\left( k,x,u\right) \right) -\varphi \left( k,x\right) , $$

$$ G^d\left( k,z,\gamma ^d\right) =-\varphi \left( k+1,\theta \left( k,z,\gamma ^d\right) \right) +\varphi \left( k,x\left( k\right) \right) $$

$$ +\, \varphi ^d \left( k,z, t_F, x_F^d \right) - \varphi ^d \left( k,z,t_I, x^d_I \right) , $$

$$ R^d\left( k,z,t, x^d,u^d \right) = \varphi ^d(k, z,t+1, f^d\left( k,z,t,x^d,u^d\right) ) $$

$$ -\, f^k(t, x^d(k,t),u^d(k,t))- \varphi ^d(k, z,t, x^d), $$

$$ \mu ^d\left( k,z,t\right) =\sup ~\{R^d\left( k,z,t, x^d,u^d \right) :x^d \in \mathbf{X}^d (k,z,t), u^d \in \mathbf{U}^d\left( k,z,t,x^d\right) \}, $$

$$ l^d\left( k,z\right) =\inf ~\{G^d\left( k,z,\gamma ^d \right) :\, (\gamma ^d)\in {\mathbf{\Gamma }^d}(k,z), x^d \in \mathbf{X}^d (k,z,t_F)\}, $$

$$ \mu \left( k\right) =\left\{ \begin{array}{ll} \sup \{R\left( k,x,u\right) :x\in \mathbf{X}(k), u\in \mathbf{U}\left( k,x\right) \}, \quad t\in \mathbf{K}\backslash \mathbf{K'}, \\ -\inf \{l^d\left( z\right) :\, x\in \mathbf{X}\left( k\right) , \; u^v\in \mathbf{U}^v \left( k,x\right) \}, \quad k\in \mathbf{K'}, \end{array} \right. $$

$$ l=\inf \{G\left( x\right) :\, x\in \mathbf{\Gamma }\cap \mathbf{X}\left( k_F\right) \}. $$

Here $\varphi \left( k,x\right)$ is an arbitrary functional and $\varphi ^d(k,z,t,x^d)$ is an arbitrary parametric family of functionals with parameters k and z.

We note that L(m) and I(m) coincide for $m\in \mathbf{D}$.

Theorem 1 allows us to reduce the solution of the optimal control problem posed to an extremum study of the constructions R, G and $R^d$, $G^d$ by the arguments for each k and t, respectively. Theorem 2 indicates a way to construct improvement methods. One of the variants of these methods is implemented below.

4 Sufficient Conditions in the Bellman Form

One of the possible ways to set a pair $(\varphi ,~ \tilde{\varphi }^d )$ is to require fulfillment of condition $\inf \limits _{\{m_u\} }L=0$ for any $m_x$. Here $m_u=(u(k),~ u^v(k),~ u^d(k,t))$ is a set of control functions from the sets $\mathbf{U},~~ \mathbf{U}^v,$ and $\mathbf{U}^d$, respectively, $m_x=(x(k),~~ \tilde{x}^d(k,t))$ is a set of state variables of upper and lower levels. Such a requirement leads directly to concrete optimality conditions of the Bellman type that can also be used to construct effective iterations of process improvement. Let $\mathbf{{\Gamma }}^d_F\left( z\right) ={\mathbb R}^{n(k)}$, $\theta \left( z,\gamma ^d\right) = \theta \left( z, x_F^d\right)$. There are no other restrictions on the state variables.

The following recurrent chain is obtained with respect to the Krotov-Bellman functionals $\varphi$ and $\varphi ^d\left( z\right)$ of two levels:

$$ \varphi \left( k,x\right) =\sup \limits _{u\in \mathbf{U}\left( k,x\right) } \varphi \left( k+1,f\left( k,x\left( k\right) ,u\right) \right) , \quad k\in \mathbf{K}\backslash \mathbf{K'}\backslash {k_F}, $$

$$\varphi \left( k_F, x\right) =-F\left( x\right) ,$$

$$\begin{aligned} \varphi ^d(k,t)=\sup \limits _{u^d\in \mathbf{U^d}\left( z,t,x^d\right) }\Big (\varphi ^d \left( k,t+1,f^d\left( k,t,x^d\left( k,t\right) ,u^d\right) \right) \end{aligned}$$

(3)

$$ -\, f^k(t, x^d(k,t),u^d(k,t))\Big ), $$

$$ \varphi ^d\left( z,t_F,x_F^d\right) = \varphi \left( k+1,\theta \left( z,x_F^d \right) \right) , $$

$$ \varphi \left( k,x\right) = \sup \limits _{ u^v \in \mathbf{U}^v\left( t,x\right) }\varphi ^d\left( z, \tau \left( z\right) , \xi \left( z\right) \right) , \quad k\in \mathbf{K'}, $$

which is resolved in the order from $k_F$ to $k_I$. Suppose that a solution to this chain $\left( \varphi \left( k,x\left( k\right) \right) ,~ \varphi ^d\left( z,t,x^d\right) \right)$ exists and, moreover, that there are controls corresponding to this solution $\tilde{u}\left( k,x\right) , \; \tilde{u}^v\left( k,x\right) , \; \tilde{u}^d\left( z,t,x^d\right)$, obtained from the maximum operations in 3. Substituting the found controls in the right parts of the given discrete formulas, we obtain

$$ x\left( k+1\right) =f\left( k,x\left( t\right) ,\tilde{u}\left( k,x\left( t\right) \right) \right) , \quad x\left( k_I\right) =x_I, \quad k\in \mathbf{K}\backslash \mathbf{K'}\backslash {k_F}, $$

$$ x\left( k+1\right) = \theta \left( k,x\left( k\right) ,\tilde{u}^v\left( k,x\left( k\right) \right) , \gamma ^d\left( \tilde{z}\right) \right) , $$

$$ x^d(k,t+1)=f^d\left( k,x\left( k\right) , \tilde{u}^v \left( k,x\left( k\right) \right) ,t,x^d,\tilde{u}^d\left( \tilde{z}(k),t,x^d\right) \right) , $$

$$ t_I=\tau \left( \tilde{z}(k)\right) , \quad x^d\left( t _I\right) =\xi \left( \tilde{z}(k)\right) , \quad \tilde{z}(k)=\left( k,x\left( k\right) , \tilde{u}^v\left( k,x\left( k\right) \right) \right) $$

for $k\in \mathbf{K'}$. The solution of this chain is

$$ \left( x\left( k\right) ,~u\left( k\right) \right) _*, \quad k\in \mathbf{K}\backslash \mathbf{K}', $$

$$ \left( x\left( k\right) ,~ \hat{u}\left( k\right) , ~x^d\left( k,t \right) , ~u^d\left( k,t \right) \right) _*, \quad k\in \mathbf{K'}, \quad t \in \mathbf{T}\left( z_*(k)\right) . $$

If this solution exists, it sets the optimal heterogeneous discrete process $m_*$. We note that the functional $\varphi ^d(z,t,x^d)$ in this case can be considered independent of x, because it “serves” a family of problems for different initial conditions.

The first variant of these conditions is obtained in [8, 11].

5 The Approximate Synthesis of Optimal Control

Suppose that $\mathbf{X}(k)= {\mathbb R}^{m(k)}$, $\mathbf{X}^d(z,t)={\mathbb R}^{n(k)}$, $x^d_I =\xi \left( z\right)$, $k_I$, $x_I$, $k_F$, $t_I(k)$, $t_F(k)$ are given, $x^d_F\in {\mathbb R}^{n(k)}$, and lower-level systems do not depend on control $u^v$.

We will develop the method based on the principles of expansion [9] and localization [10]. The task of improvement is to build an operator $\eta (m),~ \eta : \mathbf{D}\rightarrow \mathbf{D}$, such that $I(\eta (m))\le I(m)$. For some given initial element, such an operator generates improving, specifically a minimizing sequence $\{m_s\}: m_{s+1}=\eta (m_s)$.

According to the localization principle, the task of improving an element $m^\mathrm{I}$ resolves itself into the problem of the minimum of the intermediary functional

$$\begin{aligned} I_\alpha (m) = \alpha I(m) + (1-\alpha )J(m^\mathrm{I}, m), \quad \alpha \in [0,1], \end{aligned}$$

(4)

where $J(m^\mathrm{I}, m)$ is the functional of a metric type. By varying $\alpha$ from 0 to 1, we can achieve the necessary degree of proximity $m_{\alpha }$ to $m^\mathrm{I}$ and effectively use the approximations of the constructions of sufficient conditions in the neighbourhood of $m^\mathrm{I}$. As a result, we obtain an algorithm with the parameter $\alpha$, which is a regulator configurable for a specific application. This parameter is chosen so that the difference $I(m^\mathrm{I})-I(m_{\alpha })$ is the largest; then the corresponding element $m_{\alpha }$ is taken as $m^\mathrm{II}$. We consider the intermediary functional of the form

$$ I_{\alpha }=\alpha I +\left( 1-\alpha \right) \left( \sum \limits _{\mathbf{K}\backslash \mathbf{K'}\backslash k_F}\frac{1}{2}|\varDelta u \left( k\right) |^2 + \sum \limits _{\mathbf{K}'} \sum \limits _{\mathbf{T}(z)\backslash t_F}\frac{1}{2}|\varDelta u^d\left( k,t\right) |^2 \right) , $$

where $\alpha \in [0,1], \varDelta u=u- u^\mathrm{I},~ \varDelta u^d=u^d- u^{d\mathrm I}.$

According to said extension principle for the given element $m^\mathrm{I}\in \mathbf{D}$, we need to find an element $m^\mathrm{II}\in \mathbf{D}$ for which $I_{\alpha } (m^\mathrm{II})= L_{\alpha } \left( m^\mathrm{II}\right) <I_{\alpha } (m^\mathrm{I})= L_{\alpha } \left( m^\mathrm{I}\right) ,$ or $L_{\alpha } \left( m^\mathrm{II}\right) - L_{\alpha } \left( m^\mathrm{I}\right) < 0.$ We consider the increment of the functional $L_{\alpha } (m)$:

$$ \varDelta L_\alpha \approx G^\mathrm{T}_ {x_F} \varDelta x_F +\frac{1}{2}\varDelta x_F ^\mathrm{\mathrm{T}}G^\mathrm{T}_ {x_Fx_F} \varDelta x_F $$

$$ -\sum \limits _{\mathbf{K}\backslash \mathbf{K'}\backslash k_F} \Big (R^\mathrm{T}_x\varDelta x+ R^\mathrm{T}_u\varDelta u+ \frac{1}{2}\varDelta u ^\mathrm{\mathrm{T}}R_{uu}\varDelta u $$

$$ +\,\frac{1}{2}\varDelta x ^\mathrm{\mathrm{T}}R_{xx}\varDelta x +\varDelta u ^\mathrm{\mathrm{T}}R_{ux}\varDelta x \Big ) +\sum \limits _{\mathbf{K'}\backslash k_F}\Big (G^{d\mathrm{T}}_{x^d_F}\varDelta x^d_F +G^{d\mathrm{T}}_x\varDelta x $$

$$ +\,\frac{1}{2}\varDelta x^{d\mathrm{T}}_F G^{d\mathrm T}_ {x^d_Fx^d_F} \varDelta x^d_F +\frac{1}{2}\varDelta x ^\mathrm{T}G^{d\mathrm T}_ {xx} \varDelta x+ \varDelta x^{d\mathrm{T}}_F G^{d\mathrm T}_ {x^d_Fx}\varDelta x \Big ) $$

$$ - \sum \limits _{\mathbf{T}(z)\backslash t_F} \Big (R^{d \mathrm{T}}_{x^d}\varDelta x^d+ R^{d \mathrm{T}}_x\varDelta x+ R^{d\mathrm{T}}_{u^d}\varDelta u^d +\frac{1}{2}\varDelta u^{d\mathrm{T}} R^d_{u^d u^d}\varDelta u^d $$

$$ +\, \frac{1}{2}\varDelta x^{d \mathrm{T}}R^d_{x^dx^d}\varDelta x^d+\varDelta x ^\mathrm{T}R^d_{xx^d}\varDelta x^d +\varDelta x ^\mathrm{T}R^d_{xu^d}\varDelta u^d +\varDelta u ^{d \mathrm{T}}R^d_{u^dx^d}\varDelta x^d \Big ), $$

where $\varDelta u=u- u^\mathrm{I},~ \varDelta x=x- x^\mathrm{I},~ \varDelta u^d=u^d- u^{d\mathrm I},~ \varDelta x^d=x^d- x^{d\mathrm I},~ \varDelta x^d_F=x^d_F- x^{d\mathrm I}_F,$ and $x_F=x(k_F).$ Here the functions $R,~ G,~ R^d,$ and $G^d$ are defined for the functional $I_\alpha$, and their first and second derivatives are calculated at $u=u^\mathrm{I}(k),~ x=x^\mathrm{I}(k),~ x^d=x^{d\mathrm{I}}(k,t),$ and $u^d=u^{d\mathrm{I}} (k,t).$ We suppose that matrices $R_{uu}$ and $R^d_{u^du^d}$ are negative definite (this can always be achieved by choosing a parameter $\alpha$ [10]). We find $\varDelta u, \varDelta u^d$ such that $\sum \limits _{\mathbf{K}\backslash \mathbf{K'}\backslash k_F},$ $\sum \limits _{\mathbf{T}(z)\backslash t_F}$ reach their respective maximum values. It is easy to see that

$$ \varDelta u=-(R_{uu})^{-1}(R_u +R_{ux}\varDelta x(k)), $$

$$\varDelta u^d=-(R^d_{u^du^d})^{-1}(R^d_{u^d}+R^d_{u^dx}\varDelta x (k)+R^d_{u^dx^d}\varDelta x^d(k,t)). $$

We substitute the found formulas for the control increments into the formula for the increment of the functional $\varDelta L_\alpha$. Then we perform the necessary transformations and denote the result by $\varDelta M_\alpha$. We obtain

$$ \varDelta M_\alpha \approx G^\mathrm{T}_x\varDelta x+\frac{1}{2}\varDelta x^\mathrm{T} G_{xx}\varDelta x -\sum \limits _{\mathbf{K}\backslash \mathbf{K'}\backslash k_F} \Big ( (R_x- R_{xu}R_{uu}^{-1}R^\mathrm{T}_u)\varDelta x $$

$$ +\,\frac{1}{2}\varDelta x^\mathrm{T}\left( R_{xx}- R_{xu} R_{uu}^{-1}R^\mathrm{T} _{xu}\right) \varDelta x-\frac{1}{2} R^\mathrm{T}_u R_{uu}^{-1} R_u\Big ) $$

$$ +\sum \limits _{\mathbf{K'}\backslash k_F}\Big (G^{d\mathrm T}_{x^d_F}\varDelta x^d_F+\frac{1}{2}\varDelta x_F^{d\mathrm T} G^d_{x^d_F x^d_F}\varDelta x^d_F + G^{d\mathrm{T}} _x\varDelta x+\frac{1}{2}\varDelta x^\mathrm{T} G^d_{xx}\varDelta x $$

$$ +\,\varDelta x_F^{d\mathrm T} G^d_{x^d_Fx}\varDelta x \Big )- \sum \limits _{\mathbf{T}(z)\backslash t_F} \Big (R^d _{x^d}- R^d_{x^du^d}(R^d_{u^du^d})^{-1} R^{d\mathrm T}_{u^d} \Big )\varDelta x^d $$

$$ +\,\frac{1}{2}\varDelta x^{d\mathrm{T}}\left( R^d_{x^dx^d}- R^d_{x^du^d} (R^d_{u^du^d})^{-1}R_{x^du^d}^{d\mathrm T} \right) \varDelta x^d $$

$$ +\left( R^{d\mathrm{T}}_x- R^d_{xu^d}(R^d_{u^du^d})^{-1} R^d_{u^d}\right) \varDelta x+\frac{1}{2}\varDelta x^\mathrm{T} \left( R^d_{xx}- R^d_{xu^d} (R^d_{u^du^d})^{-1} R^d\mathrm{T}_{xu^d}\right) \varDelta x $$

$$+\, \left( \varDelta x^\mathrm{T} \left( R^d_{xx^d}- R^d_{xu^d} (R^d_{u^du^d})^{-1}R^{d\mathrm{T}}_{x^du^d} \right) \varDelta x^d-\frac{1}{2}R^{d\mathrm{T}}_{u^d} (R^d_{u^du^d})^{-1}R^d_{u^d})\right) . $$

We define the functions $\varphi , \varphi ^d$ as $\varphi =\psi ^\mathrm{T} \left( k\right) x\left( k\right) +\frac{1}{2}\varDelta x^\mathrm{T} \left( k\right) \sigma \left( k\right) \varDelta x\left( k\right) ,$

$$\varphi ^d=\lambda ^\mathrm{T}\left( k,t\right) x(k)+\psi ^{d\mathrm T} \left( k,t\right) x^d\left( k,t\right) +\frac{1}{2}\varDelta x^{d\mathrm{T}} \left( k,t\right) \sigma ^d\left( k,t\right) \varDelta x^d \left( k,t\right) $$

$$ +\,\varDelta x^\mathrm{T}\left( k\right) \varLambda \left( k,t\right) \varDelta x^d\left( k,t\right) +\frac{1}{2}\varDelta x^\mathrm{T}\left( k\right) S\left( k,t\right) \varDelta x\left( k\right) , $$

where $\psi , \psi ^d, \lambda$ are vector functions and $\sigma ,~ \sigma ^d,~ S,~\varLambda$ are matrices, and so that the increment of the functional $\varDelta M_\alpha$ does not depend on $\varDelta x,~ \varDelta x_F,$ $\varDelta x^d,$ $\varDelta x^d_F.$ The last requirement will be achieved if

$$ R_x- R_{xu}R_{uu}^{-1}R^\mathrm{T} _u=0, $$

$$ R_{xx}- R_{xu} R_{uu}^{-1}R^\mathrm{T} _{xu}=0, $$

$$ R^d_x- R^d_{xu^d}\left( R^d_{u^du^d}\right) ^{-1}R^{d\mathrm T}_{u^d} =0, $$

$$ R^d _{x^d}- R^d_{x^du^d}(R^d_{u^du^d})^{-1} R^{d\mathrm T} _{u^d}=0, $$

$$ R^d_{x^dx^d}- R_{x^du^d}(R^d_{u^du^d})^{-1}R_{x^du^d}^\mathrm{T} =0, $$

$$ R^d_{xx}- R_{xu^d}(R^d_{u^du^d})^{-1}R_{xu^d}^\mathrm{T}=0, $$

$$ R^d_{xx^d}- R_{xu^d}(R^d_{u^du^d})^{-1}R_{x^du^d}^\mathrm{T} =0, $$

$$ G_x=0, ~~ G^d_x=0, ~~ G^d_{x^d_F}=0, ~~G_{xx}=0, ~ ~G^d_{x^d_Fx^d_F}=0,~ ~G^d_{x^d_Fx}=0,~~ G^d_{xx}=0. $$

Transformation of these conditions leads to a Cauchy problem for HDS with respect to $\psi ,~\psi ^d,\lambda ,$ $\sigma ,~ \sigma ^d,~ S,$ and $\varLambda$, with initial conditions on the right end:

$$ \psi (k_F)=-\alpha F_x,~~ \sigma (k_F)=-\alpha F_{xx},~ $$

$$ \psi (k)=H_x-\left( f^T_x\sigma \left( k+1\right) f_u+H_{xu}\right) \left( f^T_u\sigma \left( k+1\right) f_u+H_{uu}\right) ^{-1}H_u, $$

$$ \sigma (k)= f^\mathrm{T} _x\sigma \left( k+1\right) f_x+H_{xx} $$

$$-\left( f^\mathrm{T}_x\sigma \left( k+1\right) f_u+ H_{xu}\right) \left( f^\mathrm{T}_u\sigma \left( k+1\right) f_u+H_{uu}\right) ^{-1} $$

$$ \left( f^\mathrm{T}_x\sigma \left( k+1\right) f_u+H_{xu}\right) ^ \mathrm{T}, ~k \in {\mathbf{K}\backslash \mathbf{K'}\backslash k_F}, $$

$$ \psi (k)=H_x+\xi ^\mathrm{T}_x H_{x^d} +\xi ^\mathrm{T}_x\psi ^d(k,t_I)+ \lambda (t_I)- \lambda (t_F), ~k \in \mathbf{K'}, $$

$$ \sigma \left( k\right) =\theta ^\mathrm{T}_x\sigma \left( k+1\right) \theta _x+H_{xx}+\xi ^\mathrm{T}_x\theta _{x^d}(t_I)\sigma (k+1)\theta _x+\theta ^\mathrm{T} _x\sigma (k+1)\theta _{x^d}(t_I)\xi _x $$

$$ +\,\xi ^\mathrm{T}_x\theta ^\mathrm{T}_{x^d}(t_I)\sigma \left( k+1\right) \theta _{x^d}(t_I)\xi _x+\xi ^\mathrm{T} _x\sigma ^d\left( k,t_I\right) \xi _x + S\left( k,t_I \right) $$

$$ +\,\xi _{xx}\psi ^d(t_I) +\xi ^T_x\sigma ^d (k,t_I)\xi _x +\xi ^\mathrm{T}_x\varLambda (t_I), ~k \in \mathbf{K'}, $$

$$ \psi ^d=H^d_{x^d}-\left( f^{d\mathrm T}_{x^d}\sigma ^d\left( k,t+1\right) f^d_{u^d}+H^d_{x^du^d}\right) \left( f^{d\mathrm T}_{u^d}\sigma ^d\left( k,t+1\right) f^d_{u^d}+H^d_{u^du^d}\right) ^{-1}H^d_{u^d}, $$

$$ \psi ^d\left( k,t_F\right) =H_{x^d_F}, $$

$$ \lambda (k,t)= \lambda (k,t+1)+H^d_x-(\varLambda (k,t+1)f^d_{u^d}+f^{d\mathrm T}_x\sigma ^d(k,t+1)f^d_{u^d}+H^d_{xu^d}) $$

$$ \left( f^{d\mathrm T}_{u^d}\sigma \left( k,t+1\right) f^d_{u^d}+H^d_{u^du^d}\right) ^{-1}H^d_{u^d}, ~~\lambda (k,t_F)=0, $$

$$ \sigma ^d(k,t)= f^{d\mathrm T} _{x^d}\sigma ^d\left( k,t+1\right) f^d_{x^d}+H^d_{x^dx^d}-\left( f^{d\mathrm T}_{x^d}\sigma ^d\left( k,t+1\right) f^d_{u^d}+H^d_{x^du^d}\right) $$

$$ \left( f^{d\mathrm T}_{u^d}\sigma \left( k,t+1\right) f^d_{u^d}+H^d_{u^du^d}\right) ^{-1} \left( f^{d\mathrm T}_{x^d}\sigma ^d\left( k,t+1\right) f^d_{u^d}+H^d_{x^du^d}\right) ^ \mathrm{T}, $$

$$ \sigma ^d\left( k,t_F\right) =\theta ^\mathrm{T}_{x^d_F}\sigma \left( k+1\right) \theta _{x^d_F}+H_{x^d_Fx^d_F}, $$

$$ \varLambda \left( k,t\right) = f^{d\mathrm T} _{x}\varLambda \left( k,t+1\right) f^d_{x^d}+H^d_{xx^d}-\left( f^{^d\mathrm T}_{x}\varLambda \left( k,t+1\right) f^d_{u^d}+H^d_{xu^d}\right) $$

$$ \left( f^{d\mathrm T}_{u^d}\sigma ^d\left( k+1\right) f^d_{u^d}+H^d_{u^du^d}\right) ^{-1} \left( f^{d\mathrm T}_{x^d}\sigma ^d\left( k,t+1\right) f^d_{u^d}+H^d_{x^du^d}\right) ^ \mathrm{T}, $$

$$ \varLambda \left( k,t_F\right) = \theta ^\mathrm{T} _x\sigma \left( k+1\right) \theta _{x^d}+ H_{xx^d}, $$

$$ S(k,t)=S(k,t+1)+f^{d\mathrm T}_x\varLambda ^{d\mathrm T}(k,t+1)+ \varLambda (k,t+1)f^d_{x}+H^d_{xx}+ f^{d\mathrm T}_x\sigma ^d(k,t+1)f^d_x $$

$$ -\left( f^{^d\mathrm T}_{x}\varLambda \left( k,t+1\right) f^d_{u^d}+H^d_{xu^d}\right) \left( f^{d\mathrm T}_{u^d}\sigma ^d\left( k+1\right) f^d_{u^d}+H^d_{u^du^d}\right) ^{-1} $$

$$ \left( \left( f^{^d\mathrm T}_{x}\varLambda \left( k,t+1\right) f^d_{u^d}+H^d_{xu^d}\right) \right) ^T,~ S\left( k,t_F \right) =0, $$

where

$$ H=\psi ^\mathrm{T}\left( k+1\right) f(k,x(k),u(k))-\frac{1}{2}\left( 1-\alpha \right) |\varDelta u \left( k\right) |^2, ~k \in {\mathbf{K}\backslash \mathbf{K'}\backslash k_F} $$

and

$$ H=\psi ^\mathrm{T} \left( k+1\right) \theta \left( k,x\left( k\right) ,x^c_I,x^c_F\right) ~k \in \mathbf{K'}, $$

$$ H^d=\psi ^{d\mathrm T}(k,t+1) f^d(k,t,x(k),x^d,u^d)- f^k(t,x^d,u^d)- \frac{1}{2}\left( 1-\alpha \right) |\varDelta u^d \left( k\right) |^2, $$

$x\left( k_I\right) =x_I,$  $x\left( k_F\right) =x_F,$  $x^d\left( k,t_I\right) =x^d_I,$  $x^d\left( k,t_F\right) =x^d_F.$

Wherein

$$ \varDelta u \left( k\right) = -\left( f^\mathrm{T} _u\sigma \left( k+1\right) f_u+H_{uu}\right) ^{-1}\left( H_u +\left( f^\mathrm{T} _x\sigma \left( k+1\right) f_u+H_{xu}\right) ^ \mathrm{T} \varDelta x(k)\right) , $$

$$ \varDelta u^d \left( k,t\right) = -(H^d_{u^du^d})^{-1}\Big ( H^d_{u^d}+(\varLambda ^T f^d_{u^d}+H^d_{xu^d})^\mathrm{T}\varDelta x(k) $$

$$ +\left( \sigma ^df^d_{u^d}+H^d_{x^du^d}\right) ^\mathrm{T}\varDelta x^d(k,t)\Big ). $$

We note that the formulas obtained for the control increments of the upper and lower levels depend on the state increments of the same levels. The method then gives a solution to the problem in the form of approximately optimal linear synthesis.

6 Iterative Procedure

Based on the formulas obtained, we can formulate the following iterative procedure:

• 1. We calculate the initial HDS from left to right for $u=u_s(k),$ $u^d=u^d_s(k,t)$ with the given initial conditions to obtain the corresponding trajectory $(x_s(k),~ x^d_s(k,t))$.

• 2. We resolve the HDS from right to left with respect to $\psi \left( k\right)$, $\psi ^d\left( k,t\right)$, $\lambda (k,t)$, $\sigma (k),~\sigma ^d(k,t),~\varLambda (k,t),$ and S(k, t).

• 3. We find $\varDelta u,~ \varDelta u^d$ and new controls $u=u_s(k)+ \varDelta u,$ $u^d=u^d_s(k,t)+ \varDelta u^d$.

• 4. With the controls found and the initial condition $x(k_I)=x_I$, we calculate the initial HDS from left to right. This defines a new element $m_{s+1}.$

The iteration process ends when $|I_{s+1}- I_{s}| \approx 0$ with a specified accuracy.

Theorem 3

Suppose that the indicated iteration procedure is developed for a given HDS and the functional I is bounded from below. Then it generates an improving sequence of elements $\{m_s\}\in \mathbf{D}$, convergent in terms of the functional, i.e., there is a number $I^*$ such that $I^*\le I(m_s),~ I(m_s)\rightarrow I^*$.

Proof

The proof follows directly from the monotonicity property with respect to the functional of the improvement operator under consideration. Thus, we obtain a monotonic numerical sequence

$$\{I_s\}=\{I(m_s)\}, \quad I_{s+1}\le I_s,$$

bounded from below, which according to the well-known analysis theorem converges to a certain limit: $I_s\rightarrow I_*$.

Remark 1

The equations for the matrices $\sigma , \sigma ^d$ are analogs of the matrix Riccati equations and can therefore have singular points. Points $k^*\in \mathbf{K}$, $t^*\in \mathbf{T}(k)$ are called singular if there are changes in the sign of definiteness of matrices $R_{uu}$, $R_{u^du^d}^d$. In these cases, by analogy with homogeneous discrete processes, singular points can be shifted to the points $k_I,~ t_I(k)$ due to the special choice of the parameter $\alpha ,$ and we can find the control increments by the modified formulas [13]. In the particular case when the discrete process of the lower level does not depend on x and $u^d$, these formulas have the simplest form:

$$ R_{uu}(k_I)\varDelta u(k_I)=0,~~ R^d_{u^du^d}(k,t_I)\varDelta u^d(k,t_I)=0 . $$

The last equalities are systems of linear homogeneous algebraic equations with degenerate matrices $R_{uu}(k_I)$, $R^d_{u^du^d}(k,t_I)$ and therefore always have non-zero solutions.

Remark 2

If $\sigma = 0, ~ \sigma ^d = 0, ~ \varLambda = 0$ in the resulting algorithm, then we obtain the first-order improvement method. In this case, the formulas $\varDelta u, ~ \varDelta u^d$ will still depend on the state increments. Consequently, the resulting solution, as before, is an approximate synthesis of optimal control.

7 Example

We illustrate the work of the method with an example. Let the HDS be given:

$$ x^d (t+1)= -2x^d (t)+( u^d_1 -1)^2, ~ x^d(0)=1, t=0,1,2,3, $$

$$ I^0= \frac{1}{2}(x^d (t))^2+\frac{1}{3}(u^d_1)^3, $$

$$ x^d(t+1)= (t -u^d_2)^2,~ t=4,5,6,~ I^1=\frac{1}{2}(x^d)^2+u^d_2, $$

$$ I=x^d(7) \rightarrow \min . $$

Fig. 1.

Control variables in different iterations

It is easy to see that $K={0,1,2}.$ Since $x^d$ is a linking variable in the two periods under consideration, we can write the process of the upper level in terms of this variable:

$$x(0)=x^d(0,0), ~ x(1)=x^d(0,4),~ x(2)=x^d(1,7), ~x^d(1,4)=x(1).$$

Then $\theta =x^d(0,4),~\xi =x(1),~ I=x(2).$

Since at both stages the process of the lower level does not depend on the state variables of the upper level, then $\lambda (0,t)=\lambda (1,t)=0,~\varLambda (0,t)= \varLambda (1,t)=0,~S(0,t)=S(1,t)=0.$

We obtain

$$ \psi (2)=-\alpha ,~ \sigma (2)=0,~\psi (1)=\psi (2)+\psi ^d(1,4),~ \sigma (1)=2\sigma ^d(1,4) $$

$$ H^d(0,t)=\psi ^d(0,t+1)(-2x^d+ (u^d_1 -1)^2)-\frac{1}{2}(x^d (t))^2-\frac{1}{3}(u^d_1)^3 -\frac{1}{2}(1-\alpha )(\varDelta u^d_1)^2, $$

$$ H^d(1,t)=\psi ^d(1,t+1)(t -u^d_2)^2 -\frac{1}{2}(x^d)^2-u^d_2-\frac{1}{2}(1-\alpha )(\varDelta u^d_2)^2, $$

$$ \psi ^d(0,t)=-2\psi ^d(0,t+1)-x^d-4\sigma ^d(0,t+1)(1-u^d_1)(4(u^d_1 -1)^2)\sigma ^d(0,t+1) $$

$$ +\,2\psi ^d(0,t+1)-2u^d_1-(1-\alpha ))^{-1} (2\psi ^d(0,t+1)( u^d_1 -1)-(u^d_1)^2),~\psi ^d(0,4)=\psi (2), $$

$$ \sigma ^d(0,t)=4\sigma ^d(0,t+1) -1-(4\sigma ^d(0,t+1)(1-u^d_1))^2)(4(u^d_1 -1)^2)\sigma ^d(0,t+1) $$

$$ +\,2\psi ^d(0,t+1)-2u^d_1-(1-\alpha ))^{-1}, $$

$$ \psi ^d(1,t)=-x^d,~ \psi ^d(1,7)=0,~ \sigma ^d(1,t)=-1,~ \sigma ^d(1,7)=0, $$

$$ \varDelta u^d_1=(2\psi ^d(0,t+1)-2u^d_1 -(1-\alpha ))^{-1}(2\psi ^d(0,t+1)( u^d_1-1)-(u^d_1)^2 $$

$$ +\,2\sigma ^d(0,t+1)( u^d_1-1)\varDelta x^d(0,t), $$

$$ \varDelta u^d_2=-(2\psi ^d(1,t+1) -(1-\alpha ))^{-1}(2\psi ^d(1,t+1)(t-u^d_2)+1). $$

Fig. 2.

State variables in different iterations

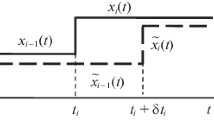
Numerical experiments show that the improvement of the functional does not depend significantly on the choice of the parameter $\alpha$ and occurs in almost one iteration. The result of calculations is shown for $\alpha =0.76$ and $u(t)=1,t=0,..,6$. The functional value is improved from 25 to 0.64 in one iteration. Initial and resulting controls and states are shown in Figs. 1 and 2.

For comparison, calculations using the gradient method were also performed. The result is obtained in six iterations, while the value of the functional is 2.87. This indicates the efficiency of the proposed method.

8 Conclusion

This paper considers HDS with intermediate criteria. On the basis of an analogue of Krotov’s sufficient optimality conditions, a method for the approximate synthesis of optimal control is constructed, its algorithm formulated, and an illustrative example given to demonstrate the efficiency of the proposed method.