Advances in Computational Mechanics to Address Challenges in Crystal Plasticity FEM

Abstract

Image-based computational models are essential for predicting microstructure-property relationships. Crystal plasticity finite element models, or CPFEM, constitute a major part of these computational models. These models generally adopt conventional finite element analysis tools such as available commercial codes. However, they face severe challenges when modeling complex microstructures undergoing extreme phenomena. This chapter examines a few challenges of conventional CPFEM and proposes remedies through advanced methods of computational mechanics. The methods discussed include element stabilization, multi-time-domain subcycling, and efficiency enhancement through adaptivity. It demonstrates the need for such numerical advances and the advantages gained. It provides motivation for looking beyond the available tools and making fundamental advances in field of computational mechanics that can benefit predictive modeling.

1 Introduction

Structural materials, like metals and alloys, are often characterized by microstructural heterogeneities in the form of nonuniform grain distributions, multi-colony sites, or polyphase aggregates in a polycrystalline ensemble. Morphological and crystallographic characteristics of microstructures strongly govern their mechanical behavior and failure response. For example, disparities in grain size, crystallographic orientations, micro-texture, and slip system resistance cause large stress concentrations and grain boundary dislocation pileups, leading to localized plastic flow and crack nucleation in Ti alloys (Sinha et al. 2006). Robust predictive models of deformation and failure, incorporating microstructural features and physical mechanisms, are necessary for effective material simulation and design.

The recent years have seen a surge in the use of image-based computational micro-mechanics models for predicting microstructure-property relationships. For polycrystalline microstructures undergoing large plastic deformation, image-based computational modeling entails determining micromechanical solution fields in statistically equivalent representative volume elements (SERVEs) of the material microstructure by executing computational methods like the finite element method (FEM), boundary element method (BEM), or fast Fourier transform (FFT) method. A SERVE is an optimally small computational domain that is created to capture the statistics of characteristic morphological and crystallographic variables in experimentally obtained electron backscattered diffraction (EBSD) or scanning electron microscopy (SEM) images. Methods of generating SERVEs are discussed in a previous chapter (by Ghosh and Groeber) of this handbook. The SERVE creation is generally followed by conforming mesh generation through discretization of the microstructure into simple geometric elements. Figure 1 shows a 3D SERVE constructed from a 2D EBSD scan of a Ti-7Al specimen and strain evolution in the image-based crystal plasticity finite element analysis.

Fig. 1

(a) EBSD scan of the alloy Ti-7Al, (b) 529-grain 3D SERVE of dimension 300 μm showing < c > -axis misorientation and pole figures comparing SERVE data to EBSD, (c) contour plot of plastic strain at 20% strain with an applied compressive strain rate of 10⁴ s⁻¹

A majority of the computational models for polycrystalline microstructures undergoing large plastic deformation implement crystal plasticity constitutive models. Crystal plasticity finite element models, e.g., in Pierce et al. (1983), Busso et al. (2000), Staroselsky and Anand (2003), Matous and Maniatty (2004), Bridier et al. (2009), Roters et al. (2010a, b), Hasija et al. (2003), Deka et al. (2006), Venkataramani et al. (2007), Anahid et al. (2011), Meissonnier et al. (2001), Dunne et al. (2012), and Kalidindi and Schoenfeld (2000), generally incorporate these constitutive models in conventional finite element analysis codes like ABAQUS, LS-DYNA, etc. for full field analysis of short- and long-range evolution of state variables. Image-based CPFEM, in which microstructural SERVEs are modeled for predicting complex deformation mechanisms including crack nucleation, twin propagation, etc., are discussed in Thomas et al. (2012), Shahba and Ghosh (2016), Cheng and Ghosh (2015, 2017), and Ozturk et al. (2017).

A number of challenges arise when using CPFEM for modeling deformation mechanisms in complex microstructures, especially those involving phenomena like localization, twinning, crack propagation, fatigue, etc. Special methods in advanced computational mechanics should be developed to overcome these challenges and render robust predictive tools. This chapter begins with a brief description of CPFEM formulations, crystal plasticity constitutive relations, and their implementation. Subsequently, it examines three challenges that commonly persist with conventional CPFEM and offers remedies for overcoming them.

• Element Stabilization: Plastic incompressibility causes volumetric locking of commonly used tetrahedral elements in CPFE analyses. Special element technology should be developed for stabilizing spurious modes in these elements.

• Time-Domain Subcycling for Disparate Deformation Rates: Modeling localization phenomena, e.g., discrete twin evolution, in CPFEM often has low computational efficiency due to very fine simulation time steps. This is a major bottleneck in predicting rapidly evolving twin bands. A multi-time-domain subcycling algorithm can improve computational efficiency through the introduction of complementary sub-domains with selective fine and coarse time stepping.

• Enhanced Efficiency with Adaptive CPFEM: Conventional 3D CPFEM with high-resolution mesh can be computationally prohibitive, especially with algorithms for solving complex constitutive models. Increased efficiency can compromise accuracy due to the use of coarse mesh and simplified computational domains. Hierarchical adaptive methods in CPFEM are capable of providing a solution to this shortcoming.

2 Crystal Plasticity FE Formulation and Solution Methods

Finite deformation, crystal plasticity finite element models typically invoke an incremental solution method, where the time (or equivalent loading) domain is discretized into finite number of steps. In an updated Lagrangian formulation (Bathe 2006) for a body under quasi-static conditions, the principle of virtual work for an increment transcending discrete temporal points t and t +  Δt is written as:

(1)

where $\varOmega ^{t}\subset \mathcal {R}^{3}$ is the computational domain at time t and ${\mathbf {E}}^{t+\triangle t}_{t}$ and ${\mathbf {S}}^{t+\triangle t}_{t}$ correspond to the Green-Lagrange strain and the second Piola-Kirchhoff (PK) stress tensors, respectively, with respect to the reference configuration at time t. The weak form at time t + △t requires the following relations:

(2a)

(2b)

(2c)

(2d)

In these relations, σ is the Cauchy stress, u is the displacement, b is the body force per unit volume, δu is a displacement variation, F is the deformation gradient, and J is its determinant or Jacobian. All quantities in Eqs. (2) are at time t + △t and referred to the configuration at time t. The second Piola-Kirchhoff (PK) stress and the Green-Lagrange strain are, respectively, decomposed as:

(3)

where △S^t denotes the increment of second PK stress from time t to t + △t and the Green-Lagrange strain tensor is decomposed into a linear part $\triangle {\mathbf {e}}^{t}(\triangle \mathbf {u}) = \frac {1}{2}\left [ \left (\frac {\partial \triangle \mathbf {u}}{\partial {\mathbf {x}}^t}\right )^T+ \frac {\partial \triangle \mathbf {u}}{\partial {\mathbf {x}}^t} \right ]$ and a nonlinear part given as $\triangle \boldsymbol {\eta }^{t}(\triangle \mathbf {u})=\frac {1}{2} \left (\frac {\partial \triangle \mathbf {u}}{\partial {\mathbf {x}}^t}\right )^T \frac {\partial \triangle \mathbf {u}}{\partial {\mathbf {x}}^t}$. Substituting the strain decomposition, the incremental crystal plasticity constitutive relation $\triangle {\mathbf {S}}^{t} = \mathbb {C}^t(\mathbf {u}): \triangle {\mathbf {E}}^{t}(\mathbf {u}) \approx \mathbb {C}^t(\mathbf {u}): \triangle {\mathbf {e}}^{t}(\mathbf {u})$, and the relation δE^t ≈ δe^t in Eq. (1), the linearized weak form is written as:

(4)

where $\mathbb {C}^t$ is the local material tangent stiffness matrix. The nonlinear weak form in Eq. (4) is solved by using an iterative scheme such as the Newton-Raphson method (Bathe 2006). In the i-th Newton-Raphson iteration, the spatially discretized linearized Eq. (4) is written as:

(5)

where ${\mathbf {K}}_{t}^i$ is the global tangent stiffness matrix, △uⁱ⁺¹ = △uⁱ + u is the displacement update, and $\boldsymbol {b}_{t+\triangle t}-{\mathbf {R}}_t^i$ is the residual force vector for every iteration. These are, respectively, expressed as:

where $\mathbb {C}^{t,i}$ is the elastoplastic tangent stiffness matrix in the i-th iteration; B and B_NL are the linear and nonlinear strain-displacement matrices, respectively; and N is the matrix of shape functions. The Newton-Raphson iterations continue till the residual $\boldsymbol {b}_{t+\triangle t}-{\mathbf {R}}_t^i$ reaches a predetermined tolerance.

2.1 Crystal Plasticity Constitutive Models

Crystal plasticity constitutive models account for dislocation glide on crystallographic slip systems. A significant body of work exists on micromechanical modeling using crystal plasticity models due to glide on slip systems, using, e.g., power law description (Pierce et al. 1983; Asaro and Needleman 1985), the thermally activated theory of plastic flow (Kocks et al. 1975), or the dislocation density-based models (Roters et al. 2010a, b). While computational mechanics advances are in general independent of the constitutive relations used, a crystal plasticity constitutive model for hcp materials developed in Cheng and Ghosh (2015, 2017) is summarized here.

2.1.1 Kinematic Relations, Flow Rule, and Slip System Resistances

The deformation gradient at time t admits a multiplicative decomposition into elastic and plastic components as:

$$\displaystyle \begin{aligned} {\mathbf{F}}^t_0={\mathbf{F}}^{e}{\mathbf{F}}^{p} ~~~\mbox{where}~~\det {\mathbf{F}}^{e} > 0~~\mbox{and}~~ \det~{\mathbf{F}}^{p}=1 {} \end{aligned} $$

(6)

where F^e accounts for elastic stretching and rigid-body rotation of the crystal lattice, while F^p corresponds to the incompressible plastic flow due to slip. The second Piola-Kirchoff stress is expressed in terms of the elastic Green-Lagrange strain tensor ${\mathbf {E}}^{e}\left (=\frac {1}{2}\left ({\mathbf {F}}^{eT}{\mathbf {F}}^{e}-\mathbf {I}\right )\right )$ as:

$$\displaystyle \begin{aligned} \mathbf{S}=\mathbb{C}^{e}:{\mathbf{E}}^{e} {} \end{aligned} $$

(7)

where $\mathbb {C}^{e}$ is a fourth-order anisotropic elasticity tensor. The evolution of plastic deformation is expressed in terms of plastic velocity gradient L^p as:

$$\displaystyle \begin{aligned} {\mathbf L}^p = \dot{\mathbf{F}}^p {{\mathbf{F}}^p}^{-1} = \sum \limits_{\alpha=1} ^{N_{\mathrm{slip}}} {\dot \gamma^{\alpha} {\mathbf{s}}_0^{\alpha} } ~~~\mbox{where}~~ {\mathbf{s}}_0^{\alpha} = {\mathbf{m}}_{0}^\alpha \otimes {\mathbf{n}}_{0}^{\alpha} \end{aligned} $$

(8)

Here $\dot {\gamma }^{\alpha }$ is the slip rate on a slip system α, N_slip is the total number of slip systems, and the Schmid tensor ${\mathbf {s}}_0^\alpha$ associated with α-th slip system is expressed in terms of the slip direction ${\mathbf {m}}_{0}^{\alpha }$ and slip plane normal ${\mathbf {n}}_{0}^{\alpha }$ in the reference configuration. The dislocation glide-based slip rate on the slip system α is described in Pierce et al. (1983) and Cheng and Ghosh (2015, 2017) using a power law as:

$$\displaystyle \begin{aligned} \dot{{\gamma}}^{\alpha}=\dot{\gamma}_{0}^{\alpha}\left|\frac{\tau^{\alpha}-s_{a}^{\alpha}}{s_{*}^{\alpha}}\right|{}^{\frac{1}{m}}\mathrm{sign}(\tau^{\alpha}-s_{a}^{\alpha}) {} \end{aligned} $$

(9)

where $\dot {\gamma }_{0}^{\alpha }$ is a reference slip rate for slip system α and m is the exponent representing strain-rate sensitivity. The resolved shear stress on slip system α is expressed as $\tau ^{\alpha }={\mathbf {F}}^{eT}{\mathbf {F}}^{e}\mathbf {S} : {\mathbf {s}}_0^{\alpha }$. The athermal shear resistance $s^{\alpha }_{a}$ is due to the interaction of the stress field between parallel dislocation lines and from grain boundaries, and the thermal shear resistance $s^{\alpha }_{*}$ is due to local repelling obstacles, such as forest dislocations and dislocation jogs.

Two types of dislocations are considered in the evolution of athermal $s_{a}^\alpha$ and thermal $s_{*}^\alpha$ shear resistances. These are (i) statistically stored dislocations (SSDs) associated with the homogeneous components of plastic flow characterized by vanishing net Burgers vector and (ii) geometrically necessary dislocations (GNDs) corresponding to stored polarized dislocation densities. GND accumulation is necessary for accommodating crystal lattice curvatures in single crystal bending or near-grain boundaries of polycrystalline aggregates. The athermal and thermal hardening rates due to the evolution of SSDs are given as:

$$\displaystyle \begin{aligned} {\dot{s}}^{\alpha}_{a,\mathrm{SSD}}=\sum_{\beta=1}^{N} h^{\alpha \beta }_a~~{|\dot{\gamma }}^{\beta }{\mathrm{sin}(\mathbf{n_0}}^{\alpha },{\mathbf{t_0}}^{\beta })| ~~~\mbox{and}~~~ {\dot{s}}^{\alpha }_{*,\mathrm{SSD}}=\sum_{\beta=1}^{N} h^{\alpha \beta }_*~~{|\dot{\gamma }}^{\beta }{\mathrm{cos}(\mathbf{n_0}}^{\alpha },{\mathbf{t_0}}^{\beta })| {}\end{aligned} $$

(10)

where t₀^β is the dislocation line tangent vector for edge dislocation on the slip plane β and the coefficient matrices $h_a^{\alpha \beta }$ and $h_*^{\alpha \beta }$ represent the hardening of athermal and thermal shear resistances on the slip system α due to activity on slip system β, respectively. The GND contributions to the slip system hardening are derived from two sources, viz., (i) dislocation components $\rho _{\mathrm {GND},P}^\alpha$ parallel to the slip plane α that cause hardening due to the athermal shear resistance $s_{a}^\alpha$ and (ii) forest dislocation components $\rho _{\mathrm {GND},F}^\alpha$, which contribute to hardening due to thermal shear resistance $s_{*}^\alpha$ as:

$$\displaystyle \begin{aligned} s^{\alpha}_{a,\mathrm{GND}}=c_1Gb\sqrt{{\rho }^{\alpha }_{P,\mathrm{GND}}}~~~\mbox{and}~~~ s^{\alpha}_{*,\mathrm{GND}}=\frac{Q_{\mathrm{slip}}}{c_2c_3b^2}\sqrt{{\rho }^{\alpha }_{F,\mathrm{GND}}}\end{aligned} $$

(11)

where G is the shear modulus, $Q_{\mathrm {slip}}^{\alpha }$ is the effective activation energy for dislocation slip, and c₁, c₂, c₃ are constants representing the passing stress, jump-width, and obstacle-width, respectively. GND accumulation can be measured in terms of the curl of the plastic deformation gradient per unit area in the reference configuration, which corresponds to the Nye’s dislocation density tensor $\boldsymbol {\varLambda } = -{(\boldsymbol {\nabla }_{X} \times {{\mathbf {F}}^{{p^T}}})^T}$ (Anahid et al. 2011). The Nye’s tensor is related to the GND density components on each slip system as (Cheng and Ghosh 2017):

$$\displaystyle \begin{aligned} \boldsymbol{\varLambda}=\sum_{\alpha=1}^{\mathrm{nslip}}\rho_{\mathrm{GND},s}^{\alpha}\mathbf{{b_0}^{\alpha}\otimes\mathbf{{m_0}^{\alpha}}}+\rho_{\mathrm{GND},et}^{\alpha}\mathbf{ {b_0}^{\alpha}\otimes\mathbf{{t_0}^{\alpha}}}+\rho_{\mathrm{GND},en}^{\alpha}\mathbf{{b_0}^{\alpha}\otimes\mathbf{{n_0}^{\alpha}}} {}\end{aligned} $$

(12)

where ρ_GND,s, ρ_GND,et, and ρ_GND,en are the GND density components with screw, in-slip-plane edge, and normal-to-slip-plane edge characteristics, per unit volume in the reference configuration and $\mathbf b_0^\alpha$ is the Burgers vector for a slip system α. For hcp crystals, there are more slip systems than the number of components in Λ, and hence ρ_GND,s, ρ_GND,et, and ρ_GND,en are obtained by solving a constrained minimization problem of minimizing the L₂ norm of the GND densities subject to the constraint Eq. (12) (Anahid et al. 2011). Screw and edge GND components ρ_GND,s, ρ_GND,et, and ρ_GND,en on each slip system contribute, respectively, to the parallel ($\rho _{\mathrm {GND},P}^\alpha$) and forest ($\rho _{\mathrm {GND},F}^\alpha$) components of GNDs. The total athermal and thermal resistances are expressed as the sum of a part related to the evolving dislocation structure and another related to defects such as Peierls resistance, impurities, and point defects, as:

$$\displaystyle \begin{aligned} s_a^{\alpha}=s_{a,0}^{\alpha}+\sqrt{(s^{\alpha}_{a,\mathrm{SSD}})^2+(s^{\alpha}_{a,\mathrm{GND}})^2}~~\mbox{and}~~ s_*^{\alpha}={s}_{*,0}^{\alpha}+\sqrt{(s^{\alpha}_{*,\mathrm{SSD}})^2+(s^{\alpha}_{*,\mathrm{GND}})^2}\end{aligned} $$

(13)

where $s_{a,0}^{\alpha }$ and ${s}_{*,0}^{\alpha }$ are initial resistances, independent of the dislocation structure.

2.1.2 Numerical Implementation of Crystal Plasticity Constitutive Model

The numerical time integration algorithm integrates the set of coupled differential equations in the nonlocal constitutive model using the following steps (details provided in Cheng and Ghosh 2015, 2017):

Step A::

Update stresses, plastic strains, and all state variables, keeping the nonlocal GND density and twin variables fixed, with known values of deformation variables at time t, as well as a given deformation gradient F(t + △t);

Step B::

Update the GND densities and their rates of hardening by evaluating ∇_X ×F^pT, using values in adjacent elements.

An implicit update algorithm is implemented in step A with update in step B (Cheng and Ghosh 2015, 2017). For step A, the algorithm assumes that the primary unknown variable is the second Piola-Kirchhoff stress S and seeks its solution from a set of six nonlinear equations by a Newton-Raphson iterative solver while updating other deformation and state variables.

(14)

where N_tot is the total number of slip systems and B^α is defined as:

(15)

with $\mathbf {A}(t+\triangle t)={\mathbf {F}}^{p^{-T}}(t) {\mathbf {F}}^{T}(t+\triangle t) \mathbf {F}(t+\triangle t){\mathbf {F}}^{p^{-1}}(t)$. The trial stress is expressed as ${\mathbf {S}}^{tr}=\mathbb {C}:\frac {1}{2}\left ( \mathbf {A}(t+\triangle t)-\mathbf {I} \right )$. In the iterative solution of Eq. (14), a residual is defined for i-th iteration the as:

(16)

the i + 1-th iteration update to S is obtained as:

(17)

In this update procedure for S(t + △t), the slip system resistances are held fixed. After convergence, the increment of shear resistances from SSDs are updated using Eqs. (10). The next step B computes the GND densities and associated hardening increments. A nonlocal, invoking the element gradient operator is implemented to evaluate Λ. The gradient operator is calculated from nodal values using element shape functions. A super-convergent patch recovery (SPR) method is implemented to evaluate the nodal values of F_p from Gauss quadrature points to evaluate ∇_X ×F^pT at quadrature points. Evolution of plastic strain in image-based CPFEM simulations of a SERVE is shown in Fig. 1c.

3 Stabilization of Four-Noded Tetrahedral Elements for CPFEM

Polycrystalline microstructures of metals and alloys often have sharp and tortuous grain boundaries and multiple grain junctions. Discretization, conforming to these domains in 3D, is conveniently accomplished using four-noded tetrahedral or TET4 elements. However, it has been observed, e.g., in Matous and Maniatty (2004), Gee et al. (2009), and de Souza Neto et al. (2005), that these elements suffer from severe volumetric locking when simulating incompressible materials. Crystal plasticity constitutive models exhibit near isochoric plastic flow (det F^p = 1) and large volumetric strains in TET4 elements. High stresses induce high spurious dilatational energy and considerable error due to element locking. This is attributed to low incompressibility constraint ratio, defined as the ratio of number of degrees of freedom to the number of incompressibility constraints in the FE mesh.

A number of methods have been proposed for the stabilization of volumetric locking in TET4 elements (Gee et al. 2009; de Souza Neto et al. 2005; Dohrmann et al. 2000; Nguyen-Thoi et al. 2009). A key idea in these methods is to associate nodal points with patches corresponding to an assembly of surrounding sub-elements and subsequently to selectively integrate the dilatational and deviatoric parts of the FE weak form over these patches. This process reduces the incompressibility constraint ratio. However, these methods are not effective for anisotropic CPFE formulations for which the stress or the elastoplastic tangent stiffness tensor cannot be split into volumetric and deviatoric components. A finite deformation element formulation with a F-bar patch method has been introduced in de Souza Neto et al. (2005), while mixed elements have been proposed in Matous and Maniatty (2004) with augmentation strain fields in conjunction with a linearly interpolated pressure field.

Based on developments in Cheng et al. (2016), this section discusses three locking-free stabilized finite element formulations for CPFE analysis. They include a node-based uniform strain (NUS) element, a locally integrated B-bar (LIB)-based element, and a F-bar patch (FP)-based element.

3.1 Node-Based Uniform Strain and Locally Integrated B-Bar Elements

The node-based uniform strain (NUS) formulation, introduced in Dohrmann et al. (2000), assigns a patch of sub-elements $\hat {\varOmega }^{s}=\sum _{i=1}^{N^{s}} \alpha _{s}^{i} \:\varOmega _{s}^{i}$ to a node s in the finite element mesh as shown in Fig. 2a. Here N^s is the number of TET4 elements attached to a node s, $\varOmega _{s}^{i}$ is the volume contribution of the i-th element to the patch $\hat {\varOmega }^{s}$, and $\alpha _{s}^{i}$ is a scalar weighting factor. Within each patch, the strain increment $\hat {\mathbf {e}}^{s}$ is uniform and obtained by weighted averaging from surrounding elements as:

(18)

wⁱ is a relative volume-based weight for element i and $\triangle \hat {\mathbf {q}}^{s}$ is the nodal displacement vector. $\hat {\mathbf {B}}^{s,t}$ is a strain-displacement matrix associated with the patch s, obtained by weighted assembling B^{i, t} from surrounding elements. The NUS formulation yields a constant tangent modulus and stress over the patch s, and one-point numerical integration is sufficient. However, this element can exhibit spurious zero or low-energy modes, causing large element distortion (Gee et al. 2009).

Fig. 2

(a) 2D nodal patch in the NUS method, (b) nodal patch with strain distributions in the LIB method, and (c) patch of elements in the F-bar patch method

To overcome shortcomings of the NUS element for CPFE analysis with anisotropic elastoplastic stiffness matrix, a locally integrated B-bar (LIB) element is proposed in Cheng et al. (2016). This method alleviates volumetric locking without introducing spurious zero-energy modes. The strain increment is decomposed into volumetric and deviatoric parts by splitting the gradient matrix as e = e^vol + e^dev = B^vol△q + B^dev△q. For reduced constraints, only the volumetric part of the strain increment e^vol is assumed to be uniform inside the patch for each node s. The uniform volumetric strain increment $\hat {\mathbf {e}}^{s,\mathrm {vol}}$ is obtained as:

(19)

$\bar {\mathbf {B}}^{s,\mathrm {vol}}$ is the volumetric part of the gradient matrix associated with a patch s. It is assembled from the B^{i, vol} matrices of the surrounding elements with weights wⁱ. The deviatoric part of the strain increment e^dev is constant in each of the contributing TET4 elements. This yields separate distributions of the volumetric and deviatoric strain increments over the domain, as illustrated in Fig. 2b. Each TET4 element is divided into four sub-domains of equal volume. Within each sub-domain, the volumetric and deviatoric parts of the strain increment are constant. The LIB element selectively reduces the volumetric strain components over the patch and keeps the deviatoric strain components unchanged.

3.2 F-Bar Patch-Based (FP) Element

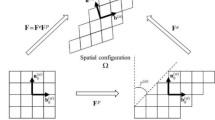
The F-bar patch (FP) formulation (de Souza Neto et al. 2005) has been shown to alleviate volumetric locking without introducing spurious zero-energy modes. The F-bar patch method modifies the deformation gradient for weak enforcement of incompressibility in the element, rather than point-wise enforcement. The deformation gradient is decomposed into isochoric and volumetric components as:

$$\displaystyle \begin{aligned} \mathbf{F}={\mathbf{F}}_{\mathrm{iso}} {\mathbf{F}}_{\mathrm{vol}}~~~~\mbox{where}~~ {\mathbf{F}}_{\mathrm{iso}}=\left( \mathrm{det} \mathbf{F} \right) ^ {-\frac{1}{3}} \mathbf{F} ~~\mbox{and}~~ {\mathbf{F}}_{\mathrm{vol}}=\left( \mathrm{det} \mathbf{F} \right) ^{\frac{1}{3}} \mathbf{I} \end{aligned} $$

(20)

Incompressibility in constitutive relations is enforced over a patch of elements, rather than in each element. This requires that elements in the mesh be assigned to non-overlapping patches as illustrated in Fig. 2c. For a patch $\mathscr {P}$ of a set of elements, with deformed and undeformed volumes $\varOmega ^{t+\triangle t}_{\mathrm {patch}}$ and $\varOmega ^{0}_{\mathrm {patch}}$, respectively, the deformation gradient in element $K \in \mathscr {P}$ is modified as:

(21)

3.3 Performance of TET4 Element Stabilization in CPFEM

The performance of the locally integrated B-bar (LIB) element and the F-bar patch element with a patch size of 8 tetrahedrons (FP8) has been studied in Cheng et al. (2016) for CPFEM analysis of polycrystalline materials. Simulation results for a bicrystal compression test and a polycrystalline bending test of the hcp magnesium alloy AZ31 are compared with those for the standard TET4 element. The reference solution is for simulations with the B-bar stabilized eight-noded hexahedral element.

• Bicrystal compression test: A bicrystal of dimensions of 10 × 10 × 10 μm is simulated under uniaxial compression using the standard TET4, LIB, and FP8 elements in CPFEM. Material constitutive models are given in Cheng and Ghosh (2015). The grain boundary is characterized by crystal orientations, which have Euler angles $\left [ 0^\circ , 0^\circ , 0^\circ \right ]$ and $\left [0^\circ , 90^\circ , 0^\circ \right ]$ in the ZXZ convention for crystals 1 and 2, respectively, as shown in Fig. 3a. Displacement boundary conditions are applied on the top surface. A reference solution of the loading direction stress σ_zz for CPFE analysis with hexahedral elements with B-bar stabilization is shown in Fig. 3b. Results using the standard, LIB and FP8 TET4 elements are shown in Fig. 3c, e, respectively. Non-smooth distribution of the local stress with high stress concentration is observed at the grain boundary using standard TET4 element, compared to other stabilized elements. The stress error is evaluated as the L2 norm of the difference with the reference solution as $\left \Vert e\right \Vert { }_{L2}=\frac {\left [\int _{\varOmega }\left ({\sigma }_{ij}-{\sigma }_{ij}^{ref}\right )\left ({\sigma }_{ij}-{\sigma }_{ij}^{ref}\right )d\varOmega \right ]^{\frac {1}{2}}}{\left (\int _{\varOmega }{\sigma }_{ij} {\sigma }_{ij} d\varOmega \right )^{\frac {1}{2}}}$. The corresponding error plots for different elements with increasing mesh densities are shown in Fig. 4a. The average convergence rate for LIB and FP8 elements is 0.75. For CPFE analysis, these elements exhibit similar results with much smaller errors compared to the standard TET4 element. The evolution of hydrostatic stress at the grain boundary with increasing strain is plotted in Fig. 4b. Unrealistically large stresses are observed with conventional TET4 elements, while the LIB and FP8 elements produce results that are consistent with the stabilized hexahedral element.

  Fig. 3

  

  (a) Boundary conditions and crystallographic orientations in the bicrystal compression test; distribution of loading direction stress at 5% strain using simulation results of (b) eight-noded B-bar hexagonal elements with a mesh of 18,081 nodes, (c) standard TET4 element, (d) LIB element, and (e) FP8 element, all with a mesh of 11,862 nodes

  Fig. 4

  

  (a) Stress error plot with increasing degrees of freedom and (b) evolution of maximum hydrostatic stress with strain for different element formulations

• Micro-twin nucleation in polycrystalline magnesium alloy: CPFE simulations are conducted for twin nucleation using a microstructural model of the polycrystalline Mg alloy AZ31 shown in Fig. 5a. The 40 × 40 × 40 μm statistically equivalent virtual microstructure with 103 grains of average size of 10 μm is developed from electron backscattered diffraction data. The microstructure is discretized into 113, 425 TET4 elements. Displacement boundary conditions are applied at a rate of 0.004 μm/s on the two surfaces in Y-direction, which bend the microstructure about the X-axis on Y-Z plane. Details of the twin nucleation model are given in Sect. 4.1. The GND density contour plots in Fig. 5b, c show highest GND concentrations close to grain boundaries. The conventional TET4 element shows a much stiffer response in Fig. 6b compared to the other elements. The FP8 element shows a slightly lower level of locking than LIB elements due to a lower constraint ratio. The twin nucleation predictions in Fig. 6a show a much earlier twin nucleation time (97 s) with the TET4 elements in comparison with the LIB element (160 s) and FP8 element (180 s).

  Fig. 5

  

  Schematic of the polycrystalline AZ31 SERVE showing the applied boundary conditions; GND densities distribution after 500s using: (b) TET4 and (c) FP8 elements

  Fig. 6

  

  (a) Micro-twin dissociation distance as a function of loading time and (b) loading direction stress at a material point with loading time

In summary, both the LIB and FP elements stabilize the local stresses and GND distributions in CPFE analyses and converge to the reference solution. The FP element is capable of providing slightly better results than the LIB element for an optimal patch size. A study on computational efficiency in Cheng et al. (2016) have shown that the FP element outperforms the LIB element with a considerably lower simulation time. From accuracy and efficiency considerations, the FP element is deemed more suitable for stabilized CPFE analysis.

4 Multi-Time-Domain Subcycling for Discrete Twin Evolution

Deformation twinning is a critical deformation mechanism that causes change in lattice orientations with localized deformation inside thin twin bands. Twinning can induce characteristic features like plastic anisotropy, tension-compression asymmetry, and local softening in the material response. Many crystal plasticity-based twinning models adopt a twin volume fraction approach that treats twin evolution in the same way as slip (Staroselsky and Anand 2003; Izadbakhsh et al. 2011; Zhang and Joshi 2012). These approaches do not account for deformation heterogeneity within discrete twins. Explicit twin formation models within the CPFE framework have been proposed based on phenomenological twin formation criteria and adaptive mesh generation methods in Abdolvand and Daymond (2013) and Knezevic et al. (2016). Explicit twinning models hold promise, provided the physics of twin nucleation, propagation, and interactions are correctly accounted for. The author has recently implemented an image-based crystal plasticity FE model with discrete twin evolution in Cheng and Ghosh (2017) and Cheng et al. (2018) to study deformation and twinning mechanisms in polycrystalline microstructures of Mg alloys.

A major difficulty with image-based CPFE simulations of polycrystalline microstructures delineating explicit twin formation is the high demands on computing time. This is attributed to the discrepant deformation rates between the domains of rapidly evolving twins and the surrounding crystalline matrix. The high rates of twin evolution in localized bands lead to numerical instability with the stiff nonlinear crystal plasticity constitutive equations, requiring very fine simulation time steps. A quantitative study on the critical time step size required for numerical stability for a CPFE simulation of a Mg alloy with evolving explicit twins has been conducted in Ghosh and Cheng (2018). The study shows that while 97% of elements require a minimum time step size of Δt = 10 s, only 3% of the elements located in localized twin bands require a significantly smaller time step of Δt = 0.0391 s. The reduction in time step size corresponds to a factor of ∼255. Requiring all elements in the computational domain to be integrated with the smaller step size can cause a huge loss of efficiency and could potentially be computationally intractable. While single time step methods to accelerate slip-based crystal plasticity models have been proposed, e.g., in Roters et al. (2010a), they are insufficient for twin evolution models.

4.1 Crystal Plasticity Constitutive Models with Twinning

The crystal plasticity constitutive models in Sect. 2.1 are extended in this section to account for both dislocation glide and twinning on crystallographic slip and twin systems. Twinning reorients the crystallographic lattice symmetrically by reflection across a mirror or twin plane in the reference configuration. In the twinned regions, plastic flow takes place by gliding of twin partial dislocations on twin planes, as well as by dislocation glide. The plastic velocity gradient in twinned region is subsequently expressed as:

$$\displaystyle \begin{aligned} {\mathbf L}^p = \dot{\mathbf{F}}^p {{\mathbf{F}}^p}^{-1} = \sum \limits_{\beta=1} ^{N_{\mathrm{twin}}} {\dot \gamma^{\beta}_{tw} {\mathbf{s}}_{0,tw}^{\beta}} + \sum \limits_{\alpha=1} ^{N_{\mathrm{slip}}} {\dot{\tilde{\gamma}}^{\alpha} \tilde{\mathbf{s}}_{0,\mathrm{slip}}^{\alpha} } ~\mbox{where}~{\mathbf{s}}_{0,tw}^{\beta} = {\mathbf{m}}_{0,tw}^\beta \otimes {\mathbf{n}}_{0,tw}^{\beta} {} \end{aligned} $$

(22)

$\dot \gamma ^{\beta }_{tw}$ is the shearing rate on a twin system β, $\dot {\tilde {\gamma }}^{\alpha }$ is the slip rate in the reorientated slip system α, N_twin is the number of twin systems, ${\mathbf {m}}_{0,tw}^{\beta }$ is the twin shearing direction vector, and ${\mathbf {n}}_{0,tw}^{\beta }$ is the twin plane normal in the reference configuration. Dislocation slip in the twinned volume occurs on a slip plane $\tilde {\mathbf {n}}_{0,\mathrm {slip}}^{\alpha }$ in the direction $\tilde {\mathbf {m}}_{0,\mathrm {slip}}^{\alpha }$, with mirror symmetry to the directions ${\mathbf {n}}_{0,\mathrm {slip}}^{\alpha }$ and ${\mathbf {m}}_{0,\mathrm {slip}}^{\alpha }$ in the matrix region. Twin nucleation and propagation models, developed in Cheng and Ghosh (2015, 2017) for hcp materials, are summarized here.

• Twin nucleation: The twin nucleation model is based on the elastic dislocation theory of twin nucleation by non-planar dissociation of a sessile pyramidal $\left < c+a \right >$ dislocation. Three simultaneous conditions should be satisfied for the dissociation process to spontaneously occur and form a stable twin nucleus. They are (i) dissociation condition, E_ini ≥ E_tw(d = 0) + E_r; (ii) irreversibility condition, $E_{\mathrm {ini}} > E_F\left (d=d_{s},\tau _{tw}\right )$; and (iii) reliability condition, d_s > 2r₀. Here E_ini is the initial system energy prior to dissociation, corresponding to the dislocation line self-energy of sessile pyramidal $\left < c+a \right >$ dislocations, E_tw is the self-energy of the twinning dislocation loop, E_r is the self-energy of stair-rod dislocations, and E_F is the post-dissociation total system energy. The distance d is the separation distance between two partial dislocations and d_s is the stable separation distance. Detailed description of the various energies and other critical parameters in the twin nucleation model are provided in Cheng and Ghosh (2015, 2017).

• Explicit twin propagation: Twin propagation involves two motions, viz., twin elongation by rapid gliding of twin partial dislocations on twin planes and twin thickening by migrating twin boundaries from the current twin planes to every other $\left \{10\bar {1}2\right \}$ twin plane (Keshavarz and Ghosh 2013, 2015). Gliding of twin partial dislocations occurs by a mixed shear-shuffle process, for which twin propagation is deemed as thermal activation process. The velocity of twin partial dislocation on a twin plane is expressed as:

  

  (23)

  where f_shuffle is the shuffling frequency, λ_shear is the shear distance, b_tw represents the Burgers vector on a twin system, τ is the effective resolved shear stress on the twin plane, and A_P is the shearing area. The term $\exp \left (-\frac {\triangle F-\tau A_{P} b_{tw}}{K_{B}T}\right )$ is the probability of gliding with an internal energy barrier △F. The twin boundary migrates when the twin partial dislocation glides on the adjacent twin plane.

A stimulated slip model is used to model thickening of twins. It assumes the existence of immobile lattice dislocations, which penetrate multiple twin planes. The velocity of twin partial dislocations crossing twin planes has been derived as:

(24)

where d_tw denotes the distance between twin planes, △t_tw is the average time required to meet a promoter, P_promoter is the fraction of dislocations that act as promoters, ρ_tot is the total dislocation density, and v_glide and l_tw are, respectively, the velocity and length of moving dislocations. The time-averaged, twin system plastic shear rate in Eq. (22) due to twinning is obtained from the Orowan equation as:

(25)

where $\dot {\gamma }_{0,tw}=\rho _{tw} b_{tw} f_{\mathrm {shuffle}}\lambda _{\mathrm {shear}}$ and ρ_tw is the density of twin partial dislocations. For $\left \{10\bar {1}2\right \}$ twin in Mg, $\gamma _{tw}^{\mathrm {max}}=0.1289$. In simulations, the shear on a twin system quickly reaches this upper bound once an integration point is twinned.

The complex interaction between dislocations and twin boundaries is modeled by the evolution of a slip/twin system resistance in which Eq. (25) is reduced to a conventional shear resistance-based power law model as:

(26)

For a twin system α, the rate of shear resistance is expressed as $\dot {s}^\alpha _{tw}=\sum\limits _{\beta = 1}^{N_{\mathrm {slip}}} {h^{\alpha \beta } } | {\dot {\tilde {\gamma }}^{\beta } } |$, where the hardening matrix h^αβ quantifies hardening due to dislocation slip in the twinned regions. Implementation of twin evolution in the CPFEM framework is discussed in Cheng and Ghosh (2017) and Cheng et al. (2018).

4.2 Adaptive Subcycling for Accelerated CPFEM

An adaptive multi-time-domain subcycling algorithm is developed in Cheng and Ghosh (2017) and Ghosh and Cheng (2018) to avert the low efficiency due to minimum critical time step requirements, by activating a differential temporal resolution in the computational domain. The algorithm partitions the microstructural domain into sub-domains that are classified as critical (high strain rate) and noncritical (low-strain rate). For optimal efficiency, time integration in each sub-domain is conducted with its own independent time step, as determined from stability and accuracy criteria. For a twinned microstructure, regions of twin bands are solved with fine time steps, while the remaining regions use coarse time steps. A schematic layout of the algorithm is shown in Fig. 7. With a known state at time t, the integration algorithm for the time increment t to t + △t solves the noncritical sub-domain problem using the coarsest possible time increment △t and the critical sub-domain problem using fine time steps △τ ≪△t. To achieve global equilibrium for the computational domain, the different sub-domains are coupled, and residuals at the interfaces of discrepant time steps in the assembled sub-domains are minimized using a predictor-corrector scheme. The subcycling algorithm evaluates displacement correctors by equilibrating nodal residual forces since displacement fields at nodal points of adjacent sub-domains will not satisfy compatibility in general. Decomposition of the computational domain necessitates the evaluation of critical time steps for each element. With known state variables at time t, the critical time increment in each element is estimated from convergence of time integration of the constitutive model. If the time integration fails to converge, a scaled reduction of the original time increment is made. The essential steps in a staggered algorithm for evolving twins are given next and detailed in Cheng and Ghosh (2017) and Ghosh and Cheng (2018).

• 1. At time t compute trial displacements and partition coarse and fine sub-domains;

• 2. Solve the coarse sub-domains with the larger time increment △t;

• 3. Solve the fine sub-domains with scaled time increments △τ_i;

• 4. From the coarse and fine sub-domain residuals, obtain displacement corrector;

• 5. Check for equilibrium, update twin domains, and nucleate new twins.

Fig. 7

Schematic of the subcycling algorithm showing partitioning and equilibrating domains

Two factors affect the computational speedup with the subcycling method. They are (i) the ratio of degrees of freedom (DOF) in fine timescale sub-domain to the DOF of entire domain, i.e., $\frac {N^F}{N^{\mathrm {total}}}$, and (ii) the ratio of fine time step △τ to coarse time step △t, i.e., $\frac {\triangle \tau }{\triangle t}$. In Ghosh and Cheng (2018) it is shown that $\frac {\triangle t}{\triangle \tau }$ and $\frac {N^{\mathrm {total}}}{N^F}$ are the key factors in reducing the number of operations. Higher acceleration rates can be achieved by the subcycling method if the deformation is localized in smaller regions and if deformation rates exhibit more heterogeneity. The effectiveness of the twin evolution algorithm with subcycling is tested for single and polycrystalline microstructures.

• Deformation-Induced Twin Evolution in Single Crystal Mg: A single crystal simulation of pure Mg is conducted in Cheng and Ghosh (2017) to validate the subcycling-accelerated CPFE model for discrete twin evolution. The microstructure, shown in Fig. 8a, has a dimension of 20 × 10 × 10 μm with an Euler angle orientation of [0^∘, 5^∘, 0^∘] in the ZXZ convention. It is discretized into 67,418 TET4 (FP8) elements with 13,021 nodes. The calibrated constitutive parameters for CPFE analysis are provided in Cheng and Ghosh (2017). A uniaxial, constant strain rate of 1 × 10⁻⁴ is applied in a compressive manner on the top surface, which causes the formation of $\left \{10\bar {1}2\right \}$ tension twins. The 5^∘ tilt in the crystal orientation makes the Schmid factor of twin variant 1 to be highest among all 6 twin variants. Thus only twin variant 1 is formed during simulations.

  Fig. 8

  

  (a) A pure Mg single crystal computational model subjected to constant strain rate, uniaxial loading, (b) simulated twins, and (c) Lagrangian strain E_yy at 1% strain, using the subcycling-induced CPFE model with a time step △t = 10 s

The evolved discrete twins and Lagrangian strain distribution at 1% strain are shown in Fig. 8b, c, respectively. The [0^∘, 5^∘, 0^∘] orientation causes the $\left (\bar {1}102\right ) \left [ 1\bar {1}01\right ]$ twin variant to have the highest Schmid factor. The only exception is that a $\left (10\bar {1}2\right ) \left [\bar {1}011\right ]$ twin variant (variant 4 of the extension twin systems) occurs at the upper left corner of the model due to the local stress state. The localized strain distribution is caused by easy gliding of twins. Approximately 3.6 times speedup is achieved with subcycling without any loss of accuracy.

• Twin Evolution in Polycrystalline RVE: An image-based RVE of the Mg alloy AZ31 containing 620 grains of average grain size of 32 μm in a 300 × 300 × 300 μm box is shown in Fig. 9a. A uniaxial, compressive strain rate of 1 × 10⁻³ s⁻¹ is applied normal to transverse direction (TD) surface. The figure shows texture with the propagation of twin bands, where the lattice in the twinned region is reorientated by nearly 86^∘. The volume-averaged stress-strain response from CPFE simulations are compared with experimental results from Beyerlein et al. (2011) in Fig. 9b. The CPFE simulation with subcycling algorithm has a speedup by a factor of 6. In summary, the multi-time-domain subcycling enhanced CPFEM is highly effective for predicting nucleation and propagation of explicit twins in single crystal and polycrystalline microstructures of metals and alloys.

  Fig. 9

  

  (a) Texture evolution with deformation in contour plots of the angles between the [0001] lattice axis in each grain and the ND direction (Z-axis) at 2% strain and (b) volume-averaged stress-strain response compared with experimental results in Beyerlein et al. (2011)

5 Adaptive Hierarchical CPFEM with Enhanced Wavelet Basis

Image-based CPFE modeling of polycrystalline materials, e.g., in Roters et al. (2010b), Meissonnier et al. (2001) and Cheng and Ghosh (2017) often requires very high 3D resolution for accurate representation of realistic microstructures. This can incur prohibitively high computational costs in simulating deformation leading to localized phenomena like fatigue failure or deformation twin evolution. A few alternative computational methods have emerged to efficiency-related shortcomings of CPFEM. The elastic-viscoplastic self-consistent models in Lebensohn and Tome (1994) treat grains as embedded inclusions in a homogeneous medium and avoid the need to represent stress heterogeneity inside each grain. The fast Fourier transformation (FFT)-based methods in Moulinec and Suquet (1998) and Lebensohn et al. (2012), and discussed in another chapter of this part, are very efficient, especially for large regular sampling grid simulations with periodicity. The use of FFT methods for discontinuous or high gradient fields can however lead to truncation errors due to the Gibbs phenomenon, propagating from the discontinuity. Regularization methods are being applied to correct this effect, e.g., in Gottlieb et al. (1992). These approaches can also have suboptimal convergence rates due to nonconforming sampling grids that require a large number of degrees of freedom. The present section however seeks an adaptive enrichment method for optimally augment the efficiency of CPFEM while retaining accuracy.

A wavelet-basis enhanced adaptive hierarchical CPFEM has been developed in Azdoud and Ghosh (2017) and Azdoud et al. (2017) to improve computational efficiency and accuracy of FE analyses of polycrystalline microstructures. The method adaptively creates an optimal discretization space conforming to the solution profile by projecting the solution onto a set of scaling and multi-resolution wavelet basis functions. The multi-resolution property is particularly advantageous for approximating a field using a minimal set of wavelet basis functions. The second generation family of wavelets (Sweldens 1998) is used to generate hierarchical shape functions using the so-called lifting scheme. Given the scaling functions at a coarse and fine scale, the lifting scheme defines a set of wavelet functions that complement the coarser set of interpolation functions to uniquely project any function decomposed on a finer set. Complex irregular meshes are easily constructed for these wavelet bases, which make them ideal candidates for enrichment functions in the wavelet-enhanced hierarchical FEM. A summary of the methods and results from Azdoud and Ghosh (2017) and Azdoud et al. (2017) are presented here.

5.1 Wavelets for Optimal Enrichment Basis Functions

Wavelet basis functions span the space of square integrable functions L²(R) through translation and dilation of the scaling function φ(x), which satisfies the refinement condition $\varphi (x)=\sum _{k=1}^{N_{\mathrm {filt}}}h_k \varphi (x)(2x-k)$. Parameters h_k and N_filt characterize the wavelet basis and correspond to the components of a low-pass filter. These functions can be used for optimal multi-resolution hierarchical enrichment, conforming to the solution estimate $\tilde {\mathbf {u}}$ profile. Properties that render them ideal for multi-scale enrichment (Azdoud and Ghosh 2017; Azdoud et al. 2017) are:

• Compact support: Wavelet functions have compact support. Solutions in wavelet bases do not exhibit spurious instabilities, such as the Gibbs phenomena.

• Multi-resolution: Wavelet bases have multi-resolution characteristics that represent the differences between hierarchical scales. Wavelet functions with the Reisz basis property avoid aliasing by ensuring completeness of each scale.

• Compatibility with FE discretization: Second-generation wavelet functions (Sweldens 1998) can be constructed from any irregular hierarchical FE mesh.

• Vanishing moments: The integral of wavelet functions over any domain is zero. Thus a small coefficient has negligible contribution to the solution.

The lifting scheme creates wavelets for the hierarchical FE shape functions. A lazy wavelet $\tilde {\varphi }^{l-1}_{\beta }$ is first created from hierarchical shape functions, followed by transformation through the lifting scheme by adding vanishing moments to yield:

$$\displaystyle \begin{aligned} \varphi^{l-1}_{\beta}(\mathbf{x})=\tilde{\varphi}^{l-1}_{\beta}(\mathbf{x})-\sum_{\lambda}^R a_{\lambda} N^{l-1}_{\lambda}(\mathbf{x}) \end{aligned} $$

(27)

Here l denotes the scale, $N^{l-1}_{\lambda }$ is a standard FE shape function at scale l − 1 and coefficient a_λ is chosen from the condition: $\int _{\varOmega } \varphi ^{l-1}_{\beta }(\mathbf {x})d\varOmega =0 \quad\forall \beta \in [1,p(l)]$. Each scale of wavelets represents a Reisz basis in Ω. Adding $N^{l-1}_{\lambda }$ extends the compact support of the wavelet function $\varphi ^{l-1}_{\beta }$ to the whole domain, i.e., $\bigcup _{\beta }^{p(l)}\mathrm {supp}( \varphi ^{l-1}_{\beta })=\varOmega$. The lifting scheme with R = 2 is sufficient for all the above properties.

5.2 Adaptive Solution Enhancement with Wavelet Basis Functions

The hierarchical wavelet-enhancement is based on the finite deformation crystal plasticity FE formulation summarized in Sect. 2. The solution in the Newton-Raphson algorithm corresponds to the i-th iterative correction u of the displacement increment △uⁱ in a time step between t and t +  Δt. In the proposed algorithm (Azdoud et al. 2017), an adaptive enhancement is made to the first iterate of the solution, i.e., Δuⁱ⁼¹ = u. It is premised upon finding an optimal discretization space V^h(t)(Ω) for u =  Δuⁱ⁼¹ that will reduce the discretization error to within a prescribed tolerance. Assume that the approximate solution u^h at time t has been evaluated on the discretized space V^h(t)(Ω) ⊂ V (Ω) as:

$$\displaystyle \begin{aligned} {\mathbf{u}}^{h}(\mathbf{x})=\sum_{{\alpha}}^m {\mathbf{u}}^{h}_{\alpha} N_{\alpha}(\mathbf{x})+\sum_{{\beta}}^{m_{\mathrm{enr}}(t)} {\mathbf{w}}_{\beta}^{h} \varphi_{\beta}^{(t)}(\mathbf{x})~~~ \forall \mathbf{x} \in \varOmega \end{aligned} $$

(28)

The standard finite element basis N_α corresponds to the approximation of u in the original coarse FE discretization space at time t₀ with m as the number of nodes in this mesh. The adaptive method introduces a set of enrichment functions $\lbrace \varphi \rbrace ^{m_{\mathrm {enr}}}$ in the hierarchy, which expand the discretization space V^h(Ω) to an enriched space $V^{h_{\mathrm {enr}}}(\varOmega )\supset V^h(\varOmega )$. m_enr corresponds to the number of additional enrichment nodes that are hierarchically added to the initial number m. Assume that the set {ϕ}ⁿ is an arbitrarily large (n →∞) and sufficient set of multi-scale hierarchical enrichment functions for the coarse discretization space {N}^m. The functions in the set {ϕ}ⁿ are the standard C⁰ hierarchical FEM shape functions obtained by uniform subdivision of the coarse mesh. For the increment Δt ∈ t → t +  Δt, the adaptive method finds an optimal set $\lbrace \varphi \rbrace ^{m_{enr}(t+\Delta t)}\subset \lbrace \phi \rbrace ^n$ such that:

$$\displaystyle \begin{aligned} \Vert \mathbf{u}-{\mathbf{u}}^{h_{enr}}\Vert{\leq}\epsilon~~\mbox{where}~~ {\mathbf{u}}^{h_{enr}}(\mathbf{x}){=}\sum_{{\alpha}}^m {\mathbf{u}}^{h_{enr}}_{\alpha} N_{\alpha}(\mathbf{x})+\sum_{{\beta}}^{m_{enr}(t+\Delta t)} {\mathbf{w}}_{\beta}^{h_{enr}} \varphi_{\beta}^{t+\Delta t}(\mathbf{x})~~ \forall \mathbf{x} {\in} \varOmega \end{aligned} $$

(29)

An iterative error estimation-solution enrichment algorithm is implemented with iteration steps denoted by k. The resulting algorithm for a time step from t → t +  Δt has two iterative loops, viz., (i) iterations for the first estimate of u, in which the enrichment functions $\lbrace \varphi \rbrace ^{m_{\mathrm {enr}}(t+\Delta t)}$ are sought, and (ii) the Newton-Raphson iterations for the constitutive update. The adaptive iterative scheme for an iteration step (k + 1) to determine $\lbrace \varphi \rbrace ^{m_{\mathrm {enr}}(t+\Delta t)}$ is presented in Azdoud et al. (2017).

5.3 Results with Adaptive CPFEM for Polycrystals

The effectiveness of the adaptive, wavelet-enhanced hierarchical CPFE model is examined in this example. A polycrystalline microstructure of the hcp Ti6242 alloy, containing 208 grains in a computational microstructure of dimensions 124 × 124 × 124 μm is simulated under uniaxial displacement conditions. The z-axis misorientation distribution is shown in Fig. 10a. The loading is applied uniformly on the top surface (z = 124 μm) with a displacement ramp from u_z = 0 to u_z = 3 μm, while the surface (z = 0) is constrained with u_x = u_y = u_z = 0. The transversely elastic stiffness coefficients and crystal plasticity parameters are given in Azdoud and Ghosh (2017) and Azdoud et al. (2017).

Fig. 10

(a) A 208 grain polycrystalline microstructure showing z-axis misorientation distribution, (b) node enrichment positions, where the black spheres, red cubes, and green octahedra denote the enrichment scales 1, 2, and 3, respectively, and (c) contour plot of error e_l(%) for the wavelet adapted model with 42,000 enrichment DoFs

For the elasticity problem only, the wavelet adaptivity admits three scales of enrichment. The coarse-scale solution u^h is computed on a mesh composed of N_e = 9485 tetrahedral elements with N_n = 1, 778 nodes. The mesh for the fine-scale reference FE solution u^f, as well as the adapted FE model with three scales of enrichment, both have N_e = 4, 856, 320 tetrahedral elements and N_n = 821, 569 nodes. A total of 14,000 enrichment functions are used, with 5568 functions at scale 1, 6730 functions at scale 2, and 1702 functions at scale 3. In Fig. 10b, nodal positions of the 14, 000 enriched function $\lbrace \varphi \rbrace ^{m_{\mathrm {enr}}}$ are predominantly in regions of large error near highly misoriented grain boundaries. Figure 10c shows the magnitude of the displacement error $e_l=\sqrt {\frac {({\mathbf {u}}^{h_{enr}}-{\mathbf {u}}^f)^T({\mathbf {u}}^{h_{\mathrm {enr}}}-{\mathbf {u}}^f)}{({\mathbf {u}}^f)^T({\mathbf {u}}^f)}} \times 100 (\%)$ for the adapted solution ${\mathbf {u}}^{h_{enr}}$. The convergence rate of the solution with the adaptive hierarchical FE method is compared to that of a uniformly enriched FE method in Fig. 11a. The average convergence rate for the adaptive method is ${\sim }\mathcal {O}(N^{-1.22})$ compared to ${\sim }\mathcal {O}(N^{-0.99})$ for the standard FEM. The evolution of the number of enrichment functions with the number of iterations is depicted in Fig. 11b for a tolerance 𝜖 = 0.002. Convergence is generally reached in under five iterations. The CPU time for different simulations show a significant gain in efficiency with reduced error for the adaptive method in comparison with a uniformly refined mesh.

Fig. 11

(a) Log-log plot of the L₂ norm of displacement error as a function of DoF and (b) evolution of the number of $\tilde {\mathbf {u}}^*$ enrichment functions as a function of the number of iterations

For crystal plasticity simulations, convergence rates of the wavelet-enriched adaptive method are compared with that for the uniformly refined hierarchical FEM solutions in Fig. 12a, b. The convergence rates are calculated from displacement and stress errors. The adaptive method converges faster than the uniformly refined hierarchical FEM simulations. For the adaptive method, the convergence rate is ${\sim }\mathcal {O}(N^{-1.509})$ for the displacement norm and ${\sim }\mathcal {O}(N^{-0.861})$ for the stress norm, while those for the uniformly refined model are ${\sim }\mathcal {O}(N^{-1.179})$ and ${\sim }\mathcal {O}(N^{-0.733})$, respectively. In conclusion, the proposed adaptive wavelet enrichment method is robust with reduced computational costs while preserving the accuracy of local fields. It is very efficient when a conforming mesh cannot be obtained, such as for heterogeneous materials.

Fig. 12

Log-log plot of convergence rates of (a) displacement error $e_{ \boldsymbol {u}^f}$, (b) stress error $e_{ \boldsymbol {\sigma }^f}$ as a function of degrees of freedom at the end of simulation

6 Conclusions

This chapter emphasizes the need to explore novel methods and algorithms in computational mechanics to facilitate robust and efficient crystal plasticity FE-based modeling of deformation and failure in metals and alloys. Image-based CPFE models incorporate characteristic microstructural features, as well as underlying physical mechanisms. The claim for such innovative developments is made through three challenging problems that are often bottlenecks in crystal plasticity modeling of extreme mechanisms such as twinning and localization. Remedies to these challenges are developed through methods of element stabilization, multi-time-domain subcycling, and efficiency enhancement through wavelet enhanced hierarchical adaptivity. Many other opportunities exist in the crystal plasticity FE modeling arena. For example, when modeling fatigue failure, it is necessary to conduct simulations for a large number of cycles with a high time resolution to reach local states of crack nucleation and growth. A powerful, multi-resolution wavelet transformation induced multi-time scaling (WATMUS) algorithm has been developed in Chakraborty and Ghosh (2013) and Joseph et al. (2010) for accelerated cyclic simulations. The WATMUS methodology introduces wavelet decomposition of displacements and all associated variables in the finite element formulation to decouple the response into a monotonic cycle-scale behavior and oscillatory fine timescale behavior. In conclusion, this chapter provides motivation to look beyond available tools and make fundamental advances for effective predictive capabilities. Many of these codes will be hosted at the JHU Software Hub cited in Ghosh (2018).