Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A program obfuscator is a compiler that takes a program as input, and outputs a functionally equivalent program that is hard to reverse engineer. Early works by Hada [24] and Barak et al. [6] provided rigorous definitional treatment of obfuscation, but also showed the impossibility of achieving strong security notions for general circuits. In particular Virtual Black-Box (VBB) security, where interaction with the obfuscated program can be simulated using only black-box access to the obfuscated program, was proven impossible in general.

Constructing secure obfuscators, even heuristically, is a very challenging task. Indeed, until recently, candidate obfuscators were only known to exist for a few simple function classes. The game changer in this field had been the introduction of graded encoding schemes (GES) by Garg, Gentry and Halevi [20] and follow-up constructions by Coron, Lepoint and Tibouchi [18, 19]. GES allow to encode ring elements (from some underlying ring) in a way that hides the identity of the ring element, but still allows algebraic manipulation on the encoding (addition and multiplication). Each encoding is associated with a level, which is a positive integer (or more generally an integer vector). Addition is only allowed within a level, and in multiplication the level of the output is the sum of the levels of the inputs. A GES allows to test if the contents of an encoding is the zero element, but only at a predetermined “zero-test level”, and not beyond. Thus GES allows arithmetic operations of bounded degree.

Garg et al. [21] presented a candidate obfuscator for general circuits based on GES. They conjectured, with some supporting evidence, that their obfuscator is a secure indistinguishability obfuscator (iO). Indistinguishability obfuscation is a weak security notion and it first glance it may seem useless. However, Sahai and Waters [32] showed that iO is actually sufficient for a wide variety of applications. Numerous follow-up works showed how to use iO to construct many desirable cryptographic primitives, thus establishing iO itself as one of the most important cryptographic primitives. The goal of formally establishing the security of obfuscation candidates had since been central in cryptographic research.

Brakerski and Rothblum [12] presented a similar obfuscator candidate, and proved its security in the generic GES model. This model addresses adversaries that are restricted to algebraic attacks on the encoding scheme, i.e. generate encodings, perform algebraic manipulations and test for zero, while being oblivious to the representation of the element. This is modeled by representing the encodings using random strings, thus making them completely opaque. The algebraic functionality is provided as oracle. Other candidate obfuscators with generic proofs followed [1, 5, 28]. Pass, Seth and Telang [31] replaced the generic model with a strong notion of “uber-assumption”.

The constructions mentioned so far were all based on converting the obfuscated program into a branching program, thus having computational cost which scaled with the formula size of the program to be obfuscated.Footnote 1 This was improved by newer constructions that used composite order GES (where the underlying ring is isomorphic to \(\mathbb {Z}_N\) for a composite N). In a nutshell, composite order rings allow for “slotted” representation of elements via the Chinese Remainder Theorem, so that each ring element is viewed as a tuple of slots, and algebraic operations are performed slot-wise. In particular, Zimmerman [34] and Applebaum and Brakerski [2] presented obfuscators whose overhead relates to the circuit size of the program and not its formula size. However, using known candidate GES, the underlying encodings again incorporated overhead that depends on the formula size. Nonetheless, these constructions carry the promise that given more efficient GES candidates, the dependence on the formula size can be completely removed. Proofs in generic models were provided.

Since the generic model restricts the adversary beyond its actual attack capabilities, such proofs should be taken only as evidence in lieu of standard model proofs. In order for the evidence to carry more weight, we should be prudent and use models that pose as few restrictions as possible on the adversary.

For example, [2, 5, 34] consider a model where one assumes that not only encodings of different elements appear to the adversary as independent uniform strings, but also if the same element is computed in two different ways then it will have two independent-looking representations. This is a fairly strong assumption and in particular one that does not hold in cryptographic multilinear-maps, if such exist [7]. It is shown in [2] that the suggested obfuscation scheme actually breaks if one is allowed to even test for zero at levels below the zero-test level. They therefore proposed a more robust obfuscator that is secure in the unique representation model of [10–12], in which each ring element has a unique representation. Unfortunately, this added security came at a cost of reducing efficiency, specifically the number of “input slots” goes up from 2 to \(n+2\) (where n is the input length). This directly translates to an efficiency loss in the construction.Footnote 2 Boneh, Wu and Zimmerman [8] proposed a way to immunize GES so that zero encodings cannot be created below the zero-test level.

A notable progress in the study of secure obfuscation had been made recently by Gentry, Lewko, Sahai and Waters [22]. They showed an obfuscator whose security is based on an assumption in the standard model. It is yet unclear whether their hardness assumption holds true in known candidate GES (recent attacks [16, 30] suggest it might not). It should further be noted that this construction again requires a large number of input slots (essentially proportional to the formula size of the obfuscated circuit).Footnote 3

We see that the attempts to come up with a more realistic security model comes at the cost of increasing the number of required slots, and therefore reducing the efficiency. It is not clear whether this trade-off is necessary.

Does a stronger security model come at the cost of efficiency?

In this work, we show that at least in the generic model, one does not need to pay in efficiency to achieve better security.

We proceed to consider an even more conservative security model, one where even finding a non-trivial encoding of the zero element is assumed to obliterate security completely.Footnote 4 This model is motivated by new attacks on the security of all known proposed GES candidates [15–17, 20, 25, 30], showing that having access to encodings of the ring’s zero element results, in some cases, in a complete security breach. Indeed, current attacks do not work with just any non-trivial zero encoding, however they do raise concern that having an adversary access an encoding of zero might be a vulnerability. This concern had been significantly heightened recently as Miles, Sahai and Zhandry [29] presented an attack on obfuscators that are based on the [20] GES candidate. This new attack again makes crucial use of top-level encodings of zero (but does not require “low-level” zero encodings like some prior attacks).

To hedge against these risks, Badrinarayanan, Miles, Sahai and Zhandry [3] proposed to avoid zeros completely. Namely, to construct an obfuscator in such a way that the adversary is unable to generate such encodings altogether. However, this seems to defeat the purpose, since zero-testing is the way to extract information out of an encoding for functionality purposes. They get around this barrier in a creative way, by only obfuscating evasive functions, where finding an accepting input using oracle access is (unconditionally) hard.Footnote 5 Classes of evasive functions have played an important role in the study of obfuscation, since many classes that are desirable to obfuscate are evasive (e.g. various variants of point functions, starting with the work of Canetti [14]) and one could hope that they can even be obfuscatable in the strong VBB setting. (See [4] for more information and the state of the art about evasive functions.) Badrinarayanan et al. show that when their obfuscator is applied to an evasive function, the adversary is unable to find an encoding of zero. The proof here is in the generic model as well. The restriction to evasive functions, however, excludes interesting function classes such as conjunctions [10, 13]. We therefore address the following question.

Can we obfuscate non-evasive functions in the zero-sensitive model?

Perhaps surprisingly, we answer this question in the affirmative, and show that our obfuscator (the same as above) is secure in a zero-sensitive model, even for some non-evasive function classes, and in particular for worst-case conjunctions.

1.1 Our Results

A More Efficient Circuit Obfuscator. We present a new direct circuit obfuscator, i.e. one that does not go through branching programs. Our construction is inspired by the “robust obfuscator” \(\mathsf {RobustObf}\) of [2]. However, whereas \(\mathsf {RobustObf}\) works over a composite order graded encoding scheme with \((n+2)\) message slots, our obfuscator only requires 3 slots. Our obfuscator provides equivalent level of security to \(\mathsf {RobustObf}\) in the unique representation generic GES model (see details below). This improvement translates directly to a factor n improvement in the size of the encodings, and a \( poly (n)\)-factor improvement in the computational complexity of generating and evaluating the obfuscated program.Footnote 6 We therefore show that at least in the generic model, there is no real efficiency gain to working in a less secure model. We hope that our techniques can be translated to reduce the number of required slots in the non-generic setting as well, in particular in the [22] scheme.

We prove that the resulting obfuscator is indistinguishability secure in the unique representation graded encoding model. The proof outline is similar in spirit to that of the robust obfuscator of [2], while incorporating some proof techniques from [34]. In particular, we rely on the sub-exponential hardness of factoring the order of the underlying ring, in addition to the security of the generic model. In contrast, [2] work in a model where the order of the ring is hidden so that factoring it is information theoretically hard.

We note that one can consider many variants of the generic model: known modulus, unknown modulus and information theoretic hardness, computational hardness. Furthermore, [34] also shows how to prove VBB security at the cost of increasing the size of the obfuscator by additional \(n^2\) encodings. Our improvement can be applied to all of these variants, transforming them to the unique representation model while preserving the number of slots as constant. For the sake of concreteness, we chose to prove in a setting that we found interesting.

The Zero-Sensitive Oracle and All-or-Nothing Functions. We show that the [3] approach discussed above can be extended even beyond evasive functions. This may come as a surprise since applying our obfuscator to non-evasive functions gives the adversary access to zero encodings. As a motivating example, consider the class of conjunctions that had been studied in [10]. One can think of a conjunction as string-matching with wildcards. Namely, the function is defined by a string \(v \in \{0,1,\star \}^n\), and \(f_v(x)=1\) if and only if for all i, either \(v[i]=x[i]\) or \(v[i]=\star \). Indeed, some distributions on this class of functions are evasive, but what if we want to obfuscate it in the worst case?

Naturally, in the worst case there could be an adversary that can find an accepting input (more generally, no function class is evasive in the worst case except the zero function). However, the critical observation is that this does not necessarily hinder security, since given an accepting input, one can learn the entire function. In the case of conjunctions this is easy to do by taking an accepting x and flipping each of its bits in turn to see if this bit is a wildcard (and switching it back afterwards). Therefore, if we find an accepting input, we should not expect the obfuscator to hide anything anyway!

We generalize this property and define All-or-Nothing (AoN) function classes to be ones where if an adversary finds an accepting input, then it can recover the function in its entirety (a formal definition is provided). We would like to show that indeed such function classes can be securely obfuscated even in a setting where a non-trivial zero encoding implies that the GES is insecure.

In the proof of [3] for evasive functions, proving security was split into two tasks: presenting a simulator, and showing that the adversary cannot compute encodings of zero. Our notion of security, however, requires additional definitional treatment, since we would like successful simulation even in the case where an accepting input had been found, and we cannot tell in advance whether such an input will be found or not. We therefore define a new generic model where the GES oracle keeps track of the encodings that the adversary generates, and if one of those is a non-trivial zero, then the adversary gets access to a decoding oracle that allows to decode any given encoding to obtain the plaintext. This is how we model the risk in non-trivial zeros.

Finally, we prove that our obfuscator is indeed a secure VBB obfuscator for AoN functions in our new zero-sensitive model. Interestingly, we don’t need to use complexity leveraging here and we can prove VBB security without increasing the number of encodings. We view this as evidence that AoN functions may be strictly easier to obfuscate than general functions, and are perhaps a good candidate for VBB obfuscation in the standard model.

What GES Candidate To Use? We stress that our work is completely abstract and not directly related to any specific GES candidate, but naturally it would be more convincing if it could be instantiated with one. To date, the only candidate composite order GES is that of [18, 19], and indeed this candidate can be used with our scheme. We stress that the only known attacks on this candidate uses encodings of zero, and there are no known attacks in the zero evading model (this is also true for the [20] candidate). In fact, even in the “standard” model, the attacks of [17, 29] do not seem to apply to our obfuscator when instantiated with [18, 19]. However, these attacks suggest that obfuscators such as ours might be vulnerable to future attacks. The goal of finding secure instantiations of composite order candidate GES is a very important one, but orthogonal to the contributions of this paper.

1.2 Our Techniques

Our Obfuscator. Our building block is a graded encoding scheme whose plaintexts are elements in a composite order ring. We denote the encoding of the element a by \([{a}]\). Encodings can be added, subtracted, multiplied and tested for zero (subject to constraints imposed by the levels, which we will ignore in this outline since they are similar to previous works). We think of a itself as a tuple of elements via the Chinese Remainder Theorem. Each sub-ring is of high cardinality and it is assumed that “isolating” the components of an encoded element is computationally hard (in the generic model this relates to the hardness of factoring the order of the ring). The [2] obfuscator (following [10–12]) adds an additional layer on top of this encoding and rather than encoding \([{a}]\) itself, it produces a pair of encodings \([{r}]\) and \([{r\cdot a}]\), for a random r, i.e. the plaintext value is the ratio between the values in the two encodings. This “rational encoding” plays an important role in both functionality and security. For the purpose of this outline only, we use \([{a}]^{\scriptscriptstyle {\Diamond }}\) as shorthand notation for the pair \([{r}], [{r\cdot a}]\). It can be shown that rational encodings can be added and multiplied, subject to constraints as in previous works.

The starting point of our construction is the “robust obfuscator” from [2]. This obfuscator, in turn, is derived from a simpler solution [2, 34] that applies in a more forgiving generic model. In the “simple obfuscator”, for each input bit i, two encodings are given as a part of the obfuscator. These encodings are of the form \([{(y_i,b)}]^{\scriptscriptstyle {\Diamond }}\), for \(b \in \{0,1\}\), where \(y_i\) is a random value that is the same whether \(b=0\) or 1. The weakness of this scheme stems from the ability to subtract the two encodings that correspond to the same i, and cancel out the \(y_i\) value to obtain an encoding of the form \([{(0,1)}]^{\scriptscriptstyle {\Diamond }}\), which in turn allows to test whether the second slot of a given encoding is zero or not (via multiplying by \([{(0,1)}]^{\scriptscriptstyle {\Diamond }}\) and zero-testing). In the less restrictive multiple representation generic model, this attack is prevented by disallowing to test for zero in some situations. However, this cannot be avoided in a model where each element has a unique representation since one can always test for zero by comparing to a known encoding of zero.

The robust obfuscator from [2] prevents this problem by adding n additional slots to the encodings, and publishing, for each input bit of the obfuscated function, the values \([{w_{i,b}}]^{\scriptscriptstyle {\Diamond }}\), for \(b \in \{0,1\}\), where \(w_{i,b}={(y_i, b, \rho _{1,b}, \ldots , \rho _{n,b})}\). The \(\rho \) values are uniform and independent, and therefore subtracting \([{w_{i,1}}]^{\scriptscriptstyle {\Diamond }}-[{w_{i,0}}]^{\scriptscriptstyle {\Diamond }}\) here will not cancel out the \(\rho \) values. The \(\rho \) values should be eliminated in the end of the computation, and this is done by providing additional encodings of a special form \(\hat{w}_{i, b} = (\hat{y}_i, \beta _{i,b}, \hat{\rho }_{1,b}, \ldots , \hat{\rho }_{i-1,b}, 0,\hat{\rho }_{i+1,b}, \ldots , \hat{\rho }_{n,b})\). Namely, encodings that zero out the ith \(\rho \) value. In the evaluation, the value \(\prod _i \hat{w}_{i, x_i}\) is computed and multiplied with the result of the computation so far, thus zeroing out the last n slots. Note that even though the \(\rho \) values can be zeroed out, this does not enable the previous attack. This is due to the level constraints that impose structural limitations. In particular, \([{\hat{w}_{i,0}}]^{\scriptscriptstyle {\Diamond }}\) and \([{w_{i,1}}]^{\scriptscriptstyle {\Diamond }}\) cannot be used in the same computation, which is in contrast to \([{w_{i,0}}]^{\scriptscriptstyle {\Diamond }}\) and \([{w_{i,1}}]^{\scriptscriptstyle {\Diamond }}\) that cannot be prevented from interacting (at a high level, this is because each input bit can be used many times in the circuit, but the \(\hat{w}\) values are designed to only be used once).

Our modification to this scheme is quite simple. We observe that the use of n different \(\rho \) slots is only due to the cancellation step via \(\hat{w}\), where we need to enforce that an adversary must use a \([{\hat{w}_{i,b}}]^{\scriptscriptstyle {\Diamond }}\) value for each and every i. The reason is that this use prevents the dangerous mix-and-match of \([{w_{i,0}}]^{\scriptscriptstyle {\Diamond }}\) and \([{w_{i,1}}]^{\scriptscriptstyle {\Diamond }}\). We notice, however, that since rational encodings can be added and not just multiplied, one could enforce that an \(\hat{w}_{i,b}\) is used for every i using a sum rather than a product. We set \(\hat{w}_{i, b} = (\hat{y}_i, \beta _{i,b}, \hat{\rho }_{i})\), thus reducing the number of sub-rings to only 3. We choose the \(\hat{\rho }_i\) values at random, subject to the constraint that \(\sum _i \hat{\rho }_i = 0\). This means that in order to zero-out the \(\hat{\rho }\) coordinate, an adversary needs to use a \([{\hat{w}_{i,b}}]^{\scriptscriptstyle {\Diamond }}\) element for every i. As before, we must prevent \([{\hat{w}_{i,0}}]^{\scriptscriptstyle {\Diamond }}\) and \([{\hat{w}_{i,1}}]^{\scriptscriptstyle {\Diamond }}\) from interacting, since taking their difference zeros out the \(\hat{\rho }\) coordinate and is therefore dangerous, but this is done in the same way as previous works.

Proving Security. As has been shown in a number of previous works, in the generic model, the adversary is limited to applying arithmetic circuits over the encodings received as input, and testing the output for zero. The simulator, therefore, generates a collection of random strings to play the role of the encodings in the obfuscated program, and then to answer queries of the form of an arithmetic circuit, determining whether applying this circuit to the encodings at hand evaluates to zero.Footnote 7 The problem is that the simulator needs to do this with only oracle access to the obfuscated circuit. Namely, it does not fully know what is the plaintext in the encoding that it generated.

We use a proof practice that started with [10]. They notice that if we use rational encoding as described above, then the polynomial computed by an arithmetic circuit can be decomposed into a sum of terms that we call semi-monomials. A semi-monomial is a polynomial of the form \(M(\vec {r})Q(\vec {w})\), where \(M(\vec {r})\) is a product of “randomizing” variables, and \(Q(\vec {w})\) is a polynomial in the “content” variables. Since the randomizer variables are random and independent, the task of testing the polynomial for zero is identical to the task of finding whether there exists a non-zero semi-monomial.

We distinguish between semi-monomials that are “valid”, in the sense that they represent a legal evaluation of the circuit on an input, and ones that are “invalid”. We show how to test if a semi-monomial is valid or not, and that an invalid semi-monomial cannot zero-out, regardless which circuit had been obfuscated, assuming the hardness of factoring the ring order. We show that “valid” monomials zero-out if and only if the obfuscated circuit accepts their associated input x.

Therefore, our proof strategy is straightforward. We extract semi-monomials from the circuit one after the other.Footnote 8 For each semi-monomial, we check whether it is invalid, in which case we can immediately return that the arithmetic circuit computes a non-zero. If the semi-monomial is valid for some input x, we query the obfuscated circuit oracle on x. If it rejects, then the answer is again non-zero, but if it accepts, then the answer is still undetermined and we need to proceed to the next semi-monomial.

This process takes \(2^n\) time in the worst case, since there can be at most \(2^n\) valid semi-monomials. Thus the running time of our iO simulator is exponential in the input length. However, in the case of AoN functions, the situation is much simpler and in fact only one semi-monomial needs to be inspected. The reason is that if the extracted x is an accepting input for the circuit, then we don’t need to proceed at all, since for AoN functions, we can efficiently learn the code of the circuit, which allows us to continue the simulation trivially by just assigning the right values to the \(\vec {w}\) variables. This completes the proof.

1.3 Paper Organization

In Sect. 2 we present our new generic model as well as our new zero-sensitive model, which is a new contribution. Section 3 features the specifics of our obfuscator, and security is proven in Sect. 4, where we also define the class of AoN functions. Due to space constraints, much of the technical content is deferred to the full version [9].

2 The Generic GES Model and Our New Zero-Sensitive Variant

We would like to prove the security of our construction against generic adversaries. To this end, we will use the generic graded encoding scheme model, adapted from [5, 10–12], which is analogous to the generic group model (see Shoup [33] and Maurer [27]).

There are various flavors of generic models suggested in the literature. In this work, we follow [2, 10] and use the unique-representation model, where each element in the underlying ring, at each level, has a unique representation. This is in contrast to the multiple-representation model [2, 5, 34] which (roughly) states that if the same element is being computed via different computational paths, then each path will lead to a different and independent representation of that element. While the latter model makes the task of proving security easier, it is inadequate in some situations, as we described in the introduction. We note that a proof in the unique representation model immediately carries over to the multiple representation model, but not the other way around. We provide a definition of this model in Sect. 2.1 below.

We then introduce our zero-sensitive model. This model is motivated by recent attacks that leverage non-trivial encodings of zero. In this model we treat a non-trivial encoding of zero at any level as perilous. In particular, once such an encoding had been generated, the GES oracle will no longer keep any secret, and surrender the plaintexts of all encodings to the adversary. As we explained above, we can prove security of all-or-nothing functions in this model. See Sect. 2.2 for details.

Lastly, in Sect. 2.3, we define indistinguishability and virtual black-box obfuscation in the presence of our oracles.

2.1 The Ideal GES Oracle

We present the “online” variant of the unique representation model. As shown in previous works, this variant is equivalent to the “offline” variant up to negligible statistical distance. See [2, 10] for more details. We model the GES using an oracle \(\mathcal{RG}\) which implements the functionality of a GES in which the representations of elements are uniform and independent random strings.

The Online \(\mathcal{RG}\) Oracle. The online \(\mathcal{RG}\) oracle is implemented by an online polynomial time process, which samples representations for ring elements on-the-fly. Specifically, the oracle will maintain a table of entries of the form \((\mathbf {v}, a, \mathsf {label}_{\mathbf {v}, a})\), where \(\mathsf {label}_{\mathbf {v},a} \in \{0,1\}^t\) is the representation of \([{a}]_{{\mathbf {v}}}\) in \(\mathcal{RG}\), and F is either a formal variable or an arithmetic circuit over formal variables. The table is initially empty and is filled as described below.

  • Whenever a sampling query is made, \(\mathcal{RG}\) generates an element a from \(\mathcal {R}\) (or the appropriate sub-ring), and a uniform length t label. It then stores the tuple \((\mathbf {0}, a, \mathsf {label}_{\mathbf {0}, a})\) in its table.

  • For encoding and arithmetic operations, the oracle takes the input labels and finds appropriate entries in the table that correspond to these labels. If such don’t exist then \(\bot \) is returned. Otherwise, the oracle retrieves the appropriate \((\mathbf {v}, a)\) values to perform the operation. It then checks that the level values are appropriate (e.g. \(\mathsf {encRand}\) can only be applied to level zero encodings, addition can only take two operands of the same level), and computes the output of the operation. It then performs the computation on the ring elements. Finally, the oracle needs to return an encoding of an element of the form \((\mathbf {v}', a')\). To do this, the oracle checks whether \((\mathbf {v}', a')\) is already in the table, and if so returns the appropriate \(\mathsf {label}_{\mathbf {v}', a'}\). Otherwise it samples a new uniform label, and inserts a new entry into the table. Otherwise it samples a new uniform label, and inserts a new entry into the table.

  • Extraction is trivial in our representation, one can just use \(\mathsf {label}_{\mathbf {v}', a'}\) as the extracted value for \([{a}]_{{\mathbf {v}}}\).

  • Zero testing is performed by finding the appropriate entry in the table and checking whether the respective ring element is indeed 0.

2.2 The Zero-Sensitive Generic Model

We propose a new generic model that incorporates the zero-evading requirement of [3] into the generic GES model. Whereas our oracle is a modification of the unique representation generic model presented above, similar modifications can be made to other generic models in the literature.

We propose a generic model with an additional decoding functionality which will allow the adversary to retrieve the plaintext of any encoding of its choosing, once an encoding of zero had been generated. Some care needs to be taken, since it is easy to produce “syntactic zeros” which are harmless. E.g. subtracting an encoding from itself will produce such a zero encoding, or less trivially, computing an expression of the form \((A+B)*C-(C*A+C*B)\). These expressions will evaluate to zero regardless of the values that are actually encoded in A, B, C and we refer to them as “trivial” or “syntactic” zeros. Such encodings of zero are unavoidable, but they are not dangerous. (Indeed, in known instantiations of GES [18–20], syntactic zeros are always encoded by the all-zero string and thus provide no meaningful information.) We design an oracle that whenever a non-syntactic zero is created (or rather, when it could potentially be created), enables the decoding feature.

We consider the encodings that are generated by the \(\mathsf {encRand}\) function as atomic variables, and for every encoding generated by the adversary throughout the computation, we maintain its representation as an algebraic circuit over these variables. Whenever two syntactically different such arithmetic circuits evaluate to the same value, we enable the decoding feature. Details follow.

The \(\mathcal{RG}_\mathcal{Z}\) Oracle. The new oracle is based on the functionality of the oracle \(\mathcal{RG}\) defined in Sect. 2.1. It will maintain a table similarly to \(\mathcal{RG}\), but in addition each entry in the table will contain an additional value in the form of an arithmetic circuit over the formal variables \(X_1, X_2, \ldots \). Elements encoded at level \(\mathbf {0}\) will not have a circuit associated with them, but whenever \(\mathsf {encRand}\) is executed, the resulting element will be stored in the table together with a new variable \(X_i\). It will also maintain a global binary state \(\mathsf {decode}\) which is initialized to \(\mathsf {false}\).

When the arithmetic functionality of \(\mathcal{RG}_\mathcal{Z}\) is called, say on operands \(A_1, A_2\) whose table entries are \((\mathbf {v}_1, a_1, A_1, C_1)\), \((\mathbf {v}_1, a_2, A_2, C_2)\), it performs exactly as \(\mathcal{RG}\) and computes the values \((\mathbf {v}', a')\) corresponding to the level and value of the result. In addition \(\mathcal{RG}_\mathcal{Z}\) also defines \(C' = C_1 \mathsf {op} C_2\), where \(\mathsf {op}\) is the arithmetic operation to be performed (e.g. \(C'=C_1+C_2\) or \(C' = C_1 \times C_2\)). Then, just like in \(\mathcal{RG}\), we search the table to find whether \((\mathbf {v}', a')\) already appears. If it does not, then a new label \(A'\) is generated, \((\mathbf {v}', a', A', C')\) is stored in the table, and \(A'\) is returned. However, if there already exists \((\mathbf {v}', a', A'', C'')\) in the table, then there is potential for a non-trivial zero in the case where \(C' \not \equiv C''\). This equivalence is easy to check (even in polynomial time using Schwartz-Zippel). If the circuits are equivalent: \(C' \equiv C''\), then there is no risk, the table entry does not change and \(A''\) is returned. However, if indeed \(C' \not \equiv C''\), then the adversary can create a non-trivial zero (since he generated the element \(a'\) in two syntactically different ways). Therefore, in this event, \(\mathcal{RG}_\mathcal{Z}\) sets \(\mathsf {decode}= \mathsf {true}\).

As explained above, \(\mathcal{RG}_\mathcal{Z}\) also provides an additional decoding functionality: \(\mathsf {Decode}(A)\). This function, upon receiving an encoding A as input, first checks the \(\mathsf {decode}\) variable. If \(\mathsf {decode}=\mathsf {false}\) then it returns \(\bot \). Otherwise, it searches the table for and entry whose label is A, and returns the corresponding “plaintext” value a.

Non-trivial Zeros in the Unique Representation Model. Our zero evading model has unique representations, in the sense that the oracle assigns a single string to each ring element. This state of affairs may be confusing, since if there is only one representation for each element (in particular, the zero element), it may seem that the distinction between trivial and non-trivial zeros is meaningless. While this intuition is true in the standard model, in a generic model the \(\mathcal{RG}\) oracle can judge whether an encoding of zero is trivial or not even though they are represented by the same string, since it can keep track of the path the adversary took in generating said encoding. In fact, security in our model is stronger than in a model that allows multiple representations. Details follow.

We note that unique representation GES (call it uGES for short) is effectively equivalent to multiple representations GES (mGES) in which zero-testing can be performed anywhere below level \(\mathbf {v}_{\text {zt}}\) and not just at \(\mathbf {v}_{\text {zt}}\) itself. This is because the adversary can always think about the first representation of a specific element as the “real” one. Whenever it sees a new encoding, it can subtract it from all previous ones that it saw in the same level, and test for zero, thus discovering if two different encodings in fact refer to the same element. Therefore, by using uGES we only give the adversary extra power. Another advantage of using uGES is that the extraction procedure becomes trivially defined and does not need additional machinery. One can thus think of our use of uGES as a formalism that allows us to seamlessly handle cases such as mGES with low-level zero-testing (and extraction).

2.3 Obfuscation in the Generic GES Model

These definitions are fairly standard and originate from [10]. We start with correctness, which should hold with respect to an arbitrary GES implementation.

Definition 2.1

(Preserving Functionality). A GES-based obfuscation scheme \((\mathsf {Obf},\mathsf {Eval})\) for \(\mathcal {C}\) is functionality preserving if for every instantiation \(\mathcal {G}\) of GES, every \(n\in \mathbb {N}\), every \(C_K \in \mathcal {C}\) where \(K\in \{0,1\}^{m(n)}\), and every \(x \in \{0,1\}^n\), with all but \(\mathsf {negl}(\lambda )\) probability over the coins of \(\mathsf {Obf},\mathsf {Eval}\) and the GES oracle \(\mathcal {G}\) it holds that:

$$\begin{aligned} \mathsf {Eval}^{\mathcal {G}}(1^n,1^{\lambda }, \hat{C},x)=C_{K}(x),\qquad \text {where } \hat{C}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}\mathsf {Obf}^{\mathcal {G}}(1^n,1^{\lambda },K). \end{aligned}$$

We define Indistinguishability Obfuscator with respect to some (possibly inefficient) GES instantiation. Our definition is formulated in terms of unbounded simulation which is equivalent to the more standard indistinguishability-based definition (cf. [12]).

Definition 2.2

(Indistinguishability/VBB Security [6]). A GES-based obfuscation scheme \((\mathsf {Obf},\mathsf {Eval})\) for \(\mathcal {C}\) is called an Indistinguishability Obfuscator (iO) with respect to some GES instantiation \(\mathcal {G}\) (which possibly contains a decode function) if for every polynomial size adversary \(\mathcal {A}\), there exists a (computationally unbounded) simulator \(\mathcal {S}\), such that for every \(n \in \mathbb {N}\) and for every \(C_K \in \mathcal {C}\) where \(K\in \{0,1\}^{m(n)}\):

$$\big | \Pr [\mathcal {A}^{\mathcal {G}}(1^{\lambda },\hat{C}) = 1 ] - \Pr [\mathcal {S}^{C_K}(1^{|K|},1^n,1^{\lambda }) = 1] \big | = \mathsf {negl}(\lambda ), $$

where \(\hat{C}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \$}\mathsf {Obf}^{\mathcal {G}}(1^n,1^{\lambda },K)\). If the simulator can be implemented by polynomial size circuits than the obfuscator is Virtually Black-Box (VBB) secure.

3 Description of Our Obfuscator and Its Correctness

3.1 Setting and Definitions

We define \(\mathcal {C}=\left\{ \mathcal {C}_K\right\} _{K\in \left\{ 0,1\right\} ^*}\) to be a family of efficiently computable functions with n-bit inputs, representation size \(m=m(n)\) and universal evaluator \(\mathcal {U}\). And we let \(\hat{\mathcal {U}}\) be the arithmetized version of \(\mathcal {U}\). That is, an arithmetic circuits with \(\{+,\times \}\) gates such that for any field \(\mathbb {F}\) if \((x,K)\in \left\{ 0,1\right\} ^{n+m}\subseteq \mathbb {F}^{n+m}\), then \(\hat{\mathcal {U}}(x,K)=C_K(x)\). We also denote by \(D_{\hat{\mathcal {U}}}\) the degree of the polynomial computed by \(\hat{\mathcal {U}}\).

We define the multiplicity of input wire i as follows. We consider an enumeration of the wires of \(\hat{\mathcal {U}}\) in topological order, such that the first \(n+m\) wires refer to the wires of the x, C inputs. For each wire i we define a vector \(\mathbf {s}_i\in \mathbb {Z}^{n+m}\) as follows. If \(i\le n+m\), then \(\mathbf {s}_i=\mathbf {e}_i\) (the ith indicator vector). For a wire i which is the output wire of a gate whose input wires are \(j_1,j_2\), we define \(\mathbf {s}_{i}=\mathbf {s}_{j_1}+\mathbf {s}_{j_2}\). The multiplicity is defined to be \(M_i=\mathbf {s}_\mathrm {out}\left[ i\right] \), where “out” is the output wire of \(\hat{\mathcal {U}}\).

3.2 The Obfuscator \(\mathsf {Obf}\)

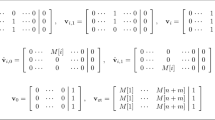
For all \(i\in \left[ n\right] \), \(b\in \left\{ 0,1\right\} \) we define \(\mathbf {v}_{i,b}\in \mathbb {Z}^{\left( n+m+1\right) \times 4}\) as \(\mathbf v_{i,b}=\mathbf {e}_i\otimes \left[ b,1,1-b,0\right] \). We further define \(\hat{\mathbf {v}}_{i,b}=\mathbf {e}_i\otimes \left[ \left( 1-b \right) \cdot M\left[ i \right] ,0,b\cdot M\left[ i \right] ,1\right] \).

For all \(i\in \left\{ n+1,\dots ,n+m \right\} \) we define \(\mathbf {v}_{i}=e_i\otimes \left[ 1,1,1,0\right] \). We define \(\mathbf {v}_0=\mathbf {e}_{n+m+1}\otimes \left[ 1,1,1,0\right] \) and \(\mathbf {v}^*=\mathbf {e}_{n+m+1}\otimes \left[ 0,0,0,1\right] \). Lastly, we define: \(\mathbf {v}_{\mathrm {zt}}=\left( \mathbf {s}_\mathrm {out}+\mathbf {e}_{n+m+1}\right) \otimes \left[ 1,1,1,0\right] +\left( \sum _{i=1}^{n+m}\mathbf {e}_i\right) \otimes \left[ 0,0,0,1\right] +D\cdot \mathbf {v}^*\in \mathbb {Z}^{(n+m+1)\times 4} \), where \(D=D_{\hat{\mathcal {U}}}+n\). We note that for all \(x\in \left\{ 0,1\right\} ^n\) it holds that \(\mathbf {v}_{\text {zt}}=\mathbf {v}_0+\sum _{i=1}^n\left( M\left[ i\right] \cdot \mathbf {v}_{i,x_i}+\hat{\mathbf {v}}_{i,x_i} \right) + \sum _{i=n+1}^{n+m}M\left[ i\right] \cdot \mathbf {v}_i+D\cdot \mathbf {v}^* \). We illustrate the various level vectors in Fig. 1.

Fig. 1.
figure 1

The level vectors for the obfuscator.

Full size image

The Obfuscator \(\mathsf {Obf}\) :

  • Input: Circuit identifier \(K\in \left\{ 0,1\right\} ^m\) where \(C_K\in \mathcal {C}\) and a security parameter \(\lambda \).

  • Output: Obfuscated program with the same functionality as \(C_K\).

  • Algorithm:

    1. 1.

      Instantiate a 3-composite graded encoding scheme

      $$\begin{aligned} \left( params,evparams\right) =\mathrm {InstGen}(1^{\lambda +\log \Vert \mathbf {v}_{\text {zt}}\Vert _1},1^{3},\mathbf {v}_{\text {zt}}). \end{aligned}$$
    2. 2.

      For all \(i\in \left[ n\right] \), compute random encodings \(R_{i,b}=\left[ r_{i,b}\right] _{\mathbf {v}_{i,b}}\) as well as encodings of \(Z_{i,b}=\left[ r_{i,b}\cdot w_{i,b}\right] _{\mathbf {v}_{i,b}+\mathbf {v}^*}\), where \(w_{i,b}=\left( y_i,b,\rho _{i,b}\right) \) and \(y_i,\rho _{i,b}\) are uniform.

    3. 3.

      For all \(i\in \left[ i\right] \), compute random encodings: \(\hat{R}_{i,b}=\left[ \hat{r}_{i,b}\right] _{\hat{\mathbf {v}}_{i,b}}\) as well as encodings of \(\hat{Z}_{i,b}=\left[ \hat{r}_{i,b}\cdot \hat{w}_{i,b}\right] _{\hat{\mathbf {v}}_{i,b}+\mathbf {v}^*}\), where \(\hat{w}_i=(\hat{y}_i,\hat{\beta }_i,\hat{\rho }_i)\), where \(\hat{y}_i,\hat{\beta }_i,\left\{ \hat{\rho }_i\right\} _{i\ne n}\) are all uniform but \(\hat{\rho }_n=-\sum _{i=1}^{n-1}\hat{\rho }_i\).

    4. 4.

      For all \(i\in \left\{ n+1,\dots ,n+m\right\} \), compute random encodings \(R_i=\left[ r_i\right] _{\mathbf {v}_i}\) as well as encodings of \(Z_i=\left[ r_i\cdot w_i\right] _{\mathbf {v}_i+\mathbf {v}^*}\), where \(w_i=(y_i,K_{i-n},\rho _i)\), where \(K_i\) is the ith bit of the circuit description and \(y_j,\rho _{i}\) are uniform.

    5. 5.

      Compute random encoding \(R_0=\left[ r_0\right] _{\mathbf {v}_0}\) and \(Z_0=\left[ r_0\cdot w_0\right] _{\mathbf {v}_0+D\mathbf {v}^*}\), where \(w_0=\left( \sum _{i\in [n]}\hat{w}_i\right) \cdot (y_0,1,0)\) and \(y_0=\hat{\mathcal {U}}(y_1,\dots ,y_{n+m})\).

    6. 6.

      The obfuscated program will contain the following:

      • The evaluation parameters evparams.

      • For all \(i\in [n], b\in \{0,1\}\) the elements \(R_{i,b},Z_{i,b},\hat{R}_{i,b},\hat{Z}_{i,b}\).

      • For all \(i\in \{n+1,\dots ,n+m\}\) the elements \(R_i,Z_i\).

      • The elements \(R_0,Z_0\).

We denote by \(\mathcal {D}_\lambda (n,K)\) the distribution over the encoded ring elements the obfuscator outputs according to the construction. Evaluating an obfuscated program is done in a straightforward manner, similarly to previous works. See full version [9] for details.

4 Security

This section contains security proofs for \(\mathsf {Obf}\) for all-or-nothing functions (defined in Sect. 4.1) in the zero-sensitive \(\mathcal{RG}_\mathcal{Z}\) model (Sect. 4.2).

Due to space limitations we are only able to present the outline of the security analysis. The proof in the classical generic model follows fairly similar lines and is outline in the end of Sect. 4.2. Many details are missing in this high level presentation and we encourage the reader who wishes to see the entire analysis in context to refer to the full version [9].

4.1 All-or-Nothing (\(\mathsf {AoN}\)) Functions

We define a category of “all or nothing” functions. These are functions such that are either evasive or perfectly learnable, namely, finding an accepting input for a function in the class implies that the code of the function can be retrieved. This class is an extension of the class of evasive functions. For simplicity we provide the definition in the standalone setting, but it can be extended to the auxiliary input setting as well.

Definition 4.1

An ensemble of functions \(\mathcal {C}= \{ \mathcal {C}_n \}\) is \(\mathsf {AoN}\) if for any \(\text{ ppt }\) algorithm \(\mathcal {A}\), there exists a \(\text{ ppt }\) algorithm \(\mathcal {B}\) such that for all \(C \in \mathcal {C}_n\),

$$ \mathop {\Pr }\limits _r\left[ \left( C\left( \mathcal {A}^C\left( 1^n; r\right) \right) =1\right) \wedge \left( \mathcal {B}^C(1^n; r) \ne C\right) \right] =\mathsf {negl}(\lambda )~, $$

that is \(\mathcal {A}, \mathcal {B}\) use the same random tape r.

We can also define an average-case analogue:

Definition 4.2

An ensemble of functions \(\mathcal {C}= \{ \mathcal {C}_n \}\) together with distributions \(\{\mathcal {D}_n\}\) over \(\mathcal {C}\) is average-case \(\mathsf {AoN}\) if for any \(\text{ ppt }\) algorithm \(\mathcal {A}\), there exists a \(\text{ ppt }\) algorithm \(\mathcal {B}\) such that:

$$ \mathop {\Pr }\limits _{r,\;C\leftarrow \mathcal {D}_n}\left[ \left( C\left( \mathcal {A}^C\left( 1^n; r\right) \right) =1\right) \wedge \left( \mathcal {B}^C(1^n; r) \ne C\right) \right] =\mathsf {negl}(\lambda )~, $$

that is \(\mathcal {A}, \mathcal {B}\) use the same random tape r.

Note that we ask that \(\mathcal {B}\) outputs the exact code of C, given only black box access. Therefore, \(\mathsf {AoN}\) function classes which are not evasive need to have programs with unique representations. This indeed holds for classes such as conjunctions.

4.2 Zero-Sensitive Security for All-or-Nothing Functions

The following theorem states the VBB security of \(\mathsf {Obf}\) for any class of \(\mathsf {AoN}\) functions. We note that while we provide a proof for worst-case \(\mathsf {AoN}\), the average case setting follows by a similar proof (note that there could exist function classes that are average case \(\mathsf {AoN}\) but not worst case \(\mathsf {AoN}\)).

Theorem 4.3

Assuming factoring is hard then if \(\mathcal {C}\) is a family of \(\mathsf {AoN}\) functions, then \(\mathsf {Obf}\) is VBB-secure with respect to the oracle \(\mathcal{RG}_\mathcal{Z}\).

Proof

In order to prove VBB security, we want to define an efficient simulator \(\mathcal {S}\) that will simulate the view of the adversary using only an oracle access to \(C_K\).

Similarly to the definition of the \(\mathcal{RG}_\mathcal{Z}\) oracle in Sect. 2.2, the simulator \(\mathcal {S}\) will need to act differently when a non-trivial encoding of zero is encountered (that is, simulate the performance of \(\mathcal{RG}_\mathcal{Z}\) when \(\mathsf {decode}=\mathsf {true}\)). The simulator will maintain a variable \(\mathsf {decode}\) that upon initialization will be set to \(\mathsf {false}\) and only when we encounter a non-trivial encoding of zero it will be set to \(\mathsf {true}\). As long as \(\mathsf {decode}=\mathsf {false}\), we use the hardness of factorization in order to show that finding non-trivial zero using invalid monomials is unlikely, therefore up to the point where such encoding is found, the simulator will not use the factorization of the ring at all. The factorization will only be used afterwards in order to continue the simulation after \(\mathsf {decode}\) was set to \(\mathsf {true}\).

Initialization: The simulator generate a number \(N\) which it knows how to factor into three factors \( p_1,p_2,p_3 \) (which have \(\gcd (p_i,p_j)=1\) for \(i\ne j\), but does not have to be primes). In similar with the \(\mathcal{RG}_\mathcal{Z}\) oracle, the simulator will also create a table \(\mathcal {L}\). For each encoding the obfuscator outputs, \(\mathcal {S}\) will create a row in the table associating random label string with the formal variable represented by the encoding and the appropriate level of the encoding. \(\mathcal {S}\), just like the obfuscator, will output a list of label strings for each of the obfuscated encodings and give them to the adversary. The only difference between the simulator and the oracle here is that the ring element is not stored in the table at this point.

\(\mathcal {S}.\mathsf {Add}(\mathrm {enc}_1,\mathrm {enc}_2),\mathcal {S}.\mathsf {Mult}(\mathrm {enc}_1,\mathrm {enc}_2),\mathcal {S}.\mathsf {Negate}(\mathrm {enc})\) : Given an arithmetic operation (Add, Mult, Negate), the simulator will construct an arithmetic-circuit \(A_\mathrm {res}=A_{\mathsf {enc}_1}\;\mathrm {op}\;A_{\mathsf {enc}_2}\) (where \(A_{\mathsf {enc}_1}\) and \(A_{\mathsf {enc}_2}\) are the arithmetic-circuits associated with \(\mathsf {enc}_1\) and \(\mathsf {enc}_2\) respectively) and check if it is equivalent to one of the other elements in the table with the same level. It can easily be done by subtracting \(A_\mathrm {res}\) from the arithmetic-circuit in the table and using \( \mathsf {isZero} \) procedure. If they are equivalent, the simulator will response with the same label. Otherwise, the simulator will create a new row in \(\mathcal {L}\) containing a new label, \(A_\mathrm {res}\) and the new level. Outputs the label to the adversary.

\(\mathcal {S}.\mathsf {isZero}(\mathrm {enc})\) : The \( \mathsf {isZero} \) algorithm works differently when \(\mathsf {decode}\) is set to \(\mathsf {true}\) or \(\mathsf {false}\).

The Case Where \(\mathsf {decode}=\mathsf {false}\) : The simulator will check if \(\mathrm {enc}\) is in \(\mathcal {L}\). If not it will output \(\bot \), otherwise the simulator use the following algorithm:

  1. 1.

    Use the \(\mathsf {AoNZero}\) algorithm from Lemma 4.5 on the arithmetic-circuit associated with \(\mathsf {enc}\) in order to determine whether it evaluates to zero or in order to find an accepting input. If the algorithm output a decision regarding the evaluation of the arithmetic-circuit output it.

  2. 2.

    Otherwise, we note that the adversary together with the simulator up to this point is an efficient algorithm that finds an accepting input. From the definition of the function class (Definition 4.1) we can use the \( \mathcal {B}\) algorithm associated with this combined algorithm in order to find the code of the obfuscated circuit C.

  3. 3.

    Generate values to all the formal variables given in the initialization step using the known factorization of the ring. And store the values for future use.

    We note that when we choose random variables, we could have broken consistency with previous queries, as it could have been that using these values previous \( \mathsf {isZero} \) calls would have response with true. But note that such inconsistency can only occur with negligible probability.

  4. 4.

    Set \(\mathsf {decode}=\mathsf {true}\) and run \(\mathcal {S}.\mathsf {isZero}(\mathrm {enc})\) again.

Remark 4.4

The \(\mathsf {isZero}\) algorithm this case can only return that the value is indeed “zero” if the encoded element is a trivial zero. In any other case we either output “non-zero” or we change to the case where \(\mathsf {decode}=\mathsf {true}\).

The Case Where \(\mathsf {decode}=\mathsf {true}\) : In this case, the simulator has already assigned values to each of the formal variables in the table \(\mathcal {L}\), and therefore it can easily evaluate the result of the arithmetic-circuit associated with \(\mathsf {enc}\) and reply to the \(\mathsf {isZero}\) accordingly.

\(\mathcal {S}.\mathsf {Decode}(\mathsf {enc})\) : If \(\mathsf {decode}=\mathsf {false}\) simply return \(\bot \) as this is what the simulator will do. We note that in every arithmetic operation that the adversary does, we initiate \(\mathsf {isZero}\) on all the elements at the same level. Therefore, if the adversary succeeded in finding a non-trivial zero or received the same element in two different ways, the simulator will change \(\mathsf {decode}\) to be \(\mathsf {true}\). Thus in that case, the simulator has already assigned values to all the formal variables used in the arithmetic-circuit associated with \( \mathrm {enc} \). By substituting those variables into this arithmetic-circuit results the decoded value of \( \mathrm {enc} \) which we can output to the adversary.

Correctness: We want to show the correctness of the \( \mathcal {S}.\mathsf {isZero} \) procedure in both cases. We note that if \(\mathsf {decode}=\mathsf {true}\), the simulator already knows the function evaluated and it have assignments to all the formal variables that are in use, therefore, it is clear that substituting this values in the arithmetic-circuit associated with the encoding the adversary wish to zero test will yield a correct answer.

On the other hand, while \(\mathsf {decode}=\mathsf {false}\), the correctness is immediate from the correctness of Lemma 4.5 together with the definition of the \(\mathsf {AoN}\) class and the hardness of factoring. But using the hardness of factoring is delicate since \(\mathcal {S}\) knows factors of \(N\), therefore we cannot simply solve factoring using the simulator, because in order to construct the simulator those factors are needed to be known in advanced. We note that once \(\mathsf {decode}=\mathsf {true}\) the hardness of factoring doesn’t play a role in the correctness of the simulator.

Because we only care when \(\mathsf {decode}=\mathsf {false}\), we can construct a new simulator \(\mathcal {S}_1\) that will abort when \(\mathsf {decode}=\mathsf {true}\). It is clear that if \(\mathsf {AoNZero}\) in \(\mathcal {S}\) broke factoring while \(\mathsf {decode}=\mathsf {false}\) so it must during \(\mathcal {S}_1\). Now, we introduce the simulator \(\mathcal {S}_2\) which is similar to \(\mathcal {S}_1\) only that \(\mathcal {S}_2\) does not know any proper factors of \(N\). We notice that those factors are only being used when we set \(\mathsf {decode}=\mathsf {true}\), and since \(\mathcal {S}_1\) aborts when \(\mathsf {decode}\) is set to \(\mathsf {true}\) the behavior of \(\mathcal {S}_1\) and \(\mathcal {S}_2\) is the same, and therefore the behavior of \(\mathcal {S}_2\) and \(\mathcal {S}\) is the same as long as \(\mathsf {decode}=\mathsf {false}\).

Now, we want to bound the probability that \(\mathsf {AoNZero}\), when being used in the \(\mathcal {S}\) during the time \(\mathsf {decode}=\mathsf {true}\), will output a factor or fail (which occurs only in negligible probability as explained in Lemma 4.5). We note that in simulator \(\mathcal {S}_2\) the probability to either of those event is negligible since factoring is hard. Thus, because the behavior of \(\mathcal {S}\) and \(\mathcal {S}_2\) is the same as long as \(\mathsf {decode}=\mathsf {false}\), the probability will have to be negligible in \(\mathcal {S}\).

Lemma 4.5

Let C be from a family of \(\mathsf {AoN}\) functions. There exists an algorithm \(\mathsf {AoNZero}^C\) that when given an arithmetic circuit A either determines whether it evaluates to zero, outputs an accepting input for C or output a non-trivial factor of \(N\).

4.3 Indistinguishability Obfuscation in the Classic Generic Model

In a nutshell, the proof in the classic generic model is simpler since the detection of non-trivial zeros and the decode oracle are not required. However, we cannot rely on recovering the code of the circuit when an accepting input is encountered. Therefore, we have to go over all semi-monomials, and only if all of them are valid and correspond to an accepting input, we declare that the result is zero. This requires computation that scales with \(2^n\) and therefore we must take are parameters large enough to make factoring hard even for such algorithms. See details in the full version [9].