Quantitative Analysis of 3D T1‐Weighted Gadolinium (Gd) DCE‐MRI with Different Repetition Times

Abstract

Dynamic contrast-enhanced MRI (DCE-MRI) acquires T₁-weighted MRI scans before and after injection of an MRI contrast agent such as gadolinium (Gd). Gadolinium causes the relaxation time to decrease, resulting in higher MR image intensities after injection followed by a gradual decrease in image intensities during wash out. Gd does not pass the intact blood–brain barrier (BBB), thus its dynamics can be used to quantify pathology associated with BBB leaks. In current clinical practice, it is suggested to use the same pulse sequence for pre-injection T₁ calibration and Gd concentration calculation in the DCE image sequence based on the spoiled gradient recalled echo (SPGR) signal equation. A common method for T₁ estimation is using variable flip angle (VFA). However, when the parameters such as the repetition time (TR) for image acquisition could be tuned differently for T₁ estimation and DCE acquisition, the popular dcemriS4 software package that handles only a fixed TR often results in discrepancies in Gd concentration estimation. This paper reports a quick solution for calculating Gd concentrations when different TRs are used. First, the pre-injection T₁ map is calculated by using the Levenberg-Marquardt algorithm with VFA acquisition, then, because the TR used for DCE acquisition is different from the VFA TR, the equilibrium magnetization is updated with the TR for DCE, and the Gd concentration is calculated thereafter. In the experiments, we first simulated Gd concentration curves for different tissue types and generated the corresponding VFA and DCE image sequences and then used the proposed method to reconstruct the concentration. Comparing with the original simulated data allows us to validate the accuracy of the proposed computation. Further, we tested performance of the method by simulating different amounts of K^trans changes in a manually selected region of interest (ROI). The results showed that the new method can estimate Gd dynamics more accurately in the case where different TRs are used and be sensitive enough to detect slight K^trans changes in DCE-MRI.

1 Introduction

Dynamic contrast-enhanced (DCE) MRI has been widely used in many clinical studies for noninvasive detection and characterization of diseases [1]. For example, it can not only quantify pathologies of brain tumor associated with blood–brain barrier (BBB) leakage [2], but also study possible BBB disruption in aging, dementia, stroke and multiple sclerosis [3]. In acquiring DCE-MRI, a contrast agent (CA) such as gadolinium (Gd) is injected into the blood stream while acquiring a series of T₁-weighted MR images. CA concentration can be calculated from MR image intensities for quantitative pharmacokinetic analysis [4]. The injection of Gd results in T₁ relaxation time changes compared to the pre-injection T₁ (denoted as T₁₀). Therefore, DCE-MRI acquisition generally consists of two stages. The first stage is to estimate an intrinsic tissue T₁ map. This estimation can be done by acquiring images with variable flip angles. The second stage is to estimate the time varying T₁(t) map sequence from the DCE-MRI sequence right before and after Gd injection.

To accurately estimate the pre-injection longitudinal relaxation time map T₁₀, the variable flip-angle (VFA) spoiled gradient recalled echo (SPGR) method provides high spatial resolution with relatively short acquisition times and is commonly used in basic and clinical research [5]. Specifically, by capturing T₁-weighted MR images at different flip angles, T₁₀ can be calculated using the Levenberg-Marquardt algorithm based on the SPGR signal equation. Next, for computing the Gd concentration from the DCE-MRI image sequences, the same SPGR signal equation is employed to estimate the time varying T₁(t) map sequences. In the dcemriS4 software [6], the CA.fast function can be used for this task.

However, in practice the parameters for image acquisition might have been tuned differently for T₁ calibration and for DCE acquisition stages. For example, in some of our clinical research data, different repetition times (TR) had been used. Because the equilibrium magnetization and T₁₀ are estimated using one TR value, and the DCE acquisitions use another, the parameters estimated from the SPGR signal equation may generate discrepancies when applied to DCE. In this paper, we present a simple and practical solution for calculating Gd concentrations when different TRs are used for T₁ calibration and DCE acquisition.

The major steps remain the same as the dcemriS4 package. Specifically, first, the tissue T₁₀ map is calculated by using the Levenberg-Marquardt algorithm with variable flip angles. Then, because the TR used for DCE acquisition is different the one used for T₁₀ calibration, a new equilibrium magnetization map is calculated with the new TR, so that the SPGR signal equation can better fit the DCE image sequence. Then, the Gd concentration is calculated in a similar way.

In experiments, we first modified the dcemriS4 software package so that different TRs can be used for calculating Gd concentration from DCE-MRI image sequences. Then, we investigated the performance of the modification using simulated Gd concentration signals and different levels of K^trans changes in a manually marked ROI. After simulating Gd concentration curves for different brain tissues, we generated the DCE-MRI image sequences and then estimated the concentration curves using the proposed method. In this way, the estimation accuracy can be calculated.

For 3D DCE image series, spatially correlated Gaussian noises are added to the simulated DCE-MRI image sequences with predefined K^trans changes in a manual ROI. This allows us to compare two groups of DCE-MRI sequences, one with and another without K^trans changes. After simulating DCE-MRI sequences with different conditions and re-calculating K^trans, we use the SPM package to highlight group differences [7]. The experimental results showed that the new method can estimate Gd dynamics more accurately in the case of different TRs, and it is sensitive to K^trans changes in DCE-MRI.

2 Method

2.1 Estimation of T₁ from SPGR Images

In MR imaging, the T₁ relaxation time, or the spin-lattice relaxation time, measures how quickly the net magnetization vector recovers to its ground state along the direction of the main magnetic field B₀. Generally, the measured SPGR signal intensity can be defined as a function of the longitudinal relaxation time $T_{10}$, the repetition time $TR$, the flip angle $\theta$, and the equilibrium longitudinal magnetization $M_{0}$ as,

$$ S_{0} = \frac{{M_{0} (1 - { \exp }( - TR/T_{10} )){ \sin }(\theta )}}{{1 - { \exp }( - TR/T_{10} ){ \cos }(\theta )}} . $$

(1)

Variable flip angle acquisitions are commonly used to estimate the intrinsic relaxation time maps. Given a series of ($N$) flip angles $\theta_{1} , \ldots \theta_{N}$ and corresponding SPGR images $S_{1} , \ldots S_{N}$, with a fixed repetition time TR, the nonlinear least squares algorithm aims to estimate $M_{0}$ and $T_{10}$ by minimizing the sum of squared errors between the left and right sides of Eq. (1) normalized/weighted by the expected signal standard deviation. The Levenberg-Marquardt algorithm is one such method for estimating $M_{0}$ and $T_{10}$. This can be achieved by using the M0.fast function in the dcemriS4 package.

2.2 Estimation of Gd Concentration from DCE-MRI Sequences

During DCE-MRI acquisition, a series of MRI images are captured while the contrast agent Gd is injected into the blood stream. Herein, we denote the DCE image sequence as $I_{t}$, with $t = 1, \ldots T$, and $T$ is the number of DCE images captured. The first several ($P$) frames are pre-injection acquisitions, and the contrast agent injection starts from frame $P + 1$. Therefore, Eq. (1) can be directly used for calculating the dynamic $T_{1} (t)$ by simply modifying the equation to:

$$ \frac{1}{{T_{1} (t)}} = \frac{ - 1}{TR}{ \ln }\left[ {\frac{{M_{0} \sin \left( \theta \right) - I_{t} }}{{M_{0} \sin \left( \theta \right) - I_{t} { \cos }(\theta )}}} \right]. $$

(2)

However, because of the multi-variable nature of the SPGR signal equation, the parameters estimated for one case may result in discrepancies when applied to another imaging case, particularly for new TR values. It has been suggested that the $P$ pre-injection frames of the DCE image sequences can be used to “normalize” the relaxation time sequences [8]. Thus, by replacing $S_{0}$ with the average of the first $P$ pre-injection frames, the following equation is used:

$$ I_{t} - S_{0} = \frac{{M_{0} (1 - { \exp }( - TR/T_{1} ({\text{t}}))){ \sin }(\theta )}}{{1 - { \exp }( - TR/T_{1} \left( {\text{t}} \right)){ \cos }(\theta )}} - \frac{{M_{0} \left( {1 - \exp \left( { - TR/T_{10} } \right)} \right)\sin \left( \theta \right)}}{{1 - \exp \left( { - TR/T_{10} } \right)\cos \left( \theta \right)}}, $$

(3)

where $S_{0} = {\text{average}}(I_{t} ,t = 1, \ldots P)$. Then, we can calculate the relaxation time by:

$$ \frac{1}{{T_{1} (t)}} = \frac{ - 1}{TR}{ \ln }\left[ {\frac{1 - (A + B)}{{1 - { \cos }(\theta )(A + B)}}} \right], $$

(4)

where $A = \frac{{I_{t} - S_{0} }}{{M_{0} \sin \left( \theta \right)}}$ and $B = \frac{{1 - \exp \left( { - \frac{TR}{{T_{10} }}} \right)}}{{1 - \exp \left( { - \frac{TR}{{T_{10} }}} \right)\cos \left( \theta \right)}}$. It has been assumed that the pulse sequence for T₁ calibration and DCE acquisition is set to be the same during MRI scanning, i.e., $TR$ remains the same in $T_{10}$ estimation (Sect. 2.1) and Gd concentration computation (Sect. 2.2).

2.3 Improvement of Dynamic $\varvec{T}_{1} (\varvec{t})$ Computation from DCE-MRI

In clinical practice, we found that the repetition time (TR) for T₁ estimation and DCE acquisition are often different. The effect is that the replacement of $S_{0}$ with the average of the pre-injection DCE images may result in discrepancies because the VFA images and DCE images have different TRs. Basically, denoting the new repetition time of DCE as $TR_{n}$, the parameters estimated in Sect. 2.1 will not hold during DCE concentration estimation because $S_{0} \ne I_{\text{pre}} = {\text{average}}(I_{t} ,t = 1, \ldots P)$ for the new flip angle $\theta_{n}$ of DCE, i.e.,

$$ I_{\text{pre}} \ne \frac{{M_{0} \left( {1 - \exp \left( { - TR/T_{10} } \right)} \right)\sin \left( {\theta_{n} } \right)}}{{1 - \exp \left( { - TR/T_{10} } \right)\cos \left( {\theta_{n} } \right)}}. $$

(5)

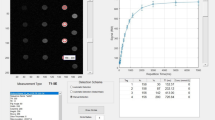
As shown in Fig. 1, we optimized $M_{0}$ and $T_{10}$ using four flip angles (2º, 7º, 18º and 25º) and tested the reconstructed SPGR images by using different TR and $\theta$ and computed the difference between the reconstructed images and the original captured images. When TR remains the same (top row), we can precisely reconstruct the SPGR images with different flip angles, while, when TR is different (bottom row), the reconstructed image demonstrated larger errors. The reason is not because the equilibrium magnetization and the intrinsic $T_{10}$ maps are changed due to the acquisition parameter change, but because the original estimation of the multi-variate nonlinear equation (Eq. (1)) only applies to the original TR value.

Fig. 1.

Reconstructing SPGR images using the same $T_{10}$ map with different TRs. Top: reconstruction using the same TR (5 ms) during T₁ calibration; (a) is the SPGR image captured using TR = 5, $= 12^\circ$, and (b) is the reconstructed image using Eq. (1) with the same parameters. (c) shows the difference image between images (b) and (a). Bottom: reconstruction using different TR. (d) is the average of pre-injection DCE captured using TR = 3.14, $\theta = 10^\circ$, (e) is the reconstructed MR image using Eq. (1), and (f) is the difference between images (e) and (d).

To remedy this discrepancy we can use all the flip angles and TR values during T₁ calibration and DCE acquisition to estimate M₀ and T₁₀ in Eq. (1). However, this requires more acquisitions at different combinations of flip angles and TR values. In practice, these extended multiple acquisitions may not be available.

As mentioned in Introduction, the problem that we are often facing is that TR values may be different during T₁ calibration and DCE acquisition, and there is only one fixed TR and flip angle during DCE acquisition. Therefore, we can assume that the estimated $T_{10}$ relaxation time map (an intrinsic property of tissues) is fixed and will estimate a new equilibrium magnetization map that better fits the new flip angle $\left( {\theta_{n} } \right)$ and the new TR, i.e., $TR_{n}$. Therefore, by solving

$$ I_{\text{pre}} = \frac{{M_{n} \left( {1 - \exp \left( { - TR_{n} /T_{10} } \right)} \right)\sin \left( {\theta_{n} } \right)}}{{1 - \exp \left( { - TR_{n} /T_{10} } \right)\cos \left( {\theta_{n} } \right)}}, $$

(6)

we get a new equilibrium magnetization map $M_{n}$ for the new flip angle and new TR,

$$ M_{n} = \frac{{I_{\text{pre}} \left( {1 - \exp \left( { - TR_{n} /T_{10} } \right)\cos \left( {\theta_{n} } \right)} \right)}}{{(1 - \exp \left( { - TR_{n} /T_{10} } \right))\sin \left( {\theta_{n} } \right)}}. $$

(7)

Notice that although the real equilibrium magnetization has not been changed, we simply did not estimate it well particularly for the new TR value because of the lack of available TR and flip angles values during T₁ calibration in Sect. 2.1. Re-calculating $M_{n}$ here makes the SPGR signal intensity equation better fits the new TR value for different flip angles. Finally, the new relaxation rates $1/T_{1} (t)$ can be calculated using Eq. (4), by applying the new parameters: $M_{n}$, $TR_{n}$, and $\theta_{n}$.

2.4 Summary of the Gd Concentration Computation Algorithm

The improved algorithm for computing Gd Concentration from DCE-MRI with different TRs is summarized as follows:

• Stage 1. Calculate tissue relaxation T₁₀ map. Input SPGR images $S_{i}$ with corresponding acquisition TR and flip angles $\theta_{i}$, $i = 1, \ldots , N$, and apply the dcemriS4 package to compute $M_{0}$ and $T_{10}$ using the Levenberg-Marquardt algorithm.

• Stage 2. Calculate Gd concentration from DCE-MRI image sequences using the following three steps:

  • Step 2.1. Input the pre-injection DCE image frames $I_{t} ,t = 1, \ldots P$, and calculate their average image as $I_{\text{pre}}$, and use Eq. (7) to calculate the new equilibrium magnetization map $M_{n}$ using the new TR and flip angle for DCE acquisition, i.e., $TR_{n}$ and $\theta_{n}$.

  • Step 2.2. For the entire DCE-MRI sequence $I_{t} ,t = 1, \ldots T$, calculate the relaxation rates $1/T_{1} (t)$ by replacing $M_{0}$ with $M_{n}$ and $\theta$ with $\theta_{n}$ in Eq. (4).

  • Step 2.3. Calculate Gd concentration using the following equation:

  • $$ C\left( t \right) = \frac{1}{\gamma }\left( {\frac{1}{{T_{1} \left( t \right)}} - \frac{1}{{T_{10} }}} \right), $$

    (8)

    where γ is the relaxivity of Gd, for which we assume an in-vitro value of $3.9[{\text{mMol}}]^{ - 1} s^{ - 1}$ [9]. The pharmacokinetic model used by dcemriS4 is the extended Tofts model [4] convolved with a population average of directly measured AIFs, modeled as a bi-exponential function [10]. This model can be used to determine K^trans, the transfer constant, which is a reflection of permeability, capillary surface area, and blood flow [11].

3 Experiments

3.1 Evaluation Using Simulated MR Signals

First, we evaluated the accuracy of the algorithm using simulated MR signals from Gd concentration curves. Specifically, after a bolus injection of dose D (mmol/kg), given the values of the transfer constant $K^{trans}$, the rate constant $k_{ep}$, we can use the following equation to simulate the Gd concentration curve [4]:

$$ C\left( t \right) = DK^{trans} \mathop \sum \limits_{i = 1}^{2} a_{i} [\exp \left( { - k_{ep} t} \right) - exp( - m_{i} t)]/[m_{i} - k_{ep} ], $$

(9)

where $a_{1} = 3.99$ kg/liter, $a_{2} = 4.78$ kg/liter, $m_{1} = 0.144$/min, and $m_{2} = 0.0111$/min Subsequently, the relaxation rate $R_{1} \left( t \right) = 1/T_{1} (t)$ can be obtained from Eq. (8), and the corresponding MR signal $S(t)$ can be calculated using Eq. (1). Then, temporally correlated Gaussian noises are added to the simulated MR signals. By setting the typical mean values of $K^{trans}$ to 0.119, 0.071, 0.034 for CSF, GM, and WM, and those of $k_{ep}$ to 0.480, 0.534, and 0.457, respectively, we simulated the concentration curves of different tissues shown as blue curves in Fig. 2. These blue curves were used to generate MR signals, and the proposed algorithm (the method with Step 2.1 included) and the original algorithm (without Step 2.1) were used to reconstruct these concentration signals. We used TR = 3.14 ms, and $\theta = 10^\circ$ for DCE, which are different than those used for simulating the flip angle MR signals (TR = 5 ms, and $\theta = 2^\circ , 7^\circ , 18^\circ , 27^\circ$). After reconstruction, the recovered green curves were vertically shifted. For conveniently comparing their shapes, we shifted them back so the pre-injection concentration is zero. It can be seen from Fig. 2 that the green curves cannot fully recover the contrast of the original $C(t)$. Quantitatively, the areas under the curves (AUC) for red ones have small difference from the blue ones: 0.3 %, 0.8 %, and 4.0 %, and those for the green curves are more different from the blue curves: 45.0 %, 45.1 %, and 42.2 %, for CSF, GM, and WM, respectively.

Fig. 2.

The original and the reconstructed Gd concentration signals. Blue: original simulated concentration; red: reconstructed concentration using our method (with Step 2.1); green: original method (without Step 2.1). (Color figure online)

3.2 Application in Gd DCE-MRI Analysis

We applied the proposed algorithm in pre-processing of DCE-MRI datasets by simulating K^trans change. Because of lack of ground truth for DCE-MRI images, first, we generated simulated DCE-MRI datasets from a segmented image using realistic $K^{trans}$ and $k_{ep}$ parameters for different tissue types, including WM, GM, and CSF. Then, $K^{trans}$ and $k_{ep}$ are subject to a spatially correlated Gaussian distribution for different tissue types, and a manually selected region of interest (ROI) was used to simulate the “abnormal” region, wherein the mean values of $K^{trans}$ and $k_{ep}$ are set differently.

The detailed simulation steps are as follows. First, we set the mean values of $K^{trans}$ and $k_{ep}$ for different tissues according to the segmented MR image, then, the standard deviation (std) of $K^{trans}$ is set to x% of the mean values. In this way we generated the $K^{trans}$ map for every voxel in the segmented MR image and spatially smoothed it with a 3 × 3 × 3 window. A group of 10 $K^{trans}$ maps are generated to act as the control group. Another study group was generated in a similar way, and additionally the $K^{trans}$ values within the manual ROI (see Fig. 3) were shifted, and the shifting parameter is subject to a Gaussian distribution $N(m,\delta )$, with $m$ as y% of the $K^{trans}$ mean, and $\delta$ the prescribed std for $m$. In summary, x% reflects the variability of $K^{trans}$ for each tissue type, and y% is the amount of relative changes of $K^{trans}$ to simulate the abnormality within ROI. In the simulation, we kept $k_{ep}$ unchanged as the desired mean values of different tissue types.

Fig. 3.

Group comparison of $K^{trans}$ change in ROI. The segmented image with a manual ROI is used to simulate the $K^{trans}$ maps of two groups, one with and another without $K^{trans}$ shifts in the ROI. The –log(p) maps show group differences for different amount of shifts by applying SPM on the reconstructed $K^{trans}$ maps.

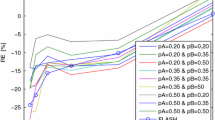
According to these settings, each experiment was performed by first simulating the two groups of $K^{trans}$ maps with different parameters (x% and y%), and the VFA images, as well as the DCE-MRI image sequence were then simulated in a similar way as Sect. 3.1 (Gaussian noises are added to the simulated images). Then, we used the proposed method to calculate the Gd concentration maps and computed the $K^{trans}$ maps using the Tofts model. Finally, we applied the SPM package for statistical analysis, where a $7{\text{mm}} \times 7{\text{mm}} \times 7{\text{mm}}$ spatial smoothing window was applied on the resultant $K^{trans}$ maps before calculating the p-value map. We tested the conditions when x% = 10 % and 20 %, and y% = 1 %,…7 %, respectively. Figure 3(a) shows the segmented image used as the template image for the simulation, and the brown region is the manually picked abnormal region. In the subsequent images in Fig. 3, we show the –log(p) maps when x% = 10 % and y% = 1 %,…5 %. It can be seen that at the variability level of 10 % (std of $K^{trans}$ is 10 % of its mean), the method can catch the shape of the abnormal ROI when the different between control and abnormal is 4 % ~ 5 %.

Figure 4 plots the mean and std of the p-values within the ROI for two different $K^{trans}$ variability levels: x % = 10 % and 20 %. It can be seen that as more variability appears in $K^{trans}$ for the tissues, the minimal change that can be detected has been increased. Notice that these experiments have not incorporated image registration errors in the simulation. In real cases, the sensitivity for detecting permeability between groups could also be affected by image registration errors.

Fig. 4.

The mean and std of p-values within the ROI under different simulation conditions.

Finally, it is worth noting that the objective of this paper is to evaluate the proposed method on simulated Gd concentrations to show that concentration maps can be estimated more accurately, particularly when the repetition time is different for T₁ calibration and DCE acquisition. In our recent study [12], the proposed method was applied to analyze real DCE-MRI imaging data for quantifying group differences of Gd dynamics between young and old healthy adults.

4 Conclusion

This paper presents a simple yet effective solution for calculating Gd concentrations when different TRs are used during T1 calibration and DCE acquisition. We showed that due to the limited number of VFA acquisitions during baseline calibration, the SPGR signal equation, as a multi-variate nonlinear function, has not been calibrated well enough to account for different TR values. To remedy this shortcoming, we first used the Levenberg-Marquardt method to estimate the intrinsic T₁ relaxation time from different flip angle acquisition, and then recalculate the equilibrium magnetization map using the pre-injection DCE images acquired with a new TR and new flip angle. The modified SPGR signal equation is thus tuned to the new TR and flip angle and can better represent the DCE image sequences. Gd concentration dynamics are then calculated. In experiments with simulated DCE-MRI, we showed that the new method can generate more accurate concentration maps, and hence improve the quantitative analysis of DCE-MRI for human brain BBB analysis.