Keywords

1 Introduction

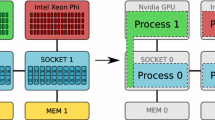
Parallelism in todays computer architectures is pervasive not only in systems from large supercomputers to laptops, but also in small portable devices like smartphones and watches. Along with parallelism, the level of heterogeneity in modern computing systems is also gradually increasing. Multicore CPUs are combined with discrete high-performance GPUs, or even become integrated parts with them as a system-on-chip (SoC) like in the NVIDIA Tegra mobile family of devices. To extract full performance from systems like these, the heterogeneity makes the parallel programming for technical computing problems extremely challenging, especially in modern applications that require fast linear algebra on many independent problems that are of size \(\mathcal {O}\)(100) and smaller. According to a recent survey among the Sca/LAPACK and MAGMA [17] users, 40 % of the responders needed this functionality for applications in machine learning, big data analytics, signal processing, batched operations for sparse preconditioners, algebraic multigrid, sparse direct multifrontal solvers, QR types of factorizations on small problems, astrophysics, and high-order FEM. At some point in their execution, applications like these must perform a computation that is cumulatively very large, but whose individual parts are very small; when such operations are implemented naively using the typical approaches, they perform poorly. To address the challenges, we designed a standard for Hybrid Batched BLAS [6], and developed innovative algorithms [10], data and task abstractions [1], as well as high-performance implementations based on the standard that are now released through MAGMA 2.0 [5, 9]. Figure 1 illustrates how the need for batched operations and new data types arises in areas like linear algebra (Left) and machine learning (Right). The computational characteristics in these cases are common to many applications, as already noted: the overall computation is very large but is made of operations of interest that are in general small, must be batched for efficiency, and various transformations must be explored to cast the batched small computations to regular and therefore efficient to implement operations, e.g., GEMMs. We note that applications in big data analytics and machine learning target higher dimension and accuracy computational approaches (e.g., ab initio-type) that model mutilinear relations, thus, new data abstractions, e.g., tensors, may be better suited vs. the traditional approach of flattening the computations to linear algebra on two-dimensional data (matrices). Indeed, we developed these tensor data abstractions and accelerated the applications using them significantly [1] compared to other approaches.

Fig. 1.
figure 1

Left: Example of a \(4^{th}\)-order tensor contractions design using Einstein summation notation and a Domain Specific Embedded Language (or DSEL). Right: Illustration of batched computations needed in machine learning.

Full size image

There is a lack of sufficient optimizations on the batched GEMMs needed and targeted in this paper. We show this in comparison to vendor libraries like CUBLAS for NVIDIA GPUs and MKL for Intel multicore CPUs. Related work on GEMM and its use for tensor contractions [1] target only GPUs and for very small sizes (16 and below). Batched GEMM for fixed and variable sizes in the range of \(\mathcal {O}\)(100) and smaller were developed in [2]. The main target here is multicore CPUs and GPUs for sizes up to 32.

2 Contributions to the Field

The evolution of semiconductor technology is dramatically transforming the balance of future computer systems, producing unprecedented changes at every level of the platform pyramid. From the point of view of numerical libraries, and the myriad of applications that depend on them, three challenges stand out: (1) the need to exploit unprecedented amounts of parallelism; (2) the need to maximize the use of data locality and vectorized operations; and (3) the need to cope with component heterogeneity. Below, we highlight our main contributions related to the algorithm’s design and optimization strategies aimed at addressing these challenges on multicore CPU and GPU architectures:

Exploit Parallelism and Vector Instructions: Clock frequencies are expected to stay constant, or even decrease to conserve power; consequently, as we already see, the primary method of increasing computational capability of a chip will be to dramatically increase the number of processing units (cores), which in turn will require an increase of orders of magnitude in the amount of concurrency that routines must be able to utilize as well as increasing the computational capabilities of the floating point units by extending it to the classical Streaming SIMD Extensions set (SSE-1, to SSE-4) in the earlier 2000, and recently to Advanced Vector Extensions (AVX, AVX-2, AVX-3). We developed specific optimization techniques that demonstrate how to use the many cores (currently multisocket 10–20 cores for the Haswell CPU and \(15 \times 192\) CUDA cores for the K40 GPU) to get optimal performance. The techniques and kernels developed are fundamental and can be used elsewhere.

Hierarchical Communication Techniques that Maximizes the Use of Data Locality: Recent reports (e.g., [7]) have made it clear that time per flop, memory bandwidth, and communication latency are all improving, but at exponentially different rates. So computation on very small matrices, that can be considered as computation-bound on old processors, is, –today and in the future– communication-bound and depends from the communication between levels of the memory hierarchy. We demonstrate that, performance is indeed harder to get on new manycore architectures unless hierarchical communications and optimized memory management are considered in the design. We show that, only after we developed multilevel memory design, our implementations reach optimal performance.

Performance Analysis and Autotuning: We demonstrate the theoretical maximal performance bounds that could be reached for computation on very small matrices. We studied various instructions and performance counters, as well as proposed a template design with different tunable parameters in order to evaluate the effectiveness of our implementation and optimize it to reach the theoretical limit.

3 Experimental Hardware

All experiments are done on an Intel multicore system with two 10-cores Intel Xeon E5-2650 v3 (Haswell) CPUs, and a Kepler Generation Tesla K40c GPU. Details about the hardware are illustrated in Fig. 2. We used gcc compiler 5.3.0 for our CPU code (with options -std=c++14 -O3 -avx -fma), as well as the icc compiler from the Intel suite 2016.0.109, and the BLAS implementation from MKL (Math Kernel Library) 16.0.0 [12]. We used CUDA Toolkit 7.5 for the GPU. For the CPU comparison with the MKL library we used two implementations: (1) An OpenMP loop statically or dynamically unrolled among the cores (we choose the best results), where each core computes one matrix-matrix product at a time using the optimized sequential MKL dgemm routine, and (2) The batched dgemm routine that has been recently added to the MKL library.

Fig. 2.
figure 2

Memory hierarchies of the experimental CPU and GPU hardware

Full size image

4 Methodology, Design, and Optimization

To evaluate the efficiency of our algorithms we derive theoretical bounds for the maximum achievable performance \(P_{max} = F / T_{min}\), where F is the number of operations needed by the computation and \(T_{min}\) is the fastest time to solution. For simplicity, consider \(C = \alpha A B + \beta C\) on square matrices of size n. We have \(F \approx 2 n^3\) and \(T_{min} = min_T( T_{Read(A,B,C)} + T_{Compute(C)} + T_{Write(C)})\). Note that we have to read/write \(4 n^2\) elements, or \(32 n^2\) Bytes for double precision (DP) calculations. Thus, if the maximum achievable bandwidth is B (in Bytes/second), and we assume \(T_{Compute(C)}\rightarrow 0\) for very small computation, then \(T_{min} = T_{Read(A,B,C)} + T_{Write(C)} = 4 n^2 / B\) in DP. Note that this time is theoretically achievable if the computation totally overlaps the data transfer and does not disrupt the maximum rate B of read/write to the GPU memory. Thus,

$$\begin{aligned} P_{max} = \frac{2 n^3 B}{32 n^2} = \frac{n B}{16} \text {~in DP}. \end{aligned}$$

The achievable bandwidth can be obtained by benchmarks. For our measures, we used the STREAM benchmark [16] and the Intel memory latency checker 3.0 tool for CPU, and the NVIDIA’s bandwidthTest for GPU. Our tests show that the practical CPU bandwidth we are able to achieve using different benchmarks is about 44 GB/s per socket. On the K40 GPU with ECC on the peak is 180 GB/s, so in that case \(P_{max}\) is 2.75 n GFlop/s per socket for the CPU and 11.25 n GFlop/s for the K40 GPU. The curve representing this theoretical maximal limit is denoted by the “upper bound” line on Figs. 5 and 8. Thus, when \(n=16\) for example, we expect a theoretical maximum performance of 180 GFlop/s in DP on the K40 GPU.

4.1 Programming Model, Performance Analysis, and Optimization for CPUs

The design of our code is done using new features of C++ for better re-usability and adaptability of the code. By using advanced template techniques we can create high-level interfaces [15] without adding any cost even for small matrix-matrix products. To do so, we have designed a batch structure which will contain a C++ vector for the data and static dimensions. By using the C++ constexpr keyword and integral constants we can make a generic batched code that will dispatch at compile time the correct version depending on the size of matrices. We use this environment for each code sequence we generate.

The implementation of a matrix-matrix products kernel for very small matrices for CPUs requires specific design and optimisations. As we can store three double precision matrices of size up to \(32 \times 32\) in the L1 cache of an Intel Xeon E5-2650 v3 processor, one can expect that any implementation will not suffer from data cache misses. This can be seen on Fig. 5b where the performance of an ijk implementation, which is not cache-aware and cannot be vectorized, is pretty close to the ikj one. For smaller sizes, the ijk implementation is even more efficient than the ikj one, as it optimizes the number of stores (Fig. 3a). To obtain a near optimal performance, we conduct an extensive study over the performance counters using the PAPI [18] tools. Our analysis concludes that in order to achieve an efficient execution for such computation, we need to maximize the occupancy and minimize the data traffic while respecting the underlying hierarchical memory design. Unfortunately, today’s compilers cannot introduce highly sophisticated cache/register based loop transformations and, consequently, this kind of optimization effort should be studied and implemented by the developer [13]. This includes techniques like reordering the data so that it can be easily vectorized, reducing the number of instructions so that the processor spends less time in decoding them, prefetching the data that will be reused in registers, and using an optimal blocking strategy.

Data Access Optimizations and Loop Transformation Techniques. In our design, we propose to order the iterations of the nested loops in such a way that we increase locality and expose more parallelism for vectorization. The matrix-matrix product is an example of perfectly nested loops which means that all the assignment statements are in the innermost loop. Hence, loop unrolling, loop peeling, and loop interchange can be useful techniques for such algorithm [3, 4]. These transformations improve the locality and help to reduce the stride of an array based computation. In our approach, we propose to unroll the two inner-most loops so that the accesses to matrix B are independent from the loop order, which also allows us to reorder the computations for continuous access and improved vectorization. This technique enables us to prefetch and hold some of the data of B into the SIMD registers. Here, we manage to take advantage from the knowledge of the algorithm, and based on the principle of locality of references [11], to optimize both the temporal and spatial data locality.

Register Data Reuse and Locality. Similarly to the blocking strategies for better cache reuse in numerically intensive operations (e.g., large matrix-matrix products), we focus on register blocking to increase the performance. Our study concludes that the register reuse ends up being the key factor for performance. The idea is that when data is loaded into SIMD register, it will be reused as much as possible before its replacement by new data. The amount of data that can be kept into registers becomes an important tuning parameter. For example, an \(8 \times 8\) matrix requires 16 256-bit AVX-2 registers to be completely loaded. As the targeted hardware consists of only 16 256-bit AVX-2 registers, one can expect that loading the whole B will not be optimal as we will have to reload the vectors for A and C. However, if we load only 8 registers for B, which is equal to 4 rows, we can compute a row of C at each iteration and reuse these 8 registers for each iteration. We propose an auto-tuning process to check all the possible scenarios and provide the best option. This reduces the number of load, store, and total instructions from \(\mathcal {O}(n^2)\) to \(\mathcal {O}(n)\), compared to a classical ijk or ikj implementation as depicted in Figs. 3a, b, and 5a, respectively.

Algorithmic Advancements. Algorithm 1 is an example of our methodology for a matrix-matrix product of \(16 \times 16\) matrices. In this pseudo-code, we start by loading four 256-bit AVX-2 registers with values of B which correspond to the first row. These registers are reused throughout the algorithm. In the main loop (Lines 4–14), we start by computing the first values of every multiplication (stored into a register named M = A \(\times \) B) based on the prefetched register in line 1. Then, we iterate on the remaining rows (Lines 7–11) loading B, multiplying each B by a value of A, and adding the result into M. Once the iteration over a row is accomplished, the value of M is the final result of A \(\times \) B and thus, we can load the initial values of C, multiply by \(\alpha \) and \(\beta \), and store it back before moving toward the next iteration such a way to minimize the load/store as shown in Fig. 3. Each C ends up being loaded/stored once. We apply this strategy to matrix sizes ranging from 8 to 32 as for smaller sizes the whole matrix can fit in registers. Different blocking strategies (square versus rectangular) have been studied through our auto-tuning process in order to achieve the best performance. We generate each matrix-matrix product function at compile time with C++ templates. The matrix size is passed as a function parameter using C++ integral constants.

figure a
Fig. 3.
figure 3

CPU Performance counters measurement of the memory accesses

Full size image

Effect of the Multi-threading. As described above, operating on matrices of very small sizes is memory-bound computation and thus, increasing the number of CPU cores may not always increase the performance since the performance will be limited by the bandwidth which can be saturated by a few cores. We performed a set of experiments towards clarifying this behaviour and illustrate our findings in Fig. 4b. As shown, the notion of perfect speed-up does not exist for a memory-bound algorithm, and adding more cores increases the performance slightly. We performed a bandwidth evaluation when varying the number of cores to find that a single core can achieve about 18 GB/s while 6 and 8 cores (over the available 10 cores) can reach about 88 % and 93 % of the practical peak bandwidth, which is about 44 GB/s.

Fig. 4.
figure 4

CPU Performance analysis

Full size image

Effect of the NUMA-Socket and Memory Location. We also studied NUMA-socket (non-uniform memory access) [8] when using two Xeon sockets as seen in Fig. 4a. A standard memory allocation puts all of the data in the memory slot associated to the first socket until it gets filled, then starts filling the second socket. Since the problem size we are targeting is very small, most of the data is allocated on one socket, and thus using extra 10 cores of the second socket will not increase the performance. This is due to the fact that the data required by the cores of the second socket goes through the memory bus of the first socket, and thus is limited by the bandwidth of one socket (44 GB/s). There are ways to overcome this issue. By using NUMA with the interleave=all option, which spreads the allocation over the two sockets by memory pages, we can improve the overall performance. However, for very small sizes, we observe that such solution remains far from the optimal bound since data is spread out over the memory of the two sockets without any rules that cores from socket 0 should only access data on socket 0, and vice versa. To further improve performance, we use a specific NUMA memory allocation, which allows us to allocate half of the matrices on each socket. As shown in Fig. 4a, this allows our implementation to scale over the two sockets and to reach close to the peak bound.

Fig. 5.
figure 5

Experimental results of the matrix-matrix multiplication on CPU’s

Full size image

4.2 Programming Model, Performance Analysis, and Optimization for GPUs

Our goal is to minimize coding effort and to design one kernel that can be easily adapted for very small matrix size computations, providing very efficient execution. To design a GEMM kernel in CUDA to take advantage of the available threads, thread blocks, and streaming multiprocessors (SMs) of a GPU, the computation must be partitioned into blocks of threads (also called thread blocks, or simply TBs) that execute independently from each other on the multiprocessors of the GPU. We use a hierarchical blocking model of both communications and computations, similarly to the MAGMA batched GEMM kernel [2] for medium and large sizes. We designed CUDA C++ templates to enable unified code base for all the small sizes. Templates enable an easy instantiation of a kernel with a specific precision and tuning parameters.

A Cache-Based Approach. Unlike multi-core CPUs, the L1 cache (per SM) is not intended for global memory accesses, which are cached only in the L2. The L2 cache is shared among all SMs, which makes it difficult to use for cache-based optimizations, since all TBs will be sharing it (L2 cache is up to 1.5 MB). However, a modern Kepler GPU has a 48 KB per SM of a read-only cache (rocache), which can be used for global memory reads. A possible implementation that takes advantage of this is to read the input matrices A and B through the read-only cache. Each matrix computation is associated to one TB that is configured with \(\textsf {M}\times \textsf {N}\) threads, where each thread is responsible for computing one output element of the resulting matrix C. Thus, each thread reads an entire row of A and entire column of B. This cache-based design ideally assumes that most of the global memory accesses hit in the rocache. This kernel does not use the shared memory, and so it does not need any synchronization points.

A Shared Memory Based Approach. Another approach is to use shared memory (shmem) for data reuse rather than rocache. We refer to this implementation as the MAGMA kernel, since it is distributed within the MAGMA library. We performed an extensive set of auto-tuning and performance counter analysis to optimize and improve this implementation. The matrices A and B are loaded by block into the shared memory, and the corresponding block of the matrix C is held into registers. Prefetching can also be used to load the next blocks of A and B. The prefetching can be done through either the shared memory or the register, and is controlled by a tunable parameter. This implementation is very well parametrized, and can work for any dimension with tunable block sizes for A, B, and C.

Fig. 6.
figure 6

Performance counters measurement on the K40 GPU

Full size image

Instruction Mix. We performed a detailed performance study based on the collection and analysis of hardware counters. Counter readings were taken using performance tools (Nvidia’s CUPTI and PAPI CUDA component [14]). Our analysis shows that it is important to pay attention to the instruction mix of the GPU kernel, in particular when operating on matrices of such very small sizes. Integer instructions, which are used for loop counters and memory address calculations, can be quite an overhead in such computations. Moreover, our study showed that a loop with predefined boundary can be easily unrolled and optimized by the Nvidia compiler. We adopt an aggressive approach to produce a fully unrolled code for every size of interest. We add the sizes M, N, and K to the template parameters such a way to use a unified code base to produce a fully unrolled and optimized implementation for any of these very small sizes. Figure 6a shows the ratio of integer instructions to the total number integer and floating point instructions, the MAGMA kernel has the smallest ratio for most sizes. An interesting observation of the CUBLAS implementation, for this range of matrices, is that it uses a fixed blocking size of 16\(\times \)16. This explains the drops at sizes 16 and 32, where the problem size matches the internal blocking size.

Fig. 7.
figure 7

Performance counters measurement on the K40 GPU

Full size image
Fig. 8.
figure 8

Performance counters measurement and efficiency of our design for the matrix-matrix multiplication on the K40 GPU

Full size image

Thread Block-Level Aggregation. We further improved the proposed design by another optimization that helps significantly increase the performance for the tiny sizes (e.g. less than 12). Multiple TBs, each is assigned for one problem, are aggregated together into one larger TB. The motivation behind this technique is to increase the number of threads, especially when the TB configuration has few warps or even less than a warp. Aggregation is controlled through an additional parameter tba, which controls the number of TBs to be fused together. Figure 6b shows the impact of tba on performance. For example, we achieve a speed-up of 6.8\(\times \) for size 2 and 3.8\(\times \) for size 3. The performance improvement reaches 24 % at size 8. Beyond size 10, setting tba larger than 1 does not achieve any gains because the resources required by one fused TB become expensive, which affects the number of residing TBs per SM. Some curves look incomplete, since a large value of tba sometimes requires more threads than the hardware-defined maximum number of threads allowed per TB.

Performance Counter Analysis. Figure 7 shows two of the key factors to high performance on a GPU: the achieved occupancy and the efficiency of global memory reads. The first one is the ratio between the number of active warps per active cycles and the maximum number of warps that can run on an SM. The second is defined as the ratio between the load throughput requested by the kernel, and the actual required throughput needed to fulfil the kernel load requests. Our proposed MAGMA implementation achieves more than 75 % occupancy in most cases, which is nearly the upper limit for the other design. It can also achieve very high occupancy (\(\approx \)90 %) even for very small matrices, thanks to the TB-level aggregation. On the other hand, the MAGMA approach is at least 90 % efficient in reading from global memory, which means that the kernel encounters very little overhead in terms of load instructions replays.

5 Conclusions and Future Directions

We presented work motivated by a large number of applications, ranging from machine learning to big data analytics, that require fast linear algebra on many independent problems that are of size 32 and smaller. The use of batched GEMM for small matrices is fundamental for obtaining high performance in applications like these. We presented specialized algorithms for these cases – where the overall computation is memory bound but still must be blocked – to obtain performance that is within 90 % of the optimal, significantly outperforming currently available state-of-the-art implementations and vendor-tuned math libraries. Here, the optimal is the time to just read the data once and write the result, disregarding the time to compute. The algorithms were designed for modern multi-core CPU and GPU architectures. The optimization techniques and algorithms can be used to develop other batched Level 3 BLAS and to accelerate numerous applications that need linear algebra on many independent problems.

Future work includes further optimizations and analyses, e.g., on how high performance can go using CUDA. It is known that compilers have their limitations in producing top performance codes for computations like these, thus, requiring the use of lower level programming languages. Current results used intrinsics for multi-core CPUs and CUDA for GPUs, combined with auto-tuning in either case, to quickly explore the large algorithmic variations developed in finding the fastest one. Future work includes also use in applications, development of application-specific optimizations, data abstractions, e.g., tensors, and algorithms that use them efficiently.