Zero-Error Capacity of Quantum Channels

Abstract

This chapter presents the classical zero-error capacity of quantum channels, which is a generalization of the zero-error capacity of discrete memoryless channels. Initially, we present the main concepts and definitions related to the zero-error capacity of quantum channels. Then, we discuss an equivalent definition for the capacity in terms of graphs. Some properties of quantum states reaching the zero-error capacity are investigated, as well as an upper bound for the zero-error capacity in terms of the Holevo-Schumacher-Westmoreland capacity. The chapter ends with a discussion about the superactivation of the zero-error capacity of quantum channels. Superactivation is a surprising result with no counterpart in classical theory; we exhibit quantum channels such that one channel use cannot transmit any classical information, whereas two uses can.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Quantum zero-error information theory deals with techniques, protocols and analyzes methods to allow communication of classical or quantum information through quantum noisy channels, with the main requirement that no errors can be tolerated. This new research field aims to generalize and extend the classical zero-error theory proposed by Shannon and outlined in Chap. 4

Because quantum mechanics has many features not present in the classical world, e.g. entanglement , one may expect that developments in this area should not only generalize definitions and results from classical theory but they must go beyond. This is exactly what has been happening! As we already know, a classical channel has an asymptotically positive zero-error capacity if and only if the one-shot capacity is positive, i.e., N(1) > 1. One of the most impressive results in quantum zero-error information theory is that there exist quantum channels such that no information can be perfectly transmitted with a single use, whereas the communication is possible with two channel uses. This phenomenon is known as superactivation of the quantum zero-error capacity.

In this chapter we present the classical zero-error capacity of quantum channels, which is a generalization of the zero-error capacity of discrete memoryless channels. Section 5.1 deals with main concepts and definitions. In Sect. 5.2, an equivalent definition for the quantum zero-error capacity is given in terms of graphs. Some properties of quantum states reaching the channel capacity are investigated in Sect. 5.3. Section 5.4 presents an upper bound for the quantum zero-error capacity in terms of the Holevo-Schumacher-Westmoreland capacity and, finally, Sect. 5.5 discusses the superactivation of the zero-error capacity of quantum channels.

5.1 Classical Zero-Error Capacity of Quantum Channels

In quantum information theory, the Holevo-Schumacher-Westmoreland (HSW) capacity can be understood as a quantum version of the ordinary capacity of classical channels originally defined by Shannon. Fundamentally, the parallel is due to the communication protocol used by the HSW capacity: quantum codewords are composed by tensor product of quantum states and collective measurements can be made at the channel output.

The first zero-error capacity of quantum channels was defined taking into account the HSW communication protocol, with the restriction that the probability of decoding errors should be zero. In this sense, the classical zero-error capacity (CZEC) of a quantum channel can be viewed as the “error-free” version of the HSW capacity, as well as the quantum generalization of the zero-error capacity of classical channels.

Given an arbitrary quantum channel, we ask for the maximum amount of classical information per channel use that can be transmitted with zero probability of error. For this purpose, we consider a d-dimensional quantum channel $\mathcal{E}\equiv \left \{E_{a}\right \}$ as a completely positive tracing preserving map . Let $\mathcal{S}$ be a subset of quantum states belonging to a d-dimensional Hilbert space $\mathcal{H}$. States $\rho _{i} \in \mathcal{S}$ will be called input states .

Initially, a sender Alice chooses a message from a set $\left \{1,\ldots,m\right \}$ containing m classical messages. The encoder maps this message into an n-tensor product of quantum states of $\mathcal{S}$. The resulting state is called quantum codeword , which is sent through the noisy quantum channel $\mathcal{E}$. The receiver Bob performs a collective measurement with a POVM on the received state. The measurement output becomes argument of the decoding function. The decoder has to decide which message was sent by Alice considering that errors are not allowed. The sketch of the communication protocol is shown in Fig. 5.1.

Fig. 5.1

Quantum zero-error communication system

The error-free communication protocol can be summarized as follows.

• The source alphabet is the set $\mathcal{S} = \left \{\rho _{1},\ldots,\rho _{\ell}\right \}$, where $\mathcal{S}\subseteq \mathcal{H}$;

• In order to be transmitted through the quantum channel, classical messages are mapped into tensor products of quantum states in $\mathcal{S}$;

• At the channel output, the decoder performs collective measurements in order to estimate the message that was sent.

Taking this into account, we can now define error-free quantum codes.

Definition 5.1 ((m, n) Error-Free Quantum Code).

An (m, n) error-free quantum code for a quantum channel $\mathcal{E}$ is composed of:

• 1. a set of indexes $\left \{1,\ldots,m\right \}$, each one associated with a classical message;

• 2. an encoding function

  $$\displaystyle{ f_{n}: \left \{1,\ldots,m\right \} \rightarrow \mathcal{S}^{\otimes n} }$$

  (5.1)

  leading to codewords $f_{n}(1) = \overline{\rho }_{1},\ldots,f_{n}(m) = \overline{\rho }_{m}$, $\overline{\rho }_{i} \in \mathcal{S}^{\otimes n}$;

• 3. a decoding function

  $$\displaystyle{ g: \left \{1,\ldots,k\right \} \rightarrow \left \{1,\ldots,m\right \} }$$

  (5.2)

  that deterministically associates each of the possible measurement results performed by a POVM $\mathcal{M} = \left \{M_{i}\right \}_{i=1}^{k}$ with a message. The decoding function has the following property:

  $$\displaystyle{ \Pr [g(\mathcal{E}(f_{n}(i)))\neq i] = 0\forall i \in \left \{1,\ldots,m\right \}. }$$

  (5.3)

Clearly, the rate of this code is $R_{n} = \frac{1} {n}\log m$ bits per channel use.

With these codes we can now define the classical zero-error capacity (CZEC) of a quantum channel .

Definition 5.2 (Quantum Zero-Error Capacity [11]).

Let $\mathcal{E}(\cdot )$ be a TPCP map that represents a quantum noisy channel. The quantum zero-error capacity of $\mathcal{E}$, denoted by $C^{(0)}(\mathcal{E})$, is the highest superior limit of achievable rates with zero-error decoding probability, i.e,

$$\displaystyle{ C^{(0)}(\mathcal{E}) =\sup _{ \mathcal{S}}\sup _{n} \frac{1} {n}\log \alpha _{n}(\mathcal{E}), }$$

(5.4)

where $\alpha _{n}(\mathcal{E}) = m$ is the maximum number of classical messages that can be transmitted without errors when an (m, n) error-free quantum code is used with input alphabet $\mathcal{S}$.

For a given (m, n) error-free quantum code attaining the quantum zero-error capacity of $\mathcal{E}$, we define an optimum pair $(\mathcal{S},\mathcal{M})$.

Definition 5.3 (Optimum Pair $(\mathcal{S},\mathcal{M})$ [15]).

An optimum pair $(\mathcal{S},\mathcal{M})$ is composed by a set of input states $\mathcal{S}$ and a POVM $\mathcal{M}$ for which the quantum zero-error capacity is reached.

We are interested in scenarios where the classical zero-error capacity of a quantum channel is non-zero. This is only possible when at least two input states are non-adjacent. Definition 5.4 synthesizes this idea.

Definition 5.4 (Adjacency of Quantum States ).

Let $\mathcal{E}$ be a quantum channel and $\rho _{i},\rho _{j} \in \mathcal{S}$ two quantum states, i ≠ j, from the input alphabet of the channel. We say that ρ _i and ρ _j are non-adjacent (orthogonal or distinguishable) in the output of $\mathcal{E}$ if the Hilbert subspaces spanned by the supports of ρ _i and ρ _j are orthogonal. We denote it by $\rho _{i} \perp _{\mathcal{E}}\rho _{j}$.

Adjacency of quantum states can be generalized to tensor product, as illustrated in Fig. 5.2. Let $\hat{\rho }_{i}$ and $\hat{\rho }_{j}$ be two input tensor products $\hat{\rho }_{i} =\rho _{i,1} \otimes \ldots \otimes \rho _{i,n}$ and $\hat{\rho }_{j} =\rho _{j,1} \otimes \ldots \otimes \rho _{j,n}$. If there is at least one $\rho _{i,k} \perp _{\mathcal{E}}\rho _{j,k}$, then $\hat{\rho }_{i} \perp _{\mathcal{E}}\hat{\rho }_{j}$.

Fig. 5.2

Two quantum states $\hat{\rho }_{i}$ e $\hat{\rho }_{j}$ are distinguishable if there is at least one $\rho _{i,k} \perp _{\mathcal{E}}\rho _{j,k}$, 1 ≤ k ≤ n

Taking adjacency into account , a quantum channel $\mathcal{E}$ has positive zero-error capacity if and only if the set $\mathcal{S}$ contains at least two non-adjacent states.

Example 5.1 (Quantum Channel with a Vanishing Zero-Error Capacity).

Suppose that a depolarizing quantum channel can transmit an input state ρ intact with probability 1 − p or exchange it by a complete mixed state with probability p, as discussed in Example 3.15. Let d be the dimension of the input Hilbert state $\mathcal{H}$ and let $\mathbb{1}_{d}$ be the identity matrix of dimension d. This channel is shown in Fig. 5.3.

Fig. 5.3

Quantum depolarizing channel

Recall that the formal representation of this channel is given by

$$\displaystyle{ \mathcal{E}(\rho ) = (1 - p)\rho + p\frac{1} {d}\mathbb{1}_{d}, }$$

(5.5)

where 0 < p < 1. To check if this channel has positive zero-error capacity, we verify if there exist at least two different states, ρ _i and ρ _j , which are distinguishable at the channel output, i.e.,

$$\displaystyle\begin{array}{rcl} \mathop{\mathrm{Tr}}\nolimits [\mathcal{E}(\rho _{i})\mathcal{E}(\rho _{j})]& =& \mathop{\mathrm{Tr}}\nolimits \left [\left ((1 - p)\rho _{i} + p\frac{1} {d}\mathbb{1}_{d}\right )\left ((1 - p)\rho _{j} + p\frac{1} {d}\mathbb{1}_{d}\right )\right ] {}\\ & =& \mathop{\mathrm{Tr}}\nolimits \left [(1 - p)^{2}\mathop{ \mathrm{Tr}}\nolimits [\rho _{ i}\rho _{j}] + \frac{p(1 - p)} {d} \mathop{\mathrm{Tr}}\nolimits [\rho _{i} +\rho _{j}] + \frac{p^{2}} {d^{2}}\mathbb{1}_{d}\right ] {}\\ &>& 0, {}\\ \end{array}$$

for any 0 < p < 1. This way, the zero-error capacity of the depolarizing quantum channel $\mathcal{E}$ is zero, i.e., $C^{(0)}(\mathcal{E}) = 0$.

Example 5.2 (Quantum Channel with Positive Zero-Error Capacity).

Suppose a quantum channel $\mathcal{E}$ in an 8-dimensional Hilbert space. Consider a set of classical messages $\left \{0,1,\ldots,7\right \}$ associated with a set of pure quantum input states $\mathcal{S} = \left \{\rho _{0} = \left \vert 0\right \rangle \left \langle 0\right \vert,\rho _{1} = \left \vert 1\right \rangle \left \langle 1\right \vert,\ldots,\rho _{7} = \left \vert 7\right \rangle \left \langle 7\right \vert \right \}$, in which 0 ↦ ρ ₀, 1 ↦ ρ ₁, …, 7 ↦ ρ ₇. Let $\mathcal{M}$ be a POVM specified by $\mathcal{M} = \left \{M_{i} = \left \vert i\right \rangle \left \langle i\right \vert \right \}_{i=0}^{7}$. Notice that $\sum _{i=0}^{7}M_{i} =\mathbb{1}$. We consider that the quantum channel acts on the input as shown in Fig. 5.4a.

Fig. 5.4

Diagrams representing the transitions performed by the channel ɛ over the input. (a ) A discrete memoryless channel. (b ) A subset of non-adjacent states at the channel output

This channel has positive zero-error capacity because it is possible to identify a subset of non-adjacent states at the channel output, as shown in Fig. 5.4b. This subset is composed by $\left \{\rho _{0},\rho _{1},\rho _{3},\rho _{5},\rho _{7}\right \}$ and it is maximal. We have that

$$\displaystyle\begin{array}{rcl} C^{(0)}(\mathcal{E})& \geq & \frac{1} {1}\log _{2}5 {}\\ & \geq & 2.321\text{ bits per symbol per channel use.} {}\\ \end{array}$$

It is important to emphasize that it is not possible to state that the zero-error capacity of this quantum channel is equal to 2. 321 bits per channel use, since the supremum (5.4) should be taken over all sets $\mathcal{S}$ and over all zero-error quantum codes of length n.

5.2 Representation in Graphs

The zero-error capacity of quantum channels allows for a representation in terms of graphs [11, 14], as does the zero-error capacity of classical channels. Given a quantum channel and a set $\mathcal{S}$ of input states, we can construct a characteristic graph as follows.

Definition 5.5 (Characteristic Graph ).

Let $\mathcal{E}$ be a quantum channel. For a given set of input states $\mathcal{S} = \left \{\rho _{1},\rho _{2},\ldots,\rho _{\ell}\right \}$, we can build a characteristic graph $\mathcal{G}$ with vertices and edges given by

• 1. $V (\mathcal{G}) = \left \{1,2,\ldots,\ell\right \}$, where each vertex is associated with an input state in $\mathcal{S}$;

• 2. $E(\mathcal{G}) = \left \{(i,j)\vert \rho _{i} \perp _{\mathcal{E}}\rho _{j};\rho _{i},\rho _{j} \in \mathcal{S};i\neq j\right \}$.

This notion of characteristic graph can be extended to the n-tensor product of states in $\mathcal{S}$, $\mathcal{S}^{\otimes n}$, giving rise to the graph $\mathcal{G}^{n}$, where $V (\mathcal{G}^{n}) = V (\mathcal{G})^{n}$ and two vertices in $V (\mathcal{G}^{n})$ are connected if and only if the corresponding n-tensor input states are non-adjacent at the channel output, i.e.,

• 1. $V (\mathcal{G}^{n}) = \left \{1,2,\ldots,\ell\right \}^{n}$,

• 2. $E(\mathcal{G}^{n}) = \left \{(i_{1}\ldots i_{n},j_{1}\ldots j_{n})\vert \rho _{i_{k}} \perp _{\mathcal{E}}\rho _{j_{k}}\right \}$ for at least one k, 1 ≤ k ≤ n; $\rho _{i_{k}},\rho _{j_{k}} \in \mathcal{S}$.

With this representation we can verify that vertices connected by an edge in the graph $\mathcal{G}^{n}$ correspond to mutually non-adjacent product states at the channel output. Therefore, the maximum amount of messages that can be transmitted by an (m, n) error-free quantum code with input alphabet $\mathcal{S}$ is given by the clique number of $\mathcal{G}^{n}$, denoted by $\omega (\mathcal{G}^{n})$, i.e., $\omega (\mathcal{G}^{n}) =\alpha _{n}(\mathcal{E})$. Moreover, we can give an alternative, equivalent definition of the zero-error capacity of quantum channels in terms of graph theory.

Definition 5.6 (Classical Zero-Error Capacity of a Quantum Channel).

The zero-error capacity of a quantum channel $\mathcal{E}$ is given by

$$\displaystyle{ C^{(0)}(\mathcal{E}) =\sup _{ \mathcal{S}}\sup _{n} \frac{1} {n}\log \omega (\mathcal{G}^{n}), }$$

(5.6)

where the supremum is taken over all input sets $\mathcal{S}$ and over all codes of length n.

Example 5.3 (Zero-Error Capacity from a Graph).

Let’s return to the channel $\mathcal{E}$ of Example 5.2 and illustrated in Fig. 5.4a. The characteristic graph associated with the subset $\mathcal{S}$ is shown in Fig. 5.5. The clique number of this characteristic graph is 5, corresponding to the pairs $\left \{(0,1),(1,3),(3,5),(5,7),(7,0)\right \}$. The clique of the characteristic graph of $\mathcal{E}$ is shown in Fig. 5.5 with dotted edges.

Fig. 5.5

Characteristic Graph of $\mathcal{E}$ from Example 5.2

5.3 Quantum States Attaining the Zero-Error Capacity

We turn our attention to the subset $\mathcal{S} =\{ \rho _{1},\ldots,\rho _{l}\}$ that reaches the supremum (5.6). Note that states $\rho _{i} \in \mathcal{S}$ can be either pure or mixed states . It turns out that the zero-error capacity of a quantum channel can always be reached by a set of quantum pure states.

Proposition 5.1.

The zero-error capacity of quantum channels can be achieved by a set $\mathcal{S}$ composed only of pure quantum states, i.e., $\mathcal{S} =\{\rho _{i} = \vert v_{i}\rangle \langle v_{i}\vert \}$ .

To prove the proposition, consider a quantum channel with Kraus operators $\mathcal{E}\equiv \{ E_{a}\}$, and assume that the capacity is reached by a subset $\mathcal{S}$ that contains mixed states. Then, we show that it is always possible to write a new subset $\mathcal{S}'$ composed only of pure states that also achieves the channel capacity.

Initially, note that two quantum states ρ and σ have orthogonal supports if and only if $\text{Tr}\left (\rho \sigma \right ) = 0$. We can write

$$\displaystyle\begin{array}{rcl} \text{Tr}\left (\mathcal{E}(\rho _{i})\mathcal{E}(\rho _{j})\right )& =& \text{Tr}\left (\sum _{a}\sum _{r}\lambda _{i_{r}}E_{a}\vert v_{i_{r}}\rangle \langle v_{i_{r}}\vert E_{a}^{\dag }\sum _{ b}\sum _{s}\lambda _{j_{s}}E_{b}\vert v_{j_{s}}\rangle \langle v_{j_{s}}\vert E_{b}^{\dag }\right ) \\ & =& \text{Tr}\left (\sum _{a}\sum _{r}\sum _{b}\sum _{s}\lambda _{i_{r}}\lambda _{j_{s}}E_{a}\vert v_{i_{r}}\rangle \langle v_{i_{r}}\vert E_{a}^{\dag }E_{ b}\vert v_{j_{s}}\rangle \langle v_{j_{s}}\vert E_{b}^{\dag }\right ) \\ & =& \sum _{a,r,b,s}\lambda _{i_{r}}\lambda _{j_{s}}\vert \vert \langle v_{i_{r}}\vert E_{a}^{\dag }E_{ b}\vert v_{j_{s}}\rangle \vert \vert ^{2}, {}\end{array}$$

(5.7)

where $\rho _{i} =\sum _{s}\lambda _{i_{s}}\vert v_{i_{s}}\rangle \langle v_{i_{s}}\vert$. Suppose that $\rho _{i}\perp _{\mathcal{E}}\rho _{j}$, then $\langle v_{i_{r}}\vert E_{a}^{\dag }E_{b}\vert v_{j_{s}}\rangle = 0$ for all indexes r and s. Now, without loss of generality, define a new set $\mathcal{S}' =\{ \vert v_{1_{1}}\rangle,\ldots,\vert v_{l_{1}}\rangle \}$, where $\vert v_{i_{1}}\rangle \in \text{supp} \rho _{i}$ is a pure state in the support of ρ _i . It is clear that if ρ _i and ρ _j are non-adjacent, then

$$\displaystyle\begin{array}{rcl} \text{Tr}\left (\mathcal{E}(\vert v_{i_{1}}\rangle )\mathcal{E}(\vert v_{j_{1}}\rangle )\right )& =& \text{Tr}\left (\sum _{a}E_{a}\vert v_{i_{1}}\rangle \langle v_{i_{1}}\vert E_{a}^{\dag }\sum _{ b}E_{b}\vert v_{j_{1}}\rangle \langle v_{j_{1}}\vert E_{b}^{\dag }\right ) \\ & =& \text{Tr}\left (\sum _{a}\sum _{b}E_{a}\vert v_{i_{1}}\rangle \langle v_{i_{1}}\vert E_{a}^{\dag }E_{ b}\vert v_{j_{1}}\rangle \langle v_{j_{1}}\vert E_{b}^{\dag }\right ) \\ & =& \sum _{a,b}\vert \vert \langle v_{i_{1}}\vert E_{a}^{\dag }E_{ b}\vert v_{j_{1}}\rangle \vert \vert ^{2} \\ & =& 0. {}\end{array}$$

(5.8)

Note that all non-adjacency relationships in $\mathcal{S}$ are at least preserved when using the subset $\mathcal{S}'$. In terms of graphs, the characteristic graph $\mathcal{G}'$ due to $\mathcal{S}'$ can be obtained from $\mathcal{G}$, the characteristic graph due to $\mathcal{S}$, by probably adding a number of edges but never deleting edges. Because adding new vertices never decreases the clique number of a graph, we can conclude that the subset $\mathcal{S}'$ also attains the quantum zero-error capacity.

Now the relationship between orthogonality at the channel input and non-adjacency at the channel output is investigated. It is straightforward to see that two non-adjacent quantum states are necessarily orthogonal at the channel input. At a first glance, we can think that maximizing the number of pairwise non-adjacent quantum states requires pairwise orthogonal states at the channel input. Surprisingly, it turns out that there exist quantum channels such that we can do better by choosing a subset $\mathcal{S}$ where not all states are pairwise orthogonal.

To illustrate this feature, we present a mathematically motivated example of a quantum channel for which the capacity is attained by a set of non-orthogonal input states. In addition, the channel gives rise to the pentagon graph for the subset reaching the capacity.

Example 5.4.

Let e be a quantum channel with operation elements {E ₁, E ₂, E ₃} given by

$$\displaystyle\begin{array}{rcl} & E_{1} = \left [\begin{array}{*{10}c} 0.5& 0 & 0 & 0 & \frac{\sqrt{49902}} {620} \\ 0.5&-0.5& 0 & 0 & 0\\ 0 & 0.5 &-0.5 & 0 & 0 \\ 0 & 0 & 0.5 &-\frac{\sqrt{457}} {50} & \frac{\sqrt{457}} {50} \\ 0 & 0 & 0 & -0.62 & -\frac{289} {1550} \end{array} \right ],\quad E2 = \left [\begin{array}{*{10}c} 0.5& 0 & 0 & 0 &-\frac{\sqrt{49902}} {620} \\ 0.5&0.5& 0 & 0 & 0\\ 0 &0.5 &0.5 & 0 & 0 \\ 0 & 0 &0.5& \frac{\sqrt{457}} {50} & -\frac{\sqrt{457}} {50} \\ 0 & 0 & 0 & 0.5 & 0.5 \end{array} \right ],& {}\\ & E3 = 0.3\vert 4\rangle \langle 4\vert, & {}\\ \end{array}$$

where β = { | 0〉, …, | 4〉} is the computational basis for the Hilbert space of dimension five. Consider the following set $\mathcal{S}$ of input states for $\mathcal{E}$:

$$\displaystyle{ \mathcal{S} = \left \{\vert v_{1}\rangle = \vert 0\rangle,\vert v_{2}\rangle = \vert 1\rangle,\vert v_{3}\rangle = \vert 2\rangle,\vert v_{4}\rangle = \vert 3\rangle,\vert v_{5}\rangle = \frac{\vert 3\rangle + \vert 4\rangle } {\sqrt{2}} \right \}. }$$

(5.9)

In order to construct the characteristic graph $\mathcal{G}$, we need to explicit all adjacency relations between states in $\mathcal{S}$. If the channel outputs $\mathcal{E}(\vert v_{i}\rangle )$ are calculated for every $\vert v_{i}\rangle \in \mathcal{S}$, one can verify that

$$\displaystyle\begin{array}{rcl} \vert v_{1}\rangle \perp _{\mathcal{E}}\vert v_{3}\rangle,\qquad \vert v_{1}\rangle \perp _{\mathcal{E}}\vert v_{4}\rangle,\qquad \vert v_{2}\rangle \perp _{\mathcal{E}}\vert v_{4}\rangle,& & {}\\ \vert v_{2}\rangle \perp _{\mathcal{E}}\vert v_{5}\rangle,\qquad \text{and}\qquad \vert v_{3}\rangle \perp _{\mathcal{E}}\vert v_{5}\rangle.& & {}\\ \end{array}$$

These relations give rise to the pentagon as characteristic graph, as it is illustrated in Fig. 5.6a.

Fig. 5.6

(a ) Characteristic graph $\mathcal{G}$ for the subset $\mathcal{S}$ containing non-adjacent input states. (b ) Characteristic graph for a subset $\mathcal{S}'$ of mutually orthogonal input states. In this case, the transmission rate is less than C ⁽⁰⁾(pentagon) for any zero-error quantum code with alphabet $\mathcal{S}'$

It is important to note that if we replace the state $\vert v_{5}\rangle = \frac{\vert 3\rangle +\vert 4\rangle } {\sqrt{2}}$ with the state | 4〉, then the subset $\mathcal{S}$ becomes the (orthonormal) basis β. For the subset β, the characteristic graph is shown in Fig. 5.6b. The zero-error capacity of the former graph is $C_{0} = \frac{1} {2}\log 5$ bits/use, whereas the latter has zero-error capacity C ₀ = 1 bit/use. Because there is no other subset of input states giving rise to a graph with C ₀ ≥ 1, the zero-error capacity of $\mathcal{E}$ is

$$\displaystyle{C^{(0)}(\mathcal{E}) = \frac{1} {2}\log 5\text{ bits/use}.}$$

5.4 Relation with Holevo-Schumacher-Westmoreland Capacity

Quantum channels have different kinds of capacity, depending mainly on if the information to be sent is either classical or quantum and on the communication protocol [17]. When classical messages are mapped into tensor products at the channel input and collective measurements are performed at the channel output, the capacity of the quantum channel to convey classical information with a negligible error probability after many channel uses, denoted by C _1, ∞ , is given by the Holevo-Schumacher-Westmoreland (HSW) theorem [10, 20].

As we already mentioned, the HSW capacity can be understood as a generalization of the ordinary capacity of classical channels. According to the HSW theorem, this capacity is given by

$$\displaystyle{ C_{1,\infty }(\mathcal{E}) \equiv \max _{p_{i},\rho _{i}}\chi _{p_{i},\rho _{i}}, }$$

(5.10)

where

$$\displaystyle{ \chi _{p_{i},\rho _{i}} = S\left (\mathcal{E}\left (\sum _{i}p_{i}\rho _{i}\right )\right ) -\sum _{i}p_{i}S\left (\mathcal{E}(\rho _{i})\right ). }$$

(5.11)

The term S(⋅ ) in (5.11) stands for the von Neumann entropy ; the maximum (5.10) takes into account all possible input ensembles {ρ _i , p _i } for the quantum channel $\mathcal{E}$; $\chi _{p_{i},\rho _{i}}$ is known as the Holevo quantity.

Theorem 5.1 (Bound on the Quantum Zero-Error Capacity).

The zero-error capacity of a quantum channel $\mathcal{E}$ is upper bounded by the HSW capacity, i.e.,

$$\displaystyle{ C^{(0)}(\mathcal{E}) \leq C_{ 1,\infty }(\mathcal{E}) \equiv \max _{p_{i},\rho _{i}}\chi _{p_{i},\rho _{i}}. }$$

(5.12)

To prove the theorem, we assume that Alice sends to Bob a message chosen uniformly from the set {1, …, 2^nR}. If we define a random variable X representing indexes of classical messages, then

$$\displaystyle{ H(X) = nR, }$$

(5.13)

where H stands for the classical Shannon entropy [1]. Let Y be a random variable representing POVM outputs. Using the definition of mutual information , we get

$$\displaystyle\begin{array}{rcl} nR& =& H(X) = H(X\vert Y ) + I(X,Y ).{}\end{array}$$

(5.14)

Because the quantum code is error-free, H(X | Y ) = 0. Suppose that Alice encodes the message i as $\overline{\rho }_{i} =\rho _{i_{1}} \otimes \ldots \otimes \rho _{i_{n}}$. Applying the Holevo bound we get

$$\displaystyle\begin{array}{rcl} nR& =& I(X,Y ) \\ & \leq & S\left (\sum _{i=1}^{2^{nR} } \frac{1} {2^{nR}}\mathcal{E}(\overline{\rho }_{i})\right ) -\sum _{i=1}^{2^{nR} } \frac{1} {2^{nR}}S(\mathcal{E}(\overline{\rho }_{i})).{}\end{array}$$

(5.15)

Remember that $\mathcal{E}(\overline{\rho }_{i}) = \mathcal{E}(\rho _{i_{1}}) \otimes \ldots \otimes \mathcal{E}(\rho _{i_{n}})$. Hence, we can apply the subadditivity of the von Neumann entropy, S(A, B) ≤ S(A) + S(B):

$$\displaystyle\begin{array}{rcl} nR& \leq & \sum _{j=1}^{n}S\left (\sum _{ i=1}^{2^{nR} } \frac{1} {2^{nR}}\mathcal{E}(\rho _{i_{j}})\right ) -\sum _{i=1}^{2^{nR} } \frac{1} {2^{nR}}\sum _{j=1}^{n}S(\mathcal{E}(\rho _{ i_{j}})) \\ & =& \sum _{j=1}^{n}\left [S\left (\sum _{ i=1}^{2^{nR} } \frac{1} {2^{nR}}\mathcal{E}(\rho _{i_{j}})\right ) -\sum _{i=1}^{2^{nR} } \frac{1} {2^{nR}}S(\mathcal{E}(\rho _{i_{j}}))\right ].{}\end{array}$$

(5.16)

Because the capacity (5.10) is calculated by taking the ensemble that gives the maximum, we can conclude that each term on the right side of (5.16) is less than or equal to $C_{1,\infty }(\mathcal{E})$. Then,

$$\displaystyle{ nR \leq nC_{1,\infty }(\mathcal{E}) }$$

(5.17)

and the inequality follows for all zero-error quantum block codes of length n and rate R. This is an intuitive result, since one would expect to increase the information transmission rate whenever a small probability of error is allowed.

Example 5.5.

Consider the quantum channel of the Example 5.4 and the set $\mathcal{S}$ of non-orthogonal states giving rise to the pentagon as characteristic graph. Obviously, we do not know if $\mathcal{S}$ attains the supremum (5.10). However, $\mathcal{S}$ does attain the zero-error capacity of $\mathcal{E}$, which is $C_{0}(G_{5}) = \frac{1} {2}\log 5$ bits per use. In this case, a simple calculation shows that the χ quantity for the family $\{\mathcal{S},p_{i} = 1/5\}$ is greater than C ₀(G ₅), i.e.,

$$\displaystyle\begin{array}{rcl} \chi _{\{\mathcal{S},1/5\}}& =& \frac{1} {5}\left [S\left (\mathcal{E}\left (\sum _{i=1}^{5}\vert v_{ i}\rangle \langle v_{i}\vert \right )\right ) -\sum _{i=1}^{5}S(\mathcal{E}(\vert v_{ i}\rangle \langle v_{i}\vert ))\right ] \\ & =& 1.53 \\ & \geq & C_{0}(G_{5}) \\ & =& 1.16. {}\end{array}$$

(5.18)

5.5 Superactivation of Zero-Error Capacity

A well-known result in classical zero-error communication asserts that a discrete memoryless channel has positive zero-error capacity if and only if N(1) > 1. Therefore, if one use of the channel cannot transmit zero-error information, then many uses cannot either. Thanks to entanglement , the capacity of quantum channels to carry classical or quantum information behaves significantly different from the corresponding classical capacity. Concerning the zero-error capacity, there are quantum channels such that the use of entangled input states allows for a positive zero-error capacity even when the one-shot capacity is zero.¹ This phenomenon is known as superactivation of zero-error capacity of quantum channels.

The activation of zero-error capacity was first demonstrated by Duan and Shi [8] in a scenario of a multipartite communication system, where m senders want to send classical messages to n receivers using a noisy multipartite quantum channel. Afterwards, superactivation was found on several classes of one sender/one receiver quantum channels.

5.5.1 Activation of Zero-Error Capacity on Multipartite Quantum Channels

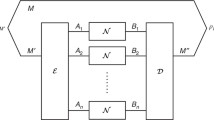
Consider a scenario where n senders, S ₁, …, S _n , want to communicate with m receivers, R ₁, …, R _m , using a multipartite quantum communication channel , $\mathcal{E}$. Figure 5.7 illustrates the general setup of this system. As a reasonable assumption, Duan and Shi considered that the senders can use LOCC (local operations and classical communication) in order to prepare and code the quantum state to be transmitted [8]. At the channel output, the receivers can also use LOCC to decode the output message.

Fig. 5.7

An (m, n) multipartite quantum channel. When the senders want to transmit the message k, they start with the state | 0〉 ⊗ … ⊗ | 0〉. Then, LOCC is used to encode | 0〉^⊗m into a quantum stated ρ _k , which is transmitted through the channel $\mathcal{E}_{m,n}$. At the channel output, receivers make use of LOCC to decode $\mathcal{E}_{m,n}(\rho _{k})$ and get an estimation of the original message k

Let $\mathcal{E}$ be an (m, n) multipartite quantum channel defined as the following positive trace-preserving map:

$$\displaystyle{\mathcal{E}_{m,n}: \mathcal{B}(\mathcal{H}_{S})\longrightarrow \mathcal{B}(\mathcal{H}_{R}),}$$

where $\mathcal{H}_{S} = \mathcal{H}_{S_{1}} \otimes \ldots \otimes \mathcal{H}_{S_{m}}$ and $\mathcal{H}_{R} = \mathcal{H}_{R_{1}} \otimes \ldots \otimes \mathcal{H}_{R_{n}}$ are the state spaces of senders and receivers, respectively. In order to transmit a message, the senders start with a state | 0〉 ⊗ … ⊗ | 0〉 and prepare the input quantum codeword $\rho \in \mathcal{H}_{S}$ using LOCC. At the channel output, the receivers make use of LOCC to decode the output state $\mathcal{E}_{m,n}(\rho )$. The communication scheme is illustrated in Fig. 5.8.

Fig. 5.8

Example of a $\mathcal{E}_{1,2}$ channel whose zero-error capacity can be activated. Although no perfect transmission can be archived with a single use, a sender can transmit one bit of information by using the channel twice. The zero-error capacity of this channel is at least 0. 5 bits per channel use

As an example, define σ ₀ = | β ₀₀〉〈β ₀₀ | and $\sigma _{1} = \frac{1} {3}(\mathbb{1} -\sigma _{0})$, where $\vert \beta _{00}\rangle = \frac{\vert 00\rangle +\vert 11\rangle } {\sqrt{2}}$ stands for the Bell state . Consider the following one sender (Charlie) two receivers (Alice an Bob) quantum channel

$$\displaystyle{ \mathcal{E}_{1,2}(\rho ) =\langle 0\vert \rho \vert 0\rangle \sigma _{0} +\langle 1\vert \rho \vert 1\rangle \sigma _{1}, }$$

(5.19)

which takes a qubit ρ into two qubits—one qubit for each receiver. It is straightforward to see that there exists just one pair of adjacent input states for this channel, corresponding to the qubits | 0〉 and | 1〉, since $\mathcal{E}_{1,2}(\vert 0\rangle \langle 0\vert ) =\sigma _{0}$ and $\mathcal{E}_{1,2}(\vert 1\rangle \langle 1\vert ) =\sigma _{1}$. Although σ ₀ and σ ₁ are orthogonal quantum states, Alice and Bob are not able to distinguish them after a single use of the channel. This arises from the fact that no quantum communication is allowed between the receivers. Because the one-shot zero-error capacity of this channel is zero, one may think that no zero-error information can be transmitted, even after many channel uses. Shannon proved that this assertion is always true for classical channels. Thanks to entanglement, quantum channels behave drastically different from classical channels. Now suppose that the Charlie uses the channel $\mathcal{E}_{1,2}(\rho )$ twice to transmit ρ ^⊗2 = | 00〉 or ρ ^⊗2 = | 01〉. The corresponding received states are

$$\displaystyle\begin{array}{rcl} \mathcal{E}_{1,2}^{\otimes 2}(\vert 00\rangle \langle 00\vert )& =& \sigma _{ 0} \otimes \sigma _{0},{}\end{array}$$

(5.20)

$$\displaystyle\begin{array}{rcl} \mathcal{E}_{1,2}^{\otimes 2}(\vert 01\rangle \langle 01\vert )& =& \sigma _{ 0} \otimes \sigma _{1}.{}\end{array}$$

(5.21)

No matter what are the messages transmitted by Charlie, | 00〉 or | 01〉, Alice and Bob always will share the Bell state σ ₀ = | β ₀₀〉. In order to complete the communication, Alice and Bob make use of the shared state | β ₀₀〉 to teleport the second qubit, e.g., Alice teleports his part of the entangled state σ ₀ or σ ₁ to Bob. Finally, Bob performs a projective measurement in order to distinguish between σ ₀ or σ ₁. Because we are able to transmit two messages without confusion using the channel twice, the zero-error capacity is, at least,

$$\displaystyle{C^{(0)}(\mathcal{E}_{ 1,2}) \geq \frac{1} {2}\log 2 = 0.5\text{ bits per channel use}.}$$

This is an amazing result with no counterpart in classical zero-error information theory . A single use of $\mathcal{E}_{1,2}$ cannot transmit error-free messages, whereas two uses can! This phenomenon is called activation of the zero-error capacity.

Considering that senders and receivers agree on the LOCC protocol above, Duan and Shi proved the following theorem:

Theorem 5.2 (Activation of the Zero-Error Capacity on Multipartite Quantum Channels).

For any m > 1 or n > 1, there exist (m,n) multipartite quantum channels for which one use of channel cannot transmit zero-error classical information, whereas two or more uses can.

To prove the theorem, it is sufficient to explicit two multipartite quantum channels, $\mathcal{E}_{1,2}$ and $\mathcal{E}_{2,1}$, for which the zero-error capacity can be activated. That is because any (m, n) multipartite quantum channels can be extended to an (m + m′, n + n′) channel, m′ and n′ positive integers, by ignoring the input from the additional m′ senders and setting to | 0〉 the output to all the additional n′ receivers.

Consider a (2, 1) multipartite quantum channel $\mathcal{E}_{2,1}$ from two senders, Alice and Bob, to one receiver, Charlie,

$$\displaystyle{ \mathcal{E}_{2,1}: \mathcal{B}(\mathcal{H}_{S})\longrightarrow \mathcal{B}(\mathcal{H}_{R}), }$$

(5.22)

where $\mathcal{H}_{S} = \mathcal{H}_{S_{A}} \otimes \mathcal{H}_{S_{B}}$ and $\mathcal{H}_{R} = \mathcal{H}_{R_{C}}$. The state spaces of Alice and Bob, $\mathcal{H}_{S_{A}}$ and $\mathcal{H}_{S_{B}}$, are four dimensional spaces. The output state space $\mathcal{H}_{R_{C}}$ is a qubit. The quantum channel $\mathcal{E}_{2,1}$ is defined as follows:

$$\displaystyle{ \mathcal{E}_{2,1}(\rho ) = \text{Tr}\left (P_{0}\rho \right )\vert 0\rangle \langle 0\vert + \text{Tr}\left (P_{1}\rho \right )\vert 1\rangle \langle 1\vert, }$$

(5.23)

where P ₀ is a projector onto the state space $\mathcal{S}_{0} \subset \mathcal{H}_{S}$ spanned by the (unnormalized) vectors

$$\displaystyle\begin{array}{rcl} \vert \psi _{1}\rangle & =& \vert 00\rangle -\vert 11\rangle, \\ \vert \psi _{2}\rangle & =& \vert 22\rangle -\vert 33\rangle, \\ \vert \psi _{3}\rangle & =& \vert 20\rangle -\vert 31\rangle, \\ \vert \psi _{4}\rangle & =& \vert 02\rangle + \vert 13\rangle, \\ \vert \psi _{5}\rangle & =& \vert 30\rangle -\vert 03\rangle, \\ \vert \psi _{6}\rangle & =& \vert 10\rangle -\sqrt{2}\vert 21\rangle + \vert 32\rangle, \\ \vert \psi _{7}\rangle & =& \vert 01\rangle + \sqrt{2}\vert 12\rangle + \vert 23\rangle, \\ \vert \psi _{8}\rangle & =& \vert 10\rangle -\vert 32\rangle -\vert 01\rangle + \vert 23\rangle,{}\end{array}$$

(5.24)

and P ₁ is the projector onto $\mathcal{S}_{1}$, which is the orthogonal complement of $\mathcal{S}_{0}$, i.e., $\mathcal{S}_{1} = \mathcal{S}_{0}^{\perp }$. The vectors | ψ _i 〉 were carefully chosen in order to span a completely entangled state subspace. Consequently, $\mathcal{S}_{0}$ has no product state, which means that $\mathcal{S}_{0}$ does not have any state | ϕ〉 such that | ϕ〉 = | ϕ _A 〉 ⊗ | ϕ _B 〉, $\vert \phi _{A}\rangle \in \mathcal{H}_{S_{A}}$ and $\vert \phi _{B}\rangle \in \mathcal{H}_{S_{B}}$. Because any quantum codeword ρ prepared by Alice and Bob using LOCC is necessarily a product state , it turns out that $\text{Tr}\left (P_{0}\rho \right )> 0$ as well as $\text{Tr}\left (P_{1}\rho \right )> 0$. As a consequence, the corresponding outputs of the channel (5.23) are always non-orthogonal mixed states. Therefore, there are no pairs of adjacent states at the channel input and the one-shot zero-error capacity is zero, i.e., no classical information can be transmitted with a single use of the $\mathcal{E}_{2,1}$ channel. However, the use of entanglement between two uses of channel enables the transmission of a classical bit with a zero probability of error.

Let | Φ〉 be the following bipartite quantum state:

$$\displaystyle{ \vert \varPhi \rangle = \frac{1} {2}(\vert 00\rangle + \vert 11\rangle + \vert 22\rangle + \vert 33\rangle ). }$$

(5.25)

Because $\vert \varPhi \rangle \in \mathcal{H}_{S} \otimes \mathcal{H}_{S}$, we denote by | Φ〉 _AA′ the multipartite state | Φ〉 prepared by Alice, where A and A′ denote the first and the second component of | Φ〉, respectively. The same holds for the state | Φ〉 _BB′ prepared by Bob. Define U _i  = | 0〉〈0 | − | 1〉〈1 | + | 2〉〈2 | − | 3〉〈3 | as an operator that acts on the component i of | Φ〉, where i ∈ { A, A′, B, B′}. In order to activate the zero-error capacity of the channel, the senders use the quantum channel twice in the following way:

• 1. Alice locally prepares the state | Φ〉, denoted by | Φ〉 _AA′. Bob does the same, getting | Φ〉 _BB′;

• 2. Using LOCC, Alice and Bob agree on who will transmit the message (one bit) to Charlie. Without loss of generality, suppose that Alice sends the message (the bit “0”) to Charlie;

• 3. Alice and Bob transmit the first components of their bipartite state, i.e., the components A and B of | Φ〉 _AA′ and | Φ〉 _BB′, respectively. This is the first use of the channel;

• 4. The second components of each state | Φ ^A〉 and | Φ〉 _BB′ are sent;

• 5. After the second round, Charlie performs a joint projective measurement in order to estimate the message sent by Alice and Bob. As will be explained below, the received state is given by

  $$\displaystyle{ \mathcal{E}_{2,1}^{\otimes 2}(\vert \varPhi \rangle _{ AA'} \otimes \vert \varPhi \rangle _{BB'}) = \frac{\vert 00\rangle \langle 00\vert + \vert 11\rangle \langle 11\vert } {2}. }$$

  (5.26)

• 6. Instead, if Alice chooses to send the bit “1,” then she applies the operator U _i to one of the components A or A′ of | Φ〉 _AA′. As will be demonstrated next, the whole received state by Charlie is

  $$\displaystyle{ \mathcal{E}_{2,1}^{\otimes 2}(U_{ A\text{ or }A'}\vert \varPhi \rangle _{AA'} \otimes \vert \varPhi \rangle _{BB'}) = \frac{\vert 01\rangle \langle 01\vert + \vert 10\rangle \langle 10\vert } {2}. }$$

  (5.27)

It is straightforward to see that the two possible output quantum states (5.26) and (5.27) are orthogonal , i.e., they can be fully distinguished by Charlie using a projective measurement. Figure 5.9 illustrates the communication protocol.

Fig. 5.9

Example of a $\mathcal{E}_{2,1}$ channel whose one-shot zero-error capacity is equal to zero. Figure illustrates how Alice and Bob can use the channel twice in order to transmit one bit to Charlie without confusion. The zero-error capacity of this channel is at least 0. 5 bits/use

By linearity, the output of the quantum channel (5.23) after two channel uses can be written as

$$\displaystyle\begin{array}{rcl} \mathcal{E}_{2,1}^{\otimes 2}(\rho )& =& \text{Tr}\left ((P_{ 0} \otimes P_{0})\rho \right )\vert 00\rangle \langle 00\vert + \text{Tr}\left ((P_{0} \otimes P_{1})\rho \right )\vert 01\rangle \langle 01\vert \\ & & +\text{Tr}\left ((P_{1} \otimes P_{0})\rho \right )\vert 10\rangle \langle 10\vert + \text{Tr}\left ((P_{1} \otimes P_{1})\rho \right )\vert 11\rangle \langle 11\vert.{}\end{array}$$

(5.28)

Before the first transmission and supposing that Alice wishes to send the message “0,” the global system state at the channel input is given by

$$\displaystyle\begin{array}{rcl} \vert \varPhi \rangle _{AA'} \otimes \vert \varPhi \rangle _{BB'}& =& 1/4(\vert 00\mathbf{00}\rangle + \vert 00\mathbf{11}\rangle + \vert 00\mathbf{22}\rangle + \vert 00\mathbf{33}\rangle \\ & & +\vert 11\mathbf{00}\rangle + \vert 11\mathbf{11}\rangle + \vert 11\mathbf{22}\rangle + \vert 11\mathbf{33}\rangle \\ & & +\vert 22\mathbf{00}\rangle + \vert 22\mathbf{11}\rangle + \vert 22\mathbf{22}\rangle + \vert 22\mathbf{33}\rangle \\ & & +\vert 33\mathbf{00}\rangle + \vert 33\mathbf{11}\rangle + \vert 33\mathbf{22}\rangle + \vert 33\mathbf{33}\rangle ).{}\end{array}$$

(5.29)

Unfortunately, we cannot directly apply the above state to the composite channel (5.28) in order to get the output state after the second channel use. To see this, first note that we have written in bold the components of the global input state (5.29) that belongs to Bob. However, the expression of $\mathcal{E}_{2,1}^{\otimes 2}(\rho )$ presumes that the components of ρ must be organized in an order compatible with the original transmission protocol. For example, the second trace operator in (5.28), $\text{Tr}\left ((P_{0} \otimes P_{1})\rho \right )$, means that we must apply P ₀ to the components A and B of | Φ〉 _AA′ and | Φ〉 _BB′, respectively. Analogously, the projector P ₁ must be applied to the parts A′ and B′ of the corresponding quantum systems. For instance, we can manipulate (5.29) to fulfill this requirement. We call ρ = | Φ ₀〉〈Φ ₀ | the state of the system corresponding to the message “0,” where

$$\displaystyle\begin{array}{rcl} \vert \varPhi _{0}\rangle & =& \vert \varPhi _{ABA'B'}\rangle \\ & =& 1/4(\vert 0\mathbf{0}0\mathbf{0}\rangle + \vert 0\mathbf{1}0\mathbf{1}\rangle + \vert 0\mathbf{2}0\mathbf{2}\rangle + \vert 0\mathbf{3}0\mathbf{3}\rangle \\ & & +\vert 1\mathbf{0}1\mathbf{0}\rangle + \vert 1\mathbf{1}1\mathbf{1}\rangle + \vert 1\mathbf{2}1\mathbf{2}\rangle + \vert 1\mathbf{3}1\mathbf{3}\rangle \\ & & +\vert 2\mathbf{0}2\mathbf{0}\rangle + \vert 2\mathbf{1}2\mathbf{1}\rangle + \vert 2\mathbf{2}2\mathbf{2}\rangle + \vert 2\mathbf{3}2\mathbf{3}\rangle \\ & & +\vert 3\mathbf{0}3\mathbf{0}\rangle + \vert 3\mathbf{1}3\mathbf{1}\rangle + \vert 3\mathbf{2}3\mathbf{2}\rangle + \vert 3\mathbf{3}3\mathbf{3}\rangle ).{}\end{array}$$

(5.30)

Now supposing that Alice wants to transmit the message “1” and that she applies the operator U _i to any of the components of | Φ〉 _AA′, we have

$$\displaystyle\begin{array}{rcl} U_{i}\vert \varPhi \rangle _{AA'}& =& (\vert 0\rangle \langle 0\vert -\vert 1\rangle \langle 1\vert + \vert 2\rangle \langle 2\vert -\vert 3\rangle \langle 3\vert )\frac{1} {2}(\vert 00\rangle + \vert 11\rangle + \vert 22\rangle + \vert 33\rangle ) {}\\ & =& \frac{1} {2}(\vert 00\rangle -\vert 11\rangle + \vert 22\rangle -\vert 33\rangle ). {}\\ \end{array}$$

The whole state of the system before the transmission is

$$\displaystyle\begin{array}{rcl} U_{i}\vert \varPhi \rangle _{AA'} \otimes \vert \varPhi \rangle _{BB'}& =& 1/4(\vert 00\mathbf{00}\rangle + \vert 00\mathbf{11}\rangle + \vert 00\mathbf{22}\rangle + \vert 00\mathbf{33}\rangle \\ & & -\vert 11\mathbf{00}\rangle -\vert 11\mathbf{11}\rangle -\vert 11\mathbf{22}\rangle -\vert 11\mathbf{33}\rangle \\ & & +\vert 22\mathbf{00}\rangle + \vert 22\mathbf{11}\rangle + \vert 22\mathbf{22}\rangle + \vert 22\mathbf{33}\rangle \\ & & +\vert 33\mathbf{00}\rangle -\vert 33\mathbf{11}\rangle -\vert 33\mathbf{22}\rangle -\vert 33\mathbf{33}\rangle ).{}\end{array}$$

(5.31)

In the same way, we can manipulate the above state in order to apply the channel $\mathcal{E}_{2,1}(\rho )$ twice:

$$\displaystyle\begin{array}{rcl} \vert \varPhi _{1}\rangle & =& \vert \varPhi _{ABA'B'}\rangle \\ & =& 1/4(\vert 0\mathbf{0}0\mathbf{0}\rangle + \vert 0\mathbf{1}0\mathbf{1}\rangle + \vert 0\mathbf{2}0\mathbf{2}\rangle + \vert 0\mathbf{3}0\mathbf{3}\rangle \\ & & -\vert 1\mathbf{0}1\mathbf{0}\rangle -\vert 1\mathbf{1}1\mathbf{1}\rangle -\vert 1\mathbf{2}1\mathbf{2}\rangle -\vert 1\mathbf{3}1\mathbf{3}\rangle \\ & & +\vert 2\mathbf{0}2\mathbf{0}\rangle + \vert 2\mathbf{1}2\mathbf{1}\rangle + \vert 2\mathbf{2}2\mathbf{2}\rangle + \vert 2\mathbf{3}2\mathbf{3}\rangle \\ & & -\vert 3\mathbf{0}3\mathbf{0}\rangle -\vert 3\mathbf{1}3\mathbf{1}\rangle -\vert 3\mathbf{2}3\mathbf{2}\rangle -\vert 3\mathbf{3}3\mathbf{3}\rangle ).{}\end{array}$$

(5.32)

Finally, the reader can verify that

$$\displaystyle{\mathcal{E}_{2,1}^{\otimes 2}(\vert \varPhi _{ 0}\rangle \langle \varPhi _{0}\vert ) = \frac{\vert 00\rangle \langle 00\vert + \vert 11\rangle \langle 11\vert } {2} }$$

and

$$\displaystyle{\mathcal{E}_{2,1}^{\otimes 2}(\vert \varPhi _{ 1}\rangle \langle \varPhi _{1}\vert ) = \frac{\vert 01\rangle \langle 01\vert + \vert 10\rangle \langle 10\vert } {2} }$$

are orthonormal quantum states. In summary, one use of the quantum channel always leads to non-orthogonal mixed states and, therefore, the channel one-shot zero-error capacity vanishes. In contrast, using the channel twice, Alice and Bob can agree on a LOCC protocol in order to send one message to Charlie without confusion. Therefore, the asymptotical zero-error capacity of this channel is

$$\displaystyle{C^{(0)}(\mathcal{E}_{ 2,1}) \geq \frac{1} {2}\log 2 = 0.5\text{ bits per channel use}.}$$

Besides its amazing feature of having the zero-error capacity activated, the channel $\mathcal{E}_{2,1}(\rho )$ has another interesting property. Alice and Bob can use the channel twice to send one bit of information to Charlie without leaking any information about the transmitted message to the other sender.

For instance, the activation of the zero-error capacity was shown in a context of a multiuser quantum channel , where senders and receivers share a classical channel to run a LOCC protocol. A natural question is whether there exist one-sender one-receiver quantum channels such that the zero-error capacity can be activated, i.e., quantum channels that a single sender cannot perfectly transmit a message to a single receiver just using the channel once, whereas such transmission is possible using the channel twice. Surprisingly, these quantum channels exist; this feature was discovered simultaneously by Duan [7] and by Cubitt et al. [5]. The so-called superactivation of the zero-error capacity is explained in the next section.

5.5.2 Superactivation of the Classical Zero-Error Capacity of Quantum Channels: Part I

In this section, we present the first of two mathematical developments that lead to a surprising result about the zero-error capacity of quantum channels. By using different frameworks, Duan [7] and Cubitt et al. [5] were able to construct families of one-sender one-receiver quantum channels whose zero-error capacities can be superactivated.

Initially, we describe the construction of two quantum channels, $\mathcal{S}$ and $\mathcal{F}$, that have a vanishing zero-error capacity. In contrast, when used together, the quantum channel $\mathcal{S}\otimes \mathcal{F}$ has a positive zero-error capacity, i.e., $C^{(0)}(\mathcal{S}\otimes \mathcal{F})> 0$. This is not yet an example of superactivation. However, if we construct a quantum channel $\mathcal{E} = \mathcal{S}\oplus \mathcal{F}$ as the direct sum of $\mathcal{S}$ and $\mathcal{F}$,

$$\displaystyle{ \mathcal{E}(\rho ) = \mathcal{S}(P_{0}\rho P_{0}) + \mathcal{F}(P_{1}\rho P_{1}), }$$

(5.33)

where P ₀ and P ₁ are specific projectors over the input state space, then it can be showed that the channel $\mathcal{E}$ has the one-shot zero-error capacity equal to zero, whereas classical information can be transmitted making use of the direct sum channel twice. The setup is showed in Fig. 5.10.

Fig. 5.10

A quantum channel $\mathcal{E}$ whose zero-error capacity can be superactivated. The channel $\mathcal{E}$ is the direct sum of $\mathcal{S}$ and $\mathcal{F}$, two quantum channels with a vanishing one-shot zero-error capacity with the property that $C^{(0)}(\mathcal{S}\otimes \mathcal{F})> 0$. The channel $\mathcal{E}$ has a one-shot zero-error capacity equal to zero, but when used twice, Bob can perfectly distinguish between two output states $\mathcal{E}^{\otimes 2}(\vert \varPhi _{0}\rangle \langle \varPhi _{0}\vert )$ and $\mathcal{E}^{\otimes 2}(\vert \varPhi _{1}\rangle \langle \varPhi _{1}\vert )$

Consider a quantum channel $\mathcal{E}$ with Kraus operators $\mathcal{E}\equiv \{ E_{k}\}_{k=1}^{n}$, where $\mathcal{E}(\rho ) =\sum _{k}E_{k}\rho E_{k}^{\dag }$ and ∑ _k E _k ^† E _k  = I. According to (5.8), if the quantum channel $\mathcal{E}$ has positive zero-error capacity, then there exist at least two orthogonal input states | ψ ₀〉, | ψ ₁〉 such that

$$\displaystyle\begin{array}{rcl} \text{Tr}\left (\mathcal{E}^{\dag }(\vert \psi _{ 0}\rangle \langle \psi _{0}\vert )\mathcal{E}(\vert \psi _{1}\rangle \langle \psi _{1}\vert )\right )& =& \sum _{a,b}\vert \vert \langle \psi _{0}\vert E_{a}^{\dag }E_{ b}\vert \psi _{1}\rangle \vert \vert ^{2} \\ & =& 0, {}\end{array}$$

(5.34)

which means that

$$\displaystyle{ \text{Tr}\left (E_{a}^{\dag }E_{ b}\vert \psi _{0}\rangle \langle \psi _{1}\vert \right ) = 0 }$$

(5.35)

for all 1 ≤ a, b ≤ n. It is evident that operators E _a ^† E _b play an important role in studying the zero-error capacity of quantum channels. Define

$$\displaystyle{ \mathcal{K}(\mathcal{E}) = \text{span}\{E_{a}^{\dag }E_{ b}: 1 \leq a,b \leq n\}. }$$

(5.36)

In linear algebra, a basis $\mathcal{B}$ of a matrix space vector is called unextendible if $\mathcal{B}^{\perp }$ contains no rank-one matrices. Consequently, $\mathcal{B}^{\perp }$ contains only matrices with rank two or more and, therefore, we say that $\mathcal{B}^{\perp }$ is a completely entangled state space. When $\mathcal{B}^{\perp }$ contains at least one rank-one matrix, the basis $\mathcal{B}$ is called extendible . This kind of partition of a state space has interesting applications in quantum information theory, specially in distinguishability of general quantum states and subspaces. Some references about unextendible basis can be found at Further Reading section. For our purposes, we just mention an important property of unextendible basis. It was shown that if the dimension of a matrix subspace $\mathcal{B}$ is $\text{dim}(\mathcal{B}) <2d - 1$, where d is the dimension of the whole matrix space, then $\mathcal{B}$ is always extendible.

We turn our attention to (5.35). First note that the operator | ψ ₀〉〈ψ ₁ | is orthogonal to E _a ^† E _b for all 1 ≤ a, b ≤ n, i.e., $\vert \psi _{0}\rangle \langle \psi _{1}\vert \in \mathcal{K}(\mathcal{E})^{\perp }$. Moreover, the operator | ψ ₀〉〈ψ ₁ | has rank equal to one. Therefore, we conclude that if a quantum channel $\mathcal{E}\equiv \{ E_{k}\}_{k=1}^{n}$ has positive one-shot zero-error capacity , then $\mathcal{K}(\mathcal{E})$ is extendible. The converse is also true, as states the following lemma [7].

Lemma 5.1.

Let $\mathcal{E}\equiv \{ E_{k}\}_{k=1}^{n}$ be a quantum channel with Kraus operators E _k . The channel $\mathcal{E}$ has positive zero-error capacity if and only if $\mathcal{K}(\mathcal{E})$ is extendible.

Another property of $\mathcal{K}(\mathcal{E})$ is $\mathcal{K}(\mathcal{E})^{\dag } = \mathcal{K}(\mathcal{E})$. Note that $\mathcal{K}(\mathcal{E})^{\dag } =\{ K^{\dag },K \in \mathcal{K}(\mathcal{E})\}$. Moreover, because $\mathcal{E}$ is trace preserving , it turns out that $I \in \mathcal{K}(\mathcal{E})$. In fact, these two properties are necessary and sufficient conditions to guarantee the existence of a quantum channel from an input state space of operators $\mathcal{B}(\mathcal{H}_{d})$ to the output state space $\mathcal{B}(\mathcal{H}_{d'})$.

Lemma 5.2 (Duan [7]).

Let $\mathcal{M}$ be a matrix subspace of $\mathcal{B}(\mathcal{H}_{d})$ . There is a quantum channel $\mathcal{E}$ from $\mathcal{B}(\mathcal{H}_{d})$ to $\mathcal{B}(\mathcal{H}_{d'})$ such that $\mathcal{K}(\mathcal{E}) = \mathcal{M}$ if and only if $\mathcal{M}^{\dag } = \mathcal{M}$ and $I \in \mathcal{M}$ .

The conditions in Lemmas 5.1 and 5.2 are important because they allow to construct quantum channels whose zero-error capacity can be superactivated . As already mentioned, this can be achieved by finding two quantum channels, $\mathcal{S}$ and $\mathcal{F}$, with vanish zero-error capacity, whereas $\mathcal{S}\otimes \mathcal{F}$ has positive zero-error capacity. This can be done by writing down two partitions of a state space, say $\mathcal{K}(\mathcal{S})$ and $\mathcal{K}(\mathcal{F})$, with the following properties: $\mathcal{K}(\mathcal{S})$ and $\mathcal{K}(\mathcal{F})$ are unextendible, whereas $\mathcal{K}(\mathcal{S}) \otimes \mathcal{K}(\mathcal{F})$ is extendible.

Example 5.6 (Superactivation of the Zero-Error Capacity of Quantum Channels).

Let $\mathcal{K}(\mathcal{S})$ be the matrix state space spanned by the vectors:

$$\displaystyle\begin{array}{rcl} S_{1}& =& \vert 0\rangle \langle 0\vert + \vert 1\rangle \langle 1\vert, \\ S_{2}& =& \vert 2\rangle \langle 2\vert + \vert 3\rangle \langle 3\vert, \\ S_{3}& =& \vert 2\rangle \langle 0\vert -\vert 0\rangle \langle 2\vert, \\ S_{4}& =& \vert 3\rangle \langle 0\vert + \vert 0\rangle \langle 3\vert, \\ S_{5}& =& \vert 1\rangle \langle 3\vert + \vert 3\rangle \langle 1\vert, \\ S_{6}& =& \cos \theta \vert 0\rangle \langle 1\vert +\sin \theta \vert 2\rangle \langle 3\vert -\vert 1\rangle \langle 2\vert, \\ S_{7}& =& \cos \theta \vert 1\rangle \langle 0\vert +\sin \theta \vert 3\rangle \langle 2\vert -\vert 2\rangle \langle 1\vert, \\ S_{8}& =& \sin \theta \vert 0\rangle \langle 1\vert -\cos \theta \vert 2\rangle \langle 3\vert -\sin \theta \vert 1\rangle \langle 0\vert +\cos \theta \vert 3\rangle \langle 2\vert,{}\end{array}$$

(5.37)

where 0 < θ < π∕2 is a parameter. The reader can verify that $\mathcal{K}(\mathcal{S})^{\perp } = \mathcal{K}(\mathcal{S})$ and $I \in \mathcal{K}(\mathcal{S})$. In addition, consider the matrix state space spanned by the following vectors:

$$\displaystyle\begin{array}{rcl} F_{1}& =& \vert 0\rangle \langle 0\vert -\vert 1\rangle \langle 1\vert, \\ F_{2}& =& \vert 2\rangle \langle 2\vert -\vert 3\rangle \langle 3\vert, \\ F_{3}& =& \vert 2\rangle \langle 0\vert + \vert 0\rangle \langle 2\vert, \\ F_{4}& =& \vert 3\rangle \langle 0\vert -\vert 0\rangle \langle 3\vert, \\ F_{5}& =& \vert 1\rangle \langle 3\vert -\vert 3\rangle \langle 1\vert, \\ F_{6}& =& \cos \theta \vert 0\rangle \langle 1\vert +\sin \theta \vert 2\rangle \langle 3\vert + \vert 1\rangle \langle 2\vert, \\ F_{7}& =& \cos \theta \vert 1\rangle \langle 0\vert +\sin \theta \vert 3\rangle \langle 2\vert + \vert 2\rangle \langle 1\vert, \\ F_{8}& =& -\sin \theta \vert 0\rangle \langle 1\vert +\cos \theta \vert 2\rangle \langle 3\vert +\sin \theta \vert 1\rangle \langle 0\vert -\cos \theta \vert 3\rangle \langle 2\vert.{}\end{array}$$

(5.38)

The reader can easily verify that $\mathcal{K}(\mathcal{F})$ satisfies the Hermitian condition , $\mathcal{K}(\mathcal{F})^{\dag } = \mathcal{K}(\mathcal{F})$. Moreover, the subspaces $\mathcal{K}(\mathcal{S})$ and $\mathcal{K}(\mathcal{F})$ are orthogonal with respect to the Hilbert-Schmidt inner product .

The two matrix vectors state spaces $\mathcal{K}(\mathcal{S})$ and $\mathcal{K}(\mathcal{F})$ has the following desirable properties:

• (a) $\mathcal{K}(\mathcal{S})$ and $\mathcal{K}(\mathcal{F})$ are unextendible, i.e., they are completely entangled state spaces;

• (b) $\mathcal{K}(\mathcal{S}) \otimes \mathcal{K}(\mathcal{F})$ is extendible.

In order to verify property (a), define a rank-one matrix | ψ〉〈ϕ | orthogonal to $\mathcal{K}(\mathcal{S})$, where | ψ〉 = ∑ _i = 0 ³ c _i  | i〉 and | ϕ〉 = ∑ _j = 0 ³ d _j  | j〉. Then, for each k = 1, …, 8, $\text{Tr}\left (S_{k}\vert \psi \rangle \langle \phi \vert \right ) = 0$ implies c _i  = d _i  = 0 for all 0 ≤ i ≤ 3, i.e., the orthogonal complement of $\mathcal{K}(\mathcal{S})$ has no rank-one matrices and, therefore, $\mathcal{K}(\mathcal{S})$ is unextendible. The same holds for the subspace $\mathcal{K}(\mathcal{F})$.

Property (b) can be demonstrated by defining the quantum state

$$\displaystyle{ \vert \varPhi _{0}\rangle = \frac{\vert 00\rangle + \vert 11\rangle + \vert 22\rangle + \vert 33\rangle } {2} }$$

(5.39)

and the operator U = | 0〉〈0 | − | 1〉〈1 | + | 2〉〈2 | − | 3〉〈3 | . The reader can verify that the following quantum state

$$\displaystyle{ \vert \varPhi _{1}\rangle = (I \otimes U)\frac{\vert 00\rangle + \vert 11\rangle + \vert 22\rangle + \vert 33\rangle } {2} }$$

(5.40)

gives rise to the rank-one matrix | Φ ₁〉〈Φ ₁ | orthogonal to $\mathcal{K}(\mathcal{S}) \otimes \mathcal{K}(\mathcal{S})$, i.e.,

$$\displaystyle{\text{Tr}\left (S_{i} \otimes F_{j}\vert \varPhi _{1}\rangle \langle \varPhi _{1}\vert \right ) = 0\qquad \forall i,j = 1,\ldots,8.}$$

Therefore, the vector space $\mathcal{K}(\mathcal{S}) \otimes \mathcal{K}(\mathcal{S})$ is extendible because $(\mathcal{K}(\mathcal{S}) \otimes \mathcal{K}(\mathcal{S}))^{\perp }$ has a rank-one matrix.

According to Lemma 5.2, the corresponding quantum channels $\mathcal{S}$ and $\mathcal{F}$ have no zero-error capacity when used individually, whereas the channel $\mathcal{S}\otimes \mathcal{F}$ has positive zero-error capacity. By using $\mathcal{S}\otimes \mathcal{F}$, a sender can prepare one of the entangled states  | Φ ₀〉 and | Φ ₁〉 to transmit a classical message to a receiver, since the latter can perfectly distinguish between $\mathcal{S}\otimes \mathcal{F}(\vert \varPhi _{0}\rangle )$ and $\mathcal{S}\otimes \mathcal{F}(\vert \varPhi _{1}\rangle )$.

As already mentioned, this is not yet an example of superactivation, since $\mathcal{S}$ and $\mathcal{F}$ are different channels. However, if we consider the direct sum channel $\mathcal{S}\oplus \mathcal{F}$ (5.33),

$$\displaystyle{\mathcal{E}(\rho ) = \mathcal{S}(P_{0}\rho P_{0}) + \mathcal{F}(P_{1}\rho P_{1}),}$$

with P ₀ = | Φ ₀〉〈Φ ₀ | and P ₁ = I − | Φ ₀〉〈Φ ₀ | , then it is clear that a single use of the channel $\mathcal{E}$ cannot transmit classical information without error. In contrast, one can verify that when the channel $\mathcal{E}$ is used twice, then Bob is able to distinguish between the two orthogonal states , $\mathcal{E}^{\otimes 2}(\vert \varPhi _{0}\rangle )$ and $\mathcal{E}^{\otimes 2}(\vert \varPhi _{1}\rangle )$. Therefore, the use of entanglement between two uses of a quantum channel can superactivate the zero-error capacity of the channel. Finally, we can conclude that the asymptotic zero-error capacity of $\mathcal{E}$ is

$$\displaystyle{C^{(0)}(\mathcal{E}) \geq 0.5\text{ bits per channel use}.}$$

A short remark on the construction of the quantum channels $\mathcal{S}$ and $\mathcal{F}$ should be given. First, note that

$$\displaystyle{M =\sum _{ i=1}^{8}S_{ i}^{\dag }S_{ i} =\sum _{ i=1}^{8}F_{ i}^{\dag }F_{ i},}$$

where

$$\displaystyle{ M = \left [\begin{array}{*{10}c} 4&0&0&0\\ 0 &4 &0 &0 \\ 0&0&4&0\\ 0 &0 &0 &4 \end{array} \right ]. }$$

In order to construct the corresponding trace-preserving quantum operations $\mathcal{E}$ we only need to define the sets

$$\displaystyle{ \mathcal{S}\equiv \left \{S_{i}M^{-\frac{1} {2} }\right \}_{i=1}^{8}\quad \text{and}\quad \mathcal{F}\equiv \left \{F_{i}M^{-\frac{1} {2} }\right \}_{i=1}^{8}, }$$

(5.41)

where

$$\displaystyle{ M^{-\frac{1} {2} } = \left [\begin{array}{*{10}c} 0.5& 0 & 0 & 0\\ 0 &0.5 & 0 & 0 \\ 0 & 0 &0.5& 0\\ 0 & 0 & 0 &0.5 \end{array} \right ]. }$$

5.5.3 Superactivation of the Classical Zero-Error Capacity of Quantum Channels: Part II

This section describes a different approach to determine necessary and sufficient conditions for the existence of quantum channels, $\mathcal{S}$ and $\mathcal{F}$, whose one-shot zero-error capacities are zero, while the composite channel $\mathcal{S}\otimes \mathcal{F}$ has positive (one-shot) zero-error capacity.

Consider a quantum channel $\mathcal{S}: \mathcal{B}(\mathcal{H}) \rightarrow \mathcal{B}(\mathcal{H})$. The channel $\mathcal{S}$ has a vanishing one-shot zero-error capacity if and only if all quantum states in $\mathcal{H}$ are adjacent, i.e.,

$$\displaystyle{ \forall \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}: \text{Tr}\left (\mathcal{S}(\vert \psi \rangle )^{\dag }\mathcal{S}(\vert \varphi \rangle )\right )\neq 0. }$$

(5.42)

Let $\mathcal{S}^{{\ast}}$ be the adjoint² (or dual) of $\mathcal{S}$ with respect to the Hilbert-Schmidt inner product. Because the cyclic property of the trace ,

$$\displaystyle\begin{array}{rcl} \text{Tr}\left (\mathcal{S}(\vert \psi \rangle )^{\dag }\mathcal{S}(\vert \varphi \rangle )\right )& =& \text{Tr}\left (\psi \cdot \mathcal{S}(\mathcal{S}(\vert \varphi \rangle ))\right ) \\ & =& \text{Tr}\left (\psi \cdot \mathcal{S}^{{\ast}}\circ \;\mathcal{S}(\vert \varphi \rangle )\right ),{}\end{array}$$

(5.43)

where ψ ≡ | ψ〉〈ψ | and $\mathcal{S}(\mathcal{S}(\cdot )) \equiv \mathcal{S}\circ \mathcal{S}(\cdot )$ were defined for short.

Conversely, a quantum channel has positive zero-error capacity if and only if there exists at least one pair of non-adjacent states in $\mathcal{H}$, i.e.,

$$\displaystyle{ \exists \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}: \text{Tr}\left (\mathcal{S}(\vert \psi \rangle )^{\dag }\mathcal{S}(\vert \varphi \rangle )\right ) = 0, }$$

(5.44)

or, equivalently,

$$\displaystyle{ \exists \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}: \text{Tr}\left (\psi \cdot \mathcal{S}^{{\ast}}\circ \mathcal{S}(\vert \varphi \rangle )\right ) = 0. }$$

(5.45)

The problem of finding quantum channels whose zero-error capacities can be superactivated is reformulated as follows. One needs to find two quantum channels $\mathcal{S}$, $\mathcal{F}$, such that

• (a)
  $$\displaystyle{ \forall \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}: \text{Tr}\left (\psi \cdot \mathcal{S}^{{\ast}}\circ \;\mathcal{S}(\vert \varphi \rangle )\right )\neq 0, }$$

  (5.46)

  which means $C^{(0)}(\mathcal{S}) = 0$;

• (b)
  $$\displaystyle{ \forall \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}: \text{Tr}\left (\psi \cdot \mathcal{F}^{{\ast}}\circ \;\mathcal{F}(\vert \varphi \rangle )\right )\neq 0, }$$

  (5.47)

  which means $C^{(0)}(\mathcal{F}) = 0$;

• (c)
  $$\displaystyle{ \exists \vert \alpha \rangle,\vert \phi \rangle \in \mathcal{H}^{\otimes 2}: \text{Tr}\left (\alpha \cdot (\mathcal{S}^{{\ast}}\circ \mathcal{S}) \otimes (\mathcal{F}^{{\ast}}\circ \mathcal{F})(\vert \phi \rangle \right ) = 0, }$$

  (5.48)

  which means $C^{(0)}(\mathcal{S}\otimes \mathcal{F})> 0$.

The composite map $\mathcal{S}^{{\ast}}\circ \mathcal{S}$ plays an important role in studying the zero-error capacity. A map $\mathcal{N}$ is called conjugate-divisible if it can be decomposed as $\mathcal{N} = \mathcal{S}^{{\ast}}\circ \mathcal{S}$. Before enunciating a theorem that establishes necessary and sufficient conditions for the existence of conjugate-divisible maps and gives a full characterization of its corresponding Choi-Jamiołkowski matrices, it is helpful to define positive-semidefinite states and subspaces, as well as conjugate-symmetric states and subspaces.

For bipartite states $\vert \phi \rangle _{AB} \in \mathcal{H}_{AB}$ with basis | i _A 〉 | j _B 〉, there exists an isomorphism with the space of d _A × d _A matrices in the following way:

$$\displaystyle{\vert \phi \rangle _{AB} =\sum _{ij}M_{ij}\vert i_{A}\rangle \vert j_{B}\rangle.}$$

In this way, the bipartite state | ϕ〉 _AB is said to be positive-semidefinite if the corresponding matrix $M_{\vert \phi \rangle _{AB}} = [M_{ij}]$ is positive-semidefinite. Analogously, a subspace $\mathcal{H}_{AB}$ is positive-semidefinite if it can be spanned by a set of positive-semidefinite states.

A bipartite state or operator $\vert \phi \rangle _{AB} \in \mathcal{H}_{AB}$ is conjugate-symmetric in a given basis | i _A 〉 | j _B 〉 if it is invariant under the flip operation :

$$\displaystyle{\mathbb{F}\left (\sum _{ij}c_{ij}\vert i_{A}\rangle \vert j_{B}\rangle \right ) =\sum _{ij}\bar{c}_{ij}\vert j_{A}\rangle \vert i_{B}\rangle.}$$

The effect of the flip operation is to interchange the two parties and complex conjugation. Similarly, a subspace is said to be conjugate-symmetric if it is invariant under the same operation.

Theorem 5.3 (Existence of Conjugate-Divisible Maps [5]).

Given a subspace $\mathcal{H}_{AB} \subseteq \mathcal{H}^{\otimes 2}$ such that $\text{supp}\left (\text{Tr}_{B}\left (\mathcal{H}_{AB}\right )\right ) = \mathcal{H}$ , there exists a conjugate-divisible map with (in general non-standard) Choi-Jamiołkowski matrix σ _AB such that $\text{supp}(\sigma _{AB}) = \mathcal{H}_{AB}$ if and only if $\mathcal{H}_{AB}$ is a positive-semidefinite and conjugate-symmetric subspace.

The notation $\text{supp}\left (\text{Tr}_{B}\left (\mathcal{H}_{AB}\right )\right )$ stands for $\bigcup _{\vert \phi \rangle \in \mathcal{H}_{AB}}\text{supp}\left (\text{Tr}_{B}\left (\vert \phi \rangle \langle \phi \vert \right )\right )$. Now requirements (a) to (c) can be converted into necessary and sufficient conditions for the maps to satisfy (5.46) to (5.48). Let $\sigma _{\mathcal{S}}$ and $\sigma _{\mathcal{F}}$ be the Choi-Jamiołkowski matrices corresponding to the conjugate-divisible maps $\mathcal{N}_{\mathcal{S}} = \mathcal{S}^{{\ast}}\circ \mathcal{S}$ and $\mathcal{N}_{\mathcal{F}} = \mathcal{F}^{{\ast}}\circ \mathcal{F}$, respectively. Equations (5.46) and (5.47) can be rewritten as

$$\displaystyle\begin{array}{rcl} \forall \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}: \text{Tr}\left (\psi \cdot \mathcal{S}^{{\ast}}\circ \;\mathcal{S}(\vert \varphi \rangle )\right )& =& \text{Tr}\left (\psi \cdot \text{Tr}_{ A}\left (\sigma _{S} \cdot \varphi ^{T}\otimes\mathbb{1}\right )\right ) \\ & =& \text{Tr}\left (\sigma _{\mathcal{S}}\cdot \varphi \otimes \psi \right ) \\ & \neq & 0, {}\end{array}$$

(5.49)

and

$$\displaystyle{ \forall \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}: \text{Tr}\left (\sigma _{\mathcal{F}}\cdot \varphi \otimes \psi \right )\neq 0. }$$

(5.50)

Therefore, if $\mathcal{H}_{\sigma _{\mathcal{S}}},\mathcal{H}_{\sigma _{\mathcal{F}}} \subseteq \mathcal{H}^{\otimes 2}$ are the subspaces spanned by the support of $\sigma _{\mathcal{S}}$ and $\sigma _{\mathcal{F}}$, respectively, it is necessary and sufficient to require that their orthogonal complements contain no product states , i.e.,

$$\displaystyle{ \nexists \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}\;:\; \vert \psi \rangle \otimes \vert \varphi \rangle \in \mathcal{H}_{\sigma _{\mathcal{S}}}^{\perp },\mathcal{H}_{\sigma _{ \mathcal{F}}}^{\perp }. }$$

(5.51)

We turn our attention to (5.48) in order to find necessary and sufficient conditions to the joint map $\mathcal{S}\otimes \mathcal{F}$ to fulfill the corresponding requirement. Without loss of generality, fix the states | α〉 and | ϕ〉 to be maximally entangled in the following way. Let | ω〉 be the full rank (unnormalized) state  | ω〉 = ∑ _i  | i〉 | i〉 and define | α〉 = (U ⊗ V ) | ω〉, | ϕ〉 = (W ⊗ X) | ω〉, where U, V, W, X are unitary. Again, if $\sigma _{\mathcal{S}}$ and $\sigma _{\mathcal{F}}$ are the Choi-Jamiołkowski matrices corresponding to the conjugate-divisible maps $\mathcal{N}_{\mathcal{S}} = \mathcal{S}^{{\ast}}\circ \mathcal{S}$ and $\mathcal{N}_{\mathcal{F}} = \mathcal{F}^{{\ast}}\circ \mathcal{F}$, respectively, then

$$\displaystyle\begin{array}{rcl} 0& =& \text{Tr}\left (\alpha \cdot (\mathcal{S}^{{\ast}}\circ \mathcal{S}) \otimes (\mathcal{F}^{{\ast}}\circ \mathcal{F})(\vert \phi \rangle \right ) \\ & =& \text{Tr}\left (\alpha \cdot \mathcal{N}_{\mathcal{S}}\otimes \mathcal{N}_{\mathcal{F}}(\vert \phi \rangle \right ) \\ & =& \text{Tr}\left (\alpha \cdot \text{Tr}_{A}\left (\sigma _{S} \otimes \sigma _{F} \cdot \phi ^{T}\otimes\mathbb{1}\right )\right ) \\ & =& \text{Tr}\left (\sigma _{S} \otimes \sigma _{F} \cdot \phi ^{T}\otimes \alpha \right ) \\ & =& \text{Tr}\left (\sigma _{S} \otimes \sigma _{F} \cdot (U \otimes V \omega ^{T}U^{T} \otimes V ^{T}) \otimes (W \otimes X\omega W^{\dag }\otimes X^{\dag })\right ) \\ & =& \text{Tr}\left (\left (U \otimes W\sigma _{\mathcal{S}}U^{T} \otimes W^{\dag }\right )^{T} \cdot \left (V \otimes X\sigma _{ F}V ^{T} \otimes X^{\dag }\right )\right ) \\ & =& \text{Tr}\left (\sigma _{\mathcal{S}}^{T} \cdot \left (U \otimes V \sigma _{ \mathcal{F}}U^{\dag }\otimes V ^{\dag }\right )\right ). {}\end{array}$$

(5.52)

Besides fulfilling the requirements (5.51), the support of the Choi-Jamiołkowski matrices $\sigma _{\mathcal{S}}$ and $\sigma _{\mathcal{F}}$ must be related by

$$\displaystyle{\mathcal{H}_{\sigma _{\mathcal{F}}}^{T} = (U \otimes V )\mathcal{H}_{\sigma _{ \mathcal{S}}}^{\perp }.}$$

Because conjugate-symmetry, Schmidt-rank, and positive-semidefiniteness are invariant under the transpose operation, we can write

$$\displaystyle{ \mathcal{H}_{\sigma _{\mathcal{F}}} = (U \otimes V )\mathcal{H}_{\sigma _{\mathcal{S}}}^{\perp }. }$$

(5.53)

Moreover, if a subspace is conjugate-symmetric , then so is its orthogonal complement. Considering the fact that Schmidt-rank is invariant under unitary operations, all the conditions can be expressed in terms of a single subspace $\mathcal{H}_{2} \subseteq \mathcal{H}^{\otimes 2}$. Finally, (5.51) and (5.53), together with Theorem 5.3, give necessary and sufficient conditions to guarantee the existence of two quantum channels $\mathcal{S}$ and $\mathcal{F}$ such that $C^{(0)}(\mathcal{E}) = C^{(0)}(\mathcal{F}) = 0$, while the composite channel $\mathcal{S}\otimes \mathcal{F}$ has positive one-shot zero-error capacity. All of these conditions are grouped in Theorem 5.4

Theorem 5.4 (Superactivation of the One-Shot Zero-Error Capacity [5]).

If there exists a subspace $\mathcal{H}_{2} \subseteq \mathcal{H}^{\otimes 2}$ and unitaries U,V satisfying

$$\displaystyle\begin{array}{rcl} \nexists \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}\;:\; \vert \psi \rangle \otimes \vert \varphi \rangle \in \mathcal{H}_{2}^{\perp },& &{}\end{array}$$

(5.54)

$$\displaystyle\begin{array}{rcl} \nexists \vert \psi \rangle,\vert \varphi \rangle \in \mathcal{H}\;:\; \vert \psi \rangle \otimes \vert \varphi \rangle \in \mathcal{H}_{2},& &{}\end{array}$$

(5.55)

$$\displaystyle\begin{array}{rcl} \mathbb{F}(\mathcal{H}_{2}) = \mathcal{H}_{2},& &{}\end{array}$$

(5.56)

$$\displaystyle\begin{array}{rcl} \mathbb{F}(U \otimes V \cdot \mathcal{H}_{2}) = U \otimes V \cdot \mathcal{H}_{2},& &{}\end{array}$$

(5.57)

$$\displaystyle\begin{array}{rcl} \exists \{M_{i} \geq 0\}\;:\; \mathcal{H}_{2} \equiv \text{s}pan\{M_{i}\},& &{}\end{array}$$

(5.58)

$$\displaystyle\begin{array}{rcl} \exists \{M_{j} \geq 0\}\;:\; U \otimes V \cdot \mathcal{H}_{2}^{T} \equiv \text{s}pan\{M_{ j}\},& &{}\end{array}$$

(5.59)

then there exist quantum channels $\mathcal{S}$ and $\mathcal{F}$ whose one-shot zero-error capacity is zero, whereas the joint channel $\mathcal{S}\otimes \mathcal{F}$ has positive zero-error capacity.

In Theorems 5.4, (5.54) and (5.55) fulfill requirements (5.46) and (5.47), i.e., they impose that the one-shot zero-error capacity of the channels $\mathcal{S}$ and $\mathcal{F}$ are both equal to zero. Equation (5.57) ensures that the joint channel $\mathcal{S}\otimes \mathcal{F}$ has positive zero-error capacity, whereas (5.56), (5.58), and (5.59) are necessary and sufficient conditions to guarantee the existence of the corresponding quantum channels, as stated in Theorem 5.3.

5.6 Further Reading

In this chapter, we revisited the classical zero-error capacity of quantum channels proposed by Medeiros [11]. This chapter is based on his thesis, but many articles published previously built up his theory [12–14, 16].

Many alternative definitions to the zero-error capacity of a quantum channel can also be found in the literature. Medeiros and Assis proposed a version in which the maximum amount of quantum information sent through quantum channels without errors is considered, the so-called quantum zero-error capacity of a quantum channel [14]. Other variants proposed by Winter et al. are shown in Chap. 8 and can also be found detailed in papers by these authors [4, 6, 9].

Superactivation was first described by Duan and Shi [8] for a scenario of multiple senders and receivers. Using the concept of unextendible basis [3, 19, 22], Duan [7] demonstrated the existence of one-sender one-receiver quantum channel whose zero-error capacity can be activated. This phenomena was independently studied by Cubitt et al., which proved a more general result on the superactivation of the asymptotic zero-error capacity [5]. Park and Lee [18] showed that the zero-error capacity of qubit channels cannot be superactivated.

Cubitt and Smith [2] considered the scenario where two quantum channels $\mathcal{S}$ and $\mathcal{F}$ have a vanishing zero-error capacity, whereas the joint channel $\mathcal{S}\otimes \mathcal{F}$ could transmit quantum information at a positive rate and with probability of error equal to zero. The authors called this effect the super-duper-activation of the quantum zero-error capacity. Various examples of low dimensional quantum channels whose one-shot classical and quantum zero-error capacities can be superactivated were described by Shirokov and Shulman [21].