Abstract
A novel analytic approximate technique, namely optimal variational method (OVM), is employed to propose an approach to solve some nonconservative nonlinear oscillators. Different from perturbation methods, the validity of the OVM is independent on whether or not there exist small physical parameters in the considered nonlinear equations. This procedure offers a promising approach by constructing a generalized Lagrangian and a generalized Hamiltonian for nonlinear oscillators. An excellent agreement has been found between the analytical results obtained by the proposed method and numerical integration results.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Quadratic Damping
- Optimal Variational Method (OVM)
- Numerical Integration Results
- Nonlinear Oscillations
- Approximate Analytical Techniques
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The entire conventional theory of Lagrangian representation in the space of the generalized coordinates of conservative Newtonian systems subject to holonomic constrains is based on the often tacit assumption that constrains are frictionless. But in practice, holonomic constrains are realized by mechanical means. Therefore, the presence of frictional forces is inevitable whenever holonomic constrains occur and in turn, a Lagrangian representation that does not reflect this dissipative nature commonly is considered a first approximation of the system. For computing a Lagrangian for dynamical systems with more general Newtonian forces are nowadays applicable only to systems with force derivable from a potential function (basically conservative systems). But conservative systems do not exist in our Newtonian environment. In consequence, Lagrangian representation of conservative Newtonian systems is in general only a crude approximation of physical reality. The problem of the existence of a Lagrangian or Hamiltonian can be studied today with a variety of modern and sophisticated mathematical tools which include the use of functional analysis, prolongation theory, and differential geometry. This question is called as “Inverse problem in Newtonian Mechanics” and consists in the identifications of the methods for the construction of a Lagrangian or Hamiltonian from given equation of motion [1–3].
The aim of this paper is to construct approximations to periodic solutions and frequencies of nonlinear oscillators with linear and cubic elastic restoring force and quadratic damping. These oscillators are examples of nonconservative dynamical systems. Such systems with linear and cubic elastic restoring force and quadratic damping appropriately describe those real systems for which the damping of the oscillations is produced by a turbulent liquid flow inside the damper. A typical example of an oscillator with quadratic damping is the suspension of a vehicle equipped with hydraulic shock absorbers. Suspensions with nonlinear elastic and damping characteristics are frequently utilized, because nonlinearity limits displacements and velocity reduces the extreme values of the acceleration and leads to a more uniform dynamic loading of the suspensions. The damping nonlinearity is usually achieved by using hydraulic or hydropneumatic shock absorbers. If v is the velocity of the sprung mass, for small values of v, the flow of the oil in the shock absorber is laminar and the damping characteristic is linear. As v increases, the flow becomes turbulent and the characteristic takes a parabolic form. When the velocity reaches a certain “critical” value, the pressure inside the shock absorber becomes large enough to bring about the opening of the relief valves, and this modifies the further dependence of the damping force on velocity [4]. Quadratic damping is a subject of interest for many scientists [5–9].
In this paper we consider a nonlinear oscillator with linear and cubic elastic restoring force and quadratic damping in the form
subject to initial conditions
where dot denotes derivative with respect to time and α, β, A are known constants, A > 0.
In the last few decades, considerable work has been invested in developing new methods for analytical and numerical solutions of strongly nonlinear oscillators, but it is still difficult to obtain convergent results in cases of strong nonlinearity. There is a great need for effective algorithms to avoid shortcomings of some traditional techniques. In this way, recently, many new approaches have been proposed for determining periodic solutions and frequencies to nonlinear oscillators by using a mixture of methodologies [10–20].
In what follows, we construct approximations to periodic solutions and frequencies of nonlinear oscillators by applying the optimal variational method. The most significant features of this new approach are the optimal control of the convergence of approximations and its excellent accuracy. Different from other methods, the validity of the OVM is independent on whether or not there exist small parameters in the considered nonlinear equations. Our procedure is very effective and this work demonstrates the validity and great potential of the OVM.
2 Basic Formulation of the OVM
In order to develop an application of the OVM, we consider the following differential equation of the nonlinear oscillations
with the initial conditions
where f is a nonlinear function. In our procedure, f does not need to contain a small parameter.
Variational principle can be easily established if there exists a functional called the action functional or action for short:
where T is the period of the nonlinear oscillator, \(T = 2\pi /\Omega\), and \(\Omega\) is the frequency of the system (3), which admits as extremals the solutions of Eqs. (3) and (4) and L is the generalized Lagrangian of the system (3). On physical grounds, the primary significance of this principle rests on the fact that the acting forces of Newtonian system (3) need not necessarily be derivable from a potential.
We assume that the solutions of Eq. (3) can be expressed in the form
where C i,i = 1,2,…,s + 1 are arbitrary parameters at this moment and s is a positive integer number.
Substituting Eq. (6) into Eq. (5), it results in
where
is the residual.
Equation (7) can be rewritten in the form
Applying the Ritz method, we require
From Eqs. (10) and initial conditions (4) which become
we can obtain optimally the parameters C i, i = 1,2,…,s + 1 and the frequency \(\Omega\).
We remark that expression (6) is not unique. We can alternatively choose another expression of the solution in the form
or, if the function f from Eq. (3) is an odd function:
and so on, where \(C^{\prime}_{i}\) and \(C^{\prime\prime}_{j}\) are the convergence control parameters. With these parameters known, the approximate solution is well determined.
Another possibility to determine the optimal values of these parameters C i is to solve the system
where \(R(x,C_{i} ,\Omega )\) is the residual given by Eq. (8) and \(x_{i} \in \left( {0,\pi } \right)\), i = 1,2,…,s + 2.
The parameters C i and the frequency \(\Omega\) can be determined by the least square method, the Galerkin method, the collocation method and so on [10], [18], [19].
The Hamiltonian of Eq. (3) can be expressed in the form
where p is the generalized momenta
If the Lagrangian is independent of time, then also the Hamiltonian is independent of time and results that
where t 0 is a fixed value of t such that \(t_{0} \in [0,\pi /\Omega ]\).
On the other hand, the parameters C i, i = 1,2,…,s + 1 and Ω from Eq. (17) can be determined from the conditions
3 The Oscillator with Linear and Cubic Elastic Restoring Force and Quadratic Damping
The system described by Eqs. (1) and (2) is a nonconservative system, but we try to determine a generalized Lagrangian L in the form
where F, X, Y, and G are unknown functions. The expression (19) is not unique, because it is well known that the generalized Lagrangian L is not unique. Our problem consists in studying the conditions under which there exist the Lagrangian given by Eq. (19) such that Lagrange’s equation in L coincide with
where \(h(t,u,\dot{u})\) is an arbitrary function such that \(h(t,u,\dot{u}) \ne 0\). It is clear that the Eq. (1) and the equation
have the same solutions, because \(h(t,u,\dot{u}) \ne 0\).
From Eq. (19), we can write
Substituting Eqs. (22) and (23) into Eq. (20) we have
If we choose
then, from Eq. (26) we deduce that
For simplification, we choose C 1 = C 2 = 0 into Eq. (27), then substituting Eqs. (25) and (27) into Eq. (24) it follows that
Into Eq. (28) we choose
From Eqs. (28), (29) and (30) we obtain
The Lagrangian L given by Eq. (19) can be obtained from Eqs. (27), (30), (31) and by integrating the last term in Eq. (19). In this way, we can write the generalized Lagrangian in the form
The generalized momenta becomes
The generalized Hamiltonian given by Eq. (15) can be written
The generalized Lagrangian given by Eq. (33) and therefore the generalized Hamiltonian given by Eq. (35) are independent of time, and therefore from Eqs. (35), (17) and (4) we obtain
We rewrite Eq. (36) in the form
Equations (1) and (37) are equivalent because they have the same solutions. For Eq. (37) we suppose that the solution (6) has the form (s = 5)
The action functional (5) is very difficult to solve with the solution (38), but in this case we use Eq. (37). Substituting Eq. (38) into Eq. (37), we obtain
where \(\tau =\Omega t\).
4 Numerical Examples
In order to show the validity of the OVM, Eq. (39) has been numerically solved for the case α = 1/2, β = 1 and A = 1. Making collocation in 7 points for Eq. (39), we obtain
and therefore the solution (38) becomes
Figure 1 shows the comparison between the present solution and the numerical integration results obtained using a fourth-order Runge–Kutta scheme.
5 Conclusions
In this paper, an efficient variational approach, called the optimal variational method (OVM) is employed to propose a new analytic approximate solution for some nonlinear oscillators with linear and cubic elastic restoring force and quadratic damping.
Our construction of the variational approach is different from the classical variational approach especially referring to the involvement of some initially unknown parameters C 1, C 2, …, which ensure a fast convergence of the solution. Also, the generalized Lagrangian and the generalized Hamiltonian are given in a proper manner. It should be underlined that the form of the generalized Lagrangian (19) is currently not found in the literature. Moreover, the arbitrary function h from (20) and the equivalence of the Lagrangians are completing a new approach to Lagrangian function and variational principle.
Our procedure is valid even if the nonlinear equations do not contain any small or large parameters. The OVM provides us with a simple and rigorous way to control and adjust the convergence of a solution through the parameters C i which are optimally determined. This version of variational approach proves to be very rapid, effective, and accurate. We proved this comparing the solution obtained by the proposed method with the solutions obtained via numerical integration using a fourth-order Runge–Kutta scheme. Actually, the capital strength of the OVM is its fast convergence to the exact solution, which proves that this method is very efficient in practice.
References
Santilli R.M.: Foundations of theoretical mechanics I. The inverse problem in Newtonian mechanics, Springer, Berlin (1984)
Obădeanu V., Marinca V.: The inverse problem in analytical mechanics, West Publishing House, Timişoara (1992)
Obădeanu V. Marinca V: On the inverse problem in Newtonian mechanics Tensor N.S 48 30–35 (1989)
Dincă F., Teodosiu C.: Nonlinear and random vibrations, Academic Press, New York (1973)
Cveticanin L.: Oscillator with strong quadratic damping force, Pub. Inst. Math. 85 119–130 (2009)
Pakdemirli M.: A comparison of two perturbation methods for vibrations of systems with quadratic and cubic nonlinearities, Mech. Res. Commun. 21 203–208 (1994)
Kovacic I., Rakaric Z.: Study of oscillators with non-negative real-power restoring force and quadratic damping Nonlin. Dyn. 64 293–304 (2011)
Ji J., Yu L., Chert Y.: Amplitude modulated motions in a two degree-of-freedom system with quadratic nonlinearities under parametric excitation: experimental investigation, Mech. Res. Commun. 26 499–505 (1999)
Starosvetsky Y., Gendelman O.V.: Vibration absorption in systems with a nonlinear energy sink: Nonlinear damping, J. Sound Vibr. 324 916–939 (2009)
Herişanu N., Marinca V.: Optimal homotopy perturbation method for a non-conservative dynamical system of a rotating electrical machine, Zeit. fur Naturfors. A 8–9 509-516 (2012)
Beléndez A., Méndez D.I., Fernández E., Marini S., Pascual I.: An explicit approximate solution to the Duffing-harmonic oscillator by a cubication method Phys. Lett. A 373 2805–2809 (2009)
Mickens R.E., Oyedeji K.: Comments on the general dynamics of the nonlinear oscillator J. Sound Vibr. 330, 4196 (2011)
Wu B.S., Lim C.W., Li P.S.: A generalization of the Senator–Bapat method for certain strongly nonlinear oscillators Phys. Lett. A 341 164–169 (2005)
Pakdemirli M., Karahan M.M.F., Boyacı H.: Forced vibrations of strongly nonlinear systems with multiple scales Lindstedt Poincare method Math. Comput. Appl. 16 879–889 (2011)
Pilipchuk V., Olejnik P., Awrejcewicz J.: Transient friction-induced vibrations in a 2-DOF model of brakes, J. Sound Vibr. 344, 297–312 (2015)
Natsiavas S., Paraskevopoulos E.: A set of ordinary differential equations of motion for constrained mechanical systems, Nonlinear Dyn 79 1911–1938 (2015)
Chen Y.M., Liu J.K.: A modified Mickens iteration procedure for nonlinear oscillators J. Sound Vibr. 314 465–473 (2008)
Herisanu N., Marinca V.: An iteration procedure with application to van der Pol oscillator, Int. J. Nonlinear Sci. Numer. Simulation 10 353–361 (2009)
Marinca V., Herisanu N.: The Optimal Homotopy Asymptotic Method. Engineering Applications, Springer (2015)
Lee K.C.: Energy Methods in Dynamics, Springer Berlin Heidelberg (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Marinca, V., Herişanu, N. (2016). The Oscillator with Linear and Cubic Elastic Restoring Force and Quadratic Damping. In: Awrejcewicz, J. (eds) Dynamical Systems: Theoretical and Experimental Analysis. Springer Proceedings in Mathematics & Statistics, vol 182. Springer, Cham. https://doi.org/10.1007/978-3-319-42408-8_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-42408-8_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42407-1
Online ISBN: 978-3-319-42408-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


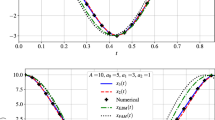


 approximate solution;
approximate solution;  numerical integration results
numerical integration results