A Competitive Memetic Algorithm for Carbon-Efficient Scheduling of Distributed Flow-Shop

Abstract

Considering the energy conservation and emissions reduction, carbon-efficient scheduling becomes more and more important to the manufacturing industry. This paper addresses the multi-objective distributed permutation flow-shop scheduling problem (DPFSP) with makespan and total carbon emissions criteria (MODPFSP-Makespan-Carbon). Some properties to the problem are provided, and a competitive memetic algorithm (CMA) is proposed. In the CMA, some search operators compete with each other, and a local search procedure is embedded to enhance the exploitation. Meanwhile, the factory assignment adjustment is used for each job, and the speed adjustment is used to further improve the non-dominated solutions. To investigate the effect of parameter setting, full-factorial experiments are carried out. Moreover, numerical comparisons are given to demonstrate the effectiveness of the CMA.

1 Introduction

Nowadays, global warming becomes a serious public problem. Carbon dioxide (CO₂) produced during the combustion process of fossil fuel is believed to be a critical reason that causes the global warming. As fossil fuel is the main source of energy, massive amounts of CO₂ are released to the atmosphere. Realizing the danger of climate, many policies and treaties are made to restrict the emissions of greenhouse gas. About half of the world’s total energy consumption is contributed by industry sector [1]. Therefore, it is imperative for manufacturing industry to implement the energy-efficient scheduling in order to reduce carbon footprints.

Under the situation, much research has been carried out about energy-saving and low-carbon. In [2], several dispatching rules were proposed relying on the estimation of inter-arrival time between jobs to control the turn on/turn off time of machines, and a multi-objective mathematical programming model was developed to minimize the energy consumption and total completion time. In [3], the turn on/off framework was applied to the single machine scheduling, and a greedy randomized multi-objective adaptive search algorithm was proposed to optimize total energy consumption and total tardiness. The framework was extended to the flexible flow shop scheduling [4], and genetic algorithm (GA) and simulated annealing (SA) were hybridized to minimize the makespan and the total energy consumption. Another energy saving technique is speed scaling [5]. In such a case, machines can be run at varying speeds, and the lower speed results in lower energy consumption and longer processing time. Some researchers assumed that the speed range of machine is continuous adjustable. For example, the performance of several algorithms was studied in terms of the management of energy and temperature [6]. Others considered that there are a number of discrete speeds are available for machines. Two mixed integer programming (MIP) models were presented and their performances were investigated for the permutation flow shop scheduling problem (PFSP) with makespan and peak power consumption [7]. To reduce the carbon emissions and makespan for the PFSP, an NEH-Insertion procedure was developed based on the problem properties, and a multi-objective NEH and an iterative greedy (IG) algorithm were proposed [8]. To solve the multi-mode resource constrained project scheduling with makespan and carbon emissions criteria, a Pareto-based estimation of distribution algorithm (EDA) was proposed [9].

With market dispersing throughout the world, manufacturing is changing from the traditional pattern in one single factory into the co-production among multi-factories [10]. Distributed manufacturing enables companies to improve production efficiency and profit [11]. There exist two sub-problems: allocating jobs to suitable factories and scheduling jobs on machines in each factory. Since the coupled two sub-problems cannot be solved sequentially if high performance is required, distributed scheduling is more difficult to solve [12]. Currently, the distributed PFSP (DPFSP) has been a hot topic. In [12], six MIP models and two factory assignment rules as well as several heuristics and variable neighborhood descent methods were developed. Besides, tabu search [13], EDA [14], hybrid immune algorithm [15], IG [16], and scatter search [17] have been developed to solve the DPFSP. Moreover, the DPFSP with reentrant constraint [18] have also been studied. Most of the above research only considered the time-based objectives. In this paper, the multi-objective DPFSP with carbon emissions and makespan criteria is studied. Inspired from the good performance of memetic algorithms in solving the complex optimization problems [19], we extend the competitive memetic algorithm (CMA) for the DPFSP [20] to a multi-objective version. Especially, several specific search operators are designed according to the problem characteristics. Due to the complexity brought by the optimization of the carbon emission, the sharing phase is replaced by the adjustment phase in the CMA to effectively reduce the carbon emission. In addition, some properties will be analyzed, and the effectiveness will be demonstrated by numerical comparisons.

2 Problem Description

The following notions will be used to describe the MODPFSP-Makespan-Carbon.

• f: total number of factories; n: total number of jobs;

• m: number of machines in each factor; s: number of speeds alternative to machines;

• S: discrete set of s different processing speeds, S = {v ₁, v ₂, …, v _s};

• n _k : number of jobs in the factory k; O _i,j : operation of job i on machine j;

• p _i,j : standard processing time of O _i,j ; V _i,j : processing speed of O _i,j ;

• C _i,j : the completion time of O _i,j ; C(k): the completion time of factory k;

• PP _j,v : energy consumption per unit time when machine j is run at speed v;

• SP _j : energy consumption per unit time when machine j is run at standby mode;

• π ^k: the processing sequence in the factory k; Π: a schedule, Π = (π ¹, π ², …, π ^f; V).

The problem is described as follows. There are f identical factories, each of which is a permutation flow shop with m machines. Each of n jobs can be assigned to any one of the f factories for processing. Each operation O _i,j has a standard processing time p _i,j . Each machine can be run at s different speeds S, and it cannot change the speed during processing an operation. When operation O _i,j is processing at speed V _i,j , the actual processing time becomes p _i,j /V _i,j . Machines will not be shut down before all jobs are completed. If there is no job processed on machine j, it will be run at a standby mode. The makespan C _max is calculated as follows.

$$ C_{{\pi^{k} (1),1}} = p_{{\pi^{k} (1),1}} /V_{{\pi^{k} (1),1}} $$

(1)

$$ C_{{\pi^{k} (i),1}} = C_{{\pi^{k} (i - 1),1}} + p_{{\pi^{k} (i),1}} /V_{{\pi^{k} (i),1}} $$

(2)

$$ C_{{\pi^{k} (1),j}} = C_{{\pi^{k} (1),j - 1}} + p_{{\pi^{k} (1),j}} /V_{{\pi^{k} (1),j}} $$

(3)

$$ C_{{\pi^{k} (i),j}} = \hbox{max} \{ C_{{\pi^{k} (i - 1),j}} ,C_{{\pi^{k} (i),j - 1}} \} + p_{{\pi^{k} (i),j}} /V_{{\pi^{k} (i),j}} $$

(4)

$$ C(k) = C_{{\pi^{k} \left( {n_{k} } \right),m}} $$

(5)

$$ C_{\hbox{max} } = \hbox{max} \{ C(1),C(2), \ldots ,C(f)\} $$

(6)

Let x _kjv (t) and y _kj (t) be the following binary variables:

$$ x_{kjv} (t) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;{\text{machine}}\;j\;{\text{in}}\;{\text{factory}}\;k\;{\text{is}}\;{\text{run}}\;{\text{at}}\;{\text{speed}}\;v\;{\text{at}}\;{\text{time}}\;t} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(7)

$$ y_{kj} (t) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;{\text{machine}}\;j\;{\text{in}}\;{\text{factory}}\;k\;{\text{is}}\;{\text{run}}\;{\text{at}}\;{\text{standby}}\;{\text{mode}}\;{\text{at}}\;{\text{time}}\;t} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(8)

The total carbon emissions (TCE) can be calculated as follows:

$$ \begin{aligned} TCE = \varepsilon \cdot TEC \\ = \varepsilon \cdot \sum\nolimits_{k = 1}^{f} {\int_{0}^{C(k)} {\left( {\sum\nolimits_{v = 1}^{s} {\sum\nolimits_{j = 1}^{m} {PP_{jv} \cdot x_{kjv} (t)} } + \sum\nolimits_{j = 1}^{m} {SP_{j} \cdot y_{kj} (t)} } \right)} } dt \\ \end{aligned} $$

(9)

where TEC is the total energy consumption and ε refers to the emissions per unit of consumed energy.

A Gantt chart of problem with 2 factories is shown in Fig. 1. Since C(1) > C(2), C _max = C(1). Take the situation at time t ₁ to explain how TCE is calculated. In the factory F ₁, machine M ₁ is in the standby mode, while M ₂ and M ₃ are in processing mode. Assuming that M ₂ and M ₃ are run at speed v and u, the energy consumption of factory F ₁ at time t ₁ is P(t ₁) = SP ₁ + PP _2v  + PP _3u . Similarly, the energy consumption of each factory at different time points can be calculated as Fig. 2. The area between the curve and time axis is energy consumption of the corresponding factory. Then, TCE can be obtained by accumulating the energy consumption of each factory.

Fig. 1.

Gantt chart of the DPFSP

Fig. 2.

Energy consumption

For the MODPFSP-Makespan-Carbon, it assumes that when V _i,j is increased from v to u, the energy consumption increases while processing time decreases.

$$ p_{i,j} /u < p_{i,j} /v $$

(10)

$$ PP_{j,u} \cdot p_{i,j} /u > PP_{j,v} \cdot p_{i,j} /v $$

(11)

Based on the assumption, two properties for the PFSP were given in [8]. Here, one more property is given and extended to those of the MODPFSP-Makespan-Carbon.

Property 1

[8]. If two schedules π ₁ and π ₂ satisfy (1) $\forall i \in \{ 1,2, \ldots ,n\} ,j \in \{ 1,2, \ldots ,m\}$, V _i,j (π ₁) = V _i,j (π ₂), (2) C _max(π ₁) < C _max(π ₂), then, TCE(π ₁) < TCE(π ₂). That is $\pi_{1} \succ \pi_{2}$.

Property 2

[8]. If two schedules π ₁ and π ₂ satisfy (1) C _max(π ₁) = C _max(π ₂), (2) $\forall i \in \{ 1,2, \ldots ,n\} ,j \in \{ 1,2, \ldots ,m\}$, V _i,j (π ₁) ≤ V _i,j (π ₂), (3) $\exists i \in \{ 1,2, \ldots ,n\}$, $j \in \{ 1,2, \ldots ,m\}$, V _i,j (π ₁) < V _i,j (π ₂), then, TCE(π ₁) < TCE(π ₂). That is $\pi_{1} \succ \pi_{2}$.

Property 3.

If two schedules π ₁ and π ₂ satisfy (1) $\forall i \in \{ 1,2, \ldots ,n\} ,j \in \{ 1,2, \ldots ,m\}$, V _i,j (π ₁) = V _i,j (π ₂), (2) TCE(π ₁) < TCE(π ₂), then, C _max(π ₁) < C _max(π ₂). That is $\pi_{1} \succ \pi_{2}$.

Proof.

The TCE of π ₁ and π ₂ can be calculated in the following ways:

$$ TCE(\pi_{1} ) = \varepsilon \cdot (\sum\nolimits_{j = 1}^{m} {SP_{j} \times t_{j}^{\text{idle}} (\pi_{1} )} + \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{m} {PP_{{j,V_{i,j} }} \times p_{i,j} /V_{i,j} } } ) $$

(12)

$$ TCE(\pi_{ 2} ) = \varepsilon \cdot (\sum\nolimits_{j = 1}^{m} {SP_{j} \times t_{j}^{\text{idle}} (\pi_{ 2} )} + \sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{m} {PP_{{j,V_{i,j} }} \times p_{i,j} /V_{i,j} } } ) $$

(13)

where $t_{j}^{\text{idle}}$ represents the total idle time of machine M _j .

Since TCE(π ₁) < TCE(π ₂), it has $\sum\nolimits_{j = 1}^{m} {t_{j}^{\text{idle}} (\pi_{1} )} < \sum\nolimits_{j = 1}^{m} {t_{j}^{\text{idle}} (\pi_{2} )}$. Thus, $\exists j' = 1,2, \ldots ,{\kern 1pt} m$, $t_{j'}^{\text{idle}} (\pi_{1} ) < t_{j'}^{\text{idle}} (\pi_{2} )$. So, ${\kern 1pt} {\kern 1pt} t_{j'}^{\text{idle}} (\pi_{1} ) + \sum\nolimits_{i = 1}^{n} {p_{i,j'} /V_{i,j} } < t_{j'}^{\text{idle}} (\pi_{2} ) + \sum\nolimits_{i = 1}^{n} {p_{i,j'} /V_{i,j} }$. According to the definition of C _max in a PFSP, it has $C_{\hbox{max} } (\pi_{1} ) = t_{j}^{\text{idle}} (\pi_{1} ) + \sum\nolimits_{i = 1}^{n} {p_{i,j} /V_{i,j} }$, ${\kern 1pt} {\kern 1pt} \forall j = 1,2, \ldots ,m$. Therefore, $C_{\hbox{max} } (\pi_{1} ) < C_{\hbox{max} } (\pi_{2} )$.

Property 4.

For a schedule Π, keep the speeds of all operations unchanged and change the job processing sequence in the factory with maximum completion time (denoted as F _m ). If the completion time of F _m is decreased, then the carbon emissions of F _m are also decreased. That is, if C _max(Π) is decreased, then TCE(Π) is decreased.

Property 5.

For a schedule Π, keep the speeds of all operations unchanged and change the job processing sequence in F _m . If the carbon emissions of F _m are decreased, then the completion time of F _m is also decreased. That is, if TCE(Π) is decreased, then C _max(Π) is decreased.

Property 6.

For a schedule Π, if it keeps the completion time of each factory unchanged and slows down the speeds of some operations, the TCE(Π) will be decreased while C _max(Π) will remain the same.

3 CMA for MODPFSP-Makespan-Carbon

3.1 Encoding Scheme

In the CMA, an individual X _l is represented by a job-factory matrix J - F and a velocity matrix A. J - F is a 2-by-n matrix, where the first row is job permutation sequence and the second row is factory assignment sequence. A is a n-by-m matrix, where element $A_{i,j} \in \{ 1,2, \ldots ,s\}$ represents the processing speed of O _i,j . An instance with f = 2, n = 5, m = 4, s = 3 is shown in Fig. 3. J - F implies that jobs J ₁ and J ₂ are assigned to F ₁ with the processing sequence π ¹ = {1, 2}, and jobs J ₃, J ₅, J ₄ are assigned to F ₂ with the sequence π ² = {3, 5, 4}. In matrix A, for example, A _2,3 = 3 means that the operation O _2,3 is processed at speed v ₃.

Fig. 3.

An example for encoding scheme

3.2 Solution Updating Mechanism, Initialization and Archive

In the CMA, once a new individual X _l ’ is generated, it will be compared with its original one X _l , and the acceptance rule is based on the dominance relationship between the two individuals: (1) If $X_{l} \text{'} \succ X_{l}$, $X_{l} = X_{l} '$; (2) If $X_{l} \succ X_{l} '$, remain X _l unchanged; (3) If X _l and X _l ’ are non-dominated, then randomly choose one as new X _l .

In the initialization phase, all population size (PS) individuals are generated randomly to achieve enough diversity. Besides, a Pareto archive (PA) is used to record the explored non-dominated solutions and a temporal archive (TA) is used to store the newly found non-dominated solutions in each generation.

3.3 Competition

Adjusting the job processing sequence or the processing speed will impact the objective value, so three operators are designed, including SU, SD and CS.

SU: the operator is to increase the speed of an operation for optimizing makespan. Since the C _max of the DPFSP will be decreased only by improving the schedule in F _m , SU is designed to randomly choose an operation O _i,j from the factory F _m ; if A _i,j  = a<s, then increase A _i,j to b (a < b≤s).

SD: the operator is to decrease the speed of an operation for optimizing TCE. Since the reduction of carbon emissions of any factory contributes to the reduction of TCE, factory F _k is randomly selected in SD. Then, randomly choose an operator O _i,j from F _k ; if A _i,j  = a>1, then decrease A _i,j to b (1 ≤ b<a).

CS: based on the Properties 4 and 5, the operator is to change job processing sequence in a factory to decrease C _max and TCE simultaneously. CS is designed to randomly select a job J* from F _m , then insert J* into a new position in F _m .

In each generation, the objective of each individual is normalized as follows:

$$ g_{p} \left( {X_{l} } \right) = (f_{p} \left( {X_{l} } \right) - f_{p}^{\hbox{min} } )/(f_{p}^{\hbox{max} } - f_{p}^{\hbox{min} } ) $$

(14)

where g _p (X _l ) denotes the normalized value of the p-th objective, f _p (X _l ) denotes the value of the p-th objective, $f_{p}^{ \hbox{max} }$ and $f_{p}^{ \hbox{min} }$ denote the maximum and minimum value of the p-th objective in the current population.

It can be seen from Fig. 4 that the normalized objective space is divided into three areas by α ₁, α ₂ and α ₃. Obviously, individuals belonging to Ω₁ has better performance on the TCE while is relatively weaker on the C _max. Individuals in Ω₂ are just the opposite. Individuals in Ω₃ have better balance between the two objectives. Since individuals in Ω₁, Ω₂ and Ω₃ have different features, we make a distinction among them by choosing different operators for individuals in different areas. To be specific, individuals in Ω₁ execute operator SU to make an emphasis on optimizing C _max, and those in Ω₂ execute operator SD to focus on the reduction of TCE, and those in Ω₃ carry out operator CS to optimizing both of the two objectives.

Fig. 4.

Normalized objective space

The size of the corresponding area is decided by the angles α ₁, α ₂ and α ₃, namely, the use ranges of SU, SD and CS is controlled by the three angles. In the beginning of the CMA, we set α ₁ = α ₂ = α ₃ = π/6. Later, the performance of the operators may be different at different evolution phase. Besides, to adaptively adjust the use ranges of SU, SD and CS, a competition is performed among α ₁, α ₂ and α ₃ based on the performance of operators in each generation.

To evaluate the three operators, the score of operator K denoted will be calculated after every execution. Because SU and SD are designed to optimize single objective, the score of SU or SD is calculated as follows:

$$ S_{r} (K) = \hbox{max} \left\{ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} f* (X_{l} )- f*(X_{l} ')} \right\}/f*(X_{l} ) $$

(15)

where f*(X _l ) = f ₁(X _l ) when K = SU, and f*(X _l ) = f ₂(X _l ) when K = SD.

CS is to optimize both C _max and TCE, so its score is calculated as follows:

$$ S_{r} ({\text{CS}}) = \hbox{max} \left\{ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} f_{1} \left( {X_{l} } \right) - f_{1} (X_{l} ')} \right\}/f_{1} (X_{l} ) + \hbox{max} \left\{ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} f_{2} \left( {X_{l} } \right) - f_{2} (X_{l} ')} \right\}/f_{2} (X_{l} ) $$

(16)

Let IN _q be the number of individuals in the area Ω _q . The average score of operator K is calculated as $AVS(K) = \sum\nolimits_{r = 1}^{IN*} {S_{r} (K)} /IN*$, where IN* = IN ₁ when K = SU, IN* = IN ₂ when K = SD, and IN* = IN ₃ when K = CS.

Then, the values of α ₁, α ₂ and α ₃ are redefined as follows:

$$ \alpha_{q} = (\pi /2 - 3\beta )*AVS(K)/\sum\nolimits_{K} {AVS(K)} + \beta $$

(17)

where β is a small angle that guarantees α _q  ≠ 0. Here, it sets β = π/60.

3.4 Local Intensification

It is widely recognized that local search is helpful to intensify the exploitation ability of memetic algorithms [19]. Based on the SD and CS, two more local search operators SD_2 and CS_2 are presented.

SD_2: randomly select an operation O _i,j from the factory with maximum energy consumption (denoted as F _c ), if A _i,j  = a>1, then decrease A _i,j to b (1 ≤ b<a).

CS_2: randomly select a job from F _c , and insert it into a new position in F _c .

In the local intensification phase, a non-dominated solution in the current population is selected to perform local search for LS times. The local search procedure which includes SU, CS, SD_2 and CS_2 is illustrated in Fig. 5. When F _m  = F _c , only CS is performed to avoid the repeated modification of the processing speeds.

Fig. 5.

Pseudocode of local search procedure

3.5 Adjustment

There are two steps in the adjustment phase. The first step is factory assignment adjustment, and the second step is speed adjustment.

In the factory adjustment, four adjusting schemes are designed. (1) Randomly select a job from factory F _m , and insert it into all possible positions of another factory. (2) Randomly select a job from factory F _m , and exchange its position with all jobs in another factory. (3) Randomly select a job from factory F _c , and insert it into all possible positions of another factory. (4) Randomly select a job from factory F _c , and exchange its position with all jobs in another factory.

Each individual chooses one of the above schemes to search better factory assignments. Let P* be the set of non-dominated solutions that newly generated when X _l execute the factory assignment adjustment. Then, randomly select a non-dominated solution X* from $X_{l} \cup P*$, and set X _l  = X*.

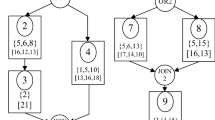
In the speed adjustment, according to the Property 5, a solution can be improved by adjusting the processing speeds without deteriorating the completion time of each factory. Therefore, the speed adjustment is performed on each solution in the TA. After the adjustment, solutions in the TA are used to update the PA. Since the completion time of a factory will not be longer if the critical path [21] remains the same, the speed adjustment is implemented on the operations that are not on the critical paths (called non-critical operations). An example of speed adjustment is shown in Fig. 6. Firstly, the critical path of each factory is found, as the arrowed line. Secondly, for each factory, the non-critical operations are selected to execute the speed adjustment from the final job back to the first. For example, the operations in Fig. 6(a) are to be adjusted in the order {O_3,2 → O_3,1 → O_2,1 → O_1,3}.

Fig. 6.

Illustration of speed adjustment

The procedure of speed adjustment for one factory is described as Fig. 7. And the flowchart of the CMA is illustrated in Fig. 8.

Fig. 7.

The procedure of speed adjustment

Fig. 8.

Flowchart of the CMA

4 Computational Results

The CMA is coded in C language, and all the tests are run on the same PC with an Intel(R) core(TM) i5-3470 CPU @ 3.2 GHz/ 8 GB RAM under Microsoft Windows 7. The stopping criterion is set as 0.5 × n seconds CPU time.

Since there is no benchmark for the MODOFSP-Makespan-Carbon, we generate test instances based on the test data as [8]. To be specific, f = {2, 3, 4, 5}, n = {20, 40, 60, 80, 100}, m = {4, 8, 16}, v = {1, 1.3, 1.55, 1.75, 2.10}, p _i,j is uniformly distributed within 5 ~ 50, PP _j,v  = 4×v ², SP _j  = 1. Clearly, there are 15 combinations of n × m. For each combination, 10 instances are randomly generated, and each instance is extended to f = {2, 3, 4, 5}. Thus, it has 15 × 10 × 4=600 instances in total for evaluation.

The CMA contains two parameters: PS and LS. To investigate the influences of PS and LS on the performance of the CMA, we set PS with four levels {10, 20, 30, 40} and LS with four levels {0, 100, 200, 300}, and then 4² full-factorial experiments are employed. To carry out the experiments, 60 instances are generated randomly, where each corresponds to a combination of f × n×m. For each instance, 16 combinations of PS × LS are tested. For each combination of PS × LS, the CMA is run 10 times independently and the obtained non-dominated solutions E _{c_i} (c_i = 1, 2, …, 16) are stored. The final non-dominated solutions FE are obtained by integrating E ₁, E ₂, …, E ₁₆. Then, the contribution of a certain combination (CON) is calculated as $CON(c\_i) = \left| {E'_{c\_i} } \right|/\left| {FE} \right|$, where $E'_{c\_i} = \{ X_{l} \in E_{c\_i} \left| {\exists X_{l'} \in FE,{\kern 1pt} X_{l} = X_{l'} } \right.\}$.

After all the instances are tested, the average CON of each combination is calculated as the response variable (RV) value. The results are listed in Tables 1 and 2, and the interval plots of PS and LS are shown in Fig. 9.

Table 1. RVs of full-factorial experiments.

Table 2. Result of analysis of variance.

Fig. 9.

Interval plot

From the Table 2, it can be seen that the influences of PS and LS are both significant with 95 % confidence interval. From Fig. 9, we know that the value of PS should neither be too small nor too large. A large PS may lead to an insufficient evolution, while a small PS is harmful to the diversity of the population. Similarly, a large LS is benefit to the exploitation, but a too large LS costs much of computation time on the local minima. According to the results of experiments, an appropriate combination of parameters is suggested as PS = 20 and LS = 200.

Since there is no published paper for solving the MODPFSP-Makespan-Carbon, the CMA is compared with the NSGA-II [22] and random algorithm (RA). In the NSGA-II, the population size is equal to PS in the CMA, and the crossover rate and mutation rate are set as 0.9 and 1/n as suggested in [22]. The stopping criteria of NSGA-II and RA are also set as 0.5 × n seconds CPU time. There are several performance metrics for multi-objective problems [23]. In this paper, we focus on the quality of the obtained non-dominated solutions. Thus, the coverage metric (CM) is used for evaluation. The CM is defined as follows:

$$ C\left( {E_{1} ,E_{2} } \right) = \left| {\{ X_{2} \in E_{2} \left| {\exists X_{1} \in E_{1} ,X_{2} \prec X_{1} {\kern 1pt} or{\kern 1pt} X_{2} = X_{1} } \right.\} } \right|/\left| {E_{2} } \right| $$

(21)

where C(E ₁, E ₂) denotes the percentage of the solutions in E ₂ that are dominated by or the same as the solutions in E ₁.

For each instance, the CMA, NSGA-II and RA are run 10 times independently within 0.5 × n seconds CPU time. The CM is applied to pairwise comparison between the CMA and NSGA-II as well as the CMA and RA. For the same combination of f × n×m, the average CM of 10 instances is calculated. The comparison results are listed in Tables 3, 4, 5 and 6 grouped by different number of f. From Tables 3, 4, 5 and 6, it can be seen that the proposed CMA is superior to NSGA-II and RA at all sets of instances. Besides, hypothesis testing is carried out on C(CMA,NSGA-II) and C(NSGA-II,CMA) as well as C(CMA,RA) and C(RA,CMA), and all the resulted p-values are equal to 0. So, it is demonstrated that the difference between C(CMA,NSGA-II) and C(NSGA-II,CMA) as well as the difference between C(CMA,RA) and C(RA,CMA) are significant with 95 % confidence interval. Thus, it is concluded that the CMA is more effective than the NSGA-II and RA in terms of the quality of the obtained solutions.

Table 3. Comparisons of algorithms (f = 2).

Table 4. Comparisons of algorithms (f = 3).

Table 5. Comparisons of algorithms (f = 4).

Table 6. Comparisons of algorithms (f = 5).

5 Conclusions

This is the first work to consider the carbon-efficient scheduling for the distributed permutation flow shop scheduling problem with makespan and total carbon emissions criteria. Some properties were analyzed, a competitive memetic algorithm was proposed, the effect of parameter setting was investigated, and the effectiveness of the designed CMA was demonstrated. Future work could focus on the design of the new search operators and new mechanisms to perform competition. It is also interesting to studying the carbon-efficient scheduling for other distributed scheduling problems.