Computer Simulations of the Tumor Vasculature: Applications to Interstitial Fluid Flow, Drug Delivery, and Oxygen Supply

Welter, Michael; Rieger, Heiko

doi:10.1007/978-3-319-42023-3_3

Michael Welter² &
Heiko Rieger²

Part of the book series: Advances in Experimental Medicine and Biology ((AEMB,volume 936))

2491 Accesses
12 Citations

Abstract

Tumor vasculature, the blood vessel network supplying a growing tumor with nutrients such as oxygen or glucose, is in many respects different from the hierarchically organized arterio-venous blood vessel network in normal tissues. Angiogenesis (the formation of new blood vessels), vessel cooption (the integration of existing blood vessels into the tumor vasculature), and vessel regression remodel the healthy vascular network into a tumor-specific vasculature. Integrative models, based on detailed experimental data and physical laws, implement, in silico, the complex interplay of molecular pathways, cell proliferation, migration, and death, tissue microenvironment, mechanical and hydrodynamic forces, and the fine structure of the host tissue vasculature. With the help of computer simulations high-precision information about blood flow patterns, interstitial fluid flow, drug distribution, oxygen and nutrient distribution can be obtained and a plethora of therapeutic protocols can be tested before clinical trials. This chapter provides an overview over the current status of computer simulations of vascular remodeling during tumor growth including interstitial fluid flow, drug delivery, and oxygen supply within the tumor. The model predictions are compared with experimental and clinical data and a number of longstanding physiological paradigms about tumor vasculature and intratumoral solute transport are critically scrutinized.

Access provided by Autonomous University of Puebla. Download chapter PDF

Computational Simulation of Tumor-Induced Angiogenesis

Physics of the tumor vasculature: Theory and experiment

Article 08 February 2016

Computational modeling of flow-mediated angiogenesis: Stokes–Darcy flow on a growing vessel network

Article 17 September 2023

Keywords

3.1 Introduction

One of the hallmarks of cancer is angiogenesis, the formation of new blood vessels via sprouting, which fuels tumor growth with additional nutrients [62]. Angiogenesis, vessel cooption (the integration of existing blood vessels into the tumor vasculature), dilatation, and vessel regression remodel the healthy vascular network of the host into a tumor specific vasculature that is different from the arterio-venous blood vessel network of the host tissue [75]. Consequently blood flow, oxygen and nutrient supply, and interstitial fluid flow have tumor specific abnormalities [161] that have dramatic consequences for anti-cancer treatment: (a) tumor vasculature is chaotic, lacking a hierarchical organization, and spatially inhomogeneous comprising regions with low microvascular density (like a necrotic core). As a result, severe hypoxia (deprivation from oxygen) [71] can impede the effectiveness of radiation and chemo therapies [58], and promote invasive growth (migration of tumor cells and penetration of tissue barriers). (b) Tumor vessel walls are leaky, i.e. have a high permeability for blood plasma, and a functioning lymphatic drainage is absent in most malignant tumors, leading to bulk flow of free water in the interstitial space, denoted as interstitial fluid flow (IFF), and a concomitantly elevated interstitial fluid pressure (IFP) [75]. The resulting excessive extravasation of liquid may release most drug prematurely, leading to a retarded delivery into the tumor center, especially in large tumor [74, 81, 76]. Indeed high IFP is regarded as an obstacle in cancer therapy [64, 102]. Therapeutic concepts like vessel normalization via anti-angiogenic therapy have been developed [77] that actually decrease IFP and improve drug penetration in tumors [157].

However, a mechanistic understanding of vascular network formation and various treatment strategies is still lacking and calls for a quantitative analysis of the underlying physics. Drug delivery as well as oxygen supply are determined by blood and interstitial fluid flow, for which reason such an analysis must focus on the relation between the intra- and extra-vascular transport characteristics and the tumor vasculature morphology. Moreover, the analysis must account of the fact that tumor blood vessel networks emerge from, and are connected to the normal, arterio-venous, vasculature of the host.

In this chapter we review the current state of mathematical modeling and simulation of vascularized tumor growth and discuss predictions made by our models for vascular morphology, drug delivery and oxygenation. It is organized as follows: The first section provides an overview of the physiological basics of vascularized tumor growth. It follows a section on obstacles to treatment of cancer. In the subsequent model part we review our work and the related literature, comprising models of vascular network formation, tumor growth, interstitial fluid flow, drug delivery and oxygenation. Then we discuss the various predictions made, limitations of our models, and finally provide an outlook to future work. For further reading on our work, see [11, 90, 165, 166, 168, 169, 167]

3.1.1 Physiological Basics

Normal vasculatures are organized in capillaries, small vessels by which most of the solute exchange of nutrients and wastes with blood takes place, and in arterial and venous trees, respectively. Capillaries are organized as homogeneously distributed dense network, the capillary plexus. The walls of capillaries consist mostly of endothelial cells (ECs). This network is supplied by arterial and drained by adjacent arioles and venules, respectively. Arterioles and venules join into larger arteries and veins which eventually join at the heart. Their walls recruit additional cells such as pericytes and smooth muscle cells for reinforcement and control over their diameter. This vascular organization thus minimizes the power required to drive blood and to simultaneously maintain the volume of circulated blood [105]. Normally, maintenance of the vasculature depends on a balance of pro-and antiangiogenic factors such as blood flow and metabolic demand, mediated by a complex biochemical signaling network not yet fully understood. This system adapts the microvascular density (MVD) to the nutrient demand of tissue and regulates development of blood vessels into vascular trees. Components of this system have been studied (see below, in the context of tumors), however the big picture is still elusive.

A solid tumor typically starts off as an avascular multicellular spheroid. It is initially formed, when cells undergo mutations disabling their regulatory circuits for proliferation and apoptosis (programmed cell death) allowing them to divide an infinite number of times. After an initial phase of exponential growth, the radius of a spheroid in nutrient solution continues to grow linearly [20, 39] since proliferation of tumor cells (TCs) is restricted to a few cell layers behind the tumor-tissue interface. Vascularized tumors also show a linear growth regime [38, 66]. TCs beyond an annular outer shell enter a quiescent state due to nutrient and space restrictions or die off (necrosis). Thus a necrotic core develops, and an equilibrium between proliferation and death is established, limiting the size of the spheroid to approximately 1 mm³. We consider only oxygen as representative of nutrients, which is a common simplification in mathematical models, although tumor metabolism depends on other nutrients and waste products as well. Notably, TCs can switch to a glucose-based metabolism, allowing them to survive hypoxic conditions. Not all tumors start as avascular spheres though. Some types, e.g. glioma brain tumors and breast tumors, incorporate (coopt) the blood vessel network of the host at the beginning of growth [67, 122]. In this process, TCs preferably proliferate around blood vessels, apparently while displacing or destroying cells of normal tissue [37]. The ability to metastasize may develop at a later point in time.

Oxygen in tissue has a high diffusion coefficient of ca. 2 mm²∕s, but it is also bound and consumed which leads to an approximately exponential decrease of the concentration around blood vessels. The range up to which the concentration decreases to zero is typically 100 μm in tumors [25]. In normal tissues it lies between 50 μm (brain) and 150 μm (breast). This diffusion range is thus a major determining factor of the mean intercapillary distance required for adequate oxygen supply. Neither normal cells nor TCs remain viable beyond it. Normal cells as well as tumor cells can respond to hypoxia by releasing chemical compounds known as growthfactors (GFs) which are essential mediator molecules of angiogenic signals. VEGF is a well-known major player [25, 101, 26, 94] but there are many more with various function. They diffuse through tissue where they bind to receptors at blood vessels and collectively they loosen the cell layers of vascular walls, and stimulate ECs to proliferate and to migrate away from their parent vessel. ECs follow GF gradients to the source of GF (chemotaxis) trailed by more ECs that form a new sprout [108, 49, 143]. This process is known as angiogenesis. If the tip encounters another vessel it will fuse with it and mature into a perfused capillary. Otherwise the sprout retracts after some time.

Hence, a hypoxic tumor spheroid might develop a phenotype that enables pro-angiogenic signaling by GFs in an effort to improve its oxygen supply. Like diffusion of oxygen, the angiogenic signal has a finite range. The area where neovascularization is visible in glioma [66] and melanoma [38] is restricted to a 200 μm annular shell around the invasive edge. However, in microscopy images of mammary carcinoma in mice, increased branching and dilation is observed up to ca. 1 mm from the edge [10, Fig.1]. Neovasculature as well as preexisting vessels are coopted when the tumor grows past them. For unknown reasons, tumor vascular network formation is not properly controlled. As a result, dense chaotic vascular excrescence develops (s. Fig. 3.1b), that is very unlike a well ordered normal capillary bed (s. Fig. 3.1a). The additional vessel may provide nutrients required for growth. However, they are often dysfunctional, in some cases even hindering growth [130].

A few 100 μm into the tumor interior, angiogenesis stops and endothelial cells a switch to circumferential growth leading to vaso-dilation. Tumor vessels of Melanoma and Glioma tend to dilate to a maximum radius of ca. 25 μm but no further. Moreover, many vessels undergo a process of regression, until eventual collapse of the lumen and pinch off of blood flow [38, 67]. GFs produced in the tumor interior are partially responsible for the concomitant detachment of supporting cells from the vascular tube, but they also promote ECs survival. Another crucial factor for survival is blood flow, where Angiopoietins (Ang-1/2) among others act as regulatory molecules [53, 21]. They are expressed by ECs in reaction to the shear stress which is exerted by the blood flow on the vessel wall [7]. Ang-2, a negative regulator of angiogenesis, promoting regression, is frequently overexpressed in tumors [67]. ECs apparently switch from angiogenesis to circumferential growth depending on the sensed direction of the GF concentration gradient [143], which is by the ephB4 guidance molecule [43].

Only few dilated vessels survive this thinning process, leading to a very sparse network of isolated vessels. Viable TCs remain as cuffs around these vessels. Beyond the diffusion range of oxygen, TCs die of hypoxia, whereupon large necrotic regions emerge in the tumor interior. Thus, a normal blood vessel network is progressively transformed into a tumor specific vasculature by the angiogenic activity that is mostly confined to an area around the tumor edge. The result is a compartmentalization into a ca. 200 μm wide band around the periphery where the MVD is elevated to ca. 1. 5 times the baseline normal tissue MVD. The MVD decreases sharply into the tumor interior to approximately half of the MVD of normal tissue [66, 38]. Images of experimental tumors are reprinted in Figs. 3.1 and 3.2. Quantitative morphological data from [38] is reprinted in Fig. 3.3.

Normally, only a small amount of blood plasma leaks from blood vessels through nanometer sized gaps between ECs whereupon it becomes part of the interstitial fluid (IF). IF is absorbed into lymphatic channels which eventually feed the liquid back into the blood stream. Leakiness of tumor vessels is caused by huge gaps present in their walls due to missing ECs [25] leaving holes of the size of micrometers. The permeability of the vessel walls therefore increased by two orders of magnitude [83]. Moreover, tumors often lack functional lymphatic vessels, although they can induce lymphangiogenesis similar to regular angiogenesis and can metastasize through lymphatics in the tumor periphery [153]. The lack of lymphatics as well as vascular hyper-permeability lead to the phenomenon of elevated interstitial fluid pressure (IFP), an elevation of the hydrostatic pressure of the IF which approaches the level of blood pressure [152]. The IFP in the tumor interior is relatively homogeneous at levels between 10 and 40 mmHg. Across the tumor boundary it drops down to the level of normal tissue where the IFP is zero in good approximation. The interstitial fluid flows through tissue like water or oil flows through a porous medium, e.g. through rock. In tissues, cells and ECM assume the role of the medium. Consequently, IF flows predominantly in radial direction out of the tumor spheroid. Peak velocities between 0. 1 and 0. 2 μm/s were measured near the boundary of a 1 cm sized tumor [73]. Elsewhere, velocities are much lower due to shallower IFP gradients. This may drive TCs into the surrounding lymphatics and wash out drug from the tumor.

3.1.2 Obstacles to Cancer Treatment

This section reviews biophysically relevant obstacles to treatment most of which are founded in the peculiarities of tumor blood vessel networks. Current cancer-killing drugs have poor selectivity, i.e. they are toxic to normal cells, too. Therefore, it is not possible to simply increase the dose to compensate for inadequacies of the vasculature [102].

Since tumor vasculatures are heterogeneous, one can find areas in tumors, so called hot-spots, where the MVD is locally increased. The MVD at hot-spots is used as indicator for malignancy and tumor progression with varying success [38]. Therefore a solid understanding of the interactions between vascular network formation and growth dynamics of the tumor spheroid is required.

The reasons for poor drug delivery are manifold. In addition to premature release and washout due to excessive extravasation, the vasculature is sparse in large areas of the tumor and therefore the efficacy of drugs depends on the ability to penetrate tissue well. However penetration is often poor, instead, strong drug concentration gradients emerge around blood vessels, and persist over long periods of time [121]. Vascular normalization strategies can help [80], but other approaches should be considered, too, such as alteration of tissue permeability.

The discovery of tumor induced angiogenesis [45], and VEGF, sparked the development of a new type of treatment in which the vasculature is targeted with angiogenesis suppressing agents to deprive the tumor of nutrients. This is a so-called anti-angiogenic therapy, today often used concomitantly to other measures, such as chemotherapy. Vascular normalization is a more recent concept, where a balance between excessive pruning and a reduction of angiogenic activity is to be effectuated in order to reduce leakiness and thus improve blood flow [78]. However the underlying mechanisms are still poorly understood. What works for one kind of tumor can have an adverse effect in another type of tumor [102]. Relief of mechanical stress on blood vessels is now also seen as therapeutic opportunity [79] to improve blood flow.

Moreover, the success of ordinary chemo and radiation therapy is tied to the oxygenation status of the tumor. For instance, some chemotherapeutics work poorly in oxygen deprived environments due the chemical reactions involved. Other drugs can only kill cycling (proliferating) cells and are therefore unefficative against tumor cells (TCs) which are quiescent. Hypoxic TCs are also resistant to radiation therapy since oxygen is required so that ionizing radiation can produce DNA damaging compounds [85]. Hypoxia also promotes invasive growth, i.e. the tendency and ability of TCs to migrate increases [113]. Hence, hypoxia is generally associated with poor prognosis [19, 63].

It is possible to obtain important tumor characteristic data such as perfusion, blood volume and hypoxia status from patients using positron emission tomography (PET) and other imaging methods. However the interpretation of raw sensor data requires theoretical models. Moreover the resolution of current methods is limited to a voxel size of ca. 1 mm³. On the other hand, microscopic information are hardly accessible experimentally. Direct measurements by invasive probes are limited to small sample sizes and may be afflicted with systematic errors [159]. Interstitial fluid flow velocities are measured by invasive microscopy [76], not applicable to humans. Concentration distributions of drugs were measured by microscopy of dissected tumorous tissue [121], exploiting auto-fluorescence. In this regard theoretical models and computer simulation can provide insight into the tumor micro environment in order to foster the understanding of macroscopic phenomena and therapy failures.

3.2 Theoretical Models

This section reviews basic theory and modeling approaches of mathematical models of tumor growth and its microenvironment. See also the Refs. [158, 95, 134, 124] for reviews of recent work.

3.2.1 The Bulk of Tissue

There are two approaches to describe tissues. In continuum mechanics conservation equations are formulated for mass, momentum and sometimes energy, and on the other hand, in particle methods, particles represent either cells or macroscopic sections of tissue and move according to Newtons equations of motion. Fluids and deformable bodies are described in this way, too. But for living tissues, addition and removal of mass and momentum due to growth and death needs to be taken into account. The simplest form of mass conservation to satisfy this is the partial differential equation (PDE)

$$\displaystyle\begin{array}{rcl} \frac{d\rho } {dt} = -\rho \nabla \boldsymbol{u} +\alpha \text{,}& &{}\end{array}$$

(3.1)

where $\rho =\rho (\boldsymbol{x},t)$ is the density depending on space and time, d ρ∕dt is total derivative in time which can be expanded into $d\rho /dt = \partial \rho /\partial t +\boldsymbol{ u}\nabla \rho$, ∇ is the Nabla operator, $\boldsymbol{u}$ is the local velocity, and α embodies local sources and drains. The general form of momentum equations is

$$\displaystyle\begin{array}{rcl} \frac{d(\rho \boldsymbol{u})} {dt} = \nabla \cdot \boldsymbol{\sigma } +\boldsymbol{ f}\text{,}& &{}\end{array}$$

(3.2)

where $\boldsymbol{\sigma }$ is the Cauchy stress tensor and $\boldsymbol{f}$ is the total body force, accounting for gravity for instance. In reality, biological tissues are highly complex materials [162, see the review]. On short time scales, they show elastic behavior which is usually neglected in models of tumor growth. On long time scales, i.e. days, residual stresses are relaxed by rearrangement of ECM fibers and cell adhesion molecules, leading to viscous behavior. Moreover, cells show active responses to stimuli, e.g. migratory behavior. In practice, growing tumors are therefore often modeled like (viscous) liquids, including an isotropic (solid) pressure, friction, and adhesion forces. Inertial forces can be neglected since tissue growth and cell migration happens at very low Reynolds numbers (Re ≪ 1). Conservation of energy is mostly not considered, assuming a homogeneous constant temperature. The growth of multicellular spheroids [4, 8, 3, 32, 163] and tumors in general [178, 151, 117] was described using continuum models of a single homogeneous material.

Current state of the art are multi-phase or mixture models where mass, momentum and stress are given as summations over contributions from cells of different types, ECM and water. These phases coexist in space, so that each phase occupies a fraction of the unit volume, given as volume fraction ϕ _i of phase i. The motion of the cell population is often modeled analogous to fluid flow through a porous medium, where the ECM takes the role of the medium. The “flow” thus represents migratory motion in response to solid pressure. Depending on the choice of components and their stress tensors, mixture models describe various growth phenomena, and found numerous applications to study avascular [22, 96, 5, 171, 32, 135] and vascular tumor growth [18, 29, 148, 97, 70]. Cell-cell adhesion may be modeled by an effective surface tension forces, following [17], allowing the study of growth induced morphological instabilities of the interface between cell populations.

In [169] we introduced a continuum model of the tumor spheroid, closely following [117] and the refs. therein. In principle, a common volume fraction ϕ and a common migration velocity v _ϕ is defined for TCs and normal tissue cells. The interface between TCs and normal cells is defined via an auxiliary function, using the Level Set method [139]. Thus the interface is defined as 0-level of the auxiliary function providing the closest distance from the interface within some proximity of the interface. In real tissues, cell-cell adhesion causes a certain degree of smoothness of the tissue interfaces. This has been neglected, but still our model predicts approximately spherical growth under the assumption of equal motilities of TCs and normal cells. The basic mechanism of tumor expansion of this model is based on an increased tolerance to solid pressure of tumor cells, leading to proliferation whereas proliferation of nearby normal cells is inhibited, eventually leading to apoptosis.

In particle based models, matter is described from the frame of reference that is anchored to a point on a material. In actual computations, a material such as a fluid, is divided into thousands to millions of pieces, represented by particles that move and interact with each other. In biological applications, the particle count is not conserved in general. Instead particles are allowed to replicate or vanish to reflect growth and regression of real tissues. In microscopic systems, particles can be conveniently identified with individual cells. Their time dynamics can be described simply by Newtons equation of motion for each particle as in molecular dynamics simulations, i.e.

$$\displaystyle\begin{array}{rcl} \frac{\partial m_{i}v_{i}} {\partial t} = F_{i}(x_{0},\ldots,x_{N},\ldots )\text{,}& & {}\\ \end{array}$$

where m _i, v _i, x _i denote the mass, velocity and position of the i-th particle, and F _i denotes the force on the particle depending on the current state of the system. These equations must be solved numerically in a discrete time-stepping scheme. In between time steps, an extra step can be added to account for proliferation and death of particles. Continuous space particle models were used to study the growth dynamics of multicellular spheroids [125, 39] and of tissues that are in competition with each other [12]. The dynamics can also be described by stochastic processes and be simulated by Monte-Carlo methods (see below).

In cellular automata models, particles are confined to sites on a lattice. Particles may be able to hop or proliferate to neighboring sites. Due to its simplicity this is a popular approach to study tumor growth [2, 11, 16, 90, 164, 111, 42, 41] and angiogenesis [6, 112, 164, 115]. In the latter case, particles represent pipe segments of a network. It is however more adequate to think of the network as a dynamically changing graph as in mathematical graph theory. The space-time dynamics can be determined by deterministic rules which are applied once per discrete time step, or by stochastic processes, or a mix of both. A stochastic process is formally described by the Master Equation for the rate of change of the probability P _k to find the system in state k = 1. . n

$$\displaystyle\begin{array}{rcl} \frac{dP_{k}} {dt} =\sum _{l}A_{kl}P_{l}.& & {}\\ \end{array}$$

The matrix A _kl contains the transition rates according to which the system transitions from state l to k with probability A _kl dt.

Bartha and Rieger proposed a simple particle model of individual TCs [11]. Therein, lattice sites are identified with the potential location of one and only one TC, assuming that TCs cannot move but proliferate to neighboring sites. Given a small initial tumor nucleus, proliferation is consequently confined to the tumor rim, yielding linear growth dynamics of tumor spheroids. Moreover, TCs can be flagged as dead in case that the oxygen concentration becomes too low. Dead TC occupy lattice sites, prohibiting proliferation thereto, but are otherwise inert. Thus the size and spatial distribution of necrotic regions can be analyzed. This model is simple but in conjunction with a model of tumor vascular remodeling it is sufficient to predict realistic morphologies of tumor vasculatures [90, 165, 166]. However, the representation of individual cells in three dimensions at macroscopic system sizes is computationally costly. Therefore coarser grained models are better suited there.

3.2.2 Solutes in the Bulk of Tissue

The simplest general partial differential equation to describe the transport of the concentration $c(\boldsymbol{x},t)$ of one species is the diffusion-advection-reaction equation

$$\displaystyle\begin{array}{rcl} \frac{\partial c} {\partial t} + \nabla \cdot (c\boldsymbol{u}) = \nabla \cdot (D\nabla c) + R\text{,}& &{}\end{array}$$

(3.3)

where the substance diffuses with diffusion constant D and is carried with the flow of the solute with velocity $\boldsymbol{u}$. The reaction term R can comprise sources and drains, e.g. vessels are sources of oxygen whereas binding and consumption may be represented by a homogeneous drain distribution. In multi-components system, each component i is associated with the concentration c _i each of which is governed by an equation of type (3.3) [117]. Then R (or rather R _i) also comprise transition rates between compartments. This way, drug binding to different intracellular compartments was described in simulations of drug concentrations in tumors [141]. The advection term in calculations of oxygen distributions is usually neglected since oxygen transport is dominated by diffusion due to its low molecular weight. Moreover, it is sufficient to consider quasi stationary distributions where $\partial c/\partial t = 0$ since equilibration times are much shorter than growth processes in tissues [11]. Thus we obtain

$$\displaystyle\begin{array}{rcl} 0 = D\nabla ^{2}c + R\text{,}& &{}\end{array}$$

(3.4)

assuming equal concentration c in all compartments and a constant oxygen diffusion coefficient D.

Balance equations like (3.2, 3.2, 3.3) can only be solved analytically in special cases. Often solutions are calculated numerically with the help of finite difference (FD) [93] or finite element methods (FEM) or some variation thereof. FEM have the advantage that they can be applied straight forwardly to unstructured meshes and therefore work well for arbitrary domain shapes. However, FD methods are easier to implement for regular grids, making them well suited for problems where the expansion of a tumor within a rectangular domain is considered. The application of difference operators leads to systems of linear or non-linear equations in the solution values at grid points. The obtained system matrices are usually sparse, for which many specialized tools are available including direct factorization, fast Fourier transformation, multi-grid, and iterative preconditioned Krylov subspace methods.

3.2.3 Normal Blood Vessel Networks

A model for tumor vascularization must start with the blood vessel network of the healthy tissue surrounding the tumor, since, during growth, the tumor coopts the existing tissue vasculature and generates new vessels via angiogenesis. In early models of angiogenesis, the initial network consisted only of a single parent vessel [6]. These models adequately describe angiogenesis in the rabbit eye model [51]. Essentially, a small tumor on the cornea of the rabbit eye stimulates vascular sprouting in a few large parent vessels from up to 1 mm away. These sprouts branch excessively and form a dense capillary mesh between the tumor and the parent vessels. Similar configurations were considered in later theoretical work [146, 145, 173, 172]. However, in reality, the bulk of tissue is interspersed with vessels which may be coopted by the tumor. Therefore, recent works consider a capillary plexus, often represented by a network of segments which are arranged in a regular pattern, e.g. as square or hexagonal grid, omitting supplying arteries and draining veins [2, 23, 111, 164, 16, 11, 90, 174, 173]. Blood flow is computed assuming a fixed blood pressure at boundaries of the simulation box. In [165] a honeycomb pattern is used in place of a square pattern [11] allowing for more realistic branching angles. Other authors use random arrangements of lines [50] or voronoi cells as basis for vascular networks [128].

Only a few attempts have been made to incorporate physiologically relevant arterio-venous vessel networks. First works focused on algorithmic construction of arterial trees branch by branch [132, 133]. At each step, the existing tree is first geometrically scaled to increase in dimension. This increases the distance between vessels, implying that tissue oxygenation would worsen each step. However a new segment is added according to some optimality criterion in order to supply the voxel in space that is most in need of oxygen. Thus, oxygenation stays approximately constant. This process is repeated until the desired size is reached.

Later, Gödde and Kurz [52] developed a relatively simple lattice based growth model comprising the entire vasculature including arteries, capillaries and veins. Therefore, such an arterio-venous vasculature construction model was implemented for the study of tumor growth [166]. In the following we sketch the construction principle (s. Fig. 3.4): first arterial and venous trees are simultaneously grown by successive attachment of bifurcations at randomly selected tree tips. A bifurcation is simply a Y-shaped arrangement of three segments as depicted in Fig. 3.4h. Lattice sites and bonds can only be occupied once, thus growth terminates eventually when no further free sites are available. Thus the space is divided into areas with only arterial and only venous vessels, respectively (s. Fig. 3.4b). Proper interdigitating trees are obtained by the second stage of the algorithm where vascular trees are remodeled, allowing well perfused branches to expand and weakly perfused branches to regress (s. Fig. 3.4c–e). To this end, each remodeling sweep is preceded with determination of vascular radii, addition of temporary connecting segments (capillaries), and computation of blood flow rates and shear stress f. Capillaries are removed again before the vascular trees are altered, however, they are added again for the final output. An overview of our implementation is given below, but a definition in every detail is beyond the scope of this chapter.

As input, the locations of tree roots and their type, i.e. arterial or venous, are given and mark the starting sites for growth (s. Fig. 3.4a). In previous work their selection was arbitrary, i.e. we considered a wide range of configurations using single pairs of nodes, two pairs [166], or occupation of entire side faces of the cuboid simulation domain [169]. In pseudo code, the first stage of random growth reads as follows

nodes = rootNodes // a list

while nodes not empty:

nd = RemoveRandomItem(nodes)

// return removed item

newNodes

= TryAppendBifurcation(nd)

// return list of nodes;

may be empty

nodes += newNodes // append

TryAppendBifurcation probes orientations along the axes of the lattice, taking already occupied sites into account, and picks an admissible configuration randomly if there are any, adding it to the network. The loop terminates when no more space is available, i.e. the list sites is empty. Such as state is depicted in Fig. 3.4b. The second stage is more involved due to the dependence on blood flow. Hence, we define

function

CapillariesRadiiAndBloodflow():

ComputeRadii()

AddCapillaries()

ComputeFlow()

The function ComputeRadii traverses each vascular tree in a simple depth first traversal and determines the radius of each segment starting from tree tips up to root nodes. Murray’s law is utilized to determine the radius of a parent branch r _p when the radii of child branches r _c, 1,r _c, 2 are known, which states that $r_{p}^{\alpha } = r_{c,1}^{\alpha } + r_{c,2}^{\alpha }$, with an exponent α between 2. 7 and 3 depending on the tissue. The radii of the arterial and venous tree tips are all equal, respectively. Each of the two is an input parameter. The function AddCapillaries loops over all nodes of the network, and attempts find neighbors of opposing type (arterial or venous), to which, if admissible, a capillary segment is added. This is carried out again under the exclusion of overlap with other segments. Moreover, (i) in general, at any point, at most three segments are allowed to join at a node. Potential additions of capillaries violating this rule are rejected. (ii) We found it useful for promotion of growth to allow capillaries between vessels of a radius up to a limit of 5 to 20 μm, rather than creating only tip-to-tip connections as done in Ref. [52]. ComputeFlow computes blood pressure, flow rates, and shear stress f associated with nodes and vessels as discussed in Sect. 3.2.5 (see below). The main loop of the second stage of the algorithm is as follows

for iter = 0 to maxIter:

CapillariesRadiiAndBloodflow()

RemoveCapillaries()

event = dictionary()

// map nodes to events

for each Node nd in network:

event[nd]

= DetermineRemodelingEvent()

// does the work

for each Node nd in network:

// in random order

if events[nd] == REGRESSION:

Remove(nd)

else if events[nd] == GROWTH:

added

= TryAppendBifurcation(nd)

if not added: // space is

occupied

TryAppendSingleSegment(nd)

// prepare final output

CapillariesRadiiAndBloodflow()

Segments marked as capillaries have to be removed again, which is carried out by RemoveCapillaries. The function DetermineRemodelingEvent determines whether a node is marked for REGRESSION, GROWTH, or for another event denoted NONE, indicating no change. Remove(nd) also removes adjacent vessel segments. However, since only tree tips are allowed to regress there is only one such segment. Moreover, we found the attempt to insert a single segment to help with grow into crowded spaces. Hence TryAppendSingleSegment acts analogous to TryAppendBifurcation but adds just a single segment.

The following definition of DetermineRemodelingEvent is to some degree arbitrary. However the essential mechanism is growth of perfused branches while others regress. First, let p _G, p _R, and p _N be probabilities for growth, regression and no change. We define them differently for nodes that are perfused (q > 0 in at least one adjacent segment) on the one hand, and nodes that are unperfused on the other hand (q = 0 for all adjacent segments). For unperfused nodes we simply define

$$\displaystyle\begin{array}{rcl} p_{G}& =& p_{G,x}{}\end{array}$$

(3.5)

$$\displaystyle\begin{array}{rcl} p_{R}& =& 1 - p_{G,x}{}\end{array}$$

(3.6)

$$\displaystyle\begin{array}{rcl} p_{N}& =& 0\text{,}{}\end{array}$$

(3.7)

where p _G, x determines the rate of regression and is chosen less then 1∕2 to obtain p _G < p _R. Figure 3.4e was obtained with p _G, x = 0. 4. Thus unperfused nodes may clear space for growing branches. To define probabilities for circulated branches, let f _max be the maximal shear stress taken over all segments, and f be the shear stress average of segments at the considered node. Hence we define the growth “signal” $f_{sig} = f/(\,f +\epsilon _{1}f_{max})$, where ε ₁ ≪ 1 is small number. Taking $\epsilon _{1} = 10^{-2}$ one obtains a rapidly increasing function in f which approaches nearly one (0. 99 for $\epsilon _{1} = 10^{-2}$) for f = f _max (see below). The probabilities are defined using f _sig as follows

$$\displaystyle\begin{array}{rcl} p_{G}& =& f_{sig}^{\beta }{}\end{array}$$

(3.8)

$$\displaystyle\begin{array}{rcl} p_{R}& =& (1 - f_{sig})^{\beta }{}\end{array}$$

(3.9)

$$\displaystyle\begin{array}{rcl} p_{N}& =& 1 - p_{G} - p_{R}\text{,}{}\end{array}$$

(3.10)

where β is an exponent larger or equal to one. As a result the growth probability p _G never assumes the value one, which is useful in two-dimensional cases where very well perfused vessels would otherwise form bottlenecks. Moreover taking β > 1 stabilizes moderately perfused vessels, for which then p _N > 0 is obtained. One of the corresponding events is preliminarily picked using tower sampling. However certain conditions need to be fulfilled to be admissible. To grow, a node has to have less than three adjacent segment. To regress, the node has to be a tip node, having only one attached segment. If any of these conditions is not fulfilled, NONE is assigned to the node.

Finally we want to add some remarks. First, by setting appropriate values for the lattice constant and capillary radii, the MVD and vascular volume rBV of generated networks can be adjusted. Secondly, in two dimensions large areas may be left void, depending on selection of root nodes. Such cases were rejected in Ref. [166].

Moreover we found it helpful to vary p _G, x ≤ 1∕2 in proportion to the local concentration of growth factors. A corresponding distribution may be incorporated into the model for instance adopting the simplified model in Ref. [11]. This model variant has the advantage that it does not require manual tuning of p _G, x. Biologically it is justified since vascular sprouts grown by angiogenic signaling via growth factors are also initially not perfused. In the model, unperfused vessels that remain from the first stage of the algorithm, can guide growing branches into a proper tree-like morphology when contact is made with perfused branches.

The extension to FCC lattices seems over complicated, but FCC lattices can be represented by layers of two-dimensional triangular lattices which are offset from each other according to the well known-stacking order ABCABC…(s. Fig. 3.4g). We actually organize sites as sites of a three-dimensional cubic lattice that is spatially distorted to coincide with the conceptual FCC lattice. Neighbors of a given site must correspond to the FCC lattice. Therefore, exploiting translational symmetry, we store precomputed neighbor lists, for a total of six of exemplary sites. Generation of arterio-venous initial networks was carried out again using Y-junctions as structural elements of growth, following the original proposal [52]. Additional rotational degrees of freedom simply add to the number of probed configurations of which one admissible is picked for addition to the network.

3.2.4 Tumor Vascular Remodeling

Bartha and Rieger [11] originally considered a model of tumor vascularization including the processes angiogenesis, cooption, vessel dilatation, regression and collapse (s. Fig. 3.5a). Its basic ingredients are as follows: Vessel segments representing a vascular network, mathematically described as a graph, occupy bonds on a lattice. Junctions (nodes) coincide with sites of the lattice. Various properties are associated with vessels and nodes, such as blood pressure p, radius r, blood flow rates q, and shear stress exerted by the blood flow on vessel walls f. Furthermore, there is a concentration distribution of VEGF representative of all GFs, as well as a tissue oxygen concentration distribution. The system state at t = 0 comprises an initial network as described above, and small tumor spheroid in the center of the system. The growth of the spheroid depends on the local oxygen concentration, allowing cell proliferation if the concentration is sufficiently high. If the oxygen concentration drops to hypoxic levels then GFs are locally produced and diffuse into tissue. Diffusion through tissue can be modeled by reaction-diffusion equations (3.4), however simplified models were used [11].

The spatio-temporal evolution of the network is determined by stochastic and continuous processes, reflecting sprouting angiogenesis, vessel dilation, collapse, and regression, respectively (s. Fig. 3.5b–f). In practice, time is advanced in discrete steps of length Δ t = 1 h, and these processes are defined approximately as simple local updating rules:

Angiogenesis::: A new segment is added with non-zero probability, connecting the current site $\boldsymbol{x}$ and a distant site $\boldsymbol{x}^{{\prime}}$ under the following conditions: Both sites are occupied by circulated vessels, the GF concentration at $\boldsymbol{x}$ is sufficiently high, the distance of $\boldsymbol{x}$ to other branching points is at least d ^(br, min), the distance $\vert \boldsymbol{x} -\boldsymbol{ x}^{{\prime}}\vert $ is small enough, and no site on the path is occupied by TCs. These conditions reflect lateral inhibition of sprouting (for a modeling approach see [15]), finite growth length of sprouts [108], and the switch to circumferential growth within tumors [43].
Dilation::: There is a non-zero probability that the radius r of a vessel segment is increased by the amount corresponding to the addition of 10 μm (diameter of an EC) to its circumference, under the following conditions: the local GF concentration is sufficiently high, the segment is located within the tumor, and r is smaller than the upper limit r ^(max). The latter condition accounts for observations in real tumors [38, 66], however the mechanism that limits dilation is unknown. It should be emphasized that this process is particular important for blood flow characteristics within the tumor since the blood flow varies with the fourth power of the radius and only modest vessel radius increase by a factor of 2 or 3 has leads to an extreme increase in blood flow.
Collapse::: A vessel segment surrounded by TCs has a non-zero probability to be removed if the wall shear stress f is less than the threshold f _crit. This process reflects the dependence of vessel survival and maturation on blood flow [67].
Regression::: An uncirculated vessel segment has a non-zero probability to be removed if the oxygen concentration is less than a threshold, reflecting complete disintegration of unperfused sections of the vasculature.

One time step comprises the application of these rules at all sites occupied by the network and subsequent recomputation of blood flow, oxygen distribution, and time propagation of other model components such as the tumor spheroid. The probabilities are given as fractions Δ t∕τ _proc of the time step Δ t and process specific time constants τ _proc, requiring Δ t < τ _proc.

In [11] the network was represented by sequences of 10 μm wide pieces, representing endothelial cells that occupy lattice sites. However, it is much more computationally efficient to associate vessel segments with a series of lattice bonds and allow for segments longer than a single bond. However we still use a basic lattice constant h _(tum) of 10 μm, to allow for a sufficiently high resolution of the tumor neovascular plexus. To conserve memory we store pointers to segments in a hash table [156] using a pair of sites indices as key. The lattice constant h _(gen) of the initial network synthesis model corresponds is normally larger than h _(tum). This is well defined since for proper choice of h _(gen), e.g. 100 μm, the location of initial vessels coincides with bonds and sites of the finer h _(tum) = 10 μm lattice.

In subsequent work [165] we considered a minor extension to the angiogenesis process where sprouts grow over a period of time. Instead of creating a “bridge” instantly, a sprout segment is added and extended with additional segments in subsequent time steps until a timer t _sp associated with the sprout runs out. This allows for emulation of tip splitting by sprouting off of a growing sprout and fusion of sprouting branches [165].

To make the model applicable to arterio-venous initial networks, we incorporated a stability variable w associated with segments [166], reflecting the wall strength of vessels, allowing for thick vessels to be more resistant to collapse. The wall strength, w, is continuously decreased at rate Δ w until zero, and only then a segment is allowed to collapse (be deleted).

3.2.5 Computation of Blood Flow and Hematocrit

Circulated vessel, i.e. vessels which are perfused at rates q > 0, can be determined with the help of the biconnected component graph algorithm [68]. To robustly handle general cases, including arterio-venous networks, we first make an ad hoc augmentation to the network: all boundary (root) nodes are connected temporarily to an extra node which is added. Then the set of perfused vessel is the biconnected component that comprises all edges for which a loop, without repetition of nodes or edges (simple cycle), exists which they are part of and which also runs through the extra node (see also [156]). For partially remodeled square or other regular networks, the augmentation can be omitted, using any of the boundary nodes instead.

Depending on the application, blood flow can be considered on various scales, from computation of the velocity field on micrometer scale to bulk perfusion measured in $ml\ blood\ ml\ tissue^{-1}min^{-1}$ as obtained for instance by positron emission tomography (PET). For pipe networks of tumors models, blood flow is approximated as ideal laminar flow, where the flow rates q define the blood volume throughput per time through each pipe. Blood pressure, p, is associated with nodes. Thus, q is determined by Poiseuille’s law

$$\displaystyle\begin{array}{rcl} q = \frac{\pi r^{4}} {8\eta } \frac{\varDelta p} {l} \text{,}& &{}\end{array}$$

(3.11)

where r is the vessel radius, η the viscosity, l the length, and Δ p denotes the blood pressure difference between the ends of the segment. Conservation of mass requires that the flow into a node equals the flow out of the node, analogous to Kirchoff’s laws of electricity, i.e.

$$\displaystyle\begin{array}{rcl} \sum _{i}q_{i} = 0\text{,}& &{}\end{array}$$

(3.12)

where i indexes vessels adjacent to a given node under consideration. Together with boundary conditions, a system of equations is obtained which is sparse and can be solved with direct factorization or preconditioned conjugate gradient.

Blood contains red blood cell (RBC) causing non-Newtonian behavior, i.e. its viscosity η(r, H) depends on the vessel radius r and on blood hematocrit H, where hematocrit is the blood volume fraction of RBCs. The viscosity is commonly expressed by the decomposition into the product of the blood plasma viscosity η _plasma, which is constant, and a correction factor, the relative viscosity η _rel(r, H). Pries et al. [120] derived a well-known phenomenological formula for η _rel(r, H) which is easy to incorporate. The distribution of hematocrit is sensitive to blood flow rates, i.e., at bifurcations, RBCs tend to flow into the faster perfused vascular branch which is the well-known phase separation effect. Pries and Secomb [118], developed a phenomenological formula that describes this effect in dependence on flow rates of the vessels at the bifurcation. This allows the computation of the hematocrit in downstream branches. Under assumption of given flow rates, the hematocrit distribution can thus be propagated downstream through the network. By iteration, a self-consistent solution for the hematocrit distribution and blood flow rates can be computed [118], which is utilized in several works [2, 16, 111, 115, 165, 167]. However, as a first approximation, it may be sufficient to consider a constant prescribed hematocrit as in [11, 168, 169]. This is justified because in spite of a wide value range of the relative viscosity ($\eta _{rel}(r = 25\,\upmu \mathrm{m},H = 0.15) \approx 1.5$, $\eta _{rel}(r = 5\,\upmu \mathrm{m},H = 0.6) = 8$), the dependence of the flow resistance on on r ⁴ plays a much greater role.

3.2.6 Time Dependent Intravascular Tracer Concentration

Rather than computing stationary concentration distributions, we are interested in following an injected bolus of some substances during the transit through the vascular network. For this purpose, Mc Dougall and Anderson [146] already adopted a method from petrol engineering, originally developed to predict solute transport through porous rock. It allows for computation of time dependent concentrations of a tracer c associated with segments of a vascular networks. Essentially tracer flows into nodes where it accumulates, amounting to mass m. From there it is distributed downstream in proportion to the flow rates q of downstream vessels. This procedure, akin to the upwind-differencing scheme for advection equations, is applied repeatedly in time steps of length Δ t. The amounts of substance from upstream vessels, added into downstream nodes, is accordingly Δ m = cq Δ t. Thus, given a time dependent inlet concentration c _in(t), the method yields concentrations c(t) of each vessel. Transvascular loss was not considered although the method would be straight forward to extend to take this into account.

We applied the method to networks created by our tumor growth simulation for regular [165, 168] and arterio-venous initial networks [166]. However, in our network model, the assumption that network edges are of constant length, and short compared to their radius is violated, leading to an amplified propagation velocity. Therefore we track the position of the interface that separates clean blood from tracer “contaminated” blood and moves with the velocity of blood flow. Similar models were developed for the simulation of capillary rise in network models of porous materials [1] and are widely used there, e.g. in [123].

3.2.7 Interstitial Fluid Pressure

Interstitial fluid flow (IFF) is modeled as liquid flowing through a porous medium [81, 83, 173, 24, 174, 176, 137, 138], where tissue cells and the fibers of the extracellular matrix assume the role of the medium. Fluid and medium are described in general within the framework of mixture theory with the help of distributions of their local volume fraction and their velocity distributions. However, the medium is often assumed rigid. The volume fraction of the liquid is identified with the porosity ε which describes the amount of space available per unit volume within the medium. This space is filled by definition with the liquid. Assuming rigidity and (quasi) stationary flow, the system is characterized by the spatial velocity field of the liquid, v(x), where x is the space coordinate. The velocity v is determined by the gradient of the IFP p _i according to the well-known Darcy’s Law

$$\displaystyle\begin{array}{rcl} v = -K\nabla p_{i}\text{,}& &{}\end{array}$$

(3.13)

where the permeability constant K is the product of an intrinsic permeability constant of the medium, the porosity and the inverse fluid viscosity. Usually, K is obtained directly from experimental data for a specific tissue type. Assuming incompressibility and constant permeability, the mass conservation equation obtained is a Poisson equation in p _i:

$$\displaystyle\begin{array}{rcl} & & \nabla \cdot v = -K\nabla ^{2}p_{ i} = Q\text{,}{}\end{array}$$

(3.14)

where $Q = J_{v} + J_{l}$ was added to represent sources and drains with contributions from vessels, J _v, and lymphatics, J _l. We adopted this simple approach to determine IFP and IFF in vascular networks of simulated tumors [169]. Some authors consider IFF within a fully coupled mixture model, where v is the relative velocity between the IF and a moving cell population [171]. Other authors incorporate IFF into models of tumor growth and allow compression of blood vessels due to elevated IFP [174]. Penta and Ambrosi used data of a simulated microscopic volume [114] to predict IFF in macroscopic systems. Zhao et al. [176] used imaging data of real tumors as basis for simulations using a continuum model.

3.2.8 Transvascular Fluid Exchange

The net transvascular liquid flux J _v is driven predominantly by the difference of blood to interstitial fluid pressure. This is expressed by Starling equation

$$\displaystyle\begin{array}{rcl} J_{v} = L_{p}S\left [\,p_{v} - p_{i} +\sigma _{T}(\pi _{v} -\pi _{i})\right ]\text{,}& &{}\end{array}$$

(3.15)

where L _p is the hydraulic permeability of vessel walls, S is the vascular surface area within a given control volume, p _v is the blood pressure, p _i is the interstitial pressure, $\sigma _{T}$ is the average osmotic reflection coefficient and π _v and π _i are the osmotic pressures of plasma and IF, respectively [81]. The osmotic term $\sigma _{T}(\pi _{v} -\pi _{i})$ represents forces generated by dissolved substances and can be considered as a constant offset from p _v at an experimentally determined value. This model of liquid exchange is straight forward to apply if the vascular network is considered as homogeneous phase [81].

Otherwise (3.14) may be taken as definition of a local source strength of a spatially varying IFP distribution. This is facilitated by letting the vessel network occupy the same lattice used for discretization of (3.14) as done in Refs. [173, 24, 174]. Then each node of the vessel network j corresponds to a discretization site of (3.14), so that the flux between them is directly proportional to (3.15) with suitable choice of S corresponding to the surface area of vessels adjacent to node j. Using the standard finite difference stencil for the Laplace operator in (3.14) one obtains a combined system of equations, equivalent to Kirchhoff’s laws. The same strategy can be used to simulate drug delivery [141, 138] and oxygenation [33, 86, 103, 142, 44]. We add that drainage due to lymphatics J _l is in all of the literature known to us modeled as continuous sink density analogous to (3.15).

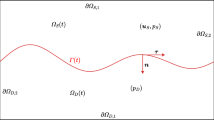
More generally, vessels can be considered as line-like sources akin to the Dirac δ distribution [69, 14], a concept which has been formulated mathematically rigorously for the solution of elliptic equations with Dirac terms by finite element methods [34] and applied to IFF [28]. We can thus replace (3.15) by the distribution

$$\displaystyle\begin{array}{rcl} & & J(\boldsymbol{y}) =\int _{\varGamma }L_{p}2\pi r(\tilde{p}_{v} - p_{i})\delta (\boldsymbol{x} -\boldsymbol{ y})dx{}\end{array}$$

(3.16)

where $\boldsymbol{x}$, $\boldsymbol{y}$ are spatial coordinates on the network and in the bulk of tissue respectively. Γ is the set of one-dimensional curves (or line segments) that describes the vascular network, $\tilde{p}_{v}$ is the effective blood pressure including the osmosis terms, and r is the vessel radius. The permeability L _p, blood pressure $\tilde{p}_{v}$ and radius r can vary depending on the position on the network $\boldsymbol{x}$.

The latter approach was taken by us to simulate IFF in simulated tumors grown within synthetic arterio-venous vasculatures [169]. We took inspiration from immersed boundary methods [116] and replaced the Dirac δ distribution with a smoothed kernel δ _ε of width ε > 0 to allow for resolution of the source distribution J on a grid of finite cell size. Thus the source distribution of vessels is “smeared” over nearby grid cells, very similar to the method used by [14].

3.2.9 Interstitial Drug Transport

Spatio-temporal distributions of macro-molecules were studied theoretically with the help of homogeneous compartment models in spherical symmetry, incorporating diffusion and interstitial fluid flow [13, 81]. In a similar way [176] albumin concentrations were simulated in a continuous but non-symmetrical tumorous tissue. In a theoretical study of drug transport in tumors, [141] the discrete nature of blood vessels was accounted for on the basis of a tumor grown in an square-patterned initial network (t = 0).

We followed [141] in the development of a simple model of drug transport guided by data for Doxorubicin, a common chemotherapy drug [169]. In this model, the local drug concentration is divided among an extracellular compartment with concentration $s_{1}(\boldsymbol{x})$ [169, Eqn. 20] and an intracellular compartment with concentration $s_{2}(\boldsymbol{x})$ [169, Eqn. 21] where drug is bound immobile. The extracellular concentration s ₁ is subject to diffusion and advection with the liquid velocity v _l according to (3.3). Vessels are sources and drains of drug (s. Sects. 3.2.8, and 3.2.10) comprising diffusive and advective transvascular flux densities [169, Eqn. 23]. Lymphatics can sink drug by advection, assuming that the drug concentration within lymphatics is approximately equal to the concentration in tissue. Consequently, drug diffusion into lymphatics is neglected. Both compartments 1 and 2 exchange drug via rates k ₁₂ and k ₂₁ depending on assumed trans-membrane diffusion coefficient and cell surface area. For simplicity, degradation of drug molecules is neglected. In future this should be straight forward to add, provided experimental data. The initial condition is a system clean of drug. Drug is inserted via the vasculature where the intravascular concentration s ^v(t) is homogeneous in space and follows a exponentially decaying pulse in time, imitating an injection.

We applied the model to study drug transport in tissues supplied by tumor vascular networks embedded within synthetic initial arterio-venous networks [169]. A cohort of tumors was considered. We first simulated tumor growth and then considered drug transport for stationary final (t = 800 h) configurations. Interstitial fluid velocity distributions $v_{l}(\boldsymbol{x})$ were determined prior to computation of drug concentrations.

3.2.10 Oxygen Transport

Oxygen diffuses across the blood tissue interface with a net flux that depends on the difference of oxygen partial pressure (PO2) at the vessel wall and within blood [65]. As oxygen diffuses into tissue, its concentration in blood is reduced, leading to a gradient across the micro-vasculature of ca. 100 mmHg at the arterial side and 40 mmHg at the venous side. The coupling of transvascular oxygen flux with the tissue PO2therefore poses a difficult problem for the computation of intravascular and tissue oxygen distributions.

This problem has been solved for simple configurations where single, straight artificial capillaries are considered. Based on original ideas of Krogh [87], current sophisticated theoretical models achieve very good agreement with experimental data [106, 107, 65, 104].

For many applications it may be sufficient to simply consider a constant blood PO2. Then the tissue PO2distributions P _t can by computed by solution of the reaction diffusion equation (3.4). This is very common approach in the literature on models of tumor growth. In other works the tissue oxygen distribution is analyzed in detail based on stationary configurations of disjoint collections of lines or points (in two-dimensions) representing sources of oxygen [35, 142, 86, 103, 33, 44, 89, 88]. The limitation of such models is however that the PO2in each source must be given as input.

In tumor however, low flow rates may lead to depletion of intravascular oxygen over short distances, making it necessary to model intravascular PO2variations. However due to the complexity of tumor blood vessel networks, intravascular oxygen distributions are hard to predict without actually simulating them. Some authors attacked this problem [69, 57, 136, 55, 56, 160, 127, 46, 126, 167] and computed self-consistent solutions of the equations for intravascular advection of oxygen and diffusion of oxygen in tissue for systems comprising realistic blood vessel networks. For numerical methods, see [136, 57, 167].

To cope with the computation of intravascular PO2distributions in complex networks compromises must be made (see [54] for a review). Most importantly, vessels are treated as one-dimensional line segments and intravascular PO2variations in the radial direction are neglected. Instead, the average over the cross-sectional area is considered, P(x), depending only on the position on the center line x. This is justified because radial variations of intravascular oxygen concentrations are relatively small as revealed by theoretical calculations [104].

In the modeling of intravascular oxygenation it is crucial to take into account that oxygen is, for the most part, bound to hemoglobin in red blood cells (RBCs). The steady state of the binding and unbinding processes is described in good approximation by the Hill-curve [54]

$$\displaystyle\begin{array}{rcl} S(\,P) = \frac{P^{n}} {P^{n} + P_{50}^{n}}\text{,}& &{}\end{array}$$

(3.17)

where P is the partial pressure of oxygen, S(P) is the fraction of oxygen bound relative to the maximal capacity, c ₀ is the concentration of oxygen in RBCs at full saturation, n is the Hill exponent and P ₅₀ denotes the partial pressure of oxygen where $S(P_{50}) = 1/2$. Hence, the total concentration of oxygen c is given by

$$\displaystyle\begin{array}{rcl} c =\alpha P + Hc_{0}S(\,P)\text{,}& &{}\end{array}$$

(3.18)

where H is the hematocrit and $\alpha =\alpha _{p} + H\alpha _{rbc}$ is the effective solubility in blood and α _p, α _rbc the solubility in plasma and RBCs, respectively.

In large scale network models it is infeasible to compute all microscopic details of spatio-temporal intravascular PO2distributions and outward diffusion. Instead, the net transvascular flux per blood-tissue interface surface area j _tv is determined by the effective, network dependent, mass transfer coefficient (MTC) γ, similar to L _p of Eq. (3.15)

$$\displaystyle\begin{array}{rcl} j_{tv} =\gamma (\,P - P_{t})\text{,}& &{}\end{array}$$

(3.19)

where P _t is the PO2 at the inner wall of the vessel lumen, and P is the average partial pressure in blood. Note that γ represents an effective radial diffusion coefficient of oxygen in blood. L _p of the Starling equation, on the other hand, represents the permeability of the wall. In small vessels, blood tends to form an RBC-rich core and a RBC-free boundary layer. For larger vessels (r > 100 μm), the discrete nature of RBCs plays a lesser role. Therefore the MTC is function of the vessel radius r, hematocrit H, and blood oxygen saturation S [65]. The functional dependency γ(r, H, S) can be obtained from single capillary simulations and experiments. Moreover, since vessels are much longer than their diameter it is reasonable to assume that the tissue PO2is homogeneous over the vessel circumference [136]. Thus, integration yields a transvascular oxygen flux per length amounting to 2π r j _tv, The change of the oxygen flux along the vessel axis is therefore simply given by the

$$\displaystyle\begin{array}{rcl} q \frac{dc} {dx} = -2\pi rj_{tv}\text{,}& &{}\end{array}$$

(3.20)

where q is the blood flow rate, and x denotes the longitudinal space coordinate on the vessel axis. In order to determine the oxygen distribution across an entire network, assumptions must be made on the distribution at vessel junctions, e.g. instant equilibration of the partial pressure of oxygen flowing into a junction. With the help of mass balance equations, the concentration of outflowing oxygen can be computed. Thus the solution for the oxygen concentration can be propagated downstream assuming a known tissue PO2distribution and a given PO2at the inlets (see [136, 167]).

Locally, at the blood-tissue interface, j _tv is also subject to Fick’s law $j_{tv} = -\alpha \nabla P$, in addition to (3.19). This relation can be utilized to obtain boundary conditions for a diffusion equation that determines the tissue PO2[57]. However in this chapter we want to consider the network as volumetric sources of oxygen $J_{tv}(\boldsymbol{x})$. This is well-defined since the oxygen flux into tissue is already known from (3.19). Therefore, J _tv may be formulated with the help of the Dirac δ distribution in analogy to (3.16) [136, 167].

The tissue oxygen concentration c _t = α _t P _t is determined by the diffusion equation for the partial pressure P _t

$$\displaystyle\begin{array}{rcl} 0 =\alpha _{t}D\nabla ^{2}P_{ t} - M(\,P_{t}) + J_{tv}\text{,}& &{}\end{array}$$

(3.21)

where D is the diffusion coefficient of oxygen in tissue, M(P) is the partial pressure dependent consumption rate. A good approximation of M(P) is the well-known Michaelis-Menten relation

$$\displaystyle\begin{array}{rcl} M(\,P) = M_{0} \frac{P} {P + P_{50}^{{\prime}}}\text{,}& &{}\end{array}$$

(3.22)

which tends to zero for small P, assumes the value M ₀∕2 for $P = P_{50}^{{\prime}}$ and goes asymptotically to the maximal consumption rate M ₀. For some problems like tumor oxygenation it is usually assumed that the oxygen concentration is rather low, i.e. $P_{t} < P_{50}^{{\prime}}$. Then it is sufficient to use a linear approximation $M(P) \approx -\lambda P$ for some rate coefficient $\lambda$. In physiological conditions, where $P > P_{50}^{{\prime}}$, M(P) is often approximated by zero order kinetics M(P) ≈ M ₀.

Discretization of the model equations yields a complex system of non-linear equations. Following [136, 14] we developed a new numerical scheme based on finite differences which is sufficiently efficient, allowing us to study three-dimensional networks in a simulation box of ca. 0. 5 cm³ at reasonable accuracy [167]. Our method was applied to study the relation of vascular morphology to clinical data of tissue blood oxygen saturation in human breast cancers. Hsu and Secomb [69, 136] formulated a solution to the system of equations with the help of a Green’s function method. Their method was applied to study oxygenation by various small network sections obtain from animal models as well as synthetic human brain vasculatures [126].

Methods developed for the study of oxygen distributions are also applicable to distributions of other substances like drugs which may be simpler since oxygen adds the complication of hemoglobin binding which leads to nonlinear systems of equations.

3.3 Discussion of Model Predictions

Current state of the art models of vascularized solid tumor growth and capillary network remodeling predict the morphological compartmentalization of tumor blood vessel networks in good agreement with experimental data of melanoma and glioma [38, 67, 66]. From the obtained configurations, of which one is shown in Figs. 3.6 and 3.7 conclusions can be drawn on the mechanisms of vascularization. Further conclusions, using model extensions, can be drawn for interstitial fluid flow and solute transport, as discussed in the following.

3.3.1 Vascular Morphology and Compartmentalization

Typical vascular compartmentalization is characterized by dense chaotic vascular sprouting within an annular shell of a width amounting to ca. 200 μm around the invasive edge, and a sharp decrease of vascular density into tumor spheroid. The normal vasculature is progressively transformed while the invasive edge moves forward, leaving predominantly isolated vessels behind. The ingredients, to obtain such characteristics from theoretical models comprise an expanding tumor spheroid, an initial capillary network, blood flow, a growthfactor concentration distribution, an oxygen concentration distribution, and processes reflecting co-option, angiogenesis, vaso-dilation, regression and collapse [11, 90]. The basic mechanism of this remodeling was identified as shear stress correlated collapse. Dilatation causes a decrease in flow rates and shear stress since the blood volume that the tumor vasculature conducts per time is limited by the flow resistance of the surrounding vasculature. This leads to removal of segments according to the collapse rule, redirecting blood flow to other vessels. As a result, blood flow and shear stress is stabilized above the critical collapse threshold in surviving vessels. Remaining dead ends are rapidly removed by the regression process.

In synthetic capillary-only initial networks (CNs), vessels of identical diameter are laid out in regular square or hexagonal patterns. However, it is hardly possible to select realistic blood flow boundary conditions for such networks of macroscopic size beyond a few hundred micrometers. For instance, imposing a homogeneous blood pressure gradient yields tumor vascular networks where tumor vessels survive preferably in the direction parallel to the imposed gradient [11, 165]. The explanation is simply that vessel segments of linear chains that run, on average, perpendicular to the gradient, lie on approximately equal blood pressure potentials and therefore no significant blood flow can occur, resulting in collapse of these vessels.

In reality, the capillary plexus is however supplied and drained by adjacent arterioles and venules which exhibit irregular spatial configurations. Therefore, there is no global flow direction, which is why arterio-venous initial networks (AVNs) abolish this artifact in model predictions [166]. In AVNs blood flow depends on only a few boundary conditions at in-and outlets for which experimental reference values for pressure or blood flow can be used. Models based on synthetic arterio-venous networks predict vascular morphologies which obey realistic compartmentalization of MVD and radii. However, in addition to dilated capillaries, the tumor center also exhibits higher-caliber vessels co-opted from the initial network. Such vessels exhibit a radius r larger than the maximal dilation threshold r _max and are therefore not subject to dilation. As a result, predictions of flow rate q are a factor of 10 larger than predicted for CNs.

Model predictions of average quantities such as radial distributions of MVD, blood flow, oxygenation and tumor density are robust against model alterations, as studied in Refs [165, 166]. This is true in particular for the rather drastic alteration of the introduction of arterio-venous blood vessel networks (AVNs) [166]. Other model variations, such as calculation of blood flow in conjunction with varying hematocrit, or use of spatially varying collapse probabilities, do not change predictions qualitatively [165]. The parameters vessel collapse probability p ^(col), wall degradation rate Δ w, critical collapse shear stress f ^(col) and contact inhibition length of angiogenesis d ^(br, min) correlate with the MVD obtained for the tumor center. The MVD at the invasive edge is determined by the MVD of the original network and the contact inhibition length d ^(br, min). A certain invariance against model details is expected and even required, because it would be implausible if the results were dependent on a specific abstraction of the biological reality (within reasonable accuracy).

Our model predicts that MVD of the tumor interior, MVD at the tumor periphery, and tumor expansion speed are uncorrelated if the peripheral blood vessel network can support the metabolic demand of tumor cells required for growth [11]. Growth within AVNs additionally leads to clustering of vessels in clusters of differing size and density depending on the initial network configuration [166]. The density of such hot-spots is used as a diagnostic tool [38]. However these results suggest that it rather unreliable. A recent meta-study [110] of clinical data comes to the same conclusion. Correlations between MVD and the outcome of the disease is likely due to metastases which was not considered.

We add that we considered the line density L _D, the summed lengths of vessel segments within a given region per volume of this region, as a measure for MVD. It is however not the same as the histological MVD because vessels in parallel to the cutting-plane which contribute to L _D cause L _D to overestimate the MVD by a factor of approximately two.

3.3.2 Fractal Properties of Tumor Vasculatures

Following [11], fractal dimension numbers were computed for vascular networks. Fractal dimension d _f is an extension of the conventional dimension to self-similar (fractal) objects. For instance a line has d _f = 1, but a fractal curve within the two-dimensional plane can have d _f between 1 and 2 depending on how densely it permeates space. d _f = 2 corresponds to a solid object like a disc. For real objects of finite size several approximative metrics exists, e.g. the number obtained by box-counting [98]. Useful model systems are percolation clusters: In conventional percolation, sites of a lattice are randomly occupied with probability p. At some critical probability p _c, a percolating cluster forms that spans across the lateral size of the considered domain. The dimension of this cluster is exactly known d _f ^perc = 1. 891 [149]. Similarly, a system-spanning cluster can be created from an invasive growth process into a heterogeneous matrix, the dimension of which is known and amounts to $d_{f}^{inv-perc} = 1.81$ in two dimensions [47].

Gazit [48] measured the dimension of photographs of tumor vascular networks and obtained d _f ^exp = 1. 89 ± 0. 04, in good agreement with d _f ^inv−perc and therefore hypothesized that fractal properties of tumor vascular networks emerge from angiogenic sprouting into a heterogeneous extracellular matrix. Bartha and Rieger [11] obtained d _f = 1. 85 by box-counting from the entire vasculature that was changed by tumor vascular remodeling. Since no ECM heterogeneities were modeled, it was hypothesized that the mechanism leading to the fractal properties is a random dilution process similar to conventional percolation. Later simulations predicted d _f between 1. 6 and 1. 9, correlated with the tumor MVD, where the parameters critical collapse shear-stress f ^(col) and collapse probability p ^(col) were varied, with similar results respectively [165]. Fractal dimensions of tumor vascular networks obtained from simulations based on three-dimensional AVNs [168] yielded d _f = 2. 51 ± 0. 03, in good agreement with percolation theory and [90] where tumors in three-dimensional CNs are considered. However, accurate measurement of fractal dimensions of real and simulated tumor vascular networks is hardly possible due to their limited size [11]. Moreover different methods were used: theoretical values were determined by two-or three-dimensional box-counting, whereas Gazit [48] considered two-dimensional projections of real vasculatures. We conclude that fractal dimension is mostly a function of MVD and that it is not a reliable means to determine mechanism of vascularization in tumors.

Morphological analysis was approached from another angle in [166], where frequency distributions of (i) local MVD, (ii) area of clusters of necrotic tissue, and (iii) area of hot-spots of high MVD were computed for tumors grown in two-dimensional AVNs. Predicted distributions show good agreement with a power law, and exhibit all the same exponent of − 1. 4. Such an algebraic decrease, in contrast to an exponential decrease, is known for systems at a critical threshold where systems undergo a phase transition. In the case of percolation, the critical threshold at p = p _c marks the transition from isolated clusters to a single connected region. Bartha and Rieger [11] suggested that the tumor vasculature is driven automatically into a state akin to the critical percolation cluster by the mechanism of shear-stress correlated vascular collapse. As a result vessels permeate through the entire tumor, robust against moderate variations in f ^(col) and p ^(col). These predictions are experimentally testable and, if confirmed, would support that real vascular networks of the interior of tumors are the result of a dilution process rather than the result of sprouting growth into a heterogeneous environment.

3.3.3 Interrelation of Initial and Emergent Tumor Vasculature

High-caliber arterioles and venules ( > 50 μm radius) protruding into the tumor form a backbone of stable vessels in-between which thinner vessels form short and straightforward paths [166]. The flow resistance decreases in proportion to 1∕r ⁴ with radius r and is therefore, in comparison to capillaries, extremely low in such high-caliber vessels. Therefore, in analogy to electrical networks, the blood pressure (voltage) drop across them is also low. In zero-th order approximation the blood pressure is constant, i.e. high-caliber vessels act like a pressure boundary condition for adjacent capillaries. Short, directed paths, have a survival advantage as discussed above in the context of CNs. The distribution of tumor vessels thus becomes dependent on initial (t = 0) vascular networks and is generally heterogeneous and anisotropic.

Assuming an arteriole runs near a venule then a large spatial blood pressure gradient is present. When a tumor grows near this area, a connection (short cut) is formed by angiogenesis, imposing the spatial gradient onto blood flow through this newly formed vessel which is the more stable the steeper the gradient. We attempted to quantify this dependence by correlation of tumor MVD (t > 0) versus the magnitude of blood pressure differences in-between vessels of initial (t = 0) AVNs. For this purpose, an auxiliary “pressure” field $p(\boldsymbol{x})$ was computed as function of space $\boldsymbol{x}$ at t = 0 that interpolates approximately the blood pressure p _v in spaces between vessels [166] and is determined by ∇² p + a ⋅ (p _v − p) = 0, where a is zero in empty space and a ≫ 1 at sites coincident with vessels. We plotted the magnitude of the gradient | | ∇p | | as local averages taken over small boxes versus the local MVD at t = 1200 h Predicted correlation coefficients ranged from 0. 2 to 0. 5 per simulation. A correlation coefficient of 0. 9 was obtained for averages over entire tumors of a cohort of simulations [166]. This finding may eventually be useful for model validation by experiments, should it become possible to scan real three-dimensional vasculatures of host tissues prior inoculation with TCs.

Somewhat different vascular configurations are indeed observed in real tumors of the same tissue, e.g. breast tumors [40]. Predictions outlined above suggest that heterogeneity of the initial vascular network has a strong impact on the emerging tumor vasculature rather than heterogeneity of the ECM through which vascular sprouts grow as originally proposed by Gazit [48].

3.3.4 Blood Flow and Blood Borne Drug Transport

McDougall et al. [146, 145] first considered conduction of a tracer substance through tumor vascular networks using a simulation model of a time-dependent intravascular concentration distribution that was previously used in geo-engineering. Following them, intravascular tracer conduction was studied in stationary tumor vascular networks based on CNs [165] and AVNs [166, 168]. Simply, a pulse, or a constant infusion, is applied at inlet vessels, which is from there propagated down-stream through the vascular network. The unspectacular model predictions show tracer flowing through networks within a duration of seconds (AVNs) and ca. 1 min (CNs).

McDougall et al., on the other hand, consider a model system based on angiogenesis experiments on the cornea of a rabbit eye [51] (rabbit-eye model). There, the tumor is not connected to an extensive vascular network, but instead, a single parent vessel spawns a few sprouts (angiogenesis) which travel a long distance of ca. 1 mm and branch into a dense network permeating a tumor spheroid and adjacent tissue. It was concluded that the tumor vasculature conducts drug poorly and that most drug bypasses the tumor. The cause of this contradiction appears to be dilution of the tracer concentration within the dense network near the tumor and much lower flow rates leading to transit times of the order of 10–30 min. Moreover a vascular adaptation model was considered, leading to formation of shunts that bypass the tumor network [145].

A good perfusion is consistent with several clinical studies of human tumors based on PET measurements [170, 99, 92, 72] where elevated perfusion rBF by factors of 4. 7 to 5. 2 were observed [167, Tbl. 4]. Blood flow velocities in tumors predicted by our model are of the order of 1 mm/s, similar to blood flow in normal human micro vessels [100]. Our model predicts arterio-venous short-cuts within the tumor, i.e. vaso-dilation gives rise to mostly very well perfused vascular threads connecting arterioles with venoules [165, Fig. 8]. Such shunts were suggested in the experimental literature where “flow hotspots” are frequently found in tumors of patients [129]. However, it is well-known that blood flow in animal models is can be severely reduced to only 0. 1 to 1 mm/s. The exact causes for discrepancy are presumably vessel compression and excessive blood plasma extravasation [175, 82], both of which were not considered here.

3.3.5 Interstitial Fluid Flow

Interstitial fluid flow (IFF) in tumorous tissue has been considered theoretically for some time, for instance within the framework of continuum models [76, 83, 176]. More recent models incorporate a discrete tumor vasculatures, e.g. based on the rabbit-eye model [173, 172], and remodeling of capillary networks (CNs) [174].

Welter and Rieger [169] considered IFF and extravascular drug transport in tumors grown within synthetic arterio-venous networks. Predicted interstitial fluid pressure (IFP) distributions exhibit an average radial profile that increases sharply from the tumor edge into the tumor center (s. Fig. 3.8). There, the IFP approaches a plateau value asymptotically, close to the level of blood pressure, amounting to ca. 6.5 kPa (49 mmHg) [169, Fig. 4 and 5]. This is expected due to the high vascular permeability, implying a small pressure drop across the vessel wall. The plateau value lies above experimentally observed mean values taken over various human tumors, but it is still lower than the absolute maximal observed IFP [83, Tbl. 1]. Since the IFP is generally assumed to rise very close to the level of blood pressure, this is rather indicative of overestimated blood pressure. IFF distributions, i.e. the scaled negative gradient of the IFP, follow trivially and exhibit the expected sharp rise at the tumor rim amounting to a maximal value of 0. 2 μm/s in good agreement with the literature. As a novel prediction due to the discrete AVN model used, the IFP and IFF distributions exhibit heterogeneity, i.e. they vary spatially in-between vessels of different blood pressure values. Thus vessels are predicted to drain the interstitial fluid in some instances [169, Fig. 4C].

It was often suggested that an elevated IFP poses a barrier to drug delivery [102, 64, 76, 174]. However, the reason for this cannot simply be a decreased transvascular hydrostatic pressure gradient that drives extravasation according to the Starling equation (3.15). To the contrary, in standard modeling approaches (s. Sect. 3.2.7), interstitial fluid flow is analogous to an electrical current flowing through a chain of resistors, of which one resistor, namely leaky tumor vessel walls, is particularly small (s. Fig. 3.9). Thus, an increase in leakiness, i.e. an elevation of IFP, would actually increase the liquid flux throughout the tumor, as predicted by our model. However, the analysis was restricted to good perfusion, where only a negligible liquid fraction escapes in spite of leakiness. Otherwise the way through tumorous tissue into lymphatics could presumably present an alternative well conducting pathway, draining downstream vessels of blood plasma, resulting in reported low flow velocities [82].

The recent theoretical work [174], using CNs and a sophisticated model of tumor growth that incorporates vessel compression due to IFP, comes to similar conclusions about the role of various permeabilities However, it was concluded that IFP is a barrier with little supporting numerical evidence, i.e. no simulation of actual drug transport was performed.

3.3.6 Interstitial Drug Transport

Experimentally, penetration experiments are performed for homogeneous cells layers and genetic causes for drug resistance are examined. However direct observation of drug distribution in tumors is difficult due to a lack of suitable markers. As a result there is only little experimental where spatial distributions of drug were measured [102, 177, 121] and quantitative data is scarce.

In oder to shed light on barriers to drug delivery, transport through tissue by advection and diffusion after extravasation must be taken into account. For this purpose, we analyzed a simple model, according to which, we computed time-dependent concentration distributions of drug in simulated tissues containing a vascularized tumor, grown in three-dimensional AVNs [169]. The considered tumors were static, and obtained by simulations guided by melanoma and glioma. In addition to concentration distributions, we also computed maps of time-independent metrics of doses delivered to the intracellular compartment: the local maximal concentration s ₂ taken over time (ICMAX) and the time integral of s ₂, respectively (ICAUC). The computation was stopped after a simulated time of 96 h.

Anti-cancer drugs come in a variety of kinds, from light molecules e.g. Cisplatin or Doxorubicin ( ≈ 543 g/mol) to heavy nano particles and viruses as carrier systems. We considered a base case guided by Doxorubicin since it is experimentally relatively well studied and widely used [121, 177].

Our model predicts that, in general, the dose delivered is subject to a compartmentalization similar to the vascular density (MVD), where metrics ICAUC and ICMAX likewise reflect the distribution of the MVD [169, Fig. 9]. Hence the average dose within the center of the tumor spheroid is significantly lower than in normal tissue, unless stated otherwise, and doses are highest at the tumor edge. This result provides an additional explanation of the incompletely understood success of combination therapies of anti-angiogenic agents and chemotherapy, whereas a single drug fails to improve survival [78]. TCs behind the tumor edge might be killed by high doses of chemotherapeutics, effective against cycling cells, whereas the TC population of the tumor center is reduced by necrosis caused by hypoxia. A monotherapy might leave the one or the other part of the TC population unaffected. The mechanism by which combination therapies are known to act is suppression of the activity caused by vascular growth factors, leading to a decreased vascular permeability. This allows overall better delivery of chemotherapeutics due to improved perfusion [78]. We also considered the case of a prolonged infusion which yielded similar results but with higher magnitudes of concentrations and doses.

Variation of the various permeabilities showed that average doses delivered with the permeability. Doses showed the highest sensitivity with respect to interstitial hydraulic and diffusive permeabilities which were varied simultaneously. See Fig. 3.9b, where a 10× increase in permeability leads to a similarly drastic increase in extravasation and IFF, not as obtained by other cases. As a result, more drug is delivered into tissue as well. However, the mechanism only works under the assumption that blood flow is sufficently high that it is not disturbed much by extravasation. As suggested before [174], this could be exploited for therapy. However an increased IFF could aggravate tumor invasion and metastatic dissemination [140]. Moreover, angiogenic normalization therapy, i.e. a reduction of permeability and pruning of vessels [78], might be ineffective or even detrimental for tumors where blood flow is negligibly impaired.

Doxorubicin and lighter molecules have the advantage that diffusion helps to distribute a substantial dose homogeneously around blood vessels regardless of IFF. This was demonstrated in recent simulations of another group [141] where very smooth and homogeneous concentration distributions of the more diffusive drug Cisplatin (300 g/mol) arising from extravasation from a CN were predicted.

Since the diffusion coefficient decreases with the molar mass of the solute, transport of drugs like nano-particles is strongly advection dominated. Simulation of the flow of such particles predicted interstitial drug concentrations that follow the stream of interstitial fluid in significant concentrations through the largest parts of the tumor spheroid, starting from the initial insertion through the vasculature (s. Fig. 3.10). As a result small isolated islands were predicted to exist right behind the invasive edge of the tumor where no significant dose had been delivered within the time frame of the simulation of 96 h. Presumably, this discrepancy to earlier work [76] is caused by the discrete nature of the blood vessel network considered allowing for flow in-between vessel of different blood pressure levels. Thus radial flow component vanishes by chance at some places as dictated by the random configuration of the vascular network. This suggests that a mono-therapy with agents of high molar mass would be prone to recurring cancer.

3.3.7 Oxygen Distribution

Extremely good perfusion of tumor vessels cannot be assumed for tumors in general. This necessitates consideration of spatially varying substance concentrations because a substantial fraction may be lost during the transit through the tumor. Maps of tissue and intravascular oxygen partial pressure (PO2) distributions were calculated previously for small system volumes of the order of 0. 1 mm³ [136, 54]. Our recently developed computational method allows for computation of PO2distributions in macroscopic simulation boxes of ca. 0. 5 cm³ on standard hardware (i7-2600K, 3.4 GHz, 4 GB Ram) within hours to a fair degree of accuracy [167]. It is still computationally expensive, however, few simplifying assumptions need to be made for the vascular network. Computed distributions of PO2and blood oxygen saturation are shown in Fig. 3.11a, b.

Critical to performance and accuracy is the regularization of the singular source term (3.16), containing Dirac δ distributions, in conjunction with an efficient numerical scheme for the solution of the diffusion equation. In general the method should yield a sparse system matrix to enable numerical solutions in $O(n\,\log n)$ time in the number of unknowns n. In future, adaptive tesselation of the tissue domain may be used to increase accuracy [34].

The computation of intravascular PO2distributions [167] was applied to the case of breast tumors for which several groups measured hemoglobin concentrations c _Hb and average blood oxygen saturations Y in large cohorts of patients [60, 144, 155, 154]. They determined average concentrations of total hemoglobin c _Hb, oxyhemoglobin c _HbO, deoxyhemoglobin c _HbD, and tissue blood oxygen saturations $Y = c_{HbO}/c_{Hb}$ within normal and tumorous tissue sections. Obtained tumor hemoglobin concentrations c _Hb(tumor) were always larger than hemoglobin concentrations in normal tissue c _Hb(normal). This is already explained by an increase in regional blood volume rBV due to vaso-dilation. However, the blood oxygen saturation in tumors Y (tumor) was sometimes larger or smaller than the blood oxygen saturation in normal tissue Y (normal), divided approximately to equal numbers among patients. Moreover, high hemoglobin concentrations were correlated with high saturations, but tumors with low hemoglobin concentration exhibited a wider range of blood oxygen saturations.

We considered tumor vascular networks (t = 800 h) obtained from simulation of tumor growth and vascular remodeling. A large cohort of 90 different networks was simulated emulating a cohort of patients. Regional blood volume rBV, perfusion rBF, hemoglobin concentrations c _Hb, oxy-hemoglobin concentrations, deoxy-hemoglobin concentrations, oxygen saturation Y, as well as tissue and vascular oxygen partial pressure distributions P, and P _t were calculated for initial networks and final tumor networks (t = 800 h). Transient behavior such as transient hypoxia due to temporary occlusion of blood vessels was not considered. In our base case (BASE), different initial (t = 0) vascular configurations lead to a spread in tumor oxygen saturations, but it did not predict the clinically observed dependency of Y (tumor) versus Y (normal) since predicted Y (tumor) were always larger than Y (normal). Therefore we considered a phenomenological ad-hoc extension of the model by vaso-compression. On average, taken over the cohort of tumors, the proposed alteration results in a reduction of the radii of arterioles and venules that are thicker than the maximal dilation radius r ^(max), whereas the radii of smaller vessels are not much affected on average. This modified model predicts saturations Y in good agreement with mammography data (see Fig. 3.12). The reasons for this better agreement are a reduction of blood flow, thus draining a greater fraction of the supplied O2in order to meet metabolic demand. Moreover, Y is the volume weighted average of the local blood saturation S(P). Therefore compression reduces the weight of dilated arterio-venous shunts which generally exhibit a high saturation S. Cases for which drastically increased metabolic oxygen consumption rates M ₀, decreased maximal dilatation radii r ^(max), and stochastic variations thereof were considered, failed to predict the clinically observed distributions. Therefore our results suggest that a decreased tissue blood oxygen saturation relative to baseline normal tissue of the same patient is indicative of vessel compression which could be exploited in therapy. The clinical data might imply that tumor vascular networks that exhibit higher saturations than normal are vastly different in their vascular architecture than networks that exhibit low saturations. However, our simulations suggest that these networks nevertheless share the traits of typical tumor vascular networks as outlined in the introduction.

For models of tumor growth, it is a very convenient approximation to consider a model of oxygenation where the intravascular PO2distribution is constant. Then only the tissue PO2distribution needs to be calculated. There are however qualitative difference in its predictions that one should be aware of (s. Fig. 3.11d). The constant-PO2approximation fails to predict local oxygen depletion in vessels threading the tumor center. More importantly it over-estimates the PO2in the neo-vascular plexus around the tumor periphery. The depletion of oxygen predicted by the full model is a consequence of a redirection of most hematocrit into the tumor center due to the phase separation effect (s. Fig. 3.11c). Therefore the densely vascularized capillary plexus around the invasive edge is deprived of red blood cells and thus the oxygen capacity of blood therein drastically reduced.

3.4 Limitations and Outlook

Although current models produce predictions that are in many respect in good agreement with experiments, there are some severe limitations. For one, many predictions were obtained by first simulating tumor growth by a simplified model. Then additional quantities relevant for tumor growth were computed, e.g. interstitial fluid flow or intravascular oxygen distributions [169, 167]. Other works have other limitations, e.g. oversimplified vascular networks of host tissue [95, 174, 141, 131]. It may be worth to develop an integrated model combining all aspects into time dependent simulation of tumor growth. This may be particularly important for the study of pharmacokinetics where IFF, drug transport, oxygenation and tumor growth are tightly coupled.

Furthermore, To obtain a more faithful cohort of initial blood vessel networks, a systematic analysis of initial networks could be carried out. Experimental data of blood volume, rBV, perfusion rBF, and so on, could be used to select a cohort of networks that satisfies experimentally observed statistical distributions. Current networks are unrealistic in some aspects, e.g. they contain no anastomosis, i.e. cross-links between vascular trees [100].

Therefore it would be ideal to use real scanned and digitized blood vessel networks (s. Fig. 3.13 for examples). In principle it is possible to automatically reconstruct networks from voxel data. However, current state of the art microscopy methods can only see through a tissue slab up to a maximal depth of ca. 250 μm [27]. Recently, data obtained from micro computed tomography (μ-CT) was used by Stamatelos et al. [147] to reconstruct large parts of the vascular system of an animal-model breast tumor. However, it is questionable if all capillaries were captured since the resolution of the scanner was only 8 μm, and many dead ends were in the reconstructed network. Similar results were obtained for other cranial [61] and coronary [91] blood vessel networks. A data base of many large scale networks of normal tissues and corresponding tumor networks at different growth stages could be built. Not only would this eliminate the need to construct artificial initial networks, but it would also allow for a detailed comparison between model predictions and real tumor networks.

A major limitation of our model is the restricted applicability to only well perfused tumors. However in animal models blood flow velocities are generally lower amounting to 0.1–1 mm/s [109, 9]. The prediction of good perfusion is inherent to our basic model of vascular remodeling since tumor vessels can only dilate, not shrink, leading to well conducting arterio-venous shunts. The prediction of high flow rates allows for neglect of blood plasma loss due to extravasation, which we justify by a simple worst case estimation of lost plasma amounting to ca. 0. 1 %. Therefore, extravasation of plasma cannot be the only cause for low blood flow, but rather it likely aggravates the situation if vessels are constricted by solid pressure for instance.

Consequently, it would be worthwhile to explore extensions to vascular dilation and regression processes rather than limiting blood flow by ad-hoc shrinkage of arterial radii, as done in [167]. One such possible extension already exists in the vascular adaptation model [119]. Essentially, a shrinking-tendency is balanced by a wall shear-stress dependent growth signal. Moreover, compression of blood vessels is insufficiently understood. Forces involved were studied quantitatively, separately (see Refs. below). However, their interplay is not understood or studied much. Obviously, the deformation of vessel walls is governed by a balance of forces which are tensile and compressive stress within the vessel wall, blood pressure, interstitial fluid pressure, and solid pressure. Solid pressure compresses vessels [31, 150, 30] and there is evidence that an elevated IFP aids in compression of vessels [59, 36]. There is, to our knowledge, no predictive model of the response of the vessel wall that takes these factors into account. A physical consideration based on first principles e.g. with the help of a elasto-plastic mechanical model of vascular walls in combination with a mechanical model of tissue could help elucidate the forces involved and ultimately yield better predictions of blood flow.

With an ad-hoc extension to emulate compression, our model predicts regional blood flow rBF that is about a factor of 5–10 above measured data from breast tumors [167, Tbl. 4]. This apparent deficiency might be founded in the size of the considered tumors (4 mm in diameter, simulated, versus centimeter sized real tumors), since in tumor xenografts [84] blood flow rBF of experimental tumors (2–0.3 ml/g/min) correlates negatively with size (0.1–10 cm³ tumor volume), consistent with predictions of our model. The reasons for this size dependency are currently unknown. However, it suggests that either normal vasculatures can only provide a constant blood flow rate per surface area of the tumor spheroid into the tumor, or that the abnormal organization of the tumor vasculature is only affecting blood flow velocities in tumors much larger than theoretically studied.

References

Aker E, JØrgen MÅlØy K, Hansen A, Batrouni G (1998) A two-dimensional network simulator for two-phase flow in porous media. Trans Porous Media 32(2):163–186. doi:10.1023/A:1006510106194
Google Scholar
Alarcon T, Byrne H, Maini P (2003) A cellular automaton model for tumour growth in inhomogeneous environment. J Theor Biol 225:257–274
Article CAS PubMed Google Scholar
Ambrosi D, Ateshian GA, Arruda EM, Cowin SC, Dumais J, Goriely A, Holzapfel GA, Humphrey JD, Kemkemer R, Kuhl E, Olberding JE, Taber LA, Garikipati K (2011) Perspectives on biological growth and remodeling. J Mech Phys Solids 59(4):863–883
Article PubMed PubMed Central Google Scholar
Ambrosi D, Mollica F (2004) The role of stress in the growth of a multicell spheroid. J Math Biol 48(5):477–499
Article CAS PubMed Google Scholar
Ambrosi D, Preziosi L (2009) Cell adhesion mechanisms and stress relaxation in the mechanics of tumours. Biomech Model Mechanobiol 8(5):397–413
Article PubMed Google Scholar
Anderson A, Chaplain MAJ (1998) Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Biol 60(857–900):857–899
Article CAS PubMed Google Scholar
Ando J, Yamamoto K (2013) Flow detection and calcium signalling in vascular endothelial cells. Cardiovasc Res 99(2):260–268
Article CAS PubMed Google Scholar
Armstrong NJ, Painter KJ, Sherratt JA (2006) A continuum approach to modelling cell-cell adhesion. J Theor Biol 243(1):98–113
Article CAS PubMed PubMed Central Google Scholar
Baish JW, Netti PA, Jain RK (1997) Transmural coupling of fluid flow in microcirculatory network and interstitium in tumors. Microvasc Res 53:128–141
Article CAS PubMed Google Scholar
Baish JW, Stylianopoulos T, Lanning RM, Kamoun WS, Fukumura D, Munn LL, Jain RK (2011) Scaling rules for diffusive drug delivery in tumor and normal tissues. Proc Natl Acad Sci USA 108(5):1799–1803
Article CAS PubMed PubMed Central Google Scholar
Bartha K, Rieger H (2006) Vascular network remodeling via vessel cooption, regression and growth in tumors. J Theor Biol 241:903–918. doi:http://dx.doi.org/10.1016/j.jtbi.2006.01.022. http://www.sciencedirect.com/science/article/pii/S0022519306000373
Google Scholar
Basan M, Prost J, Joanny JF, Elgeti J (2011) Dissipative particle dynamics simulations for biological tissues: rheology and competition. Phys Biol 8(2):026,014
Google Scholar
Baxter LT, Jain RK (1989) Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvasc Res 37:77–104
Article CAS PubMed Google Scholar
Beard DA (2001) Computational framework for generating transport models from databases of microvascular anatomy. Ann Biomed Eng 29(10):837–843
Article CAS PubMed Google Scholar
Bentley K, Gerhardt H, Bates PA (2008) Agent-based simulation of notch-mediated tip cell selection in angiogenic sprout initialisation. J Theor Biol 250(1):25–36. doi:http://dx.doi.org/10.1016/j.jtbi.2007.09.015. http://www.sciencedirect.com/science/article/pii/S0022519307004432
Google Scholar
Betteridge R, Owen MR, Byrne HM, Alarcon T, Maini PK (2006) The impact of cell crowding and active cell movement on vascular tumour growth. Netw Heterog Media 1(4):515–535
Article Google Scholar
Brackbill JU, Kothe DB, Zemach C.: A continuum method for modeling surface tension. J Comput Phys 100:335–354 (1992). doi:10.1016/0021-9991(92)90240-Y
Article CAS Google Scholar
Breward CJ, Byrne HM, Lewis CE (2003) A multiphase model describing vascular tumour growth. Bull Math Biol 65(4):609–640
Article PubMed Google Scholar
Brown JM, Wilson WR (2004) Exploiting tumour hypoxia in cancer treatment. Nat Rev Cancer 4(6):437–447
Article CAS PubMed Google Scholar
Bru A, Albertos S, Subiza JL, Lopez J, Garcia-Asenjo, Bru I (2003) The universal dynamics of tumor growth. Biophys J 85:2948–2961
Article CAS PubMed PubMed Central Google Scholar
Buchanan CF, Verbridge SS, Vlachos PP, Rylander MN (2014) Flow shear stress regulates endothelial barrier function and expression of angiogenic factors in a 3D microfluidic tumor vascular model. Cell Adh Migr 8(5):517–524
Article PubMed PubMed Central Google Scholar
Byrne H, Preziosi L (2003) Modelling solid tumour growth using the theory of mixtures. Math Med Biol 20(4):341–366
Article PubMed Google Scholar
Byrne HM, Owen MR, Alarcon T, Murphy J, Maini PK (2006) Modelling the response of vascular tumours to chemotherapy: a multiscale approach. Math Models Methods Appl Sci 16(Supp 01):1219–1241. doi:10.1142/S0218202506001522
Article CAS Google Scholar
Cai Y, Xu S, Wu J, Long Q (2011) Coupled modelling of tumour angiogenesis, tumour growth and blood perfusion. J Theor Biol 279(1):90–101. http://dx.doi.org/10.1016/j.jtbi.2011.02.017. http://www.sciencedirect.com/science/article/pii/S0022519311001196
Google Scholar
Carmeliet P, Jain R (2000) Angiogenesis in cancer and other diseases. Nature 407:249–257
Article CAS PubMed Google Scholar
Carmeliet P, Jain RK (2011) Molecular mechanisms and clinical applications of angiogenesis. Nature 473(7347):298–307
Article CAS PubMed PubMed Central Google Scholar
Cassot F, Lauwers F, Fouard C, Prohaska S, Lauwers-Cances V (2006) A novel three-dimensional computer-assisted method for a quantitative study of microvascular networks of the human cerebral cortex. Microcirculation 13(1):1–18
Article CAS PubMed Google Scholar
Cattaneo L, Zunino P (2014) A computational model of drug delivery through microcirculation to compare different tumor treatments. Int J Numer Method Biomed Eng 30(11):1347–1371
Article CAS PubMed Google Scholar
Chaplain MA, Graziano L, Preziosi L (2006) Mathematical modelling of the loss of tissue compression responsiveness and its role in solid tumour development. Math Med Biol 23:197–229
Article CAS PubMed Google Scholar
Chauhan VP, Boucher Y, Ferrone CR, Roberge S, Martin JD, Stylianopoulos T, Bardeesy N, DePinho RA, Padera TP, Munn LL, Jain RK (2014) Compression of pancreatic tumor blood vessels by hyaluronan is caused by solid stress and not interstitial fluid pressure. Cancer Cell 26(1):14–15
Article CAS PubMed PubMed Central Google Scholar
Chauhan VP, Martin JD, Liu H, Lacorre DA, Jain SR, Kozin SV, Stylianopoulos T, Mousa AS, Han X, Adstamongkonkul P, Popovi? Z, Huang P, Bawendi MG, Boucher Y, Jain RK (2013) Angiotensin inhibition enhances drug delivery and potentiates chemotherapy by decompressing tumour blood vessels. Nat Commun 4:2516
Google Scholar
Ciarletta P, Ambrosi D, Maugin GA, Preziosi L (2013) Mechano-transduction in tumour growth modelling. Eur Phys J E Soft Matter 36(3):23
Article CAS PubMed Google Scholar
Da ̧su A, Toma-Da ̧su I, Karlsson M (2003) Theoretical simulation of tumour oxygenation and results from acute and chronic hypoxia. Phys Med Biol 48(17):2829–2842
Google Scholar
D’Angelo C (2012) Finite element approximation of elliptic problems with dirac measure terms in weighted spaces: applications to one- and three-dimensional coupled problems. SIAM J Numer Anal 50(1):194–215
Article Google Scholar
Degond P, Mas-Gallic S (1989) The weighted particle method for convection-diffusion equations. Part 1: the case of an isotropic viscosity. Math Comput 53(188):485–507
Google Scholar
DelGiorno KE, Carlson MA, Osgood R, Provenzano PP, Brockenbough JS, Thompson CB, Shepard HM, Frost GI, Potter JD, Hingorani SR (2014) Response to Chauhan et al.: interstitial pressure and vascular collapse in pancreas cancer-fluids and solids, measurement and meaning. Cancer Cell 26(1):16–17
Article CAS PubMed PubMed Central Google Scholar
Döme B, Hendrix MJ, Paku S, Tovari J, Timar J (2007) Alternative vascularization mechanisms in cancer: pathology and therapeutic implications. Am J Pathol 170(1):1–15
Article PubMed PubMed Central CAS Google Scholar
Döme B, Paku S, Somlai B, Tímár J (2002) Vascularization of cutaneous melanoma involves vessel co-option and has clinical significance. J Pathol 197(3):355–362
Article PubMed Google Scholar
Drasdo D, Höhme S (2005) A single-cell-based model of tumor growth in vitro: monolayers and sphereoids. Phys Biol 2:133–147
Article CAS PubMed Google Scholar
Du J, Li FH, Fang H, Xia JG, Zhu CX (2008) Microvascular architecture of breast lesions: evaluation with contrast-enhanced ultrasonographic micro flow imaging. J Ultrasound Med 27(6):833–842
PubMed Google Scholar
Enderling H, Anderson AR, Chaplain MA, Beheshti A, Hlatky L, Hahnfeldt P (2009) Paradoxical dependencies of tumor dormancy and progression on basic cell kinetics. Cancer Res 69(22):8814–8821
Article CAS PubMed Google Scholar
Enderling H, Hlatky L, Hahnfeldt P (2009) Migration rules: tumours are conglomerates of self-metastases. Br J Cancer 100(12):1917–1925
Article CAS PubMed PubMed Central Google Scholar
Erber R, Eichelsbacher U, Powajbo V, Korn T, Djonov V, Lin J, Hammes HP, Grobholz R, Ullrich A, Vajkoczy P (2006) EphB4 controls blood vascular morphogenesis during postnatal angiogenesis. EMBO J 25(3):628–641
Article CAS PubMed PubMed Central Google Scholar
Espinoza I, Peschke P, Karger CP (2013) A model to simulate the oxygen distribution in hypoxic tumors for different vascular architectures. Med Phys 40(8):081,703
Google Scholar
Folkman J (1971) Tumor angiogenesis: therapeutic implications. N Engl J Med 285(21):1182–1186
Article CAS PubMed Google Scholar
Fraser GM, Goldman D, Ellis CG (2013) Comparison of generated parallel capillary arrays to three-dimensional reconstructed capillary networks in modeling oxygen transport in discrete microvascular volumes. Microcirculation 20(8):748–763
CAS PubMed PubMed Central Google Scholar
Furuberg L, Feder J, Aharony A, Jossang T (1988) Dynamics of invasion percolation. Phys Rev Lett 61(18):2117–2120
Article CAS PubMed Google Scholar
Gazit Y, Berk DA, Michael Leunig LTB, Jain RK (1995) Scale-invariant behavior and vascular network formation in norma and tumor tissue. Phys Rev Lett 75(12):2428–2431
Article CAS PubMed Google Scholar
Gerhardt H, Golding M, Fruttinger M, Ruhrberg C, Lundkvist A, Abramsson A, Jeltsch M, Mitchell C, Alitalo K, Shima D, Betsholz C (2003) VEGF guides angiogenic sprouting utilizing endothelial tip cell filopodia. J Cell Biol 161(6):1163–1177
Article CAS PubMed PubMed Central Google Scholar
Gevertz JL (2011) Computational modeling of tumor response to vascular-targeting therapies–part I: validation. Comput Math Methods Med 2011:830,515
Google Scholar
Gimbrone M, Cotran R, Leapman S, Folkman J (1974) Tumor growth and neovascularization: an experiment model using the rabbit cornea. J Natl Cancer Inst 52:413–427
PubMed Google Scholar
Gödde R, Kurz H (2001) Structural and biophysical simulation of angiogenesis and vascular remodeling. Dev Dyn 220(4):387–401
Article PubMed Google Scholar
Goettsch W, Gryczka C, Korff T, Ernst E, Goettsch C, Seebach J, Schnittler HJ, Augustin HG, Morawietz H (2008) Flow-dependent regulation of angiopoietin-2. J Cell Physiol 214(2):491–503
Article CAS PubMed Google Scholar
Goldman D (2008) Theoretical models of microvascular oxygen transport to tissue. Microcirculation 15(8):795–811
Article PubMed PubMed Central Google Scholar
Goldman D, Bateman RM, Ellis CG (2004) Effect of sepsis on skeletal muscle oxygen consumption and tissue oxygenation: interpreting capillary oxygen transport data using a mathematical model. Am J Physiol Heart Circ Physiol 287(6):H2535–2544
Article CAS PubMed Google Scholar
Goldman D, Bateman RM, Ellis CG (2006) Effect of decreased O2 supply on skeletal muscle oxygenation and O2 consumption during sepsis: role of heterogeneous capillary spacing and blood flow. Am J Physiol Heart Circ Physiol 290(6):H2277–2285
Article CAS PubMed Google Scholar
Goldman D, Popel AS (2000) A computational study of the effect of capillary network anastomoses and tortuosity on oxygen transport. J Theor Biol 206(2):181–194
Article CAS PubMed Google Scholar
Gray LH, Conger AD, Ebert M, Hornsey S, Scott OCA (1953) The concentration of oxygen dissolved in tissues at the time of irradiation as a factor in radiotherapy. Br J Radiol 26(312):638–648. doi:10.1259/0007-1285-26-312-638. http://dx.doi.org/10.1259/0007-1285-26-312-638. PMID:13106296
Google Scholar
Griffon-Etienne G, Boucher Y, Brekken C, Suit HD, Jain RK (1999) Taxane-induced apoptosis decompresses blood vessels and lowers interstitial fluid pressure in solid tumors: clinical implications. Cancer Res. 59(15):3776–3782
CAS PubMed Google Scholar
Grosenick D, Wabnitz H, Moesta KT, Mucke J, Schlag PM, Rinneberg H (2005) Time-domain scanning optical mammography: II. Optical properties and tissue parameters of 87 carcinomas. Phys Med Biol 50(11):2451–2468
Article PubMed Google Scholar
Guibert R, Fonta C, Plouraboue F (2010) Cerebral blood flow modeling in primate cortex. J Cereb Blood Flow Metab 30(11):1860–1873. doi:10.1038/jcbfm.2010.105
Article PubMed PubMed Central Google Scholar
Hanahan D, Weinberg RA (2011) Hallmarks of cancer: the next generation. Cell 144(5):646–674
Article CAS PubMed Google Scholar
Harris AL (2002) Hypoxia–a key regulatory factor in tumour growth. Nat Rev Cancer 2(1):38–47
Article CAS PubMed Google Scholar
Heldin CH, Rubin K, Pietras K, Ostman A (2004) High interstitial fluid pressure – an obstacle in cancer therapy. Nat Rev Cancer 4(10):806–813
Article CAS PubMed Google Scholar
Hellums JD, Nair PK, Huang NS, Ohshima N (1996) Simulation of intraluminal gas transport processes in the microcirculation. Ann Biomed Eng 24(1):1–24
Article CAS PubMed Google Scholar
Holash J, Maisonpierre PC, Compton D, Boland P, Alexander CR, Zagzag D, Yancopoulos GD, Wiegand SJ (1999) Vessel cooption, regression, and growth in tumors mediated by angiopoietins and VEGF. Science 284(5422):1994–1998
Article CAS PubMed Google Scholar
Holash J, Wiegand S, Yancopoulos G (1999) New model of tumor angiogenesis: dynamic balance between vessel regression and growth mediated by angiopoietins and VEGF. Oncogene 18:5356–5362
Article CAS PubMed Google Scholar
Hopcroft J, Tarjan R (1973) Algorithm 447: efficient algorithms for graph manipulation. Commun ACM 16(6):372–378. doi:10.1145/362248.362272. http://doi.acm.org/10.1145/362248.362272
Article Google Scholar
Hsu R, Secomb TW (1989) A green’s function method for analysis of oxygen delivery to tissue by microvascular networks. Math Biosci 96(1):61–78
Article CAS PubMed Google Scholar
Hubbard M, Byrne H (2013) Multiphase modelling of vascular tumour growth in two spatial dimensions. J Theor Biol 316(0):70–89. http://dx.doi.org/10.1016/j.jtbi.2012.09.031. http://www.sciencedirect.com/science/article/pii/S0022519312005097
Google Scholar
Höckel M, Vaupel P (2001) Tumor hypoxia: definitions and current clinical, biologic, and molecular aspects. J Natl Cancer Inst 93(4):266–276. doi:10.1093/jnci/93.4.266. http://jnci.oxfordjournals.org/content/93/4/266.abstract
Article PubMed Google Scholar
Ito M, Lammertsma AA, Wise RJ, Bernardi S, Frackowiak RS, Heather JD, McKenzie CG, Thomas DG, Jones T (1982) Measurement of regional cerebral blood flow and oxygen utilisation in patients with cerebral tumours using 15O and positron emission tomography: analytical techniques and preliminary results. Neuroradiology 23(2):63–74
Article CAS PubMed Google Scholar
Jain RK (1987) Transport of molecules across tumor vasculature. Cancer Metastasis Rev 6(4):559–593
Article CAS PubMed Google Scholar
Jain RK (1987) Transport of molecules in the tumor interstitium: a review. Cancer Res 47(12):3039–3051
CAS PubMed Google Scholar
Jain RK (1988) Determinants of tumor blood flow: a review. Cancer Res 48:2641–2658
CAS PubMed Google Scholar
Jain RK (1999) Transport of molecules, particles, and cells in solid tumors. Annu Rev Biomed Eng 1:241–263
Article CAS PubMed Google Scholar
Jain RK (2005) Normalization of tumor vasculature: an emerging concept in antiangiogenic therapy. Science 307(5706):58–62
Article CAS PubMed Google Scholar
Jain RK (2013) Normalizing tumor microenvironment to treat cancer: bench to bedside to biomarkers. J Clin Oncol 31(17):2205–2218
Article CAS PubMed PubMed Central Google Scholar
Jain RK (2014) An indirect way to tame cancer. Sci Am 310(2):46–53
Article PubMed Google Scholar
Jain RK (2015) Antiangiogenesis strategies revisited: from starving tumors to alleviating hypoxia. Cancer Cell 26(5):605–622
Article CAS Google Scholar
Jain RK, Baxter LT (1988) Mechanisms of heterogeneous distribution of monoclonal antibodies and other macromolecules in tumors: significance of elevated interstitial pressure. Cancer Res 48(24 Pt 1):7022–7032
CAS PubMed Google Scholar
Jain RK, Stylianopoulos T (2010) Delivering nanomedicine to solid tumors. Nat Rev Clin Oncol 7(11):653–664
Article CAS PubMed PubMed Central Google Scholar
Jain RK, Tong RT, Munn LL (2007) Effect of vascular normalization by antiangiogenic therapy on interstitial hypertension, peritumor edema, and lymphatic metastasis: insights from a mathematical model. Cancer Res. 67(6):2729–2735
Article CAS PubMed PubMed Central Google Scholar
Kallinowski F, Schlenger KH, Kloes M, Stohrer M, Vaupel P (1989) Tumor blood flow: the principal modulator of oxidative and glycolytic metabolism, and of the metabolic micromilieu of human tumor xenografts in vivo. Int J Cancer 44(2):266–272
Article CAS PubMed Google Scholar
Karakashev SV, Reginato MJ (2015) Progress toward overcoming hypoxia-induced resistance to solid tumor therapy. Cancer Manag Res 7:253–264
PubMed PubMed Central Google Scholar
Kelly CJ, Brady M (2006) A model to simulate tumour oxygenation and dynamic [18F]-Fmiso PET data. Phys Med Biol 51(22):5859–5873
Article CAS PubMed Google Scholar
Krogh A (1919) The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. J Physiol (Lond) 52(6):409–415
Article CAS Google Scholar
Lagerlöf JH, Kindblom J, Bernhardt P (2014) The impact of including spatially longitudinal heterogeneities of vessel oxygen content and vascular fraction in 3D tumor oxygenation models on predicted radiation sensitivity. Med Phys 41(4):044,101
Google Scholar
Lagerlöf JH, Kindblom J, Cortez E, Pietras K, Bernhardt P (2013) Image-based 3D modeling study of the influence of vessel density and blood hemoglobin concentration on tumor oxygenation and response to irradiation. Med Phys 40(2):024,101
Google Scholar
Lee D, Rieger H, Bartha K (2006) Flow correlated percolation during vascular remodeling in growing tumors. Phys Rev Lett 96(5):058,104–1–058,104–4. doi:10.1103/PhysRevLett.96.058104. http://link.aps.org/doi/10.1103/PhysRevLett.96.058104
Lee J, Beighley P, Ritman E, Smith N (2007) Automatic segmentation of 3D micro-CT coronary vascular images. Med Image Anal 11(6):630–647
Article PubMed Google Scholar
Leenders KL, Beaney RP, Brooks DJ, Lammertsma AA, Heather JD, McKenzie CG (1985) Dexamethasone treatment of brain tumor patients: effects on regional cerebral blood flow, blood volume, and oxygen utilization. Neurology 35(11):1610–1616
Article CAS PubMed Google Scholar
LeVeque RJ (2007) Finite difference methods for ordinary and partial differential equations – steady-state and time-dependent problems. SIAM
Book Google Scholar
Logsdon EA, Finley SD, Popel AS, Gabhann FM (2014) A systems biology view of blood vessel growth and remodelling. J Cell Mol Med 18(8):1491–1508
Article PubMed Google Scholar
Lowengrub JS, Frieboes HB, Jin F, Chuang YL, Li X, Macklin P, Wise SM, Cristini V (2010) Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity 23(1):R1–R9
Article PubMed PubMed Central Google Scholar
Macklin P, Lowengrub J (2007) Nonlinear simulation of the effect of microenvironment on tumor growth. J Theor Biol 245:677–704
Article CAS PubMed Google Scholar
Macklin P, McDougall S, Anderson AR, Chaplain MA, Cristini V, Lowengrub J (2009) Multiscale modelling and nonlinear simulation of vascular tumour growth. J Math Biol 58:765–798
Article PubMed Google Scholar
Mandelbrot BB (1983) The fractal geometry of nature. Freeman, San Francisco
Google Scholar
Mankoff DA, Dunnwald LK, Gralow JR, Ellis GK, Charlop A, Lawton TJ, Schubert EK, Tseng J, Livingston RB (2002) Blood flow and metabolism in locally advanced breast cancer: relationship to response to therapy. J Nucl Med 43(4):500–509
PubMed Google Scholar
Marieb E, Hoehn K (2013) Human anatomy & physiology. Pearson, San Francisco
Google Scholar
McDonald DM, Choyke PL (2003) Imaging of angiogenesis: from microscope to clinic. Nat Med 9(6):713–725
Article CAS PubMed Google Scholar
Minchinton AI, Tannock IF (2006) Drug penetration in solid tumours. Nat Rev Cancer 6(8):583–592
Article CAS PubMed Google Scholar
Mönnich D, Troost EG, Kaanders JH, Oyen WJ, Alber M, Thorwarth D (2011) Modelling and simulation of [18F]fluoromisonidazole dynamics based on histology-derived microvessel maps. Phys Med Biol 56(7):2045–2057
Article PubMed Google Scholar
Moschandreou TE, Ellis CG, Goldman D (2011) Influence of tissue metabolism and capillary oxygen supply on arteriolar oxygen transport: a computational model. Math Biosci 232(1):1–10
Article CAS PubMed PubMed Central Google Scholar
Murray C (1926) The physiological principle of minimum work: the vascular system and the cost of blood volume. Proc Natl Acad Sci USA 12:207–214
Article CAS PubMed PubMed Central Google Scholar
Nair PK, Hellums JD, Olson JS (1989) Prediction of oxygen transport rates in blood flowing in large capillaries. Microvasc Res 38(3):269–285
Article CAS PubMed Google Scholar
Nair PK, Huang NS, Hellums JD, Olson JS (1990) A simple model for prediction of oxygen transport rates by flowing blood in large capillaries. Microvasc Res 39(2):203–211
Article CAS PubMed Google Scholar
Nehls V, Herrmann R, Hühnken M (1998) Guided migration as a novel mechanism of capillary network remodeling is regulated by fibroblast growth factor. Histochem Cell Biol 109:319–329
Article CAS PubMed Google Scholar
Netti PA, Roberge S, Boucher Y, Baxter LT, Jain RK (1996) Effect of transvascular fluid exchange on pressure-flow relationship in tumors: a proposed mechanism for tumor blood flow heterogeneity. Microvasc Res 52(1):27–46
Article CAS PubMed Google Scholar
Nico B, Benagiano V, Mangieri D, Maruotti N, Vacca A, Ribatti D (2008) Evaluation of microvascular density in tumors: pro and contra. Histol Histopathol 23(5):601–607
PubMed Google Scholar
Owen MR, Alarcon T, Maini PK, Byrne HM (2009) Angiogenesis and vascular remodelling in normal and cancerous tissues. J Math Biol 58(4–5):689–721
Article PubMed Google Scholar
Peirce SM, Van Gieson EJ, Skalak TC (2004) Multicellular simulation predicts microvascular patterning and in silico tissue assembly. FASEB J 18(6):731–733
CAS PubMed Google Scholar
Pennacchietti S, Michieli P, Galluzzo M, Mazzone M, Giordano S, Comoglio PM (2003) Hypoxia promotes invasive growth by transcriptional activation of the met protooncogene. Cancer Cell 3(4):347–361
Article PubMed Google Scholar
Penta R, Ambrosi D (2015) The role of the microvascular tortuosity in tumor transport phenomena. J Theor Biol 364(0):80–97
Google Scholar
Perfahl H, Byrne HM, Chen T, Estrella V, Alarcon T, Lapin A, Gatenby RA, Gillies RJ, Lloyd MC, Maini PK, Reuss M, Owen MR (2011) Multiscale modelling of vascular tumour growth in 3D: the roles of domain size and boundary conditions. PLoS One 6(4):e14,790
Article CAS Google Scholar
Peskin CS (2002) The immersed boundary method. Acta Numer 11:479–517. doi:10.1017/S0962492902000077. http://dx.doi.org/10.1017/S0962492902000077
Article Google Scholar
Preziosi L, Tosin A (2009) Multiphase modelling of tumour growth and extracellular matrix interaction: mathematical tools and applications. J Math Biol 58:625–656
Article PubMed Google Scholar
Pries A, Secomb T, Gaehtgens P, Gross J (1990) Blood flow in microvascular networks. Experiments and simulation. Circ Res 67:826–834
Article CAS PubMed Google Scholar
Pries AR, Reglin B, Secomb TW (2005) Remodeling of blood vessels: responses of diameter and wall thickness to hemodynamic and metabolic stimuli. Hypertension 46(4):725–731
Article CAS PubMed Google Scholar
Pries AR, Secomb TW, Gessner T, Sperandio MB, Gross JF, Gaehtgens P (1994) Resistance to blood flow in microvessels in vivo. Circ Res 75(5):904–915
Article CAS PubMed Google Scholar
Primeau AJ, Rendon A, Hedley D, Lilge L, Tannock IF (2005) The distribution of the anticancer drug Doxorubicin in relation to blood vessels in solid tumors. Clin Cancer Res 11(24 Pt 1):8782–8788
Article CAS PubMed Google Scholar
Raica M, Cimpean AM, Ribatti D (2009) Angiogenesis in pre-malignant conditions. Eur J Cancer 45(11):1924–1934
Article CAS PubMed Google Scholar
Rieger H, Thome C, Sadjadi Z (2015) Meniscus arrest dominated imbibition front roughening in porous media with elongated pores. J Phys Conf Ser 638(1):012,007. http://stacks.iop.org/1742-6596/638/i=1/a=012007
Google Scholar
Rieger H, Welter M (2015) Integrative models of vascular remodeling during tumor growth. Wiley Interdiscip Rev Syst Biol Med 7(3):113–129. doi:10.1002/wsbm.1295. http://dx.doi.org/10.1002/wsbm.1295
Article CAS PubMed PubMed Central Google Scholar
Roose T, Chapman S, Maini P (2007) Mathematical models of avascular tumor growth. SIAM Rev 49(2):179–208. doi:10.1137/S0036144504446291. http://epubs.siam.org/doi/abs/10.1137/S0036144504446291
Article Google Scholar
Safaeian N, David T (2013) A computational model of oxygen transport in the cerebrocapillary levels for normal and pathologic brain function. J Cereb Blood Flow Metab 33(10):1633–1641
Article CAS PubMed PubMed Central Google Scholar
Safaeian N, Sellier M, David T (2011) A computational model of hemodynamic parameters in cortical capillary networks. J Theor Biol 271(1):145–156
Article PubMed Google Scholar
Safaeian N (2012) Computational modelling of capillaries in neuro-vascular coupling: A Thesis Presented for the Degree of Doctor of Philosophy in Mechanical Engineering at the University of Canterbury, Christchurch. University of Canterbury
Google Scholar
Sahani DV, Kalva SP, Hamberg LM, Hahn PF, Willet CG, Saini S, Mueller PR, Lee TY (2005) Assessing tumor perfusion and treatment response in rectal cancer with multisection ct: initial observations. Radiology 234:785–792
Article PubMed Google Scholar
Sainson RC, Harris AL (2007) Anti-Dll4 therapy: can we block tumour growth by increasing angiogenesis? Trends Mol Med 13(9):389–395
Article CAS PubMed Google Scholar
Sanga S, Sinek JP, Frieboes HB, Ferrari M, Fruehauf JP, Cristini V (2006) Mathematical modeling of cancer progression and response to chemotherapy. Expert Rev Anticancer Ther 6(10):1361–1376
Article CAS PubMed Google Scholar
Schreiner W (1993) Computer generation of complex arterial tree models. J Biomed Eng 15(2):148–150
Article CAS PubMed Google Scholar
Schreiner W, Buxbaum P (1993) Computer-optimization of vascular trees. IEEE Trans Biomed Eng 40(5):482–491
Article CAS PubMed Google Scholar
Scianna M, Bell CG, Preziosi L (2013) A review of mathematical models for the formation of vascular networks. J Theor Biol 333:174–209
Article CAS PubMed Google Scholar
Sciume G, Shelton S, Gray W, Miller C, Hussain F, Ferrari M, Decuzzi P, Schrefler B (2013) A multiphase model for three-dimensional tumor growth. New J Phys 15:015,005
Google Scholar
Secomb TW, Hsu R, Park EYH, Dewhirst MW (2004) Green’s function methods for analysis of oxygen delivery to tissue by microvascular networks. Ann Biomed Eng 32(11):1519–1529
Article PubMed Google Scholar
Sefidgar M, Soltani M, Raahemifar K, Bazmara H, Nayinian SM, Bazargan M (2014) Effect of tumor shape, size, and tissue transport properties on drug delivery to solid tumors. J Biol Eng 8:12
Article PubMed PubMed Central CAS Google Scholar
Sefidgar M, Soltani M, Raahemifar K, Sadeghi M, Bazmara H, Bazargan M, Naeenian MM (2015) Numerical modeling of drug delivery in a dynamic solid tumor microvasculature. Microvasc Res 99(0):43–56
Google Scholar
Sethian JA, Smereka P (2003) Level set methods for fluid interfaces. Ann Rev Fluid Mech 35(1):341–372. http://www.annualreviews.org/doi/abs/10.1146/annurev.fluid.35.101101.161105
Shieh AC, Swartz MA (2011) Regulation of tumor invasion by interstitial fluid flow. Phys Biol 8(1):015,012
Google Scholar
Sinek JP, Sanga S, Zheng X, Frieboes HB, Ferrari M, Cristini V (2009) Predicting drug pharmacokinetics and effect in vascularized tumors using computer simulation. J Math Biol 58(4–5):485–510
Article PubMed Google Scholar
Skeldon AC, Chaffey G, Lloyd DJ, Mohan V, Bradley DA, Nisbet A (2012) Modelling and detecting tumour oxygenation levels. PLoS ONE 7(6):e38,597
Article CAS Google Scholar
Song JW, Munn LL (2011) Fluid forces control endothelial sprouting. Proc Natl Acad Sci USA 108(37):15,342–15,347
Google Scholar
Spinelli L, Torricelli A, Pifferi A, Taroni P, Danesini G, Cubeddu R (2005) Characterization of female breast lesions from multi-wavelength time-resolved optical mammography. Phys Med Biol 50(11):2489–2502
Article PubMed Google Scholar
McDougall SR, Anderson A, Chaplain MAJ (2006) Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: clinical implications and therapeutic targeting strategies. J Theor Biol 241:564–589
Article PubMed Google Scholar
McDougall SR, Anderson A, Chaplain MAJ, Sherratt J (2002) Mathematical modelling of flow through vascular networks: implications for tumor-induced angiogenesis and chemotherapy strategies. Bull Math Biol 64:673–702
Article CAS PubMed Google Scholar
Stamatelos SK, Kim E, Pathak AP, Popel AS (2014) A bioimage informatics based reconstruction of breast tumor microvasculature with computational blood flow predictions. Microvasc Res 91:8–21
Article PubMed Google Scholar
Stamper IJ, Byrne HM, Owen MR, Maini PK (2007) Modelling the role of angiogenesis and vasculogenesis in solid tumour growth. Bull Math Biol 69(8):2737–2772
Article CAS PubMed Google Scholar
Stauffer D, Aharony A (1994) Introduction to percolation theory. CRC Press, London
Google Scholar
Stylianopoulos T, Martin JD, Chauhan VP, Jain SR, Diop-Frimpong B, Bardeesy N, Smith BL, Ferrone CR, Hornicek FJ, Boucher Y, Munn LL, Jain RK (2012) Causes, consequences, and remedies for growth-induced solid stress in murine and human tumors. Proc Natl Acad Sci USA 109(38):15101–15108
Article CAS PubMed PubMed Central Google Scholar
Swanson KR, Rockne RC, Claridge J, Chaplain MA, Alvord EC, Anderson AR (2011) Quantifying the role of angiogenesis in malignant progression of gliomas: in silico modeling integrates imaging and histology. Cancer Res 71(24):7366–7375
Article CAS PubMed PubMed Central Google Scholar
Swartz MA, Lund AW (2012) Lymphatic and interstitial flow in the tumour microenvironment: linking mechanobiology with immunity. Nat Rev Cancer 12(3):210–219
Article CAS PubMed Google Scholar
Tammela T, Alitalo K (2010) Lymphangiogenesis: molecular mechanisms and future promise. Cell 140(4):460–476
Article CAS PubMed Google Scholar
Taroni P (2012) Diffuse optical imaging and spectroscopy of the breast: a brief outline of history and perspectives. Photochem Photobiol Sci 11(2):241–250
Article CAS PubMed Google Scholar
Taroni P, Torricelli A, Spinelli L, Pifferi A, Arpaia F, Danesini G, Cubeddu R (2005) Time-resolved optical mammography between 637 and 985 nm: clinical study on the detection and identification of breast lesions. Phys Med Biol 50(11):2469–2488
Article PubMed Google Scholar
Cormen TH, Leiserson CE, RLR, Stein C (2009) Introduction to algorithms, 3rd edn., chap. 22 MIT Press, Cambridge
Google Scholar
Tong RT, Boucher Y, Kozin SV, Winkler F, Hicklin DJ, Jain RK (2004) Vascular normalization by vascular endothelial growth factor receptor 2 blockade induces a pressure gradient across the vasculature and improves drug penetration in tumors. Cancer Res 64(11):3731–3736. doi:10.1158/0008-5472.CAN-04-0074. http://cancerres.aacrjournals.org/content/64/11/3731.abstract
Article CAS PubMed Google Scholar
Tracqui P (2009) Biophysical models of tumour growth. Rep Prog Phys 72(5):056,701
Google Scholar
Tsai AG, Johnson PC, Intaglietta M (2003) Oxygen gradients in the microcirculation. Physiol Rev 83(3):933–963
Article CAS PubMed Google Scholar
Tsoukias NM, Goldman D, Vadapalli A, Pittman RN, Popel AS (2007) A computational model of oxygen delivery by hemoglobin-based oxygen carriers in three-dimensional microvascular networks. J Theor Biol 248(4):657–674
Article CAS PubMed PubMed Central Google Scholar
Vaupel P, Kallinowski F, Okunieff P (1989) Blood flow, oxygen and nutrient supply, and metabolic microenvironment of human tumors: a review. Cancer Res 49(23):6449–6465. http://cancerres.aacrjournals.org/content/49/23/6449.abstract
CAS PubMed Google Scholar
Verdier C, Etienne J, Duperray A, Preziosi L (2009) Review: rheological properties of biological materials. Comptes Rendus Physique 10(8):790–811. http://dx.doi.org/10.1016/j.crhy.2009.10.003. http://www.sciencedirect.com/science/article/pii/S1631070509001492. Complex and biofluidsFluides complexes et biologiques
Google Scholar
Volokh KY (2006) Stresses in growing soft tissues. Acta Biomater 2(5):493–504
Article CAS PubMed Google Scholar
Weislo R, Dzwinel W, Yuen DA, Dudek AZ (2009) A 3-D model of tumor progression based on complex automata driven by particle dynamics. J Mol Model 15(12):1517–1539
Article CAS Google Scholar
Welter M, Bartha K, Rieger H (2008) Emergent vascular network inhomogeneities and resulting blood flow patterns in a growing tumor. J Theor Biol 250(2):257–280. http://dx.doi.org/10.1016/j.jtbi.2007.09.031. http://www.sciencedirect.com/science/article/pii/S0022519307004584
Google Scholar
Welter M, Bartha K, Rieger H (2009) Vascular remodelling of an arterio-venous blood vessel network during solid tumour growth. J Theor Biol 259(3):405–422. http://dx.doi.org/10.1016/j.jtbi.2009.04.005. http://www.sciencedirect.com/science/article/pii/S0022519309001635
Google Scholar
Welter M, Fredrich T, Rinneberg H, Rieger H (2015, Submitted) Relation between tumor oxygenation, vascular remodeling, and blood flow: a computational model with applications to breast cancer. PLOS Comp Biol [10pt]
Google Scholar
Welter M, Rieger H (2010) Physical determinants of vascular network remodeling during tumor growth. Eur Phys J E Soft Matter 33(2):149–163
Article CAS PubMed Google Scholar
Welter M, Rieger H (2013) Interstitial fluid flow and drug delivery in vascularized tumors: a computational model. PLoS ONE 8(8):e70,395. doi:10.1371/journal.pone.0070395. http://dx.doi.org/10.1371%2Fjournal.pone.0070395
Google Scholar
Wilson CB, Lammertsma AA, McKenzie CG, Sikora K, Jones T (1992) Measurements of blood flow and exchanging water space in breast tumors using positron emission tomography: a rapid and noninvasive dynamic method. Cancer Res 52(6):1592–1597
CAS PubMed Google Scholar
Wise SM, Lowengrub JS, Frieboes HB, Cristini V (2008) Three-dimensional multispecies nonlinear tumor growth–I model and numerical method. J Theor Biol 253:524–543
Article CAS PubMed PubMed Central Google Scholar
Wu J, Long Q, Xu S, Padhani AR (2009) Study of tumor blood perfusion and its variation due to vascular normalization by anti-angiogenic therapy based on 3d angiogenic microvasculature. J Biomech 42(6):712–721. http://dx.doi.org/10.1016/j.jbiomech.2009.01.009. http://www.sciencedirect.com/science/article/pii/S0021929009000281
Google Scholar
Wu J, Xu S, Long Q, Collins MW, Konig CS, Zhao G, Jiang Y, Padhani AR (2008) Coupled modeling of blood perfusion in intravascular, interstitial spaces in tumor microvasculature. J Biomech 41(5):996–1004
Article PubMed Google Scholar
Wu M, Frieboes HB, McDougall SR, Chaplain MA, Cristini V, Lowengrub J (2013) The effect of interstitial pressure on tumor growth: coupling with the blood and lymphatic vascular systems. J Theor Biol 320(0):131–151. doi:10.1016/j.jtbi.2012.11.031. http://www.sciencedirect.com/science/article/pii/S0022519312006200
Google Scholar
Yuan F, Salehi HA, Boucher Y, Vasthare US, Tuma RF, Jain RK (1994) Vascular permeability and microcirculation of gliomas and mammary carcinomas transplanted in rat and mouse cranial windows. Cancer Res 54(17):4564–4568
CAS PubMed Google Scholar
Zhao J, Salmon H, Sarntinoranont M (2007) Effect of heterogeneous vasculature on interstitial transport within a solid tumor. Microvasc Res 73:224–236
Article CAS PubMed Google Scholar
Zheng JH, Chen CT, Au JL, Wientjes MG (2001) Time- and concentration-dependent penetration of doxorubicin in prostate tumors. AAPS PharmSci 3(2):E15
Article CAS PubMed Google Scholar
Zheng X, Wise SM, Cristini V (2005) Nonlinear simulation of tumor necrosis, neo-vascularization and tissue invasion via an adaptive finite-element/level-set method. Bull Math Biol 67:211–259
Article CAS PubMed Google Scholar

Download references

Author information

Authors and Affiliations

Theoretical Physics, Saarland University, Campus E2 6, 66123, Saarbrücken, Germany
Michael Welter & Heiko Rieger

Authors

Michael Welter
View author publications
You can also search for this author in PubMed Google Scholar
Heiko Rieger
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Heiko Rieger .

Editor information

Editors and Affiliations

H. Lee Moffitt Cancer Center & Research Institute, Tampa, Florida, USA
Katarzyna A. Rejniak

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Welter, M., Rieger, H. (2016). Computer Simulations of the Tumor Vasculature: Applications to Interstitial Fluid Flow, Drug Delivery, and Oxygen Supply. In: Rejniak, K. (eds) Systems Biology of Tumor Microenvironment. Advances in Experimental Medicine and Biology, vol 936. Springer, Cham. https://doi.org/10.1007/978-3-319-42023-3_3

Download citation

DOI: https://doi.org/10.1007/978-3-319-42023-3_3
Published: 14 October 2016
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42021-9
Online ISBN: 978-3-319-42023-3
eBook Packages: Biomedical and Life SciencesBiomedical and Life Sciences (R0)

Publish with us

Policies and ethics